the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Retrospective forecasts of the upcoming winter season snow accumulation in the Inn headwaters (European Alps)
Kristian Förster
Florian Hanzer
Elena Stoll
Adam A. Scaife
Craig MacLachlan
Johannes Schöber
Matthias Huttenlau
Stefan Achleitner
Ulrich Strasser
This article presents analyses of retrospective seasonal forecasts of snow accumulation. Re-forecasts with 4 months' lead time from two coupled atmosphere–ocean general circulation models (NCEP CFSv2 and MetOffice GloSea5) drive the Alpine Water balance and Runoff Estimation model (AWARE) in order to predict mid-winter snow accumulation in the Inn headwaters. As snowpack is hydrological storage that evolves during the winter season, it is strongly dependent on precipitation totals of the previous months. Climate model (CM) predictions of precipitation totals integrated from November to February (NDJF) compare reasonably well with observations. Even though predictions for precipitation may not be significantly more skilful than for temperature, the predictive skill achieved for precipitation is retained in subsequent water balance simulations when snow water equivalent (SWE) in February is considered. Given the AWARE simulations driven by observed meteorological fields as a benchmark for SWE analyses, the correlation achieved using GloSea5-AWARE SWE predictions is r = 0.57. The tendency of SWE anomalies (i.e. the sign of anomalies) is correctly predicted in 11 of 13 years. For CFSv2-AWARE, the corresponding values are r = 0.28 and 7 of 13 years. The results suggest that some seasonal prediction of hydrological model storage tendencies in parts of Europe is possible.
Seasonal prediction based on climate models (CMs) is an emerging field in hydrology (e.g. Yuan et al., 2015; Svensson et al., 2015; Mackay et al., 2015) complementing current progress in predicting long-term developments in changing hydrological conditions as a consequence of anthropogenic greenhouse gas emissions. In contrast to climate change projections, seasonal predictions focus on hydrological states of the upcoming months from their dependence on initial states (Warner, 2011). These can provide “climate services”: a set of tools, products, and information serving decision makers and practitioners and bringing all types of information on climate research into practice at all levels of society (Vaughan and Dessai, 2014). This makes them relevant for detecting anticipated short-term changes in hydrological systems as requested by international research programmes such as the World Climate Research Programme (WCRP, e.g. Kirtman and Pirani, 2009), Future Earth (Greenslade and Berkhout, 2014), and more specialized programmes such as the International Network for Alpine Research Catchment Hydrology (INARCH; Pomeroy et al., 2015), which is part of the Global Energy and Water Cycle Exchanges Project (GEWEX; Chahine, 1992). In this context, seasonal predictions contribute both to coping with the WCRP “Grand Challenges” (Reid et al., 2010) and to detecting short-term changes in coupled hydrological–societal systems. The latter consideration of water and humans (Sivapalan et al., 2012) seeks to better understand interactions between society and hydrological systems for which seasonal predictions can also be seen as relevant. The goal of the current scientific decade, Panta Rhei – Everything Flows, of the International Association of Hydrological Sciences (IAHS) is to better understand these interactions over different timescales (Montanari et al., 2013).
Seasonal outlooks of hydrological variables have been prepared for decades. Antecedent hydrological and meteorological data have been used to predict monthly to seasonal streamflow using statistical methods (e.g. regression models) in various hydrological regimes (Pagano et al., 2004; Robertson and Wang, 2012; Schick et al., 2015). Another common way to predict future hydrological states is to run a process-based hydrological model based on known initial states and force it with ensembles of meteorological data observed in the past. This methodology is well known and referred to as ensemble streamflow prediction (ESP; Wood and Lettenmaier, 2008). The development of this method goes back to the 1970s and 1980s (Twedt et al., 1977; Day, 1985) and framed the development of statistical seasonal hydrological forecasting. ESP is a very useful method for studying the influence of meteorological boundary conditions (obtained from observed long-term records) on the results of hydrological forecasting models. In contrast, the reversed ESP experiment is based on actual meteorological forcing but involves an ensemble of initial states, which makes it an appropriate method to study the influence of initial conditions on forecast results. The combination of both methods is also the subject of recent research on predictability of hydrological systems (e.g. the VESPA approach; Wood et al., 2016). In the last decades, coupled atmosphere–ocean general circulation models (AOGCMs) have become a viable method for seasonal predictions (Svensson et al., 2015). These climate model-based forecasts provide future meteorological/climatological conditions for the following weeks (sub-seasonal forecasts), months (seasonal forecasts), or decades (decadal forecasts) on a physical basis rather than based on statistics. An overview of the state of the art of CM-based seasonal predictions is provided by Doblas-Reyes et al. (2013) and Yuan et al. (2015). Like numerical weather prediction, seasonal forecasts are an initial-state problem since predictions of the atmospheric states of the upcoming months strongly depend on the initial states of the atmosphere, oceans, land, and sea ice. In contrast to weather predictions however, the need for considering ocean and sea ice dynamics is crucial since these components of the climate system affect atmospheric phenomena on timescales beyond typical weather predictions. Another important difference from numerical weather predictions is the dependence of seasonal predictions on boundary conditions. Like long-term climate predictions, which are based on anthropogenic greenhouse gas emissions, CM-based seasonal predictions require adequate definitions of boundary conditions (Doblas-Reyes et al., 2013).
The skill of CM-based seasonal predictions is not distributed equally in space and time (Smith et al., 2012; Kim et al., 2012; Kirtman et al., 2014). For instance, the skill in Europe is much lower than in the tropics, where phenomena like El Niño–Southern Oscillation (ENSO) are predictable with higher accuracy (Yuan et al., 2015). Current progress on improving predictability has been recently reported by Scaife et al. (2014), who demonstrated skilful prediction of the North Atlantic Oscillation (NAO), a feature that is relevant for seasonal predictions in Europe. Bruno Soares and Dessai (2015) found that there is a mismatch in supply and demand regarding seasonal forecast products which is limited by skill levels in some regions although the authors also detected additional non-scientific reasons for this mismatch like, e.g. insufficient communication of forecasts to the users.
In general, hydrological forecast models are quite sensitive to initial hydrological conditions such as antecedent rainfall, soil moisture, and snow water equivalent (SWE). Uncertainties in the data of antecedent meteorological conditions influence the quality of process-based hydro-meteorological models at hourly resolution, e.g. in the case of 2-day flood forecasts (Achleitner et al., 2012) or 1-month sub-seasonal streamflow drought forecasts (Fundel et al., 2013). Statistical seasonal streamflow forecast models can be improved when initial conditions with respect to soil moisture and groundwater flow (Robertson et al., 2013) or snow water equivalent (Pagano et al., 2004) are considered. Discharge from alpine catchments is known to be related to snow and ice melt (Viviroli et al., 2003; Kaser et al., 2010). For hydropower generation it is interesting to know if a winter season is above or below average regarding the accumulation of snow. For water management demands such as efficient hydropower production, large efforts have been made to measure SWE in catchments of reservoirs (Painter et al., 2016; Krajči et al., 2017; Schattan et al., 2017), to simulate distributed SWE in basins of reservoirs and water intakes (Schöber et al., 2012; Hanzer et al., 2016), to improve flood forecasts with distributed SWE data (Schöber et al., 2014), and to model future runoff under climate change conditions in snow- and ice-melt-dominated catchments (Barnett et al., 2005; Schaefli et al., 2007; Finger et al., 2012; Hanzer et al., 2017). Gridded SWE data used for initialization of a process-based hydrological model improved predictions of SWE with lead times up to 1 month (Jörg-Hess et al., 2015). Seasonal streamflow and reservoir inflow predictions in snow-dominated basins were quite skilful during the snowmelt season and showed larger uncertainties during the rest of the year (Schick et al., 2015; Anghileri et al., 2016).

Figure 1Map of the Inn headwaters upstream of the Kirchbichl gauging station. Major land use classes are shown along with the topography.
Besides hydropower, seasonal prediction of the accumulation of snow may be relevant to estimate the future evolution of snow depth on skiing slopes for the winter tourism business (Abegg et al., 2013; Marke et al., 2015). Well-focussed, sustainable operation of artificial snow production could result in significant savings with respect to energy costs and water use (Hanzer et al., 2014; Olefs et al., 2010).
In the present study, we focus on a way to make seasonal hydrological predictions more exploitable in the context of water resource planning in the Alps. We present a systematic evaluation of predicting above- and below-average snow accumulation, which is expected to significantly influence runoff in spring and early summer. To achieve this goal, CM-based seasonal forecasts are employed as input data to a water balance model that predicts snow water equivalent (SWE) and runoff in the Inn headwaters. A new aspect of this work is the focus on hydrological storage instead of instantaneous hydrological fluxes and the seasonal prediction of SWE in general. It is expected that the focus on integrated storage (e.g. mid-winter snow accumulation) is more robust than considering instantaneous fluxes (e.g. precipitation, runoff) in seasonal predictions.
Moreover, we focus on the winter season as extratropical seasonal forecasts appear to have the highest skill in this season (e.g. Riddle et al., 2013; Scaife et al., 2014; Kang et al., 2014). There are a number of reasons for this, including winter being the season when the stratosphere is active, which is known to affect predictions (e.g. Domeisen et al., 2015; Scaife et al., 2016; Butler et al., 2016). The winter season also shows much stronger dynamical connections to the tropics, allowing high predictability of tropical rainfall (Kumar et al., 2013) to be transmitted into the extratropics (Greatbatch et al., 2012; Molteni et al., 2015; Scaife et al., 2017).
Based on this, the research question remains as follows: can we detect above- or below-average snow conditions based on CM-based seasonal predictions in the Alps? To answer this, CM-based and hydrological modelling is applied in an Alpine case study. In Sect. 2 the relevant information about the study area, the climate data, the CM-based seasonal predictions, the water balance model, and the methodology for detecting the predictability of snow accumulation are described. In Sect. 3, the results are presented, compiled, and discussed. Finally, Sect. 4 provides concluding remarks and an outlook for future work.
2.1 Study area
The Inn headwaters catchment upstream of the Kirchbichl gauging station covers an area of 9310 km2 and is located in Switzerland and Austria (see Fig. 1). The Inn river is the main tributary to the upper Danube. Elevations in the catchment range between 486 and 4049 m a.s.l., with a mean elevation of approximately 2000 m a.s.l. About 3 % of the catchment area is covered by glaciers. During the winter season runoff is lowest since a major fraction of precipitation is accumulated as snow cover. In spring snowmelt causes an increase in runoff reaching its maximum in August, when glacier melt is highest. For the period 1985–2009, the average areal precipitation and runoff amount to 1225 and 1000 mm yr−1 respectively. In the second half of the 20th century, several reservoirs were built in the study area. Their total capacity is 638 × 106 m3.
2.2 Climate data and seasonal predictions
2.2.1 Climate data
The climate data provided by the HISTALP project (Historical Instrumental Climatological Surface Time Series of the Greater Alpine Region; Auer et al., 2007) constitute a suitable data set for studying climatology and long-term changes of temperature and precipitation in the Alps. The data have been compiled for a long period of time (1800–2010) and include a dense observational station network from different countries in the greater Alpine region. Moreover, it has been quality-checked and homogenized (Auer et al., 2007; Chimani et al., 2013). Mean temperature and precipitation depth are provided on a grid with a temporal resolution of 1 month and a spatial resolution of 5 arcmin (approx. 6 km).
2.2.2 Climatological forecasts
In the framework of this study, the term “climatological forecasts” refers to simulations based on long-term averages of air temperature and precipitation depth for each month based on the HISTALP data. For instance, considering a climatological forecast for January, mean air temperature and precipitation depth are computed through averaging each variable over all Januaries in a multi-year period (i.e. 1996–2009).
2.2.3 Climate model-based seasonal predictions
In this study, two different AOGCMs are utilized as input data for further analyses of seasonal predictions. As outlined earlier, the requirements of CM-based seasonal predictions exceed the extent of numerical weather predictions with respect to the forecast horizon and the number of subsystems of the climate system that need to be considered. Due to the extended forecast horizon, oceans and sea ice need to be incorporated in the models as well (see, e.g., Smith et al., 2012; Doblas-Reyes et al., 2013; Yuan et al., 2015). In this study, two different AOGCMs are applied independently:
-
The NCEP (National Centers for Environmental Prediction) Coupled Forecast System model version 2 (CFSv2; Saha et al., 2014) is an operational seasonal prediction system. Forecasts are initialized 4 times a day. The horizontal resolution is 0.5∘ (approx. 40 km). In order to derive monthly forecasts, runs between the 8th day of the previous month and the 7th day of the current month are utilized in order to generate a lagged ensemble. This methodology was proposed by Yuan et al. (2013), who applied this method to re-forecasts. Since re-forecasts are only available for every 5th day, a typical ensemble of CFSv2 re-forecasts comprises 24 members per month. The archive of re-forecasts includes data from 1985 to 2009. The maximum lead time is 9 months.
-
MetOffice Global Seasonal forecast system version 5 (GloSea5) is a seasonal prediction system that runs operationally at the MetOffice (MacLachlan et al., 2015; Scaife et al., 2014). Compared to CFSv2, it has a higher ocean horizontal resolution (0.25∘, approx. 20 km). The data applied in this study were provided by the SPECS project (“Seasonal-to-decadal climate Prediction for the improvement of European Climate Services”, http://www.specs-fp7.eu/) and cover the period between 1996 and 2010. Re-forecasts for winter were used with initial start dates: 25 October, 1 November, and 9 November. For each date, three runs are available which gives a lagged ensemble of nine members per winter. This subset of hindcasts has a lead time of 4 months for each run.
Systematic analyses are performed for 1996–2009 (the period in which both models are available). Only those re-forecasts that start in November are considered. The lead time is limited to 4 months to predict snow conditions in February. Monthly grids of the climate models with their original grid spacing (as specified above) are used as forcing data for the water balance model which is described in the next section.
2.3 Water balance simulations using AWARE
The Alpine Water balance and Runoff Estimation model (AWARE; Förster et al., 2016) is a deterministic hydrological model operating on a regular grid at 1-month time steps. The model has been designed to estimate anomalies in hydrological variables at the catchment scale from anomalies in meteorological fields predicted by climate models. The coarse temporal resolution allows one to carry out seasonal predictions considering a large number of individual runs at a minimum of computational costs which justifies the coarse time step. As the study's focus is on anomalies in seasonal characteristics, using a monthly scale water balance model is feasible (Kling et al., 2012; Bock et al., 2016), and these models are also applied for seasonal hydrological predictions (Bell et al., 2017).
Required meteorological forcing data include both mean monthly air temperature and monthly precipitation totals provided as grids or station data, which makes the model parsimonious with respect to data requirements. Altitudinal gradients are applied in order to realistically redistribute temperature and precipitation on the model grid. In general, this feature results in a decrease in temperature with increasing elevation and an increase in precipitation on the mountains. For each grid cell the relative contributions of rainfall and snowfall are computed taking into account two threshold temperature values. If the air temperature falls below the lower threshold temperature, the monthly precipitation depth is assumed to be snowfall only. Likewise, air temperatures exceeding the upper threshold indicate rainfall only. In order to enable the occurrence of both snow and rain, a transition range between both thresholds is defined. Based on air temperature, the fraction of rain and snow is linearly interpolated between these two thresholds. Even though the model is also capable of reading shortwave radiation fields (Förster et al., 2016) in order to improve ice-melt prediction, only a simplified snow- and ice-melt simulation using air temperature is possible. This simplification considers the fact that air temperature and precipitation are readily available and more predictable compared to some other meteorological fields. In order to perform simulations with this minimal input of data, the Thornthwaite (1948) evapotranspiration approach is applied. The soil water balance is computed following the approach of McCabe and Markstrom (2007). Linear storage is applied in order to account for the recession of runoff typically related to groundwater processes.
The spatial resolution of the Inn headwaters setup in the AWARE model is 1000 m. Besides a grid-based model domain, AWARE assumes a baseline (reference) meteorological data set for calibration, which is shown in Fig. 2 using the HISTALP data from 1996 to 2009 as the reference period (this run is herein referred to as HISTALP-AWARE). The Nash–Sutcliffe model efficiency (NSE) amounts to E = 0.92 which could be considered very good model performance. As suggested by Schaefli and Gupta (2007), the benchmark Nash–Sutcliffe model efficiency is computed as well (Eb = 0.45). This benchmark NSE value accounts for strong effects of seasonality (Eq. A1 in Sect. A in the Appendix). While the standard NSE indicates if a model is better than the average of observed values, the benchmark NSE proves if the model performance exceeds the corresponding value of a simple model that simply predicts long-term averages for each month. Since the benchmark NSE is also greater than 0, the model is more skilful than applying long-term averages. According to Klemeš (1986) a split sample test is applied including an independent validation period ranging from 1984 to 1995. The corresponding NSE and benchmark NSE are E = 0.91 and Eb = 0.25 respectively. A possible reason for the lower Eb value might be the fact that the validation period has seen an advancing of glaciers due to positive glacier mass balances. In contrast, the calibration period is characterized by a shrinkage of glacier volumes. Both processes are not incorporated in the model so far. However, as the model performance of the validation period is still comparable to the calibration period, the model is found to be suitable for prediction. The mismatch of runoff simulations in winter, especially in March, can be attributed to the effects of reservoirs on river flow in the catchment area which are not represented in the model so far. In this period water is released from seasonal storage filled in summer.
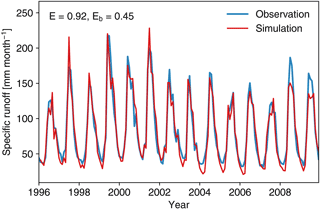
Figure 2Specific runoff hydrographs for observed and modelled runoff at Kirchbichl gauging station and the corresponding performance measures E (Nash–Sutcliffe model efficiency, NSE) and Eb (benchmark NSE).
Another advantage of the 1-month time step is the lower complexity with respect to downscaling of climate model data. Current approaches focus on statistical (e.g. Crochemore et al., 2016) or dynamical downscaling (e.g. Förster et al., 2014) of coarse atmospheric data fields (e.g. derived by climate models). AWARE builds upon a simple and robust approach which is based on anomalies. For instance, Marzeion et al. (2012) successfully add anomalies from other data sets to a reference climatology to compute glacier mass balances at the global scale. In order to account for different spreads of distributions, standardized anomalies are considered in our study. According to Wilks (2006) this approach is feasible when “working simultaneously with batches of data that are related, but not strictly comparable”. This is a typical situation for observational data and re-forecasts. Standardized anomalies zx are simply computed for a variable x, taking into consideration its long-term mean for a given month and the corresponding empirical standard deviation (Wilks, 2006):
Given that two data sets x and y are comparable (e.g. reference climatology and the climatology of re-forecasts), their standardized anomalies zx and zy could be comparable as well. Based on the assumption that zx = zy, Eq. (1) can be rearranged to
Anomalies of the climate model (i.e. y − ) can easily be transformed to the climatology of the reference data set (i.e. x). Mean values and standard deviations are computed separately for each month and climate data set including HISTALP, CFSv2, and GloSea5. In this way, anomalies predicted by the climate models can be reliably transformed to typical anomalies of the observational data.
2.4 Model experiment for analysing the predictability of snow accumulation
The long-term simulations of the water balance provide monthly snapshots of valid system states for each state variable at any point in time. For each CM-based seasonal prediction run starting in November, system states for SWE, soil moisture, and groundwater storage computed for October are defined as initial states. In total four AWARE runs driven with different forcing data sets are available for each winter season between 1997 and 2009 (November to February, NDJF):
-
HISTALP-AWARE: long-term continuous run based on observed HISTALP data (see Sect. 2.2.1 and Fig. 2).
-
CF-AWARE: climatological forecasts (CF) with average conditions computed using HISTALP (see Sect. 2.2.2).
-
GloSea5-AWARE: CM-based seasonal forecast using GloSea5 (ensemble mean of nine members).
-
CFSv2-AWARE: CM-based seasonal forecast using CFSv2 (ensemble mean of 24 members).
The ensemble provided by each CM-based seasonal forecast of meteorological quantities is averaged prior to the water balance simulations. In general, ensemble seasonal predictions are subject to low signal-to-noise ratios. The signal in the ensemble mean is small in most cases and using members individually will mask the signal (Scaife et al., 2014; Eade et al., 2014). In general, each ensemble member of input data is individually processed in hydrological forecasting, which is why the averaging is typically implemented afterwards. However, a skill improvement has been reported in recent seasonal prediction studies (e.g. Bell et al., 2017), in which the concept of averaging is applied prior to hydrological simulations. This approach seems feasible given that the time step of hydrological simulations is 1 month. Although the hydrological model is a conceptual model that mimics the basic physical principles, the temporal scale does not allow for capturing the full dynamics of hydrological processes that are typically studied on smaller scales. Thus, the coarse temporal resolution of the modelling approach is to a certain degree “statistical” in nature which justifies the application of mean ensemble inputs. Moreover, the utilization of standardized anomalies applied to CM-based seasonal forecasts in the AWARE model accounts for variance corrections to the ensemble mean values as suggested by Eade et al. (2014). Appropriate uncertainty can also be added to the predictions to ensure reliable probabilistic forecasts.
The basin-average time series of these water balance simulations are directly comparable. While the continuous long-term simulation represents a reference run (#1) serving as benchmark for seasonal predictions, the climatological forecasts (#2) help to judge whether anomalies will be above or below average. Correlations between the reference run and the water balance simulations forced by CM-based forecasts (#3 and #4) are computed to assess the predictive skill. Moreover, the tendency or sign of anomalies is compared through counting the coincidence of above- or below-average anomalies in the reference run and the seasonal predictions.
A set of skill measures is used throughout the study in order to quantify the model skill of the different forecasts (CF-AWARE, GloSea5-AWARE, CFSv2-AWARE). Besides correlation and hit rate (i.e. the number of correctly predicted states divided by the total number of winters), other measures to assess the skill of the models are considered. For instance, the standard deviation of a single time series is a measure used to compare the variability of forecasts. In contrast, the root mean square error (RMSE) also involves observed time series and provides insight into the absolute difference between time series. Since quadratic differences are summarized, a greater weight is assigned to larger differences, thus making RMSE sensitive to greater mismatches. In order to show the accuracy of the models in predicting the tendencies of anomalies (hit rate), the Brier skill score (BSS) is also computed (see Eqs. A2 and A4 in Sect. A along with a brief description in the Appendix). In general, a skill score judges the improvement of a forecast system relative to a reference (climatology). A value of 0 indicates that the forecast system is not better than the reference. In contrast, a value of 1 indicates a perfect match of forecasts and observations. The BSS is related to the hit rate which has already been defined (higher hit rates go in hand with higher BSS). Finally, the mean absolute error (MAE, Eq. A3) skill is comparable to RMSE but does not account for quadratic weighting of differences. Like BSS, MAE can be computed as a skill score (MAESS; Eq. A4), which is a measure for the differences in absolute terms. In this way, it is less sensitive than RMSE to large differences but rather includes a reference run.
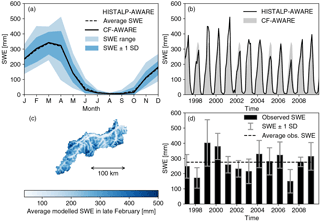
Figure 3Observed and simulated snow states. (a) Range and standard deviation of SWE time series computed for single years and the corresponding mean monthly averages derived from AWARE using HISTALP data (HISTALP-AWARE). Average SWE conditions computed using climatological forecasts (CF-AWARE) are displayed as well. (b) This plot shows the same data but as time series between 1997 and 2009. (c) Map showing the average spatial SWE distribution computed for February. (d) SWE observations in February collected from stations in the study area above 1400 m a.s.l. (Schöber et al., 2016). The error bars show the ±1 SD (standard deviation) of observations for each year (see Schöber et al., 2016, for further details on SWE sampling).
3.1 Long-term simulations and climatological forecast of SWE
While the applicability of AWARE to reconstruct the water balance in terms of observed runoff time series was demonstrated in Sect. 2.3, it is necessary to evaluate the model experiments HISTALP-AWARE and CF-AWARE with respect to SWE prior to the analyses of CM-based SWE forecasts. Figure 3a demonstrates the annual cycle of modelled SWE. The black dashed line is the mean value of all years computed using the reference run (HISTALP-AWARE). It compares well with the black bold line which represents the climatological simulations based on AWARE using average air temperature and precipitation depth for each month (CF-AWARE). Thus, a climatological forecast is suitable to compute average snow conditions. Figure 3c shows the spatial distribution of average SWE in February. The averages of SWE on the model highlights the typical snow distribution with highest values on the mountains and lower values in the valleys. Full time series are shown in Fig. 3b. The boundary conditions of the climatological forecast are equal in each year. However, the initial conditions differ according to the initialization each year in October which is obtained from the long-term run. Figure 3d depicts a subset of SWE observations compiled by Schöber et al. (2016). In contrast to the cited study, which explains the methodology of SWE sampling in detail, here only stations above 1400 m a.s.l. have been selected in order to better match the average catchment elevation (Sect. 2.1). The correlation between computed SWE in February and the SWE observations in February is r = 0.65 (Fig. 3b vs. Fig. 3d). This comparison should be interpreted with caution. First, despite the fact that a sub-selection of stations that better match the mean elevation of the catchment has been chosen for this analysis, the full range of elevation bands in the basin is not fully covered by the observational data set. Moreover, scaling issues limit spatial and temporal representativeness, since averaged point-scale measurements recorded on a weekly scale are compared to basin-scale water balance simulation with 1-month time step. However, observed and computed SWE compare reasonably well. This underlines the applicability of AWARE to predict SWE.
3.2 CM-based seasonal predictions using AWARE
In the next step, anomalies computed using AWARE forced by CM-based seasonal forecasts are compared to the corresponding values of the reference run (HISTALP-AWARE, #1). This evaluation is demonstrated in Fig. 4 for temperature, precipitation depth, and SWE in February. Anomalies in temperature and precipitation depth refer to the period November to February (NDJF) in each winter and represent average values at the basin scale (i.e. the mean of all grid points of the meteorological fields in AWARE). In this way, the values are subject to the statical transformations and elevation-dependent redistributions as outlined in Sect. 2.3. The anomalies of the reference AWARE run driven by HISTALP are shown in the top panels of Fig. 4 (HISTALP-AWARE). Their correlation is set to 1 by definition since this run is viewed as a reference run. The seasonal forecasts computed using AWARE driven by GloSea5-AWARE (centre) and CFSv2-AWARE (bottom) are also displayed. In addition, Table 1 (first model experiment column) provides a summary of skill measures for temperature, precipitation, and SWE.
Table 1Skill measures for basin-scale averages of NDJF temperature, NDJF precipitation, and SWE in February. For each experiment, results for GloSea5-AWARE and CFSv2-AWARE are summarized. The first experiment (full dynamical model runs) refers to the standard setting of CM-based seasonal forecasts using AWARE (Sect. 3.2), while the other two experiments replace CM-based time series with climatology (Sect. 3.3). Skill measures: r, Pearson correlation coefficient; SD, standard deviation of time series; RMSE, root mean square error; hit rate, number of correctly predicted states (out of 13); BSS, Brier skill score; MAESS, mean absolute error skill score. Please note that the units of SD and RMSE are those of the input time series. HISTALP-AWARE is the reference used in the calculations of r, RMSE, hit rate, BSS, and MAESS.
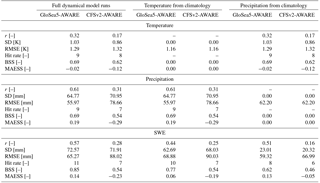
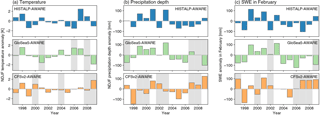
Figure 4Anomalies of (a) basin-scale NDJF temperature, (b) NDJF areal precipitation depth, and (c) snow accumulation in February. Water balance simulations driven by CM-based seasonal forecasts are compared to water balance simulation driven by HISTALP. Shaded areas indicate years in which the sign of anomalies does not match the reference run.
Correlation coefficients computed for NDJF temperature anomalies range from r = 0.17 (CFSv2-AWARE) to r = 0.32 (GloSea5-AWARE). Tendencies in anomalies (i.e. the prediction of correct signs of anomalies) also vary between the models. This becomes obvious when counting the shaded areas indicating a mismatch between the seasonal forecast and the reference run. While GloSea5-AWARE correctly predicted the sign of temperature anomalies in 9 of 13 winters, the hit rate achieved for CFSv2-AWARE only amounts to 8 of 13 (see Table 1). The differences between GloSea5-AWARE and CFSv2-AWARE in terms of standard deviation are small. Hence, both model settings show a similar variability of forecasts which can be attributed to the standardized anomaly approach. GloSea5-AWARE shows a smaller RMSE than CFSv2-AWARE does. A similar ranking of skill is obvious when considering BSS and MAESS. The latter suggests that both model runs (GloSea5-AWARE and CFSv2-AWARE) are less skilful than climatology (MAESS < 0). However, the positive BSS values highlight the capability of predicting the tendency of temperature anomalies.
In the case of GloSea5-AWARE, the hit rate of correctly predicted anomalies regarding precipitation is 9 of 13 (r = 0.61). As for temperature, the model skill of precipitation predictions computed by CFSv2-AWARE is also lower (hit rate 7 of 13, r = 0.31). This finding holds also true for the other skill measures, namely RMSE, BSS, and MAESS. However, the number of correctly predicted tendencies achieved using GloSea5-AWARE could be considered to be a good result since the seasonal forecasts include a lead time of 4 months. Single months show lower scores, suggesting that temporal integration improves the robustness of results consistent with our approach using hydrological storage rather than fluxes. In our study, we found monthly correlations computed for precipitation forecasts ranging from −0.29 to 0.30 (GloSea5-AWARE) and −0.11 to 0.15 (CFSv2-AWARE). These are generally lower than the corresponding values achieved for the averaged NDJF forecasts (GloSea5-AWARE: 0.61; CFSv2-AWARE: 0.31). Similar values of the same order have been observed for SWE forecasts (GloSea5-AWARE: 0.57; CFSv2-AWARE: 0.28).
Given the skill measures from Table 1 (first column) and the coincidence of anomalies highlighted in Fig. 4c the predictive skill achieved for precipitation depth also prevails for SWE in February. Even though correlation coefficients are slightly lower compared to precipitation depth (GloSea5-AWARE: r = 0.57; CFSv2-AWARE: r = 0.28), SWE values in February computed by AWARE driven by CM-based forecasts compare well to those of the reference run (HISTALP-AWARE). The hit rate achieved using GloSea-AWARE even reaches 11 of 13 while the hit rate of CFSv2-AWARE remains at the level of 7 of 13. An increase in skill in terms of RMSE, BSS, and MAESS is also at least partially obvious for both models, indicating that some skill measures suggest that SWE predictions are more robust than precipitation predictions.
A Bernoulli experiment helps to judge whether these hit rates differ from the performance of a “fair coin” for predicting above- and below-average conditions. The null hypothesis states that the hit rate of the seasonal forecasts does not differ from a random 50 : 50 probability (binomial test). Given the total number of winters n = 13 and a level of significance of α = 0.05, the null hypothesis is rejected for hit rates above 9 of 13. This means that according to the results shown in Fig. 4 and Table 1, for seasonal predictions of SWE using GloSea5 this test rejects the null hypothesis, indicating significant skill. In contrast, the scores for CFSv2 are not significant.
Regardless the limitations discussed with respect to observed SWE, the correlations are much lower if the observations from Fig. 3d are involved in skill computations. The correlation between observed anomalies and GloSea5 is r = 0.21, while the corresponding value achieved using CFSv2 is only r = 0.11. These values are much lower than the correlations achieved using the reference run (HISTALP-AWARE). This finding might also be related to possible mismatches in representativeness between observations and simulations. However, the comparison between HISTALP-AWARE and the CM-based seasonal forecasts highlights GCM forecast skill and acknowledges the fact that the water balance model is never perfect since it introduces uncertainties into hydrological forecasts, too. Due to the reasonably good agreement between seasonal forecasts and the reference run, the skill of CM-based forecasts is considered promising.
Figure 5 depicts time series of the water balance of the snow storage for each year and each AWARE model run. Monthly precipitation (divided into rainfall and snowfall), cumulative snowmelt, and SWE are plotted. Moreover, the snow accumulation of the reference run (HISTALP-AWARE, #1) and the climatological forecast (CF-AWARE, #2) are displayed. The latter is subject to the same forcing in each year but is initialized according to the system states of AWARE in late autumn. If the SWE computed by HISTALP-AWARE exceeds the corresponding value of CF-AWARE, above-average snow accumulation prevails. Accordingly, the opposite is true for below-average conditions. A similar comparison is possible for the predictions of GloSea5-AWARE and CFSv2-AWARE. If the CM-based forecast and HISTALP-AWARE simultaneously indicate either above- or below-average conditions, the label “HIT” is added to the corresponding seasonal forecast. The overall hit rate can be seen in Table 1. Even though monthly precipitation depth differs between HISTALP-AWARE and the CM-based forecasts, the NDJF precipitation totals might compensate for this monthly scale differences resulting in a good match of SWE values in February. This is obvious for many of the winter seasons shown in Fig. 5 (e.g. 1998/1999 and 2000/2001) and confirms the previous finding that improved model skill is possible when storage instead of instantaneous fluxes is considered.
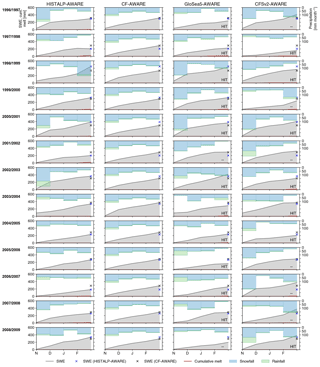
Figure 5Water balance of the basin-scale snow storage for each year and each forcing data set used for AWARE simulations. CF is the climatological forecast (long-term averages of HISTALP) which can be viewed as forecast yielding average conditions. The evolution of snow accumulation is categorized either “HIT” or “–” if the sign of anomalies obtained from HISTALP-AWARE and CM-based AWARE runs matches or mismatches respectively.
3.3 The role of temperature and precipitation for SWE forecasts
In order to show the importance of both temperature and precipitation in SWE forecasting, Table 1 summarizes the skill measure previously introduced for two other model experiments in which either temperature or precipitation is replaced by climatological forecasts: (i) temperature from climatology is combined with precipitation forecasts from the climate models (second column of Table 1) or (ii) precipitation from climatology is combined with temperature forecasts from the climate models (third column of Table 1). If one variable is replaced by climatology the standard deviation of anomalies is 0 since the climatological forecasts have no deviations from climatology. This is in line with zero skill in terms of BSS and MAESS (see temperature skills in the second column and precipitation skills in the third column). The skill measures of the respective variable that has not changed in this way are subject to the same characteristics as in the full dynamical run (first column). For instance, if temperature is replaced by climatology, precipitation skills are equal to those in the full dynamic run (e.g. compare the first and second columns for precipitation).
In the case of SWE, the effects of replacing either temperature or precipitation differ in terms of model skill. First, a drop in correlation is obvious in both cases. If temperature is replaced by climatology the hit rate of GloSea5-AWARE decreases only slightly to 10 but remains at 7 for CFSv2-AWARE. If precipitation is replaced by climatology hit rates decrease in both cases and the standard deviation is much lower than in the full dynamic run. This indicates that the variability in SWE forecasts is mainly prescribed by precipitation in the current study setup. However, the influence of temperature would likely increase for predictions of SWE in the ablation season.
Surprisingly, the RMSE in terms of SWE re-forecasts is lowest in the model run in which precipitation is replaced by climatology. Since this finding is confirmed neither by comparing MAESS (which computes similar error statistics but with linear instead of quadratic weighting of errors) values nor by considering any of the other skill measures, it is likely that this effect is explained by the low variability of SWE in this experiment combined with the quadratic weighting of errors in RMSE computations. This comparison underlines the need for different skill measures in the process of evaluating forecasts.
3.4 Model skill and its relation to other studies
Compared to findings reported in the literature, the results achieved in this study are promising given that the skill for Europe is generally found to be low. For instance, according to Weisheimer and Palmer (2014) the skill of DJF temperature is “marginally useful” using ECMWF's System4. Even the rating for DJF precipitation is found to be “not useful” (see Fig. 5 in Weisheimer and Palmer, 2014). Similarly, Kim et al. (2012) found some skill in terms of correlation for wintertime temperature predictions using System4. However, their study also suggests low absolute correlation coefficients for precipitation forecasts and for both temperature and precipitation forecasts achieved using CFSv2. A direct comparison to the results presented in this study is not possible since GloSea5 was not addressed in these studies. Moreover, given that only one single catchment is considered, a ranking of models is beyond the scope of this article. The predictability for SWE detected in this study could be related both to some amount of skill in precipitation prediction and to previous findings on the persistence of SWE predictions with shorter-term forecast horizons. For instance, in the case of Alpine snow cover, Jörg-Hess et al. (2015) underline the persistence of SWE predictions at least up to a lag of 2 weeks.
In this study, a systematic evaluation of CM-based seasonal winter forecasts starting in November has been performed using a water balance model. A new method has been developed focussing on hydrological storage instead of instantaneous hydrological fluxes. SWE was chosen as predictand here, and two independent climate models were used as input data for monthly scale distributed water balance model. A robust approach based on standardized anomalies was applied in order to bridge the gap in scale between GCMs and the water balance model. In this way, basin-scale averages of temperature and precipitation depth are temporally integrated in order to achieve November to February (NDJF) averages and totals respectively. Given a lead time of 4 months, the application of the water balance model then allows predicting SWE in February, which is relevant for many sectors like water management or hydropower generation. Based on year-by-year evaluation of re-forecasts using different skill measures and a binomial test, the results achieved using GloSea5-AWARE and CFSv2-AWARE indicate that dynamical (CM-based) seasonal forecasts can provide skill. A sensitivity analysis using different configurations of input data sets showed that SWE forecasts benefit from the skill in precipitation forecasts, especially in terms of variability and hit rate/Brier score. These findings might be related to the hydro-climatological characteristics of the study area where snow accumulation is the major process during winter, while snowmelt as a strong temperature-dependent process is less important in this time (Fig. 5). In other environments the relative role of temperature and precipitation might look different.
Regarding predictability, the location of the study area is also of particular interest in the process of interpreting the results. Due to the fact that the Alps are situated in a transition zone between northern and southern Europe, the influence of large-scale climate patterns, such as the NAO, should be analysed in more detail in the future. It is also known that ENSO impacts the climate in Europe in late winter and sudden stratospheric warming is also important (Ineson and Scaife, 2008; Scaife et al., 2016). The first assessment of possible connections between the NAO and snow- and glacier-related states only resulted in low correlations (cf. Beniston and Jungo, 2002; Scherrer et al., 2004; Bartolini et al., 2009; Marzeion and Nesje, 2012). However, in the southern and western parts of the Alps this relationship between NAO and snow and ice properties might be explained more clearly. Recent improvements regarding CM-based seasonal predictions might explain our detectable skill (Scaife et al., 2014). Future work should address climatological processes that are related to model skill and involve other basins in different parts of the Alps.
Besides studying the climatological perspective of predictability, the results also revealed uncertainties involved in hydrological modelling using the water balance model and scaling issues regarding the representativeness of point-scale SWE observations. These findings also suggest improvements regarding both the provision of basin-scale SWE observations and the water balance model to be considered in future work. Low-flow conditions in March might be better predicted if the model accounted for artificial reservoirs in the study area. Moreover, better representation of changes in glaciated area is currently being investigated through coupling AWARE with a glacier evolution model developed by Marzeion et al. (2012). These features will be added to the model in the future.
However, the results of this study show that it is possible to detect skilful signals from dynamical (CM-based) seasonal predictions of hydrological storage in Europe, where seasonal prediction is still challenging. The results suggest that seasonal prediction of hydrological model storage tendencies is possible, although the skill of such predictions is in many cases low in Europe. Overall this study suggests that focussing on hydrological storage rather than hydrological fluxes might help in exploiting seasonal predictions. The first results of the methodology are promising for practical application, with hit rates above 70 % seen as a reasonable target accuracy. Since snowmelt predictions are of particular interest in the study area, a similar approach could be applied to CM-based seasonal forecasts initialized in May. Future research should also address predictability studies in other regions. Moreover, it would be interesting to study the predictability of other types of hydrological storage such as glaciers, lakes, or groundwater, as well as exploring probabilistic forecasting.
CFSv2 re-forecasts (https://nomads.ncdc.noaa.gov/data/cfsr-rfl-mmda/flxf/) as well as the HISTALP data (http://www.zamg.ac.at/histalp/index.php) are available for free.
The definition of the Nash–Sutcliffe model efficiency E and the benchmark Nash–Sutcliffe model efficiency Eb (Schaefli and Gupta, 2007) reads as follows:
In this equation, time series of observed qobs and modelled qsim quantities are considered for all time steps t. qbench(t) is the time-dependent benchmark value at timestep t. qbench(t) is a long-term average computed for the month of time step t. The original definition of Schaefli and Gupta (2007) refers to daily series for which the long-term average for a specific calendar day is applied. According to Schaefli and Gupta (2007) Eb indicates if the model “has greater explanatory power than already contained in the seasonality of the driving forces (the climate)”. If qbench(t) = is assumed, Eb is equal to the Nash–Sutcliffe model efficiency E. In contrast to E, Eb presumes the climatological mean of each time step as a benchmark against which all elements of the time series are compared. Since seasonality is inherent in many time series, generally Eb ≤ E holds.
A widely used measure to evaluate the accuracy of forecasts is the Brier score B (Wilks, 2006):
This is a special case of the ranked probability score (RPS; see, e.g., Hersbach, 2000) that restricts the evaluation of forecasts to two categories (e.g. above or below average). The forecast fi computed for each year i is compared to the corresponding state observed in that year oi, whereby fi and oi are dichotomous states (0 or 1). The Brier score B is the average of the squared differences between fi and oi. The average refers to a range of N years. The best value that can be achieved in this way is 0, indicating a perfect forecast skill. In contrast, 1 indicates that all forecasts are wrong.
Another skill measure for forecasts is the MAE which characterizes, similar to RMSE, differences between the forecasted value qf and the observed value qo (in units of the underlying time series):
If − is replaced by (qf,i(t) − qo,i(t))2 and the square root is calculated from Eq. (A3), this equation yields the RMSE. In contrast to RMSE, MAE is less sensitive to larger differences between qf,i and qo,i. Moreover, the MAE is comparable to the continuous ranked probability score (CRPS) used for probabilistic forecasts (Hersbach, 2000; Trinh et al., 2013) and can be used for single-value (deterministic) forecasts.
In order to compare these skill measures computed for different forecasts to a reference forecast (i.e. climatology), a skill score S measure is typically calculated. For instance, the MAESS (SMAESS) can be derived using
where Mforecast is the MAE of the forecast system and Mreference is the MAE of the climatological forecast. Similarly, Eq. (A4) can be applied to derive a BSS SBSS through replacing M by B.
KF prepared the manuscript with contributions from all co-authors, designed the study, and performed the water balance simulations and predictability analyses. KF and FH developed the AWARE model, which was designed for this kind of study. ES contributed to downscaling of climate model output and reviewed the literature with respect to connections between snow and glacier observations and the NAO index. AAS and CM computed and provided the GloSea5 re-forecasts and helped with data usage, interpretation of the results, and improving the methodology. Snow observations in the study area were evaluated by JS, who also contributed to interpreting anomalies in SWE. MH coordinated the project. SA and US were the key researchers of the project. They supervised the scientific work and helped discuss the results and improve the methodology.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Sub-seasonal to seasonal hydrological forecasting”. It is not associated with a conference.
This work was carried out as part of the W01 MUSICALS II – Multiscale
Snow/Ice Melt Discharge Simulation for Alpine Reservoirs project at alpS – Centre
for Climate Change Adaptation in Innsbruck, Austria. The K1-Centre
alpS is funded through the Federal Ministry of Transport, Innovation and
Technology (BMVIT), the Federal Ministry of Science, Research and Economy (BMWFW),
and the Austrian federal states of Tyrol and Vorarlberg
within the scope of COMET – Competence Centers for Excellent Technologies.
The COMET programme is managed by the Austrian Research Promotion Agency (FFG).
We want to thank Tiroler Wasserkraft AG (TIWAG) for the collaboration
and for co-funding the project. Additional thanks go to the NOAA (National Oceanic
and Atmospheric Administration) National Centers for Environmental Prediction (NCEP)
for the provision the CFSv2 data. The retrospective forecasts of the
GloSea5 model were kindly provided by the SPECS project (Seasonal-to-decadal
climate Prediction for the improvement of European Climate Services;
http://www.specs-fp7.eu/). We would like to thank Felix Oesterle, who
wrote the script to automatically retrieve and convert CFSv2 data. Assistance
with HISTALP data provided by Anna-Maria Tilg and Barbara Chimani is greatly
appreciated. Adam A. Scaife and Craig MacLachlan were supported by the joint DECC/Defra MetOffice
Hadley Centre Programme (GA01101). The publication of this article was funded
by the Open Access fund of Leibniz Universität Hannover. We wish to thank
two anonymous reviewers for their helpful comments that helped to improve the manuscript.
The publication of this article was funded by the open-access
fund of Leibniz Universität Hannover.
Edited by: Quan J. Wang
Reviewed by: two anonymous referees
Abegg, B., Steiger, R., and Walser, R.: Herausforderung Klimawandel: Chancen und Risiken für den Tourismus in Graubünden, Amt für Wirtschaft und Tourismus, Chur, Innsbruck, 2013. a
Achleitner, S., Schöber, J., Rinderer, M., Leonhardt, G., Schöberl, F., Kirnbauer, R., and Schönlaub, H.: Analyzing the operational performance of the hydrological models in an alpine flood forecasting system, J. Hydrol., 412–413, 90–100, https://doi.org/10.1016/j.jhydrol.2011.07.047, 2012. a
Anghileri, D., Voisin, N., Castelletti, A., Pianosi, F., Nijssen, B., and Lettenmaier, D. P.: Value of long-term streamflow forecasts to reservoir operations for water supply in snow-dominated river catchments, Water Resour. Res., 52, 4209–4225, https://doi.org/10.1002/2015WR017864, 2016. a
Auer, I., Böhm, R., Jurkovic, A., Lipa, W., Orlik, A., Potzmann, R., Schöner, W., Ungersböck, M., Matulla, C., Briffa, K., Jones, P., Efthymiadis, D., Brunetti, M., Nanni, T., Maugeri, M., Mercalli, L., Mestre, O., Moisselin, J.-M., Begert, M., Müller-Westermeier, G., Kveton, V., Bochnicek, O., Stastny, P., Lapin, M., Szalai, S., Szentimrey, T., Cegnar, T., Dolinar, M., Gajic-Capka, M., Zaninovic, K., Majstorovic, Z., and Nieplova, E.: HISTALP – historical instrumental climatological surface time series of the Greater Alpine Region, Int. J. Climatol., 27, 17–46, https://doi.org/10.1002/joc.1377, 2007. a, b
Barnett, T. P., Adam, J. C., and Lettenmaier, D. P.: Potential impacts of a warming climate on water availability in snow-dominated regions, Nature, 438, 303–309, https://doi.org/10.1038/nature04141, 2005. a
Bartolini, E., Claps, P., and D'Odorico, P.: Interannual variability of winter precipitation in the European Alps: relations with the North Atlantic Oscillation, Hydrol. Earth Syst. Sci., 13, 17–25, https://doi.org/10.5194/hess-13-17-2009, 2009. a
Bell, V. A., Davies, H. N., Kay, A. L., Brookshaw, A., and Scaife, A. A.: A national-scale seasonal hydrological forecast system: development and evaluation over Britain, Hydrol. Earth Syst. Sci., 21, 4681–4691, https://doi.org/10.5194/hess-21-4681-2017, 2017. a, b
Beniston, M. and Jungo, P.: Shifts in the distributions of pressure, temperature and moisture and changes in the typical weather patterns in the Alpine region in response to the behavior of the North Atlantic Oscillation, Theor. Appl. Climatol., 71, 29–42, https://doi.org/10.1007/s704-002-8206-7, 2002. a
Bock, A. R., Hay, L. E., McCabe, G. J., Markstrom, S. L., and Atkinson, R. D.: Parameter regionalization of a monthly water balance model for the conterminous United States, Hydrol. Earth Syst. Sci., 20, 2861–2876, https://doi.org/10.5194/hess-20-2861-2016, 2016. a
Bruno Soares, M. and Dessai, S.: Exploring the use of seasonal climate forecasts in Europe through expert elicitation, Clim. Risk Manage., 10, 8–16, https://doi.org/10.1016/j.crm.2015.07.001, 2015. a
Butler, A. H., Arribas, A., Athanassiadou, M., Baehr, J., Calvo, N., Charlton-Perez, A., Déqué, M., Domeisen, D. I. V., Fröhlich, K., Hendon, H., Imada, Y., Ishii, M., Iza, M., Karpechko, A. Y., Kumar, A., MacLachlan, C., Merryfield, W. J., Müller, W. A., O'Neill, A., Scaife, A. A., Scinocca, J., Sigmond, M., Stockdale, T. N., and Yasuda, T.: The Climate-system Historical Forecast Project: do stratosphere-resolving models make better seasonal climate predictions in boreal winter?, Q. J. Roy. Meteorol. Soc., 142, 1413–1427, https://doi.org/10.1002/qj.2743, 2016. a
Chahine, M. T.: GEWEX: The global energy and water cycle experiment, Eos Trans. Am. Geophys. Un., 73, 9–14, 1992. a
Chimani, B., Matulla, C., Böhm, R., and Hofstätter, M.: A new high resolution absolute temperature grid for the Greater Alpine Region back to 1780, Int. J. Climatol., 33, 2129–2141, https://doi.org/10.1002/joc.3574, 2013. a
Crochemore, L., Ramos, M.-H., and Pappenberger, F.: Bias correcting precipitation forecasts to improve the skill of seasonal streamflow forecasts, Hydrol. Earth Syst. Sci., 20, 3601–3618, https://doi.org/10.5194/hess-20-3601-2016, 2016. a
Day, G. N.: Extended Streamflow Forecasting Using NWSRFS, J. Water Resour. Pl. Manage., 111, 157–170, https://doi.org/10.1061/(ASCE)0733-9496(1985)111:2(157), 1985. a
Doblas-Reyes, F. J., García-Serrano, J., Lienert, F., Biescas, A. P., and Rodrigues, L. R. L.: Seasonal climate predictability and forecasting: Status and prospects, WIREs Clim. Change, 4, 245–268, https://doi.org/10.1002/wcc.217, 2013. a, b, c
Domeisen, D. I. V., Butler, A. H., Fröhlich, K., Bittner, M., Müller, W. A., and Baehr, J.: Seasonal Predictability over Europe Arising from El Niño and Stratospheric Variability in the MPI-ESM Seasonal Prediction System, J. Climate, 28, 256–271, https://doi.org/10.1175/JCLI-D-14-00207.1, 2015. a
Eade, R., Smith, D., Scaife, A., Wallace, E., Dunstone, N., Hermanson, L., and Robinson, N.: Do seasonal-to-decadal climate predictions underestimate the predictability of the real world?, Geophys. Res. Lett., 41, 5620–5628, https://doi.org/10.1002/2014gl061146, 2014. a, b
Finger, D., Heinrich, G., Gobiet, A., and Bauder, A.: Projections of future water resources and their uncertainty in a glacierized catchment in the Swiss Alps and the subsequent effects on hydropower production during the 21st century, Water Resour. Res., 48, W02521, https://doi.org/10.1029/2011WR010733, 2012. a
Förster, K., Meon, G., Marke, T., and Strasser, U.: Effect of meteorological forcing and snow model complexity on hydrological simulations in the Sieber catchment (Harz Mountains, Germany), Hydrol. Earth Syst. Sci., 18, 4703–4720, https://doi.org/10.5194/hess-18-4703-2014, 2014. a
Förster, K., Oesterle, F., Hanzer, F., Schöber, J., Huttenlau, M., and Strasser, U.: A snow and ice melt seasonal prediction modelling system for Alpine reservoirs, Proc. Int. Assoc. Hydrol. Sci., 374, 143–150, https://doi.org/10.5194/piahs-374-143-2016, 2016. a, b
Fundel, F., Jörg-Hess, S., and Zappa, M.: Monthly hydrometeorological ensemble prediction of streamflow droughts and corresponding drought indices, Hydrol. Earth Syst. Sci., 17, 395–407, https://doi.org/10.5194/hess-17-395-2013, 2013. a
Greatbatch, R. J., Gollan, G., Jung, T., and Kunz, T.: Factors influencing Northern Hemisphere winter mean atmospheric circulation anomalies during the period 1960/61 to 2001/02, Q. J. Roy. Meteorol. Soc., 138, 1970–1982, https://doi.org/10.1002/qj.1947, 2012. a
Greenslade, D. and Berkhout, F.: Future Earth-Research for Global Sustainability, in: EGU General Assembly Conference Abstracts, vol. 16, 27 April–2 May 2014, Vienna, Austria, 2014. a
Hanzer, F., Marke, T., and Strasser, U.: Distributed, explicit modeling of technical snow production for a ski area in the Schladming region (Austrian Alps), Cold Reg. Sci. Technol., 108, 113–124, https://doi.org/10.1016/j.coldregions.2014.08.003, 2014. a
Hanzer, F., Helfricht, K., Marke, T., and Strasser, U.: Multilevel spatiotemporal validation of snow/ice mass balance and runoff modeling in glacierized catchments, The Cryosphere, 10, 1859–1881, https://doi.org/10.5194/tc-10-1859-2016, 2016. a
Hanzer, F., Förster, K., Nemec, J., and Strasser, U.: Projected cryospheric and hydrological impacts of 21st century climate change in the Ötztal Alps (Austria) simulated using a physically based approach, Hydrol. Earth Syst. Sci. Discuss., https://doi.org/10.5194/hess-2017-309, in review, 2017. a
Hersbach, H.: Decomposition of the Continuous Ranked Probability Score for Ensemble Prediction Systems, Weather Forecast., 15, 559–570, https://doi.org/10.1175/1520-0434(2000)015<0559:DOTCRP>2.0.CO;2, 2000. a, b
Ineson, S. and Scaife, A. A.: The role of the stratosphere in the European climate response to El Niño, Nat. Geosci., 2, 32–36, https://doi.org/10.1038/ngeo381, 2008. a
Jörg-Hess, S., Griessinger, N., and Zappa, M.: Probabilistic Forecasts of Snow Water Equivalent and Runoff in Mountainous Areas, J. Hydrometeorol., 16, 2169–2186, https://doi.org/10.1175/JHM-D-14-0193.1, 2015. a, b
Kang, D., Lee, M.-I., Im, J., Kim, D., Kim, H.-M., Kang, H.-S., Schubert, S. D., Arribas, A., and MacLachlan, C.: Prediction of the Arctic Oscillation in boreal winter by dynamical seasonal forecasting systems, Geophys. Res. Lett., 41, 3577–3585, https://doi.org/10.1002/2014GL060011, 2014. a
Kaser, G., Großhauser, M., and Marzeion, B.: Contribution potential of glaciers to water availability in different climate regimes, P. Natl. Acad. Sci. USA, 107, 20223–20227, https://doi.org/10.1073/pnas.1008162107, 2010. a
Kim, H.-M., Webster, P. J., and Curry, J. A.: Seasonal prediction skill of ECMWF System 4 and NCEP CFSv2 retrospective forecast for the Northern Hemisphere Winter, Clim. Dynam., 39, 2957–2973, https://doi.org/10.1007/s00382-012-1364-6, 2012. a, b
Kirtman, B. and Pirani, A.: The State of the Art of Seasonal Prediction: Outcomes and Recommendations from the First World Climate Research Program Workshop on Seasonal Prediction, B. Am. Meteorol. Soc., 90, 455–458, https://doi.org/10.1175/2008BAMS2707.1, 2009. a
Kirtman, B., Power, S. B., Adedoyin, J. A., Boer, G. J., Camilloni, I., Doblas-Reyes, F. J., Fiore, A. M., Kimoto, M., Meehl, G. A., Prather, M., Sarr, A., Schar, C., Sutton, R., van Oldenborgh, G. J., Vecchi, G., and Wang, H. J.: Near-term climate change: projections and predictability, in: Climate change 2013: the physical science basis: contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M. M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, 2014. a
Klemeš, V.: Operational testing of hydrological simulation models, Hydrolog. Sci. J., 31, 13–24, https://doi.org/10.1080/02626668609491024, 1986. a
Kling, H., Fuchs, M., and Paulin, M.: Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios, J. Hydrol., 424-425, 264–277, https://doi.org/10.1016/j.jhydrol.2012.01.011, 2012. a
Krajči, P., Kirnbauer, R., Parajka, J., Schöber, J., and Blöschl, G.: The Kühtai data set: 25 years of lysimetric, snow pillow, and meteorological measurements, Water Resour. Res., 53, 5158–5165, https://doi.org/10.1002/2017WR020445, 2017. a
Kumar, A., Chen, M., and Wang, W.: Understanding Prediction Skill of Seasonal Mean Precipitation over the Tropics, J. Climate, 26, 5674–5681, https://doi.org/10.1175/JCLI-D-12-00731.1, 2013. a
Mackay, J., Jackson, C., Brookshaw, A., Scaife, A., Cook, J., and Ward, R.: Seasonal forecasting of groundwater levels in principal aquifers of the United Kingdom, J. Hydrol., 530, 815–828, https://doi.org/10.1016/j.jhydrol.2015.10.018, 2015. a
MacLachlan, C., Arribas, A., Peterson, K. A., Maidens, A., Fereday, D., Scaife, A. A., Gordon, M., Vellinga, M., Williams, A., Comer, R. E., Camp, J., Xavier, P., and Madec, G.: Global Seasonal forecast system version 5 (GloSea5): A High-Resolution Seasonal Forecast System, Q. J. Roy. Meteorol. Soc., 141, 1072–1084, https://doi.org/10.1002/qj.2396, 2015. a
Marke, T., Strasser, U., Hanzer, F., Stötter, J., Wilcke, R. A. I., and Gobiet, A.: Scenarios of Future Snow Conditions in Styria (Austrian Alps), J. Hydrometeorol., 16, 261–277, https://doi.org/10.1175/JHM-D-14-0035.1, 2015. a
Marzeion, B. and Nesje, A.: Spatial patterns of North Atlantic Oscillation influence on mass balance variability of European glaciers, The Cryosphere, 6, 661–673, https://doi.org/10.5194/tc-6-661-2012, 2012. a
Marzeion, B., Jarosch, A. H., and Hofer, M.: Past and future sea-level change from the surface mass balance of glaciers, The Cryosphere, 6, 1295–1322, https://doi.org/10.5194/tc-6-1295-2012, 2012. a, b
McCabe, G. J. and Markstrom, S. L.: A Monthly Water-Balance Model Driven By a Graphical User Interface, US Geological Survey Open-File report, https://pubs.usgs.gov/of/2007/1088/ (last access: 22 February 2017), 2007. a
Molteni, F., Stockdale, T. N., and Vitart, F.: Understanding and modelling extra-tropical teleconnections with the Indo-Pacific region during the northern winter, Clim. Dynam., 45, 3119–3140, https://doi.org/10.1007/s00382-015-2528-y, 2015. a
Montanari, A., Young, G., Savenije, H., Hughes, D., Wagener, T., Ren, L. L., Koutsoyiannis, D., Cudennec, C., Toth, E., Grimaldi, S., Blöschl, G., Sivapalan, M., Beven, K., Gupta, H., Hipsey, M., Schaefli, B., Arheimer, B., Boegh, E., Schymanski, S. J., Di Baldassarre, G., Yu, B., Hubert, P., Huang, Y., Schumann, A., Post, D. A., Srinivasan, V., Harman, C., Thompson, S., Rogger, M., Viglione, A., McMillan, H., Characklis, G., Pang, Z., and Belyaev, V.: Panta Rhei – Everything Flows: Change in hydrology and society – The IAHS Scientific Decade 2013–2022, Hydrolog. Sci. J., 58, 1256–1275, https://doi.org/10.1080/02626667.2013.809088, 2013. a
Olefs, M., Fischer, A., and Lang, J.: Boundary Conditions for Artificial Snow Production in the Austrian Alps, J. Appl. Meteorol. Clim., 49, 1096–1113, https://doi.org/10.1175/2010JAMC2251.1, 2010. a
Pagano, T., Garen, D., and Sorooshian, S.: Evaluation of official western US seasonal water supply outlooks, 1922–2002, J. Hydrometeorol., 5, 896–909, https://doi.org/10.1175/1525-7541(2004)005<0896:EOOWUS>2.0.CO;2, 2004. a, b
Painter, T. H., Berisford, D. F., Boardman, J. W., Bormann, K. J., Deems, J. S., Gehrke, F., Hedrick, A., Joyce, M., Laidlaw, R., Marks, D., Mattmann, C., McGurk, B., Ramirez, P., Richardson, M., Skiles, S. M., Seidel, F. C., and Winstral, A.: The Airborne Snow Observatory: Fusion of scanning lidar, imaging spectrometer, and physically-based modeling for mapping snow water equivalent and snow albedo, Remote Sens. Environ., 184, 139–152, https://doi.org/10.1016/j.rse.2016.06.018, 2016. a
Pomeroy, J., Bernhardt, M., and Marks, D.: Water resources: Research network to track alpine water, Nature, 521, 32–32, https://doi.org/10.1038/521032c, 2015. a
Reid, W. V., Chen, D., Goldfarb, L., Hackmann, H., Lee, Y. T., Mokhele, K., Ostrom, E., Raivio, K., Rockstrom, J., Schellnhuber, H. J., and Whyte, A.: Earth System Science for Global Sustainability: Grand Challenges, Science, 330, 916–917, https://doi.org/10.1126/science.1196263, 2010. a
Riddle, E. E., Butler, A. H., Furtado, J. C., Cohen, J. L., and Kumar, A.: CFSv2 ensemble prediction of the wintertime Arctic Oscillation, Clim. Dynam., 41, 1099–1116, https://doi.org/10.1007/s00382-013-1850-5, 2013. a
Robertson, D. E. and Wang, Q. J.: A Bayesian Approach to Predictor Selection for Seasonal Streamflow Forecasting, J. Hydrometeorol., 13, 155–171, https://doi.org/10.1175/JHM-D-10-05009.1, 2012. a
Robertson, D. E., Pokhrel, P., and Wang, Q. J.: Improving statistical forecasts of seasonal streamflows using hydrological model output, Hydrol. Earth Syst. Sci., 17, 579–593, https://doi.org/10.5194/hess-17-579-2013, 2013. a
Saha, S., Moorthi, S., Wu, X., Wang, J., Nadiga, S., Tripp, P., Behringer, D., Hou, Y.-T., Chuang, H.-Y., Iredell, M., Ek, M., Meng, J., Yang, R., Mendez, M. P., van den Dool, H., Zhang, Q., Wang, W., Chen, M., and Becker, E.: The NCEP Climate Forecast System Version 2, J. Climate, 27, 2185–2208, https://doi.org/10.1175/JCLI-D-12-00823.1, 2014. a
Scaife, A. A., Arribas, A., Blockley, E., Brookshaw, A., Clark, R. T., Dunstone, N., Eade, R., Fereday, D., Folland, C. K., Gordon, M., Hermanson, L., Knight, J. R., Lea, D. J., MacLachlan, C., Maidens, A., Martin, M., Peterson, A. K., Smith, D., Vellinga, M., Wallace, E., Waters, J., and Williams, A.: Skillful long-range prediction of European and North American winters, Geophys. Res. Lett., 41, 2514–2519, https://doi.org/10.1002/2014GL059637, 2014. a, b, c, d, e
Scaife, A. A., Karpechko, A. Y., Baldwin, M. P., Brookshaw, A., Butler, A. H., Eade, R., Gordon, M., MacLachlan, C., Martin, N., Dunstone, N., and Smith, D.: Seasonal winter forecasts and the stratosphere, Atmos. Sci. Lett., 17, 51–56, https://doi.org/10.1002/asl.598, 2016. a, b
Scaife, A. A., Comer, R. E., Dunstone, N. J., Knight, J. R., Smith, D. M., MacLachlan, C., Martin, N., Peterson, K. A., Rowlands, D., Carroll, E. B., Belcher, S., and Slingo, J.: Tropical rainfall, Rossby waves and regional winter climate predictions, Q. J. Roy. Meteorol. Soc., 143, 1–11, https://doi.org/10.1002/qj.2910, 2017. a
Schaefli, B. and Gupta, H. V.: Do Nash values have value?, Hydrol. Process., 21, 2075–2080, https://doi.org/10.1002/hyp.6825, 2007. a, b, c, d
Schaefli, B., Hingray, B., and Musy, A.: Climate change and hydropower production in the Swiss Alps: quantification of potential impacts and related modelling uncertainties, Hydrol. Earth Syst. Sci., 11, 1191–1205, https://doi.org/10.5194/hess-11-1191-2007, 2007. a
Schattan, P., Baroni, G., Oswald, S. E., Schöber, J., Fey, C., Kormann, C., Huttenlau, M., and Achleitner, S.: Continuous monitoring of snowpack dynamics in alpine terrain by aboveground neutron sensing, Water Resour. Res., 53, 3615–3634, https://doi.org/10.1002/2016WR020234, 2017. a
Scherrer, S. C., Appenzeller, C., and Laternser, M.: Trends in Swiss Alpine snow days: The role of local- and large-scale climate variability, Geophys. Res. Lett., 31, L13215, https://doi.org/10.1029/2004GL020255, 2004. a
Schick, S., Rössler, O., and Weingartner, R.: Saisonale Abflussprognosen für mittelgroße Einzugsgebiete in der Schweiz: Möglichkeiten und Grenzen hydrologischer Persistenz (Seasonal runoff predictions for mesoscale catchments in Switzerland – Potentials and limitations of hydrologic persistence), Hydrol. Wasserbewirtsch., 59, 59–67, https://doi.org/10.5675/HyWa_2015,2_2, 2015. a, b
Schöber, J., Achleitner, S., Kirnbauer, R., Schöberl, F., and Schönlaub, H.: Impact of snow state variation for design flood simulations in glacierized catchments, Adv. Geosci., 31, 39–48, https://doi.org/10.5194/adgeo-31-39-2012, 2012. a
Schöber, J., Schneider, K., Helfricht, K., Schattan, P., Achleitner, S., Schöberl, F., and Kirnbauer, R.: Snow cover characteristics in a glacierized catchment in the Tyrolean Alps – Improved spatially distributed modelling by usage of Lidar data, J. Hydrol., 519, 3492–3510, https://doi.org/10.1016/j.jhydrol.2013.12.054, 2014. a
Schöber, J., Achleitner, S., Bellinger, J., Kirnbauer, R., and Schöberl, F.: Analysis and modelling of snow bulk density in the Tyrolean Alps, Hydrol. Res., 47, 419–441, https://doi.org/10.2166/nh.2015.132, 2016. a, b, c
Sivapalan, M., Savenije, H. H. G., and Blöschl, G.: Socio-hydrology: A new science of people and water, Hydrol. Process., 26, 1270–1276, https://doi.org/10.1002/hyp.8426, 2012. a
Smith, D. M., Scaife, A. A., and Kirtman, B. P.: What is the current state of scientific knowledge with regard to seasonal and decadal forecasting?, Environ. Res. Lett., 7, 015602, https://doi.org/10.1088/1748-9326/7/1/015602, 2012. a, b
Svensson, C., Brookshaw, A., Scaife, A. A., Bell, V. A., Mackay, J. D., Jackson, C. R., Hannaford, J., Davies, H. N., Arribas, A., and Stanley, S.: Long-range forecasts of UK winter hydrology, Environ. Res. Lett., 10, 064006, https://doi.org/10.1088/1748-9326/10/6/064006, 2015. a, b
Thornthwaite, C. W.: An Approach toward a Rational Classification of Climate, Geogr. Rev., 38, 55–94, https://doi.org/10.2307/210739, 1948. a
Trinh, B. N., Thielen-del Pozo, J., and Thirel, G.: The reduction continuous rank probability score for evaluating discharge forecasts from hydrological ensemble prediction systems, Atmos. Sci. Lett., 14, 61–65, https://doi.org/10.1002/asl2.417, 2013. a
Twedt, T. M., Schaake Jr., J. C., and Peck, E. L.: National Weather Service extended streamflow prediction, in: Proceedings Western Snow Conference, 18–21 April 1977, Albuquerque, New Mexico, 52–57, 1977. a
Vaughan, C. and Dessai, S.: Climate services for society: origins, institutional arrangements, and design elements for an evaluation framework, Wiley Interdiscip. Rev. Clim. Change, 5, 587–603, https://doi.org/10.1002/wcc.290, 2014. a
Viviroli, D., Weingartner, R., and Messerli, B.: Assessing the hydrological significance of the world's mountains, Mt. Res. Dev., 23, 32–40, 2003. a
Warner, T. T.: Numerical weather and climate prediction, Cambridge University Press, Cambridge, New York, 2011. a
Weisheimer, A. and Palmer, T. N.: On the reliability of seasonal climate forecasts, J. Roy. Soc. Interf., 11, 20131162, https://doi.org/10.1098/rsif.2013.1162, 2014. a, b
Wilks, D. S.: Statistical methods in the atmospheric sciences, in: no. v. 91 in International geophysics series, 2nd Edn., Academic Press, Amsterdam, Boston, 2006. a, b, c
Wood, A. W. and Lettenmaier, D. P.: An ensemble approach for attribution of hydrologic prediction uncertainty, Geophys. Res. Lett., 35, L14401, https://doi.org/10.1029/2008GL034648, 2008. a
Wood, A. W., Hopson, T., Newman, A., Brekke, L., Arnold, J., and Clark, M.: Quantifying Streamflow Forecast Skill Elasticity to Initial Condition and Climate Prediction Skill, J. Hydrometeorol., 17, 651–668, https://doi.org/10.1175/JHM-D-14-0213.1, 2016. a
Yuan, X., Wood, E. F., Roundy, J. K., and Pan, M.: CFSv2-Based Seasonal Hydroclimatic Forecasts over the Conterminous United States, J. Climate, 26, 4828–4847, https://doi.org/10.1175/JCLI-D-12-00683.1, 2013. a
Yuan, X., Wood, E. F., and Ma, Z.: A review on climate-model-based seasonal hydrologic forecasting: Physical understanding and system development, WIREs Water, 2, 523–536, https://doi.org/10.1002/wat2.1088, 2015. a, b, c, d





