the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Relative effects of statistical preprocessing and postprocessing on a regional hydrological ensemble prediction system
Sanjib Sharma
Ridwan Siddique
Seann Reed
Peter Ahnert
Pablo Mendoza
Alfonso Mejia
The relative roles of statistical weather preprocessing and streamflow postprocessing in hydrological ensemble forecasting at short- to medium-range forecast lead times (day 1–7) are investigated. For this purpose, a regional hydrologic ensemble prediction system (RHEPS) is developed and implemented. The RHEPS is comprised of the following components: (i) hydrometeorological observations (multisensor precipitation estimates, gridded surface temperature, and gauged streamflow); (ii) weather ensemble forecasts (precipitation and near-surface temperature) from the National Centers for Environmental Prediction 11-member Global Ensemble Forecast System Reforecast version 2 (GEFSRv2); (iii) NOAA's Hydrology Laboratory-Research Distributed Hydrologic Model (HL-RDHM); (iv) heteroscedastic censored logistic regression (HCLR) as the statistical preprocessor; (v) two statistical postprocessors, an autoregressive model with a single exogenous variable (ARX(1,1)) and quantile regression (QR); and (vi) a comprehensive verification strategy. To implement the RHEPS, 1 to 7 days weather forecasts from the GEFSRv2 are used to force HL-RDHM and generate raw ensemble streamflow forecasts. Forecasting experiments are conducted in four nested basins in the US Middle Atlantic region, ranging in size from 381 to 12 362 km2.
Results show that the HCLR preprocessed ensemble precipitation forecasts have greater skill than the raw forecasts. These improvements are more noticeable in the warm season at the longer lead times (> 3 days). Both postprocessors, ARX(1,1) and QR, show gains in skill relative to the raw ensemble streamflow forecasts, particularly in the cool season, but QR outperforms ARX(1,1). The scenarios that implement preprocessing and postprocessing separately tend to perform similarly, although the postprocessing-alone scenario is often more effective. The scenario involving both preprocessing and postprocessing consistently outperforms the other scenarios. In some cases, however, the differences between this scenario and the scenario with postprocessing alone are not as significant. We conclude that implementing both preprocessing and postprocessing ensures the most skill improvements, but postprocessing alone can often be a competitive alternative.
Both climate variability and climate change, increased exposure from expanding urbanization, and sea level rise are increasing the frequency of damaging flood events and making their prediction more challenging across the globe (Dankers et al., 2014; Wheater and Gober, 2015; Ward et al., 2015). Accordingly, current research and operational efforts in hydrological forecasting are seeking to develop and implement enhanced forecasting systems, with the goals of improving the skill and reliability of short- to medium-range streamflow forecasts (0–14 days) and providing more effective early warning services (Pagano et al., 2014; Thiemig et al., 2015; Emerton et al., 2016; Siddique and Mejia, 2017). Ensemble-based forecasting systems have become the preferred paradigm, showing substantial improvements over single-valued deterministic ones (Schaake et al., 2007; Cloke and Pappenberger, 2009; Demirel et al., 2013; Fan et al., 2014; Demargne et al., 2014; Schwanenberg et al., 2015; Siddique and Mejia, 2017). Ensemble streamflow forecasts can be generated in a number of ways, being the most common approach to the use of meteorological forecast ensembles to force a hydrological model (Cloke and Pappenberger, 2009; Thiemig et al., 2015). Such meteorological forecasts can be generated by multiple alterations of a numerical weather prediction model, including perturbed initial conditions and/or multiple model physics and parameterizations.
A number of ensemble prediction systems (EPSs) are being used to generate streamflow forecasts. In the United States (US), the NOAA's National Weather Service River Forecast Centers are implementing and using the Hydrological Ensemble Forecast Service to incorporate meteorological ensembles into their flood forecasting operations (Demargne et al., 2014; Brown et al., 2014). Likewise, the European Flood Awareness System from the European Commission (Alfieri et al., 2014) and the Flood Forecasting and Warming Service from the Australia Bureau of Meteorology (Pagano et al., 2016) have adopted the ensemble paradigm. Furthermore, different regional EPSs have been designed and implemented for research purposes, to meet specific regional needs, and/or for real-time forecasting applications. Two examples, among several others (Zappa et al., 2008, 2011; Hopson and Webster, 2010; Demuth and Rademacher, 2016; Addor et al., 2011; Golding et al., 2016; Bennett et al., 2014; Schellekens et al., 2011), are the Stevens Institute of Technology's Stevens Flood Advisory System for short-range flood forecasting (Saleh et al., 2016) and the National Center for Atmospheric Research (NCAR) System for Hydromet Analysis, Research, and Prediction for medium-range streamflow forecasting (NCAR, 2017). Further efforts are underway to operationalize global ensemble flood forecasting and early warning systems, e.g., through the Global Flood Awareness System (Alfieri et al., 2013; Emerton et al., 2016).
EPSs are comprised of several system components. In this study, a regional hydrological ensemble prediction system (RHEPS) is used (Siddique and Mejia, 2017). The RHEPS is an ensemble-based research forecasting system, aimed primarily at bridging the gap between hydrological forecasting research and operations by creating an adaptable and modular forecast emulator. The goal with the RHEPS is to facilitate the integration and rigorous verification of new system components, enhanced physical parameterizations, and novel assimilation strategies. For this study, the RHEPS is comprised of the following system components: (i) precipitation and near-surface temperature ensemble forecasts from the National Centers for Environmental Prediction 11-member Global Ensemble Forecast System Reforecast version 2 (GEFSRv2), (ii) NOAA's Hydrology Laboratory-Research Distributed Hydrologic Model (HL-RDHM) (Reed et al., 2004; Smith et al., 2012a, b), (iii) a statistical weather preprocessor (hereafter referred to as preprocessing), (iv) a statistical streamflow postprocessor (hereafter referred to as postprocessing), (v) hydrometeorological observations, and (vi) a verification strategy. Recently, Siddique and Mejia (2017) employed the RHEPS to produce and verify ensemble streamflow forecasts over some of the major river basins in the US Middle Atlantic region. Here, the RHEPS is specifically implemented to investigate the relative roles played by preprocessing and postprocessing in enhancing the quality of ensemble streamflow forecasts.
The goal with statistical processing is to use statistical tools to quantify the uncertainty of and remove systematic biases in the weather and streamflow forecasts in order to improve the skill and reliability of forecasts. In weather and hydrological forecasting, a number of studies have demonstrated the benefits of separately implementing preprocessing (Sloughter et al., 2007; Verkade et al., 2013; Messner et al., 2014a; Yang et al., 2017) and postprocessing (Shi et al., 2008; Brown and Seo, 2010; Madadgar et al., 2014; Ye et al., 2014; Wang et al., 2016; Siddique and Mejia, 2017). However, only a very limited number of studies have investigated the combined ability of preprocessing and postprocessing to improve the overall quality of ensemble streamflow forecasts (Kang et al., 2010; Zalachori et al., 2012; Roulin and Vannitsem, 2015; Abaza et al., 2017). At first glance, in the context of medium-range streamflow forecasting, preprocessing seems necessary and beneficial since meteorological forcing is often biased and its uncertainty is more dominant than the hydrological one (Cloke and Pappenberger, 2009; Bennett et al., 2014; Siddique and Mejia, 2017). In addition, some streamflow postprocessors assume unbiased forcing (Zhao et al., 2011) and hydrological models can be sensitive to forcing biases (Renard et al., 2010).
The few studies that have analyzed the joint effects of preprocessing and postprocessing on short- to medium-range streamflow forecasts have mostly relied on weather ensembles from the European Centre for Medium-range Weather Forecasts (ECMWF) (Zalachori et al., 2012; Roulin and Vannitsem, 2015; Benninga et al., 2017). Kang et al. (2010) used different forcing but focused on monthly, as opposed to daily, streamflow. The conclusions from these studies have been mixed (Benninga et al., 2017). Some have found statistical processing to be useful (Yuan and Wood, 2012), particularly postprocessing, while others have found that it contributes little to forecast quality. Overall, studies indicate that the relative effects of preprocessing and postprocessing depend strongly on the forecasting system (e.g., forcing, hydrological model, statistical processing technique), and conditions (e.g., lead time, study area, season), underscoring the research need to rigorously verify and benchmark new forecasting systems that incorporate statistical processing.
The main objective of this study is to verify and assess the ability of preprocessing and postprocessing to improve ensemble streamflow forecasts from the RHEPS. This study differs from previous ones in several important respects. The assessment of statistical processing is done using a spatially distributed hydrological model whereas previous studies have tended to emphasize spatially lumped models. Much of the previous studies have used ECMWF forecasts; here we rely on GEFSRv2 precipitation and temperature outputs. Also, we test and implement a preprocessor, namely heteroscedastic censored logistic regression (HCLR), which has not been used before in streamflow forecasting. We also consider a relatively wider range of basin sizes and longer study period than in previous studies. In particular, this paper addresses the following questions:
-
What are the separate and joint contributions of preprocessing and postprocessing over the raw RHEPS outputs?
-
What forecast conditions (e.g., lead time, season, flow threshold, and basin size) benefit potential increases in skill?
-
How much skill improvement can be expected from statistical processing under different uncertainty scenarios (i.e., when skill is measured relative to observed or simulated flow conditions)?
The remainder of the paper is organized as follows. Section 2 presents the study area. Section 3 describes the different components of the RHEPS. The main results and their implications are examined in Sect. 4. Lastly, Sect. 5 summarizes key findings.
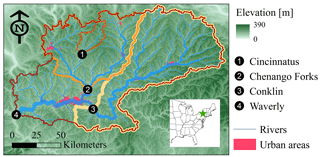
The North Branch Susquehanna River (NBSR) basin in the US Middle Atlantic region (MAR) is selected as the study area (Fig. 1), with an overall drainage area of 12 362 km2. The NBSR basin is selected as flooding is an important regional concern. This region has a relatively high level of urbanization and high frequency of extreme weather events, making it particularly vulnerable to damaging flood events (Gitro et al., 2014; MARFC, 2017). The climate in the upper MAR, where the NBSR basin is located, can be classified as warm, humid summers and snowy, cold winters with frozen precipitation (Polsky et al., 2000). During the cool season, a positive North Atlantic Oscillation phase generally results in increased precipitation amounts and occurrence of heavy snow (Durkee et al., 2007). Thus, flooding in the cool season is dominated by heavy precipitation events accompanied by snowmelt runoff. In the summer season, convective thunderstorms with increased intensity may lead to greater variability in streamflow. In the NBSR basin, we select four different US Geological Survey (USGS) daily gauge stations, representing a system of nested subbasins, as the forecast locations (Fig. 1). The selected locations are the Ostelic River at Cincinnatus (USGS gauge 01510000), Chenango River at Chenango Forks (USGS gauge 01512500), Susquehanna River at Conklin (USGS gauge 01503000), and Susquehanna River at Waverly (USGS gauge 01515000) (Fig. 1). The drainage area of the selected basins ranges from 381 to 12 362 km2. Table 1 outlines some key characteristics of the study basins.
In this section, we describe the different components of the RHEPS, including the hydrometeorological observations, weather forecasts, preprocessor, postprocessors, hydrological model, and the forecasting experiments and verification strategy.
3.1 Hydrometeorological observations
Three main observation datasets are used: multisensor precipitation estimates (MPEs), gridded near-surface air temperature, and daily streamflow. MPEs and gridded near-surface air temperature are used to run the hydrological model in simulation mode for parameter calibration purposes and to initialize the RHEPS. Both the MPEs and gridded near-surface air temperature data at 4 × 4 km2 resolution were provided by the NOAA's Middle Atlantic River Forecast Center (MARFC) (Siddique and Mejia, 2017). Similar to the NCEP stage-IV dataset (Moore et al., 2015; Prat and Nelson, 2015), the MARFC's MPEs represent a continuous time series of hourly, gridded precipitation observations at 4 × 4 km2 cells, which are produced by combining multiple radar estimates and rain gauge measurements. The gridded near-surface air temperature data at 4 × 4 km2 resolution were developed by the MARFC by combining multiple temperature observation networks as described by Siddique and Mejia (2017). Daily streamflow observations for the selected basins were obtained from the USGS. The streamflow observations are used to verify the simulated flows, and the raw and postprocessed ensemble streamflow forecasts.
Table 1Main characteristics of the four study basins.
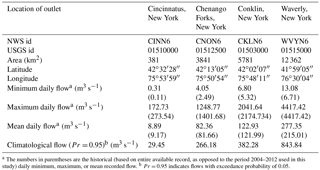
a The numbers in parentheses are the historical (based on entire available record, as opposed to the period 2004–2012 used in this study) daily minimum, maximum, or mean recorded flow. b Pr = 0.95 indicates flows with exceedance probability of 0.05.
3.2 Meteorological forecasts
GEFSRv2 data are used for the ensemble precipitation and near-surface air temperature forecasts. The GEFSRv2 uses the same atmospheric model and initial conditions as the version 9.0.1 of the Global Ensemble Forecast System and runs at T254L42 (∼ 0.50∘ Gaussian grid spacing or ∼ 55 km) and T190L42 (∼ 0.67∘ Gaussian grid spacing or ∼ 73 km) resolutions for the first and second 8 days, respectively (Hamill et al., 2013). The reforecasts are initiated once daily at 00:00 Coordinated Universal Time. Each forecast cycle consists of 3-hourly accumulations for day 1 to day 3 and 6-hourly accumulations for day 4 to day 16. In this study, we use 9 years of GEFSRv2 data, from 2004 to 2012, and forecast lead times from 1 to 7 days. The period 2004 to 2012 is selected to take advantage of data that were previously available to us (i.e., GEFSRv2 and MPEs for the MAR) from a recent verification study (Siddique et al., 2015). Forecast lead times of up to 7 days are chosen since we previously found that the GEFSRv2 skill is low after 7 days (Siddique et al., 2015; Sharma et al., 2017). The GEFSRv2 data are bilinearly interpolated onto the 4 × 4 km2 grid cell resolution of the HL-RDHM model.
3.3 Distributed hydrological model
NOAA's HL-RDHM is used as the spatially distributed hydrological model (Koren et al., 2004). Within HL-RDHM, the Sacramento Soil Moisture Accounting model with Heat Transfer (SAC-HT) is used to represent hillslope runoff generation, and the SNOW-17 module is used to represent snow accumulation and melting.
HL-RDHM is a spatially distributed conceptual model, where the basin system is divided into regularly spaced, square grid cells to account for spatial heterogeneity. Each grid cell acts as a hillslope capable of generating surface, interflow, and groundwater runoff that discharges directly into the streams. The cells are connected to each other through the stream network system. Further, the SNOW-17 module allows each cell to accumulate snow and generate hillslope snowmelt based on the near-surface air temperature. The hillslope runoff, generated at each grid cell by SAC-HT and SNOW-17, is routed to the stream network using a nonlinear kinematic wave algorithm (Koren et al., 2004; Smith et al., 2012a). Likewise, flows in the stream network are routed downstream using a nonlinear kinematic wave algorithm that accounts for parameterized stream cross-section shapes (Koren et al., 2004; Smith et al., 2012a). In this study, we run HL-RDHM using a 2 km horizontal resolution. Further information about the HL-RDHM can be found elsewhere (Koren et al., 2004; Reed et al., 2007; Smith et al., 2012a; Fares et al., 2014; Rafieeinasab et al., 2015; Thorstensen et al., 2016; Siddique and Mejia, 2017).
To calibrate HL-RHDM, we first run the model using a priori parameter estimates previously derived from available datasets (Koren et al., 2000; Reed et al., 2004; Anderson et al., 2006). We then select 10 out of the 17 SAC-HT parameters for calibration based upon prior experience and preliminary sensitivity tests. During the calibration process, each a priori parameter field is multiplied by a factor. Therefore, we calibrate these factors instead of the parameter values at all grid cells, assuming that the a priori parameter distribution is true (e.g., Mendoza et al., 2012).The multiplying factors are adjusted manually first; once the manual changes do not yield noticeable improvements in model performance, the factors are tuned up using stepwise line search (SLS; Kuzmin et al., 2008; Kuzmin, 2009). This method is readily available within HL-RDHM, and has been shown to provide reliable parameter estimates (Kuzmin et al., 2008; Kuzmin, 2009). With SLS, the following objective function is optimized:
where qi and si denote the daily observed and simulated flows at time i, respectively; Ω is the parameter vector being estimated; and m is the total number of days used for calibration. A total of 3 years (2003–2005) of streamflow data are used to calibrate the HL-RDHM for the selected basins. The first year (year 2003) is used to warm up HL-RDHM. To assess the model performance during calibration, we use the percent bias (PB), modified correlation coefficient (Rm), and Nash–Sutcliffe efficiency (NSE) (see Appendix for details). Note that these metrics are used during the manual phase of the calibration process, and to assess the final results from the implementation of the SLS. However, the actual implementation of the SLS is based on the objective function in Eq. (1).
3.4 Statistical weather preprocessor
Heteroscedastic censored logistic regression (Messner et al., 2014a; Yang et al., 2017) is implemented to preprocess the ensemble precipitation forecasts from the GEFSRv2. HCLR is selected since it offers the advantage, over other regression-based preprocessors (Wilks, 2009), of obtaining the full, continuous predictive probability density function (pdf) of precipitation forecasts (Messner et al., 2014b). Also, HCLR has been shown to outperform other widely used preprocessors, such as Bayesian model averaging (Yang et al., 2017). In principle, HCLR fits the conditional logistic probability distribution function to the transformed (here the square root) ensemble mean and bias corrected precipitation ensembles. Note that we tried different transformations (square root, cube root, and fourth root) and found a similar performance between the square and cube root, both outperforming the fourth root. In addition, HCLR uses the ensemble spread as a predictor, which allows the use of uncertainty information contained in the ensembles.
The development of the HCLR follows the logistic regression model initially proposed by Hamill et al. (2004) as well as the extended version of that model proposed by Wilks (2009). The extended logistic regression of Wilks (2009) is used to model the probability of binary responses such that
where Λ(.) denotes the cumulative distribution function of the standard logistic distribution, y is the transformed precipitation, z is a specified threshold, x is a predictor variable that depends on the forecast members, δ(x) is a linear function of the predictor variable x, and the transformation ω(.) is a monotone nondecreasing function. Messner et al. (2014a) proposed the heteroscedastic extended logistic regression (HELR) preprocessor with an additional predictor variable φ to control the dispersion of the logistic predictive distribution,
where η(.) is a linear function of φ. The functions δ(.) and η(.) are defined as follows:
and
where a0, a1, b0, and b1 are parameters that need to be estimated; x = , i.e., the predictor variable xis the mean of the transformed, via the square root, ensemble forecasts f; K is the total number of ensemble members; and φ is the standard deviation of the square-root-transformed precipitation ensemble forecasts.
Maximum likelihood estimation with the log-likelihood function is used to estimate the parameters associated with Eq. (3) (Messner et al., 2014a, b). One variation of the HELR preprocessor that can easily accommodate nonnegative variables, such as precipitation amounts, is HCLR. For this, the predicted probability or likelihood πi of the ith observed outcome is determined as follows (Messner et al., 2014b):
where λ[.] denotes the likelihood function of the standard logistic function. As indicated by Eq. (6), HCLR fits a logistic error distribution with point mass at zero to the transformed predictand.
HCLR is applied here to each GEFSRv2 grid cell within the selected basins. At each cell, HCLR is implemented for the period 2004–2012 using a leave-one-out approach. For this, we select 7 years for training and the 2 remaining years for verification purposes. This is repeated until all the 9 years have been preprocessed and verified independently of the training period. This is done so that no training data are discarded and the entire 9-year period of analysis can be used to generate the precipitation forecasts. HCLR is employed for 6-hourly precipitation accumulations for lead times from 6 to 168 h. To train the preprocessor, we use a stationary training period, as opposed to a moving window, for each season and year to be forecasted, comprised of the seasonal data from all the 7 training years. Thus, to forecast a given season and specific lead time, we use ∼ 6930 forecasts (i.e., 11 members × 90 days per season × 7 years). We previously tested using a moving window training approach and found that the results were similar to the stationary window approach (Yang et al., 2017). To make the implementation of HCLR as straightforward as possible, the stationary window is used here. Finally, the Schaake shuffle method as applied by Clark et al. (2004) is implemented to maintain the observed space–time variability in the preprocessed GEFSRv2 precipitation forecasts. At each individual forecast time, the Schaake shuffle is applied to produce a spatial and temporal rank structure for the ensemble precipitation values that is consistent with the ranks of the observations.
3.5 Statistical streamflow postprocessors
To statistically postprocess the flow forecasts generated by the RHEPS, two different approaches are tested, namely a first-order autoregressive model with a single exogenous variable, ARX(1,1), and quantile regression (QR). We select the ARX(1,1) postprocessor since it has been suggested and implemented for operational applications in the US (Regonda et al., 2013). QR is chosen because it is of similar complexity to the ARX(1,1) postprocessor but for some forecasting conditions it has been shown to outperform it (Mendoza et al., 2016). Furthermore, the ARX (1,1) and QR postprocessors have not been compared against each other for the forecasting conditions specified by the RHEPS. The postprocessors are implemented for the years 2004–2012, using the same leave-one-out approach used for the preprocessor. For this, the 6-hourly precipitation accumulations are used to force the HL-RDHM and generate 6-hourly flows. Note that we use 6-hourly accumulations since this is the resolution of the GEFSRv2 data after day 4 and this is a temporal resolution often used in operational forecasting in the US. Since the observed flow data are mean daily, we compute the mean daily flow forecast from the 6-hourly flows. The postprocessor is then applied to the mean daily values from day 1 to 7.
3.5.1 First-order autoregressive model with a single exogenous variable
To implement the ARX(1,1) postprocessor, the observation and forecast data are first transformed into standard normal deviates using the normal quantile transformation (NQT) (Krzysztofowicz, 1997; Bogner et al., 2012). The transformed observations and forecasts are then used as predictors in the ARX(1,1) model (Siddique and Mejia, 2017). Specifically, for each forecast lead time, the ARX(1,1) postprocessor is formulated as follows:
where and are the NQT-transformed observed flows at time steps i and i + 1, respectively; c is the regression coefficient; is the NQT transformed forecast flow at time step i + 1; and ξ is the residual error term. In Eq. (7), assuming that there is significant correlation between ξi+1 and , ξi+1 can be calculated as follows:
where and are the standard deviation of ξi and ξi+1, respectively; ρ(ξi+1, ξi) is the serial correlation between ξi+1 and ξi; and ϑi+1 is a random Gaussian error generated from N(0, . To estimate N(0, , the following equation is used:
To implement Eq. (7), 10 equally spaced values of ci+1 are selected from 0.1 to 0.9. For each value of ci+1, is determined from Eq. (9), using the training data to determine the other variables in Eq. (9). Then, ϑi+1 is generated from N(0, and ξi+1 is calculated from Eq. (8). The result from Eq. (8) is used with Eq. (7) to generate a trace of which is transformed back to real space using the inverse NQT. These steps are repeated to generate multiple traces for each value of ci+1. For each value of ci+1, the ARX(1,1) model is trained and used to generate ensemble streamflow forecasts, which are in turn used to compute the mean continuous ranked probability score (CRPS) for the 7-year training period under consideration. Thus, the mean CRPS is computed for each value of ci+1, and the value of ci+1 that produces the smallest mean CRPS is then selected for use in the 2-year verification period under consideration. This is repeated until all the years (2004–2012) have been postprocessed and verified independently of the training period. The ARX(1,1) postprocessor is applied at each individual lead time. Thus, at each forecast lead time, an optimal value of ci+1 is estimated by minimizing the mean CRPS following the steps previously outlined. For lead times beyond the initial one (day 1), 1-day-ahead predictions are used as the observed streamflow. For the cases in which falls beyond the historical maxima, extrapolation is used by modeling the upper tail of the forecast distribution as hyperbolic (Journel and Huijbregts, 1978).
3.5.2 Quantile regression
Quantile regression (Koenker and Bassett Jr., 1978; Koenker, 2005) is employed to determine the error distribution, conditional on the ensemble mean, resulting from the difference between observations and forecasts (Dogulu et al., 2015; López López et al., 2014; Weerts et al., 2011; Mendoza et al., 2016). QR is applied here in streamflow space, since it has been shown that, in hydrological forecasting applications, QR has similar skill performance in streamflow space as well as normal space (López López et al., 2014). Another advantage of QR is that it does not make any prior assumptions regarding the shape of the distribution. Further, since QR results in conditional quantiles rather than conditional means, QR is less sensitive to the tail behavior of the streamflow dataset and, consequently, less sensitive to outliers. Note that although QR is here implemented separately for each lead time, the mathematical notation does not reflect this for simplicity.
The QR model is given by
where is the error estimate at quantile interval τ, is the ensemble mean, and dτ and eτ are the linear regression coefficients a τ. The coefficients are determined by minimizing the sum of the residuals based on the training data as follows:
Here, ετ,i and are the paired samples from a total of N samples; ετ,i is computed as the observed flow minus the forecasted one, qτ − fτ; and wτ is the weighting function for the τth quantile defined as follows:
where ζi is the residual term defined as the difference between ετ,i and , for the quantile τ. The minimization in Eq. (11) is solved using linear programming (Koenker, 2005).
Lastly, to obtain the calibrated forecast, fτ, the following equation is used:
In Eq. (13), the estimated error quantiles and the ensemble mean are added to form a calibrated discrete quantile relationship for a particular forecast lead time and thus generate an ensemble streamflow forecast.
3.6 Forecast experiments and verification
The verification analysis is carried out using the Ensemble Verification System (Brown et al., 2010). For the verification, the following metrics are considered: Brier skill score (BSS), mean continuous ranked probability skill score (CRPSS), and the decomposed components of the CRPS (Hersbach, 2000), i.e., the CRPS reliability (CRPSrel) and CRPS potential (CRPSpot). The definition of each of these metrics is provided in the appendix. Additional details about the verification metrics can be found elsewhere (Wilks, 2011; Jolliffe and Stephenson, 2012). Confidence intervals for the verification metrics are determined using the stationary block bootstrap technique (Politis and Romano, 1994), as done by Siddique et al. (2015). All the forecast verifications are done for lead times from 1 to 7 days.
To verify the forecasts for the period 2004–2012, six different forecasting scenarios are considered (Table 2). The first (S1) and second (S2) scenario verify the raw and preprocessed ensemble precipitation forecasts, respectively. Scenarios 3 (S3), 4 (S4), and 5 (S5) verify the raw, preprocessed, and postprocessed ensemble streamflow forecasts, respectively. The last scenario, S6, verifies the combined preprocessed and postprocessed ensemble streamflow forecasts. In S1 and S2, the raw and preprocessed ensemble precipitation forecasts are verified against the MPEs. For the verification of S1 and S2, each grid cell is treated as a separate verification unit. Thus, for a particular basin, the average performance is obtained by averaging the verification results from different verification units. The streamflow forecast scenarios, S3–S6, are verified against mean daily streamflow observations from the USGS. The quality of the streamflow forecasts is evaluated conditionally upon forecast lead time, season (cool and warm), and flow threshold.
This section is divided into four subsections. The first subsection demonstrates the performance of the spatially distributed model, HL-RDHM. The second subsection describes the performance of the raw and preprocessed GEFSRv2 ensemble precipitation forecasts (forecasting scenarios S1 and S2). In the third subsection, the two statistical postprocessing techniques are compared. Lastly, the verification of different ensemble streamflow forecasting scenarios is shown in the fourth subsection (forecasting scenarios S3–S6).
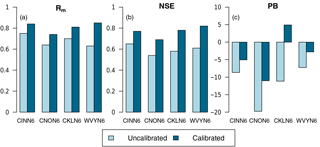
Figure 2Performance statistics for the uncalibrated and calibrated simulation runs for the entire period of analysis (years 2004–2012): (a) Rm, (b) NSE, and (c) PB.
4.1 Performance of the distributed hydrological model
To assess the performance of HL-RDHM, the model is used to generate streamflow simulations which are verified against daily observed flows, covering the entire period of analysis (years 2004–2012). Note that the simulated flows are obtained by forcing HL-RDHM with gridded observed precipitation and near-surface temperature data. The verification is done for the four basin outlets shown in Fig. 1. To perform the verification and assess the quality of the streamflow simulations, the following statistical measures of performance are employed: modified correlation coefficient, Nash–Sutcliffe efficiency, and percent bias. The mathematical definition of these metrics is provided in the appendix. The verification is done for both uncalibrated and calibrated simulation runs for the entire period of analysis. The main results from the verification of the streamflow simulations are summarized in Fig. 2.
The performance of the calibrated simulation runs is satisfactory, with Rm values ranging from ∼ 0.75 to 0.85 (Fig. 2a). Likewise, the NSE, which is sensitive to both the correlation and bias, ranges from ∼ 0.69 to 0.82 for the calibrated runs (Fig. 2b), while the PB ranges from ∼ 5 to −11 % (Fig. 2c). Relative to the uncalibrated runs, the Rm, NSE, and PB values improve by ∼ 18, 29, and 47 %, respectively. Further, the performance of the calibrated simulation runs is similar across the four selected basins, although the largest basin, WVYN6 (Fig. 2), shows slightly higher performance with Rm, NSE, and PB values of 0.85, 0.82, and −3 % (Fig. 2), respectively. The lowest performance is seen in CNON6 with Rm, NSE, and PB values of 0.75, 0.7, and −11 % (Fig. 2), respectively. Nonetheless, the performance metrics for both the uncalibrated and calibrated simulation runs do not deviate widely from each other in the selected basins, with perhaps the only exception being PB (Fig. 2c).
4.2 Verification of the raw and preprocessed ensemble precipitation forecasts
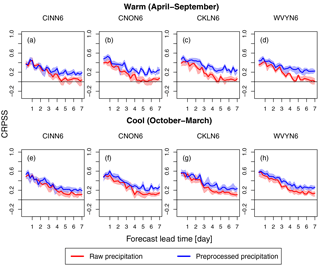
To examine the skill of both the raw and preprocessed GEFSRv2 ensemble precipitation forecasts, we plot in Fig. 3 the CRPSS (relative to sampled climatology) as a function of the forecast lead time (day 1 to 7) and season for the selected basins. Two seasons are considered: cool (October–March) and warm (April–September). Note that a CRPSS value of zero means no skill (i.e., same skill as the reference system) and a value of 1 indicates maximum skill. The CRPSS is computed using 6-hourly precipitation accumulations.
The skill of both the raw and preprocessed ensemble precipitation forecasts tends to decline with increasing forecast lead time (Fig. 3). In the warm season (Fig. 3a–d), the CRPSS values vary overall, across all the basins, in the range from ∼ 0.17 to 0.5 and from ∼ 0.0 to 0.4 for the preprocessed and raw forecasts, respectively; while in the cool season (Fig. 3e–h) the CRPSS values vary overall in the range from ∼ 0.2 to 0.6 and from ∼ 0.1 to 0.6 for the preprocessed and raw forecasts, respectively. The skill of the preprocessed ensemble precipitation forecasts tends to be greater than the raw ones across basins, seasons, and forecast lead times. Comparing the raw and preprocessed forecasts against each other, the relative skill gains from preprocessing are somewhat more apparent in the medium-range lead times (> 3 days) and warm season. That is, the differences in skill seem not as significant in the short-range lead times (≤ 3 days). This seems particularly the case in the cool season, where the confidence intervals for the raw and preprocessed forecasts tend to overlap (Fig. 3e–h).
Indeed, seasonal skill variations are noticeable in all the basins. Even though the relative gain in skill from preprocessing is slightly greater in the warm season, the overall skill of both the raw and preprocessed forecasts is better in the cool season than the warm one. This may be due, among other potential factors, to the greater uncertainty associated with modeling convective precipitation, which is more prevalent in the warm season, by the NWP model used to generate the GEFSRv2 outputs (Hamill et al., 2013; Baxter et al., 2014). Nonetheless, the warm season preprocessed forecasts show gains in skill across all the lead times and basins. For a particular season, the forecast ensembles across the different basins tend to display similar performance; i.e. the analysis does not reflect skill sensitivity to the basin size as in other studies (Siddique et al., 2015; Sharma et al., 2017). This is expected here since the verification is performed for each GEFSRv2 grid cell, rather than verifying the average for the entire basin. That is, the results in Fig. 3 are for the average skill performance obtained from verifying each individual grid cell within the selected basins.
Based on the results presented in Fig. 3, we may expect some skill contribution to the streamflow ensembles from forcing the HL-RDHM with the preprocessed precipitation, as opposed to using the raw forecast forcing. It may also be expected that the contributions are greater for the medium-range lead times and warm season. This will be examined in Sect. 4.4; prior to that we compare next the two postprocessors, namely ARX(1,1) and QR.
4.3 Selection of the streamflow postprocessor
The ability of the ARX(1,1) and QR postprocessors to improve ensemble streamflow forecasts is investigated here. The postprocessors are applied to the raw streamflow ensembles at each forecast lead time from day 1 to 7. To examine the skill of the postprocessed streamflow forecasts, Fig. 4 displays the CRPSS (relative to the raw ensemble streamflow forecasts) versus the forecast lead time for all the selected basins, for both warm (Fig. 4a–d) and cool (Fig. 4e–h) seasons. In the cool season (Fig. 4e–h), the tendency is for both postprocessing techniques to demonstrate improved forecast skill across all the basins and lead times. The skill can improve as much as 40 % at the later lead times (Fig. 4f). The skill improvements, however, from the ARX(1,1) postprocessor are not as consistent for the warm season (Fig. 4a–d), displaying negative skill values for some of the lead times in all the basins. The latter underscores an inability of the ARX(1,1) postprocessor to enhance the raw streamflow ensembles for the warm season. In some cases (Fig. 4b and e–f), the skill of the postprocessors shows an increasing trend with the lead time. This is the case since the skill is here measured relative to the raw streamflow forecasts, which is done to better isolate the effect of the postprocessors on the streamflow forecasts.
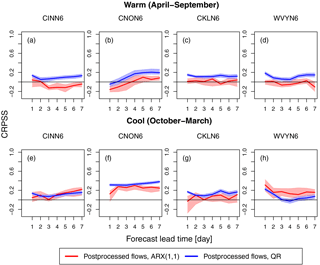
Figure 4CRPSS (relative to the raw forecasts) of the ARX(1,1) (red curves) and QR (blue curves) postprocessed ensemble flood forecasts vs. the forecast lead time during the (a)–(d) warm (April–September) and (e)–(h) cool season (October–March) for the selected basins.
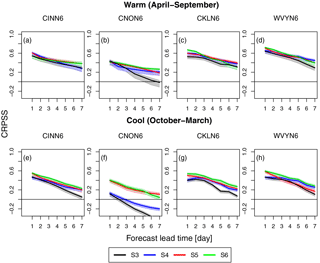
Figure 5Continuous ranked probability skill score (CRPSS) of the mean ensemble flood forecasts vs. the forecast lead time during the (a)–(d) warm (April–September) and (e)–(h) cool season (October–March) for the selected basins. The curves represent the different forecasting scenarios S3–S6. Note that S3 consists of GEFSRv2 + HL-RDHM, S4 of GEFSRv2 + HCLR + HL-RDHM, S5 of GEFSRv2 + HL-RDHM + QR, and S6 of GEFSRv2 + HCLR + HL-RDHM + QR.
The gains in skill from QR vary from ∼ 0 % (Fig. 4b at the day 1 lead time) to ∼ 40 % (Fig. 4f at lead times > 4 days) depending upon the season and lead time. The gains from ARX(1,1), however, vary from ∼ 0 % (Fig. 4g at the day 1 lead time) to a much lower level of ∼ 28 % (Fig. 4f at the day 4 lead time) during the cool season, while there are little to no gains in the warm season. In the cool season (Fig. 4e–h), both postprocessors exhibit somewhat similar performance at different lead times, with the exception of Fig. 4h, but in the warm season QR tends to consistently perform better than ARX(1,1). The overall trend in Fig. 4 is for QR to mostly outperform ARX(1,1), with the difference in performance being as high as 30 % (Fig. 4d at the day 7 lead time). This is noticeable across all the basins (except WVYN6 in Fig. 4h) for most of the lead times and for both seasons.
As discussed and demonstrated in Fig. 4, QR performs better than ARX(1,1). We also computed reliability diagrams, as determined by Sharma et al. (2017), for the two postprocessors (plots not shown) and found that QR tends to display better reliability than ARX(1,1) across lead times, basins, and seasons. Therefore, we select QR as the statistical streamflow postprocessor to examine the interplay between preprocessing and postprocessing in the RHEPS.
4.4 Verification of the ensemble streamflow forecasts for different statistical processing scenarios
In this subsection, we examine the effects of different statistical processing scenarios on the ensemble streamflow forecasts from the RHEPS. The forecasting scenarios considered here are S3–S6 (Table 2 defines the scenarios). To facilitate presenting the verification results, this subsection is divided into the following three parts: CRPSS, CRPS decomposition, and BSS.
4.4.1 CRPSS
The skill of the ensemble streamflow forecasts for S3–S6 is assessed using the CRPSS relative to the sampled climatology (Fig. 5). The CRPSS in Fig. 5 is shown as a function of the forecast lead time for all the basins, and the warm (Fig. 5a–d) and cool (Fig. 5e–h) seasons. The most salient feature of Fig. 5 is that the performance of the streamflow forecasts tends for the most part to progressively improve from S3 to S6. This means that the forecast skill tends to improve across lead times, basin sizes, and seasons as additional statistical processing steps are included in the RHEPS forecasting chain. Although there is some tendency for the large basins to show better forecast skill than the small ones, the scaling (i.e., the dependence of skill on the basin size) is rather mild and not consistent across the four basins.
In Fig. 5, the skill first increases from the raw scenario (i.e., S3, where no statistical processing is done) to the scenario where only preprocessing is performed, S4. The gain in skill between S3 and S4 is generally small at the short lead times (< 3 days) but increases for the later lead times; this is somewhat more evident for the cool season than the warm one. This skill trend between S3 and S4 is not entirely surprising, as we previously saw (Fig. 3) that differences between the raw and preprocessed precipitation ensembles are more significant at the later lead times. The skill in Fig. 5 then shows further improvements for both S5 and S6, relative to S4. Although S6 tends to outperform both S4 and S5 in Fig. 5, the differences in skill among these three scenarios are not as significant; their confidence intervals tend to overlap in most cases, with the exception of Fig. 5f, in which S4 underperforms relative to both S5 and S6. Figure 5 shows that S6 is the preferred scenario in that it tends to more consistently improve the ensemble streamflow forecasts across basins, lead times, and seasons than the other scenarios. It also shows that postprocessing alone, S5, may be slightly more effective than preprocessing alone, S4, in correcting the streamflow forecast biases.
There are also seasonal differences in the forecast skill among the scenarios. The skill of the streamflow forecasts tends to be slightly greater in the warm season (Fig. 5a–d) than in the cool one (Fig. 5e–h) across all the basins and lead times. In the warm season (Fig. 5a–d), all the scenarios tend to show similar skill, except CNON6 (Fig. 5b), with S5 and S6 only slightly outperforming S3 and S4. In the cool season (Fig. 5e–h), with the exception of CNON6 (Fig. 5f), the performance is similar among the scenarios for the short lead times, but S3 tends to consistently underperform for the later lead times relative to S4–S6. There is also a skill reversal between the seasons when comparing the ensemble precipitation (Fig. 3) and streamflow (Fig. 5) forecasts. That is, the skill tends to be higher in the cool season than the warm one in Fig. 3, but this trend reverses in Fig. 5. The reason for this reversal is that in the cool season hydrological conditions are strongly influenced by snow dynamics, which can be challenging to represent with HL-RDHM, particularly when specific snow information or data are not available. In any case, this could be a valuable area for future research since it appears here to have a significant influence on the skill of the ensemble streamflow forecasts.
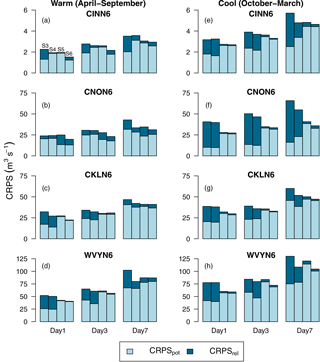
Figure 6Decomposition of the CRPS into CRPS potential (CRPSpot) and CRPS reliability (CRPSrel) for forecasts lead times of 1, 3, and 7 days during the warm (a)–(d) (April–September) and cool season (e)–(h) (October–March) for the selected basins. The four columns associated with each forecast lead time represent the forecasting scenarios S3–S6 (from left to right). Note that S3 consists of GEFSRv2 + HL-RDHM, S4 of GEFSRv2 + HCLR + HL-RDHM, S5 of GEFSRv2 + HL-RDHM + QR, and S6 of GEFSRv2 + HCLR + HL-RDHM + QR.
The underperformance of S4 in the CNON6 basin (Fig. 5f), relative to the other scenarios, is in part due to the unusually low skill of the raw ensemble streamflow forecasts of S3, so that even after preprocessing the skill improvement attained with S4 is not comparable to that associated with S5 and S6. This is also the case for CNON6 in the warm season (Fig. 5b). However, in addition, during the cool season it is likely that streamflows in CNON6 are affected by a reservoir just upstream from the main outlet of CNON6. The reservoir is operated for flood control purposes. During the cool season the reservoir affects low flows by maintaining them at a somewhat higher level than in natural conditions. Since we do not account for reservoir operations in our hydrological modeling, it is likely that one of the benefits of postprocessing is, in this case, that it corrects for this modeling bias. In fact, this is also reflected in the calibration results (e.g., in Fig. 2c), where the performance of CNON6 is somewhat lower than in the other basins. Interestingly, after postprocessing (S5 in Fig. 5f), the skill of CNON6 is as good as that of CINN6, even though at the day 1 lead time the skill for S3 is ∼ 0.1 for CNON6 (Fig. 5f) and ∼ 0.4 for CINN6 (Fig. 5e). Hence, the postprocessor seems capable of compensating somewhat for the lesser performance of CNON6 in both calibration or after preprocessing in the cool season.
4.4.2 CRPS decomposition
Figure 6 displays different components of the mean CRPS against lead times of 1, 3, and 7 days for all the basins according to both the warm (Fig. 6a–d) and cool (Fig. 6e–h) seasons. The components presented here are reliability (CRPSrel) and potential CRPS (CRPSpot) (Hersbach, 2000). CRPSrel measures the average reliability of the ensemble forecasts across all the possible events, i.e., it examines whether the fraction of observations that fall below the jth of n ranked ensemble members is equal to j∕n on average. CRPSpot represents the lowest possible CRPS that could be obtained if the forecasts were made perfectly reliable (i.e., CRPSrel = 0). Note that the CRPS, CRPSrel, and CRPSpot are all negatively oriented, with perfect score of zero. Overall, as was the case with the CRPSS (Fig. 5), the CRPS decomposition reveals that forecast reliability tends mostly to progressively improve from S3 to S6.
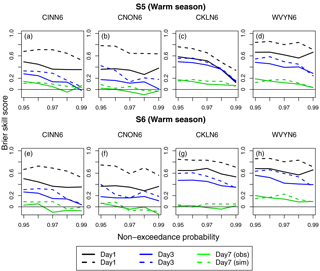
Figure 7Brier skill score (BSS) of the mean ensemble flood forecasts for S5 (a–d) and S6 (e–h) vs. the flood threshold for forecast lead times of 1, 3, and 7 days during the warm (April–September) season for the selected basins. The BSS is shown relative to both observed (solid lines) and simulated floods (dashed lines).
Interestingly, improvements in forecast quality for S5 and S6, relative to the raw streamflow forecasts of S3, are mainly due to reductions in CRPSrel (i.e., by making the forecasts more reliable), whereas for S4 better forecast quality is achieved by reductions in both CRPSrel and CRPSpot. CRPSpot appears to play a bigger role in S4 than in the other scenarios, since in many cases in Fig. 6 the CRPSpot value for S4 is the lowest among all the scenarios. The explanation for this lies in the implementation of the HCLR preprocessor, which uses the ensemble spread as a predictor of the dispersion of the predictive pdf and the CRPSpot is sensitive to the spread (Messner et al., 2014a). In terms of the warm and cool seasons, the warm season tends to show a slightly lower CRPS than the cool one for all the scenarios. There are other, more nuanced differences between the two seasons. For example, S5 is more reliable than S4 in several cases in Fig. 6, such as for the day 1 lead time in the cool season. The CRPS decomposition demonstrates that the ensemble streamflow forecasts for S5 and S6 tend to be more reliable than for S3 and S4. It also shows that the forecasts from S5 and S6 tend to exhibit comparable reliability. However, the ensemble streamflow forecasts generated using both preprocessing and postprocessing, S6, ultimately result in lower CRPS than the other scenarios. The latter is seen across all the basins, lead times, and seasons, except in one case (Fig. 6d at the day 7 lead time).
4.4.3 BSS
In our final verification comparison, the BSS values of the ensemble streamflow forecasts for S5 (Fig. 7a–d) and S6 (Fig. 7e–h) are plotted against the non-exceedance probability associated with different streamflow thresholds ranging from 0.95 to 0.99. The BSS is computed for all the basins, for the warm season, and at lead times of 1, 3 and 7 days. In addition, the BSS is computed relative to both observed (solid lines in Fig. 7) and simulated (dashed lines in Fig. 7) flows. When the BSS is computed relative to observed flows, it considers the effect on forecast skill of both meteorological and hydrological uncertainties. While the BSS relative to simulated flows is mainly affected by meteorological uncertainties. The difference between the two, i.e., the BSS relative to observed flows minus the BSS relative to simulated ones, provides an estimate of the effect of hydrological uncertainties on the skill of the streamflow forecasts. Similar to the CRPSS, the BSS value of zero means no skill (i.e., same skill as the reference system) and a value of 1 indicates perfect skill.
In general, the skill of streamflow forecasts tends to decrease with lead time across the flow thresholds and basins. In contrast to the CRPSS (Fig. 5), where S6 tends for the majority of cases to slightly outperform S5, the BSS values for the different flow thresholds appear similar for S5 (Fig. 7a–d) and S6 (Fig. 7e–h). The only exception is CKLN6 (Fig. 7c and g), where S6 has better skill than S5 at the day 1 and 3 lead times, particularly at the highest flow thresholds considered. With respect to the basin size, the skill tends to improve somewhat from the small to the large basin. For instance, for non-exceedance probabilities of 0.95 and 0.99 at the day 1 lead time, the BSS values for the smallest basin (Fig. 7a), measured relative to the observed flows, are ∼ 0.49 and 0.35, respectively. For the same conditions, both values increase to ∼ 0.65 for the largest basin (Fig. 7d).
The most notable feature in Fig. 7 is that the effect of hydrological uncertainties on forecast skill is evident at the day 1 lead time, while meteorological uncertainties clearly dominate at the day 7 lead time. With respect to the latter, notice that the solid and dashed green lines for the day 7 lead time tend to be very close to each other in Fig. 7, indicating that hydrological uncertainties are relatively small compared to meteorological ones. Hydrological uncertainties are largest at the day 1 lead time, particularly for the small basins (Fig. 7a–b and e–f). For example, for a non-exceedance probability of 0.95 and at a day 1 lead time (Fig. 7b), the BSS value relative to the simulated and observed flows are ∼ 0.79 and 0.38, respectively, suggesting a reduction of ∼ 50 % skill due to hydrological uncertainties.
In this study, we used the RHEPS to investigate the effect of statistical processing on short- to medium-range ensemble streamflow forecasts. First, we assessed the raw precipitation forecasts from the GEFSRv2 (S1), and compared them with the preprocessed precipitation ensembles (S2). Then, streamflow ensembles were generated with the RHEPS for four different forecasting scenarios involving no statistical processing (S3), preprocessing alone (S4), postprocessing alone (S5), and both preprocessing and postprocessing (S6). The verification of ensemble precipitation and streamflow forecasts was done for the years 2004–2012, using four nested gauge locations in the NBSR basin of the US MAR. We found that the scenario involving both preprocessing and postprocessing consistently outperforms the other scenarios. In some cases, however, the differences between the scenario involving preprocessing and postprocessing, and the scenario with postprocessing alone are not as significant, suggesting for those cases (e.g., warm season) that postprocessing alone can be effective in removing systematic biases. Other specific findings are as follows:
-
The HCLR preprocessed ensemble precipitation forecasts show improved skill relative to the raw forecasts. The improvements are more noticeable in the warm season at the longer lead times (> 3 days).
-
Both postprocessors, ARX(1,1) and QR, show gains in skill relative to the raw ensemble streamflow forecasts in the cool season. In contrast, in the warm season, ARX(1,1) shows little or no gains in skill. Overall, for the majority of cases analyzed, the gains with QR tend to be greater than with ARX(1,1), especially during the warm season.
-
In terms of the forecast skill (i.e., CRPSS), in the warm season the scenarios including only preprocessing and only postprocessing have a comparable performance to the more complex scenario consisting of both preprocessing and postprocessing, while in the cool season, the scenario involving both preprocessing and postprocessing consistently outperforms the other scenarios but the differences may not be as significant.
-
The skill of the postprocessing-alone scenario and the scenario that combines preprocessing and postprocessing was further assessed using the Brier skill score for different streamflow thresholds and the warm season. This assessment suggests that for high flow thresholds the similarities in skill between both scenarios, S5 and S6, become greater.
-
Decomposing the CRPS into reliability and potential components, we observed that the scenario that combines preprocessing and postprocessing results in slightly lower CRPS than the other scenarios. We found that the scenario involving only postprocessing tends to demonstrate similar reliability to the scenario consisting of both preprocessing and postprocessing across most of the lead times, basins, and seasons. We also found that in several cases the postprocessing-alone scenario displays improved reliability relative to the preprocessing-alone scenario.
These conclusions are specific to the RHEPS forecasting system, which is mostly relevant to the US research and operational communities as it relies on a weather and a hydrological model that are used in this domain. However, the use of a global weather forecasting system illustrates the potential of applying the statistical techniques tested here in other regions worldwide.
The emphasis of this study has been on benchmarking the contributions of statistical processing to the RHEPS. To accomplish this, our approach required that the quality of ensemble streamflow forecasts be verified over multiple years (i.e., across many flood cases) to obtain robust verification statistics. Future research, however, could be focused on studying how distinct hydrological processes contribute or constrain forecast quality. This effort could be centered around specific flood events rather than on the statistical, many-cases approach taken here. To further assess the relative importance of the various components of the RHEPS, additional tests involving the uncertainty to initial hydrologic conditions and hydrological parameters could be performed. For instance, the combined use of data assimilation and postprocessing has been shown to produce more reliable and sharper streamflow forecasts (Bourgin et al., 2014). The potential for the interaction of preprocessing and postprocessing with data assimilation to significantly enhance streamflow predictions, however, has not been investigated. This could be investigated in the future with the RHEPS, as the pairing of data assimilation with preprocessing and postprocessing could facilitate translating the improvements in the preprocessed meteorological forcing down the hydrological forecasting chain.
Daily streamflow observation data for the selected forecast stations can be obtained from the USGS website (https://waterdata.usgs.gov/nwis/). Multisensor precipitation estimates are obtained from the NOAA's Middle Atlantic River Forecast Center. Precipitation and temperature forecast datasets can be obtained from the NOAA Earth System Research Laboratory website (https://www.esrl.noaa.gov/psd/forecasts/reforecast2/download.html).
Modified correlation coefficient. The modified version of the correlation coefficient, called a modified correlation coefficient Rm, compares event-specific observed and simulated hydrographs (McCuen and Snyder, 1975). In the modified version, an adjustment factor based on the ratio of the observed and simulated flow is introduced to refine the conventional correlation coefficient R. The modified correlation coefficient Rm is defined as follows:
where σs and σq denote the standard deviation of the simulated and observed flows, respectively.
Percent bias. PB measures the average tendency of the simulated flows to be larger or smaller than their observed counterparts. Its optimal value is 0.0 where positive values indicate model overestimation bias, and negative values indicate model underestimation bias. The PB is estimated as follows:
where si and qi denote the simulated and observed flow, respectively, at time i.
Nash–Sutcliffe efficiency. the NSE (Nash and Sutcliffe, 1970) is defined as the ratio of the residual variance to the initial variance. It is widely used to indicate how well the simulated flows fit the observations. The range of NSE can vary between negative infinity to 1.0, with 1.0 representing the optimal value and values should be larger than 0.0 to indicate minimally acceptable performance. The NSE is computed as follows:
where si, qi, and are the simulated, observed, and mean observed flow, respectively, at time i.
Brier skill score. the Brier score (Brier, 1950) is analogous to the mean squared error, but where the forecast is a probability and the observation is either a 0.0 or 1.0. The BS is given by
where the probability of fi to exceed a fixed threshold z is
Here, n is again the total number of forecast-observation pairs, and
In order to compare the skill score of the main forecast system with respect to the reference forecast, it is convenient to define the Brier Skill Score (BSS):
where BSmain and BSreference are the BS values for the main forecast system (i.e. the system to be evaluated) and reference forecast system, respectively. Any positive values of the BSS, from 0 to 1, indicate that the main forecast system performs better than the reference forecast system. Thus, a BSS of 0 indicates no skill and a BSS of 1 indicates perfect skill.
Mean continuous ranked probability skill score. Continuous ranked probability score (CRPS) quantifies the integrated square difference between the cumulative distribution function (cdf) of a forecast, Ff(z), and the corresponding cdf of the observation, Fq(z). The CRPS is given by
To evaluate the skill of the main forecast system relative to the reference forecast system, the associated skill score, the mean continuous ranked probability skill score (CRPSS) is defined as follows:
where the CRPS is averaged across n pairs of forecasts and observations to calculate the mean CRPS of the main forecast system (CRPSmain) and reference forecast system (CRPSreference). The CRPSS varies from −∞ to 1. Any positive values of the CRPSS, from 0 to 1, indicate that the main forecast system performs better than the reference forecast system.
To further explore the forecast skill, the CRPSmain is decomposed into the CRPS reliability (CRPSrel) and potential (CRPSpot) such that CRPSmain can be calculated as follows (Hersbach, 2000):
The CRPSrel measures the average reliability of the precipitation ensembles similarly to the rank histogram, which shows whether the frequency that the verifying analysis was found in a given bin is equal for all bins (Hersbach, 2000). The CRPSpot measures the CRPS that one would obtain for a perfect reliable system. It is sensitive to the average ensemble spread and outliers.
The authors declare that they have no conflict of interest.
We acknowledge the funding support provided by the NOAA/NWS through award NA14NWS4680012.
Edited by: Shraddhanand Shukla
Reviewed by: Michael Scheuerer and two anonymous referees
Abaza, M., Anctil, F., Fortin, V., and Perreault, L.: On the incidence of meteorological and hydrological processors: effect of resolution, sharpness and reliability of hydrological ensemble forecasts, J. Hydrol., 555, 371–384, 2017.
Addor, N., Jaun, S., Fundel, F., and Zappa, M.: An operational hydrological ensemble prediction system for the city of Zurich (Switzerland): skill, case studies and scenarios, Hydrol. Earth Syst. Sci., 15, 2327–2347, https://doi.org/10.5194/hess-15-2327-2011, 2011.
Alfieri, L., Burek, P., Dutra, E., Krzeminski, B., Muraro, D., Thielen, J., and Pappenberger, F.: GloFAS – global ensemble streamflow forecasting and flood early warning, Hydrol. Earth Syst. Sci., 17, 1161–1175, https://doi.org/10.5194/hess-17-1161-2013, 2013.
Alfieri, L., Pappenberger, F., Wetterhall, F., Haiden, T., Richardson, D., and Salamon, P.: Evaluation of ensemble streamflow predictions in Europe, J. Hydrol., 517, 913–922, 2014.
Anderson, R. M., Koren, V. I., and Reed, S. M.: Using SSURGO data to improve Sacramento Model a priori parameter estimates, J. Hydrol., 320, 103–116, 2006.
Baxter, M. A., Lackmann, G. M., Mahoney, K. M., Workoff, T. E., and Hamill, T. M.: Verification of quantitative precipitation reforecasts over the southeastern United States, Weather Forecast., 29, 1199–1207, 2014.
Bennett, J. C., Robertson, D. E., Shrestha, D. L., Wang, Q., Enever, D., Hapuarachchi, P., and Tuteja, N. K.: A System for Continuous Hydrological Ensemble Forecasting (SCHEF) to lead times of 9days, J. Hydrol., 519, 2832–2846, 2014.
Benninga, H.-J. F., Booij, M. J., Romanowicz, R. J., and Rientjes, T. H. M.: Performance of ensemble streamflow forecasts under varied hydrometeorological conditions, Hydrol. Earth Syst. Sci., 21, 5273–5291, https://doi.org/10.5194/hess-21-5273-2017, 2017.
Bogner, K., Pappenberger, F., and Cloke, H. L.: Technical Note: The normal quantile transformation and its application in a flood forecasting system, Hydrol. Earth Syst. Sci., 16, 1085–1094, https://doi.org/10.5194/hess-16-1085-2012, 2012.
Bourgin, F., Ramos, M.-H., Thirel, G., and Andreassian, V.: Investigating the interactions between data assimilation and post-processing in hydrological ensemble forecasting, J. Hydrol., 519, 2775–2784, 2014.
Brier, G. W.: Verification of forecasts expressed in terms of probability, Mon. Weather Rev., 78, 1–3, 1950.
Brown, J. D. and Seo, D.-J.: A nonparametric postprocessor for bias correction of hydrometeorological and hydrologic ensemble forecasts, J. Hydrometeorol., 11, 642–665, 2010.
Brown, J. D., Demargne, J., Seo, D.-J., and Liu, Y.: The Ensemble Verification System (EVS): A software tool for verifying ensemble forecasts of hydrometeorological and hydrologic variables at discrete locations, Environ. Model. Softw., 25, 854–872, 2010.
Brown, J. D., He, M., Regonda, S., Wu, L., Lee, H., and Seo, D.-J.: Verification of temperature, precipitation, and streamflow forecasts from the NOAA/NWS Hydrologic Ensemble Forecast Service (HEFS): 2. Streamflow verification, J. Hydrol., 519, 2847–2868, 2014.
Clark, M., Gangopadhyay, S., Hay, L., Rajagopalan, B., and Wilby, R.: The Schaake shuffle: A method for reconstructing space–time variability in forecasted precipitation and temperature fields, J. Hydrometeorol., 5, 243–262, 2004.
Cloke, H. and Pappenberger, F.: Ensemble flood forecasting: a review, J. Hydrol., 375, 613–626, 2009.
Dankers, R., Arnell, N. W., Clark, D. B., Falloon, P. D., Fekete, B. M., Gosling, S. N., Heinke, J., Kim, H., Masaki, Y., Satoh, Y., Stacke, T., Wada, Y., and Wisser, D.: First look at changes in flood hazard in the Inter-Sectoral Impact Model Intercomparison Project ensemble, P. Natl. Acad. Sci. USA, 111, 3257–3261, https://doi.org/10.1073/pnas.1302078110, 2014.
Demargne, J., Wu, L., Regonda, S. K., Brown, J. D., Lee, H., He, M., Seo, D.-J., Hartman, R., Herr, H. D., and Fresch, M.: The science of NOAA's operational hydrologic ensemble forecast service, B. Am. Meteorol. Soc., 95, 79–98, 2014.
Demirel, M. C., Booij, M. J., and Hoekstra, A. Y.: Effect of different uncertainty sources on the skill of 10 day ensemble low flow forecasts for two hydrological models, Water Resour. Res., 49, 4035–4053, 2013.
Demuth, N. and Rademacher, S.: Flood Forecasting in Germany – Challenges of a Federal Structure and Transboundary Cooperation, Flood Forecasting: A Global Perspective, Elsevier, 125–151, 2016.
Dogulu, N., López López, P., Solomatine, D. P., Weerts, A. H., and Shrestha, D. L.: Estimation of predictive hydrologic uncertainty using the quantile regression and UNEEC methods and their comparison on contrasting catchments, Hydrol. Earth Syst. Sci., 19, 3181–3201, https://doi.org/10.5194/hess-19-3181-2015, 2015.
Durkee, D. J., Frye, D. J., Fuhrmann, M. C., Lacke, C. M., Jeong, G. H., and Mote, L. T.: Effects of the North Atlantic Oscillation on precipitation-type frequency and distribution in the eastern United States, Theor. Appl. Climatol., 94, 51–65, 2007.
Emerton, R. E., Stephens, E. M., Pappenberger, F., Pagano, T. C., Weerts, A. H., Wood, A. W., Salamon, P., Brown, J. D., Hjerdt, N., and Donnelly, C.: Continental and global scale flood forecasting systems, Wiley Interdisciplin. Rev.: Water, 3, 391–418, 2016.
Fan, F. M., Collischonn, W., Meller, A., and Botelho, L. C. M.: Ensemble streamflow forecasting experiments in a tropical basin: The São Francisco river case study, J. Hydrol., 519, 2906–2919, 2014.
Fares, A., Awal, R., Michaud, J., Chu, P.-S., Fares, S., Kodama, K., and Rosener, M.: Rainfall-runoff modeling in a flashy tropical watershed using the distributed HL-RDHM model, J. Hydrol., 519, 3436–3447, 2014.
Gitro, C. M., Evans, M. S., and Grumm, R. H.: Two Major Heavy Rain/Flood Events in the Mid-Atlantic: June 2006 and September 2011, J. Operat. Meteorol., 2, 152–168, https://doi.org/10.15191/nwajom.2014.0213, 2014.
Golding, B., Roberts, N., Leoncini, G., Mylne, K., and Swinbank, R.: MOGREPS-UK convection-permitting ensemble products for surface water flood forecasting: Rationale and first results, J. Hydrometeorol., 17, 1383–1406, 2016.
Hamill, T. M., Whitaker, J. S., and Wei, X.: Ensemble reforecasting: Improving medium-range forecast skill using retrospective forecasts, Mon. Weather Rev., 132, 1434–1447, 2004.
Hamill, T. M., Bates, G. T., Whitaker, J. S., Murray, D. R., Fiorino, M., Galarneau Jr., T. J., Zhu, Y., and Lapenta, W.: NOAA's second-generation global medium-range ensemble reforecast dataset, B. Am. Meteorol. Soc., 94, 1553–1565, 2013.
Hersbach, H.: Decomposition of the continuous ranked probability score for ensemble prediction systems, Weather Forecast., 15, 559–570, 2000.
Hopson, T. M. and Webster, P. J.: A 1–10-day ensemble forecasting scheme for the major river basins of Bangladesh: Forecasting severe floods of 2003–07, J. Hydrometeorol., 11, 618–641, 2010.
Jolliffe, I. T. and Stephenson, D. B.: Forecast verification: a practitioner's guide in atmospheric science, Wiley, West Sussex, England, 2012.
Journel, A. G. and Huijbregts, C. J.: Mining geostatistics, Academic Press, London, 1978.
Kang, T. H., Kim, Y. O., and Hong, I. P.: Comparison of pre-and post-processors for ensemble streamflow prediction, Atmos. Sci. Lett., 11, 153–159, 2010.
Koenker, R.: Quantile regression, Cambridge University Press, Cambridge, 38, https://doi.org/10.1017/CBO9780511754098, 2005.
Koenker, R. and Bassett Jr., G.: Regression quantiles, Econometrica, 46, 33–50, 1978.
Koren, V., Smith, M., Wang, D., and Zhang, Z.: 2.16 Use of soil property data in the derivation of conceptual rainfall-runoff model parameters, in: Proceedings of the 15th Conference on Hydrology, American Meteorological Society, Long Beach, California, 103–106, 2000.
Koren, V., Reed, S., Smith, M., Zhang, Z., and Seo, D.-J.: Hydrology laboratory research modeling system (HL-RMS) of the US national weather service, J. Hydrol., 291, 297–318, 2004.
Krzysztofowicz, R.: Transformation and normalization of variates with specified distributions, J. Hydrol., 197, 286–292, 1997.
Kuzmin, V.: Algorithms of automatic calibration of multi-parameter models used in operational systems of flash flood forecasting, Russ. Meteorol. Hydrol., 34, 473–481, 2009.
Kuzmin, V., Seo, D.-J., and Koren, V.: Fast and efficient optimization of hydrologic model parameters using a priori estimates and stepwise line search, J. Hydrol., 353, 109–128, 2008.
López López, P., Verkade, J. S., Weerts, A. H., and Solomatine, D. P.: Alternative configurations of quantile regression for estimating predictive uncertainty in water level forecasts for the upper Severn River: a comparison, Hydrol. Earth Syst. Sci., 18, 3411–3428, https://doi.org/10.5194/hess-18-3411-2014, 2014.
Madadgar, S., Moradkhani, H., and Garen, D.: Towards improved post-processing of hydrologic forecast ensembles, Hydrol. Process., 28, 104–122, 2014.
MARFC: http://www.weather.gov/marfc/Top20, last access: 1 April 2017.
McCuen, R. H. and Snyder, W. M.: A proposed index for comparing hydrographs, Water Resour. Res., 11, 1021–1024, 1975.
Mendoza, P. A., McPhee, J., and Vargas, X.: Uncertainty in flood forecasting: A distributed modeling approach in a sparse data catchment, Water Resour. Res., 48, W09532, https://doi.org/10.1029/2011wr011089, 2012.
Mendoza, P. A., Wood, A., Clark, E., Nijssen, B., Clark, M., Ramos, M. H., and Voisin, N.: Improving medium-range ensemble streamflow forecasts through statistical postprocessing, Presented at 2016 Fall Meeting, AGU, 11–15 December 2016, San Francisco, California, 2016.
Messner, J. W., Mayr, G. J., Zeileis, A., and Wilks, D. S.: Heteroscedastic extended logistic regression for postprocessing of ensemble guidance, Mon. Weather Rev., 142, 448–456, 2014a.
Messner, J. W., Mayr, G. J., Wilks, D. S., and Zeileis, A.: Extending extended logistic regression: Extended versus separate versus ordered versus censored, Mon. Weather Rev., 142, 3003–3014, 2014b.
Moore, B. J., Mahoney, K. M., Sukovich, E. M., Cifelli, R., and Hamill, T. M.: Climatology and environmental characteristics of extreme precipitation events in the southeastern United States, Mon. Weather Rev., 143, 718–741, 2015.
Nash, J. E. and Sutcliffe, J. V.: River flow forecasting through conceptual models part I – A discussion of principles, J. Hydrol., 10, 282–290, 1970.
NCAR: https://ral.ucar.edu/projects/system-for-hydromet-analysis-research-and-prediction-sharp, last access: 1 April 2017.
Pagano, T. C., Elliott, J., Anderson, B., and Perkins, J.: Australian Bureau of Meteorology Flood Forecasting and Warning, in: Flood Forecasting, Elsevier, 3–40, 2016.
Pagano, T. C., Wood, A. W., Ramos, M.-H., Cloke, H. L., Pappenberger, F., Clark, M. P., Cranston, M., Kavetski, D., Mathevet, T., and Sorooshian, S.: Challenges of operational river forecasting, J. Hydrometeorol., 15, 1692–1707, 2014.
Politis, D. N. and Romano, J. P.: The stationary bootstrap, J. Am. Stat. Assoc., 89, 1303–1313, 1994.
Polsky, C., Allard, J., Currit, N., Crane, R., and Yarnal, B.: The Mid-Atlantic Region and its climate: past, present, and future, Clim. Res., 14, 161–173, 2000.
Prat, O. P. and Nelson, B. R.: Evaluation of precipitation estimates over CONUS derived from satellite, radar, and rain gauge data sets at daily to annual scales (2002–2012), Hydrol. Earth Syst. Sci., 19, 2037–2056, https://doi.org/10.5194/hess-19-2037-2015, 2015.
Rafieeinasab, A., Norouzi, A., Kim, S., Habibi, H., Nazari, B., Seo, D.-J., Lee, H., Cosgrove, B., and Cui, Z.: Toward high-resolution flash flood prediction in large urban areas – Analysis of sensitivity to spatiotemporal resolution of rainfall input and hydrologic modeling, J. Hydrol., 531, 370–388, 2015.
Reed, S., Koren, V., Smith, M., Zhang, Z., Moreda, F., and Seo, D. J.: Overall distributed model intercomparison project results, J. Hydrol., 298, 27–60, 2004.
Reed, S., Schaake, J., and Zhang, Z.: A distributed hydrologic model and threshold frequency-based method for flash flood forecasting at ungauged locations, J. Hydrol., 337, 402–420, 2007.
Regonda, S. K., Seo, D. J., Lawrence, B., Brown, J. D., and Demargne, J.: Short-term ensemble streamflow forecasting using operationally-produced single-valued streamflow forecasts – A Hydrologic Model Output Statistics (HMOS) approach, J. Hydrol., 497, 80–96, 2013.
Renard, B., Kavetski, D., Kuczera, G., Thyer, M., and Franks, S. W.: Understanding predictive uncertainty in hydrologic modeling: The challenge of identifying input and structural errors, Water Resour. Res., 46, W05521, https://doi.org/10.1029/2009wr008328, 2010.
Roulin, E. and Vannitsem, S.: Post-processing of medium-range probabilistic hydrological forecasting: impact of forcing, initial conditions and model errors, Hydrol. Process., 29, 1434–1449, 2015.
Saleh, F., Ramaswamy, V., Georgas, N., Blumberg, A. F., and Pullen, J.: A retrospective streamflow ensemble forecast for an extreme hydrologic event: a case study of Hurricane Irene and on the Hudson River basin, Hydrol. Earth Syst. Sci., 20, 2649–2667, https://doi.org/10.5194/hess-20-2649-2016, 2016.
Schaake, J. C., Hamill, T. M., Buizza, R., and Clark, M.: HEPEX: the hydrological ensemble prediction experiment, B. Am. Meteorol. Soc., 88, 1541–1547, 2007.
Schellekens, J., Weerts, A., Moore, R., Pierce, C., and Hildon, S.: The use of MOGREPS ensemble rainfall forecasts in operational flood forecasting systems across England and Wales, Adv. Geosci., 29, 77–84, https://doi.org/10.5194/adgeo-29-77-2011, 2011.
Schwanenberg, D., Fan, F. M., Naumann, S., Kuwajima, J. I., Montero, R. A., and Dos Reis, A. A.: Short-term reservoir optimization for flood mitigation under meteorological and hydrological forecast uncertainty, Water Resour. Manage., 29, 1635–1651, 2015.
Sharma, S., Siddique, R., Balderas, N., Fuentes, J. D., Reed, S., Ahnert, P., Shedd, R., Astifan, B., Cabrera, R., Laing, A., Klein, M., and Mejia, A.: Eastern U.S. Verification of Ensemble Precipitation Forecasts, Weather Forecast., 32, 117–139, 2017.
Shi, X., Andrew, W. W., and Dennis, P. L.: How essential is hydrologic model calibration to seasonal streamflow forecasting, J. Hydrometeorol., 9, 1350–1363, 2008.
Siddique, R. and Mejia, A.: Ensemble Streamflow Forecasting across the US Mid-Atlantic Region with a Distributed Hydrological Model Forced by GEFS Reforecasts, J. Hydrometeorol., 18, 1905–1928, 2017.
Siddique, R., Mejia, A., Brown, J., Reed, S., and Ahnert, P.: Verification of precipitation forecasts from two numerical weather prediction models in the Middle Atlantic Region of the USA: A precursory analysis to hydrologic forecasting, J. Hydrol., 529, 1390–1406, 2015.
Sloughter, J. M. L., Raftery, A. E., Gneiting, T., and Fraley, C.: Probabilistic quantitative precipitation forecasting using Bayesian model averaging, Mon. Weather Rev., 135, 3209–3220, 2007.
Smith, M. B., Koren, V., Reed, S., Zhang, Z., Zhang, Y., Moreda, F., Cui, Z., Mizukami, N., Anderson, E. A., and Cosgrove, B. A.: The distributed model intercomparison project – Phase 2: Motivation and design of the Oklahoma experiments, J. Hydrol., 418, 3–16, 2012a.
Smith, M. B., Koren, V., Zhang, Z., Zhang, Y., Reed, S. M., Cui, Z., Moreda, F., Cosgrove, B. A., Mizukami, N., and Anderson, E. A.: Results of the DMIP 2 Oklahoma experiments, J. Hydrol., 418, 17–48, 2012b.
Thiemig, V., Bisselink, B., Pappenberger, F., and Thielen, J.: A pan-African medium-range ensemble flood forecast system, Hydrol. Earth Syst. Sci., 19, 3365–3385, https://doi.org/10.5194/hess-19-3365-2015, 2015.
Thorstensen, A., Nguyen, P., Hsu, K., and Sorooshian, S.: Using Densely Distributed Soil Moisture Observations for Calibration of a Hydrologic Model, J. Hydrometeorol., 17, 571–590, 2016.
Verkade, J., Brown, J., Reggiani, P., and Weerts, A.: Post-processing ECMWF precipitation and temperature ensemble reforecasts for operational hydrologic forecasting at various spatial scales, J. Hydrol., 501, 73–91, 2013.
Wang, Q., Bennett, J. C., and Robertson, D. E.: Error reduction and representation in stages (ERRIS) in hydrological modelling for ensemble streamflow forecasting, Hydrol. Earth Syst. Sci., 20, 3561–3579, https://doi.org/10.5194/hess-20-3561-2016, 2016.
Ward, P. J., Jongman, B., Salamon, P., Simpson, A., Bates, P., De Groeve, T., Muis, S., De Perez, E. C., Rudari, R., and Trigg, M. A.: Usefulness and limitations of global flood risk models, Nat. Clim. Change, 5, 712–715, 2015.
Weerts, A. H., Winsemius, H. C., and Verkade, J. S.: Estimation of predictive hydrological uncertainty using quantile regression: examples from the National Flood Forecasting System (England and Wales), Hydrol. Earth Syst. Sci., 15, 255–265, https://doi.org/10.5194/hess-15-255-2011, 2011.
Wheater, H. S. and Gober, P.: Water security and the science agenda, Water Resour. Res., 51, 5406–5424, 2015.
Wilks, D. S.: Extending logistic regression to provide full-probability-distribution MOS forecasts, Meteorol. Appl., 16, 361–368, 2009.
Wilks, D. S.: Statistical methods in the atmospheric sciences, Academic Press, Diego, California, 2011.
Yang, X., Sharma, S., Siddique, R., Greybush, S. J., and Mejia, A.: Postprocessing of GEFS Precipitation Ensemble Reforecasts over the US Mid-Atlantic Region, Mon. Weather Rev., 145, 1641–1658, 2017.
Ye, A., Qingyun, D., Xing, Y., Eric, F. W., and John, S.: Hydrologic post-processing of MOPEX streamflow simulations, J. Hydrol., 508, 147–156, 2014.
Yuan, X. and Wood, E. F.: Downscaling precipitation or bias-correcting streamflow? Some implications for coupled general circulation model (CGCM)-based ensemble seasonal hydrologic forecast, Water Resour. Res., 48, W12519, https://doi.org/10.1029/2012WR012256, 2012.
Zalachori, I., Ramos, M.-H., Garçon, R., Mathevet, T., and Gailhard, J.: Statistical processing of forecasts for hydrological ensemble prediction: a comparative study of different bias correction strategies, Adv. Sci. Res., 8, 135–141, https://doi.org/10.5194/asr-8-135-2012, 2012.
Zappa, M., Rotach, M. W., Arpagaus, M., Dorninger, M., Hegg, C., Montani, A., Ranzi, R., Ament, F., Germann, U., and Grossi, G.: MAP D-PHASE: real-time demonstration of hydrological ensemble prediction systems, Atmos. Sci. Lett., 9, 80–87, 2008.
Zappa, M., Jaun, S., Germann, U., Walser, A., and Fundel, F.: Superposition of three sources of uncertainties in operational flood forecasting chains, Atmos. Res., 100, 246–262, 2011.
Zhao, L., Duan, Q., Schaake, J., Ye, A., and Xia, J.: A hydrologic post-processor for ensemble streamflow predictions, Adv. Geosci., 29, 51–59, https://doi.org/10.5194/adgeo-29-51-2011, 2011.