the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
HESS Opinions: Linking Darcy's equation to the linear reservoir
Hubert H. G. Savenije
In groundwater hydrology, two simple linear equations exist describing the relation between groundwater flow and the gradient driving it: Darcy's equation and the linear reservoir. Both equations are empirical and straightforward, but work at different scales: Darcy's equation at the laboratory scale and the linear reservoir at the watershed scale. Although at first sight they appear similar, it is not trivial to upscale Darcy's equation to the watershed scale without detailed knowledge of the structure or shape of the underlying aquifers. This paper shows that these two equations, combined by the water balance, are indeed identical provided there is equal resistance in space for water entering the subsurface network. This implies that groundwater systems make use of an efficient drainage network, a mostly invisible pattern that has evolved over geological timescales. This drainage network provides equally distributed resistance for water to access the system, connecting the active groundwater body to the stream, much like a leaf is organized to provide all stomata access to moisture at equal resistance. As a result, the timescale of the linear reservoir appears to be inversely proportional to Darcy's “conductance”, the proportionality being the product of the porosity and the resistance to entering the drainage network. The main question remaining is which physical law lies behind pattern formation in groundwater systems, evolving in a way that resistance to drainage is constant in space. But that is a fundamental question that is equally relevant for understanding the hydraulic properties of leaf veins in plants or of blood veins in animals.
One of the more fundamental questions in hydrology is how to explain system behaviour manifest at catchment scale from fundamental processes observed at laboratory scale. Although scaling issues occur in virtually all earth sciences, what distinguishes hydrology from related disciplines, such as hydraulics and atmospheric science, is that hydrology seeks to describe water flowing through a landscape that has unknown or difficult-to-observe structural characteristics. Unlike in river hydraulics or atmospheric circulation, where answers can be found in finer grid 3-D integration of equations describing fluid mechanics, in hydrology this cannot be done without knowing the properties of the medium through which the water flows. The subsurface is not only heterogeneous, it is also virtually impossible to observe. We may be able to observe its behaviour and maybe its properties, but not its exact structure. Groundwater is not a continuous homogeneous fluid flowing between well-defined boundaries (as in open channel hydraulics), but rather a fluid flowing through a medium with largely unknown properties. In other words, the boundary conditions of flow are uncertain or unknown. As a result, hydrological models need to rely on effective, often scale-dependent, parameters, which in most cases require calibration to allow an adequate representation of the catchment. These calibration efforts typically lead to considerable model uncertainty and, hence, to unreliable predictions.
But fortunately, there is good news as well. The structure of the medium through which the water flows is not random or arbitrary; it has predictable properties that have emerged by the interaction between the fluid and the substrate. Similar structures manifest themselves in the veins of vegetation, in infiltration patterns in the soil, and in drainage networks in river basins, emerging at a wide variety of spatial and temporal scales. Patterns in vegetation or preferential infiltration in a soil can appear at relatively short, i.e. human, timescales, but surface and subsurface drainage patterns, particularly groundwater drainage patterns, evolve at geological timescales. Under the influence of strong gradients, these patterns can evolve more quickly, but even in groundwater systems with relatively small hydraulic gradients “high permeability features” appear to be present, regulating spring flow (Swanson and Bahr, 2004).
There is a debate on the physical process causing pattern formation. Most scientists agree that it has something to do with the second law of thermodynamics, but what precisely drives pattern formation is still debated. Terms in use are maximum entropy production, maximum power, minimum energy expenditure (e.g. Rodriguez-Iturbe et al., 1992, 2011; Kleidon et al., 2013; Zehe et al., 2013; Westhoff et al., 2016), and the “constructal law” (Bejan, 2015). However, this paper is not about the process that creates patterns, but rather on using the fact that such patterns exist in groundwater systems to explore the connection between laboratory and catchment scale.
How to connect laboratory scale to system scale?
Dooge (1986) was one of the first to emphasize that hydrology behaves as a complex system with some form of organization. Hydrologists have been surprised that in very heterogeneous and complex landscapes a relatively simple empirical law, such as the linear reservoir, can manifest itself. Why is there simplicity in a highly complex and heterogeneous system such as a catchment?
The analogy with veins in leaves, or in the human body, immediately comes to mind. Watersheds and catchments look like leaves. In a leaf, due to some organizing principle, the stomata, which take CO2 from the air and combine it with water to produce hydrocarbons, require access to a supply network of water and access to a drainage network that transports the hydrocarbons to the plant. Such networks are similar to the arteries and veins in our body where oxygen-rich blood enters the cells, and oxygen-poor blood is returned. The property of veins and arteries is “obviously” that all stomata in the leaf, and cells in our body, have “equal” access to water or oxygen-rich blood and can evacuate the products and residuals, respectively. Having equal access to a source or to a drain implies experiencing the same resistance to the hydraulic gradient. If a human cell has too high a resistance to the pressure exercised by the heart, then it is likely to die off. Likewise, too low resistance could lead to cell failure or erosion. As a result, the network evolves to an optimal distribution of resistance to the hydraulic gradient.
In a similar way, drainage networks have developed on the land surface of the Earth. Images from space show a wide variety of networks, looking like fractals. Rodriguez-Iturbe and Rinaldo (2001) connected these patterns to minimum energy expenditure. Hergarten et al. (2014) used the concept of minimum energy dissipation to explain patterns in groundwater drainage. Kleidon et al. (2013), however, showed that such patterns are components of larger Earth system functioning at maximum power, whereby the drainage system indeed functions at minimum energy expenditure.
In general, we see that patterns emerge wherever a liquid flows through a medium, provided there is sufficient gradient to build or erode such patterns. Likewise, such patterns must be present in the substrate through which groundwater flows, although these are generally not considered in groundwater hydrology. If such patterns were absent, then the groundwater system would be the only natural body without patterns, which is not very likely.
This paper is an opinion paper. The author does not provide proof of concept. It is purely meant to open up a debate on how the linear drainage of an active groundwater body can be connected to Darcy's law. The discussion forum of this paper contains an active debate between the author, reviewers and commenters that provides more background.
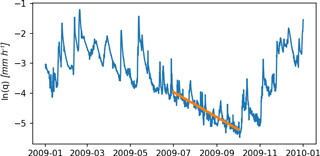
At catchment scale, the emergent behaviour of the groundwater system is the linear reservoir. Figure 1 shows a hydrograph of the Ourthe Occidentale in the Ardennes, which on a semi-log paper shows clear linear recession behaviour, overlain by short and fast rainfall responses by rapid subsurface flow, infiltration excess overland flow, or saturation overland flow. The faster processes are generally non-linear, but as the catchment dries out, the fast processes die out, the recharge to the groundwater system stops, and only the groundwater depletion remains. Even during depletion, short runoff events may superimpose the depletion process without additional recharge, in which case the depletion continues following a straight line on semi-logarithmic paper (see Fig. 1).
This behaviour is very common in first order streams, and even in higher order streams. In water resources management it is well know that recession curves of stream hydrographs can be described by exponential functions, which is congruent with the linear reservoir of groundwater depletion. It follows from the combination of the water balance with the linear reservoir concept. During the recession period there appears to be a disconnect between the root zone system that interacts with the atmosphere and the groundwater that drains towards the stream network. These two separate “water worlds” are well described by Brooks et al. (2010) and by McDonnell (2014) and are substantiated by different isotopic signatures. As a result, we see that during recession only the groundwater reservoir is active.
If during recession, the catchment is only draining from the groundwater stock, then the water balance can be described by
where Sg [L3] is the active groundwater storage and Qg [L3 T−1] is the discharge of groundwater to the stream network.
The linear reservoir concept assumes a direct proportionality between the active (i.e. dynamic) storage of groundwater and the groundwater flowing towards the drainage network:
where τ is the timescale of the drainage process, which is assumed to be constant. Combination with the water balance leads to
where Q0 is the discharge at t=0. So the exponential recession, which we observe at the outfall of natural catchments, is congruent with the linear reservoir concept. But how does this relate to Darcy's law, which applies at laboratory scale?
Darcy's law reads as follows:
where is the discharge per unit area, or filter velocity [L T−1]; k is the conductance [L T−1]; φ is the hydraulic head [L]; and x [L] is the distance along the stream line. In a drainage network, these streamlines generally form semi-circles, perpendicular to the lines of equipotential, draining almost vertically downward from the point of recharge and subsequently upward when seeping to the open drain (see Fig. 2 for a conceptual sketch).
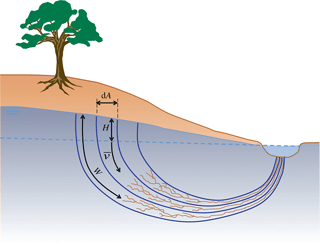
Figure 2Conceptual sketch of an unconfined phreatic groundwater body draining towards a surface drain. H is the head of the phreatic water table with respect to the nearest open water.
Henry Darcy (1803–1858) found this relationship under laboratory conditions, but the law also appears to work fine in regions with modest slopes, where one or more layers can be identified with conductivities representative for the sediment properties of these layers. In such relatively flat areas, upscaling from the laboratory scale to a region with well-defined layer structure appears to work rather well. This is clear from the many groundwater models, such as MODFLOW, that do well at representing hydraulic heads. However, such regional groundwater models are generally calibrated solely on water levels (hydraulic head) and seldom on flow velocities, transport of solutes, or flows, leading to equifinality in the determination of spatially variable k values.
Swanson and Bahr (2004) identified preferential flow even in mildly sloping terrain. Therefore it is reasonable to assume that under stronger gradients preferential flow becomes more prominent. In sloping areas, the hypothesis is that the subsurface is organized and cannot be assumed to consist of layers with relatively homogeneous properties. Under the influence of a stronger hydraulic gradient, drainage patterns occur in the substrate more or less following the hydraulic gradient along the streamlines. This happens everywhere in nature where water flows through an erodible or soluble material. An initial disturbance leads to the evolution of a drainage network that facilitates the transport of water through the erodible material. Initial disturbances can be cracks, sedimentation patterns, animal burrows, former root channels, etc. The formation of the network can be by physical erosion and deposition (breaking up, transporting, and settling particles) but can also be by chemical activity (minerals going into solution or precipitating). The latter is the dominant process in groundwater flow. The precipitation that enters the groundwater system through preferential infiltration (Brooks et al., 2009; McDonnell, 2014) is low in mineral composition and hence aggressive to the substrate. The minerals that we find in the stream during low flow (when the river is fed by groundwater) are the erosion products of the drainage network being developed. In the mineral composition of the stream we can see pattern formation at work and from the transport of chemicals by the stream we may derive the rate at which this happens.
In contrast to the physical drainage structures that we can see on the surface (e.g. river networks, seepage zones on beaches), sub-surface drainage structures are hard to observe. But they are there. On hillslopes, individual preferential sub-surface flow channels have been observed in trenches, but complete networks are hard to observe without destroying the entire network.
The hypothesis is that under the ground a drainage system evolves that facilitates the transport of water to the surface drainage network in the most efficient manner. As was demonstrated by Kleidon et al. (2013) an optimal drainage network maximizes the power of the sediment flux, which involves maximum dissipation in the part of the catchment where erosion takes place and minimum energy expenditure in the drainage network. This finding is in line with the findings of Rodríguez-Iturbe and Rinaldo (2001, p. 253), who found that minimum energy expenditure defines the structure of surface drainage. Although a surface drainage network has 2-D characteristics on a planar view, the groundwater system has a clear 3-D drainage structure. The boundary where open water and groundwater interact also has a complex shape. This is the boundary where the groundwater seeps out at atmospheric pressure, indicated in Fig. 2 by the dotted blue line. This boundary of interaction follows the stream network and moves up and down with the water level of the stream. To describe this 3-D drainage network conceptually, we can build on the analogy with a fractal-like (mostly 2-D) structure of a leaf or a river drainage network, but it is not the same.
Fractal networks can be described by width functions that determine the average distance of a point to the network. Let's call this distance W. Let's now picture a cross section over a catchment with an unconfined phreatic groundwater body draining towards an open water drain (see Fig. 2 for a conceptual sketch). At a certain infinitesimal area dA of the catchment, the drainage distance to the sub-surface network is W. The head difference to the nearest open drain is H. Darcy's equation then becomes
where rg [T] is the resistance against drainage. This way of expressing the resistance is similar to the aerodynamic resistance and the stomatal resistance of the Penman–Monteith equation. It is the resistance of the flux to a difference in head. So, instead of assuming a constant width to the drainage network, we assume a constant resistance to flow. This is in fact the purpose of veins in systems like leaves or body tissues, such as lungs or brains or muscles. The veins make sure that the resistance of liquids to reach stomata in the leaf, or cells in living tissue, is optimal and equal throughout the organ. But also in innate material, where gravity and erosive powers have been at work for millennia, the system is evolving towards an equally distributed resistance to drainage, much in line with the minimum expenditure theory of Rodriguez-Iturbe and Rinaldo (1997).
Building on Darcy's equation, an infinitesimal area dA of a catchment drains as follows:
Interestingly, this drainage (recharge to the groundwater) is downward, so that we can assume that dA lies in the horizontal plane. If we integrate the discharge over the area of the catchment that drains on the outfall, and assuming a constant resistance, we obtain
where n [–] is the average porosity of the active groundwater body (which is the groundwater body above the drainage level). We see that the areal integral of the head H equals the volume of saturated substrate above the level of the drain. Multiplied by the porosity, this volume equals the amount of groundwater stored above the drainage level, which equals the active storage of groundwater Sg. Comparison with the linear reservoir provides the following connection between the system timescale τ, the resistance rg, and the average porosity n:
As a result, we have been able to connect the timescale of the linear reservoir to the key properties of Darcy's equation, being the average porosity, the conductance and the distance to the sub-surface drainage structure, or better, to the average porosity and the resistance to drainage. This resistance to drainage is assumed to be constant in space, but will evolve over time, as the fractal structure expands. However, at a human timescale, this expansion may be considered to be so slow that the system can be assumed to be static.
In groundwater flow, connecting the laboratory scale to the system scale requires knowledge on the structure, shape, and composition of the medium that connects the recharge interface to the drain. Here we have assumed that, much like we see in a homogenous medium, the flow pattern follows streamlines perpendicular to the lines of equal head, forming semicircle-like streamlines. This implies that flow in the upper part of the streamlines is essentially vertical and that integration of Darcy's law over the cross section of a stream tube takes place in the horizontal plane, and not in a plain perpendicular to the gradient of the hillslope.
The second assumption is that, over time, patterns have evolved along these streamlines by erosion of the substrate. It is then shown that if the resistance to flow between the recharge interface and the drainage network is constant over the area of drainage, the linear reservoir equation follows from integration. This constant resistance to the hydraulic gradient is similar to what we see in leaves or body tissue.
What are the evolutionary dynamics of the drainage network? It is likely that the drainage network makes use of cracks and fissure present in the base rock, but subsequently expands and develops by minerals going into solution. As a result, these networks never stop developing, continuously refining and expanding the fractal structure. In relatively young catchments such structures may not be fully developed. By sampling the chemical contents of springs and base flow at the outfall of catchments, we may be able to determine the rate of growth of the drainage network, and – if the mineral content of the substrate is known – the origin of the erosion material. I think it is an interesting venue of research to study the expansion of such networks as a function of the mineral composition of the groundwater feeding the stream network, possibly supported by targeted use of unique tracers.
This paper does not provide an explanation for the fact that in recharge systems groundwater drains as a linear reservoir. In fact, it raises more fundamental questions: if a catchment has exponential recession, congruent with a linear reservoir, then what causes the resistance to entering the drainage network to be constant? What is the process of drainage pattern formation? If the sub-surface forms fractal-like structures, then which formation process lies behind it? The reason why this property evolves over time is still to be investigated, but it is likely that the reason should be sought, in some way or another, in the second law of thermodynamics.
We know from common practice that in mildly sloping areas, groundwater models that spatially integrate Darcy's equation are quite well capable of simulating piezometric heads. We also know that predicting the transport of pollutants in such systems is much less straightforward, requiring the assumption of dual porosities (which are in fact patterns). In more strongly sloping areas, such numerical models are much less efficient at describing groundwater flow. This can, of course, be blamed on the heterogeneity of the substrate, but one could also ask oneself the question of whether direct application of Darcy's law is the right approach at this scale. If under the stronger gradient of a hillslope preferential flow patterns have developed, then we should take the properties of these patterns into account. Fortunately, nature is kind and helpful. It has provided us with the linear reservoir that we can use as an alternative for a highly complex 3-D numerical model that has difficulty reflecting the dual porosity of patterns that we cannot observe directly, but of which we can see its simple signature: the linear reservoir with exponential recession. Hopefully groundwater modellers are going to make use of that property, particularly in larger scale modelling studies.
No data sets were used in this article.
The author declares that he has no conflict of interest.
The author would like to thank Wouter Berghuijs and Mark Cuthbert and the two
reviewers Stefan Hergarten and Axel Kleidon for the very interesting exchange
of opinions on the discussion forum that accompanied the publication of this paper
(https://www.hydrol-earth-syst-sci-discuss.net/hess-2017-580/).
Edited by: Erwin Zehe
Reviewed by: Axel Kleidon and Stefan Hergarten
Bejan, A.: Constructal law: optimization as design evolution, J. Heat Transf., 137, 061003, https://doi.org/10.1115/1.4029850, 2015.
Brooks, R., Barnard, R., Coulombe, R., and McDonnell, J. J.: Ecohydrologic separation of water between trees and streams in a Mediterranean climate, Nat. Geosci., 3, 100–104, https://doi.org/10.1038/NGEO722, 2010.
Dooge, J. C.: Looking for hydrologic laws, Water Resour. Res., 22, 46S–58S, 1986.
Hergarten, S., Winkler, G., and Birk, S.: Transferring the concept of minimum energy dissipation from river networks to subsurface flow patterns, Hydrol. Earth Syst. Sci., 18, 4277–4288, https://doi.org/10.5194/hess-18-4277-2014, 2014.
Kleidon, A., Zehe, E., Ehret, U., and Scherer, U.: Thermodynamics, maximum power, and the dynamics of preferential river flow structures at the continental scale, Hydrol. Earth Syst. Sci., 17, 225–251, https://doi.org/10.5194/hess-17-225-2013, 2013.
McDonnell, J. J.: The two water worlds hypothesis: ecohydrological separation of water between streams and trees?, WIREs, 1, 323–329, https://doi.org/10.1002/wat2.1027, 2014.
Rodríguez-Iturbe, I. and Rinaldo, A.: Fractal River Basins: Chance and Self-Organization, Cambridge University Press, Cambridge, UK, 2001.
Rodriguez-Iturbe, I., Rinaldo, A., Rigon, R., Bras, R. L., Ijjasz-Vasquez, E., and Marani, A.: Fractal structures as least energy patterns: the case of river networks, Geophys. Res. Lett., 19, 889–892, 1992.
Rodriguez-Iturbe, I., Caylor, K. K., and Rinaldo, A.: Metabolic principles of river basin organization, P. Natl. Acad. Sci. USA, 108, 11751–11755, 2011.
Swanson, S. K. and Bahr, J. M.: Analytical and numerical models to explain steady rates of spring flow, Ground Water, 42, 747–759, https://doi.org/10.1111/j.1745-6584.2004.tb02728.x, 2004.
Westhoff, M., Zehe, E., Archambeau, P., and Dewals, B.: Does the Budyko curve reflect a maximum-power state of hydrological systems? A backward analysis, Hydrol. Earth Syst. Sci., 20, 479–486, https://doi.org/10.5194/hess-20-479-2016, 2016.
Zehe, E., Ehret, U., Blume, T., Kleidon, A., Scherer, U., and Westhoff, M.: A thermodynamic approach to link self-organization, preferential flow and rainfall–runoff behaviour, Hydrol. Earth Syst. Sci., 17, 4297–4322, https://doi.org/10.5194/hess-17-4297-2013, 2013.