the Creative Commons Attribution 3.0 License.
the Creative Commons Attribution 3.0 License.
Responses of runoff to historical and future climate variability over China
Chuanhao Wu
Bill X. Hu
Guoru Huang
Peng Wang
Kai Xu
China has suffered some of the effects of global warming, and one of the potential implications of climate warming is the alteration of the temporal–spatial patterns of water resources. Based on the long-term (1960–2008) water budget data and climate projections from 28 global climate models (GCMs) of the Coupled Model Intercomparison Project Phase 5 (CMIP5), this study investigated the responses of runoff (R) to historical and future climate variability in China at both grid and catchment scales using the Budyko-based elasticity method. Results show that there is a large spatial variation in precipitation (P) elasticity (from 1.1 to 3.2) and potential evaporation (PET) elasticity (from −2.2 to −0.1) across China. The P elasticity is larger in north-eastern and western China than in southern China, while the opposite occurs for PET elasticity. The catchment properties' elasticity of R appears to have a strong non-linear relationship with the mean annual aridity index and tends to be more significant in more arid regions. For the period 1960–2008, the climate contribution to R ranges from −2.4 to 3.6 % yr−1 across China, with the negative contribution in north-eastern China and the positive contribution in western China and some parts of the south-west. The results of climate projections indicate that although there is large uncertainty involved in the 28 GCMs, most project a consistent change in P (or PET) in China at the annual scale. For the period 2071–2100, the mean annual P is projected to increase in most parts of China, especially the western regions, while the mean annual PET is projected to increase in all of China, particularly the southern regions. Furthermore, greater increases are projected for higher emission scenarios. Overall, due to climate change, the arid regions and humid regions of China are projected to become wetter and drier in the period 2071–2100, respectively (relative to the baseline 1971–2000).
Climate change has become increasingly significant (IPCC, 2013), and numerous studies have reported that climate warming is likely leading to the alteration of the hydrological cycle (Oki and Kanae, 2006; Jung et al., 2010). The dynamic properties of the hydrological cycle are governed by the interactions and feedbacks between atmospheric and land surface hydrologic processes on a catchment scale. The potential consequences of anthropogenic climate change on the hydrological cycle have received significant attention over the last 2 decades (Wang et al., 2012; IPCC, 2013).
Runoff (R), as a commonly adopted indicator of the hydrologic cycle, is critical to human lives and economic activities (Milly et al., 2005). There is a great deal of previous work exploring the impact of climate variations on R, with the motivation stemming from the region's vast resources (Christensen et al., 2004; Guo et al., 2009; Piao et al., 2010; Chen et al., 2012; Harding et al., 2012; Wang et al., 2012; Y. P. Xu et al., 2013), dangers of flooding (Kay et al., 2006, 2009, Kay and Jones, 2012; Raff et al., 2009; Liu et al., 2013; Xiao et al., 2013; Wang et al., 2013; Smith et al., 2014; Wu et al., 2014, 2015), and agricultural water uses (Vano et al., 2010). The most common practices in these previous studies are to use the hydrological models driven by the output from global climate models (GCMs) to simulate the hydrological process (e.g. R) under future climate change scenarios. However, the key issue faced by such studies is the need to convert coarse-resolution GCM outputs to local catchment-scale climatic variables at a higher spatial resolution to serve as the input to a hydrological model (Vano et al., 2015; Wu et al., 2015). The impact assessments are resource-intensive and usually subject to uncertainties related to the choice of hydrological model, GCMs, emissions scenarios, and downscaling techniques (Vano et al., 2014, 2015).
With the uncertainty in R due to climate change, simple tools able to provide robust estimates of this impact are essential to support policy and planning decisions. Climate elasticity, as an important indicator, provides a measure of sensitivity of the changes in R due to the changes in climate. Schaake (1990) made the first attempt to introduce the concept of elasticity and related the climate elasticity of R to precipitation (P). Since then numerous climate elasticity methods have been developed for evaluating the hydrologic response to climate change all over the world (Schaake, 1990; Dooge et al., 1999; Sankarasubramanian et al., 2001; Milly and Dunne, 2002; Fu et al., 2007; Zheng et al., 2009; Ma et al., 2010; Yang and Yang, 2011; Yang et al., 2014; Vano et al., 2015). Sankarasubramanian et al. (2001) provided a detailed category of climate elasticity methods for modelling climate change impacts. One of the most common methods is to analytically derive the sensitivity of R based on the Budyko hypothesis, due to its clear theory and the fact that it does not rely on a large amount of data (Yang and Yang, 2011). More importantly, the Budyko-based elasticity method can derive the climate elasticity and can also represent the impact of the catchment characteristics through the parameters of the Budyko model. Accordingly, it is widely applied for the assessment of the hydrologic impacts of climate change (Dooge et al., 1999; Zheng et al., 2009; Yang and Yang, 2011; Yang et al., 2014).
China is a vast land, spanning many degrees of latitude with complicated terrain, which results in a large regional variation in climate elasticity. The investigation of the P elasticity of R has been reported in many regions of China, such as the Miyun Reservoir basin (Ma et al., 2010), Luan River basin (X. Y. Xu et al., 2013), the headwater catchments of the Yellow River basin (Zheng et al., 2009), Poyang Lake basin (Sun et al., 2013), and Hai River and Yellow River basins (Yang and Yang, 2011; Liu and McVicar, 2012). Recently Yang et al. (2014) investigated the climate elasticity of R for the 210 catchments of China based on the Budyko-based elasticity approach. The results indicated that the P elasticity exhibits a large regional variation, with a small range in southern China, the Songhua River basin, and the north-west and a large range in the Hai River basin, the Yellow River basin, and the Liao River basin. Although the aforementioned studies have certainly made advances in understanding the climate elasticity of R in China, our knowledge about the responses of R to climate change over various temporal and spatial scales remains rather limited due to the large regional variation in climate types and catchment characteristics. The question of how climate change will affect R over China in the future is also an important problem to be addressed. Developing a more accurate and quantitative understanding of the changing water resources over various temporal and spatial scales under a changing environment is therefore a high priority for China.
Based on the unique long-term (1960–2008) land surface dataset of China and the climate projections from 28 GCMs of the Coupled Model Intercomparison Project Phase 5 (CMIP5), the objectives of this research are (1) to investigate the changes of R and climate variables and their relationship at an interannual scale; (2) to quantitatively estimate the climate elasticity and catchment properties' elasticity of R across China at both grid and catchment scales; and (3) to predict climate change and the changes in R due to future climate change for China from the CMIP5 projections at both grid and catchment scales.
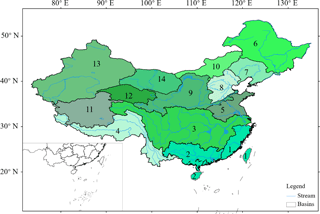
Figure 1Location of the main river basins in China. The numbers denote the river basins with increasing aridity index: (1) Southeast Drainage (0.52); (2) Pearl River (0.64); (3) Yangtze River (0.81); (4) Southwest Drainage (1.19); (5) Huaihe River (1.19); (6) Heilongjiang River (1.43); (7) Liaohe River (1.71); (8) Haihe River (2.14); (9) Yellow River (2.38); (10) Inner Mongolia River (4.41); (11) Qiangtang River (4.70); (12) Qinghai River (6.68); (13) Xinjiang River (8.09), (14) Hexi River (8.63). The numbers in the parentheses indicate the 1960–2008 mean aridity index.
2.1 Datasets
Monthly data of potential evaporation (PET) covering the period 1960–2008 over China are provided by the Terrestrial Hydrology Research Group of Princeton University (Sheffield et al., 2006, 2012). The PET is estimated by the Penman equation (Penman, 1948; Shuttleworth, 1993), using the updated meteorological dataset obtained from Sheffield et al. (2006, 2012). A long-term (1960–2008) daily land surface dataset over China, including P, surface runoff (RS), and baseflow (BS), with a 0.25∘ spatial resolution, was obtained from the Land Surface Processes and Global Change Research Group (Zhang et al., 2014). In this dataset, P is driven by interpolating gauged daily precipitation from 756 meteorological stations of the Chinese Meteorological Administration (CMA). RS and BS are derived from the Variable Infiltration Capacity (VIC) model forced by the gridded daily climate forcings (i.e. P, maximum and minimum temperature, and wind speed). VIC model parameters, including the infiltration shape parameter, the second and third soil layer depths, and the three parameters in the base flow scheme, were estimated by using an optimization algorithm of the multi-objective complex evolution of the University of Arizona (Zhang et al., 2014). The simulated monthly RS and BS match well with the observations at the large river basins in China (Zhang et al., 2014). Compared with the global product of a similar nature, this dataset provides a more reliable estimate of land surface variables over China (Nijssen et al., 2001; Adam et al., 2006; Rodell et al., 2004; Sheffield et al., 2006; Sheffield and Wood, 2007; Pan et al., 2012). In this study, the data of P, RS, and BS are initially regridded onto 0.5∘ grids over China using the linear interpolation method. All the daily data (P, RS, and BS) and monthly data (PET) are then aggregated temporally for the annual scale over China. The R was calculated by the sum of RS and BS for each of the 0.5∘ grid points.
Climate projections from 28 CMIP5 GCMs (as shown in Table 1) are provided by the Canadian Climate Data and Scenarios (CCDS, http://climate-scenarios.canada.ca/?page=main). These data, including simulations of surface air temperature (T), P, sea ice thickness, sea ice concentration, snow depth, and near-surface wind speed, are statistically downscaled and regridded onto a common 1∘ × 1∘ global grid by the CCDS. In this study, monthly P and monthly T over China, including one historical simulation for the period 1971–2000 and three emission scenarios (RCP2.6, RCP4.5, and RCP8.5) for the future period 2071–2100 from each of the 28 CMIP5 models and the multi-model ensemble of 28 CMIP5 models, are used for the projections of climate change. The data are initially disaggregated to 0.5∘ grids over China then corrected by using a “delta change” method (Wu and Huang, 2016), on the basis of the observed data of P and T as provided by the Climatic Research Unit (CRU) of the University of East Anglia (Harris et al., 2014).
Figure 2 shows the comparison of observed mean annual T and P and the corresponding simulations from 28 CMIP5 models before and after bias correction for the 14 basins in China. The basin number is consistent with that given in Fig. 1. As shown, the uncorrected model simulations tend to underestimate T and overestimate P for most of the basins, with more uncertainties for the simulation of P than for T. Compared to the uncorrected model results, the bias correction results represent large improvements and show a good agreement with the observed values for these basins. Therefore, the bias correction model simulations are acceptable for the investigation of climate change projections in this study.
As the GCM data used only consist of P and T, the PET of GCM is estimated by the Thornthwaite method (Thornthwaite, 1948) and then corrected by a multiplicative bias correction method as follows:
where PET and PET are bias-corrected annual PET and the PET calculated from the Thornthwaite method, respectively, for the ith grid point of the GCMs. and are the 49-year (1960–2008) averages of PET calculated from the Penman and Thornthwaite methods, respectively, for the ith grid point.
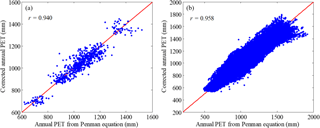
Based on the T data from the CRU, the Thornthwaite method is used to calculate PET to test the applicability of Eq. (1). Figure 3 shows a comparison of annual PET calculated from the Penman method and that from the Thornthwaite method corrected by Eq. (1) during the period 1960–2008. It is clear that the corrected PET agrees well with the PET from the Penman method, with the correlation coefficients of 0.94 and 0.958 at the catchment and grid scales, respectively. This suggests that Eq. (1) can be acceptable for the bias correction of PET in the GCMs.
Table 1CMIP5 GCMs used in this study. The GCM data were statistically downscaled and regridded onto a common 1∘ × 1∘ global grid from the Canadian Climate Data and Scenarios (CCDS).
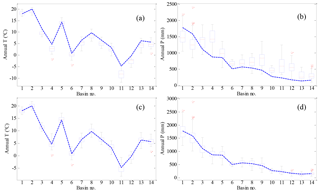
Figure 2Box plots of the simulation results of (a) mean annual T and (b) mean annual P and the bias correction results of (c) mean annual T and (d) mean annual P from 28 GCMs for the period 1971–2000 in the 14 river basins. The boxes denote the interquartile model spread (range between the 25th and 75th quantiles), with the horizontal line indicating the ensemble median and the whiskers showing the extreme range of the 28 CMIP5 model simulations. The blue dotted lines denote the observed results of mean annual T and mean annual P for the period 1971–2000. The basin number is consistent with that given in Fig. 1.
2.2 Sensitivity of runoff to climate and catchment properties
The Budyko framework has been widely used to study basin-scale water and energy balances. Two of the one-parameter formulations of the Budyko curve proposed by Choudhury (1999) (Eq. 2; see also Yang et al., 2008) and Fu (1981) (Eq. 3; see also Zhang et al., 2004) are expressed as
where n and ω are empirical parameters, representing the effects of other factors (e.g. land surface characteristics, the average slope, vegetation type or land use, and climate seasonality) on the water–energy balance (Yang et al., 2008, 2014; Roderick and Farquhar, 2011; D. Li et al., 2013). Yang et al. (2008) calibrated the parameters n and ω using long-term water balance data from 108 catchments from the non-humid regions of China and found that these two empirical parameters are linearly correlated.
Based on the Budyko hypothesis and assuming steady state conditions, Roderick and Farquhar (2011) and Yang and Yang (2011) derived the elasticity method to estimate the contribution to R from the changes in climate (represented by P and PET) and catchment properties as follows:
where εP, εPET, and εn represent the elasticity coefficients of P, PET, and catchment properties respectively and are expressed as
where , , and denote the first-order partial derivatives of the Budyko equation with respect to P, PET, and the parameter n. In this study, both Eqs. (2) and (3) are used for the estimation of the elasticity of P, PET, and catchment properties over China.
2.3 Trend estimate method
The Mann–Kendall (M–K) non-parametric test (Mann, 1945; Kendall, 1975) is an effective tool for detecting the statistical significance of trends in the time series of meteorological and hydrological variables (Yang et al., 2014; Wu and Huang, 2015). In this study, the M–K method is used to detect the significance of monotonic trends in hydroclimatic time series. The non-parametric trend slope estimator developed by Sen (1968) is used for the magnitude estimation of the trends in a hydroclimatic time series.
3.1 Interannual variability of climatic variables and runoff
The standard deviations for annual P, PET, and R are computed for each of the 0.5∘ grids in China, and the PET deviation ratio (σPET∕σP) and the R deviation ratio (σR∕σP) are calculated. The spatial distributions of PET deviation ratio and R deviation ratio across China are displayed in Fig. 4a and b. As shown, the PET deviation ratio is rather small in most parts of China, especially the southern regions, while a larger value is observed mainly in the Xinjiang region, where there are greater aridity indices. Generally, atmospheric water is enough to accommodate the limited PET in humid climates, which would lead to a limited response of PET to P variability. Specifically, the interannual variability of PET is more sensitive to that of P in arid climates (with water limits) than in humid climates (with energy limits). In contrast to the PET deviation ratio, the R deviation ratio tends to increase from arid climates to humid climates. The reason for this is that, in arid climates, the catchment water supply is very limited and gives priority to evaporation and soil storage capability, which leads to little variation in R.
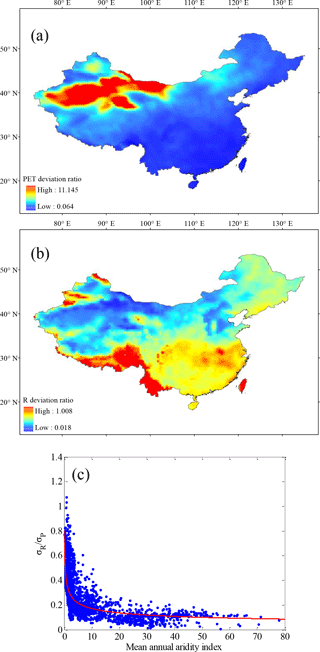
Figure 4Spatial distributions of (a) PET deviation ratio and (b) R deviation ratio and (c) the relationship between R deviation ratio and mean annual aridity index () for all 0.5∘ grid points in China.
Figure 4c shows the relationship between the R deviation ratio and mean annual aridity index () for all 0.5∘ grids in China. As indicated, is a major control for the R deviation ratio under not very dry conditions (e.g. < 10); that is, the R deviation ratio decreases with increased . However, under very dry conditions (e.g. > 10) the R deviation ratio becomes insensitive to , since in this case, other factors, such as soil storage capacity, can also have a large impact on the variation of R.
3.2 Sensitivity of runoff to climate and catchment properties
3.2.1 Climate elasticity
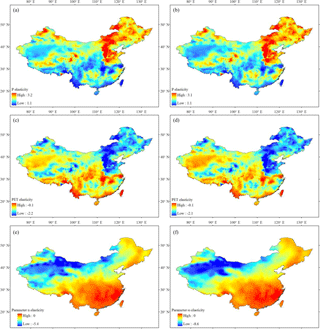
The P elasticity and PET elasticity of R based on Eqs. (2) and (3) are estimated at each of the 0.5∘ grids in China. As shown in Fig. 5, the spatial patterns of P elasticity and PET elasticity from Eqs. (2) and (3) are almost the same in all regions of China. There is a large spatial variation in P elasticity and PET elasticity, i.e. ranging from 1.1 to 3.2 and from −2.2 to −0.1 across China, respectively. In particular, P elasticity is more significant in the north-eastern and western areas than in southern China, which is in contrast to PET elasticity. Figure 6 shows the relationship between and climate (P and PET) elasticity. As shown, the P (PET) elasticity first increases (decreases) and then decreases (increases) with the increase of under not very dry conditions (i.e. < 10). However, when becomes large enough (e.g. > 10), both P and PET elasticity become insensitive to .
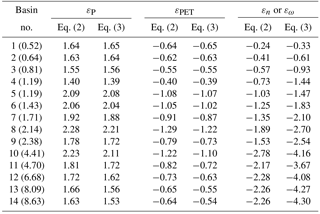
The climate elasticity estimated for each of the 14 large basins is shown in Table 2. The values of P elasticity are in the range of 1.39–2.28, with a larger (∼ smaller) elasticity in the Haihe River and Inner Mongolia River (Southwest Drainage). A similar phenomenon is found for PET elasticity, which suggests that Haihe River (Southwest Drainage) is the most (least) sensitive to PET among the 14 basins. Overall the values of P elasticity and PET elasticity derived by Eq. (2) are very close to those from Eq. (3), but the difference between them tends to be larger for dry basins with increasing aridity indices.
Table 2The estimations of P elasticity, PET elasticity, and catchment properties' elasticity of R in the 14 river basins of China based on Eqs. (2) and (3). The basin number is consistent with that given in Fig. 1. The numbers in the parentheses indicate the 1960–2008 mean aridity index.
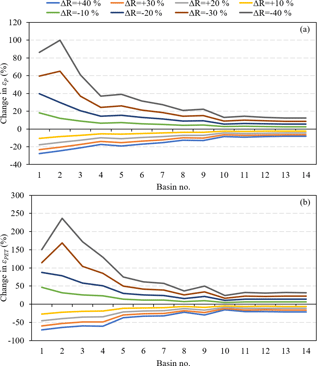
By using the estimates of climate elasticity derived by Eq. (2), the change in R as a function of the percentage change in P and PET is calculated for the 14 basins (Fig. 7). The R is positively related to P and negatively related to PET, and the magnitudes and patterns of the response of R to changes in P and PET vary on different scales. Generally, the R is more sensitive to climate in the Haihe River and Inner Mongolia River, while relatively weak sensitivity is found in the Southwest Drainage and Yangtze.
3.2.2 Catchment properties' elasticity
The spatial distributions of catchment properties' elasticity from Eqs. (2) and (3) are displayed in Fig. 5e and f. As shown, the catchment properties' elasticities for these two equations are rather similar across China, and the values of Eq. (3) are generally smaller than those from Eq. (2). Regarding the spatial pattern, the catchment properties' elasticity is very weak (approximately equal to 0) in southern China and some regions of north-eastern China, but it tends to be more significant in some water-limited regions of north-west China. Figure 6c shows the relationship between and the parameter elasticity for all 0.5∘ grids in China. It suggests that is a major control for catchment properties' elasticity across China; i.e. the catchment properties' elasticity would become stronger with increasing aridity indices. The catchment properties' elasticities estimated for the 14 large basins are shown in Table 2. The catchment properties' elasticity shows a large spatial variation, ranging from −2.78 to −0.24 for Eq. (2) and from −4.3 to −0.33 for Eq. (3). Overall, the changes in R are more sensitive to catchment properties in arid basins with larger aridity indices, which is consistent with the findings at the grid scale.
3.3 Climate change during 1960–2008
The annual trend magnitudes in P, R, PET, and aridity index during the period 1960–2008 are shown in Fig. 8a–d. As indicated, both P and R show an increasing trend mainly in the north-west and south-east regions and a decreasing trend mainly in the central region and the North China Plain. A significant increasing trend in PET is detected mainly in north-eastern China and eastern China, while the decreases mainly occur in most parts of western China. The aridity index tends to show an increasing trend in most parts of China, indicating an increasing risk of meteorological drought in these regions during the past several decades. In contrast, the decrease of aridity index is only found in some parts of western China.

Figure 6The relationship between mean annual aridity index and (a) P elasticity, (b) PET elasticity, and (c) parameter elasticity. The blue points represent the case of Eq. (2), and the red points represent the case of Eq. (3).
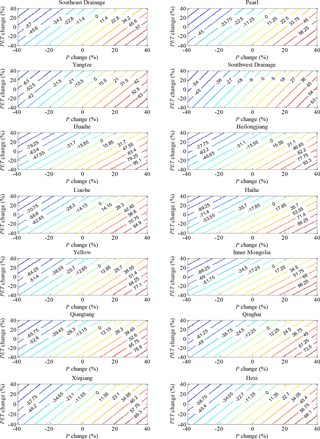
Figure 7Contour plot of percentage R change due to the changes in P and PET for the 14 river basins. The P elasticity and PET elasticity of R are estimated based on Eq. (2).
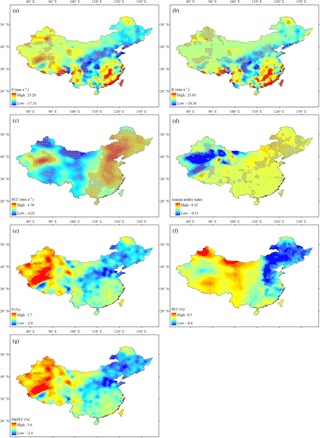
Figure 8Trend magnitudes in annual time series of (a) P, (b) R, (c) PET, and (d) aridity index for the period 1960–2008 and spatial distributions of the contributions (unit: % yr−1) of (e) P, (f) PET, and (g) climate (i.e. P and PET) to R in China for the period 1960–2008. The trend magnitudes are estimated by Sen's method. Grey dots are shown as statistically significant positive/negative trends (p < 0.05).
3.4 Changes in runoff due to climate change during 1960–2008
Using the estimates of climate elasticity from Eq. (2), the contributions of P, PET, and climate (i.e. P and PET) to R in China for the period 1960–2008 are calculated (as shown in Fig. 8e–g). A positive contribution (up to 3.7 % yr−1) from P to R is mainly recorded in western China, while a negative contribution is found mainly in north-eastern China and the North China Plain. Negative and positive contributions of PET to R mainly occur in north-eastern China and western China, respectively. The contribution of climate, i.e. the sum of the contributions from P and PET, ranges from −2.4 to 3.6 % yr−1 across China. The spatial pattern of climate is rather similar to that of P, showing a negative contribution in north-eastern China and a positive contribution in western China and some parts of the south-east. In particular, the largest positive contribution of climate occurs in the Tibetan Plateau. The contributions of P, PET, and climate (i.e. P and PET) to R in the 14 river basins for the period 1960–2008 are shown in Table 3. A positive contribution of P is detected in Southeast Drainage, Southwest Drainage, Qiangtang, Qinghai, Xinjiang and Hexi, while an opposite contribution is found in other basins. In contrast, a negative contribution of PET is found in most of the basins (except for Qiangtang and Hexi). In general, there is an increased R in Southeast Drainage, Southwest Drainage, Qiangtang, Qinghai, Xinjiang, and Hexi (from 0.06 to 1 % yr−1) and a decreased R in other basins (from −1.12 to −0.12 % yr−1).
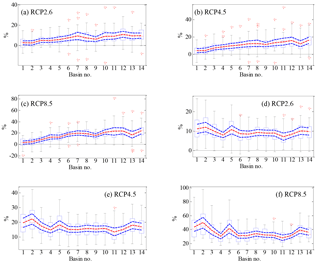
Figure 9Box plots of relative change (%) in mean annual P under (a) RCP2.6, (b) RCP4.5, and (c) RCP8.5 scenarios and in mean annual PET under (d) RCP2.6, (e) RCP4.5, and (f) RCP8.5 scenarios calculated from 28 CMIP5 models in 14 basins for the period 2071–2100 (relative to the baseline 1971–2000). The boxes denote the interquartile model spread (range between the 25th and 75th quantiles), with the horizontal line indicating the ensemble median and the whiskers showing the extreme range of the 28 CMIP5 model simulations. Red dotted lines denote the average values of the multi-model ensemble. Blue dotted lines denote the 95 % significance levels' range of the average values of the multi-model ensemble. The basin number is consistent with that given in Fig. 1.
3.5 Future climate change
Figure 9 shows the uncertainty range of the relative change in mean annual P and PET in the basins for the period 2071–2100 under the RCP2.6, RCP4.5, and RCP8.5 scenarios as predicted by 28 CMIP5 models (relative to the baseline 1971–2000). As shown, there is a large difference between different GCMs and emission scenarios, which highlights the uncertainty inherent in projections of climate change. However, overall P is projected to increase in most of the basins, and greater increases are projected for higher emission scenarios. Meanwhile, greater increases tend to be projected for more arid basins, suggesting a decreasing risk of meteorological drought in the future. The average changes (red dotted lines) of mean annual P for the 14 basins range from 2.4 to 11.0 % in RCP2.6, from 4.2 to 16.0 % in RCP4.5, and from 3.1 to 23.7 % in RCP8.5. The largest increase in the RCP2.6 and RCP8.5 scenarios is found for the Qinghai River, while the largest increase in the RCP4.5 scenario is projected for the Hexi River. For PET, there is an increase projected in all basins due to climate warming, with the largest and smallest increases in the RCP8.5 and RCP2.6 scenarios, respectively. However, a large uncertainty exists among the GCMs, which is similar to that for P. Furthermore, the uncertainty range tends to be larger with higher emission scenarios. The average changes (red dotted lines) of PET for the basins range from 7.0 to 12.0 % in RCP2.6, from 13.5 to 22.2 % in RCP4.5, and from 27.9 to 49.8 % in RCP8.5. The largest and smallest average increases are projected for the Pearl River and Qiangtang River, respectively.
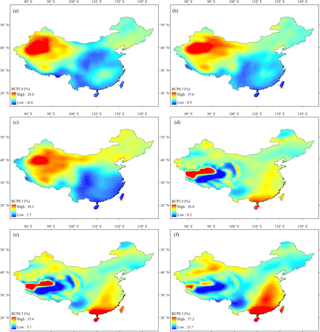
Figure 10The CMIP5 multi-model ensemble median relative change (%) in mean annual P under (a) RCP2.6, (b) RCP4.5, and (c) RCP8.5 scenarios and in mean annual PET under (d) RCP2.6, (e) RCP4.5, and (f) RCP8.5 scenarios in China for the period 2071–2100 (relative to the baseline 1971–2000).
Figure 10 displays the multi-model ensemble median relative change in mean annual P and PET in China for the period 2071–2100 (relative to the baseline 1971–2000). The projected changes in P (or PET) have a similar spatial pattern for the three emission scenarios; that is, P is projected to show an increase in western China and the north-east, and PET is projected to increase significantly in southern China and some parts of the Tibetan Plateau, especially for the RCP8.5 scenario. In addition, note that there are small changes in P and significant increases in PET projected for southern China. This would result in an increasing risk of meteorological drought in the future.
3.6 Future changes in runoff due to climate change
Based on the estimates of elasticity from Eq. (2), the percentage changes in the contributions of annual P and PET, as well as climate, to R from the 28 GCMs for the period 2071–2100 are calculated for each of the 14 basins (relative to the baseline 1971–2000). As shown in Fig. 11, the changes in P contribution mainly follow the changes in P itself (Fig. 9). A positive contribution from P is projected for most of the basins, and larger contributions occur in more arid basins, as well as in higher emission scenarios. Negative contributions of PET to R are projected for all basins due to the negative coefficients of PET elasticity. Smaller contributions of PET are mainly found in the Southwest Drainage. In contrast, larger contributions are projected mainly in the Huaihe River, Haihe River, and Inner Mongolia River, where the percentage decreases from the 28 models can be up to 25, 35, and 90 % in the RCP2.6, RCP4.5 and RCP8.5 scenarios, respectively.
Climate change is projected to reduce the R in some humid basins, such as the Southeast Drainage and Pearl River, where the average changes in the three emission scenarios range from −22.83 to −3.0 % and from −23.6 to −3.5 %, respectively (Fig. 11g–i). For other basins, particularly for arid basins, the R is projected to increase due to climate change. The largest average changes in R under the RCP2.6 and RCP4.5 scenarios are found in the Qinghai River (12.85 and 16.18 %, respectively). For the RCP8.5 scenario, they are found in the Qiangtang River (18.59 %). Note that there is an obvious decrease in R (−17.59 %) projected for the Huaihe River under the RCP8.5 scenario, which is mainly caused by the larger negative contribution of PET.
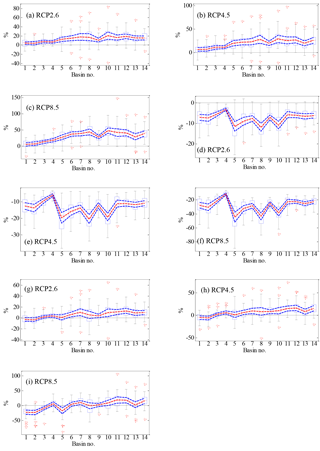
Figure 11Box plots of relative change (%) in the contributions of annual P to R under (a) RCP2.6, (b) RCP4.5, and (c) RCP8.5 scenarios, in the contributions of annual PET to R under (d) RCP2.6, (e) RCP4.5, and (f) RCP8.5 scenarios, and in the contributions of climate to R under (g) RCP2.6, (h) RCP4.5, and (i) RCP8.5 scenarios calculated from 28 CMIP5 models in 14 basins for the period 2071–2100 (relative to the baseline 1971–2000). The boxes denote the interquartile model spread (range between the 25th and 75th quantiles), with the horizontal line indicating the ensemble median and the whiskers showing the extreme range of the 28 CMIP5 model simulations. Red dotted lines denote the average values of the multi-model ensemble. Blue dotted lines denote the 95 % significance levels' range of the average values of the multi-model ensemble. The basin number is consistent with that given in Fig. 1.
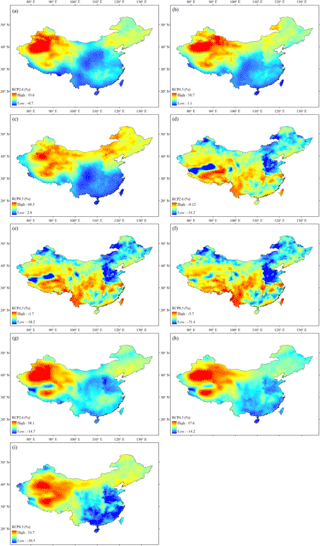
Figure 12The CMIP5 multi-model ensemble median relative change (%) in the contributions of annual P to R under (a) RCP2.6, (b) RCP4.5, and (c) RCP8.5 scenarios, in the contributions of annual PET to R under (d) RCP2.6, (e) RCP4.5, and (f) RCP8.5 scenarios, and in the contributions of climate to R under (g) RCP2.6, (h) RCP4.5, and (i) RCP8.5 scenarios in China for the period 2071–2100 (relative to the baseline 1971–2000).
Table 3The contributions of P, PET, and climate (i.e. P and PET) to R in the 14 basins of China for the period 1960–2008. The basin number is consistent with that given in Fig. 1. The numbers in the parentheses indicate the 1960–2008 mean aridity index.

Figure 12 shows the spatial distributions of the relative changes in the contributions of annual P and PET as well as climate to R in China for 2071–2100. This is based on the CMIP5 multi-model ensemble medians. Compared with the baseline 1971–2000, the increases in R due to the changes in P are projected in western China and some parts of northern China, and this phenomenon is particularly significant in the RCP8.5 scenario (up to 60.3 %). In contrast, the changes in PET are projected to reduce the R in all of China, with the larger decreases occurring mainly in the North China Plain, north-eastern China, and some parts of western China. Overall, climate change is projected to cause an obvious increase (decrease) of R in western China (southern China) under any emission scenario (Fig. 12g–i). This suggests that the arid regions (humid regions) in China will become wetter (drier) in the future.
4.1 The estimation of elasticity
The Budyko-based elasticity method is applied to quantify sensitivity of runoff to climate and catchment properties across China. Two Budyko models proposed by Choudhury (1999) and Fu (1981) are used for the comparison of the estimation of the climate elasticity of R. The results suggest that the climate elasticity is insensitive to the Budyko equations. The climate elasticity of R has been estimated in many regions of China. For example, the values of P elasticity are estimated as 2.4 for the Miyun Reservoir basin (Ma et al., 2010), 2.6 for the Luan River basin (X. Y. Xu et al., 2013), 2.1 for the headwater catchments of the Yellow River basin (Zheng et al., 2009), 1.4–1.7 for the Poyang Lake basin (Sun et al., 2013), 1.7–3.1 for the Hai River basin (Xu et al., 2014), 1.1–2.0 for southern China, the Songhua River basin, and the north-west, 2.1–4.8 for the Hai River basin, the Yellow River basin, and the Liao River basin (Yang et al., 2014), and 1.6–3.8 for the 63 catchments of China (Yang and Yang, 2011). In addition, the PET elasticity is estimated as −1.04 for the headwater catchments of the Yellow River basin (Zheng et al., 2009) and from −1 to −0.2 for the Poyang Lake basin (Sun et al., 2013). Those results are close to our results for P elasticity ranging from 1.1 to 3.2 and for PET elasticity ranging from −2.2 to −0.1 in China. It is worth noting that the values of P elasticity tend to be larger in the north-eastern and some parts of western China that are located in arid climates. This is in good agreement with the findings by Sankarasubramanian et al. (2001), which indicated that a larger P elasticity occurs in more arid regions. However, some parts of Xinjiang, which is more arid than southern China, have smaller P elasticity. Meanwhile, some parts of southern China, which is more humid than other regions in China, have larger P elasticity (Fig. 5). In addition, the Haihe River basin, located in a less arid climate than that of the north-west, shows the largest P elasticity in China (Table 2). A similar phenomenon is also introduced in Yang et al. (2014). One of the major reasons for this difference may be attributed to the impacts of human activities that alter the patterns of R in these regions. In addition, uncertainties in water budget data, such as the errors in the simulation of R and in the estimation of PET, may also contribute to this difference.
The comparisons for the estimates of εn and εω suggest that although the values of εn and εω are mainly dependent on the parameters of Budyko models, the spatial pattern of εn is consistent with that of εω at the 0.5∘ grid points over China (Fig. 5e and f). Yang et al. (2008) indicated that the parameters n and ω from Eqs. (2) and (3) are linearly correlated. We also conducted a regression analysis of εn and εω for all 0.5∘ grid points over China and found a strong linear correlation between εn and εω(εω = 1.7061εn + 0.0986, r2 = 0.96). In addition, our results show that R is more sensitive to catchment properties (εn and εω) in the more arid regions (Fig. 5e and f). The possible internal connection is that the arid regions with less vegetation coverage and stronger evaporation do not effectively hold the rainfall water that will be evaporated, leading to the smaller proportion of rainfall for R.
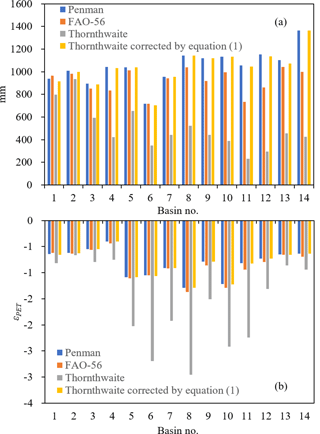
Figure 13(a) Mean annual PET calculated from the four methods for the 14 river basins of China during the period 1960–2008. (b) PET elasticity calculated from Eq. (2) based on the four PET data for the 14 river basins of China during the period 1960–2008. The basin number is consistent with that given in Fig. 1.
4.2 Sensitivity analysis for PET calculation methods
We compare four PET calculation methods, including the Penman method, the Thornthwaite method, the FAO-56 Penman–Monteith method (Allen et al., 1998), and the Thornthwaite method corrected by Eq. (1), to test the robustness of the PET elasticity result subject to PET uncertainties. In terms of mean annual PET as shown in Fig. 13a, the Thornthwaite method gives relatively low PET among the four methods, especially in arid basins (e.g. Qiangtang, Qinghai, Xinjiang, and Hexi). This is in agreement with previous studies, which indicated that the Thornthwaite method tends to underestimate PET in the arid areas (Hashemi and Habibian, 1979; Malek, 1987; Garcia et al., 2004). In contrast, the mean annual PET values from the other three methods are quite consistent, especially the Penman method and the Thornthwaite method corrected by Eq. (1). A similar result was also reported by Zeng and Cai (2016), which indicated that estimations of water balance at both annual and month scales are generally robust under various PET calculation methods (not including the Thornthwaite method). The PET elasticity calculations from the four different PET data for the 14 river basins are shown in Fig. 13b. The Thornthwaite method yields stronger PET elasticity than the other three methods in most of the basins, mainly due to the underestimation of PET. However, the other three methods give very similar results in all 14 basins. In summary, the estimation of PET elasticity is robust according to the PET calculations from the Penman method, the FAO-56 Penman–Monteith method, and the Thornthwaite method corrected by Eq. (1) but is not acceptable for the Thornthwaite method itself.
In general, the Thornthwaite method corrected by Eq. (1) significantly improves the accuracy of PET (Figs. 3 and 13a). However, it should be emphasized that the Thornthwaite method is an empirical equation that neglects the effects of atmospheric conditions, such as wind speed, humidity and radiation (McVicar et al., 2012). In addition, Eq. (1) used for the bias correction of PET is part of a delta method (Graham et al., 2007; Sperna Weiland et al., 2010), which only considers the average change but ignores the differences in the standard deviation and the coefficient of variation between the projection and baseline periods (Watanabe et al., 2012). Therefore, a more physically based PET calculation method (such as the Penman method) needs to be considered to fully understand the PET calculation uncertainties in the projections of climate change.
4.3 The projections of climate change and runoff
The hydrological impacts of climate change have been investigated in many regions of China, such as the Hanjiang basin (Chen et al., 2007; Guo et al., 2009), the catchment of the Loess Plateau (Wang et al., 2013), the Qingjiang River basin (Chen et al., 2012), the Qiantang River basin (Y. P. Xu et al., 2013), the Songhuajiang River basin (Su et al., 2015), the south-eastern Tibetan Plateau (F. Li et al., 2013), the Pearl River basin (Yan et al., 2015), the Xin River basin (Zhang et al., 2016), the subcatchments of the Yangtze and Yellow River basins (Xu et al., 2011), the Huang-Huai-Hai region (Lu et al., 2012), and 10 major river basins in China (Wang et al., 2012). There is a large uncertainty involved in these impact studies, which results in a large difference in climate projections. For example, Wang et al. (2012) indicated that the prevailing pattern of “north dry and south wet” in China will likely be exacerbated under future climate warming. However, the results of most GCMs in this study suggest that the arid regions and humid regions of China are projected to become wetter and drier in the future, respectively. The main difference between the two studies is the use of different climate models, emission scenarios, and time periods. This also demonstrates that the results of climate projections should be taken with caution, since the regional climate simulations (especially of precipitation) from the GCMs are still not robust at the present stage.
This study focuses on the hydrological change due to climate change (i.e. changes in P and PET), while the effects of the variability of catchment properties (e.g. land cover change, groundwater and river water extraction, urbanization, irrigation) on the hydrology are overlooked here. Most of the available GCMs lack key regional feedback processes involving land use, such as forest plantations, irrigation, and urbanization feedbacks that are critically important throughout China (Piao et al., 2010). The projected changes in catchment properties therefore need to be involved in the GCMs to account for their hydrological impacts. In addition, recent studies indicated that plant responses to increasing CO2 tend to keep more water on land, hence resulting in a greater increase in R (Milly and Dunne, 2016; Swann et al., 2016); that is to say, the hydrological models (e.g. VIC model), without the schemes of the plant stomatal responses to CO2, would lead to an underestimation of R under high CO2. Therefore, the implications of plants needing less water under high CO2 should be included in the assessment of hydrological impacts of climate change.
4.4 Uncertainties
Generally, a multitude of sources of uncertainty are involved in the impact assessment of climate change. In this study, uncertainty mainly comes from the GCMs, emission scenarios, the elasticity method, and the estimation error of the water budget data. To highlight the uncertainty from the GCMs, the 28 GCMs, as produced by different research institutes around the world, are used for the comparison of climate change projections. There is a large difference in the projections of P and PET among the 28 GCMs. In particular, the uncertainty range of P tends to be larger for more arid regions, while the uncertainty range of PET tends to be larger for more humid regions (Fig. 9). This highlights the impact of potential misleading conclusions if only one climate model were to be used for the impact assessments. The large uncertainty driven by the GCMs in relation to the hydrological impacts of climate change has been reported in many previous studies (Kay et al., 2009; Prudhomme and Davies, 2009; Chen et al., 2011; Teng et al., 2012; Liu et al., 2013; Wu et al., 2014, 2015). It is worth noting that although the projected ranges of P and PET show large variability in various GCMs, most project a consistent change (i.e. increase) in P and PET for the future period (Fig. 9). In contrast, the uncertainty from the emission scenarios is smaller than that from the GCMs, since the projected changes in P (or PET) show a similar pattern under all emission scenarios (Fig. 9). The main difference is that the projected changes tend to be more significant in higher emission scenarios.
The elasticity equation (i.e. Eq. 4) used in this study is driven from the linear approximation of the Budyko equation (Eqs. 2 and 3) by neglecting the higher order. Such approximation would possibly lead to uncertainty in the estimation of climate elasticity. Yang et al. (2014) indicated that the error in the estimation of elasticity tends to increase with increasing changes in P and PET, as well as the increased parameter of the Budyko equation. Future research is needed to quantify the effects of the errors on the estimation of elasticity under various climate conditions.
In addition to uncertainty in PET calculation (as discussed in Sect. 4.2), there are also uncertainties associated with the estimates of other water budget components, such as R. As shown in Fig. 14, the sensitivity of climate (i.e. P and PET) elasticity to R varies considerably between basins and tends to be larger in more humid basins. Moreover, PET elasticity is more sensitive to changes in R compared with P elasticity for all 14 basins. As indicated by Zhang et al. (2014), although the R is realistically estimated for most of the basins (especially for humid basins) in China with a small relative error, there is still a large relative error for few arid basins in western China due to the lack of meteorological observations. Therefore, the large errors in simulated R of the VIC model may result in large uncertainties in the elasticity calculation, particularly in western China. Also note that some other natural water sources, such as snow and glaciers, which may contribute to R, are overlooked in this study. Lute and Abatzoglou (2014) highlighted the importance of extreme snowfall events in shaping the interannual variability of the water balance. The melting of snow and glaciers is generally significant at a seasonal timescale in some high-altitude regions of China. Neglecting the effects of snow and glaciers would lead to a bias in the modelling of R for these regions.
In this study, the Budyko-based elasticity method was used to investigate the responses of runoff to historical and future climate variability over China at both grid and catchment scales. The climate and catchment properties' elasticities of runoff were estimated based on the long-term (1960–2008) land surface data from Zhang et al. (2014). Twenty-eight GCMs with three emission scenarios from the CMIP5 were collected for the projections of climate change and its contribution to runoff in China during the period 2071–2100. The uncertainties associated with the estimates of PET, R, and climate elasticity, as well as climate projections, are discussed in detail. The main findings are summarized as follows.
-
The interannual variability of PET is more sensitive to that of P in more arid regions, while the opposite occurs in the response of interannual variability of R to that of P. A large spatial variation exists in P elasticity (from 1.1 to 3.2) and PET elasticity (from −2.2 to −0.1) across China. The P elasticity is larger in north-eastern and western China than in southern China, which is opposite to that of PET elasticity. Among the 14 river basins, the Haihe River and Southwest Drainage have the largest and smallest climate elasticities, respectively. The catchment properties' elasticity of R is sensitive to mean annual aridity indices and tends to be stronger in more arid regions with increasing aridity indices.
-
For the period 1960–2008, the positive (negative) contributions from P to R are mainly found in western China (north-eastern China and the North China Plain), and the positive (negative) contributions of PET mainly occur in western China (north-eastern China). Overall, the climate contribution to R ranges from −2.4 to 3.6 % yr−1 across China during the period 1960–2008, with a negative contribution in north-eastern China and a positive contribution in western China and some parts of the south-west. The largest positive and negative contributions of climate occur in the Qiangtang and Haihe River basins, respectively.
-
There is a large uncertainty in climate projections among the 28 GCMs. Moreover, the uncertainty range of the P (PET) projection tends to be larger for more arid (humid) regions. However, most of the GCMs project a consistent change in annual P or annual PET. For the period 2071–2100, the P is projected to increase in most parts of China, especially the western regions, and the PET is projected to increase in all of China, particularly the southern regions. Furthermore, greater increases are projected for higher emission scenarios. Due to future climate warming, the arid regions and humid regions of China are projected to become wetter and drier in the period 2071–2100, respectively (relative to the baseline 1971–2000).
The results of this study (especially of the climate change projections) should be taken with caution, since uncertainties in the results exist because of several issues, including the different simulations of GCMs, the estimation error of climate elasticity, and the estimation error in the water budget components. A thorough investigation of the uncertainty involved in the hydrologic effects of climate change in China should be considered in future research.
The PET data are provided by the Terrestrial Hydrology Research Group of Princeton University (http://hydrology.princeton.edu/data.php; Sheffield et al., 2006, 2012). The land surface data over China, including P, RS, and BS, are provided by the Land Surface Processes and Global Change Research Group (http://hydro.igsnrr.ac.cn/resources.html; Zhang et al., 2014). The CMIP5 GCM data are obtained from the Canadian Climate Data and Scenarios (CCDS, http://climate-scenarios.canada.ca/?page=main).
The authors declare that they have no conflict of interest.
This research was supported by the Fundamental Research Funds for the
Central Universities (grant no. 21617301) and partly supported by funding
from the National Natural Science Foundation of China (grant no. 41530316)
and the National Key Research and Development Program of China (grant
no. 2016YFC0402805). We thank the editors and two reviewers for their valuable
comments that considerably helped to improve this paper.
Edited by: Jim Freer
Reviewed by: Simon Dadson and one anonymous referee
Adam, J. C., Clark, E. A., Lettenmaier, D. P., and Wood, E. F.: Correction of global precipitation products for orographic effects, J. Climate., 19, 15–38, 2006.
Allen, R., Pereira, L., Raes, D., and Smith, M.: Crop evapotranspiration – Guidelines for computing crop water requirements, FAO, Rome, 1998.
Chen, H., Guo, S. L., Xu, C. Y., and Singh, V. P.: Historical temporal trends of hydro-climatic variables and runoff response to climate variability and their relevance in water resource management in the Hanjiang basin, J. Hydrol., 344, 171–184, https://doi.org/10.1016/j.jhydrol.2007.06.034, 2007.
Chen, H., Xiang, T. T., Zhou, X., and Xu, C. Y.: Impacts of climate change on the Qingjiang watershed's runoff change trend in China, Stoch. Environ. Res. Risk A., 26, 847–858, https://doi.org/10.1007/s00477-011-0524-2, 2012.
Chen, J., Brissette, F. P., Poulin, A., and Leconte, R.: Overall uncertainty study of the hydrological impacts of climate change for a Canadian watershed, Water Resour. Res., 47, W12509, https://doi.org/10.1029/2011WR010602, 2011.
Choudhury, B. J.: Evaluation of an empirical equation for annual evaporation using field observations and results from a biophysical model, J. Hydrol., 216, 99–110, 1999.
Christensen, N. S., Wood, A. W., Voisin, N., Lettenmaier, D. P., and Palmer, R. N.: The effects of climate change on the hydrology and water resources of the Colorado River basin, Climatic Change, 62, 337–363, 2004.
Dooge, J. C., Bruen, M., and Parmentier, B.: A simple model for estimating the sensitivity of runoff to long-term changes in precipitation without a change in vegetation, Adv. Water Resour., 23, 153–163, 1999.
Fu, B. P.: On the calculation of the evaporation from land surface, Sci. Atmos. Sin., 5, 23–31, 1981.
Fu, G., Charles, S. P., and Chiew, F. H.: A two-parameter climate elasticity of streamflow index to assess climate change effects on annual streamflow, Water Resour. Res., 43, W11419, https://doi.org/10.1029/2007WR005890, 2007.
Garcia, M., Raes, D., Allen, R., and Herbas, C.: Dynamics of reference evapotranspiration in the Bolivian highlands (Altiplano), Agr. Forest Meteorol., 125, 67–82, 2004.
Graham, L. P., Andréasson, J., and Carlsson, B.: Assessing climate change impacts on hydrology from an ensemble of regional climate models, model scales and linking methods – A case study on the Lule River basin, Climatic Change, 81, 293–307, https://doi.org/10.1007/s10584-006-9215-2, 2007.
Guo S., Guo, J., Zhang, J., and Chen, H.: VIC distributed hydrological model to predict climate change impact in the Hanjiang basin, Sci. China Ser. E, 52, 3234–3239, 2009.
Harding, B. L., Wood, A. W., and Prairie, J. R.: The implications of climate change scenario selection for future streamflow projection in the Upper Colorado River Basin, Hydrol. Earth Syst. Sci., 16, 3989–4007, https://doi.org/10.5194/hess-16-3989-2012, 2012.
Harris, I., Jones, P. D., Osborna, T. J., and Lister, D. H.: Updated high-resolution grids of monthly climatic observations – the CRU TS3.10 Dataset, Int. J. Climatol., 34, 623–642, 2014.
Hashemi, F. and Habibian, M. T.: Limitations of temperature-based methods in estimating crop evapotranspiration in arid-zone agricultural projects, Agr. Forest Meteorol., 20, 237–247, 1979.
IPCC: Climate Change 2013: The Physical Science Basis, in: Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, UK and New York, NY, USA, 1535 pp., 2013.
Jung, M., Reichstein, M., Ciais, P., Seneviratne, S. I., Sheffield, J., Goulden, M. L., Bonan, G., Cescatti, A., Chen, J. Q., deJeu, R., Dolman, A. J., Eugster, W., Gerten, D., Gianelle, D., Gobron, N., Heinke, J., Kimball, J., Law, B. E., Montagnani, L., Mu, Q. Z., Mueller, B., Oleson, K., Papale, D., Richardson, A. D., Roupsard, O., Running, S., Tomelleri, E., Viovy, N., Weber, U., Williams, C., Wood, E., Zaehle, S., and Zhang, K.: Recent decline in the global land evapotranspiration trend due to limited moisture supply, Nature, 467, 951–954, 2010.
Kay, A. L. and Jones, D. A.: Transient changes in flood frequency and timing in Britain under potential projections of climate change, Int. J. Climatol., 32, 489–502, 2012.
Kay, A. L., Jones, R. G., and Reynard, N. S.: RCM rainfall for UK flood frequency estimation. II. Climate change results, J. Hydrol., 318, 163–172, https://doi.org/10.1016/j.jhydrol.2005.06.013, 2006.
Kay, A. L., Davies, H. N., Bell, V. A., and Jones, R. G.: Comparison of uncertainty sources for climate change impacts: flood frequency in England, Climatic Change, 92, 41–63, 2009.
Kendall, M. G.: Rank Correlation Methods, 4th Edn., Charles Grifin, London, 1975.
Li, D., Pan, M., Cong, Z., Zhang, L., and Wood, E.: Vegetation control on water and energy balance within the Budyko framework, Water Resour. Res., 49, 969–976, https://doi.org/10.1002/wrcr.20107, 2013.
Li, F., Zhang, Y., Xu, Z., Teng, J., Liu, C., Liu, W., and Mpelasoka, F.: The impact of climate change on runoff in the southeastern Tibetan Plateau, J. Hydrol., 505, 188–201, 2013.
Liu, L. L., Fischer, T., Jiang, T., and Luo, Y.: Comparison of uncertainties in projected flood frequency of the Zhujiang River, South China, Quatern. Int., 304, 51–61, 2013.
Liu, Q., and McVicar, T. R.: Assessing climate change induced modification of Penman potential evaporation and runoff sensitivity in a large water-limited basin, J. Hydrol., 464, 352–362, 2012.
Lu, G. H., Xiao, H., Wu, Z. Y., Zhang, S. L., and Li, Y.: Assessing the impacts of future climate change on hydrology in Huang-Huai-Hai region in China using the PRECIS and VIC models, J. Hydrol. Eng., 18, 1077–1087, 2012.
Lute, A. C. and Abatzoglou, J. T.: Role of extreme snowfall events in interannual variability of snowfall accumulation in the western United States, Water Resour. Res. 50, 2874–2888, 2014.
Ma, H. A., Yang, D. W., Tan, S. K., Gao, B., Hu, Q. F.: Impact of climate variability and human activity on streamflow decrease in the Miyun Reservoir catchment, J. Hydrol., 389, 317–324, 2010.
Malek, E.: Comparison of alternative methods for estimating ETP and evaluation of advection in the Bajah area, Iran, Agr. Forest Meteorol., 39, 185–192, 1987.
Mann, H. B.: Non-parametric tests against trend, Econometrica, 13, 245–259, 1945.
McVicar, T. R., Roderick, M. L., Donohue, R. J., Li, L. T., Van Niel, T. G., Thomas, A., Grieser, J., Jhajharia, D., Himri, Y., and Mahowald, N. M.: Global review and synthesis of trends in observed terrestrial near-surface wind speeds: implications for evaporation, J. Hydrol., 416–417, 182–205, 2012.
Milly, P. C. D. and Dunne, K. A.: Macroscale water fluxes, 2. Water and energy supply control of their interannual variability, Water Resour. Res., 38, 1206, https://doi.org/10.1029/2001WR000760, 2002.
Milly, P. C. D. and Dunne, K. A.: Potential Evapotranspiration and Continental Drying, Nat. Clim. Change, 6, 946–949, 2016.
Milly, P. C. D., Dunne, K. A., and Vecchia, A. V.: Global pattern of trends in streamflow and water availability in a changing climate, Nature, 438, 347–350, 2005.
Nijssen, B., Schnur, R., and Lettenmaier, D. P.: Global retrospective estimation of soil moisture using the Variable Infiltration Capacity land surface model, 1980–93, J. Climate, 14, 1790–1808, 2001.
Oki, T. and Kanae, S.: Global hydrological cycles and world water resources, Science, 313, 1068–1072, 2006.
Pan, M., Sahoo, A. K., Troy, T. J., Vinukollu, R. K., Sheffield, J., and Wood, E. F.: Multisource estimation of long-term terrestrial water budget for major global river basins, J. Climate, 25, 3191–3206, 2012.
Penman, H. L.: Natural evaporation from open water, bare soil and grass, P. Roy. Soc. Lond., 193, 120–145, 1948.
Piao, S., Ciais, P., Huang, Y., Shen, Z., Peng, S., Li, J., Zhou, L., Liu, H., Ma, Y., Ding, Y., Friedlingstein, P., Liu, C., Tan, K., Yu, Y., Zhang, T., and Fang, J.: The impacts of climate change on water resources and agriculture in China, Nature, 467, 43–51, 2010.
Prudhomme, C. and Davies, H. N.: Assessing uncertainties in climate change impact analyses on river flow regimes in the UK. Part 2: future climate, Climatic Change, 93, 197–222, 2009.
Raff, D. A., Pruitt, T., and Brekke, L. D.: A framework for assessing flood frequency based on climate projection information, Hydrol. Earth Syst. Sci., 13, 2119–2136, https://doi.org/10.5194/hess-13-2119-2009, 2009.
Rodell, M., Houser, P. R., Jambor, U., Gottschalck, J., Mitchell, K., Meng, C. J., Arsenault, K., Cosgrove, B., Radakovich, J., Bosilovich, M., Entin, J. K., Walker, J. P., Lohmann, D., and Toll, D.: The Global Land Data Assimilation System, B. Am. Meteorol. Soc., 85, 381–394, 2004.
Roderick, M. L. and Farquhar, G. D.: A simple framework for relating variations in runoff to variations in climatic conditions and catchment properties, Water Resour. Res., 47, W00G07, https://doi.org/10.1029/2010WR009826, 2011.
Roderick, M. L., Sun, F., Lim, W. H., and Farquhar, G. D.: A general framework for understanding the response of the water cycle to global warming over land and ocean, Hydrol. Earth Syst. Sci., 18, 1575–1589, https://doi.org/10.5194/hess-18-1575-2014, 2014.
Sankarasubramanian, A., Vogel, R. M., and Limbrunner, J. F.: Climate elasticity of streamflow in the United States, Water Resour. Res., 37, 1771–1781, 2001.
Schaake, J. C.: From climate to flow, in: Climate Change and U.S. Water Resources, edited by: Waggoner, P. E., John Wiley, New York, 177–206, 1990.
Sen, P. K.: Estimates of the regression coeffcient based on Kendall's tau, J. Am. Stat. Assoc., 63, 1379–1389, 1968.
Sheffield, J. and Wood, E. F.: Characteristics of global and regional drought, 1950–2000: Analysis of soil moisture data from off-line simulation of the terrestrial hydrologic cycle, J. Geophys. Res., 112, D17115, https://doi.org/10.1029/2006JD008288, 2007.
Sheffield, J., Goteti, G., and Wood, E. F.: Development of a 50-year high-resolution global dataset of meteorological forcings for land surface modeling, J. Climate, 19, 3088–3110, https://doi.org/10.1175/JCLI3790.1, 2006.
Sheffield, J., Wood, E. F., and Roderick, M. L.: Little change in global drought over the past 60 years, Nature, 491, 435–438, https://doi.org/10.1038/nature11575, 2012.
Shuttleworth, W. J.: Evaporation, in: Handbook of Hydrology, edited by: Maidment, D. R., McGraw-Hill, Sydney, 1993.
Smith, A., Bates, P., Freer, J., and Wetterhall, F.: Investigating the application of climate models in flood projection across the UK, Hydrol. Process., 28, 2810–2823, https://doi.org/10.1002/hyp.9815, 2014.
Sperna Weiland, F. C., van Beek, L. P. H., Kwadijk, J. C. J., and Bierkens, M. F. P.: The ability of a GCM-forced hydrological model to reproduce global discharge variability, Hydrol. Earth Syst. Sci., 14, 1595–1621, https://doi.org/10.5194/hess-14-1595-2010, 2010.
Su, B., Zeng, X., Zhai, J., Wang, Y., and Li, X.: Projected precipitation and streamflow under sres and rcp emission scenarios in the songhuajiang river basin, China, Quatern. Int., 380, 95–105, 2015.
Sun, S. L., Chen, H. S., Ju, W. M., Song, J., Zhang, H., Sun, J., and Fang, Y. J.: Effects of climate change on annual streamflow using climate elasticity in Poyang Lake Basin, China, Theor. Appl. Climatol., 112, 169–183, 2013.
Swann, A. L., Hoffman, F. M., Koven, C. D., and Randerson, J. T.: Plant responses to increasing CO2 reduce estimates of climate impacts on drought severity, P. Natl. Acad. Sci. USA, 113, 10019–10024, 2016.
Teng, J., Vaze, J., Chiew, F. H. S., Wang, B., and Perraud, J.: Estimating the Relative Uncertainties Sourced from GCMs and Hydrological Models in Modeling Climate Change Impact on Runoff, J. Hydrometeorol., 13, 122–139, 2012.
Thornthwaite, C. W.: An approach toward a rational classification of climate, Geogr. Rev., 38, 55–94, 1948.
Vano, J. A., Scott, M., Voisin, N., Stockle, C. O., Hamlet, A. F., Mickelson, K. E. B., Elsner, M. M., and Lettenmaier, D. P.: Climate change impacts on water management and irrigated agriculture in the Yakima River basin, Washington, USA, Climatic Change, 102, 287–317, https://doi.org/10.1007/s10584-010-9856-z, 2010.
Vano, J. A., Udall, B., Cayan, D. R., Overpeck, J. T., Brekke, L. D., Das, T., Hartmann, H. C., Hidalgo, H. G., Hoerling, M., McCabe, G. J., Morino, K., Webb, R. S., and Lettenmaier, D. P.: Understanding uncertainties in future Colorado River streamflow, B. Am. Meteorol. Soc., 95, 59–78, 2014.
Vano, J. A., Nijssen, B., and Lettenmaier, D. P.: Seasonal hydrologic responses to climate change in the Pacific Northwest, Water Resour. Res., 51, 1959–1976, 2015.
Wang, G. Q., Zhang, J. Y., Jin, J. L., Pagano, T. C., Calow, R., Bao, Z. X., Liu, C. S., Liu, Y. L., and Yan, X. L.: Assessing water resources in China using PRECIS projections and a VIC model, Hydrol. Earth Syst. Sci., 16, 231–240, https://doi.org/10.5194/hess-16-231-2012, 2012.
Wang, G. Q., Zhang, J. Y., Xuan, Y. Q., Liu, J. F., Jin, J. L., Bao, Z. X., He, R. M., Liu, C. S, Liu, Y. L., and Yan, X. L.: Simulating the impact of climate change on runoff in a typical river catchment of the Loess Plateau, China, J. Hydrometeorol., 14, 1553–1561, 2013.
Watanabe, S., Kanae, S., Seto, S., Yeh, P. J. F., Hirabayashi, Y., and Oki, T.: Intercomparison of bias-correction methods for monthly temperature and precipitation simulated by multiple climate models, J. Geophys. Res., 117, D23114, https://doi.org/10.1029/2012JD018192, 2012.
Wu, C. H. and Huang, G. R.: Changes in heavy precipitation and floods in the upstream of the Beijiang River basin, South China, Int. J. Climatol., 35, 2978–2992, 2015.
Wu, C. H. and Huang, G. R.: Projection of climate extremes in the Zhujiang River basin using a regional climate model, Int. J. Climatol., 36, 1184–1196, 2016.
Wu, C. H., Huang, G. R., Yu, H. J., Chen, Z. J., and Ma, J. G.: Impact of climate change on reservoir flood control in the upstream area of the Beijiang River Basin, South China, J. Hydrometeorol., 15, 2203–2218, https://doi.org/10.1175/JHM-D-13-0181.1, 2014.
Wu, C. H., Huang, G. R., and Yu, H. J.: Prediction of extreme floods based on CMIP5 climate models: a case study in the Beijiang River basin, South China, Hydrol. Earth Syst. Sci., 19, 1385–1399, https://doi.org/10.5194/hess-19-1385-2015, 2015.
Xiao, H., Lu, G. H., Wu, Z. Y., and Liu, Z. Y.: Flood response to climate change in the Pearl River basin for the next three decades, J. Hydraul. Eng., 12, 1409–1419, 2013.
Xu, H., Taylor, R. G., and Xu, Y.: Quantifying uncertainty in the impacts of climate change on river discharge in sub-catchments of the Yangtze and Yellow River Basins, China, Hydrol. Earth Syst. Sci., 15, 333–344, https://doi.org/10.5194/hess-15-333-2011, 2011.
Xu, X. Y., Yang, H. B., Yang, D. W., and Ma, H.: Assessing the impacts of climate variability and human activities on annual runoff in the Luan River basin, China, Hydrol. Res., 44, 940–952, 2013.
Xu, X. Y., Yang, D. W., Yang, H. B., and Lei, H. M.: Attribution analysis based on the Budyko Hypothesis for detecting the dominant cause of runoff decline in Haihe basin, J. Hydrol., 510, 530–540, 2014.
Xu, Y. P., Zhang, X., Ran, Q., and Tian, Y.: Impact of climate change on hydrology of upper reaches of Qiantang River Basin, East China, J. Hydrol., 483, 51–60, 2013.
Yan, D., Werners, S. E., Ludwig, F., and Huang, H. Q.: Hydrological response to climate change: The Pearl River, China under different RCP scenarios, J. Hydrol.: Reg. Stud., 4, 228–245, 2015.
Yang, H. and Yang, D.: Derivation of climate elasticity of runoff to assess the effects of climate change on annual runoff, Water Resour. Res., 47, W07526, https://doi.org/10.1029/2010WR009287, 2011.
Yang, H., Yang, D., Lei, Z., and Sun, F.: New analytical derivation of the mean annual water-energy balance equation, Water Resour. Res., 44, W03410, https://doi.org/10.1029/2007WR006135, 2008.
Yang, H., Qi, J., Xu, X., Yang, D., and Lv, H.: The regional variation in climate elasticity and climate contribution to runoff across China, J. Hydrol., 517, 607–616, 2014.
Zeng, R. and Cai, X.: Climatic and terrestrial storage control on evaporation temporal variability: Analysis of river basins around the world, Geophys. Res. Lett., 43, 185–195, https://doi.org/10.1002/2015GL066470, 2016.
Zhang, L., Hickel, K., Dawes, W. R., Chiew, F. H. S., Western, A. W., and Briggs, P. R.: A rational function approach for estimating mean annual evapotranspiration, Water Resour. Res., 40, W02502, https://doi.org/10.1029/2003WR002710, 2004.
Zhang, X., Tang, Q., Pan, M., Tang, Y.: A Long-Term Land Surface Hydrologic Fluxes and States Dataset for China, J. Hydrometeorol., 15, 2067–2084, https://doi.org/10.1175/JHM-D-13-0170.1, 2014.
Zhang, Y., You, Q., Chen, C., and Ge, J.: Impacts of climate change on streamflows under RCP scenarios: A case study in Xin River Basin, China, Atmos. Res., 178, 521–534, 2016.
Zheng, H., Zhang, L., Zhu, R., Liu, C., Sato, Y., and Fukushima, Y.: Responses of streamflow to climate and land surface change in the headwaters of the Yellow River Basin, Water Resour. Res., 45, W00A19, https://doi.org/10.1029/2007WR006665, 2009.