the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A new method, with application, for analysis of the impacts on flood risk of widely distributed enhanced hillslope storage
Peter Metcalfe
Barry Hankin
Enhanced hillslope storage is utilised in “natural” flood management in order to retain overland storm run-off and to reduce connectivity between fast surface flow pathways and the channel. Examples include excavated ponds, deepened or bunded accumulation areas, and gullies and ephemeral channels blocked with wooden barriers or debris dams.
The performance of large, distributed networks of such measures is poorly understood. Extensive schemes can potentially retain large quantities of run-off, but there are indications that much of their effectiveness can be attributed to desynchronisation of sub-catchment flood waves. Inappropriately sited measures may therefore increase, rather than mitigate, flood risk. Fully distributed hydrodynamic models have been applied in limited studies but introduce significant computational complexity. The longer run times of such models also restrict their use for uncertainty estimation or evaluation of the many potential configurations and storm sequences that may influence the timings and magnitudes of flood waves.
Here a simplified overland flow-routing module and semi-distributed representation of enhanced hillslope storage is developed. It is applied to the headwaters of a large rural catchment in Cumbria, UK, where the use of an extensive network of storage features is proposed as a flood mitigation strategy. The models were run within a Monte Carlo framework against data for a 2-month period of extreme flood events that caused significant damage in areas downstream. Acceptable realisations and likelihood weightings were identified using the GLUE uncertainty estimation framework. Behavioural realisations were rerun against the catchment model modified with the addition of the hillslope storage. Three different drainage rate parameters were applied across the network of hillslope storage.
The study demonstrates that schemes comprising widely distributed hillslope storage can be modelled effectively within such a reduced complexity framework. It shows the importance of drainage rates from storage features while operating through a sequence of events. We discuss limitations in the simplified representation of overland flow-routing and representation and storage, and how this could be improved using experimental evidence. We suggest ways in which features could be grouped more strategically and thus improve the performance of such schemes.
A catchment-based approach to flood risk management is becoming widely adopted (Werritty, 2006; Dadson et al., 2017). Its principle is that storm run-off can be managed most effectively with a combination of catchment-scale measures and downstream flood defences (Lane, 2017). An example of this approach, often referred to as natural flood management (NFM) or working with natural processes (WWNP: EA, 2014; Hankin et al., 2017), utilises soft-engineered structures and interventions that both utilise and enhance the natural processes within the catchment in order to provide flood resilience (Calder and Alywood, 2006; SEPA, 2016; Lane, 2017). It is argued that NFM is a low-cost, scalable approach that, in addition to improved flood resilience, can yield considerable benefits in terms of stakeholder engagement (Lane et al., 2011) and improved ecosystem services (Iacob et al., 2014).
A wide range of interventions are employed in NFM. These are reviewed by, amongst others, Quinn et al. (2013), EA (2014), SEPA (2016), Dadson et al. (2017) and Lane (2017). Many of these are intended to increase the capacity of hillslopes to retain fast overland run-off and release it slowly, thus reducing its contribution to the rising limb of the storm hydrograph. Measures to achieve this encompass excavated ponds, deepened or bunded existing hollows, or wooden barriers or debris dams in ephemeral channels.
The term run-off attenuation feature (RAF) has been used to refer to any structure to retain storm run-off, whether in channel (online) or on the hillslope (offline) (e.g. Barber and Quinn, 2012; Nicholson et al., 2012; Quinn et al., 2013). Here the term “enhanced hillslope storage” (EHS) is used to disambiguate online and offline approaches and will relate to any measure intended to increase the capacity of the hillslopes to retain storm run-off. EHS was implemented in the Belford Burn catchment as wooden structures and earth bunds placed across overland flow pathways identified from topographic analysis (Nicholson et al., 2012; Wilkinson et al., 2010a). In Vale of Pickering, North Yorkshire (Nisbet et al., 2011); Pontbren (Wheater et al., 2008; Nisbet and Page, 2016); and Holnicote, Devon (National Trust, 2015), blocking of moorland gullies added storage to upper parts of the catchments.
Despite the increasing use of EHS, there have been relatively few attempts to model its effects on the storm response at a catchment scale, and to quantify the requirements of a scheme to meet a certain level of flood risk mitigation. The expectation is currently that NFM will have an impact on small- to moderate-scale events. However, to be a practical strategy, it will be required to operate effectively across extreme events, but there is as yet little evidence of what will be required to have an effective impact in these conditions.
Ghimire et al. (2014) applied a fully distributed hydrodynamic model (TUFLOW) to simulate a potential single hillslope pond of capacity 27 000 m3 within the 74 km2 Tarland Burn catchment in Aberdeenshire. This showed that the intervention could reduce peak flows by 9 % for an event of the scale of the median annual flood (known as QMED). Using the fully distributed JFLOW model (Lamb et al., 2009; Environment Agency, 2013), Hankin et al. (2016, 2017) simulated the effects of multiple hillslope ponds across three catchments in Cumbria. This showed the relative impacts on the hydrograph, in terms of downstream benefits or damages avoided. The model was driven by multiple rainfall event sets incorporating spatial joint probabilities observed in the extremes from time series of observed rainfalls around the catchment (Lamb et al., 2010; Keef et al., 2013). Nicholson et al. (2012) and Wilkinson et al. (2010b) used a lumped representation in the Belford Burn catchment, whereby the storage requirement of the scheme was estimated from the reduction required to prevent damage in the hydrograph of the smallest storm that caused flooding. This indicated that 20 000 m3 of additional storage would have sufficed to prevent damage. However, the interactions of storage and the complex routing of flood waves may mean that the theoretical static storage of a scheme could be substantially underutilised, even during large events (Metcalfe et al., 2017).
The capacity of individual storage features is in the UK constrained by legislation that limits their size to 10 000 m3, above which significant legal responsibilities are imposed (Wilkinson et al., 2010b; Ghimire et al., 2014). Ghimire (2014) suggested that a network of ponds just under the critical capacity could be used to replace the single large pond first modelled. Analysis of the effects of just one of these 9500 m3 ponds indicated that it could reduce the peak of the QMED event by 2.5 %. A pond of 5200 m3 would reduce the peak of the same storm by 1 %. The storage required for a significant mitigating effect on storm flows is much greater, however. Metcalfe et al. (2017) showed that within a 29 km2 catchment, 168 000 m3 of hydrodynamic storage provided by a single large in-channel feature in the middle reaches would just have prevented flooding in a 1-in-75-year event. A scheme of a realistic scale could therefore involve installation of extremely large numbers of features on the hillslope, although the quantity required might be reduced by applying other measures such as tree-planting and online interventions.
Representing such extensive schemes within computer models will be challenging. Physically based models in general employ a gridded digital terrain model (DTM) to represent the surface. Features can be introduced into the landscape representation by raising cells on their boundary to represent wooden walls or bunds. For example, Hankin et al. (2016, 2017) simulated hillslope ponds by deepening the appropriate cells in a 2 m DTM by 1 m. This was also the approach of Ghimire et al. (2014), this time using a 5 m DTM. Hydraulic models of individual structures could be achieved by applying analogies to engineered interventions whose characteristics are understood. Metcalfe et al. (2017) modelled the effects of the wooden channel barriers by analogy with underflow sluices employed in irrigation schemes. Chow (1959) describes analytical storage–discharge relationships for such structures that utilise empirically determined parameters. Dams constructed of spaced timber members could be modelled by the Kirschmer–Mosonyi formula for flow through trash screens (Mosonyi, 1966), such as those used in the intakes to power plants and waste-water treatment works. Overflow of these structures that run out of capacity during the course of a storm event could be modelled analytically as though across a weir, another well-studied structure.
Drainage from structures to retain run-off can be by infiltration, direct evaporation from the water surface, or through permeable or “leaky” walls. It will, however, be difficult in the models mentioned to account dynamically for the drainage pathways out of large numbers of hillslope storage features. Areas will be unable to drain down during the course of a simulation, and thus the modelling approach will have limitations when applied to multiple storm events. In these cases, recovery of storage capacity during recession periods could have a significant impact on the effectiveness of a scheme through multiple events (Metcalfe et al., 2017).
Much of the effectiveness of natural and distributed flood management schemes has been attributed to their ability to desynchronise sub-catchment flood waves (Thomas and Nisbet, 2007; Blanc et al., 2012). Pattison et al. (2014) examined the interacting effects of the Eden sub-catchment flood waves using data for a large flood event in Carlisle in 2005, and concluded that their timing and magnitude predicted the majority of the variance in modelled downstream flood peaks. It will therefore be necessary to design such installations with some care. Slowing run-off that would have contributed to the hydrograph before the peak could have the effect of increasing the peak magnitude. This is called the synchronicity problem.
Peak timings vary, however, with the pattern and timing of rainfall and antecedent wetness in the catchment, and also in the way in which the hydrographs from different sub-catchments interact. Thus, it will be necessary to test the sensitivity of a design before implementation by using an appropriate model of run-off generation and mitigation measures. This might, in itself, require many model runs that reflect different event characteristics and patterns, as well as storage and drainage characteristics of features. Given the immense number of combinations of potential configurations and varieties of storm events, a pragmatic approach to evaluating the impacts of NFM would be “experimental” modelling, whereby many possible realisations of the catchment model and event sets are generated (Hankin et al., 2016, 2017). A computationally efficient run-off model and representation of hillslope storage would allow such an approach in reasonable timescales. This will necessarily involve some simplification of the hydraulic behaviour, as a fully hydrodynamic treatment will introduce complexity, additional parameters and much increased run times.
There is significant uncertainty in predictions of the spatial distribution and quantities of run-off (Beven, 2006, 2012). Attempts to assess the effectiveness of NFM will compare predictions for unaltered and modified catchments and introduce even further uncertainty. Uncertainty estimation and sensitivity analysis can provide a more realistic assessment of the reliability of predictions of the impacts of NFM (Hankin et al., 2017). These techniques will, however, also require the generation of thousands or even millions of model realisations in which parameters are sampled from prior distributions of realistic values. With continued growth in computing power it is now feasible to run the fully distributed JFLOW model over 750 km2 with a 2 m resolution grid (e.g. 175 million cells) in approximately real-time (Hankin et al., 2017). This will still require a significant commitment in time and computing power to produce more than a few scores of realisations. Thus, while high-performance computing may be fast enough for assessment for a selection of features and hillslope properties, it may still be inadequate for uncertainty analysis across larger catchments and wide-scale NFM schemes comprising the large number of features required to meet the storage requirements to significantly attenuate real flood events.
In 2016 the Life IP Natural Course project was undertaken by Lancaster University and JBA Consulting for the UK Rivers Trust. Its aim was provide better understanding of how NFM could be applied strategically to the headwaters of three catchments in Cumbria, UK (Hankin et al., 2016, 2017). Measures considered included large-scale tree-planting in order to increase evaporation losses and improve soil structure, and restoration of peat and heath to increase surface roughness. Measures to provide enhanced hillslope storage were also considered. The interventions were modelled separately, allowing the effects of each to be discerned.
Given the uncertainties in both predictions of storm run-off and the impacts of NFM, a key objective of this project was to develop an approach that could allow the modelling results to be presented to the client alongside realistic estimates of their uncertainty. This required a model that could simulate the storm run-off with sufficient computational efficiency to generate the thousands of runs required for uncertainty analysis.
Previous work has shown the importance of the drainage characteristics of features that retain run-off whilst operating across a series of closely spaced events (Metcalfe et al., 2017), as a degree of “leakiness” is required to allow the scheme to recover capacity between events. Another objective was therefore to develop an approach that could reflect drainage from “leaky” EHS and could be applied to the thousands of features required, but again without excessive computational cost. A period of three significant storms in November and December 2015, in which the catchments were badly affected, was chosen as the basis for the study. This paper documents the modelling approach that was developed and describes how it was applied in the largest of these catchments, the 223 km2 Upper Eden.
2.1 Run-off modelling
A new implementation of the semi-distributed Dynamic TOPMODEL (Metcalfe et al., 2015) was employed to predict storm run-off in both unaltered catchments models and those with the addition of hillslope storage. The original version (Beven and Freer, 2001a) has been applied in many studies (e.g. Liu et al., 2009; Page et al., 2007). In conjunction with a spatially explicit hydraulic channel routing module, the later implementation was used to evaluate the effect on flood risk of an NFM-style scheme in an agricultural catchment in North Yorkshire, UK (Metcalfe et al., 2017).
The model extends TOPMODEL (Beven and Kirkby, 1979). The basic approach in both models is the aggregation of “similar” landscape areas into hydrological response units (HRUs), which are treated during the course of a simulation as having identical hydrological responses. The units may be of arbitrary size and not necessarily spatially contiguous, although they, along with their internal states, can be mapped back into space. This “discretisation” approach significantly reduces the complexity of the landscape model whilst retaining hydrological connectivity of the hillslope. The model can therefore be run extremely quickly, and this approach therefore helped meet the objective of the LifeIP project to evaluate NFM impacts within an uncertainty framework.
In TOPMODEL the catchment classification is strictly according to the topographic wetness index (TWI), a measure of the tendency of a point on the hillslope to become saturated. An improved subsurface routing algorithm introduced in Dynamic TOPMODEL allows a more flexible approach to aggregation of catchment areas, and any characteristic or combination of characteristics may be used to identify a HRU. A routing matrix is developed from the surface topography, taken as an approximation to the hydraulic gradient, and applied to route subsurface run-off downslope through the units, with a kinematic wave relationship between specific discharge and storage deficit.
Model parameters are shown in Table 1.
Once a HRU discretisation has been defined the model can be run against rainfall and potential evapotranspiration (Ep) data for a specified time period. For that period, it produces a time series of simulated discharges at the catchment outlet and of the internal states of the HRUs. These include storage deficit, saturation excess (surface) and root zone storage. In order to reflect spatial variability, distinct rainfall and/or Ep records may be applied to the HRUs.
2.2 Overland flow-routing
Hunter et al. (2007) suggest that in some situations simplified, but physically based, surface flow models can perform as well as fully hydrodynamic formulations. In TOPMODEL and the first version of Dynamic TOPMODEL (Beven and Freer, 2001a) a network width approach was taken to routing surface flow (see Beven, 2012). In the implementation described by Metcalfe et al. (2015) semi-distributed, storage-based surface flow-routing was introduced. This uses a routing scheme similar to that applied to the subsurface. Saturation excess from upslope HRUs is routed to downslope units by a surface flow distribution matrix Wof, again derived from the surface topography:
Each row in this matrix gives the proportions of the corresponding unit's flow that is directed to other units. For example, pij is the proportion of unit i's flow that is directed to unit j, and pii is the proportion that remains within unit i. The vector r represents a lumped “river” unit such that rj is the proportion of downslope flux entering the channel network from unit number j. With an extended matrix a multi-reach river unit can also be defined. The matrix approximates transfer of flux between the different landscape units, and thence into the channel unit(s), by averaging the inter-cell slopes of the elevation raster between cells falling into each of the HRU categories.
An assumption of a linear storage–discharge relationship is now made, whereby the downslope discharge overland through a unit contour within a unit is proportional to depth of flow, i.e. specific surface excess storage s (m). This implies a uniform velocity profile, so that the specific discharge is qout = vofs, with vof (m h−1) the mean overland wave velocity within that unit. It can be shown (Metcalfe et al., 2015) that this leads to a coupled series of ordinary differential equations for the specific surface storages s across all of the HRUs:
where A and V are diagonal matrices whose leading elements are, respectively, the areas and the mean overland flow velocities. This system can be solved analytically by the so-called eigenvalue method (Dummit, 2016). During a simulation storage distributed downslope is calculated to the end of the time interval, and any directed to the channel is routed to the outlet using the network width approach. Surface excess storages thus redistributed are then added to the rainfall input for those units in the next time step. This approach allows for possible re-infiltration as “run on” if there is a soil moisture deficit in downslope units.
2.3 Modelling of enhanced hillslope storage
In order to assess the effects on the storm run-off of additional hillslope storage, simulations with identical parameters and inputs, but using representations of unaltered and modified hillslope, are undertaken and the respective results compared.
The more flexible discretisation approach introduced in Dynamic TOPMODEL allows a highly efficient way of modelling spatially distributed hillslope storage, in which areas identified with interventions can be lumped into one or more HRUs. In model realisations reflecting unaltered catchments these units behave identically to surrounding landscape areas. To then simulate the effect of applying EHS, the surface routing through these units can be altered to reflect their reduced connectivity with the hillslope. Intervention areas may be grouped into multiple units according to their characteristics. These could include, for example, height and permeability, position on the hillslope, upslope area, slope, and proximity to the channel. Even if many such aspects are identified and result in multiple groupings, this approach will substantially reduce computational overheads against a fully spatially distributed representation.
Drainage is an important aspect of hillslope storage. Between-events areas will often remain saturated and there will be little infiltration to the subsurface. There will be evapotranspiration losses, however, which will occur at the maximum potential rate from the open surface. Direct drainage from a bunded area or dam could be applied via a pipe which, ignoring friction, gives a dependence of discharge on the square of the hydrostatic head. Leaky wooden structures or permeable bunds may instead drain as though through a porous medium. In this case it is more realistic to relate output discharge linearly with the head (Beven, 2012). A structure could also be impermeable so that storage not removed by evapotranspiration is lost downslope only when the features start overflowing.
In deepened hollows and ground scrapes any overflow in excess of the storage capacity will leave the feature in a similar direction and velocity across the unmodified hillslope. In both leaky and impermeable structures, assuming they are designed to maximise interception by following the local contours, the directions are again likely to be similar. The flow rates will be more dependent on its material and construction and can, for example, be simulated by a non-contracted broad-crested weir equation (Chow, 1959; Brater and King, 1976). The semi-distributed surface routing algorithm outlined in Sect. 2.2 is now applied in order to model catchments where hillslope storage has been added by any of the methods described. The units representing storage are modified so that smaller proportions of their downslope surface flow are directed to other units than for the unaltered landscape representation, and thus features fill when there is a net input of run-off. Subsurface routing beneath the structure is unaltered.
This change in the rate of storage draining out areas due to emplacement of features with permeable walls can be emulated by reducing the effective overland flow velocity in the corresponding units. A leakiness factor Λ is defined as the proportional reduction in effective downslope flow velocities from an aggregated storage unit with respect to the unaltered hillslope. Each unit in effect behaves for the duration of a time step as a linear store with mean residence time , where vof, i is the overland flow velocity for the unaltered hillslope representation.
A modified surface distribution matrix Wof can also be used to reflect changes in the directions of downslope flow due to the presence of the storage features. For example, in a downslope pond drained by a pipe the drainage direction is likely to be towards the nearest channel. In this case, for unit i draining to reach j, the element rij of Wof is set to unity and all the other units set to zero.
For a roughly rectangular area, storage could be considered as proportional to water depth, but other storage–depth relationships could be specified for more realistic morphologies, for example in blocked gullies. A parameter exmax [L] can be introduced to control the maximum storage; if ex>exmax the structure starts to overflow. An additional overflow matrix Wover can be defined to direct excess water out of the lumped features. This matrix is likely to be identical to the unaltered surface distribution matrix, Wsurf, but could be altered, for example to emulate an overflow channel.
2.4 Uncertainty estimation framework
It has been observed that different model parameterisations can lead to similar results which meet some type of “acceptability” criteria when evaluated against observational data. This has been termed equifinality (Beven, 2006). The approach taken by the project is a form of the Generalised Likelihood Uncertainty Estimation methodology (GLUE: Beven and Binley, 1992, 2014). It accepts the possibility of many model realisations that can fit the observed behaviour. GLUE has been employed in many studies (e.g. Beven and Freer, 2001b; Blazkova and Beven, 2004; Liu et al., 2009).
Many realisations are produced using a Monte Carlo approach, whereby a large number of model parameters are sampled randomly from one or more prior distributions and are then applied in turn to the system model. For each a simulation is performed across the desired period. Each output is then scored with a likelihood or weighting function calculated from performance metrics against observational data and other criteria. This is then normalised to produce a weighting factor for the corresponding realisation.
In general only those simulations achieving an acceptability threshold are retained, yielding a “behavioural” parameter set, giving a posterior distribution of likelihoods. A triangular weighting function is common (Beven and Freer, 2001b; Beven, 2006; Blazkova and Beven, 2009; Liu et al., 2009). whereby the value is unity at the likeliest value of a predefined acceptability interval, zero at either limit, and linearly interpolated between these points. A trapezoidal form (e.g. Blazkova and Beven, 2009) could also be applied, where the value is unity between two threshold values and linearly interpolated outside these to the acceptability criteria. All of the predicted values of the observables must lie within acceptable ranges or the realisation is rejected, even if the overall sum of weights is non-zero.
An approach to incorporate this uncertainty framework into evaluation of NFM interventions is shown in Fig. 1. Weighted behavioural model realisations for the unaltered catchment model are obtained through the procedure described. One or more modifications due to the applications of interventions are applied to the catchment model, and each of the base realisations rerun against this altered model. For each altered realisation the weighting score is carried through from the baseline case. If there is available information on the likelihoods of the effects of the interventions, a score for the modified realisation can be calculated by combining it with the weighting of the associated behavioural model.
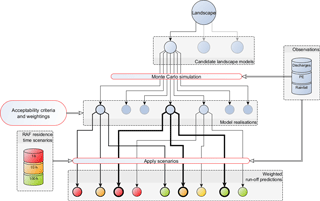
Figure 1Work flow diagram for Monte Carlo simulation of storm run-off, and selection and weighting of behavioural realisations and application of NFM scenarios for forward prediction of change. The weight of lines leading from acceptable simulations reflects the weighting likelihood score in the validity of that realisation.
The Eden headwaters in Cumbria, UK (Fig. 3), have a drainage area of 223 km2 above Great Musgrave Bridge (54.5126∘ N, 2.363234∘ W). The catchment is 55.4 % acid, improved or rough grassland and 36.0 % bog, scrub or heath. Bedrock geology is Permian and Triassic sandstones lain on Carboniferous limestones and there is some influence of groundwater pathways (Ockenden and Chappell, 2011). Tree cover is minimal, comprising just 2.5 % of its area, although there has been significant recent tree planting that is not yet thought to have had any major effect on flood peaks. Overall annual rainfall is in the region of 1200 mm, but there is a strong synoptic and orographic influence (EA, 2008).
There are two UK Environment Agency flow gauges in the catchments (see Fig. 3). Gauge number 76 806 is located at Great Musgrave Bridge and was installed in July 2000. It is of a velocity–area type and of the form of a shallow V weir 30 m in width. Gauge number 76 014 is located near Kirkby Stephen (54.482588∘ N, −2.351097∘ W) and drains an area of 69.4 km2. It dates from 1971 and is a compound broad-crested weir, also using a velocity–area method area for flow estimation.
The early autumn of 2015 was unusually dry and soil water deficits in October were more than 10 mm greater than the long-term average (Marsh et al., 2016). In November a south-westerly “atmospheric river” became established that brought warm moisture-laden air from the subtropics. A period of exceptional rainfall events followed that included storms Abigail (15–16 November), Barney (18 November) and Desmond (5–6 December). This final extra-tropical cyclone caused significant damage and over 2000 homes were flooded in Carlisle near the catchment outlet. A record 1680 m3 s−1 discharge was recorded at 09:00 GMT on 6 December at Sheepmount Weir (54.905332∘ N, 2.952091∘ W) in Carlisle. The town of Appleby (54.578719∘ N, 2.488839∘ W), was also badly affected by this event; a peak discharge of 372 m3 s−1 was recorded at 18:00 GMT on the 5 December at the Great Musgrave Bridge gauge a few kilometres upstream. Matthews et al. (2018) provide a fuller description of Storm Desmond and its hydrological extremes.
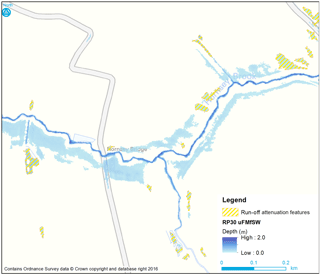
Figure 2Hydrodynamic accumulation areas within Eden, identified by JFLOW analysis for a designed storm of return period of 30 years (Hankin et al., 2017). Maximum water depths are indicated, and areas that exceed the threshold depth and other criteria (minimum area, slope angle and proximity to roads and buildings) are highlighted as potential sites for EHS.
The study period runs from close to the end of September 2015, when the soil moisture deficit was at its peak, to the recession period of Storm Desmond in early December. Processed 15 min time series of rated discharges were obtained from the EA for gauge 76 806. Tipping-bucket recorder (TBR) rainfall data at 15 min intervals were also provided by the EA and a set of these gauges lying within 10 km of the catchment was identified. Given the extreme rainfall, some gauges went off-line during the storms and were removed from the set, leaving four gauges with complete records over the period. A rainfall record was interpolated from this and met the water balance to within 5 %. This was then applied to the entire catchment area.
Although significant events, storms Abigail and Barney did not cause damaging flooding in this or downstream areas of the catchment. This suggests that a reduction of the 7.0 mm h−1 peak of Storm Desmond to that of Abigail, at 2.4 mm h−1, the larger of these storms, would be a successful outcome of any NFM intervention. This corresponds to a reduction of around 4.6 mm h−1 or 65 %. The potential for s=a large degree of uncertainty in the rating of these discharges, particularly at the extreme levels seen during Storm Desmond, should be borne in mind.
3.1 Model setup
An initial screening stage was undertaken to identify potential sites for enhancement of hillslope storage. Rainfall from a designed event of a 30-year return period was routed to the catchment outlet with JFLOW. Areas that accumulated significant water depths, such as natural depressions, flow pathways or small channels, were tagged as suitable candidates for enhanced storage (see Fig. 2). Their areas were then constrained in size to between 100 and 5000 m2 and those within 2 m of roads and buildings excluded. This yielded 4500 distinct sites of 506 m2 average area, occupying 4.0 % of the catchment and leading to a potential static storage of just over 8 million m3.
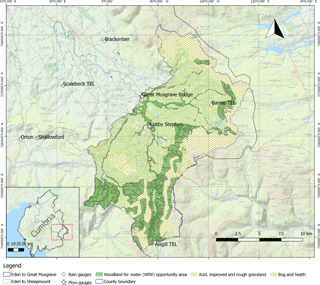
Figure 3Study catchment, the Eden headwaters to Great Musgrave Bridge (223 km2), showing context within Cumbria, UK, predominant land cover and location of TBR rain gauges and gauging stations. Woodlands for Water tree planting opportunity areas are shown. These were applied in another application of the NFM modelling framework developed for the project described, which are not discussed in detail here.
A Dynamic TOPMODEL “discretisation” was then undertaken. The catchment was divided into eight response units according to the topographic wetness index, and hillslope areas identified as potential sites for EHS were associated with an additional single response unit within the catchment. This HRU classification overrode any underlying classification determined from the TWI. This unit was thenceforth treated as a single aggregated feature bunded or dammed by a “leaky” barrier, 1 m in height with upslope sides open to receive surface run-off.
Overflow was directed over the top of the barrier in the same direction as the original distributions given by the surface flow weighting matrix. The specific overflow per unit length along the top side of the feature was calculated as though for a broad-crested weir of width 50 cm. Discharge coefficients are taken from the appropriate entries in the tables provided by Brater and King (1976). The unit took the same hydrological parameters as the surrounding regions. The unaltered overland flow velocity was taken as 100 m h−1 for all units. Three scenarios were considered, labelled RT1, RT10 and RT100, corresponding to residence times of 1, 10 and 100 h and Λ factors of 0.01, 0.1 and 1, respectively.
3.2 Monte Carlo exercise
An ensemble of 5000 parameter sets were sampled randomly from uniform prior distributions with ranges given in Table 1. The observables used to calculate likelihood weighting score were Ac, the maximum saturated contributing area, or area proportion of the catchment that generates overland flow; the Nash–Sutcliffe statistic (NSE, Nash and Sutcliffe, 1970); and qmax, the maximum simulated discharge relative to the observed rated value. The acceptability criteria for Ac were derived from considerations of physically feasible values. These could be approximated from observations across actual events, for example, by remotely sensed imaging (EA, 2013; Luscombe et al., 2015). The criteria observables are given in Table 2, alongside their limits of acceptability. The likelihood score for the NSE was the actual value calculated from the simulated discharges versus the observed, rated values. For the others, the likelihood score was triangular in the corresponding acceptability intervals, with a value of unity at the midpoint of the range. The overall weighting score for a realisation is then calculated by taking the mean of the individual scores. The behavioural sets identified by applying the limits shown in Table 2 are then used as the basis for investigation of the effects of applying a number of NFM scenarios.
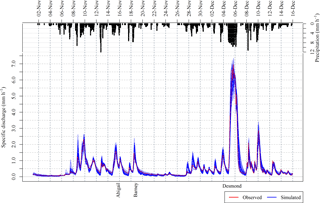
Figure 4Simulated discharges across the storm period alongside rated observed discharges at Great Musgrave Bridge. The three named storms are indicated. Rainfall is interpolated between the gauges shown in Fig. 3.
Of the 5000 realisations undertaken, 384 were identified with outputs that met the acceptability criteria given in Table 2. Figure 4 shows the discharges simulated by these behavioural cases, alongside the observed rated discharges at the EA gauge at Great Musgrave bridge.
The “dotty” plots in Fig. 5 show overall GLUE weightings against the three metrics used to select acceptable cases. The maximum saturated area, Ac, shown in the leftmost plot, has a discontinuous shape. This is because when a response unit reaches saturation it contributes its entire area at once. Within the behavioural realisations only a limited number of HRUs, along with the aggregated EHS unit, ever contribute saturated surface flow, leading to just seven distinct values for Ac. Points corresponding to likelihood weightings for realisations producing these distinct values of Ac are shown in the leftmost plot, with a distinct colour applied for each. The same colours are applied to points corresponding to the same realisations in the other plots. The stratified appearance of the NSE plot is a by-product of its correlation with the contributing area; the correlation with the maximum predicted discharge is less clear. A value of Ac of around 65 % is associated with the best NSE fits, but is spread throughout the maximum discharges. The bias towards higher values suggests that realisations producing greater quantities of fast overland flow better reflect the storm response in this period. This would be consistent with the extreme nature of the storms and observational evidence (e.g. Marsh et al., 2016).
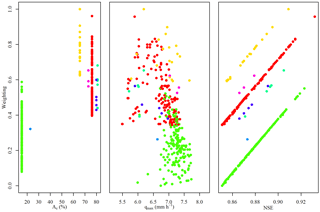
Figure 5GLUE “dotty” plots showing overall likelihood (weighting) scores calculated for the 348 behavioural run-off simulations against the three model outputs described in the text. The discontinuous appearance of the maximum saturated contributing area Ac is due to the relatively coarse discretisation applied such that once a HRU begins to produce any saturated overland flow, its entire area is added. Each unique Ac value takes a separate colour that is carried through to corresponding points in the other plots.
Parameters for each of the 384 accepted cases were applied to catchment models modified to reflect insertion of hillslope storage networks with each of the residence times considered, and the simulations rerun. Reduction in peak Δq for an intervention case is defined as the difference between a baseline case and intervention simulation based on this case. For each pair of simulations the value of Δq was multiplied by the base-case normalised weighting to reflect the likelihood of this reduction effect. The likelihood-weighted statistics for each of the events and intervention levels are given in Table 3, and the impacts on the arrival time of the main peaks of each in Table 4. The Kolmogorov–Smirnov test included is a non-parametric approach to comparing empirical distribution, equal to the maximum vertical separation of the cumulative distribution function (CDF) of the discharges. This allows an evaluation of the relative effectiveness of each intervention.
Table 3Statistics for the impacts of interventions relative to base cases on the peaks of the named storms within the simulation period. Each difference is weighted by the likelihood score for the base-case simulation. The term Δqmax (mm h−1) denotes the maximum and Med the median percentage likelihood weighted reduction in peak. K.S. is Kolmogorov–Smirnov Statistic, a non-parametric statistic equal to the maximum separation of the CDF of the simulated base-case peaks versus the peaks calculated for the intervention case. This shows that the RT10 intervention consistently has the greatest impact across the storms.
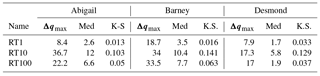
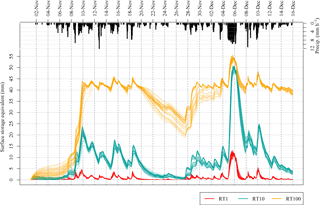
Figure 6Surface excess storages, expressed as specific rainfall equivalent, across one of the lumped RAF units with maximum storage 1 m through a single intervention case and for the three mean residences times considered. The slight excess at the peaks of the storm reflects the weir crest height of the overflow function applied.
Figure 6 shows, as rainfall-equivalent-specific surface storage within the aggregated hillslope storage unit across the entire simulation period. When this is filled, and overflow discharge predicted with a Weir equation, the crest height will lead to a slight excess over the specified maximum static storage of 1 m.
In the RT1 case the areas fill and drain quickly but appear to never fill completely. The available storage is therefore not utilised effectively: utilisation is highest at the peak of Storm Desmond, at 29 % of the theoretical hydrostatic capacity. This is equivalent to approximately 2.45 million m3 volume of storage retained across the catchment. The corresponding effect on the hydrograph is small, with a likelihood-weighted median reduction in the peak of Storm Desmond of 1.7 %. For RT10 the features appear underutilised in the earlier storms, peaking at about 50 % capacity, and recover almost all their capacity in the recession period after Storm Barney. Retained hillslope run-off across the catchment peaks at just over 10 million m3. The impact of the additional storage is significant in the final storm, and reduces the peak by a likelihood-weighted median of 5.8 % and maximum of 17.3 %, the greatest impact of any of the interventions. This intervention would not by itself have prevented flooding; however, combined with more conventional flood risk management (FRM) measures it could have had a significant mitigating effect even through this extreme event.
In the RT100 intervention the features fill completely across the course of Storm Abigail near the start of the period, and the drain-down is insufficient to allow complete recovery of capacity before the final event. They are overflowing during much of the event, with the excess following the fast pathways to the channel blocked by the hillslope. The impact is therefore much reduced compared with the 10 h case, with a median reduction of 1.9 % in the peak, although some cases do show a reduction almost as effective as RT10.
Ensemble hydrographs through each of the named storms are shown in the following figures. These present the discharges simulated for the unmodified catchment model using the parameters for each of the acceptable cases against those produced by applying the corresponding parameters to catchment models with the addition of enhanced hillslope storage.
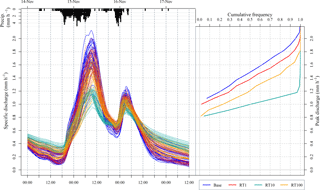
Figure 7Left: 90th percentile likelihood scored baseline and corresponding intervention cases through Storm Abigail. Right: Likelihood-weighted CDF of peak discharges for base and intervention cases. Note that, in order to share the same vertical axis, the plot axes are is transposed relative to convention.
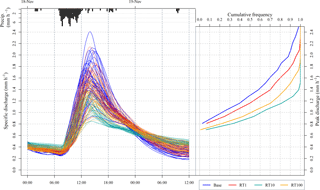
Figure 8Left: 90th percentile scored baseline and corresponding intervention cases through Storm Barney. Right: CDF of peak discharges for base and intervention cases.
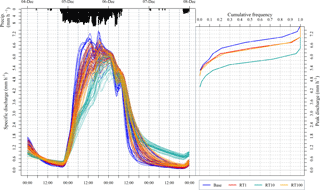
Figure 9Left: 90th percentile scored baseline and corresponding intervention cases through Storm Desmond. Left: CDF of peak discharges for base and intervention cases.
In the initial storm, Abigail, the first peak is attenuated as much by the RT100 case as the RT10 case, but in the second peak RT10 again provides much greater reduction. The RT1 case has the lowest impact on all storm peaks. The arrival of the main peak is retarded most by the RT100 case, with a median delay of 30 min. The later peak appears to be brought forward marginally by the RT100 cases, however. This may indicate that the hillslope storage unit has run out of storage and is delivering flow downslope by overflow. In all cases the recession curve is extended by the intervention, indicating that storage is draining for some time after the storm peak.
In the second event the RT100 case appears to have more impact than any of the other cases across the initial peak but then becomes less effective than RT10 through the main peak. There is less of a delay to the arrival of the main peak than for Abigail, with a median delay of only 15 min for the RT10 and RT100 cases. In the RT10 case the median brings the peak forward by 15 min. This might indicate that their effect has been to slow down fast-responding catchments so that their flood waves contribute more to the rising limb of the overall storm hydrograph.
In this largest event the RT10 case significantly outperforms the others, suggesting that it has recovered much more capacity. There is virtually no attenuation from the other cases and the peak is hardly delayed for RT1 and RT100. Figure 9 shows clearly that the RT100 units fill quickly during Abigail and remain full for the duration of Barney and Desmond. There is only a week-long period in later November when they recover a little capacity through drainage during the recession period of Barney.
The RT10 case has the greatest impact on the flood peak for all storms, with its advantage over the other cases increasing through the period. In Abigail the Kolmogorov–Smirnov distance of the RT10 case is 150 % that of the RT100 case, whereas across Desmond this has increased to 350 %.
The surface routing algorithm is computationally very efficient, particularly as it can be solved analytically. The semi-distributed representation is also straightforward and quick and allows examination of relevant characteristics such as the drainage times and multiple model runs that apply different network configurations. More sophisticated physically based modelling of surface flow will introduce computational overheads without accounting for large uncertainties in the input, and this may not add greater insight into the catchment response.
The RT10 case was significantly more effective across the largest event than the other two cases, as features had recovered capacity during the previous recession and drained sufficiently to have an impact on the flood peak in Storm Desmond. The mitigation was less across the earlier events but, given they did not cause significant flooding, this was not a consideration.
These results provide further evidence that the theoretical, static storage provided by an NFM scheme can be significantly underutilised, assuming it is configured so that it can recover capacity effectively between storms events. It has already been suggested that the effectiveness in reducing flood risk of a NFM intervention is not a simple function of the additional storage it provides, but also of its contribution to desynchronising a sub-catchment's flood wave with those downstream (Thomas and Nisbet, 2007; Blanc et al., 2012).
A more sophisticated approach to implementing NFM is probably required. For instance, the locations on the hillslopes of interventions are likely to be a significant factor on a scheme's performance as they will influence flood wave timing. In this study the network width approach to routing channel flow was applied across the entire headwater catchment, and flood wave size and timings were not available for the individual sub-catchments. It was thus unclear from the results what proportion of attenuation of storm hydrographs were due to desynchronisation of flood waves, as opposed to simple retention of surface run-off. A regression analysis similar to that undertaken by Pattison et al. (2013), including the hillslope storage location and quantities as predictor variables, could provide insight into the relative contributions of additional hillslope storage and flood wave desynchronisation on downstream flood mitigation. This can be done in a further analysis, but does raise the question of how to calibrate meaningful flood wave velocities for the individual sub-catchments.
Metcalfe et al. (2015) showed that the run-off predictions simulated by Dynamic TOPMODEL stabilised at around 8 to 12 subdivisions of the catchment. In this study eight HRUs were used: despite being at the lower limit of the region of stability identified by Metcalfe et al. (2015), the model gave good fits to the observed hydrographs, with many realisations exceeding efficiencies of 0.9 (although the uncertainties introduced through rating of discharges at extreme storm levels should be noted). The values of the maximum saturated area, Ac, were highly discontinuous, however, as when the response units start to produce saturated flow they contribute their entire area to the metric. A more fine-grained discretisation would produce a more continuous distribution which might be advantageous in terms of better identification of saturated contributing areas, in particular how the positioning of hillslope storage features in proposed schemes may influence run-off from these areas.
The features appeared to have an effect through the course of even the largest storm, although the slowest-draining cases were full and overflowing for much of the simulation period. There is, however, a possibility that features such as woody debris dams will be unable to withstand hydraulic loading across such extreme events, or across a series of storms. Complete or partial failure could lead to debris being introduced to the flood waters and potential damage or blockage of downstream infrastructure which will increase risk of flood damage. Ideally, these scenarios should be incorporated in a risk-reduction–cost matrix. There is, as yet, little information about the potential for failures that can be used to estimate residual risk, although initial findings suggest that failure sequences can behave non-linearly.
Enhanced hillslope storage was treated as a single unit in the catchment discretisation. In practise different types of interventions, e.g. hillslope ponds, bunded accumulation areas and blocked gullies, will have distinct responses under loading and their locations may also have a significant impact on the run-off. A more realistic approach would recognise the variety of interventions and group features and categorise them by their construction, geometries and position on the hillslopes. The number of possibilities will increase rapidly according to the number of varieties and configurations defined, but these are likely to be constrained by considerations of realistic design and implementation issues. In addition, the simplified representation used in this study allows for relatively rapid investigation of many different configurations. This approach can be incorporated into a sensitivity analysis to determine which characteristics are most important to the impact of enhanced hillslope storage features on the storm response. A Monte Carlo approach selecting from multiple design event sets, for example generated by the method of Keef et al. (2013), could help assess the robustness of the conclusions drawn from modelling and help to site features more strategically. It could also help identify situations where flood waves become synchronised by emplacement of features at different catchment scales.
This study has analysed the performance across a series of extreme events of a NFM scheme made up of many “leaky” features providing additional storage for hillslope run-off. The model incorporated a simplified overland routing module and achieved a high level of efficiency in simulating the observed discharges. The best baseline simulations were applied to the catchment model with the NFM features incorporated. Every variety of enhanced hillslope storage was simulated using a single simple aggregated linear store model. It showed that the combined impact could have significantly attenuated the flood peak, even during the largest storm. It also showed that their effectiveness was contingent on how their drainage characteristics would allow them to recover capacity between events.
The study demonstrates that, given a computationally efficient modelling strategy, uncertainty estimation can be applied to evaluation NFM. A well-established uncertainty analysis framework was used, whereby multiple realisations of a hillslope run-off model applied to the events were enacted and scored with a likelihood function combining output criteria. Acceptable realisations were selected according to limits of acceptability of those criteria and were likelihood-weighted according to their score. This allowed results to be presented to project and catchment stakeholders alongside meaningful estimates of their uncertainty.
The representation is efficient and allows investigation of many different configurations whilst retaining the important aspects of their behaviour and impacts, namely storage addition and residence times. It contains many assumptions and simplifications, however, and a key aim of further work will be to determine whether other significant characteristics are adequately simulated in this representation, and which will require refinement. For example, in actual applications there is likely to be a more complex storage-water–depth relationship than the straightforward equivalence used here. Hydrodynamic analysis of simulated individual structures sited in realistic topographic representations may provide insights into the applicability of the simplification across a range of loading scenarios.
The storage values considered in this study were lumped into a single HRU to maximise computational efficiency. A more sophisticated approach could utilise many more classifications that reflect their behaviour and impact on the run-off. This could include capacity, position on the hillslope, distance from access tracks and the channel, sources of construction material, and type of location (e.g. within ephemeral channels, shallow hillslope accumulation areas or on the floodplain). More work will be needed to determine which of these characteristics will be most significant and how well classifications reflect actual implementations by NFM practitioners.
It may be that the most beneficial effect of additional hillslope storage is likely to be seen on a small scale in reaches immediately downstream of a feature or sets of features. It could be, even given the overall mitigation effect, that some asynchronous flood peaks in the unmodified catchment model became synchronised when the storage was introduced and thus reduced the overall effectiveness of the interventions. Much further work is required to better understand the synchronisation problem, particularly as catchment scale increases.
Obtaining observational evidence to support modelling predictions will be difficult in the field as, by their nature, the extreme events that load features are rare, and gradual processes such as sediment deposition difficult to measure or simulate everywhere. An innovative experimental approach is needed to address these questions. Detailed hydrometric data are required, collected by instruments such as stage and flow gauges upslope, downslope and within features. However only 6 % of NFM schemes in the UK currently have any type of monitoring (JBA Trust, 2015), although some monitoring is now a condition of funding for some new schemes. The effects of the additional storage on the overall flood hydrograph will be increasingly difficult to discern as the catchment size increases, including the potential for synchronicity effects. The methodology used in this paper, however, extended to incorporate better-supported representations of small-scale impacts due to feature emplacement, may provide a productive way to advance research into natural flood management and its effectiveness.
Simulation data presented in the text are available at https://doi.org/10.13140/RG.2.2.19690.62409 (Metcalfe et al., 2018).
The authors declare that they have no conflict of interest.
This work was funded by the JBA Trust (project number W12-1866), the European Regional Development Fund, and the UK National Environmental Research Council (NERC).
This paper is dedicated to the memory of Peter Metcalfe who recently lost his
life in a climbing accident. He had just started to apply some of the methods
presented here more widely. Someone of strong commitment to everything he did,
he will be sorely missed by his friends and colleagues.
Edited by: Patricia Saco
Reviewed by: Simon Dadson and one anonymous referee
Barber, N. and Quinn, P.: Mitigating diffuse water pollution from agriculture using soft engineered runoff attenuation features, Area, 44, 454–462, 2012.
Beven, K.: A manifesto for the equifinality thesis, J. Hydrol., 320, 18–36, 2006.
Beven, K.: Rainfall-Runoff Modelling: The Primer, 2nd Edn., Wiley-Blackwell, Chichester, UK, ISBN-13: 978-0-470-71459-1, 2012.
Beven, K. and Binley, A.: The future of distributed models: model calibration and uncertainty prediction, Hydrol. Process., 6, 279–298, 1992.
Beven, K. and Binley, A.: GLUE: 20 years on, Hydrol. Process., 28, 5897–5918, 2014.
Beven, K. and Freer, J.: A Dynamic TOPMODEL, Hydrol. Process., 15, 1993–2011, 2001a.
Beven, K. and Freer, J.: Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology, J. Hydrol., 249, 11–29, 2001b.
Beven, K. J. and Kirkby, M. J.: A physically based variable contributing area model of catchment hydrology, Hydrol. Sci. B., 24, 43–69, 1979.
Blanc, J., Wright, G., and Arthur, S.: Natural Flood Management knowledge system: Part 2 – The effect of NFM features on the desynchronising of flood peaks at a catchment scale, CREW report, 2012.
Blazkova, S. and Beven, K.: Flood frequency estimation by continuous simulation of subcatchment rainfalls and discharges with the aim of improving dam safety assessment in a large basin in the Czech Republic, J. Hydrol., 292, 153–172, 2004.
Blazkova, S. and Beven, K.: A limits of acceptability approach to model evaluation and uncertainty estimation in flood frequency estimation by continuous simulation: Skalka catchment, Czech Republic, Water Resour. Res., 45, 12, 2009.
Brater, E. F. and King, H. W.: Handbook of hydraulics for the solution of hydraulic engineering problem, 6th Edn., McGraw-Hill, New York, 1976.
Calder, I. R. and Aylward, B.: Forest and floods: Moving to an evidence-based approach to watershed and integrated flood management, Water Int., 31, 87–99, 2006.
Chow, V. T.: Open channel hydraulics, McGraw-Hill Book Company, Inc., New York, 1959.
Dadson, S. J., Hall, J. W., Murgatroyd, A., Acreman, M., Bates, P., Beven, K., Heathwaite, L., Holden, J., Holman, I. P., Lane, S. N., O'Connell, E., Penning-Rowsell, E., Reynard, N., Sear, D., Thorne, C., and Wilby, R.: A restatement of the natural science evidence concerning catchment-based “natural” flood management in the United Kingdom, UK Proc. R. Soc. A, 473, 20160706, https://doi.org/10.1098/rspa.2016.0706, 2017.
Dummit, E.: Differential Equations (part 3): Systems of First-Order Differential Equations, available at: https://math.la.asu.edu/~dummit/docs/lindiff_6_systems_of_linear_differential_equations.pdf (last access: 24 April 2018), 2016.
EA – Environment Agency: River Eden, Cumbria, Catchment Flood Management Plan, Environment Agency, Bristol, UK, 2008.
EA – Environment Agency: Benchmarking the latest generation of 2D hydraulic modelling packages, Report SC120002, Environment Agency, Bristol, UK, ISBN: 978-1-84911-306-9, 2013.
EA – Environment Agency: Working with natural processes to reduce flood risk, R and D framework, Report SC130004/R2, Environment Agency, Bristol, UK, 2014.
Ghimire, S., Wilkinson, M., and Donaldson-Selby, G.: Application Of 1D And 2D Numerical Models For Assessing And Visualizing Effectiveness Of Natural Flood Management (NFM) Measures, 2014.
Hankin, B., Lamb, R., Craigen, I., Page, T., Chappell, N., and Metcalfe, P.: The Rivers Trust Life-IP Natural Course Project: Strategic Investigation of Natural Flood Management in Cumbria, JBA Consulting report number 2016s4667, JBA Consulting, Warrington, UK, 2016.
Hankin, B., Metcalfe, P., Johnson, D., Chappell, N., Page, T., Craigen, I., Lamb, R., and Beven, K.: Strategies for Testing the Impact of Natural Flood Risk Management Measures, in: Flood Risk Management, edited by: Hromadka, T. and Rao, P., InTech, Czech Republic, ISBN: 978-953-51-5526-3, 2017.
Hunter, N. M., Bates, P. D., Horritt, M. S., and Wilson, M. D.: Simple spatially-distributed models for predicting flood inundation: a review, Geomorphology, 90, 208–225, 2007.
Iacob, O., Rowan, J. S., Brown, I., and Ellis, C.: Evaluating wider benefits of natural flood management strategies: an ecosystem-based adaptation perspective, Hydrol. Res., 45, 774–787, 2014.
JBA Trust: Nature-based approaches for catchment flood management: an online catalogue, Report W15-0603, available at: http://www.jbatrust.org/wp-content/uploads/2016/02/W15-0603 (last access: 24 April 2018), 2015.
Keef, C., Tawn, J. A., and Lamb, R.: Estimating the probability of widespread flood events, Environmetrics, 24, 13–21, https://doi.org/10.1002/env.2190, 2013.
Lamb, R., Crossley, A., and Waller, S.: A fast 2D floodplain inundation model, P. I. Civil Eng.-Wat. M., 162, https://doi.org/10.1680/wama.2009.162.6.363, 2009.
Lamb, R., Keef, C., Tawn, J., Laeger, S., Meadowcroft, I., Surendran, S., Dunning, P., and Batstone, C.: A new method to assess the risk of local and widespread flooding on rivers and coasts, J. Flood Risk Manag., 3, 323–336, https://doi.org/10.1111/j.1753-318X.2010.01081.x, 2010.
Lane, S. N.: Natural flood management, Wiley Interdisciplinary Reviews: Water, 4, available at: http://www.jstor.org/stable/23020839, 2017.
Lane, S. N., Odoni, N., Landström, C., Whatmore, S. J., Ward, N., and Bradley, S.: Doing flood risk science differently: an experiment in radical scientific method, T. I. Brit. Geogr., 36, 15–36, 2011.
Liu, Y., Freer, J., Beven, K., and Matgen, P.: Towards a limits of acceptability approach to the calibration of hydrological models: Extending observation error, J. Hydrol., 367, 93–103, 2009.
Luscombe, D. J., Anderson, K., Gatis, N., Grand-Clement, E., and Brazier, R. E.: Using airborne thermal imaging data to measure near-surface hydrology in upland ecosystems, Hydrol. Process., 29, 1656–1668, 2015.
Marsh, T. J., Kirby, C., Muchan, K., Barker, L., Henderson, E., and Hannaford, J.: The winter floods of 2015/2016 in the UK – a review, Centre for Ecology & Hydrology, Wallingford, UK, 2016.
Matthews, T., Murphy, C., McCarthy, G., Broderick, C., and Wilby, R. L.: Super Storm Desmond: a process-based assessment, Environ. Res. Lett., 13, 014024, https://doi.org/10.1088/1748-9326/aa98c8, 2018.
Metcalfe, P., Beven, K., and Freer, J.: Dynamic TOPMODEL: A new implementation in R and its sensitivity to time and space steps, Environ. Modell. Softw., 72, 155–172, 2015.
Metcalfe, P., Beven, K., Hankin, B., and Lamb, R.: A modelling framework for evaluation of the hydrological impacts of nature-based approaches to flood risk management, with application to in-channel interventions across a 29-km2 scale catchment in the United Kingdom, Hydrol. Process., 31, 1734–1748, https://doi.org/10.1002/hyp.11140, 2017.
Metcalfe, P., Beven, K., Hankin, B., and Lamb, R.: Dynamic TOPMODEL simulation runs supporting Metcalfe et al. (2018), available at: https://doi.org/10.13140/RG.2.2.19690.62409, 2018.
Mosonyi, E.: Wassrekraftwerke, Band I, Niederdruckanlagen, Düsseldorf, VDI Verlag, 1966.
Nash, J. E. and Sutcliffe, J. V.: River flow forecasting through conceptual models part I – A discussion of principles, J. Hydrol., 10, 282–290, 1970.
National Trust: From source to sea: natural flood management – the Holnicote experience, Final Report to Defra, National Trust, Swindon, UK, 2015.
Nicholson, A., Wilkinson, M., O'Donnell, G. M., and Quinn, P.: Runoff attenuation features: a sustainable flood mitigation strategy in the Belford catchment, UK, Area, 44, 463–469, 2012.
Nisbet, T. and Page, T.: Case study 16. Pontbren catchment land use change study, in: How to model and map catchment processes when flood risk management planning, edited by: Hankin, B., Burgess-Gamble, L., Bentley, S., and Rose, S., Science report SC120015/R1, Environment Agency, Bristol, UK, available at: http://evidence.environment-agency.gov.uk/FCERM/Libraries/FCERM_ Project_Documents/SC120015_case_ study_16.sflb.ashx (last access: 23 December 2017), 2016.
Nisbet, T. R., Marrington, S., Thomas, H., Broadmeadow, S., and Valatin, G.: Slowing the flow at Pickering, Final Report to Defra, Project RMP5455, 2011.
Ockenden, M. C. and Chappell, N. A.: Identification of the dominant runoff pathways from data-based mechanistic modelling of nested catchments in temperate UK, J. Hydrol., 402, 71–79, 2011.
Page, T., Beven, K. J., Freer, J., and Neal, C.: Modelling the chloride signal at Plynlimon, Wales, using a modified dynamic TOPMODEL incorporating conservative chemical mixing (with uncertainty), Hydrol. Process., 21, 292–307, 2007.
Pattison, I., Lane, S. N., Hardy, R. J., and Reaney, M.: The role of tributary relative timing and sequencing in controlling large floods, Water Resour. Res., 50, 5444–5458, 2014.
Quinn, P., O'Donnell, G., Nicholson, A., Wilkinson, M., Owen, G., Jonczyk, J., Barber, N., Hardwick, M., and Davies, G.: Potential use of Runoff Attenuation Features in small rural catchments for flood mitigation, Newcastle University, Environment Agency, Royal Haskoning DHV, England, 2013.
Scottish Environment Protection Agency (SEPA): The Natural Flood Management Handbook, available at: http://www.sepa.org.uk/media/163560/sepa-natural-flood-management-handbook1.pdf (last access: 23 December 2017), 2016.
Thomas, H. and Nisbet, T.: An assessment of the impact of floodplain woodland on flood flows, Water Environ. J., 21, 114–126, 2007.
Werritty, A.: Sustainable flood management: oxymoron or new paradigm?, Area, 38, 16–23, 2006.
Wheater, H., Reynolds, B., McIntyre, N., Marshall, M., Jackson, B., Frogbrook, Z., and Chell, J.: Impacts of upland land management on flood risk: Multi-scale modelling methodology and results from the Pontbren Experiment, Flood Risk Management Research Consortium (FRMRC) Research Report UR 16, 2008.
Wilkinson, M., Quinn, P., Benson, I., and Welton. P.: Runoff management: mitigation measures for disconnecting flow pathways in the Belford Burn catchment to reduce flood risk, in: British Hydrological Society International Symposium, British Hydrological Society, Newcastle upon Tyne, 2010a.
Wilkinson, M., Quinn, P., and Welton, P.: Runoff management during the September 2008 floods in the Belford catchment, Northumberland, J. Flood Risk Manag., 3, 285–295, 2010b.