the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Impacts of changing hydrology on permanent gully growth: experimental results
Stephanie S. Day
Karen B. Gran
Chris Paola
Permanent gullies grow through head cut propagation in response to overland flow coupled with incision and widening in the channel bottom leading to hillslope failures. Altered hydrology can impact the rate at which permanent gullies grow by changing head cut propagation, channel incision, and channel widening rates. Using a set of small physical experiments, we tested how changing overland flow rates and flow volumes alter the total volume of erosion and resulting gully morphology. Permanent gullies were modeled as both detachment-limited and transport-limited systems, using two different substrates with varying cohesion. In both cases, the erosion rate varied linearly with water discharge, such that the volume of sediment eroded was a function not of flow rate, but of total water volume. This implies that efforts to reduce peak flow rates alone without addressing flow volumes entering gully systems may not reduce erosion. The documented response in these experiments is not typical when compared to larger preexisting channels where higher flow rates result in greater erosion through nonlinear relationships between water discharge and sediment discharge. Permanent gullies do not respond like preexisting channels because channel slope remains a free parameter and can adjust relatively quickly in response to changing flows.
- Article
(3070 KB) -
Supplement
(2113 KB) - BibTeX
- EndNote
Permanent gullies are first-order, deeply incised, ephemeral streams with steep head cuts. Also known as ravines (Poesen et al., 2003a), permanent gullies form part of a continuum between ephemeral gullies and perennial channels. Permanent gullies can be highly erosive, accounting for 10–94 % of the total sediment yield in a watershed (Poesen et al., 2003a, and references therein). Gullies pose a hazard to infrastructure, agricultural productivity, and human safety through rapid propagation of head cuts in both rural and urban environments, and they contribute to the rapid transport of sediment and nutrients from the uplands to main-stem channels (Bull and Kirkby, 2002; Gran et al., 2011; Poesen et al., 2003a).
Permanent gullies initiate in places where concentrated flow can erode and move sediment (Mosley, 1974; Merritt, 1984; Bennett et al., 2000; Bryan, 1990; Knapen and Poesen, 2010). These topographic lows may be subtle, but where they connect with incised river valleys, steep knickpoints can rapidly form and propagate as head cuts. Gully head cut propagation occurs primarily by groundwater sapping or piping, overland flow, or a combination of these processes. Groundwater sapping typically forms amphitheater-type head cuts (Hinds, 1925; Howard, 1988; Lamb et al., 2006) which propagate as the soil is weakened through saturation at the water table, causing failure in the sediment above (Dunne, 1990). Where groundwater follows concentrated flow paths, piping can trigger head cut initiation and drive head cut retreat (Fox and Wilson, 2010; Nichols et al., 2017; Wilson, 2009, 2011). Overland flow erosion can also cause head cut propagation in multiple ways including granular erosion and slab failure. Slab failure relies on the constant wetting and drying experienced at the head cut between events. Tension cracks form as the soil dries, and during wet times water flows into these cracks, dislodging the slab (Dietrich and Dunne, 1993; Istanbulluoglu et al., 2005). Another form of slab failure occurs in layered substrate, where a lower highly erosive layer is scoured away, leaving the upper resistant layer overhanging until it eventually breaks away (Chu-Agor et al., 2008; Holland and Pickup, 1976; Robinson and Hanson, 1994; Stein and LaTray, 2002). In both of these slab failure mechanisms, head cut retreat temporarily ceases after slab failure with the slab protecting the head cut until the slab itself is eroded away (Robinson and Hanson, 1994; Istanbulluoglu et al., 2005). Granular erosion is driven by high shear stress at steep head cut slopes and can be enhanced through focused erosion of plunge pools and impinging jet scour (Alonso et al., 2002; Flores-Cervantes et al., 2006). The focus in this paper is on permanent gullies that grow as a result of granular sediment transport in a homogeneous substrate driven primarily by overland flow.
Permanent gully initiation and growth have been found to be a function of sediment texture and erodibility, slope, land use, vegetation cover, soil moisture, head cut size, climate, and hydrology (Ambers et al., 2006; Chiverrell et al., 2007; Flores-Cervantes et al., 2006; Istanbulluoglu et al., 2005; Knapen et al., 2007; Nachtergaele et al., 2001; Poesen et al., 2003b, 2011; Stankoviansky, 2003; Vandekerckhove et al., 2000; Vanwalleghem et al., 2003, 2005), but understanding the relative importance of each factor remains a challenge. Of the many variables impacting gully erosion, the two humans most readily impact are hydrology and land cover. Here the focus is on gully response to changes in hydrology.
Hydrology is altered in agricultural areas through complex changes to the volume and/or rate at which water enters permanent gully networks as overland flow, groundwater flow, or pipe flow. Agricultural development can involve direct modification of hydrology in the form of irrigation in dry climates and sandy soils or artificial drainage in wetter climates and less permeable soils. While irrigation has little impact on overland flow due to transpiration (Haddeland et al., 2005), combined changes to land cover and drainage associated with conversion from native vegetation to row-crop agriculture tend to increase the rate and volume of water entering a stream network (Blann et al., 2009; Robinson and Rycroft, 1999; Van der Ploeg et al., 1999; Wiskow and van der Ploeg, 2003). Following harvest, fields are left bare for a portion of the year (1–6 months), which can lower evapotranspiration and increase the volume of overland flow, particularly if the ground is frozen and infiltration cannot occur (Pierson et al., 2007). In addition, the removal of roughness elements when fields are bare can increase the rates of overland flow entering gullies (Abrahams and Parsons, 1991; Einstein and Barbarossa, 1951; Eitel et al., 2011; Farres, 1978; Römkens and Wang, 1987).
Although changes to hydrology in urban areas are different from those in agricultural areas, the impacts on permanent gully hydrology can be similar, with increased impervious surface area and rerouting of water through infrastructure leading to more direct hydrologic connections between uplands and gullies. Although the presence of storm sewers and water retention ponds may mitigate the effect of increased impervious area, many urban areas see an increase in overland flow rates and the overall volume of overland flow (Arnold Jr. and Gibbons, 1996; Espey Jr. et al., 1965; Paul and Meyer, 2001; Seaburn, 1969). Increased gullying is particularly of concern in urban areas with rapid population growth, intense rainfall, and infrastructure that promotes flow concentration into erodible areas (Adediji et al., 2013; Ebisemiju, 1989).
Permanent gullies evolve over shorter timescales than larger preexisting channels. Previous numerical and physical experiments of gully evolution identified two stages to gully growth: an early stage of rapid evolution and a later stage of growth within a more static form (Parker, 1977; Kosov et al., 1978; Parker and Schumm, 1982; Sidorchuk, 1999; Bennett et al., 2000). During this early phase, gullies should be more responsive to changes in hydrology as both channel cross-sectional geometry and longitudinal profile geometry are more adaptable. During the latter phase, changes in hydrology would be accommodated through erosion focused on head cuts at the channel tips and channel incision and widening with ensuing adjustments to side slopes (Sidorchuk, 1999, 2006).
Because anthropogenic alterations to the landscape involve both changes in flow rate and volume, we chose to investigate those two aspects of hydrologic change using a physical experimental basin. Two different experimental substrates were used to measure the effects of changing flow rates on both detachment-limited and transport-limited systems. These two types of erosion represent a continuum, where the volume of sediment carried out of the system is controlled by the ability of the flow to dislodge sediment from the substrate vs. the ability of the flow to carry easily eroded sediment. Commonly “detachment-limited” is used to describe bedrock rivers, while “transport-limited” is used to describe alluvial rivers. Given that permanent gullies are incisional systems and may be down-cutting through nonalluvial substrate, the detachment-limited model may be more appropriate for permanent gully systems than classic transport-limited models for alluvial systems.
Physical experiments, like the ones we discuss here, offer a setting where most variables can be controlled and timescales for channel evolution are greatly reduced. Moreover, using experiments allows us to make measurements at a high spatial and temporal density to ensure that much of the variability in the system is captured. Such experiments are not intended as scale models; rather, they are small systems in which scale-independent processes can be studied under controlled conditions (Paola et al., 2009). As such the experiments presented here add to the body of literature focused on channel formation across a continuum of scales from rills over short timescales to head-cutting rivers over much longer timescales (i.e., Stein and LaTray, 2002; Grovers et al., 2007). The discussion of this work focuses on permanent gullies or ravines because these features tend to form over relatively short timescales geologically, but similar timescales over which preexisting channel networks might also evolve, thus allowing for a comparison between the two. Permanent gullies can also cause deep and rapid incision, potentially having a significant effect on infrastructure. Here we utilize physical experiments of permanent gullies to focus on a basic question: how does changing the flow rate of a fixed quantity of water change the total volume of sediment removed and the morphology of the resulting permanent gully?
We performed experiments at the St. Anthony Falls Laboratory at the University of Minnesota, in Minneapolis, Minnesota. These experiments tested how different overland flow rates affect erosion and permanent gully growth on a series of permanent gullies initiated through base level fall, a common feature of post-glacial landscapes in the Upper Midwest, USA (Belmont et al., 2011; Gran et al., 2013; Lenhart et al., 2013). We represented a range of natural permanent gullies using two different substrates. These substrates varied in material and grain size, with one representing a more cohesive detachment-limited system and the other a transport-limited system. The fine-grained substrate was composed of 12 µm ceramic spheres (Zeeospheres) with a density of 2.5 g cm−3 (Zeeospheres G series data sheet, 2018). The natural cohesion of this substrate caused it to behave as a detachment-limited system, as empirically shown in the results section of this paper. The coarser substrate was composed of quartz sand with a median grain size of 96 µm and a density of 2.65 g cm−3 (AGSCO technical data, 2018). This sand lacked cohesion and behaved as a transport-limited system. The experimental basin size varied for each material type; the basin used with the fine-grained substrate was 1 × 1 m, while the basin filled with the sand substrate was 2 × 4 m, thus allowing room for the more rapid growth of the permanent gullies in the more easily erodible substrate. For both substrates, water flowed out through a 0.076 m wide notch at the downstream end of the basin (Fig. 1). To initiate each run, we dropped the notch to 0.14 m below the surface of the substrate, thus creating a single abrupt base level drop. During each run a knickpoint developed at this notch and propagated upstream, carving a deep channel in the substrate.

Figure 1The experimental setup shown here allows water to flow from a settling basin over an erodible substrate and out through a 7.6 × 14 cm notch. The flow rates entering the basin range from 4 × 10−6 to 311 × 10−6 m3 s−1 and are controlled by a constant head tank. For each run a constant volume of water either 190 or 380 L is run over the erodible substrate. This figure shows the setup for the fine-grained substrate. The sand substrate setup was similar, although the erodible substrate was larger.
To initialize each run, the substrate material was mixed with water and smoothed into the basin to create a flat bed. Experiments began with a fully saturated bed to ensure that water flowed over the surface rather than infiltrating into it. We determined that the bed was at saturation and no longer oversaturated when there was no longer water on the surface of the sediment and water was no longer flowing out the downstream outlet. We analyzed the bed saturation by visual inspection rather than waiting a standard length of time because changes in humidity and temperature affected evaporation rates. Beginning with a saturated substrate allowed us to assume that the net flow was relatively constant in the cross-channel direction and no water was lost to infiltration into dry sediment.
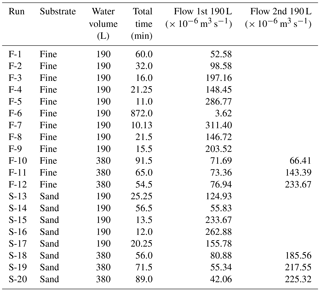
For each experimental run, water flowed over the uniform substrate as overland flow. We generated an even sheet flow by allowing water to flow over a broad crested weir as water was added to an upstream settling basin (Fig. 1). We controlled the flow rate of the water entering the settling basin with a constant-head tank, which received water from a tank with a predetermined volume of water (190 or 380 L). The flow rate was held constant through the entire run when only 190 L of water were used. When 380 L of water were used, the flow rate was held constant for the first 190 L, then increased and held constant for the second 190 L. Flow rates varied from 4 to 311 mL s−1 (4 × 10−6 to 311 × 10−6 m3 s−1) in the fine-grained substrate and 55 to 262 mL s−1 (55 × 10−6 to 262 × 10−6 m3 s−1) in the sand (Table 1; Fig. 2).
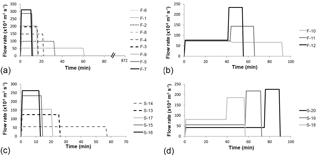
Figure 2These hydrographs show the range of flow rates tested. Each set of curves is for a separate set of experimental runs: (a) 190 L of water over the fine-grained substrate, (b) 380 L of water over the fine-grained substrate, (c) 190 L of water over the sand substrate, (d) 380 L of water over the sand substrate.
We collected topographic data before, during, and after each experimental run using a fully automated topographic scanner developed by engineers at the St. Anthony Falls Laboratory. The topographic scanner uses a standard laser that collects 2000 points per second in a gridded pattern. Data were collected with 20 × 25 mm point spacing and approximately 0.5 mm vertical resolution. For each experiment, we collected 2–5 topographic scans per 190 L of water. The experiment was paused at these intervals to complete the scans, ensuring that no data were lost in areas where water was present.
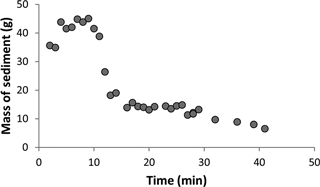
Topographic data were gridded to form a digital elevation model (DEM). To determine the total volume of sediment removed during each experimental run, we subtracted the DEM of the last scan from the DEM created from the initial scan over the flat initial surface. At each cell the vertical change was multiplied by the area of the cell to give a volume change. The total volume change was summed for each experimental run. We also calculated the volume of sediment eroded at intermediate scans to measure sediment flux over time. Because these data only provide coarse temporal measurements of sediment flux, we sampled sediment flux out of the experiment for 5 s every minute during experimental run F-11 to measure sediment flux at higher time resolution.
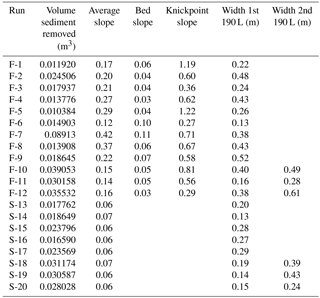
We imported the DEMs into ArcGIS to measure channel width and slope using the profile tool in the 3-D analyst toolbox. Channel width is defined as the distance between channel banks on a cross section. Where multiple channels formed, the cross section was selected just below the confluence of these channels. In the fine-grained substrate, channel width was roughly equal to the valley width along the full channel length. In the sand substrate, channels meandered, and therefore we measured channel width in the most upstream portion of the channel where migration had not yet occurred, and the valley width was equal to the channel width. We also measured the channel length and used this measurement to approximate knickpoint retreat rate. In both substrates we measured the channel length from the outlet to the break in slope at the flat upland surface. Slope was measured along the channel profile. In the fine-grained substrate we measured channel slope three separate ways: along the bed, along the knickpoint, and the average channel slope along the complete channel, including both channel bed and knickpoint zones. Where there was more than one knickpoint, we measured the bed slope and knickpoint slope for each section and averaged. Only one slope measurement, the average channel slope, was made on channels formed in the sand substrate because knickpoints were less prominent. In both substrates, average channel slope is a function of channel length, because elevation change for each channel is the same.
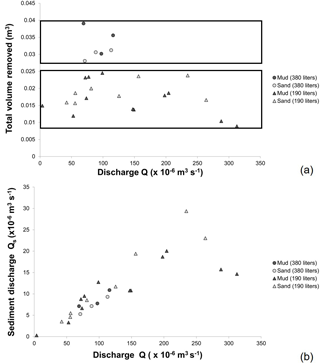
Figure 3The results from these experiments show that the total volume of sediment removed is not dependent on flow rate (a) or that sediment discharge is linearly related to water discharge (b). These charts also show that while sediment discharge is the same for the 380 L runs as it is for the 190 L runs at a given discharge, the total volume of sediment removed is greater in the 380 L runs.
These experiments show that the total eroded volume shows no consistent trend with flow rate. For all 190 L experimental runs, the volume of sediment removed ranges from 8.9 × 10−3 to 2.4 × 10−2 m3 with no clear trend (Fig. 3a). This result was the same for both the sand and the fine-grained substrate. Similarly, there is no trend in the volume of sediment removed in the 380 L runs, yet the volume of eroded sediment is greater (2.8 × 10−2 to 3.9 × 10−2 m3) than for the 190 L runs (Fig. 3). Put another way, the sediment discharge is linearly related to water discharge (Fig. 3b). For a natural system this implies that in a given storm event the amount of sediment eroded from a permanent gully is proportional to the amount of precipitation rather than the storm intensity, assuming flow rate generates shear stresses that surpass the critical shear stress of the sediment.
In experimental run F-11, the sediment discharge peaked early and rapidly decreased (Fig. 4). This pattern is also seen in several other experimental runs using the coarser resolution erosion data collected from the topographic scans, most prominently in run F-6 (Fig. 5). The experimental runs where this pattern was observed were also those where the channel interacted with a wall (see Supplement). After a channel touches a wall it is no longer able to widen, and flow preferentially remains against that smooth surface. While it was observed that the channels appeared to propagate most rapidly early in the experiment and then slow with each successive time interval, the scan data suggest that the total volume of sediment removed was relatively constant throughout the experiment except where the channel interacted with a wall. For the 380 L runs, where discharge was increased, there was a corresponding increase in sediment discharge, which was then maintained throughout the second half of the experiment.
3.1 Channel morphology
While sediment volumes removed are roughly the same in the fine-grained and sand channels, there are differences in how they erode. Channels in the fine-grained substrate erode primarily via head cut propagation. In contrast channels in the sand substrate erode due to head cut propagation as well as lateral channel migration (see Supplement).
The experiments also demonstrate a relationship between channel width and discharge. Generally, higher flows resulted in shorter, wider channels (Table 2). In particular, the 380 L runs reveal both the importance the total flow volume has for erosion volumes and how increasing flow rate affects channel geometry. In the cohesive fine-grained substrate, higher flows in the second half of the experiment formed a wider channel upstream of the already eroded gully, without altering the preexisting channel during the rest of the experiment (Fig. 6). Channel widths before the increased flow ranged from 0.16 to 0.40 m for a flow rate of 73 × 10−6 to 77 × 10−6 m3 s−1 and increased to 0.28 to 0.61 m for flow rates ranging from 143 × 10−6 m to 234 × 10−6 m3 s−1. The channels formed in the sand substrate responded differently; these channels widened along the entire channel length when flow was increased (Fig. 6). In the sand channels widths varied from 0.14 to 0.19 m for initial flows which varied from 42 × 10−6 to 81 × 10−6 m3 s−1, and the entire channel width increased to 0.24 to 0.43 m for the higher flows ranging from 185 × 10−6 to 225 × 10−6 m3 s−1 (Table 2).
The hydraulic geometry equation for width developed by Leopold and Maddock (1953) was used to quantify the relationship between width, W, and discharge, Q, for these experiments to determine how the experimental channels compare with natural channels:
where a and b are constants. The range of empirically derived exponents for b is between 0.3 and 0.5, derived from field measurements of both bedrock and alluvial streams (Knighton, 1998; Leopold and Maddock, 1953; Montgomery and Gran, 2001; Whipple, 2004). Studies of rills and ephemeral gullies have found that these relationships hold with a b value of 0.4–0.5 (Natchergaele et al., 2002; Torri et al., 2006).
To test how well these field-measured values describe our experimental channels, we calculated width using the reported values for b and iterated to find the best fit for a. In addition, we also iterated to determine what b value most accurately describes the trend in our experimental data. The root mean square error (RMSE) was calculated for each data set and is reported as a percentage of the average measured width value.
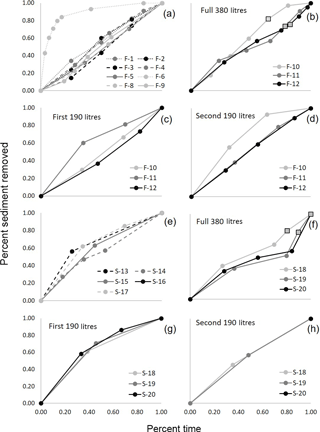
Figure 5In general, sediment discharge was near constant throughout the experiments, as indicated by the linear relationship between percent time elapsed and percent of total sediment removed in the graphs above. This result was generally consistent between for both fine-grained substrate (a–d) and the sand substrate (e–h). Results from the 190 L runs are graphed in (a) and (e) and the 380 L runs are graphed in (b) and (f) with the first half broken out in (c) and (g) and the second half in (f) and (h).
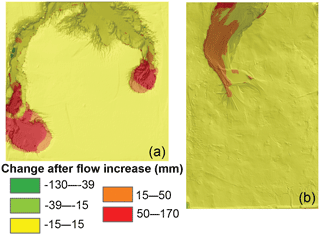
Figure 6These differenced DEMs show how changes in flow impact channel width. In the fine-grained runs (a) the width changed in the newly formed channel, while in the sand runs (b) the channel width was altered along the entire channel length. Flow is bottom to top in both images.

Figure 7Channel width can be modeled using the hydraulic geometry relationship (Eq. 1). In both plots the solid black line is a 1 : 1 line. (a) The relationship measured in the channels formed in the fine-grained substrate has a constant b value that is less than the values commonly observed in nature. (b) The relationship measured in the channels formed in the sand substrate has a constant b value of 0.4, which is in the intermediate range of the commonly proposed constants.
Using the field-derived b exponents ranging from 0.3 to 0.5, the RMSE is 29–31 % of the average measured width in the fine-grained substrate. The best fit for the experimental data results in a b value of 0.27, resulting in an RMSE of 28.5 % (Fig. 7). In the sand substrate the best fit for the data falls within the range of field-derived exponents. The error is minimized when b is 0.39, resulting in an RMSE of 9 % (Fig. 7).
3.2 Modeled sediment transport
Results from these experiments appear to conflict with standard sediment transport equations which generally predict a nonlinear increase in sediment flux as discharge increases (e.g., Engelund and Hansen, 1967; Meyer-Peter and Müller, 1948; Parker, 1990; Wilcock and Crowe, 2003), yet these equations typically include an additional factor, often slope, which, if also varied, can account for changes in discharge resulting in a linear increase in sediment flux. Below are examples of commonly used sediment transport models that, when applied to these experiments, account for the linear nature of the sediment flux discharge relationship.
Commonly erosion in detachment-limited systems is modeled by the stream power incision model (Howard and Kirby, 1983):
where k, md and nd are constants, dzdt−1 is vertical erosion rate, and S is the slope. In the detachment-limited fine-grained substrate, all erosion took place at the knickpoint and therefore we consider only knickpoint retreat rate and use Sk, knickpoint slope, in place of S. Because this rate is a horizontal retreat rate rather than vertical incision rate we must convert Eq. (2) appropriately:
where U is the knickpoint retreat rate. The exponents md and nd have been derived for a variety of natural environments. Typically the md ∕ ratio (concavity index) is approximately 0.35–0.6 (Whipple and Tucker, 1999; Baldwin et al., 2003). The exponent nd ranges between two-thirds and five-thirds depending on the erodibility of the substrate where more easily eroded sediment has a lower value for the exponent nd (Foley, 1980; Howard and Kirby, 1983; Whipple et al., 2000). The exponents md and nd for uniform detachment-limited landscapes (i.e., badlands) reported by Howard and Kirby (1983) are four-ninths and two-thirds, respectively. While the md ∕ ratio is slightly higher than reported elsewhere, we used these values to model erosion in our experiments because, like the badlands, our experimental setup was spatially homogeneous and easily eroded. RMSE was measured between the calculated U and the measured U and minimized by modifying the coefficient k. The RMSE was 25 % of the measured average knickpoint retreat rate for the fine-grained substrate. The detachment-limited equation is not appropriate for the sand substrate because there is both headward and lateral erosion, which is not captured by the equation. In addition, the knickpoint slope cannot be measured in the sand substrate.
Sediment loads from the sand substrate were modeled with the transport-limited equation (Pelletier, 2011):
where k, mt and nt are constants and qs is the volumetric unit sediment flux. This equation can be derived from the Engelund and Hansen (1967) equation where both mt and nt equal five-thirds. The Engelund and Hansen (1967) equation is ideal because it does not have an incipient motion threshold as many other sediment transport equations do. Here again the RMSE was measured between the measured and calculated qs and minimized using the coefficient k. The RMSE was 41 % of the average volumetric unit sediment discharge for the sand substrate. The transport-limited equation was also tested with the fine-grained substrate. For this test the average slope was used for S and the RMSE calculated was 86 % of the average volumetric unit sediment discharge. This high RMSE value supports the observation that the fine-grained substrate does not behave as a transport-limited system.
Our experiments demonstrate that, over a range of conditions, the sediment volume eroded during permanent gully growth under application of a fixed volume of water is independent of the rate at which the water is supplied. Thus, sediment discharge is linearly related to water discharge in both detachment-limited and transport-limited systems. These results contrast with data from many preexisting streams where changing flow intensity has resulted in increased erosion volume (i.e., Boateng et al., 2012; Ma et al., 2010; Naik and Jay, 2011), yet these data may not be directly applicable to early-stage gullies. We suggest that because gullies are actively evolving in response to a given hydrology, the channel morphology that develops reflects that hydrology, with erosion balanced by altering channel slope. This is supported by sediment transport Eqs. (4) and (5) which, when applied to our experiments, predict the measured sediment discharges by including the effects of both discharge and slope. In preexisting channels where channel slope may take tens of thousands of years to adjust to changing flows, both equations would predict a nonlinear increase in sediment discharge with increasing water discharge. Gullies evolve more rapidly in response to the imposed discharge and can balance erosion by adjusting channel slope in response to a change in the hydrologic regime.
Moreover, our findings suggest that anthropogenic changes to the discharge regime could affect channel morphology (i.e., channel width), without changing sediment output derived from permanent gullies. Where water discharge was increased in the 380 L runs, the channel quickly evolved in response to the new discharge by creating a wider channel. In these experiments the observed response to the increased discharge differed for the fine-grained and sand substrate (Fig. 6), suggesting cohesion may be an important factor in how a channel initially responds to a new discharge regime.
The results of our experiments follow the hydraulic geometry relationship for width in Eq. (1), although with lower exponents than usually measured in field studies for alluvial and bedrock channels (Knighton, 1998; Leopold and Maddock, 1953; Montgomery and Gran, 2001; Whipple, 2004) and rills and ephemeral gullies (Nachtergaele et al., 2002; Torri et al., 2006). While this relationship is typically applied to describing width or discharge changes in a single channel, it works here for these separate channels because each comparable channel is carving through the same substrate. In the fine-grained substrate the empirical exponent b for these data is lower than has been derived for natural channels. This may be a result of the steep channel walls developed in these experiments; in natural permanent gullies where near-vertical channel walls are less common, we expect that this exponent would be closer to the reported values. In the sand substrate where steep channel walls could not develop, the empirical exponent b is 0.39, which is only slightly lower than the range typically considered for alluvial channels (Rodriquez-Iturbe and Rinaldo, 1997), but similar to exponents found in rills and ephemeral gullies (Nachtergaele et al., 2002; Torri et al., 2006).
Channel width has also been modeled by Wells et al. (2013), who found that both slope and discharge play a role in setting channel width. This relationship was tested for the results of these experiments, yet it was not as strong as the relationship with discharge alone. Slope in the Wells et al. (2013) study could not change during the experiment, which contrasts with our experiments where slope is a free parameter that adjusts to discharge. This finding further supports the distinction between rapidly evolving channels like permanent gullies, and more stable systems where slope does not change as quickly, causing channel adjustments to occur primarily through changes in channel width and through a nonlinear erosion response.
Experiments focused on head cut growth completed by Bennett et al. (2000) also reported a linear relationship between water discharge and sediment discharge, yet the water discharge was lower, and the slope of the relationship was much higher in our results. This may suggest that a nonlinear relationship between sediment and water may develop over a wider range of flow rates than tested here, yet more research would be required. In addition, Bennett et al. (2000) noted two dominant processes for head cut migration: surface seal failure, which is similar to slab failure reported in other papers, and plunge pool scour, where head cut migration is driven by undercutting. Although both of these mechanisms could lead to large blocks of sediment collecting at the base of the head cut, creating periods of quiescence in head cut migration, the authors do not indicate that head cut migration stalled in their experiments. The erosion mechanisms described by Bennett et al. (2000) are similar to the mechanisms observed in our experiments, in that there was a continuous head cut propagation, although we did not observe significant plunge pool development.
In a numerical study, Istanbulluoglu et al. (2005) tested the effect of changing rain intensity while storm volume was held constant. The modeled results of their study showed an increase in the volume of sediment eroded as intensity increased. This result is in direct conflict with our results, yet there are many distinctions between the two studies that may explain this discrepancy. The Istanbulluoglu et al. (2005) model assumed gully erosion due to slab failure in a detachment-limited system. While the fine-grained substrate in our physical experiments was also detachment limited, erosion occurred grain by grain rather than as large blocks. Once these grains were detached, the flow was easily able to carry them through the channel and there was no measurable deposition in any of the experimental runs. In contrast, erosion in the slab failure model occurred in response to pore pressure build up in tension cracks resulting in large failures. This slab failure model does not require that the flow be able to carry the detached sediment and often resulted in deposition at the toe of the knickpoint, which increases resistance to future failure.
It is likely that both slab failure and granular knickpoint propagation occur in permanent gullies throughout the world. The relative importance of each process is dependent on the substrate and the knickpoint slope. Tension cracks develop behind steep slopes where shrinkage occurs due to desiccation and horizontal tensile stresses generated in large part by gravity are greater than the tensile strength of the sediment (Darby and Thorne, 1994). Cracks like this are likely to form on the landscape above steep head cuts in cohesive sediment, between storm events. In neither our study nor the Bennett et al. (2000) did we model individual storm events rather than a constant overland flow. If we had, it is likely we would have also developed tension cracks in the cohesive substrates. Because this was outside of the scope of these experiments it is difficult to form accurate conclusions on how the development of tension cracks and the subsequent failure events would have altered these results, but an analogous study that encouraged erosion by slab failure would be a useful extension.
Our experimental results are not clear with regard to Sidorchuk's (1999) two-stage gully evolution model. For most runs it appears that the second stage of gully evolution was not achieved. In a few specific cases, most notably runs F-6 and F-11, there does appear to be an early peak and later decrease and stabilization in sediment discharge. Surprisingly the results of these runs were not among the lowest total sediment discharges, as might be expected where the second stage was achieved. It is possible that if all the runs were allowed to continue we may have reached a stable system where the second stage of gully evolution was achieved. If this was allowed to occur, we would anticipate that additional water at the same discharge rate would not cause measurable erosion, potentially altering the relationship we have observed. What is not clear is how long it takes for this steady state to occur, and how this may relate to discharge.
Based on the results of this study and the comparison with previous gully studies, it is important to consider a wide range of variables when mitigating permanent gully erosion. The results from our experiments suggest that during early stages of permanent gully growth, increasing overland flow rates will not result in increased sediment yield, if the volumes of water delivered are not changed. Moreover, while sediment loads are not affected by changing flow rates, channel morphology is. Another important variable to consider is the mode of head cut retreat. The experimental results apply in environments with steep slopes where erosion is grain-by-grain. In places where tension cracks develop, the slab failure mechanism highlighted by Istanbulluoglu et al. (2005) might dominate. If the tension crack failure mechanism is the dominant process of head cut retreat, flow rates and storm intensity may become more important than they were in our study because the slabs may require a higher threshold to break up and mobilize, allowing further head cut propagation.
These experiments highlight how young incising channels like permanent gullies can respond to changing hydrology differently than higher order channels that are later in their evolution. A relevant future study should investigate how natural gullies, which have a great deal more variability than this experimental system, respond to changing hydrology. The conclusions from this project are outlined below:
-
The experiments here suggest that water volume, rather than discharge, controls the total volume of erosion during permanent gully formation. This result holds true for both transport-limited and detachment-limited systems.
-
As long as slope is a free parameter in these rapidly evolving systems, changes in flow rate can be accommodated through an adjustment in both cross-sectional and longitudinal channel geometry. Wider channels were typically shorter and thus steeper.
-
In both substrates, variations in channel width were described by the hydraulic geometry relationship proposed by Leopold and Maddock (1953), with wider channels forming in response to higher discharge.
-
Sediment transport in sand and fine-grained substrates was well described by the transport-limited sediment flux equation and the detachment-limited stream power equation, respectively.
The data are provided in the Supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/hess-22-3261-2018-supplement.
The authors declare that they have no conflict of interest.
This work was funded in part by a Geological Society of America Graduate
student research grant and by the National Center for Earth-surface Dynamics (NCED),
which is funded by the Office of Integrative Activities, National
Science Foundation grant EAR-0120914. We appreciate comments and reviews
from Robert Wells and two anonymous reviewers.
Edited by: Thom Bogaard
Reviewed by: Robert Wells and two anonymous referees
Abrahams, A. D. and Parsons, A. J.: Resistance to overland flow on desert pavement and its implications for sediment transport modeling, Water Resour. Res., 27, 1827–1836, 1991.
Adediji, A., Jeje, L. K., and Ibitoye, M. O.: Urban development and informal drainage patterns: Gully dynamics in Southwestern Nigeria, Appl. Geogr., 40, 90–102, 2013.
Agsco technical Data: http://www.agsco.com/assets/pdfs/Silica-Sands-Flours-Tech-Data-Sheet-06-04-2014.pdf, last access: 7 February 2018.
Alonso, C. V., Bennett, S. J., and Stein, O. R.: Predicting head cut erosion and migration in concentrated flows typical of upland areas, Water Resour. Res., 38, 39-1–39-15, 2002.
Ambers, R. K., Druckenbrod, D. L., and Ambers, C. P.: Geomorphic response to historical agriculture at Monument Hill in the Blue Ridge foothills of central Virginia, Catena, 65, 49–60, 2006.
Arnold Jr., C. L. and Gibbons, C. J.: Impervious surface coverage: the emergence of a key environmental indicator, J. Am. Plan. Assoc., 62, 243–258, 1996.
Baldwin, J. A., Whipple, K. X., and Tucker, G. E.: Implications of the shear stress river incision model for the timescale of postorogenic decay of topography, J. Geophys. Res., 108, 2156–2202, 2003.
Belmont, P., Gran, K., Schottler, S., Wilcock, P., Day, S., Jennings, C., Lauer, J., Viparelli, E., Willenbring, J., Engstrom, D., and Parker, G.: Large shift in source of fine sediment in the Upper Mississippi River, Environ. Sci. Technol., 45, 8804–8810, 2011.
Bennett, S. J., Alonso, C. V., Prasad, S. N., and Römkens, M. J. M.: Experiments on headcut growth and migration in concentrated flows typical of upland areas, Water Resour. Res., 36, 1911–1922, 2000.
Blann, K. L., Anderson, J. L., Sands, G. R., and Vondracek, B.: Effects of agricultural drainage on aquatic ecosystems: a review, Crit. Rev. Environ. Sci. Tech., 39, 909–1001, 2009.
Boateng, I., Bray, M., and Hooke, J.: Estimating the fluvial sediment input to the coastal sediment budget: a case study of Ghana, Geomorphology, 138, 100–110, 2012.
Bryan, R. B.: Knickpoint evolution in rillwash, Catena, 17, 111–132, 1990.
Bull, L. J. and Kirkby, M. J.: Gully processes and modelling, Prog. Phys. Geogr., 21, 354– 374, 1997.
Bull, L. J. and Kirkby, M.: Channel heads and channel extension, in: Dryland Rivers: Hydrology and Geomorphology of Semi-Arid Channels, edited by: Bull, L. J. and Kirkby, M. J., Wiley, Chichester, UK, 263–298, 2002.
Chiverrell, R. C., Harvey, A. M., and Foster, G. C.: Hillslope gullying in the Solway Firth–Morecambe Bay region, Great Britain: Responses to human impact and/or climatic deterioration?, Geomorphology, 84, 317–343, 2007.
Chu-Agor, M. L., Fox, G. A., Cancienne, R. M., and Wilson, G. V.: Seepage caused tension failures and erosion undercutting of hillslopes, J. Hydrol., 359, 247–259, 2008.
Darby, S. E. and Thorne, C. R.: Prediction of tension crack location and riverbank erosion hazards along destabilized channels, Earth Surf. Proc. Land., 19, 233–245, 1994.
Dietrich, W. E. and Dunne, T.: The Channel Head, in: Channel Network Hydrology, edited by: Beven, K. J. and Kirkby, M. J., Wiley, Chichester, UK, 175–219, 1993.
Dunne, T.: Hydrology, mechanics, and geomorphic implications or erosion by subsurface flow, in: Groundwater Geomorphology: The Role of Subsurface Water in Earth-Surface Processes and Landforms, edited by: Higgins, C. G. and Coates, D. R., Geological Society of America as Special Paper 252, Geological Society of America, Colorado, Boulder, 1–28, 1990.
Ebisemiju, F. S.: The response of headwater stream channels to urbanization in the humid tropics, Hydrol. Process., 3, 237–253, 1989.
Einstein, H. A. and Barbarossa, N. L.: River channel roughness, T. Am. Soc. Civ. Eng., 117, 1121–1132, 1951.
Eitel, J. U. H., Williams, C. J., Vierling, L. A., Al-Hamdan, O. Z., and Pierson, F. B.: Suitability of terrestrial laser scanning for studying surface roughness effects on concentrated flow erosion processes in rangelands, Catena, 87, 398–407, 2011.
Engelund, F. and Hansen, E., A monograph on sediment transport in alluvial streams, TEKNISKFORLAG, Copenhagen, Denmark, 1967.
Espey Jr., W. H., Morgan, C. W., and Masch, F. D.: A study of some effects of urbanization on storm runoff from a small watershed, Tech. Rep. 44D 07-6501 CRWR-2, Ctr. for Res. in Water Resour., Univ. Texas, Austin, 1965.
Farres, P. J.: The role of time and aggregate size in the crusting process, Earth Surf. Proc. Land., 3, 243–254, 1978.
Flores-Cervantes, J. H., Istanbulluoglu, E., and Bras, R. L.: Development of gullies on the landscape: A model of headcut retreat resulting from plunge pool erosion, J. Geophys. Res., 111, 2156–2202, 2006.
Foley, M. G.: Bed-rock incision by streams, Geol. Soc. Am. Bull., 91, 2189–2213, 1980.
Fox, G. A. and Wilson, G. V.: The role of subsurface flow in hillslope and stream bank erosion: a review, Soil Sci. Soc. Am. J., 74, 717–733, 2010.
Gran, K. B., Finnegan, N., Johnson, A. L., Belmont, P., Wittkop, C., and Rittenour, T.: Landscape evolution, valley excavation, and terrace development following abrupt postglacial base level fall, Geol. Soc. Am. Bull., 125, 1068–1082, 2013.
Gran, K. B., Belmont, P., Day, S., Jennings, C., Lauer, J. W., Viparelli, E., Wilcock, P., and Parker, G.: An integrated sediment budget for the Le Sueur River basin, Final report Presented to the Minnesota Pollution Control Agency, Minnesota, 2011.
Grovers, G., Giménez, R., and Van Oost, K.: Rill erosion: Exploring the relationship between experiments, modelling and field observations, Earth-Sci. Rev., 84, 87–102, 2007.
Haddeland, I., Lettenmaier, D. P., and Skaugen, T.: Effects of irrigation on the water and energy balances of the Colorado and Mekong river basins, J. Hydrol., 324, 210–223, 2005.
Hinds, N. E. A.: Amphitheatre valley heads, J. Geol., 33, 816–818, 1925.
Holland, W. N. and Pickup, G.: Flume study of knickpoint development in stratified sediment, Geol. Soc. Am. Bull., 87, 76–82, 1976.
Howard, A. D.: Groundwater sapping experiments and modeling, in: Sapping Features of the Colorado Plateau: A Comparative Planetary Geology Field Guide, NASA, 491, 71–83, 1988.
Howard, A. D. and Kirby, G.: Channel changes in badlands, Geol. Soc. Am. Bull., 94, 739–752, 1983.
Istanbulluoglu, E., Bras, R. L., Flores-Cervantes, H., and Tucker, G. E.: Implications of bank failures and fluvial erosion for gully development: Field observations and modelling, J. Geophys. Res., 110, 2156–2202, 2005.
Knapen, A. and Poesen, J.: Soil erosion resistance effects on rill and gully initiation points and dimensions, Earth Surf. Proc. Land., 35, 217–228, 2010.
Knapen, A., Poesen, J., Govers, G., Gyssels, G., and Nachtergaele, J.: Resistance of soils to concentrated flow erosion: A review, Earth-Sci. Rev., 80, 75–109, 2007.
Knighton, D.: Fluvial forms and processes, Edward Arnold, London, p. 377, 1998.
Kosov, B. F., Nikol'skaya, I. I., and Zorina, Y. F.: Eksperimental'nyye issledovaniya ovragoobrazovaniya, in: Eksperimental'naya geomorfologiya, edited by: Makkaveev, N. I., Moscow, 113–140, 1978.
Lamb, M. P., Howard, A. D., Johnson, J., Whipple, K. X., Dietrich, W. E., and Perron, J. T.: Can springs cut canyons into rock?, J. Geophys. Res., 111, E07002, https://doi.org/10.1029/2005JE002663, 2006.
Lenhart, C. F., Titov, M. L., Ulrich, J. S., Nieber, J. L., and Suppes, B. J.: The role of hydrologic alteration and riparian vegetation dynamics in channel evolution along the lower Minnesota River, T. ASABE, 56, 549–561, 2013.
Leopold, L. B. and Maddock, T.: The hydraulic geometry of stream channels and some physiographic implications, US Geol. Survey Prof. Paper 252, US Geological Survey, Washington, D.C., 1953.
Ma, H., Yang, D., Tan, S. K., Gao, B., and Hu, Q.: Impact of climate variability and human activity on streamflow decrease in the Miyun Reservoir catchment, J. Hydrol., 389, 317–324, 2010.
Merritt, E.: The identification of four stages during micro-rill development, Earth Surf. Proc. Land., 9, 493–496, 1984.
Meyer-Peter, E. and Müller, R.: Formulas for bed-load transport, IAHR, Stockholm, 1948.
Montgomery, D. R. and Gran, K. B.: Downstream variations in the width of bedrock channels, Water Resour. Res., 37, 1841–1846, 2001.
Mosley, M. P.: Experimental study of rill erosion, T. ASAE, 17, 909–913, 1974.
Nachtergaele, J., Poesen, J., Steegen, A., Takken, I., Beuselinck, L., Vandekerckhove, L., and Grovers, G.: The value of a physically based model versus an empirical approach in the prediction of ephemeral gully erosion for loess derived soils, Geomorphology, 40, 237–252, 2001.
Nachtergaele, J., Poesen, J., Sidorchuk, A., and Torri, D.: Prediction of concentrated flow width in ephemeral gully channels, Hydrol. Process., 16, 1935–1953, 2002.
Naik, P. K. and Jay, D. A.: Distinguishing human and climate influences on the Columbia River: Changes in mean flow and sediment transport, Hydrolog. Sci. J., 404, 259–277, 2011.
Nichols, M. H., Magirl, C., Sayre, N. F., and Shaw, J. R.: The geomorphic legacy of water and erosion control structures in a semiarid rangeland watershed, Earth Surf. Proc. Land., 43, 909–918, 2017.
Paola, C., Straub, K., Mohrig, D., and Reinhardt, L.: The “unreasonable effectiveness” of stratigraphic and geomorphic experiments, Earth-Sci. Rev., 97, 1–43, 2009.
Parker, G.: Surface-based bedload transport relation for gravel rivers, J. Hydraul. Res., 28, 417–436, 1990.
Parker, R. S.: Experimental study of basin evolution and its hydrologic implications, PhD dissertation, Colo. State Univ., Ft. Collins, 1977.
Parker, R. S. and Schumm, S. A.: Experimental study of drainage networks, in: Badland Geomorphology and Piping, edited by: Bryan, R. and Yair, A., Geobooks, Norwich, England, 153–168, 1982.
Paul, M. J. and Meyer, J. L.: Streams in the urban landscape, Ann. Rev. Ecol. Syst., 32, 333–365, 2001.
Pelletier, J. D.: Fluvial and slope-wash erosion of soil-mantled landscapes: detachment- or transport-limited, Earth Surf. Proc. Land., 37, 37–51, 2011.
Pierson, F. B., Bates, J. D., Svejcar, T. J., and Hardegree, S. P.: Runoff and erosion after cutting western Juniper, Rangeland Ecol. Manage., 60, 285–292, 2007.
Poesen, J., Nachtergaele, J., Verstaeten, G., and Valentin, C.: Gully erosion and environmental change: importance and research needs, Catena, 50, 91–133, 2003a.
Poesen, J. W. A., Torri, D. B., and VanWalleghem, T.: Gully erosion: Procedures to adopt when modelling soil erosion in landscapes affected by gullying, in: Handbook of Erosion Modelling, 1st Edn., edited by: Morgan., R. P. C. and Nearing, M. A., Blackwell Publishing Ltd., Hoboken, NJ, 360–386, 2003b.
Robinson, K. M. and Hanson, G. J.: A deterministic headcut advance model, T. ASAE, 37, 1437–1443, 1994.
Robinson, M. and Rycroft, D. W.: Agricultural Drainage, in: Agronomy Monograph 38, edited by: Skaggs, R. W. and van Schifgaarde, J., ASA, CSSA, SSSA, Madison, WI, 767–800, 1999.
Rodriquez-Iturbe, I. and Rinaldo, A.: Fractal River Basins: Chance and Self-Organization, Cambridge Univ. Press, New York, 547 pp., 1997.
Römkens, M. J. M. and Wang, J. Y.: Soil roughness changes from rainfall, T. Am. Soc. Civ. Eng., 31, 408–413, 1987.
Seaburn, G. E.: Effects of urban development on direct runoff to East Meadow Brook, Nassau County, New York, USGS Prof. Paper 627-B, US Geological Survey, Washington, 1969.
Sidorchuk, A.: Dynamic and static models of gully erosion, Catena, 37, 401–414, 1999.
Sidorchuk, A.: Stages in gully evolution and self-organized criticality, Earth Surf. Proc. Land., 31, 1329–1344, 2006.
Stankoviansky, M. I. L. O. Š.: Gully evolution in the Myjava Hill Land in the second half of the last millennium in the context of the central-European area, Geogr. Pol., 76, 89–107, 2003.
Stein, O. R. and LaTray, D. A.: Experiments and modeling of head cut migration in stratified soils, Water Resour. Res., 38, 20-1–20-12, 2002.
Torri, D., Poesen, J., Borselli, L., and Knapen, A.: Channel width–flow discharge relationships for rills and gullies, Geomorphology, 76, 273–279, 2006.
Vandekerckhove, L., Poesen, J., Oostwoud-Wijdenes, D., Nachtergaele, J., Kosmas, D., Roxo, M. J., and Figueiredo, T. D.: Thresholds for gully initiation and sedimentation in Mediterranean Europe, Earth Surf. Proc. Land., 25, 1201–1220, 2000.
Van der Ploeg, R. R., Ehlers, W., and Sieker, F.: Floods and other possible adverse environmental effects of meadowland area decline in former West Germany, Naturwissenschaften, 86, 313–319, 1999.
Vanwalleghem, T., Van Den Eeckhaut, M., Poesen, J., Deckers, J., Nachtergaele, J., Van Oost, K., and Slenters, C.: Characteristics and controlling factors of old gullies under forest in a temperate humid climate: a case study from the Meerdaal Forest (Central Belgium), Geomorphology, 56, 15–29, 2003.
Vanwalleghem, T., Poesen, J., Van Den Eeckhaut, M., Nachtergaelel, J., and Deckers, J.: Reconstructing rainfall and land-use conditions leading to the development of old gullies, Holocene, 15, 378–386, 2005.
Wells, R. R., Momm, H. G., Rigby, J. R., Bennett, S. J., Bingner, R. L., and Dabney, S. M.: An empirical investigation of gully widening rates in upland concentrated flows, Catena, 101, 114–121, 2013.
Whipple, K. X.: Bedrock rivers and the geomorphology of active orogens, Annu. Rev. Earth Planet. Sci., 32, 151–185, 2004.
Whipple, K. X. and Tucker, G. E.: Dynamics of the stream-power river incision model: Implications for height limits of mountain ranges, landscape response timescales, and research needs, J. Geophys. Res.-Solid Ea., 104, 17661–17674, 1999.
Whipple, K. X., Hancock, G. S., and Anderson, R. S.: River incision into bedrock: Mechanics and relative efficacy of plucking, abrasion, and cavitation, Geol. Soc. Am. Bull., 112, 490–503, 2000.
Wilcock, P. R. and Crowe, J. C.: Surface-based transport model for mixed-size sediment, J. Hydraul. Eng., 129, 120–128, 2003.
Wilson, G.: Understanding soil-pipe flow and its role in ephemeral gully erosion, Hydrol. Process., 25, 2354–2364, 2011.
Wilson, G. V.: Mechanisms of ephemeral gully erosion caused by constant flow through a continuous soil-pipe, Earth Surf. Proc. Land., 34, 1858–1866, 2009.
Wiskow, E. and van der Ploeg, R. R.: Calculation of drain spacings for optimal rainstorm flood control, J. Hydrol., 272, 163–174, 2003.
Zeeospheres G Series data sheet: http://www.zeeospheres.com/wp-content/uploads/2015/12/G-Series.pdf, last access: 7 February 2018.