the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Sensitivity and identifiability of hydraulic and geophysical parameters from streaming potential signals in unsaturated porous media
Anis Younes
Jabran Zaouali
François Lehmann
Fluid flow in a charged porous medium generates electric potentials called streaming potential (SP). The SP signal is related to both hydraulic and electrical properties of the soil. In this work, global sensitivity analysis (GSA) and parameter estimation procedures are performed to assess the influence of hydraulic and geophysical parameters on the SP signals and to investigate the identifiability of these parameters from SP measurements. Both procedures are applied to a synthetic column experiment involving a falling head infiltration phase followed by a drainage phase.
GSA is used through variance-based sensitivity indices, calculated using sparse polynomial chaos expansion (PCE). To allow high PCE orders, we use an efficient sparse PCE algorithm which selects the best sparse PCE from a given data set using the Kashyap information criterion (KIC). Parameter identifiability is performed using two approaches: the Bayesian approach based on the Markov chain Monte Carlo (MCMC) method and the first-order approximation (FOA) approach based on the Levenberg–Marquardt algorithm. The comparison between both approaches allows us to check whether FOA can provide a reliable estimation of parameters and associated uncertainties for the highly nonlinear hydrogeophysical problem investigated.
GSA results show that in short time periods, the saturated hydraulic conductivity (Ks) and the voltage coupling coefficient at saturation (Csat) are the most influential parameters, whereas in long time periods, the residual water content (θs), the Mualem–van Genuchten parameter (n) and the Archie saturation exponent (na) become influential, with strong interactions between them. The Mualem–van Genuchten parameter (α) has a very weak influence on the SP signals during the whole experiment.
Results of parameter estimation show that although the studied problem is highly nonlinear, when several SP data collected at different altitudes inside the column are used to calibrate the model, all hydraulic and geophysical parameters (na,Csat) can be reasonably estimated from the SP measurements. Further, in this case, the FOA approach provides accurate estimations of both mean parameter values and uncertainty regions. Conversely, when the number of SP measurements used for the calibration is strongly reduced, the FOA approach yields accurate mean parameter values (in agreement with MCMC results) but inaccurate and even unphysical confidence intervals for parameters with large uncertainty regions.
Flow through a charged porous medium can generate an electric potential (Zablocki, 1978; Ishido and Mizutani, 1981; Allègre et al., 2010; Jougnot and Linde, 2013), called streaming potential (SP). SP signals play an important role in several applications related to hydrogeology and geothermal reservoir engineering as they are useful for examining subsurface flow dynamics. During the last decade, surface SP anomalies have been widely used to estimate aquifers' hydraulic properties (Darnet et al., 2003). Interest in SP is motivated by its low cost and its high sensitivity to water flow. Either coupled or uncoupled approaches can be used for hydraulic parameter estimation from SP signals (Mboh et al., 2012). In the uncoupled approach, Darcy velocities (e.g., Jardani et al., 2007; Bolève et al., 2009) are obtained from the tomographic inversion of SP signals and are then used for the calibration of the hydrologic model. In the coupled approach, anomalies related to the tomographic inversion are avoided by inverting the full coupled hydrogeophysical model (Hinnell et al., 2010).
The SP signals have been widely studied in saturated porous media (Bogoslovsky and Ogilvy, 1973; Patella, 1997; Sailhac and Marquis, 2001; Richards et al., 2010; Bolève et al., 2009, among others). Fewer studies focused on the application of the SP signal in unsaturated flow despite the large interest in such nonlinear problems (Linde et al., 2007; Allègre et al., 2010; Mboh et al., 2012; Jougnot and Linde, 2013). Hence, in this work we are interested in the SP signals in unsaturated porous media. Our main objective is to investigate the usefulness of the SP signals for the characterization of soil parameters. For this purpose, we evaluate the impact of uncertain hydraulic and geophysical parameters on the SP signals and assess the identifiability of these parameters from the SP measurements.
The impact of soil parameters on SP signals is investigated using global sensitivity analysis (GSA). This is a useful tool for characterizing the influential parameters that contribute the most to the variability of model outputs (Saltelli et al.,1999; Sudret, 2008) and for understanding the behavior of the modeled system. GSA has been applied in several areas, for risk assessment for groundwater pollution (e.g., Volkova et al., 2008), nonreactive (Fajraoui et al., 2011) and reactive transport experiments (Fajraoui et al., 2012; Younes et al., 2016), for unsaturated flow experiments (Younes et al., 2013), natural convection in porous media (Fajraoui et al., 2017) and seawater intrusion (Rajabi et al., 2015; Riva et al., 2015). To the best of our knowledge, GSA has never been used for SP signals in unsaturated porous media. Hence, in the first part of this study, GSA is performed on a conceptual model inspired from the laboratory experiment of Mboh et al. (2012) in which SP signals are measured at different altitudes in a sandy soil column during a falling-head infiltration phase followed by a drainage phase. Four uncertain hydraulic parameters, saturated hydraulic conductivity (Ks), residual water content (θr), fitting Mualem–van Genuchten parameters (α,n) and two geophysical parameters (Archie's saturation exponent (na) and voltage coupling coefficient at saturation (Csat)), are investigated. GSA of SP signals is performed by computing the variance-based sensitivity indices using polynomial chaos expansion (PCE). To reduce the number of PCE coefficients while maintaining high PCE orders, we use the efficient sparse PCE algorithm developed by Shao et al. (2017) which selects the best sparse PCE from a given data set using the Kashyap information criterion (KIC).
In the second part of this study, we investigate the identifiability of hydrogeophysical parameters from SP measurements. For this purpose, parameter estimation is performed using two different approaches. The first is a Bayesian approach in which model parameters are treated as random variables and characterized by their probability density functions. With this approach, the prior knowledge about the model and the observed data is merged to define the joint posterior probability distribution function of the parameters. In the sequel, Bayesian analysis is conducted using the DREAM(ZS) software (Laloy and Vrugt, 2012; Vrugt, 2016) based on the Markov chain Monte Carlo (MCMC) method. MCMC has been successfully used in various inverse problems (e.g., Vrugt et al., 2003, 2008; Arora et al., 2012; Younes et al., 2017). The MCMC method yields an ensemble of possible parameter sets that satisfactorily fit the available data. These sets are then employed to estimate the posterior parameter distributions and hence the optimal parameter values and the associated 95 % confidence intervals (CIs) in order to quantify the parameters' uncertainty. The second inversion approach is the commonly used first-order approximation (FOA) approach based on the standard Levenberg–Marquardt algorithm. Two scenarios are considered to check whether FOA can provide a reliable estimation of parameters and associated uncertainties for the highly nonlinear hydrogeophysical problem investigated in the case of abundant data (small uncertainty regions) and in the case of scarcity of data (large uncertainty regions). In the first scenario, SP data collected from sensors at five different locations are taken into account for the calibration. In the second scenario, only the SP data from one sensor are used for model calibration.
The present study is set out as follows. Section 2 presents the hydrogeophysical model and the reference solution. Section 3 reports on the GSA results of SP signals. Then, Sect. 4 discusses results of parameter estimation with both MCMC and FOA approaches for the two investigated scenarios.
2.1 Test case description
The test case considered in this work is similar to the laboratory experiment developed in Mboh et al. (2012), involving a falling-head infiltration phase followed by a drainage phase (Fig. 1). This experiment is representative of several laboratory SP experiments (Linde et al., 2007; Allègre et al., 2010; Jougnot and Linde, 2013, among others). Quartz sand is evenly packed in a plastic tube with an internal diameter of 5 cm to a height of Ls=117.5 cm. The column is initially saturated with a ponding of Lw=48 cm above the soil surface. Five sensors allowing SP measurements are installed 5, 29, 53, 77 and 101 cm from the surface, respectively. The column has a zero pressure head maintained at its bottom. At the top of the column, the boundary condition corresponds to a Dirichlet condition with a prescribed pressure head condition during the falling-head phase, followed by a Neumann condition with zero infiltration flux during the drainage phase. During the falling-head phase, the prescribed pressure head htop=48 cm has an exponential behavior driven by the saturated conductivity . The falling-head phase remains until the ponding vanishes at the critical time .
2.2 Mathematical model
The total electrical current density j (A m−2) is determined from the generalized Ohm's law as follows:
where φ (V) is the streaming potential, js (A m−2) is the streaming current density and σ (S m−1) is the electrical conductivity distribution that is assumed to be isotropic.
Hence, the conservation equation is written as
In addition, the electrical conductivity distribution can be estimated using the saturation as follows (Mboh et al., 2012):
where σsat (S m−1) is the electric conductivity at saturation and na is the Archie saturation exponent (Archie, 1942).
The streaming current density (js) can be related to the Darcy velocity (q (cm min−1)) by (Linde et al., 2007; Revil et al., 2007)
where Ks (cm min−1) is the saturated hydraulic conductivity, ρ (kg min−3) is the water density, g (m s−1) is the gravitational acceleration and Csat (V Pa−1) is the voltage coupling coefficient at saturation.
Hence, the combination of the previous Eqs. (1)–(4) leads to the following partial differential equation governing the SP signals:
However, the flow through an unsaturated soil column can be modeled by the one-dimensional Richard's equation:
where H (cm) and h (cm) are, respectively, the hydraulic and pressure head, such that ; z (cm) is the depth (downward positive); Ss (–) is the specific storage; θs (cm3 cm−3) and θ (cm3 cm−3) are the saturated and actual water contents, respectively; c(h) (cm−1) is the specific moisture capacity; and K(h) (cm min−1) is the hydraulic conductivity.
The water velocity (q) is given from Darcy's law:
In the current study, the standard models of Mualem (1976) and van Genuchten (1980) are used to relate pressure head, hydraulic conductivity and water content:
where Se (–) is the effective saturation, θr (cm3 cm−3) is the residual water content, Ks (cm min−1) is the saturated hydraulic conductivity, , and α (cm−1) and n (–) are the Mualem–van Genuchten-shaped parameters.
2.3 Numerical model
Although several numerical techniques have been developed for the solution of the multidimensional Richards equation (e.g., Fahs et al., 2009; Belfort et al., 2009; Younes et al., 2013; Deng and Wang, 2017), the standard finite volume method is used here for the spatial discretization of the one-dimensional Richard's equation (Eq. 6). The integration of this equation over the finite volume (i) between and gives
Using expressions of the Darcy velocity at the element interfaces and in the case of a uniform spatial discretization with a spatial step, we obtain
Using and , the integration of Eq. (5) over the finite volume (i) yields
where the values at the interface , and are calculated using the arithmetic mean between adjacent elements (for instance, .
Then, the temporal discretization of the obtained nonlinear ODE/DAE system (9–10) is performed with the method of lines (MOL) using the DASPK (Brown et al., 1994) time solver. The MOL is suitable for strongly nonlinear systems since it allows high-order temporal integration methods with formal error estimation and control (Miller et al., 1998; Younes et al., 2009; Fahs et al., 2009, 2011). In the current study, the relative and absolute local error tolerances are fixed to 10−6.
Numerical simulations are performed assuming typical MVG hydraulic parameters for the sandy soil with (according to Carsel and Parrish, 1988) Ks=0.495 cm min−1, θs=0.43 cm3 cm−3, θr=0.045 cm3 cm−3, α=0.145 cm−1 and n=2.68. The voltage coupling coefficient at saturation is V Pa−1 and the Archie saturation exponent is na=1.6.
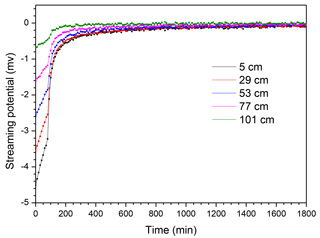
Figure 2Reference SP signals. Solid lines represent the reference SP solution and dots represent the sets of perturbed data serving as conditioning information for model calibration.
Based on these hydraulic and geophysical parameters, a reference (mesh-independent) solution is obtained using a uniform mesh of 235 cells of 0.5 cm length. Data are generated by sampling the output SP signals every 10 min during 1800 min. Figure 2 shows that the SP signals have an almost linear behavior in the saturated falling-head phase. During the drainage phase, they have a nonlinear behavior and approach zero voltage for the dry conditions occurring toward the end of the experiment. The SP signals are independent Gaussian random noises with a standard deviation of 2.73 10−5 V. This noise level was obtained by Mboh et al. (2012) from laboratory measurements. The noised data (Fig. 2) are used as “observations” in the calibration exercise.
3.1 GSA method
The aim of GSA is to assess the effect of the variation of parameters on the model output (Mara and Tarantola, 2008). Such knowledge is important for determining the most influential parameters as well as their regions and periods of influence (Fajraoui et al., 2011). The sensitivity of a model to its parameters can be assessed using variance-based sensitivity indices. These indices evaluate the contribution of each parameter to the variance of the model (Sobol', 2001). Polynomial chaos theory (Wiener, 1938) has been largely used to perform variance-based sensitivity analysis of computer models (see for instance, Sudret, 2008; Blatman and Sudret, 2010; Fajraoui et al., 2012; Younes et al., 2016; Shao et al., 2017; Mara et al., 2017). It can be stated that the PCE method is a surrogate-based approach. However, we argue that this method employs ANOVA (analysis Of variance) decomposition and hence can be considered as a spectral method (such as the Fourier amplitude sensitivity test; Cukier et al., 1973; Saltelli et al., 1999). Indeed, with this method, the sensitivity indices are directly obtained from the PCE coefficients without needing to run the surrogate model.
Let us consider a mathematical model with a random response f(ξ) which depends on (d) independent random parameters . With PCE, f(ξ) is expanded using a set of orthonormal multivariate polynomials (up to a polynomial degree p):
where is a dth-dimensional index. Sα represents the polynomial coefficients and Ψα represents the generalized polynomial chaos of degree , such as Hermite, Legendre and Jacobi polynomials, for instance. In this work, Legendre polynomials are employed because uniform distributions are considered for the parameters. The noninformative uniform distributions are used here to express the absence of prior information, which makes all possible values of the parameter equally likely.
Equation (12) is similar to an ANOVA representation of the original model (Sobol' 1993), from which it is straightforward to express V[f(ξ)], the variance of f(ξ) as the sum of the partial contribution of the inputs, as follows:
The first-order sensitivity index Si and the total sensitivity index STi are defined by
where , E(|) is the conditional expectation operator and V(|) the conditional variance. Si measures the amount of variance of f(ξ) due to ξi alone, while STi≥Si measures the amount of all contributions of ξi to the variance of f(ξ), including its cooperative nonlinear contributions with the other parameters ξj. The input/output relationship is said to be additive when , and in this case .
In the sequel, a PCE is constructed for each SP signal at each observable time. The number of coefficients for a full PCE representation is . The evaluation of the PCE coefficients requires at least P simulations of the nonlinear hydrogeophysical model. Note that P increases quickly with the order of the PCE and the number of parameters. Hence, several sparse PCE representations, in which only the significant coefficients are sought, have been proposed in the literature in order to reduce the computational cost of the estimation of the Sobol indices. For instance, Blatman and Sudret (2010) developed a sparse PCE representation using an iterative forward–backward approach based on nonintrusive regression. Fajraoui et al. (2012) developed a technique whereby only the sensitive coefficients (that affect significantly model variance) are retained in the PCE. Recently, Shao et al. (2017) developed an algorithm based on Bayesian model averaging (BMA) to select the best sparse PCE from a given data set using the KIC (Kayshap, 1982). The main idea of this algorithm is to increase the degree of an initial PCE progressively and compute the KIC until a satisfactory representation of the model responses is obtained. This algorithm is used hereafter to compute the sensitivity indices of the SP signals.
3.2 GSA results
The SP responses are considered for uniformly distributed parameters over the large intervals shown in Table 1. These intervals include the reference values reported in Mboh et al. (2012). The sensitivity indices of the six input parameters are estimated using an experimental design formed by parameter sets. The order of the sparse PCE is automatically adapted for each observable time and location. For some observable times, the PCE is highly sparse; it reaches a degree of 31 but only contains 112 nonzero coefficients.
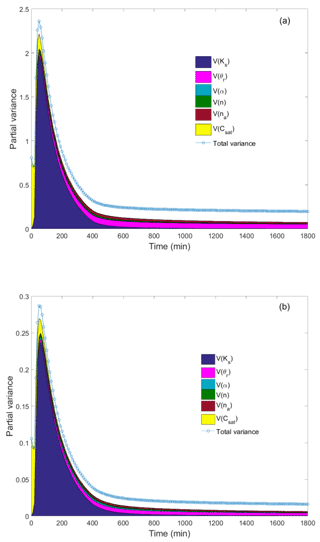
Figure 3Time distribution of the SP variance at 5 cm (a) and 77 cm (b) depth. The shaded area under the variance curve represents the partial marginal contributions of the random input parameters; the contribution of interactions between parameters is represented by the blank region between the shaded area and the variance curve.
Figure 3 depicts the temporal distribution of the streaming potential variance, represented by the blue curve, and the relative contribution of the parameters, represented by the shaded area. This figure corresponds to the temporal ANOVA decomposition for sensor 1 (5 cm from the soil surface) and for sensor 4 (77 cm from the soil surface). Interactions between parameters are represented by the blank region between the variance curves and the shaded area. Note that because a Dirichlet boundary condition with zero SP is maintained at the outlet boundary, the variance of the SP signal is zero at the bottom and reaches its maximum value near the soil surface. Hence, the variance is higher for the first sensor, located 5 cm from the soil surface (Fig. 3a) than for sensor 4, located 77 cm from the soil surface (Fig. 3b).
Table 2The first-order sensitivity index Si and the total sensitivity index STi for the SP signal 5 (a) and 77 cm (b) below the soil surface at different times.
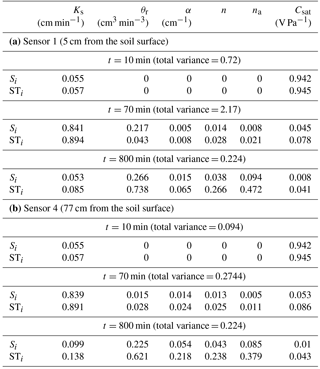
The SP signals at different altitudes exhibit similar behavior (Fig. 3). In the following, we comment on the results of sensor 1 (Fig. 3a). Because Ks varies between 0.1 and 2 cm min−1, the saturated falling-head phase remains until the ponding vanishes at . Depending on the value of Ks (see Table 1), tc varies between t1=20 min and t2=403 min. Thus, in Fig. 3a, we can see that during the first time period (t≤t1), the SP signal is strongly influenced by the value of the parameter Csat. The first-order and total sensitivity indices at t=10 min (Table 2a) confirm that only the saturated parameters Ks and Csat are influential. Csat is about 17 times more influential than Ks. As expected, the remaining parameters have no influence during the first period. The total variance is 0.72 mv, and there is no interaction between the two parameters Ks and Csat since STi=Si for both of them and .
During the second period , the flow is either saturated or unsaturated depending on the value of Ks. Figure 3a shows that the variance of the SP signal exhibits its maximum value around 2.4 mv, with strong influences of the parameters Ks and Csat and weak interactions between them (small blank region between the variance curve and the shaded area). These results are confirmed by the sensitivity indices calculated at t=70 min and reported in Table 2a for sensor 1. Both first-order and total sensitivity indices indicate that Ks is the most influential parameter. The second influential parameter is Csat, which has a total sensitivity index about 12 times less than Ks. The parameter α is irrelevant since its total sensitivity index is 109 times less than Ks and its partial variance is mv, which is less than the 95 % confidence interval associated with the SP measurement (± 0.055 mv). The total variance at t=70 min is calculated to be 2.17 mv, and the output–input relationship is close to being additive since , which means that interactions between parameters exist but are not significant.
During the third period (t≥t2), the variance of the SP signal reduces to 0.3 mv (Fig. 3a) and significant interactions are observed between parameters (large blank region between the shaded area and the variance curve). Table 2a shows that for t=800 min, which corresponds to dry conditions, the total variance is 0.22. First-order sensitivity indices are very small, except for θr. The latter is highly influential since it has a significant first-order sensitivity index (Si=0.27) and a more significant total-sensitivity index (STi=0.74). The parameters Csat and Ks are irrelevant as they have very small first-order and total sensitivity indices. Further, strong interactions are observed between the parameters since the sum of the first-order indices is far from 1 . The total sensitivity indices are significantly different from first-order sensitivity indices for almost all parameters. For instance, the ratio between these two indices is around 4 for α, 5 for na and 7 for n. The total sensitivity index of α remains small (0.065), whereas significant total sensitivity indices are obtained for n(STi=0.27) and na(STi=0.47), which indicates that these two parameters are influential (although their first-order sensitivity indices are small) because of the interaction between the parameters.
Figure 3b shows similar behavior for sensor 4 located 77 cm from the soil surface. The results in Table 2b indicate that the total variance observed at t=10, 70 and 800 min are around 8 times less than for sensor 1. For the first time period, the first and total sensitivity indices are identical to those observed for sensor 1 since saturated conditions occur inside the whole column and the same effect of Ks and Csat can be observed whatever the location inside the column. For the second time period, the sensitivity indices for sensor 4 (Table 2b) are similar to those observed for sensor 1. However, the results for the third time period show an improvement of the relevance of the parameter α, with an increase of both first and total sensitivity indices. Indeed, compared to the results of sensor 1, both first-order and total sensitivity indices tripled. Moreover, the total sensitivity index for α(STi=0.22) becomes close to that of n(STi=0.24).
In summary, the GSA applied to SP signals identifies the influential parameters and their periods of influence and shows that
-
the parameter Csat is highly influential during the first time period (t≤t1) during which no interactions are observed between parameters;
-
the parameter Ks is highly influential during the second time period during which small interactions occur between parameters;
-
the parameters θr,n and na are influential during the third time period (t≥t2) during which dry conditions occur; during this period, strong interactions take place between parameters;
-
the parameter α has no influence on the SP signals during the two first periods and presents a very small influence (Si=0.015 and STi=0.065) during the third period on sensor 1 (near the surface of the column);
-
the relevance of the parameter α improves with the distance from the soil surface, although the total variance diminishes with respect to this distance. The influence of α becomes significant (STi=0.22) on sensor 4 (located 77 cm from the soil surface) during the third period.
4.1 MCMC and FOA approaches
Calibration of computer models is an essential task since some parameters (like the Mualem–van Genuchten-shaped parameters α and n) cannot be directly measured. In such an exercise, the unknown model parameters are investigated by comparing the model responses to the observations. Recently, Mboh et al. (2012) showed that the inversion of SP signals can yield an accurate estimate of the saturated hydraulic conductivity Ks, the MVG fitting parameters α and n and the Archie saturation exponent (na). Moreover, they showed that the quality of the estimation was comparable to that obtained from the calibration of pressure heads. In their study, Mboh et al. (2012) used the FOA approach with the shuffled complex evolution optimization algorithm SCE-UA (Duan et al., 1993).
As important as the determination of the optimal parameter sets are the associated 95 % confidence intervals (CIs) to quantify the uncertainty of the estimated values. The determination of CIs is not straightforward if the observed model responses are highly nonlinear functions of model parameters (Christensen and Cooley, 1999). In the sequel, the parameter estimation is performed using two approaches: the popular FOA approach and the Bayesian approach based on the MCMC sampler. Contrarily to FOA, the MCMC method is robust since no assumptions of model linearity or differentiability are required. Furthermore, prior information available for the parameters can be included. MCMC provides not only an optimal point estimate of the parameters but also a quantification of the entire parameter space. Several MCMC strategies have been developed for Bayesian sampling of the parameter space (Gallagher and Doherty, 2007; Vrugt, 2016). In a groundwater and vadose zone modeling context, the most widely used of these strategies is the Metropolis–Hastings algorithm (Metropolis et al., 1953; Hastings, 1970). It proceeds as follows (Gelman et al., 1996).
- i.
Choose an initial candidate formed by the initial estimate of the parameter set ξ0 and the hyperparameter σ0 and a proposal distribution q that depends on the previous accepted candidate.
- ii.
A new candidate is generated from the current one xi−1 with the generator q(xi|xi−1) associated with the transition probability p(ξi|ymes,σ).
- iii.
Calculate p(ξi|ymes,σ) and compute the ratio . Additionally, draw a random number from a uniform distribution.
- iv.
If α≥u, then accept the new candidate, otherwise it is rejected.
- v.
Resume from (ii) until the chain converges or a prescribed number of iterations imax is reached.
Many improvements have been proposed in the literature to accelerate the MCMC convergence rate (e.g., Haario et al., 2006; ter Braak and Vrugt, 2008; Dostert et al., 2009, among others). Vrugt et al. (2009a, b) developed the DREAM MCMC sampler based on the differential evolution–Markov chain method of ter Braak (2006) to improve sampling efficiency. DREAM runs multiple Markov chains in parallel and uses subspace sampling and outlier chain correction to speed up MCMC convergence (Vrugt, 2016). Laloy and Vrugt (2012) developed the DREAM(ZS) MCMC sampler, in which a candidate for each chain is drawn from an archive of past states denoted Z, which plays the role of the generator q. Interested readers are referred to Vrugt (2016) for more details about the properties and implementation of DREAM and DREAM(ZS). In the current study, the DREAM(ZS) software is used for the MCMC estimation of the hydrogeophysical parameters. Note that because of the large number of model evaluations required, the MCMC method remains rarely used in practical applications compared to the FOA approach. Indeed, with FOA, the CIs are estimated once by assuming that the Jacobian remains constant within the CIs. This assumption was found to be reasonably accurate in nonlinear problems by Donaldson and Scnabel (1987). However, recently, several authors stated that parameter interdependences and model nonlinearities violate this assumption (see, for instance, Vrugt and Bouten, 2002; Vurgin et al. 2007; Gallagher and Doherty, 2007; Mertens et al., 2009; Kahl et al., 2015).
In the following, both MCMC and FOA approaches are employed for the inversion of the highly nonlinear hydrogeophysical problem using SP measurements.
4.2 Parameters estimation results
Hydrogeophysical parameters are estimated using the DREAM(ZS) MCMC sampler (Laloy and Vrugt, 2012). Independent uniform distributions are considered for model parameter priors and likelihood hyperparameters (see Table 1). The parameter posterior distribution is written as
where SS is the sum of the squared differences between the observed and modeled SP signals at time tk for N, the total number of SP observations.
The DREAM(ZS) software computes multiple sub-chains in parallel to thoroughly explore the parameter space. Taking the last 25 % of individuals (when the chains have converged) yields multiple sets used to estimate the updated parameter distributions and therefore the optimal parameter values and their CIs. In the sequel, the DREAM(ZS) MCMC sampler is used with three parallel chains.
We assume that the saturated water content has been initially measured with a fair degree of accuracy. However, instead of fixing its value (as in Kool et al. , 1987, van Dam et al., 1994, and Nützmann et al., 1998, among others), we assign a Gaussian distribution to θs to take associated uncertainty and its effect on the estimation of the rest of the parameters into account. It is assumed here that the saturated water content was accurately measured to be θs=0.43 cm3 cm−3 by weighing the saturated soil. The corresponding error measurements are independently and normally distributed with a zero mean and a standard deviation σθ=0.01 cm3 cm−3. Hence a Gaussian distribution is assigned to θs, with a mean value of 0.43 cm3 cm−3 and a 95 % CI [0.41−0.45] cm3 cm−3. The rest of the hydrogeophysical parameters have noninformative uniform distributions over the ranges reported in Table 1. The error (measurement) variance is also considered to be unknown and is simultaneously estimated with the physical parameters. Two scenarios are considered to check whether the FOA approach can provide a reliable estimation of parameters and associated uncertainties for the highly nonlinear hydrogeophysical problem investigated, both in the case of abundant data (small uncertainty regions) and in the case of scarcity of data (large uncertainty regions). In the first scenario, SP data collected from the sensors located at the five locations are taken into account for the calibration. In the second scenario, only the SP data from the first sensor located 5 cm from the soil surface serve as conditioning information for model calibration. Results of the MCMC sampler are compared to those of the FOA approach for both scenarios.
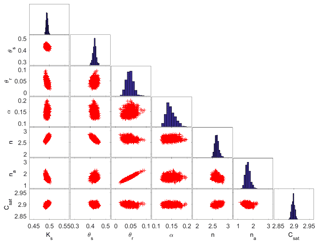
Figure 4MCMC solutions in which all SP data are considered for the calibration. The diagonal plots represent the inferred posterior probability distribution of the model parameters. The off-diagonal scatterplots represent the pairwise correlations in the MCMC drawing.
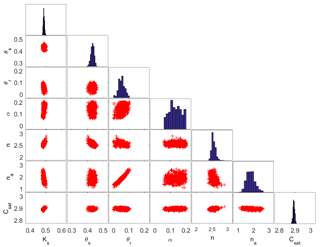
Figure 5MCMC solutions in which calibration is performed using only SP data located 5 cm from the surface. The diagonal plots represent the posterior probability distribution of the parameters. The off-diagonal scatterplots represent the pairwise correlations in the MCMC drawing.
4.2.1 Scenario 1: inversion using all SP measurements
Figure 4 shows the results obtained with MCMC when the SP data of the five sensors are used for the calibration. The “on-diagonal” plots in this figure display the posterior parameter distributions, whereas the “off-diagonal” plots represent the correlations between parameters in the MCMC sample. Figure 4 shows nearly bell-shaped posterior distributions for all parameters. A strong correlation is observed between θr and na(r=0.98).
From the obtained MCMC sample, it is straightforward to estimate the posterior 95 % confidence interval of each parameter. This as well as the mean estimate value of each parameter obtained with both MCMC and FOA approaches are reported in Table 3.
Table 3Estimated mean values (bold), confidence intervals (CIs) and size of the posterior CIs (italic) with MCMC and FOA approaches for scenario 1.

Table 4Estimated mean values (bold), confidence intervals (CIs) and size of the posterior CIs (italic) with MCMC and FOA approaches for scenario 2.

The results of this table show that the parameters are well estimated from the SP measurements since (i) identified mean values are very close to the reference solution, (ii) all confidence intervals include the reference solution and (iii) the confidence intervals are rather narrow. The saturated parameters Ks and Csat are very well estimated (with CIs around 2 %) because of data collected during the falling-head phase during which only these two parameters are influential.
The posterior CI of the parameter θs is similar to its prior CI. The parameter α is reasonably well estimated, with a CI around 35 %. Recall that this parameter had very small first-order and total sensitivity indices for sensor 1 but had more significant sensitivity indices for the sensors away from the soil surface (see results for sensor 4 in Table 2b). The parameter θr is estimated with a CI around 90 % although it was highly influential for all sensors (for instance, a first-order sensitivity index of 0.27 and a total order of 0.74 for sensor 1). The parameters n and na had similar GSA behavior to small first-order sensitivities (0.038 and 0.094, respectively, for sensor 1) and large total sensitivities (0.266 and 0.4715, respectively, for sensor 1); however, the inversion shows that the parameter n is well estimated with a CI less than 10 %, whereas the parameter na is less well estimated with a CI around 35 %. These results suggest that GSA outcomes should be interpreted with caution in the context of parameter estimation since (i) a parameter which is not relevant for the model output in one sensor can be influential for another sensor and (ii) GSA does not presume the quality of the estimation since two parameters with similar sensitivity indices can have a different quality of estimation with the inversion procedure.
Further, the results of Table 3 show that FOA and MCMC approaches yield similar mean estimated values. Moreover, very good agreement is observed between FOA and MCMC uncertainty bounds. Concerning the efficiency of the two calibration methods for this scenario, the FOA approach is by far the most efficient method since it requires only 95 s of CPU time. The MCMC method was terminated after 16 000 model runs, which required 14 116 s. The convergence was reached at around 12 000 model runs. The last 4000 runs were used to estimate the statistical measures of the posterior distribution. Recall that contrarily to FOA, MCMC can include prior information available for the parameters and allows a quantification of the entire parameter space.
4.2.2 Scenario 2: inversion using only SP measurements near the surface
In this scenario, the number of measurements used for the calibration is strongly reduced. Only SP measurements from sensor 1 (located 5 cm below the soil surface) are considered.
The results of MCMC are plotted in Fig. 5. The correlation observed between θr and na decreases slightly to r=0.95. Almost bell-shaped posterior distributions are observed for all parameters except for the parameters θr and α.
The results obtained with MCMC and FOA approaches depicted in Table 4 show the following.
-
The FOA approach yields accurate mean estimated values similar to MCMC results for all parameters.
-
The MCMC and FOA mean estimated values are close to the reference solution and to the previous scenario. The maximum difference is observed for θr for which the mean estimated value with scenario 2 is 15 % greater than for scenario 1.
-
The MCMC CIs for the parameters Ks, θs, n and Csat are close to the previous scenario. The parameters θs and n are well estimated (CIs < 10 %) and the parameters Ks and Csat are very well estimated (CIs ≤ 5 %).
-
Due to the reduction of the number of data used for model calibration in scenario 2, the MCMC CIs for the parameters na, α and θr are much larger than in the previous scenario. Indeed, compared to scenario 1, the CI for na and θr increases by around 60 %, whereas the CI of α is 3 times larger than for scenario 1.
-
The FOA method yields accurate CIs for the parameters θs, n, na and Csat, whereas it overestimates the CIs of θr (by 24 %), Ks (by 100 %) and α (by 427 %). An unphysical uncertainty region (including negative values) is obtained for the parameter α.
These results show that the FOA can fail to provide realistic parameter uncertainties and can yield larger CIs than their corresponding nonlinear MCMC counterpart. Indeed, the linearization in the FOA method assumes that the Jacobian remains constant across the CIs. This assumption was fulfilled for the first scenario in which a large number of measurements ensured small uncertainty regions. However, the assumption is not fulfilled for some parameters of the current scenario because of the large uncertainty regions induced by the reduction of the number of SP measurements.
Concerning the efficiency of the calibration methods, the FOA required approximately 174 s of CPU time, and the MCMC required many more runs to reach the convergence than in the previous scenario. Indeed, the sampler was used with 50 000 runs (35 000 runs were necessary to reach the convergence).
In this work, a synthetic test case dealing with SP signals during a drainage experiment has been studied. The test case is similar to the laboratory experiment developed in Mboh et al. (2012), involving a falling-head infiltration phase followed by a drainage phase. GSA and Bayesian parameter inference have been applied to investigate (i) the influence of hydraulic and geophysical parameters on the SP signals and (ii) the identifiability of hydrogeophysical parameters using only SP measurements. The GSA was performed using variance-based sensitivity indices which allow the contribution of each parameter (alone or by interaction with other parameters) to the output variance to be measured. The sensitivity indices have been calculated using a PCE representation of the SP signals. To reduce the number of coefficients and explore PCE with high orders, we used the efficient sparse PCE algorithm developed by Shao et al. (2017), which selects the best sparse PCE from a given data set using the Kashyap information criterion (KIC).
The GSA applied to SP signals showed that the parameters Csat and Ks are highly influential during the first period corresponding to saturated conditions. The parameters θr, n and na are influential when dry conditions occur. In such conditions, strong interactions take place between these parameters. The parameter α has a very small influence on the SP signals near the soil surface but its sensitivity increases with depth although the total variance decreases with depth.
Parameter estimation has been performed using MCMC and FOA approaches to check whether FOA can provide a reliable estimation of parameters and associated uncertainties for the highly nonlinear hydrogeophysical problem investigated. All hydraulic (Ks, θr, α and n) and geophysical (na and Csat) parameters can be reasonably estimated in the first scenario for which the whole SP data (measured at five different locations) are used as conditioning information for the model calibration. The confrontation with GSA results shows that the latter should be interpreted with caution when used in the context of parameter estimation since (i) a parameter which is not relevant for the model output in one sensor can be influential for another sensor and (ii) GSA does not presume the quality of the estimation since two parameters with similar sensitivity indices can have a different quality of estimation with the inversion procedure (see, for instance, parameters n and na). Furthermore, although the studied problem is highly nonlinear, the FOA approach provides accurate estimations of both mean parameter values and CIs in the first scenario. These results are identical to those obtained with MCMC.
When the number of SP measurements used for the calibration is considerably reduced (i.e., data are scarce), the MCMC inversion provides larger uncertainty regions of the parameters. The FOA approach yields accurate mean parameter values (in agreement with MCMC results) but inaccurate and even unphysical CIs for some parameters with large uncertainty regions.
No data sets were used in this article.
AY framed the research question, worked on sensitivity analysis and finalized the manuscript. JZ and FL worked on parameter estimation and numerical model development. MF performed simulations, analyzed the results and reviewed the manuscript.
The authors declare that they have no conflict of interest.
The authors acknowledge the financial support from the Tunisian–French joint
international laboratory NAILA (http://www.lmi-naila.com/).
Edited by: Bill X. Hu
Reviewed by: two anonymous referees
Allègre, V., Jouniaux, L., Lehmann, F., and Sailhac, P.: Streaming potential dependence on water-content in Fontainebleau sand, Geophys. J. Int., 182, 1248–1266, https://doi.org/10.1111/j.1365-246X.2010.04716.x, 2010.
Archie, G. E.: The Electrical Resistivity Log as an Aid in Determining Some Reservoir Characteristics, Transactions of the AIME, 146, 54–62, https://doi.org/10.2118/942054-G, 1942.
Arora, B., Mohanty, B. P., and McGuire, J. T.: Uncertainty in dual permeability model parameters for structured soils, Water Resour. Res., 48, https://doi.org/10.1029/2011WR010500, 2012.
Belfort, B., Ramasomanan, F., Younes, A., anf Lehmann, F.: An efficient Lumped Mixed Hybrid Finite Element Formulation for variably saturated groundwater flow, Vadoze Zone Journal, 8, 352–362, https://doi.org/10.2136/vzj2008.0108, 2009.
Blatman, G. and Sudret, B.: Efficient computation of global sensitivity indices using sparse polynomial chaos expansions, Reliability Engineering & System Safety, 95, 1216–1229, https://doi.org/10.1016/j.ress.2010.06.015, 2010.
Bogoslovsky, V. A. and Ogilvy, A. A.: Deformation of natural electric fields near drainage structures, Geophys. Prospect., 21, 716–723. https://doi.org/10.1111/j.1365-2478.1973.tb00053, 1973.
Bolève, A., Revil, A., Janod, F., Mattiuzzo, J. L., and Fry, J.-J.: Preferential fluid flow pathways in embankment dams imaged by self-potential tomography, Near Surf. Geophys., 7, 447–462, https://doi.org/10.3997/1873-0604.2009012, 2009.
Brown, P. N., Hindmarsh, A. C., and Petzold, L. R.: Using Krylov Methods in the Solution of Large-Scale Differential-Algebraic Systems, SIAM J. Sci. Comp., 15, 1467–1488, https://doi.org/10.1137/0915088, 1994.
Carsel, R. F. and Parrish, R. S.: Developing joint probability distributions of soil water retention characteristics, Water Resour. Res., 24, 755–769, https://doi.org/10.1029/WR024i005p00755, 1988.
Christensen, S. and Cooley, R. L.: Evaluation of confidence intervals for a steady-state leaky aquifer model, Adv. Water Res., 22, 807–817, https://doi.org/10.1016/S0309-1708(98)00055-4, 1999.
Cukier, R. I., Fortuin, C. M., Shuler, K. E., Petschek, A. G., and Schaibly, J. H.: Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients, I. theory, J. Chem. Phys., 59, 3873–3878, 1973.
Darnet, M., Marquis, G., and Sailhac, P.: Estimating aquifer hydraulic properties from the inversion of surface Streaming Potential (SP) anomalies, Geophys. Res. Lett., 30, https://doi.org/10.1029/2003GL017631, 2003.
Deng, B. and Wang, J.: Saturated-unsaturated groundwater modeling using 3D Richards equation with a coordinate transform of nonorthogonal grids, Applied Mathematical Modelling, 50, 39–52, doi10.1016/j.apm.2017.05.021; 2017.
Donaldson, J. R. and Schnabel, R. B.: Computational Experience with Confidence Regions and Confidence Intervals for Nonlinear Least Squares, Technometrics, 29, https://doi.org/10.2307/1269884, 1987.
Dostert, P., Efendiev, Y., and Mohanty, B.: Efficient uncertainty quantification techniques in inverse problems for Richards' equation using coarse-scale simulation models, Adv. Water Res., 32, 329–339, https://doi.org/10.1016/j.advwatres.2008.11.009, 2009.
Duan, Q. Y., Gupta, V. K., and Sorooshian, S.: Shuffled complex evolution approach for effective and efficient global minimization, J. Optimiz. Theory App., 76, 501–521, https://doi.org/10.1007/BF00939380, 1993.
Fahs, M., Younes, A., and Lehmann, F.: An easy and efficient combination of the Mixed Finite Element Method and the Method of Lines for the resolution of Richards' Equation, Environ. Modell. Soft., 24, 1122–1126, https://doi.org/10.1016/j.envsoft.2009.02.010, 2009.
Fahs, M., Younes, A., and Ackerer, P.: An Efficient Implementation of the Method of Lines for Multicomponent Reactive Transport Equations, Water Air. Soil Pollut., 215, 273–283, https://doi.org/10.1007/s11270-010-0477-y, 2011.
Fajraoui, N., Ramasomanana, F., Younes, A., Mara, T. A., Ackerer, P., and Guadagnini, A.: Use of global sensitivity analysis and polynomial chaos expansion for interpretation of nonreactive transport experiments in laboratory-scale porous media, Water Resour. Res., 47, https://doi.org/10.1029/2010WR009639, 2011.
Fajraoui, N., Mara, T. A., Younes, A., and Bouhlila, R.: Reactive Transport Parameter Estimation and Global Sensitivity Analysis Using Sparse Polynomial Chaos Expansion, Water Air. Soil Pollut., 223, 4183–4197, https://doi.org/10.1007/s11270-012-1183-8, 2012.
Fajraoui, N., Fahs, M., Younes, A. and Sudret, B.: Analyzing natural convection in porous enclosure with polynomial chaos expansions: Effect of thermal dispersion, anisotropic permeability and heterogeneity, Int. J. Heat Mass Trans., 115, 205–224, https://doi.org/10.1016/j.ijheatmasstransfer.2017.07.003, 2017.
Gallagher, M. and Doherty, J.: Parameter estimation and uncertainty analysis for a watershed model, Environ. Modell. Soft., 22, 1000–1020, https://doi.org/10.1016/j.envsoft.2006.06.007, 2007.
Gelman, A., Carlin, J., Stern, H., and Rubin, D.: Bayesian Data Analysis, Second Edition, London, Great Britain: Chapman Hall, 696 p., ISBN:0-158-48838-8, 1996.
Haario, H., Laine, M., Mira, A., and Saksman, E.: DRAM: Efficient adaptive MCMC, Statist. Comput., 16, 339–354, https://doi.org/10.1007/s11222-006-9438-0, 2006.
Hastings, W. K.: Monte Carlo Sampling Methods Using Markov Chains and Their Applications, Biometrika, 57, https://doi.org/10.2307/2334940, 1970.
Hinnell, A. C., Ferré, T. P. A., Vrugt, J. A., Huisman, J. A., Moysey, S., Rings, J., and Kowalsky, M. B.: Improved extraction of hydrologic information from geophysical data through coupled hydrogeophysical inversion, Water Resour. Res., 46, https://doi.org/10.1029/2008WR007060, 2010.
Ishido, T. and Mizutani, H.: Experimental and theoretical basis of electrokinetic phenomena in rock–water systems and its applications to geophysics, J. Geophys. Res., 86, 1763–1775, https://doi.org/10.1029/JB086iB03p01763, 1981.
Jardani, A., Revil, A., Bolève, A., Crespy, A., Dupont, J.-P., Barrash, W., and Malama, B.: Tomography of the Darcy velocity from self-potential measurements, Geophys. Res. Lett., 34, https://doi.org/10.1029/2007GL031907, 2007.
Jougnot, D. and Linde, N.: Self-Potentials in Partially Saturated Media: The Importance of Explicit Modeling of Electrode Effects, Vadose Zone J., 12, https://doi.org/10.2136/vzj2012.0169, 2013.
Kahl, G. M., Sidorenko, Y., and Gottesbüren, B.: Local and global inverse modelling strategies to estimate parameters for pesticide leaching from lysimeter studies: Inverse modelling to estimate pesticide leaching parameters from lysimeter studies, Pest Manage. Sci., 71, 616–631, https://doi.org/10.1002/ps.3914, 2015.
Kayshap, R. L.: Optimal choice of AR and MA parts in autoregressive moving average models, IEEE T. Pattern Anal., 4, 99–104, 1982.
Kool, J. B., Parker, J. C., and van Genuchten, M. T.: Parameter estimation for unsaturated flow and transport models – A review, J. Hydrol., 91, 255–293, https://doi.org/10.1016/0022-1694(87)90207-1, 1987.
Laloy, E. and Vrugt, J. A.: High-dimensional posterior exploration of hydrologic models using multiple-try DREAM (ZS) and high-performance computing, Water Resour. Res., 48, https://doi.org/10.1029/2011WR010608, 2012.
Linde, N., Jougnot, D., Revil, A., Matthäi, S. K., Arora, T., Renard, D., and Doussan, C.: Streaming current generation in two-phase flow conditions, Geophys. Res. Lett., 34, https://doi.org/10.1029/2006GL028878, 2007.
Mara, T. A. and Tarantola, S.: Application of global sensitivity analysis of model output to building thermal simulations, Build. Sim., 1, 290–302, https://doi.org/10.1007/s12273-008-8129-5, 2008.
Mara, T. A., Belfort, B., Fontaine, V., and Younes, A.: Addressing factors fixing setting from given data: A comparison of different methods, Environ. Modell. Soft., 87, 29–38, https://doi.org/10.1016/j.envsoft.2016.10.004, 2017.
Mboh, C. M., Huisman, J. A., Zimmermann, E., and Vereecken, H.: Coupled Hydrogeophysical Inversion of Streaming Potential Signals for Unsaturated Soil Hydraulic Properties, Vadose Zone J., 11, https://doi.org/10.2136/vzj2011.0115, 2012.
Mertens, J., Kahl, G., Gottesbüren, B. and Vanderborght, J.: Inverse Modeling of Pesticide Leaching in Lysimeters: Local versus Global and Sequential Single-Objective versus Multiobjective Approaches, Vadose Zone J., 8, 793, https://doi.org/10.2136/vzj2008.0029, 2009.
Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., and Teller, E.: Equation of State Calculations by Fast Computing Machines, J. Chem. Phys., 21, 1087–1092, https://doi.org/10.1063/1.1699114, 1953.
Miller, C. T., Williams, G. A., Kelley, C. T., and Tocci, M. D.: Robust solution of Richards' equation for nonuniform porous media, Water Resour. Res., 34, 2599–2610, https://doi.org/10.1029/98WR01673, 1998.
Mualem, Y.: A new model for predicting the hydraulic conductivity of unsaturated porous media, Water Resour. Res., 12, 513–522, https://doi.org/10.1029/WR012i003p00513, 1976.
Nützmann, G., Thiele, M., Maciejewski, S., and Joswig, K.: Inverse modelling techniques for determining hydraulic properties of coarse-textured porous media by transient outflow methods, Adv. Water Res., 22, 273–284, https://doi.org/10.1016/S0309-1708(98)00009-8, 1998.
Patella, D.: Introduction to ground surface self-potential tomography, Geophys. Prospect, 45, 653–681, https://doi.org/10.1046/j.1365-2478.1997.430277, 1997.
Rajabi, M. M., Ataie-Ashtiani, B., and Simmons, C. T.: Polynomial chaos expansions for uncertainty propagation and moment independent sensitivity analysis of seawater intrusion simulations, J. Hydrol., 520, 101–122, https://doi.org/10.1016/j.jhydrol.2014.11.020, 2015.
Revil, A., Linde, N., Cerepi, A., Jougnot, D., Matthäi, S., and Finsterle, S.: Electrokinetic coupling in unsaturated porous media, J. Colloid Interface Sci., 313, 315–327, https://doi.org/10.1016/j.jcis.2007.03.037, 2007.
Richards, K., Revil, A., Jardani, A., Henderson, F., Batzle, M., and Haas, A.: Pattern of shallow ground water flow at Mount Princeton Hot Springs, Colorado, using geoelectric methods, J. Volcanol. Geotherm. Res., 198, 217–232, https://doi.org/10.1016/j.jvolgeores.2010.09.001, 2010.
Riva, M., Guadagnini, A., and Dell'Oca, A.: Probabilistic assessment of seawater intrusion under multiple sources of uncertainty, Adv. Water Res., 75, 93–104, https://doi.org/10.1016/j.advwatres.2014.11.002, 2015.
Sailhac, P. and Marquis, G.: Analytic potentials for the forward and inverse modeling of SP anomalies caused by subsurface fluid flow, Geophy. Res. Lett., 28, 1851–1854, https://doi.org/10.1029/2000GL012457, 2001.
Saltelli, A., Tarantola, S., and Chan, K. P.-S.: A Quantitative Model-Independent Method for Global Sensitivity Analysis of Model Output, Technometrics, 41, 39–56, https://doi.org/10.1080/00401706.1999.10485594, 1999.
Shao, Q., Younes, A., Fahs, M., and Mara, T. A.: Bayesian sparse polynomial chaos expansion for global sensitivity analysis, Comput. Method Appl. M., 318, 474–496, https://doi.org/10.1016/j.cma.2017.01.033, 2017.
Sobol', I. M.: Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates, Math. Comput. Sim., 55, 271–280, https://doi.org/10.1016/S0378-4754(00)00270-6, 2001.
Sobol', I. M.: Sensitivity estimates for nonlinear mathematical models, Math. Model. Comput. Exp., 407–414, 1993.
Sudret, B.: Global sensitivity analysis using polynomial chaos expansions, Reliab. Eng. Syst. Safe., 93, 964–979, https://doi.org/10.1016/j.ress.2007.04.002, 2008.
ter Braak, C. J. F.: A Markov Chain Monte Carlo version of the genetic algorithm differential evolution: Easy Bayesian computing for real parameter spaces, Stat Comput., 16, 239–249, https://doi.org/10.1007/s11222-006-8769-1, 2006.
ter Braak, C. J. F. and Vrugt, J. A.: Differential Evolution Markov Chain with snooker updater and fewer chains, Statist. Comput., 18, 435–446, https://doi.org/10.1007/s11222-008-9104-9, 2008.
van Dam, J. C., Stricker, J. N. M., and Droogers, P.: Inverse Method to Determine Soil Hydraulic Functions from Multistep Outflow Experiments, Soil Sci. Soc. Am. J., 58, https://doi.org/10.2136/sssaj1994.03615995005800030002x, 1994.
van Genuchten, M. T.: A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils, Soil Sci. Soc. Am. J., 44, 892, https://doi.org/10.2136/sssaj1980.03615995004400050002x, 1980.
Volkova, E., Iooss, B., and Van Dorpe, F.: Global sensitivity analysis for a numerical model of radionuclide migration from the RRC “Kurchatov Institute” radwaste disposal site, Stoch. Env. Res. Risk A., 22, 17–31, https://doi.org/10.1007/s00477-006-0093-y, 2008.
Vrugt, J. A., Gupta, H. V., Bouten, W. and Sorooshian, S.: A Shuffled Complex Evolution Metropolis algorithm for optimization and uncertainty assessment of hydrologic model parameters, Water Resour. Res., 39, doi:10.1029/2002WR001642, 2003.
Vrugt, J. A. and Bouten, W.: Validity of First-Order Approximations to Describe Parameter Uncertainty in Soil Hydrologic Models, Soil Sci. Soc. Am. J., 66, https://doi.org/10.2136/sssaj2002.1740, 2002.
Vrugt, J. A., ter Braak, C. J. F., Clark, M. P., Hyman, J. M., and Robinson, B. A.: Treatment of input uncertainty in hydrologic modeling: Doing hydrology backward with Markov chain Monte Carlo simulation: FORCING DATA ERROR USING MCMC SAMPLING, Water Resour. Res., 44, https://doi.org/10.1029/2007WR006720, 2008.
Vrugt, J. A., ter Braak, C. J. F., Diks, C. G. H., Robinson, B. A., Hyman, J. M., and Higdon, D.: Accelerating Markov chain Monte Carlo simulation by differential evolution with self-adaptive randomized subspace sampling, Int. J. Nonlinear Sci. Numer. Simul., 10, 273–290, https://doi.org/10.1515/IJNSNS.2009.10.3.273, 2009a.
Vrugt, J. A.: Markov chain Monte Carlo simulation using the DREAM software package: Theory, concepts, and MATLAB implementation, Environ. Modell. Soft., 75, 273–316, https://doi.org/10.1016/j.envsoft.2015.08.013, 2016.
Vrugt, J. A., Robinson, B. A., and Hyman, J. M.: Self-adaptive multimethod search for global optimization in real parameter spaces, IEEE Trans. Evol. Comput., 13, 243–259, https://doi.org/10.1109/TEVC.2008.924428, 2009b.
Vugrin, K. W., Swiler, L. P., Roberts, R. M., Stucky-Mack, N. J., and Sullivan, S. P.: Confidence region estimation techniques for nonlinear regression in groundwater flow: Three case studies, Water Resour. Res., 43, W03423, https://doi.org/10.1029/2005WR004804, 2007.
Wiener, N.: The Homogeneous Chaos, Am. J. Math., 60, https://doi.org/10.2307/2371268, 1938.
Younes, A., Fahs, M., and Ahmed, S.: Solving density driven flow problems with efficient spatial discretizations and higher-order time integration methods, Adv. Water Res., 32, 340–352, https://doi.org/10.1016/j.advwatres.2008.11.003, 2009.
Younes, A., Fahs, M., and Belfort, B.: Monotonicity of the cell-centred triangular MPFA method for saturated and unsaturated flow in heterogeneous porous media, J. Hydrol., 504, 132–141, https://doi.org/10.1016/j.jhydrol.2013.09.041, 2013.
Younes, A., Mara, T. A., Fajraoui, N., Lehmann, F., Belfort, B., and Beydoun, H.: Use of Global Sensitivity Analysis to Help Assess Unsaturated Soil Hydraulic Parameters, Vadose Zone J., 12, https://doi.org/10.2136/vzj2011.0150, 2013.
Younes, A., Delay, F., Fajraoui, N., Fahs, M., and Mara, T. A.: Global sensitivity analysis and Bayesian parameter inference for solute transport in porous media colonized by biofilms, J. Contam. Hydrol., 191, 1–18, https://doi.org/10.1016/j.jconhyd.2016.04.007, 2016.
Younes, A., Mara, T., Fahs, M., Grunberger, O., and Ackerer, P.: Hydraulic and transport parameter assessment using column infiltration experiments, Hydrol. Earth Syst. Sci., 21, 2263–2275, https://doi.org/10.5194/hess-21-2263-2017, 2017.
Zablocki, C. J.: Streaming potentials resulting from the descent of meteoric water: A possible source mechanism for Kilauean self-potential anomalies, Trans. Geotherm. Resour. Counc., 2, 747–748, 1978.







