the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Developing a decision support tool for assessing land use change and BMPs in ungauged watersheds based on decision rules provided by SWAT simulation
Junyu Qi
Sheng Li
Charles P.-A. Bourque
Zisheng Xing
Fan-Rui Meng
Decision making on water resources management at ungauged, especially large-scale watersheds relies on hydrological modeling. Physically based distributed hydrological models require complicated setup, calibration, and validation processes, which may delay their acceptance among decision makers. This study presents an approach to develop a simple decision support tool (DST) for decision makers and economists to evaluate multiyear impacts of land use change and best management practices (BMPs) on water quantity and quality for ungauged watersheds. The example DST developed in the present study was based on statistical equations derived from Soil and Water Assessment Tool (SWAT) simulations and applied to a small experimental watershed in northwest New Brunswick. The DST was subsequently tested against field measurements and SWAT simulations for a larger watershed. Results from DST could reproduce both field data and model simulations of annual stream discharge and sediment and nutrient loadings. The relative error of mean annual discharge and sediment, nitrate–nitrogen, and soluble-phosphorus loadings were −6, −52, 27, and −16 %, respectively, for long-term simulation. Compared with SWAT, DST has fewer input requirements and can be applied to multiple watersheds without additional calibration. Also, scenario analyses with DST can be directly conducted for different combinations of land use and BMPs without complex model setup procedures. The approach in developing DST can be applied to other regions of the world because of its flexible structure.
Pollution from nonpoint sources poses a significant threat to ecosystems and plant and animal communities (Vörösmarty et al., 2010). Nonpoint sources of sediment, nutrients, and pesticides, primarily from agricultural lands, have been identified as major contributors to water quality degradation (Zhang et al., 2004; Ongley et al., 2010). These pollutants are difficult to control because they come from many sources (Quan and Yan, 2001). Practices such as strip cropping, terracing, crop rotation, and nutrient management can be developed to prevent soil erosion and reduce the movement of nutrients and pesticides from agricultural lands to aquatic ecosystems (D'Arcy and Frost, 2001). These pollution-prevention methods, known as best management practices (BMPs), are intended to minimize the negative environmental impact of agricultural activities, while maintaining land productivity. Reliable information on the impacts of land use change and BMPs on water quantity and quality is critical to watershed management (Panagopoulos et al., 2011).
Many studies have been conducted to evaluate the impact of land use change and BMPs on water quality based on field experiments (Novara et al., 2011; Pimentel and Krummel, 1987; Sadeghi et al., 2012; Turkelboom et al., 1997; Urbonas, 1994). Monitoring systems have been established to assess the impact of land use change and BMPs on water resources in order to capture the spatial and temporal variation in soil, climate, and topographic conditions in watersheds (Veldkamp and Lambin, 2001). Statistical models developed from field data from small watersheds are usually assumed to apply to large watersheds (Blöschl and Sivapalan, 1995; Blöschl and Grayson, 2001). Although it is not difficult to quantify soil erosion and chemical loadings in experimental plots, it is time-consuming and expensive (Mostaghimi et al., 1997). Clearly, it is not practical to conduct field experiments for every possible combination of land use and BMPs, under different biophysical conditions. As a result, it is unlikely sufficient field data could be obtained to develop management plans and conduct cost–benefit analyses. In addition, statistical models could potentially be derived from experiments; however, it is difficult to establish cause-and-effect relationships between BMPs and water quality variables under varied biophysical conditions or to quantify the impact of combined land use and BMPs on water quality at the watershed scale (Renschler and Lee, 2005).
Process-based models of hydrology can be used to extrapolate field data to fill data gaps (Borah and Bera, 2003, 2004; Singh, 1995; Singh and Woolhiser, 2002; Singh and Frevert, 2005). These process-based models provide quantitative information that is usually difficult to obtain from field experiments (Borah et al., 2002). For example, ANSWERS (Beasley et al., 1980), CREAMS (Knisel, 1980), GLEAMS (Leonard et al., 1987), AGNPS (Young et al., 1989), EPIC (Sharpley and Williams, 1990), and the Soil and Water Assessment Tool (SWAT; Arnold et al., 1998) have been used to understand surface runoff, soil erosion, nutrient leaching, and pollutant-transport processes. However, these process-based models require extensive input data and complex calibration procedures (Liu et al., 2015); watersheds with sufficient data to calibrate and validate these models are normally small, resulting in lack of representation at large spatial scales. Furthermore, once a model is calibrated, parameters become watershed-specific, which cannot be easily extended to other watersheds. In addition, these models require specialized expertise, which prevents nonexpert decision makers and economists using them (Viavattene et al., 2008).
A decision support tool could be developed by combining “decision rules” with geographic information systems (GISs) for water quality assessment in large ungauged watersheds. The “decision rules” could be based on regression equations derived from field experiments (Renschler and Harbor, 2002), or they could be defined simply as constants based on expert knowledge. Alternatively, simulations from a well-calibrated hydrological model could be used to develop statistical equation-based “decision rules”. Apart from defining “decision rules” at each grid cell, to assess water quantity and quality in streams or at subbasin and watershed outlets, the decision support tool should consider discharge, sediment, and nutrient routing within the watershed. For example, a commonly used routing method for sediments is the sediment–delivery ratio (SDR) method, which is widely employed in many GIS-based erosion models (May and Place, 2010; Wilson et al., 2001; Zhao et al., 2010). For discharge, a simple summation routing at the outlet produces acceptable accuracy for small- and medium-sized watersheds, considering that there is negligible water losses from surface runoff and streamflow. For large watersheds, water losses are generally greater. These water losses can be estimated using simple linear equations. The annual export of nutrients from watersheds (via the nutrient–delivery ratio) has been studied empirically in many studies as nutrient loading per land area (Endreny and Wood, 2003; Beaulac and Reckhow, 1982; Reckhow and Simpson, 1980).
A decision support tool developed based on “decision rules” is generally flexible and easy for decision makers and economists to use (Endreny and Wood, 2003). However, their practicality in normal circumstances, particularly with respect to their level of accuracy, needs to be evaluated. In addition, to provide sufficient “decision rules” with reasonable accuracy, fully validated hydrological models are required to be able to fill data gaps in field experiments. The present study used SWAT to provide modeled data in the development of the decision support tool. The main objective of the present study is to develop a simple decision support tool with the intent to evaluate the impact of land use change and BMPs on water resources in a large ungauged watershed in New Brunswick, Canada. This paper presents the development and testing of a decision support tool using data from two watersheds in the potato belt of New Brunswick: one small experimental watershed, with extensive monitoring and field survey data, and a larger watershed containing the smaller watershed. Specifically, this involves (1) setting up, calibrating, and validating SWAT for a small experimental watershed; (2) developing statistical equations relating water quality and quantity variables with weather, soil, land use information based on SWAT simulations for different combinations of land use and BMPs; (3) integrating the statistical equations into a decision support tool with the aid of ArcGIS; and (4) testing the decision support tool against field measurements and model simulations of stream discharge, sediment, and nutrient loadings for a large watershed.
2.1 Study sites and data collection
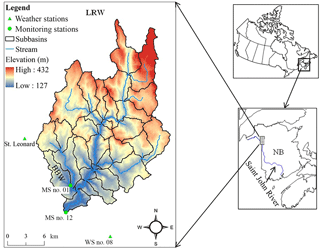
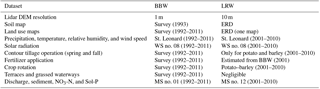
The large watershed of this study is the Little River watershed (LRW), located in the upper Saint John River valley of northwestern New Brunswick, Canada (Fig. 1). It covers an area approximately 380 km2 with a mixture of agricultural (16.2 %), forest (77 %), and residential (6.8 %) land uses (Xing et al., 2013). Elevation in the watershed ranges from 127 to 432 m a.m.s.l. (above mean sea level) (Fig. 1). The soil in the study sites is classified as mineral, derived from various parent materials. The major associations are Caribou, Carleton, Glassville, Grandfalls, Holmesville, McGee, Muniac, Siegas, Thibault, Undine, Victoria, Waasis, and one organic soil (Fig. 2). The study site belongs to the upper Saint John River valley ecoregion in the Atlantic Maritime Ecozone (Marshall et al., 1999). The climate of the region is considered to be moderately cool boreal with approximately 120 frost-free days, annually (Yang et al., 2009). Daily maximum and minimum temperatures are 24 (in July) and −18.1 ∘C (in January) based on Canadian Climate Normal station data at St. Leonard (http://climate.weather.gc.ca/climate_normals, last access: 15 July 2018). The average temperature is 3.7 ∘C and annual precipitation is 1037.4 mm (Zhao et al., 2008). About one-third of the precipitation is in the form of snow. Snowmelt leads to major surface runoff and groundwater recharge events from March to May (Chow and Rees, 2006). The land use and soil maps in the setup of SWAT for LRW were derived from publicly available data (Department of Energy and Resource Development – ERD, New Brunswick; Fig. 2).

Figure 2Slope classes created using a 10 m resolution lidar (light detection and ranging)-based DEM (digital elevation model), soil and land use maps, and land use IDs in SWAT (see Table 2 for land use ID meaning).
The small experimental watershed of the study is the Black Brook Watershed (BBW), a subbasin of LRW (Fig. 1). The BBW has been studied extensively for more than 20 years to evaluate the impact of agriculture on soil erosion and water quality (Li et al., 2014; Chow and Rees, 2006). The watershed covers an area of 14.5 km2, with 65 % being agriculture land, 21 % forest land, and 14 % residential areas and wetlands. Slopes vary from 1–6 % in the upper basin to 4–9 % in the central area. In the lower portion of the watershed, slopes are more strongly rolling at 5–16 %. Soil surveys (1:10 000 scale) identified six mineral soils, namely Grandfalls, Holmesville, Interval, Muniac, Siegas, and Undine, and one organic soil, St. Quentin (Mellerowicz, 1993).
A water-monitoring station was established at the outlet of BBW in 1992 (MS no. 01; Fig. 1) and another (MS no. 12) at the outlet of LRW in 2001. At these stations, V-notch weirs were installed, and the stage height of the water was recorded using a Campbell Scientific CR10X data logger. Stage height values were converted to total flow rates with a calibration curve function (Chow et al., 2011). Water samples were collected with an ISCO automatic sampler. Sampling frequency was set at one sample every 72 h when runoff was absent. During runoff events, sampling frequency was increased to one sample for every 5 cm change in stage height. Samples were analyzed for concentration of suspended solids, nitrate–nitrogen (NO3–N), and soluble-phosphorus (Sol–P). Detailed description of data collection procedures and sample analyses can be found in Chow et al. (2011). Weather data including daily precipitation, air temperature, relative humidity, and wind speed were acquired from the St. Leonard Environment Canada weather station (http://climate.weather.gc.ca, last access: 15 July 2018), located approximately 5 km northwest of BBW (Fig. 1). The daily average relative humidity and wind speed were calculated based on averaging hourly values. Since this weather station did not monitor daily solar radiation, the study used solar radiation collected from a weather station located approximately 10 km southeast of BBW (WS no. 08; Fig. 1).
2.2 SWAT setup, calibration, and validation for BBW and LRW
A modified version of SWAT has been developed for cold regions (Qi et al., 2016a, b, 2017a, b), and it was used for the BBW and LRW in this study. Detailed model setup, calibration, and validation for BBW can be found in Qi et al. (2017b). Specific model inputs for both watersheds are provided in Table 1. The same weather data were used for both watersheds (Table 1). The digital elevation model (DEM) for LRW and BBW were both based on high-resolution lidar (light detection and ranging) data; the first was created at 10 m and the second at 1 m resolution. The LRW was delineated into 32 subbasins from which their topographic characteristics were defined (Fig. 1). The soil types and slopes, which were classified into five separate classes, are illustrated in Fig. 2 for LRW. After combining the soil, slope, and land use maps through the ArcSWAT-interface function, 362 HRUs were subsequently created for LRW (based on thresholds: 10, 15, and 20 % for land use, soil, and slope).
Table 2Land use and land use groups for BBW and LRW.
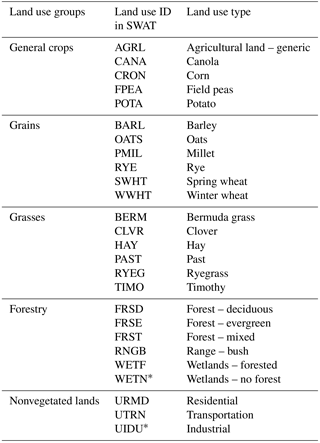
Note: “*” indicates unique land use types to LRW not present in BBW and, therefore, unaccounted for in the development of the decision support tool.
Since only one land use map was available for LRW (Table 1), assumptions were made based on information available on land use and management records for BBW to adjust the SWAT-management files for LRW as follows:
-
Potato–barley rotations were assigned to the land use ID POTA (Table 2); for other land use IDs, a single crop was considered.
-
Fertilizers were applied only to potato and barley fields, and fertilizer amounts and N:P (nitrogen-to-phosphorus) ratios were averaged for potato and barley fields over the entire watershed, based on 2001 survey data from BBW.
-
Contour tillage was applied only to potato and barley fields.
-
It was assumed that flow diversion terraces (FDTs) and grassed waterways in LRW were not used. It is worth noting that these four assumptions serve as a baseline scenario for the assessment of FDT in LRW.
To evaluate the global performance of the decision support tool for LRW, related land use and management files were prepared and accessed by SWAT. For the purpose of comparison, simulations with SWAT were produced in an initial application by setting the adjustable parameters of the model to their default values, and in a second application by setting the parameters according to values produced with a watershed-specific model calibration to BBW. This approach with model parameterization is widely accepted when applying SWAT to large ungauged watersheds (Panagopoulos et al., 2011).
2.3 Decision rules
The decision support tool was designed to use the “decision rules” to estimate annual discharge and sediment and nutrient loadings from individual grid cells:
where A is the annual discharge or sediment and nutrient loadings at the outlet of the watershed, and DRi and Ai are the delivery ratios and annual discharge or loadings, respectively, for grid cell i. For the present study, statistical equations derived from simulations of the calibrated version of SWAT for BBW were defined as the “decision rules” in the decision support tool.
2.3.1 Land use groups and BMP scenarios
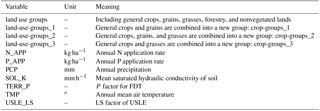
In statistical equation development, land uses in BBW (24, in total) were first classified into five land use groups according to their influences on hydrological processes (Table 2). Note that water land use type (WATR) was not used due to its small overall coverage (Fig. 2). As for watershed management, we considered three main BMPs, i.e.,
-
FDT+contour tillage,
-
contour tillage only, and
-
no-BMP (without FDT and contour tillage).
The calibrated version of the enhanced SWAT for BBW was used to generate annual outputs based on HRUs from 1992 to 2011. The model was run 3 times to generate the BMP-specific data for statistical equation development.
2.3.2 Explanatory variables selection
Explanatory candidate variables must be physically meaningful in hydrological and biochemical processes. It is worth noting that both continuous and categorical variables were included in the regression equation. The land use groups were the only categorical variable, and the remaining were all continuous variables. To detect significant predictors, the analysis of covariance (ANCOVA) was used. It requires at least one continuous and one categorical explanatory variable and is used to identify the major interaction of predictor variables. By including continuous variables, the method can reduce the variance of error to increase the statistical power and precision in estimating categorical variables (Keselman et al., 1998; Li et al., 2014). Inclusion of interaction terms in these regression models dramatically increased model performance.
In the present study, we only considered interactions between two explanatory variables at a time. Student t tests were conducted to examine the statistical significance of each level of land use groups and their interaction with the various continuous variables. When one level of land use groups (e.g., grains; Table 2) did not significantly correlate with water quality or quantity, or there were nominal interactions between a given level and other explanatory variables, this particular level of land use groups would be combined with other levels of land use groups until all new levels of land use groups were statistically significant.
Multiple linear regression analyses were used to relate annual total discharge (mm) and sediment (t ha−1), NO3–N (kg ha−1), and Sol–P (kg ha−1) loadings to the explanatory variables. These work was conducted in R (Ihaka and Gentleman, 1996). Only six continuous explanatory variables were determined for the specification of the statistical models. Annual precipitation (PCP), annual mean air temperature (TMP), and mean saturated hydraulic conductivity of soil (SOL_K) were common to the dependent variables (i.e., total discharge and sediment, NO3–N, and Sol–P loadings). The LS factor (USLE_LS) and annual N and P application rates (N_APP and P_APP) were unique to the equations addressing sediment, NO3–N, and Sol–P loading.
2.3.3 Delivery ratio definition
The LS factor of the universal soil loss equation (USLE) was determined by slope gradient (slp) and slope length (L) of individual HRUs:
where m is the equation exponent and a is the angle of the slope (in degrees). The exponent m is calculated by
where slp is in units of meters per meter (m m−1). For the decision support tool, slope length L equal to the length of the grid side and slope gradient was determined by the Slope tool in ArcGIS. The sediment–delivery ratio was not considered in the decision support tool application to BBW. We assumed that annual sediment loadings from grid cells in the decision support tool were all exported to the outlet of BBW. However, when the decision support tool was applied to LRW, the sediment–delivery ratio was used to correct estimates of sediment loading at the watershed outlet. The sediment loadings at the outlet of LRW (sed) were determined by
where sed∼ is the sediment loading calculated with the sediment loading equation (one for each BMP and land use group), and SDR is determined by the following (Vanoni, 1975):
where D (km−2) is the drainage area. For annual discharge and nutrient loadings, we assumed their delivery ratios are equal to 1.0 for all grid cells in LRW.
2.4 Decision support tool assessment
Inputs to the decision support tool included the six continuous explanatory variables and land use groups as well as information on management practices, e.g., contour tillage and FDT implementation. Simulations from each grid cell were summarized at the outlet of the study watersheds. We first tested the impact of cell size on simulations of water quantity and quality at the outlet of BBW. The cell size range was determined by considering different farmland sizes in the watershed. We assumed that farmland-based grid cells can sufficiently represent basic hydrological processes, land use change, and management practice implementations for hydrological modeling. Simulated annual water flow and sediment and nutrient loadings with the decision support tool were compared with those produced with the calibrated version of the enhanced SWAT. Subsequently, the decision support tool was applied to LRW, and the simulations were compared with the results of the uncalibrated and calibrated versions of SWAT. The purpose of this was to test if the decision support tool (i.e., land use and BMP assessment tool; LBAT) performed better, or at least as well, as both the uncalibrated and calibrated version of SWAT.
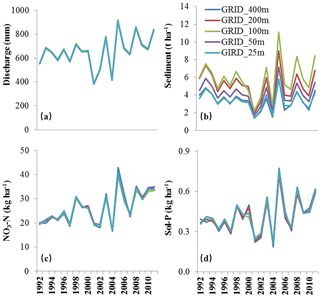
Figure 3LBAT-produced simulations of annual stream discharge and sediment, NO3–N, and Sol–P loadings determined for different DEM grid-cell sizes (i.e., 25, 50, 100, 200, and 400 m).
Model performance in terms of water quantity and quality at the outlet of the study watersheds was assessed based on the coefficient of determination (R2) and relative error (RE), i.e.,
where Oi, Pi, Oavg, and Pavg are the observed and predicted and averages of the observed (O) and predicted (P) values.
2.5 FDT assessment in LRW
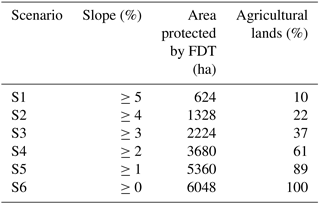
A series of FDT-implementation scenarios were set up for LBAT based on six slope classes to assess the impact of FDT on water quantity and quality on agricultural lands in LRW (Fig. 3; Table 3). From scenarios one (S1) to six (S6), the total area protected by FDT gradually increased until all agricultural lands were protected (Table 3). Mean annual simulations of total discharge and sediment, NO3–N, and Sol–P loadings from LRW from 2001 to 2010 were compared with those of the baseline scenario (FDT=0 %) for each scenario using two performance indicators, i.e., mean difference (MD) and percentage relative difference (PRD), given as follows:
-
MD=output with FDT−output without FDT, and
-
PRD (%)=MD/output without FDT×100.
3.1 Statistical equations (decision rules)
3.1.1 Model structure and coefficients
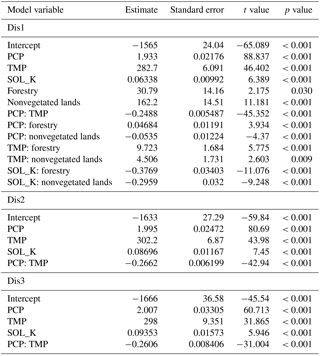
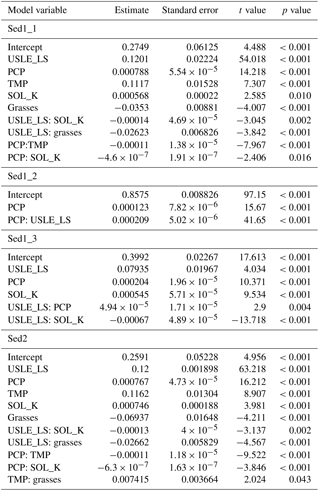
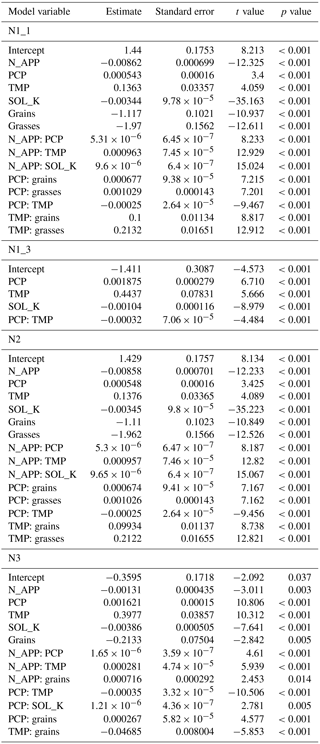
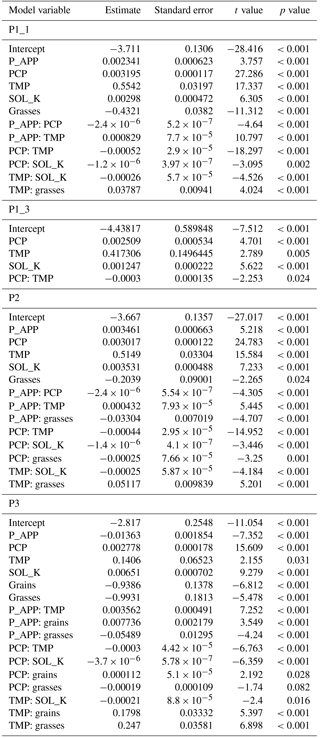
Linear regression equations and their explanatory variables for annual discharge and sediment, NO3–N, and Sol–P loadings under different combinations of land use groups and BMP scenarios are provided in Tables 4 and 5. In total, three discharge models (Dis1, Dis2, and Dis3) and five sediment (Sed1_1, Sed1_2, Sed1_3, Sed2, and Sed3), NO3–N (N1_1, N1_2, N1_3, N2, and N3), and Sol–P (P1_1, P1_2, P1_3, P2, and P3) loading models were developed. Data transformations (via logarithm and power transformations) were applied to sediment, NO3–N, and Sol–P loadings to meet the assumption of normality in multiple regression analysis (Table 4). The contour tillage and FDT were applied only to agricultural lands (including general crops, grains, and grasses; Table 4). For the no-BMP scenario, three separate sediment, NO3–N, and Sol–P loading models were developed for agricultural lands, nonvegetated lands, and forestry, and one discharge model (Dis1) for all land use groups (Table 4). It is worth noting that the sediment loading model, Sed3, was a modified version of Sed1_1 (multiplied by TERR_P) for the FDT+contour tillage scenario (Table 4), and the values of TERR_P (Qi et al., 2017b) used for Sed3 were the same as the calibrated values in SWAT for BBW (Qi et al., 2017b). Also, NO3–N and Sol–P loadings (N1_2 and P1_2) for nonvegetated lands were determined as constants, which were equal to the calculated means of NO3–N and Sol–P loadings determined by SWAT (i.e., 24 and 0.61 kg ha−1, respectively; Table 4).
In model development, three new land use groups (i.e., land-use-groups_1, land-use-groups_2, and land-use-groups_3) were formulated by combining general crops, grains, and grasses (Tables 4 and 5). For example, land-use-groups_2 was derived by combining general crops, grains, and grasses on total discharge (i.e., Dis1 model). Individual model structures are shown in Table 4, whereas the explanatory variables for these models appear in Appendix A. The coefficients estimated for the explanatory variables and their interactions, and their t-test results are also shown in Appendix A. Most of the p values for these explanatory variables were <0.001, except for several that were between 0.001 and 0.08, which were also taken as acceptable.
3.1.2 Statistical equation assessment
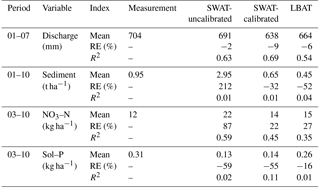
Simulations based on the statistical equations and the calculated outputs from individual HRUs for the different BMPs are compared in Table 6. In general, discharge models were able to reproduce SWAT simulations for the three BMPs, with R2 ranging from 0.86 to 0.9. Mean discharge simulated with the statistical equations was equal to that of SWAT (Table 6). Mean discharge (636 mm) for the no-BMP-case (BMP 3) was greater than that for BMPs using contour tillage and FDTs (619 and 628 mm for BMP 1 and 2, respectively), suggesting that contour tillage and FDTs can cause evapotranspiration to increase.
Models Sed1_2 and Sed1_3 were able to reproduce simulations with SWAT (yielding R2=0.71 and 0.57, respectively), and simulated mean sediment loadings were close to that of SWAT (Table 6). Models Sed1_1 and Sed2 tended to underestimate results from SWAT (Table 6), with an overall lower mean sediment loading of 10.78 vs. 12.84 and 8.31 vs. 9.4 t ha−1, respectively. Mean sediment loading with Sed3 (0.89 t ha−1) was slightly greater than that of SWAT (0.84 t ha−1), because Sed3 only took into account TERR_P, whereas SWAT took into account TERR_CN and the impact of grassed waterways. Results from the statistical equations showed that the mean sediment loading for BMP 2 (8.31 t ha−1) was significantly different than that for BMPs 1 and 3, with mean loading of 0.89 and 10.78 t ha−1 (Table 6). The smallest mean sediment loading (0.09 t ha−1) was found to occur with the forestry land use grouping (Table 6).
The four NO3–N and Sol–P loading equations explained ∼50 % of the variation in the SWAT simulations for the same variables, with R2 ranging from 0.33 to 0.59 (Table 6). Mean NO3–N and Sol–P loadings with the statistical equations were all slightly less than the values produced with SWAT for the different BMPs (Table 6). Mean NO3–N loadings were greater for BMP 1 (44 kg ha−1) than those for BMPs 2 and 3 with both giving 39 kg ha−1 (Table 6), due to increased infiltration with FDT. Mean Sol–P loading (0.8 kg ha−1) was less for BMP 3 than for BMP 2 (0.89 kg ha−1), but much greater than for BMP 1 (0.43 kg ha−1). Although contour tillage can help reduce sediment loading by modifying microtopography and reducing erosion runoff (the reason we set USLE_P<1), Sol–P transported with surface runoff increased due to reduced residue cover protecting the soil surface during winter and during the snowmelt season. When FDT was implemented with tillage, however, less surface runoff was generated due to increased infiltration, leading to a reduction in Sol–P loading. Mean NO3–N and Sol–P loadings for the forestry land grouping (10 vs. 0.06 kg ha−1) were much less than those of the crop groups (including general crops, grains, and grasses), 39 vs. 0.8 kg ha−1 (Table 6).
Table 4Statistical models based on land use groups and BMP scenarios.
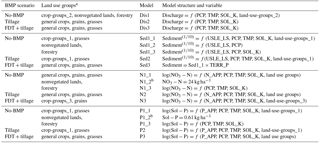
a General crops and grains are combined into one group, namely crop-groups_1 in land-use-groups_1; general crops, grains, and grasses are combined into one group, namely crop-groups_2 in land-use-groups_2; general crops and grasses are combined into one group, namely crop-groups_3 in land-use-groups_3. b Variable is set constant.
3.2 LBAT assessment
3.2.1 Impact of grid cell size on LBAT simulation
Simulations of water quantity and quality by LBAT with different grid-cell sizes (i.e., 25, 50, 100, 200, and 400 m) for BBW are shown in Fig. 3. Statistical tests indicated that grid-cell size had a significant effect on sediment loading (p value<0.01), with no effect observed for discharge and NO3–N and Sol–P loadings (p values>0.99). Increasing cell size (i.e., slope length) increased sediment loading. However, the mean slope gradient was reduced. As a result, the mean sediment loadings were correlated nonlinearly with cell size, as shown in Fig. 4. The highest mean sediment loading was found with a cell size of 100 m (5.86 t ha−1), whereas the lowest was found to occur with a cell size of 25 and 400 m (3.37 t ha−1). The LBAT with a cell size of 25 and 400 m was able to generate sediment loadings consistent with field measurements. Considering computational efficiency, we chose a grid-cell size of 400 m as the basic LBAT-simulation unit for LRW.
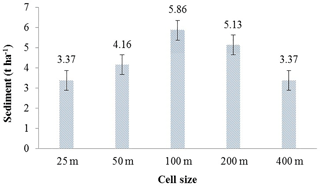
Figure 4Impact of grid-cell size on LBAT simulation of sediment loading. Mean annual sediment loadings and standard errors (vertical bars) from 1992 to 2011 are indicated.
3.2.2 LBAT vs. SWAT in LRW
Simulations of water quantity and quality with LBAT and the uncalibrated and calibrated versions of SWAT are compared with field measurements for LRW (Fig. 5). Model assessments for different simulation periods (depending on measurement availability) are shown in Table 7. It is worth noting that, to eliminate unrealistic results, USLE_LS was constrained in Sed1_2 to the nonvegetated lands:
where 1.28 is the maximum USLE_LS for BBW.
In general, the two versions of SWAT and LBAT slightly underestimated annual stream discharge, capturing its variation reasonably well (R2>0.54; Fig. 5a). The uncalibrated and calibrated versions of SWAT had the least and largest absolute values of RE ( and −9), whereas LBAT (Table 7). The uncalibrated version of SWAT severely overestimated annual sediment and NO3–N loading (RE=212 and 87, respectively; Fig. 5b and c), whereas the calibrated version of SWAT and LBAT underestimated sediment loading ( and −52, respectively) and overestimated NO3–N loading (RE=22 and 27, respectively; Table 7). In general, the calibrated version of SWAT and LBAT captured the variation in annual NO3–N loadings reasonably well (R2>0.35; Fig. 5c). However, the two versions of SWAT and LBAT failed to capture the variation in annual sediment and Sol–P loadings (low R2; Fig. 5b and d). The LBAT had the smallest absolute value of RE (i.e., ), while the uncalibrated and calibrated versions of SWAT had larger values ( and −55, respectively). These results suggested that the LBAT and the calibrated version of SWAT performed fairly equivalently in simulating annual streamflow and sediment and NO3–N loadings, with LBAT performing slightly better for annual Sol–P loading. LBAT performed noticeably better than the uncalibrated version of SWAT, especially for annual sediment and NO3–N loadings. Poor performance for both versions of SWAT and LBAT on simulation of annual sediment and Sol–P loadings in LRW might be attributable to a lack of detailed management practice and fertilizer application information from agricultural lands. We only had 1 year of data for LRW and made assumptions about rotation and management practices for other years based on information from BBW, which could introduce major input uncertainty.
Since LBAT is based on decision rules (statistical equations in this study) that were derived from SWAT simulations for BBW, its usage should be constrained to areas with soil, landscape, and land use characteristics similar to BBW. Input characteristics exceeding the range of SWAT data could lead to large errors in predictions. LBAT is flexible in its structure, and with thoughtful development of decision rules, it can be applied to diverse environments.
Table 6Comparisons of simulations of statistical models and outputs from SWAT for different land use groups and BMPs based on mean and standard deviation for the entire simulation period (1992–2011).

Note: crop groups include general crops, grains, and grasses; the statistics for discharge in no-BMP scenario are based on crop groups, nonvegetated lands, and forestry.
3.2.3 FDT assessment in LRW
Mean annual water quantity and quality simulated with LBAT for agricultural lands of LRW are shown in Table 8. The mean annual discharge for the baseline scenario was 626 mm greater than that for the six FDT scenarios (Table 8). When all agricultural lands were protected (S6), there was a 2 % reduction in discharge (equivalent to 11 mm; Table 8). With the steepest areas protected (accounting for 10 % of the total land base; S1), the mean annual sediment loading was reduced by as much as 43 % (equivalent to 4.5 t ha−1; Table 8) and by as much as 81 % (i.e., 8.57 t ha−1) with all agricultural lands protected (S6; Table 8). Mean annual Sol–P loading was reduced by 51 % (equivalent to 0.47 kg ha−1; Table 8). In contrast, increased usage of FDT tended to increase the mean annual loading of NO3–N by about 6 % when used across all agricultural lands (equivalent to 1.73 kg ha−1).
Table 8Impact of FDT on mean annual discharge and sediment, NO3–N, and Sol–P loadings simulated with LBAT under different FDT, provided in Table 3.
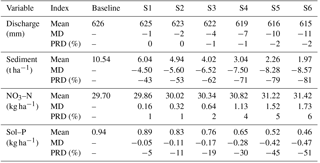
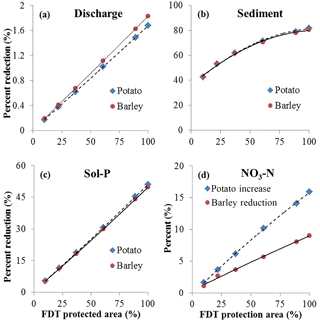
Figure 6Percentage change in discharge and sediment, NO3–N, and Sol–P loadings as a function of % area, where FDTs were used.
Percentage change (based on PRD) of water quantity and quality were plotted against percentage area of FDT for potato and barley in Fig. 6. Increasing the usage of FDT helped to reduce discharge and sediment and Sol–P loadings for both crop types (Fig. 6a–c). It is worth noting that sediment loading decreased with increasing usage of FDT (Fig. 6b). An opposite trend was observed for potato and barley with respect to the impact of FDT on NO3–N loading. With the increased usage of FDT, NO3–N loadings increased linearly for potato, while it decreased for barley. The increase for potato was nearly twice as much as the reduction for barley (Fig. 6d). Seemingly the interaction between barley and FDT had positive impacts on nitrate retention in soils, whereas the interaction between potato and FDT had an opposite effect.
These results are consistent with the results from previous studies (Yang et al., 2010, 2012), which used SWAT to assess the impact of FDT on water quantity and quality within BBW. When using SWAT, greater efforts are needed to prepare basic inputs, such as daily weather records, to proceed with its calibration and validation, involving complex scenario setup and analysis. For every new watershed, SWAT needs dedicated effort and time for its setup. LBAT, in contrast, can be used for multiple watersheds as long as they have similar environmental conditions. Scenario analysis can be directly conducted with different combinations of land use and BMPs using fewer inputs than what is required by SWAT. Also, once developed, LBAT does not require additional calibration.
The present study addresses the development of a decision support tool to assess the impact of land use change and BMPs on water quantity and quality for ungauged watersheds. An enhanced version of SWAT was calibrated and validated for a small experimental watershed. Multiple regression analyses were used to develop statistical equations based on simulations from SWAT. In total, three discharge and five sediment, NO3–N, and Sol–P loading models were developed for different combinations of land use groups and BMP scenarios. Only four common predictors (i.e., annual precipitation, annual mean air temperature, mean saturated hydraulic conductivity of soil, and land use groups) and three unique predictors (LS factor and annual nitrogen and phosphorus application rates for sediment, NO3–N, and Sol–P loading models, respectively) are required.
With the aid of ArcGIS, statistical equations were integrated into the decision support tool, i.e., the land use and BMP assessment tool (LBAT), whose basic simulation units are the DEM grid cell. The LBAT was used to simulate annual water flow and sediment and nutrient loadings at the outlet of a larger watershed, i.e., LRW. These simulations were compared with those of SWAT. Results indicated that LBAT and the calibrated version of SWAT performed equivalently with respect to annual stream discharge and sediment and NO3–N loadings. LBAT performed slightly better, when Sol–P loading was considered. Compared with the uncalibrated version of SWAT, LBAT performed better. The impact of FDT on water quantity and quality was evaluated with LBAT for LRW; its results were consistent with the results generated with SWAT for the same region in previous studies. LBAT has fewer input requirements than SWAT and can be applied to multiple watersheds without additional calibration. Also, scenario analyses can be directly conducted with LBAT without complex setup procedures. We recommend using LBAT for economic analysis and management decision making for watersheds with similar environmental conditions of New Brunswick. The LBAT developed in this study may not be directly applied to other regions; however, the approach in developing LBAT can be applied to other regions of the world because of its flexible structure.
Data used in the present study are not publicly accessible and can be required through personal contact, i.e., email: sheng.li@agr.gc.ca.
Conceptualization and methodology were developed by FRM and JQ. SL and ZX worked with the resources. JQ and CPAB prepared and wrote the paper, which was reviewed and edited by CPAB.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Coupled terrestrial-aquatic approaches to watershed-scale water resource sustainability”. It is not associated with a conference.
This research was funded by Agriculture and Agri-Food Canada (AAFC) projects
no. 1145, no. 1256, and no. 1538, and Natural Science and Engineering Research
Council (NSERC) Discovery Grants to Charles P.-A. Bourque and Fan-Rui Meng.
Edited by: Alberto Guadagnini
Reviewed by: two anonymous referees
Arnold, J. G., Srinivasan, R., Muttiah, R. S., and Williams, J. R.: Large area hydrologic modeling and assessment part I: Model development, J. Am. Water Resour. Assoc., 34, 73–89, 1998.
Beasley, D., Huggins, L., and Monke, a.: ANSWERS: A model for watershed planning, T. ASAE, 23, 938–944, 1980.
Beaulac, M. N. and Reckhow, K. H.: An Examination of Land Use–Nutrient Export Relationships, J. Am. Water Resour. Assoc., 18, 1013–1024, 1982.
Blöschl, G. and Sivapalan, M.: Scale issues in hydrological modelling: a review, Hydrol. Process., 9, 251–290, 1995.
Blöschl, G. and Grayson, R.: Spatial observations and interpolation, in: Spatial patterns in catchment hydrology: observations and modelling, edited by: Grayson, R. and Blöschl, G., Cambridge University Press, Cambridge, UK, 17–50, 2001.
Borah, D. K. and Bera, M.: Watershed-scale hydrologic and nonpoint-source pollution models: Review of mathematical bases, T. ASAE, 46, 1553, https://doi.org/10.13031/2013.15644, 2003.
Borah, D. K. and Bera, M.: Watershed-scale hydrologic and nonpoint-source pollution models: Review of applications, T. ASAE, 47, 789–803, 2004.
Borah, D. K., Demissie, M., and Keefer, L. L.: AGNPS-based assessment of the impact of BMPs on nitrate-nitrogen discharging into an Illinois water supply lake, Water Int., 27, 255–265, 2002.
Chow, L., Xing, Z., Benoy, G., Rees, H., Meng, F., Jiang, Y., and Daigle, J.: Hydrology and water quality across gradients of agricultural intensity in the Little River watershed area, New Brunswick, Canada, J. Soil Water Conserv., 66, 71–84, 2011.
Chow, T. and Rees, H.: Impacts of intensive potato production on water yield and sediment load (Black Brook Experimental Watershed: 1992–2002 summary), Potato Research Centre, AAFC, Fredericton, New Brunswick, Canada, 26–27, 2006.
D'Arcy, B. and Frost, A.: The role of best management practices in alleviating water quality problems associated with diffuse pollution, Sci. Total Environ., 265, 359–367, 2001.
Endreny, T. A. and Wood, E. F.: Watershed weighting of export coefficients to map critical phosphorous loading areas, Wiley Online Library, https://doi.org/10.1111/j.1752-1688.2003.tb01569.x (last access: 15 July 2018), 2003.
Ihaka, R. and Gentleman, R.: R: a language for data analysis and graphics, J. Comput. Graph. Stat., 5, 299–314, 1996.
Keselman, H., Huberty, C. J., Lix, L. M., Olejnik, S., Cribbie, R. A., Donahue, B., Kowalchuk, R. K., Lowman, L. L., Petoskey, M. D., and Keselman, J. C.: Statistical practices of educational researchers: An analysis of their ANOVA, MANOVA, and ANCOVA analyses, Rev. Educ. Res., 68, 350–386, 1998.
Knisel, W. G.: CREAMS: a field scale model for Chemicals, Runoff, and Erosion from Agricultural Management Systems [USA], United States, Conservation research report, Dept. of Agriculture, Tucson, Arizona, USA, 1980.
Leonard, R., Knisel, W., and Still, D.: GLEAMS: Groundwater loading effects of agricultural management systems, T. ASAE, 30, 1403–1418, 1987.
Li, Q., Qi, J., Xing, Z., Li, S., Jiang, Y., Danielescu, S., Zhu, H., Wei, X., and Meng, F.-R.: An approach for assessing impact of land use and biophysical conditions across landscape on recharge rate and nitrogen loading of groundwater, Agr. Ecosyst. Environ., 196, 114–124, https://doi.org/10.1016/j.agee.2014.06.028, 2014.
Liu, Y., Yang, W., Yu, Z., Lung, I., and Gharabaghi, B.: Estimating sediment yield from upland and channel erosion at a watershed scale using SWAT, Water Resour. Manage., 29, 1399–1412, 2015.
Marshall, I., Schut, P., and Ballard, M.: A national ecological framework for Canada: Attribute data. Ottawa, Ontario: Environmental Quality Branch, Ecosystems Science Directorate, Environment Canada and Research Branch, Agriculture and Agri-Food Canada, Ottawa, Canada, 1999.
May, L. and Place, C.: A GIS-based model of soil erosion and transport, Freshwater Forum, Freshwater Biological Association, Cumbria, UK, 2010.
Mellerowicz, K. T.: Soils of the Black Brook Watershed St. Andre Parish, Madawaska County, New Brunswick, [Fredericton], New Brunswick Department of Agriculture, Fredericton, New Brunswick, Canada, 1993.
Mostaghimi, S., Park, S., Cooke, R., and Wang, S.: Assessment of management alternatives on a small agricultural watershed, Water Res., 31, 1867–1878, 1997.
Novara, A., Gristina, L., Saladino, S., Santoro, A., and Cerdà, A.: Soil erosion assessment on tillage and alternative soil managements in a Sicilian vineyard, Soil Till. Res., 117, 140–147, 2011.
Ongley, E. D., Xiaolan, Z., and Tao, Y.: Current status of agricultural and rural non-point source pollution assessment in China, Environ. Pollut., 158, 1159–1168, 2010.
Panagopoulos, Y., Makropoulos, C., and Mimikou, M.: Reducing surface water pollution through the assessment of the cost-effectiveness of BMPs at different spatial scales, J. Environ. Manage., 92, 2823–2835, 2011.
Pimentel, D. and Krummel, J.: Biomass energy and soil erosion: Assessment of resource costs, Biomass, 14, 15–38, 1987.
Qi, J., Li, S., Li, Q., Xing, Z., Bourque, C. P.-A., and Meng, F.-R.: A new soil-temperature module for SWAT application in regions with seasonal snow cover, J. Hydrol., 538, 863–877, 2016a.
Qi, J., Li, S., Li, Q., Xing, Z., Bourque, C. P.-A., and Meng, F.-R.: Assessing an Enhanced Version of SWAT on Water Quantity and Quality Simulation in Regions with Seasonal Snow Cover, Water Resour. Manage., 30, 5021–5037, 2016b.
Qi, J., Li, S., Jamieson, R., Hebb, D., Xing, Z., and Meng, F.-R.: Modifying SWAT with an energy balance module to simulate snowmelt for maritime regions, Environ. Model. Softw., 93, 146–160, 2017a.
Qi, J., Li, S., Yang, Q., Xing, Z., and Meng, F.-R.: SWAT Setup with Long-Term Detailed Landuse and Management Records and Modification for a Micro-Watershed Influenced by Freeze-Thaw Cycles, Water Resour. Manage., 31, 3953–3974, https://doi.org/10.1007/s11269-017-1718-2, 2017b.
Quan, W. and Yan, L.: Effects of agricultural non-point source pollution on eutrophication of water body and its control measure, Acta Ecol. Sin., 22, 291–299, 2001.
Reckhow, K. and Simpson, J.: A procedure using modeling and error analysis for the prediction of lake phosphorus concentration from land use information, Can. J. Fish. Aquat. Sci., 37, 1439–1448, 1980.
Renschler, C. S. and Harbor, J.: Soil erosion assessment tools from point to regional scales – the role of geomorphologists in land management research and implementation, Geomorphology, 47, 189–209, 2002.
Renschler, C. S. and Lee, T.: Spatially distributed assessment of short-and long-term impacts of multiple best management practices in agricultural watersheds, J. Soil Water Conserv., 60, 446–456, 2005.
Sadeghi, S. H., Moosavi, V., Karami, A., and Behnia, N.: Soil erosion assessment and prioritization of affecting factors at plot scale using the Taguchi method, J. Hydrol., 448, 174–180, 2012.
Sharpley, A. N. and Williams, J. R.: EPIC-erosion/productivity impact calculator: 1. Model documentation, Technical Bulletin, United States Department of Agriculture, Washington, D.C., USA, 1990.
Singh, V. P.: Computer models of watershed hydrology, Water Resources Publications, Highlands Ranch, Colorado, USA, 1995.
Singh, V. P. and Frevert, D. K.: Watershed Models, CRC Press, Boca Raton, FL, USA, 2005.
Singh, V. P. and Woolhiser, D. A.: Mathematical modeling of watershed hydrology, J. Hydrol. Eng., 7, 270–292, 2002.
Turkelboom, F., Poesen, J., Ohler, I., Van Keer, K., Ongprasert, S., and Vlassak, K.: Assessment of tillage erosion rates on steep slopes in northern Thailand, Catena, 29, 29–44, 1997.
Urbonas, B.: Assessment of stormwater BMPs and their technology, Water Sci. Technol., 29, 347–353, 1994.
Vanoni, V. A.: Sedimentation Engineering, Manuals and Reports on Engineering Practice, American Society of Civil Engineers, New York, NY, USA, 1975.
Veldkamp, A. and Lambin, E. F.: Predicting land-use change, Agr. Ecosyst. Environ., 85, 1–6, 2001.
Viavattene, C., Scholes, L., Revitt, D., and Ellis, J.: A GIS based decision support system for the implementation of stormwater best management practices, in: 11th International Conference on Urban Drainage, Edinburgh, Scotland, UK, 2008.
Vörösmarty, C. J., McIntyre, P. B., Gessner, M. O., Dudgeon, D., Prusevich, A., Green, P., Glidden, S., Bunn, S. E., Sullivan, C. A., and Liermann, C. R.: Global threats to human water security and river biodiversity, Nature, 467, 555–561, 2010.
Wilson, C. J., Carey, J. W., Beeson, P. C., Gard, M. O., and Lane, L. J.: A GIS-based hillslope erosion and sediment delivery model and its application in the Cerro Grande burn area, Hydrol. Process., 15, 2995–3010, 2001.
Xing, Z., Chow, L., Rees, H., Meng, F., Li, S., Ernst, B., Benoy, G., Zha, T., and Hewitt, L. M.: Influences of sampling methodologies on pesticide-residue detection in stream water, Arch. Environ. Contam. Toxicol., 64, 208–218, 2013.
Yang, Q., Meng, F.-R., Zhao, Z., Chow, T. L., Benoy, G., Rees, H. W., and Bourque, C. P.-A.: Assessing the impacts of flow diversion terraces on stream water and sediment yields at a watershed level using SWAT model, Agr. Ecosyst. Environ., 132, 23–31, 2009.
Yang, Q., Zhao, Z., Benoy, G., Chow, T. L., Rees, H. W., Bourque, C. P.-A., and Meng, F.-R.: A watershed-scale assessment of cost-effectiveness of sediment abatement with flow diversion terraces, J. Environ. Qual., 39, 220–227, 2010.
Yang, Q., Benoy, G. A., Chow, T. L., Daigle, J.-L., Bourque, C. P.-A., and Meng, F.-R.: Using the Soil and Water Assessment Tool to estimate achievable water quality targets through implementation of beneficial management practices in an agricultural watershed, J. Environ. Qual., 41, 64–72, 2012.
Young, R. A., Onstad, C., Bosch, D., and Anderson, W.: AGNPS: A nonpoint-source pollution model for evaluating agricultural watersheds, J. Soil Water Conserv., 44, 168–173, 1989.
Zhang, W., Wu, S., Ji, H., and Kolbe, H.: Estimation of agricultural non-point source pollution in China and the alleviating strategies I. Estimation of agricultural non-point source pollution in China in early 21 century, Scient. Agricult. Sin., 37, 1008–1017, 2004.
Zhao, Z., Chow, T. L., Yang, Q., Rees, H. W., Benoy, G., Xing, Z., and Meng, F.-R.: Model prediction of soil drainage classes based on digital elevation model parameters and soil attributes from coarse resolution soil maps, Can. J. Soil Sci., 88, 787–799, 2008.
Zhao, Z., Benoy, G., Chow, T. L., Rees, H. W., Daigle, J.-L., and Meng, F.-R.: Impacts of accuracy and resolution of conventional and LiDAR based DEMs on parameters used in hydrologic modeling, Water Resour. Manage., 24, 1363–1380, 2010.