the Creative Commons Attribution 3.0 License.
the Creative Commons Attribution 3.0 License.
Dynamics of water fluxes and storages in an Alpine karst catchment under current and potential future climate conditions
Zhao Chen
Andreas Hartmann
Thorsten Wagener
Nico Goldscheider
Karst aquifers are difficult to manage due to their unique hydrogeological characteristics. Future climate projections suggest a strong change in temperature and precipitation regimes in European karst regions over the next decades. Alpine karst systems can be especially vulnerable under changing hydro-meteorological conditions since snowmelt in mountainous environments is an important controlling process for aquifer recharge and is highly sensitive to varying climatic conditions. Our paper presents the first study to investigate potential impacts of climate change on mountainous karst systems by using a combined lumped and distributed modeling approach with consideration of subsurface karst drainage structures. The study site is characterized by high-permeability (karstified) limestone formations and low-permeability (non-karst) sedimentary Flysch. The model simulation under current conditions demonstrates that a large proportion of precipitation infiltrates into the karst aquifer as autogenic recharge. Moreover, the result shows that surface snow storage is dominant from November to April, while subsurface water storage in the karst aquifer dominates from May to October. The climate scenario runs demonstrate that varied climate conditions significantly affect the spatiotemporal distribution of water fluxes and storages: (1) the total catchment discharge decreases under all evaluated future climate conditions. (2) The spatiotemporal discharge pattern is strongly controlled by temperature variations, which can shift the seasonal snowmelt pattern, with snow storage in the cold season (December to April) decreasing significantly under all change scenarios. (3) Increased karst aquifer recharge in winter and spring, and decreased recharge in summer and autumn, partly offset each other. (4) Impacts on the karst springs are distinct; the lowest permanent spring presents a “robust” discharge behavior, while the highest overflow outlet is highly sensitive to changing climate. This analysis effectively demonstrates that the impacts on subsurface flow dynamics are regulated by the characteristic dual flow and spatially heterogeneous distributed drainage structure of the karst aquifer. Overall, our study highlights the fast groundwater dynamics in mountainous karst catchments, which make them highly vulnerable to future changing climate conditions. Additionally, this work presents a novel holistic modeling approach, which can be transferred to similar karst systems for studying the impact of climate change on local karst water resources with consideration of their individual hydrogeological complexity and hydraulic heterogeneity.
- Article
(5688 KB) -
Supplement
(1973 KB) - BibTeX
- EndNote
The Alps, called the “water tower of Europe”, form headwaters for important regional river systems (Viviroli et al., 2007). Alpine catchments are generally characterized by above-average precipitation due to orographic effects, as well as by colder temperatures resulting in lower evapotranspiration and temporary water storage in the form of snow and ice (Zierl and Bugmann, 2005). Climate projections indicate that a shift in snow and precipitation patterns is likely to alter catchment runoff regimes (Gobiet et al., 2014). Additionally, extreme events, such as floods and droughts, are expected to increase in frequency and intensity (Dobler et al., 2013; Rössler et al., 2012). For sustainable management of water resources in Alpine areas, it is imperative to understand the complex mountainous hydrological processes (Kraller et al., 2012).
In this context, numerical models are usually applied to describe the hydrological processes in Alpine catchments (Abbaspour et al., 2007; Achleitner et al., 2009; Benischke et al., 2010; Braun and Renner, 1992; Junghans et al., 2011; Kraller et al., 2012). Lumped models are easy to use in gauged catchments because their parameters can be effectively found via calibration. For studying the spatial patterns of hydrological processes across a catchment, distributed models are required, which discretize the model domain into a grid of homogeneous subunits, for which surface and/or subsurface flow can be described by flow equations derived from basic physical laws. Previously, most distributed models focused on surface hydrological variables (e.g., vegetation, soil and snow cover) and/or anthropogenic variables (e.g., land use and water use), with relatively poor subsurface representations. Few studies (e.g., Kraller et al., 2012; Kunstmann et al., 2006; Kunstmann and Stadler, 2005) explicitly considered subsurface processes such as recharge, drainage and storage in their models for Alpine regions. It is generally accepted that the geological and lithological setting for mountainous catchments are often complex and could have significant impact on the catchment flow regime (Goldscheider, 2011; Rogger et al., 2013). The situation is even more complex when mountain ranges within a catchment consist of highly permeable limestone formations hydraulically characterized by fissures and/or conduit drainage networks, as well as concentrated discharge via springs (Goldscheider, 2005; Gremaud et al., 2009; Lauber and Goldscheider, 2014).
In order to better understand complex hydrological processes in mountainous karstic catchments as well as quantifying their dynamics, this study presents a spatially distributed investigation of the water fluxes and storages in a high-elevation Alpine catchment considering its complex subsurface heterogeneous drainage structure. The study catchment constitutes an optimal test case to explore complex hydrological processes since it includes many typical characteristics of Alpine catchments, such as a seasonal snow cover, a large range of elevations and a highly varied catchment flow regime. Furthermore, the hydrogeology in the investigated catchment is complex. It is characterized by high-permeability limestone formations (karst areas) and low-permeability Flysch sedimentary rocks (non-karst areas) as described by Goldscheider (2005). Here, we expanded an existing model (Chen and Goldscheider, 2014) by adding a snow accumulation and melting routine with high spatiotemporal resolution. We also developed a tailored calibration strategy, building on a previous sensitivity analysis by Chen et al. (2017), to calibrate the proposed catchment model reasonably and effectively.
Several recent studies indicated the significant impact of climate change on the catchment discharge behavior of Alpine areas, and demonstrated the changing characteristics of flow regimes including amount, seasonality, minima and maxima, as well as impacts on other hydrological variables, e.g., soil moisture and snow cover (Dobler et al., 2012; Jasper et al., 2004; Kunstmann et al., 2004; Middelkoop et al., 2001; Rössler et al., 2012; Zierl and Bugmann, 2005). Taylor et al. (2013) highlighted the impact of changing climatic conditions on aquifer dynamics in mountainous areas. They also pointed out that the effects of receding Alpine glaciers on groundwater systems are poorly understood. Gremaud et al. (2009) and Gremaud and Goldscheider (2010) studied a geologically complex, glacierized karst catchment in the Alps by combining tracer tests and hydrological monitoring and found that the changing hydro-meteorological conditions affect the water storage in snow and ice significantly, which have high impact on the aquifer recharge processes and discharge dynamics. Finger et al. (2013) investigated glacier meltwater runoff in a high Alpine karst catchment under present and future climate conditions using tracer experiments, karst structure modeling and glacier melt modeling. The results indicated that parts of the glacier meltwater are drained seasonally by the underlying karst system and the expected climate change may jeopardize the water availability in the karst aquifer. In order to better understand climate-change effects on complex hydrological processes in Alpine karstic environments, we assessed the impacts of varied climate conditions on the water fluxes and storages in the simulated model domain, and we identified the hydrological processes most sensitive to potential climate change. For this analysis, we used a pragmatic and widely used delta approach to project the climate change in the model domain (e.g., Dobler et al., 2012; Lenderink et al., 2007; Singh et al., 2014).
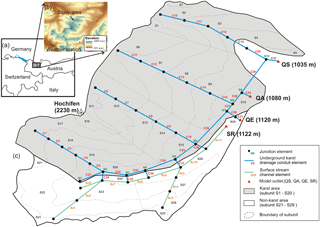
The study catchment is located in the northern Alps on the Germany/Austria border (Fig. 1a). It has an area of about 35 km2, and an altitude varying between 1000 m a.s.l. (the lowest part of the Schwarzwasser valley) and 2230 m a.s.l. (the summit of Hochifen). The climate in the area is cool-temperate and humid. The nearest permanent weather station lies to the east in the Breitach valley at an altitude of 1140 m a.s.l. There, the mean monthly temperature ranges from −2.2 ∘C in January to 14.4 ∘C in July, with an annual average of 5.7 ∘C (based on data from 1961 to 1990, available from the Water Authority Vorarlberg). The mean annual precipitation is 1836 mm with a maximum in June–August and a secondary maximum in December–January. Snow accumulates commonly between November and May.
Hydrogeologically, the investigated catchment can be divided into karst and non-karst areas, whose boundary is more or less marked by the Schwarzwasser river. The karst area is characterized by the highly permeable Schrattenkalk limestone formation (with about 100 m thickness), which is underlain by marl formations. The underground flow paths in the karst system are controlled by local folds and follow plunging synclines. The karst aquifer discharges at three major system outlets: a permanent spring (QS), a large but intermittent overflow spring (QA) and a cave that acts as overflow spring during high-flow conditions, but transforms into a swallow hole during low-flow conditions, a so-called estavelle (QE). The adjacent non-karst area consists of low-permeability Flysch formations and drains via surface streams. Several quantitative multi-tracer tests (Goldscheider, 2005; Göppert and Goldscheider, 2008; Sinreich et al., 2002) revealed two parallel drainage systems in this valley: a surface stream and a continuous underground karst drainage system along the valley axis, which are hydraulically connected via the estavelle and by diffuse seepage further upstream.
3.1 Setup of the catchment model
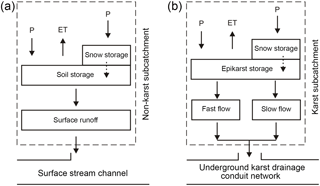
The numerical model tested and evaluated in this manuscript is an improved version of the model introduced in the study by Chen and Goldscheider (2014), which in turn has been derived from the distributed hydrologic–hydraulic water quality simulation model – the Storm Water Management Model (SWMM, version 5.0), described in Rossman (2010). The hydrological conceptual model was developed mainly based on the geologic study by Wagner (1950), the speleological investigation by the regional caving club (Höhlenverein Sonthofen, 2006) and numerous tracer tests and hydrogeological field observations by Goldscheider (2005). Additional tracer experiments by Göppert and Goldscheider (2008) and Sinreich et al. (2002) improved this conceptual model. The current catchment model is constructed by using a combined lumped and distributed modeling approach. Basically, the lumped model represents water storage and drainage in the soil and epikarst. The distributed model represents the underground karst drainage network in the karst area, and the network of surface streams in the non-karst area; these linear structures drain the flow generated from the lumped model. Compared to the earlier catchment model by Chen and Goldscheider (2014), new developments are (1) the updated model adopts the HBV-snow routine and is able to simulate snow storage and snowmelt and their influence on groundwater recharge processes (described in Sect. 3.3). (2) The earlier model considers baseflow (slow flow) as a constant value, which is insufficient for long-term climate-change impact predictions; in the updated model, we applied the linear reservoir approach by Hartmann et al. (2011) to simulate transient slow-flow components, depending on groundwater recharge and recession coefficient. (3) The laterally adjacent and hydrogeologically connected non-karst area is included in the current model domain; the updated model is able to simulate variable infiltration of surface runoff from the non-karst area into the underground karst drainage network. (4) In the updated model, the spatial discretization of the catchment area is much finer by using the elevation bands approach, which allows for a better representation of the spatial variability in meteorological variables.
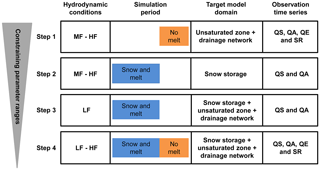
Figure 3Strategy for the multi-step model calibration, where LF, MF and HF are for low-, medium- and high-flow conditions, respectively.
Due to the new developments, the current model is able to simultaneously simulate all system outlets for a complete hydrological year, including periods of snow accumulation, snowmelt and rainfall; additionally, the current model is able to reproduce system discharge behavior during drought periods, as the system baseflow was implemented as a function of groundwater recharge and recession coefficient. In this study, the simulation started in late autumn (November 2013), during very low-flow condition. The discharge of QS during this time consists of slow-flow components from the karst aquifer. This hydrologic state was used to define the initial model condition. In total, 76 model parameters (Supplement) are considered for the model setup: (1) model parameters x1–x20 define the main hydrological processes of the unsaturated zone in the individual karst subcatchments and the top layer of the low-permeability Flysch rocks, (2) model parameters x21–x76 describe the geometry and hydraulic properties of the karst drainage conduit network as well as surface stream channels in the non-karst area.
3.2 Monitoring network and data availability
Four observation locations in the studied catchment were considered here: (1) QS at 1035 m a.s.l. in the valley, (2) QA at 1080 m a.s.l., (3) QE at 1120 m a.s.l. and (4) a gauging station (SR) at 1122 m a.s.l. quantifying the surface runoff from the upper part of Schwarzwasser valley. Hourly-measured discharges at the above-mentioned monitoring stations are used, whereas the measurements for QS and QA are available from November 2013 to October 2014 and for QE and SR only from July to October 2014. For the same period, we interpolated the meteorological data (hourly precipitation, air temperature and relative humidity) from nine weather stations (Fig. 1b) across the study catchment at a 100 m × 100 m grid resolution using combined inverse distance weighting and linear regression gridding. Mean areal precipitation and potential evapotranspiration for individual subunits are determined based on the interpolated meteorological data, in which hourly potential evapotranspiration is estimated using a modified Turc–Ivanov approach after Wendling and Müller (1984), described in Conradt et al. (2013).
3.3 Modeling snow accumulation and melting
We applied the HBV-snow routine for simulating snow accumulation and melt. The HBV model is described in various articles, e.g., Bergström (1975, 1995), Kollat et al. (2012) and Seibert (2000). We further modified the calculation of snowmelt using the approach proposed by Hock (1999), to simulate more realistic hourly-varying snowmelt in mountainous catchments:
where M is snowmelt (mm h−1), MF is melt factor (mm h−1 ∘C−1), α is radiation coefficient, I is potential clear-sky direct solar radiation at surface (W m−2), t is measured hourly air temperature (∘C) and Ts is threshold temperature (∘C) for snow melting. The melt factor and the radiation coefficient are empirical coefficients and can be estimated by model calibration. The distributed potential clear-sky direct solar radiation is dependent on surface topography and calculated with 100 m × 100 m grid resolution for the investigated area using the approach developed by Kumar et al. (1997) and a digital elevation model for the study area.
3.4 Model calibration
3.4.1 Model optimization
We used the DiffeRential Evolution Adaptive Metropolis (DREAM) by Vrugt (2016) to calibrate the model. The simultaneous minimization of the sum of the squared errors (SSE) of multiple observed time series was applied to constrain the model parameter space (described in Sect. 3.4.2), which was defined based on our previous experience in the study region (Chen and Goldscheider, 2014; Chen et al., 2017). The DREAM algorithm allows an initial population of parameter sets to converge to a stationary sample.
3.4.2 Calibration strategy
In a previous comprehensive sensitivity analysis we demonstrated that the controlling parameters exhibit varying sensitivity for different hydrodynamic conditions and for different spatially distributed model outlets (Chen et al., 2017). Based on this information, we outlined four steps to calibrate the model using different hydrodynamic system conditions and the observed time series for different outlets. Additionally, to explicitly consider or completely remove the snow dynamic during calibration, we divided the whole simulation period into a snow period (November 2013–June 2014) and a rainfall period (June 2014–October 2014). There was no snow cover anywhere in the catchment during the rainfall period.
The multi-step calibration procedure applied here is illustrated in Fig. 3. In step 1, we used the rainfall period to constrain the model parameters of the unsaturated zone and the drainage network during medium and high flows. The different hydrodynamic conditions are defined using the exceedance probability of the observed discharge at QS. In step 2, we used the snow period to constrain the parameters of snow storage during medium and high flows, whereas in the observation data the snow accumulation and melting dynamics in the catchment are clearly reflected. The time series of QS and QA are used for this calibration step. In step 3, we focused on the low flows in the same simulation period as during step 2 to further constrain the parameters of storage in snow, unsaturated zone and drainage network using the observation data of QS and QA. In step 4, the ranges of the previous parameters were constrained continuously using all flow conditions and observation time series from all four outlets.
Table 1(a) The median (q0.5) and the confidence intervals (q0.025 and q0.975) of the probabilistic precipitation scenarios for years 2030, 2050 and 2070 are explicitly given as percentage change (compared to 1990) and applied for the analysis described in Sect. 3.6. The scenarios are based on Frei (2004). (b) The median (q0.5) and the confidence intervals (q0.025 and q0.975) of the probabilistic temperature scenarios for years 2030, 2050 and 2070 are explicitly given as absolute change (compared to 1990) and applied for the analysis described in Sect. 3.6. The scenarios are based on Frei (2004).
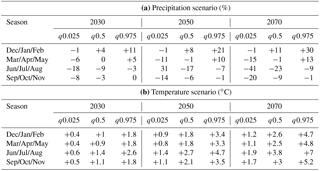
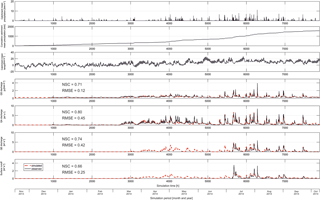
Figure 4Observed and simulated discharge of four spatially distributed model outlets QS, QA, QE and SR using the best calibrated model parameter set for the period November 2013–October 2014. Additionally, the mean catchment precipitation and temperature for the same period are shown.
The error function used in DREAM is the SSE values defined in individual calibration steps (Eq. 3 for step 1 and 4; Eq. 4 for step 2 and 3):
where Qt,o is the observed discharge at time step t, Qt,s is the simulated discharge at time step t and N is the number of measurements in the selected time series.
For each calibration step, 5000 parameter sets were generated using Latin hypercube sampling within the defined prior parameter ranges. The last 1000 parameter sets of the converged sample in each calibration step are used to represent the posterior distribution of “best” parameter sets. Posterior parameter bounds are determined using the 95 % confidence interval for these 1000 parameter sets. The parameter bounds of a previous step were adopted as a-priori parameter bounds for the subsequent calibration step.
3.5 Estimation of water storage
To understand water storage processes within the catchment, we estimated the temporary water storage volumes for the entire catchment (Eq. 5), karst area (Eq. 6) and non-karst area (Eq. 7):
Surface runoff from the non-karst area can infiltrate into the underground karst drainage network through the conduits C34–C38 constructed in the upper part of the valley (Fig. 1c). This flow is considered as allogenic recharge into the karst aquifer and was taken into account for the storage calculation for the karst and non-karst areas. Additionally we simulated the temporary subsurface water storage volume for the karst aquifer (Eq. 8):
where St, Pt, ETt, Rt and Qt are the storage, precipitation, evapotranspiration, recharge and discharge in volume at time step t (t0 is first simulation time step). The simulated temporary storage volumes for the whole catchment (St,catchment), karst area (St,karst), non-karst area (St,nonkarst) and karst aquifer (St,karstaquifer) are the absolute volumes, whereas the storage for the karst aquifer (St,karstaquifer) only describes the ground water storage in the karst aquifer. The calculation of the initial water storage volume in the karst aquifer is based on the approach introduced by Bonacci (1993):
where is the discharge from the karst aquifer at the first simulation time step and k is the recession coefficient, which can be derived by analyzing the karst spring discharge hydrograph during low-flow conditions.
3.6 Climate-change projections
The focus of this analysis is to quantify the impact of varying climate conditions on the water fluxes and storages throughout the model domain and to identify the hydrological processes most sensitive to potential climate change within the study catchment. We chose the probabilistic scenarios of precipitation and temperature by Frei (2004) for the northern Alps as the basis for our study. The median values (q0.5) and the confidence intervals (q0.025 to q0.975) of the probabilistic scenarios for years 2030, 2050 and 2070 were derived in Frei (2004) and given in Table 1. We used a delta approach to project the potential climate-change scenarios in the investigated catchment by changing precipitation and temperature time series for the pre-defined months (December–February, March–May, June–August and September–November) by a given delta (percentage or value). For the analysis, we first focused on the median climate scenarios of years 2030, 2050 and 2070 (described in Sect. 4.3.1) to better understand the general trend of the climate-change projections. In the second part of the analysis, we considered the uncertainty in the climate scenario for 2070 and estimated its impact on the simulated water fluxes and storages across the model domain (described in Sect. 4.3.2). To consider the climate-change scenario uncertainty, 1000 uniformly distributed random samples within the defined confidence intervals for the deltas of precipitation and temperature are used.
4.1 Model performance
Figure 4 shows the simulated karst spring discharges as well as the surface runoff generated from the non-karst area of the final calibrated model. The transient and highly variable discharge behavior at the four spatially distributed model outlets is simultaneously simulated at an hourly time step. The quality of the model simulation is demonstrated by two different statistical criteria, the RMSE and the Nash–Sutcliffe coefficient (NSC): RMSE values are 0.118 m3 s−1 for QS, 0.448 m3 s−1 for QA, 0.419 m3 s−1 for QE and 0.248 m3 s−1 for SR. NSC values are 0.71 for QS, 0.80 for QA, 0.74 for QE and 0.66 for SR. However, only one complete hydrological year of data can be obtained in the test site and used for this study. To better evaluate the model, we performed a split-sample test with the existing data (Supplement) that showed that we can obtain stable model parameterization and prediction with this relatively short observation period.
4.2 Estimated water fluxes and storages
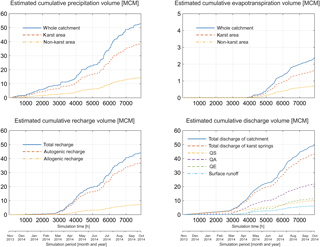
For a simulation period of about 330 days, we estimated that about 5 % of the total precipitation (52.79 MCM1) left the catchment as evapotranspiration (2.39 MCM) (Fig. 5). Furthermore, we calculated that about 84 % of the recharge (44.02 MCM) to the karst aquifer is contributed by diffuse infiltration (36.78 MCM) over the karst area. The remaining 16 % of the recharge is contributed by the allogenic recharge (7.24 MCM); i.e., direct infiltration of the surface runoff from the non-karst area into the underground karst drainage network in the upper part of the valley. The catchment is mainly drained by the karst springs. About 20 % of the total catchment discharge (49.41 MCM) is provided by QS (10.09 MCM), 44 % by QA (21.81 MCM), 23 % by QE (11.29 MCM) and 13 % by the surface runoff (6.23 MCM).
We compared the estimated water storages for the whole catchment, karst area, non-karst area and karst aquifer to better understand different storage processes (snow storage, soil water storage and subsurface water storage) in the model domain (Fig. 6). It is considered that in the simulated winter and early spring (November 2013–March 2014), the catchment water storage dynamics are mainly characterized by snow storage change in both the karst and non-karst areas. Afterwards, snowmelt (April–May 2014) led to rapidly decreasing catchment snow storage, but increasing storage in the karst aquifer as subsurface water in both fast and slow paths. During the rainfall season in the simulated summer and autumn (June–October 2014), the catchment storage is mainly characterized by subsurface water storage in the karst aquifer, while during medium and high flows the water is also stored intermittently in the top layer of the non-karst area.
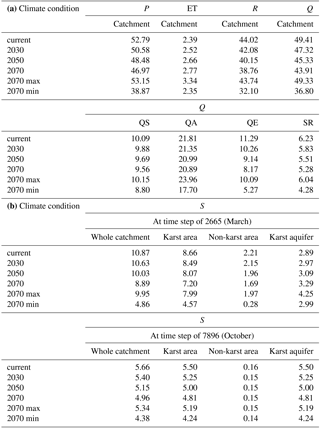
Table 2(a) Estimated total volume of precipitation (P), evapotranspiration (ET), recharge (R) and discharge (Q) under varied climate conditions (median climate scenarios of years 2030, 2050 and 2070 as well as the uncertainty in the climate scenario of 2070) for the simulated time period of 330 days and their units are MCM. (b) Estimated temporary water storage volumes (S) for the whole catchment, karst area, non-karst area and karst aquifer at time step of 2665 (March) and 7896 (October) under varied climate conditions (median climate scenarios of years 2030, 2050 and 2070 as well as the uncertainty in the climate scenario of 2070) and their units are MCM.
4.3 Assessing the impact of climate change
An overview of the change in water fluxes and storages under changing climate conditions (median climate scenarios and uncertainty in the climate scenario 2070) is given in Table 2.
4.3.1 Median climate scenarios
The simulations (Figs. 7–9) show that the water fluxes and storages are sensitive to varying climate conditions. Compared to the current situation, the precipitation over the catchment area is gradually decreasing (medians of −4.2, −8.2 and −11.0 %) for the climate scenarios of years 2030, 2050 and 2070, respectively, based on Frei (2004), whereas the evapotranspiration is increasing (medians of +5.5, +11.4 and +16.0 %). The modeled precipitation, temperature and evapotranspiration for future simulations contribute to the decreased recharge (medians of −4.4, −8.8 and −12.0 %) to the karst aquifer, whereas the recharge pattern is shifted, i.e., the recharge is increasing in winter and spring and decreasing in summer and autumn (Fig. 7).
Furthermore, the catchment water storage pattern changes significantly, especially during the normally “cold” period (from January to April). Under the current conditions, 7.74 MCM of water is stored in snow at the end of March, whereas at the same time, only 3.79 MCM as snow storage is estimated there under the conditions of 2070 (Fig. 8). This indicates that the simulated future climate conditions affect the snow storage massively. Comparatively, the catchment water storage during the rainfall season is much less influenced. For the karst aquifer, the shift of recharge pattern towards increased recharge in winter and spring, and decreased recharge in summer and autumn produces compensation, i.e., the annualized balance between recharge and discharge for the karst aquifer is constant for the simulations of years 2030, 2050 and 2070. Furthermore, the influence of the varied climate conditions on the intermediate water storage in the karst aquifer (epikarst and fast-flow path) and top layer of the non-karst area are limited.
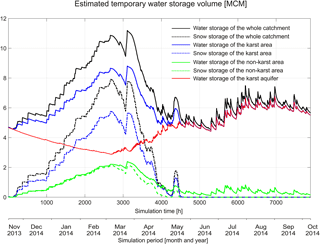
Figure 6Estimated temporary water storage volumes for the whole catchment, karst area, non-karst area and karst aquifer for the period November 2013–October 2014 on an hourly time step in million cubic meters (MCM).
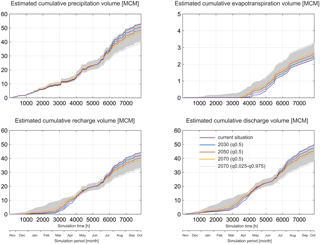
Figure 7Impacts of the median climate scenarios (q0.5) for years 2030, 2050 and 2070 as well as the uncertain climate scenarios (1000 random sampled combinations) for 2070 on the simulated precipitation, evapotranspiration, recharge and discharge for the studied catchment.
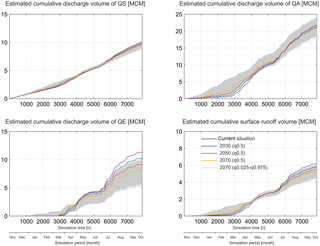
Our simulations (Fig. 9) show that the catchment discharge amount varies under changing climate conditions. The total discharge of QE is decreasing gradually (medians of 9.1, −19.0 and −27.6 %) for years 2030, 2050 and 2070, compared to the current situation. However, the deficit for QA (medians of −2.1, −3.8 and −4.2 %) and QS (medians of −2.0, −3.9 and −5.2 %) is less significant. For the total surface runoff generated from the non-karst area, climate-change effects are clearly perceptible with the total runoff decreasing (medians of −6.4, −11.4 and −15.1 %) for years 2030, 2050 and 2070. Also, the catchment discharge pattern is influenced significantly. The simulated increasingly warming winters and springs from 2030 to 2070 shift the discharge pattern of QA, QE and surface runoff continuously, while the discharge pattern of QS is quite stable until 2070.
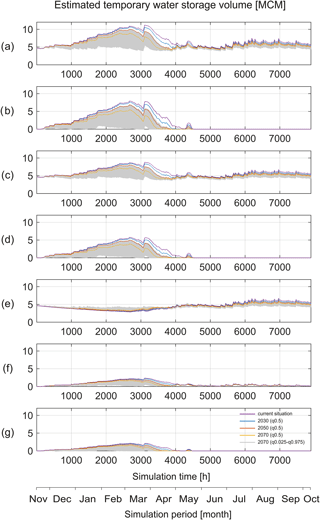
Figure 8Impacts of the median climate scenarios (q0.5) for years 2030, 2050 and 2070 as well as the uncertain climate scenarios (1000 random sampled combinations) for 2070 on (a) the simulated water storage of the whole catchment, (b) the simulated snow storage of the whole catchment, (c) the simulated water storage of the karst area, (d) the simulated snow storage of the karst area, (e) the simulated water storage of the karst aquifer, (f) the simulated water storage of the non-karst area and (g) the simulated snow storage of the non-karst area.
4.3.2 Uncertainty in the climate scenario 2070
The results show (Fig. 7) that the impacts of the possible climate scenarios for 2070 on the precipitation, evapotranspiration, recharge and catchment discharge are uncertain. Compared to the current situation, a general trend with the decrease in precipitation, recharge and catchment discharge or with the increase in evapotranspiration can be expected. In the most extreme cases, the change of precipitation varies between −26.4 and 0.7 %, evapotranspiration between −1.8 and 39.6 %, recharge to the karst aquifer between −27.1 and −0.6 % and catchment discharge between −25.5 and −0.2 %, compared to the current situation. Furthermore, the scenario runs indicate a shift of evapotranspiration, recharge and catchment discharge pattern towards increased recharge as well as catchment discharge in winter and spring and constantly increased evapotranspiration throughout the year.
Moreover, the scenario runs indicate a clear trend with the decrease in water storages for the simulated catchment (Fig. 8). Under the condition “extremely warm” of 2070, the snow storage of the catchment changes so dramatically that almost no water can be stored in snow during the normally “cold” period (from December to April). Simultaneously, the water storage pattern in the karst aquifer can be significantly shifted due to the earlier-starting snowmelt. Also, the water storage in the karst aquifer in summer and autumn are influenced strongly due to the significantly decreased recharge. This contributes to a clearly negative “balance” at the last time step of the simulation under the “extremely dry” conditions of 2070. If this negative water storage could be transferred to the coming year, it would cause more negative “balance” for the simulated karst aquifer based on the simulated climate conditions. Accordingly, the stored water resource in the karst aquifer would be decreased significantly.
Regarding the impacts of the uncertain scenarios on the karst spring discharges and surface runoff, distinct trends are identified (Fig. 9): (1) a clear trend with the decrease in QE and SR, (2) impacts on QA are highly uncertain even an increase in its total discharge is projected and (3) impacts on QS are clearly less uncertain and a general trend with decrease in QS can be expected. In the most extreme cases, compared to the current situation, the change of QS varies between −25.5 and 0.7 %, QA between −18.8 and 9.9 %, QE between −53.3 and −10.6 % and surface runoff between −31.3 and −2.9 %. QS discharge is considered as the most “robust” in the face of strongly varied climate conditions. Furthermore, a common shift of the discharge pattern of all karst springs and the surface runoff pattern are identified, i.e., increased QS, QA, QE and SR in winter and early spring.
5.1 Realism of the model simulations
In this study, the karst catchment model simultaneously simulates the transient and highly variable discharge behavior at the four model outlets. The model evaluation using different approaches indicates that the results are satisfying (described in Sect. 4.1). The previous studies have demonstrated that the model adequately represents the hydraulic processes observed in the karst aquifer and is able to transform them into realistic catchment responses during rainfall periods (Chen and Goldscheider, 2014; Chen et al., 2017). The current model represents the dominant flow process for the investigated karst catchment during low-flow conditions. During the snow accumulation period (November 2013–February 2014), the karst system was undersaturated, and QS discharged the whole catchment, while other karst springs (QA and QE) were dry and no significant surface runoff generated from the non-karst area. The simulation is consistent with our measurements and field observations. Furthermore, the current study shows that the snow dynamic reflected in the major karst springs (QS and QA) is reproduced in the model. It indicates that the model represents the recharge process driven by the snow accumulation and melting in the studied karst catchment. However, no snow observations to validate the accuracy of simulated snow accumulation and melting are available. For this reason, we developed the multi-step calibration procedure to achieve an efficient calibration of the snow model (described in Sect. 3.4.2). To more realistically simulate snowmelt and its spatial pattern in complex mountainous topography, we applied the extended snowmelt equation from Hock (1999) that considers the distributed potential clear-sky direct solar radiation, which is calculated based on a digital elevation model for the study area with 100 m resolution. Warscher et al. (2013) pointed out that the HBV approach is too simple for modeling distributed complex snow dynamics in mountainous environments, but it is the best estimation that we can obtain due to the lack of data. Therefore, the results concerning the simulated snow storage are associated with uncertainty and should be interpreted carefully.
We find that the surface runoff generated from the non-karst area is much less than the effective precipitation for the non-karst area. The reason is that the allogenic recharge leads to significant loss. This model behavior represents the conceptualization of our understanding about the hydraulic connection between the karst and non-karst areas. However, the model evaluation shows that the model underestimated the surface runoff generated from the non-karst area in response to heavy rainfall events (Fig. 4). This could be explained by an oversimplification of the complex hydrological situation in the non-karst area under-representing its runoff dynamics. Furthermore, the estimated low evapotranspiration (and very high recharge rates) for the investigated catchment appears unusual. Very high recharge rates in mountainous karst areas, ranging between 60 and 90 %, are also reported in the literature (e.g., Malard et al., 2016). In Alpine regions, low temperatures and high precipitation favor low evapotranspiration. In the elevated parts of our test site, soil and vegetation are almost entirely missing, and the limestone is extremely karstified, so that water infiltrates directly into open fractures. Hence, the high recharge rates are in accordance with our previous hydrogeological conceptual model, which is based on detailed field investigations, including 18 tracer tests (Goldscheider, 2005; Göppert and Goldscheider, 2008; Sinreich et al., 2002). The overall size of the karst system, the catchment areas of the individual springs and the general configuration of the underground drainage network are well-known. Yet, our quantification of recharge is still associated with uncertainties. Possible reasons include the following: (1) the interpolation of precipitation is uncertain. Most weather stations used for interpolation are located outside the study area, at lower elevations. Uncertainty depends on the density of observation points and the interpolation method (e.g., Ohmer et al., 2017). Increase in precipitation with elevation should also be taken into account. (2) Discharge quantities during very high-flow conditions are also uncertain. Water stages were continuously measured at all gauging stations, and numerous flow measurements (salt-dilution method) were performed to establish rating curves, which were used to obtain continuous hydrographs for all system outlets. However, most flow measurements were done during low- to moderately high-flow conditions, and the rating curves had to be extrapolated for very high flows. Therefore, substantial uncertainties have to be expected for very high-flow conditions (e.g., Baldassarre and Montanari, 2009; Coxon et al., 2015). (3) Another source of uncertainty is that sublimation from snow was not taken into account in the current model. However, some studies suggest that snow evaporation can be significant in some high-elevation catchments (e.g., Leydecker and Melack, 2000).
5.2 Hydrological process sensitivities
It is well known that long-term trends of karst aquifer dynamics (e.g., spring discharge, groundwater level) are affected mainly by regional precipitation patterns (e.g., Ma et al., 2004; Hao et al., 2006; Jia et al., 2017; Hartmann et al., 2012). In comparison to these earlier studies, our current study shows significant short-term aquifer responses to changes in hydro-meteorological conditions. The simulations demonstrate that the seasonal discharge pattern is controlled by the temporal distribution of precipitation on the one hand, and by the temperature pattern on the other hand. The snow storage in the catchment is highly sensitive to temperature variations, which can shift the seasonal patterns of snowmelt and aquifer recharge. A similar recharge pattern that strongly depends on seasonal snow accumulation and melting has been observed in other Alpine karst systems (Finger et al., 2013; Gremaud, 2011). Previous studies suggest decreasing spring discharge with increasing temperatures, as a result of increased evapotranspiration (e.g., Loáiciga et al., 1999). Our findings suggest that the extremely high recharge rates in our studied karst system will reduce the impact of rising temperatures on aquifer dynamics.
For the studied karst aquifer, due to its characteristic duality of flow and storage and additional spatially heterogeneous distributed drainage structure, the impacts of the varied climate conditions on QS, QA and QE are distinct. The simulations demonstrate well that QE is highly sensitive to changing climate conditions. The explanation is that QE acts as the highest overflow outlet of the studied karst aquifer, and its activation is strongly controlled by the hydrodynamic conditions in the karst drainage network, which are in turn highly sensitive to recharge and fast-flow processes. In contrast, QS is the lowest outlet for the karst aquifer and its discharge is “guaranteed” by the long-term water storage in matrix. Accordingly, QS is the most “robust” in the face of changing climate conditions. Under the simulated climate scenarios, QA shows a mixed character. On the one hand, the QA discharge is significantly less influenced than QE; and on the other hand, QA's discharge pattern can be more easily shifted than QS. It demonstrates well that the high permeability flow in the conduit network with less water-storage capacity is sensitive to changing hydrological conditions, while the low-permeability flow in the matrix with greater water-storage capacity is more resistant. In the non-karst area, the varied climate conditions affect the snow accumulation and melting patterns. As the non-karst and karst areas are hydraulically connected in the upper part of the valley, the predicted earlier-starting snowmelt can generate more runoff in the non-karst area which partly infiltrates into the underground drainage network leading to greater loss for the surface runoff and increased allogenic recharge to the karst aquifer.
For the current analysis, we used a pragmatic approach to analyze potential climate-change scenarios. The uncertainties in the climate scenarios were considered based on a random sampling approach. The final results indicate the impacts of the seasonal changes in the pattern of precipitation and temperature on the spatially varied hydrological processes within the catchment. Additionally, we investigated the flow exceedance probability of karst springs and surface runoff from the non-karst area (Supplement) and find that the simulated climate conditions affect the frequency and amplitude of catchment flows. This suggests that the impacts of the temporally stochastic distributions of meteorological parameters and their variability on the catchment flow dynamics should be systematically investigated.
The current work presents an investigation of the water fluxes and storages in a high-elevation Alpine catchment. We extended the existing karst catchment model developed by Chen and Goldscheider (2014) to consider spatially distributed snow dynamics and complex surface and subsurface heterogeneous drainage structures. The new model is able to simultaneously simulate the transient and highly variable discharge behavior of four spatially distributed model outlets at an hourly time step. Furthermore, we estimated the water fluxes and storages within the model domain. The results demonstrate that the spatiotemporal distribution of water fluxes and storages is controlled by the surface and subsurface hydrological setting. We find a large portion of precipitation infiltrates in the karst aquifer as autogenic recharge and contributes to surface runoff in the adjacent non-karst area, which can partly infiltrate into the karst aquifer as allogenic point recharge. In the simulation period, the catchment is mainly drained by the karst springs, about 20 % of the total catchment discharge is provided by the permanent spring QS, 44 % by the overflow spring QA, 23 % by the estavelle QE and 13 % by the surface runoff SR generated from the non-karst area. In the simulated winter and early spring (November 2013–March 2014), the catchment water storage is mainly characterized by the snow storage both in the karst and non-karst areas. During the rainfall season in the simulated summer and autumn (June–October 2014), the catchment storage is mainly characterized by the subsurface water storage in the karst aquifer.
Additionally, we studied the impacts of potential climate-change patterns on the spatially varied surface and subsurface hydrological processes in the model using a delta approach combined with a random sampling technique. The scenario runs demonstrate that the varied climate conditions affect the spatiotemporal distribution of water fluxes and storages within the catchment significantly: (1) the total catchment discharge decreases under all evaluated future climate conditions. (2) The catchment snow storage during the normally cold period from December to April decreases significantly, while the autogenic and allogenic recharge to the karst aquifer increase. (3) In the karst aquifer, due to its storage capacity, the shift of the recharge pattern towards increased recharge in winter and spring, and decreased recharge in summer and autumn offset each other under the varied climate conditions. (4) The impacts of the potential future climate conditions on the karst springs are distinct. The lowest permanent spring presents a “robust” discharge behavior, while the highest overflow outlet is highly sensitive to changing climatic conditions. This finding demonstrates that climate change impacts on karst springs do not only depend on the hydraulic characteristics of the aquifer system but also on the topographic position of the individual springs.
As our climate scenario projections use a simple delta approach, the impact of temporally stochastic distributions of meteorological parameters and their variability could not be investigated in this study. Accordingly, the results should only be applied to understand the relationship between the hydrological processes within the studied catchment and potential climate change patterns. It would be interesting to use more realistic data, i.e., the precipitation and temperature time series downscaled from regional climate models, to investigate their impact on the spatially distributed water fluxes and storages. But we warn that the measurements of meteorological variables in high-elevation mountainous environment have a quite large uncertainty. These uncertainties may have an impact on the model simulations and the understanding of derived processes. Nevertheless, there are several relevant general conclusions that can be drawn from this study. Because of their specific hydraulic characteristics, Alpine karst aquifers respond very fast and strong to hydrological events and seasonal variations, including snow accumulation and melting. The seasonal patterns of precipitation and snow regimes are projected to change in a changing climate. Alpine karst systems are especially vulnerable to these changing hydro-meteorological conditions. However, because of their hydrogeological complexity and hydraulic heterogeneity, every karst system has its individual characteristics, and different karst springs respond differently to changing climatic conditions. Therefore, site-specific investigations are required. The holistic modeling approach presented in our study can be transferred and adapted to other Alpine karst systems and can be used for studying impacts of climate change on Alpine karst water resources.
A part of the hydrological data used to support this article were provided by the responsible state authority for water resource management (Wasserwirtschaftsamt Vorarlberg) and are available upon request (wasserwirtschaft@vorarlberg.at). Another part of the hydrological data was collected by the Division of Hydrogeology at the Karlsruhe Institute of Technology (KIT) and is available from the authors upon request (zhao.chen@kit.edu). The simulation data necessary for reproducing the paper's results are also available from the authors upon request (zhao.chen@kit.edu).
The supplement related to this article is available online at: https://doi.org/10.5194/hess-22-3807-2018-supplement.
ZC developed the method and obtained all results in consultation with AH, TW and NG. ZC wrote the manuscript. The final manuscript was reviewed by all authors.
The authors declare that they have no conflict of interest.
We acknowledge the support of the Open Access Publishing Fund of Karlsruhe
Institute of Technology (KIT). We thank Clemens Mathis and Ralf Grabher from
Water Authority Vorarlberg (Austria) for providing data, Laurence Gill
(Trinity College Dublin) for inspiring discussion concerning model setup,
Joël Arnault (KIT) for providing a Matlab routine for the interpolation
of meteorological parameters and Timothy Bechtel (Franklin & Marshall
College) for proofreading the manuscript. We thank two anonymous colleagues
and Ronald Green for their constructive review comments.
The article processing charges for this open-access
publication were covered by a Research
Centre
of the Helmholtz Association.
Edited by:
Jesús Carrera
Reviewed by: two anonymous
referees
Abbaspour, K. C., Yang, J., Maximov, I., Siber, R., Bogner, K., Mieleitner, J., Zobrist, J., and Srinivasan, R.: Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT, J. Hydrol., 333, 413–430, https://doi.org/10.1016/j.jhydrol.2006.09.014, 2007.
Achleitner, S., Rinderer, M., and Kirnbauer, R.: Hydrological modeling in alpine catchments: sensing the critical parameters towards an efficient model calibration, Water Sci. Technol., 60, 1507–1514. https://doi.org/10.2166/wst.2009.488, 2009.
Benischke, R., Harum, T., Reszler, C., Saccon, P., Ortner, G., and Ruch, C.: Karstentwässerung im Kaisergebirge (Tirol, Österreich) – Abgrenzung hydrographischer Einzugsgebiete durch Kombination hydrogeologischer Untersuchungen mit Isotopenmethoden und hydrologischer Modellierung, Grundwasser, 15, 43–57, https://doi.org/10.1007/s00767-009-0124-y, 2010.
Bergström, S.: The development of a snow routine for the HBV-2 model, Nord. Hydrol., 6, 73–92, 1975.
Bergstrom, S.: The HBV model, in: Computer Models of Watershed Hydrology, edited by: Singh, V. P., Water Resources Publications: Highlands Ranch, Colorado, USA, 443–476, 1995.
Bonacci, O.: Karst springs hydrographs as indicators of karst aquifers, Hydrol. Sci. J., 38, 51–62, https://doi.org/10.1080/02626669309492639, 1993.
Braun, L. N. and Renner, C. B.: Application of a conceptual runoff model in different physiographic regions of Switzerland, Hydrol. Sci. J., 37, 217–231, https://doi.org/10.1080/02626669209492583, 1992.
Chen, Z. and Goldscheider, N.: Modeling spatially and temporally varied hydraulic behavior of a folded karst system with dominant conduit drainage at catchment scale, Hochifen–Gottesacker, Alps. J. Hydrol., 514, 41–52, https://doi.org/10.1016/j.jhydrol.2014.04.005, 2014.
Chen, Z., Hartmann, A., and Goldscheider, N.: A new approach to evaluate spatiotemporal dynamics of controlling parameters in distributed environmental models, Environ. Modell. Softw., 87, 1–16, https://doi.org/10.1016/j.envsoft.2016.10.005, 2017.
Conradt, T., Wechsung, F., and Bronstert, A.: Three perceptions of the evapotranspiration landscape: comparing spatial patterns from a distributed hydrological model, remotely sensed surface temperatures, and sub-basin water balances, Hydrol. Earth Syst. Sci., 17, 2947–2966, https://doi.org/10.5194/hess-17-2947-2013, 2013.
Coxon, G., Freer, J., Westerberg, I., Wagener, T., Woods, R., and Smith, P.: A novel framework for discharge uncertainty quantification applied to 500 UK gauging stations, Water Resour. Res., 51, 5531–5546, https://doi.org/10.1002/2014WR016532, 2015.
Di Baldassarre, G. and Montanari, A.: Uncertainty in river discharge observations: a quantitative analysis, Hydrol. Earth Syst. Sci., 13, 913–921, https://doi.org/10.5194/hess-13-913-2009, 2009.
Dobler, C., Bürger, G., and Stötter, J.: Assessment of climate change impacts on flood hazard potential in the Alpine Lech watershed, J. Hydrol., 460-461, 29–39, https://doi.org/10.1016/j.jhydrol.2012.06.027, 2012.
Dobler, C., Bürger, G., and Stötter, J.: Simulating future precipitation extremes in a complex Alpine catchment, Nat. Hazards Earth Syst. Sci., 13, 263–277, https://doi.org/10.5194/nhess-13-263-2013, 2013.
Finger, D., Hugentobler, A., Huss, M., Voinesco, A., Wernli, H., Fischer, D., Weber, E., Jeannin, P.-Y., Kauzlaric, M., Wirz, A., Vennemann, T., Hüsler, F., Schädler, B., and Weingartner, R.: Identification of glacial meltwater runoff in a karstic environment and its implication for present and future water availability, Hydrol. Earth Syst. Sci., 17, 3261–3277, https://doi.org/10.5194/hess-17-3261-2013, 2013.
Frei, C.: Die Klimazukunft der Schweiz – Eine probabilistische Projektion, available at: http://www.occc.ch/Products/CH2050/CH2050-Scenarien.pdf (last access: July 2018), 2004.
Gobiet, A., Kotlarski, S., Beniston, M., Heinrich, G., Rajczak, J., and Stoffel, M.: 21st century climate change in the European Alps – a review, Sci. Total Environ., 493, 1138–1151, https://doi.org/10.1016/j.scitotenv.2013.07.050, 2014.
Goldscheider, N.: Fold structure and underground drainage pattern in the alpine karst system Hochifen-Gottesacker, Eclogae Geol. Helv., 98, 1–17, https://doi.org/10.1007/s00015-005-1143-z, 2005.
Goldscheider, N.: Alpine Hydrogeologie, Grundwasser, 16, 1 pp., https://doi.org/10.1007/s00767-010-0157-2, 2011.
Göppert, N. and Goldscheider, N.: Solute and Colloid Transport in Karst Conduits under Low- and High-Flow Conditions, Ground Water, 46, 61–68, https://doi.org/10.1111/j.1745-6584.2007.00373.x, 2008.
Gremaud, V. and Goldscheider, N.: Climate Change Effects on Aquifer Recharge in a Glacierised Karst Aquifer System, Tsanfleuron-Sanetsch, Swiss Alps, in: Advances in Research in Karst Media, edited by: Andreo, B., Carrasco, F., Durán, J. J., and LaMoreaux, J. W., Springer Berlin Heidelberg, Berlin, Heidelberg, 31–36, 2010.
Gremaud, V., Goldscheider, N., Savoy, L., Favre, G., and Masson, H.: Geological structure, recharge processes and underground drainage of a glacierised karst aquifer system, Tsanfleuron-Sanetsch, Swiss Alps, Hydrogeol. J., 17, 1833–1848, https://doi.org/10.1007/s10040-009-0485-4, 2009.
Hao, Y., Yeh, T.-C. J., Gao, Z., Wang, Y., and Zhao, Y.: A gray system model for studying the response to climatic change: The Liulin karst springs, China, J. Hydrol., 328, 668–676, https://doi.org/10.1016/j.jhydrol.2006.01.022, 2006.
Hartmann, A., Kralik, M., Humer, F., Lange, J., and Weiler, M.: Identification of a karst system's intrinsic hydrodynamic parameters: upscaling from single springs to the whole aquifer, Environ. Earth Sci., 65, 2377–2389, https://doi.org/10.1007/s12665-011-1033-9, 2011.
Hartmann, A., Lange, J., Vivó Aguado, À., Mizyed, N., Smiatek, G., and Kunstmann, H.: A multi-model approach for improved simulations of future water availability at a large Eastern Mediterranean karst spring, J. Hydrol., 468–469, 130–138, 2012.
Hock, R.: A distributed temperature-index ice- and snowmelt model including potential direct solar radiation, J. Glaciol., 45, 101–111, https://doi.org/10.1017/S0022143000003087, 1999.
Höhlenverein Sonthofen (Ed.): Das Hölloch im Mahdtal – 100 Jahre Höhlenforschung im Kleinwalsertal, Sonthofen, 2006.
Jasper, K., Calanca, P., Gyalistras, D., and Fuhrer, J.: Differential impacts of climate change on the hydrology of two alpine river basins, Clim. Res., 26, 113–129, https://doi.org/10.3354/cr026113, 2004.
Jia, Z., Zang, H., Zheng, X., and Xu, Y.: Climate Change and Its Influence on the Karst Groundwater Recharge in the Jinci Spring Region, Northern China, Water, 9, 267, https://doi.org/10.3390/w9040267, 2017.
Junghans, N., Cullmann, J., and Huss, M.: Evaluating the effect of snow and ice melt in an Alpine headwater catchment and further downstream in the River Rhine, Hydrol. Sci. J., 56, 981–993, https://doi.org/10.1080/02626667.2011.595372, 2011.
Kollat, J. B., Reed, P. M., and Wagener, T.: When are multiobjective calibration trade-offs in hydrologic models meaningful?, Water Resour. Res., 48, W03520, https://doi.org/10.1029/2011WR011534, 2012.
Kraller, G., Warscher, M., Kunstmann, H., Vogl, S., Marke, T., and Strasser, U.: Water balance estimation in high Alpine terrain by combining distributed modeling and a neural network approach (Berchtesgaden Alps, Germany), Hydrol. Earth Syst. Sci., 16, 1969–1990, https://doi.org/10.5194/hess-16-1969-2012, 2012.
Kumar, L., Skidmore, A. K., and Knowles, E.: Modelling topographic variation in solar radiation in a GIS environment, Int. J. Geogr. Inf. Sci., 11, 475–497, https://doi.org/10.1080/136588197242266, 1997.
Kunstmann, H. and Stadler, C.: High resolution distributed atmospheric-hydrological modelling for Alpine catchments, J. Hydrol., 314, 105–124, https://doi.org/10.1016/j.jhydrol.2005.03.033, 2005.
Kunstmann, H., Schneider, K., Forkel, R., and Knoche, R.: Impact analysis of climate change for an Alpine catchment using high resolution dynamic downscaling of ECHAM4 time slices, Hydrol. Earth Syst. Sci., 8, 1031–1045, https://doi.org/10.5194/hess-8-1031-2004, 2004.
Kunstmann, H., Krause, J., and Mayr, S.: Inverse distributed hydrological modelling of Alpine catchments, Hydrol. Earth Syst. Sci., 10, 395–412, https://doi.org/10.5194/hess-10-395-2006, 2006.
Lauber, U. and Goldscheider, N.: Use of artificial and natural tracers to assess groundwater transit-time distribution and flow systems in a high-alpine karst system (Wetterstein Mountains, Germany), Hydrogeol. J., 22, 1807–1824, https://doi.org/10.1007/s10040-014-1173-6, 2014.
Lenderink, G., Buishand, A., and van Deursen, W.: Estimates of future discharges of the river Rhine using two scenario methodologies: direct versus delta approach, Hydrol. Earth Syst. Sci., 11, 1145–1159, https://doi.org/10.5194/hess-11-1145-2007, 2007.
Leydecker, A. and Melack, J.: Estimating evaporation in seasonally snow-covered catchments in the Sierra Nevada, California, J. Hydrol., 236, 121–138, https://doi.org/10.1016/S0022-1694(00)00290-0, 2000.
Loáiciga, H. A., Maidment, D. R., and Valdes, J. B.: Climate-change impacts in a regional karst aquifer, Texas, USA, J. Hydrol., 227, 173–194, https://doi.org/10.1016/S0022-1694(99)00179-1, 2000.
Ma, T., Wang, Y., and Guo, Q.: Response of carbonate aquifer to climate change in northern China: a case study at the Shentou karst springs, J. Hydrol., 297, 274–284, https://doi.org/10.1016/j.jhydrol.2004.04.020, 2004.
Malard, A., Sinreich, M., and Jeannin, P.-Y.: A novel approach for estimating karst groundwater recharge in mountainous regions and its application in Switzerland, Hydrol. Process., 30, 2153–2166, https://doi.org/10.1002/hyp.10765, 2016.
Middelkoop, H., Daamen, K., Gellens, D., Grabs, W., Kwadijk, J. C. J., Lang, H., Parmet, B. W. A. H., Schädler, B., Schulla, J., and Wilke, K.: Impact of climate change on hydrological regimes and water resources management in the Rhine Basin, Climatic Change, 49, 105–128, https://doi.org/10.1023/A:1010784727448, 2001.
Ohmer, M., Liesch, T., Goeppert, N., and Goldscheider, N.: On the optimal selection of interpolation methods for groundwater contouring: An example of propagation of uncertainty regarding inter-aquifer exchange, Adv. Water Resour., 109, 121–132, 2017.
Rogger, M., Viglione, A., Derx, J., and Blöschl, G.: Quantifying effects of catchments storage thresholds on step changes in the flood frequency curve, Water Resour. Res., 49, 6946–6958, https://doi.org/10.1002/wrcr.20553, 2013.
Rössler, O., Diekkrüger, B., and Löffler, J.: Potential drought stress in a Swiss mountain catchment-Ensemble forecasting of high mountain soil moisture reveals a drastic decrease, despite major uncertainties, Water Resour. Res., 48, W04521, https://doi.org/10.1029/2011WR011188, 2012.
Rossman, L.: Strom water management model: user's manual, version 5.0, 2010.
Taylor, R. G., Scanlon, B., Döll, P., Rodell, M., van Beek, R., Wada, Y., Longuevergne, L., Leblanc, M., Famiglietti, J. S., Edmunds, M., Konikow, L., Green, T. R., Chen, J., Taniguchi, M., Bierkens, Marc F. P., MacDonald, A., Fan, Y., Maxwell, R. M., Yechieli, Y., Gurdak, J. J., Allen, D. M., Shamsudduha, M., Hiscock, K., Yeh, P. J.-F., Holman, I., and Treidel, H.: Ground water and climate change, Nature Clim. Change, 3, 322–329, https://doi.org/10.1038/nclimate1744, 2013.
Seibert, J.: Multi-criteria calibration of a conceptual runoff model using a genetic algorithm, Hydrol. Earth Syst. Sci., 4, 215–224, https://doi.org/10.5194/hess-4-215-2000, 2000.
Singh, R., Wagener, T., Crane, R., Mann, M. E., and Ning, L.: A vulnerability driven approach to identify adverse climate and land use change combinations for critical hydrologic indicator thresholds: Application to a watershed in Pennsylvania, USA, Water Resour. Res., 50, 3409–3427, https://doi.org/10.1002/2013WR014988, 2014.
Sinreich, M., Goldscheider, N., and Hötzl, H.: Hydrogeologie einer alpinen Bergsturzmasse (Schwarzwassertal, Vorarlberg), Beit. z. Hydrogeologie, 53, 5–20, 2002.
Viviroli, D., Dürr, H. H., Messerli, B., Meybeck, M., and Weingartner, R.: Mountains of the world, water towers for humanity: Typology, mapping, and global significance, Water Resour. Res., 43, W07447, https://doi.org/10.1029/2006WR005653, 2007.
Vrugt, J. A.: Markov chain Monte Carlo simulation using the DREAM software package: Theory, concepts, and MATLAB implementation, Environ. Modell. Softw., 75, 273–316, https://doi.org/10.1016/j.envsoft.2015.08.013, 2016.
Wagner, G.: Rund um Hochifen und Gottesackergebiet: eine Einführung in die Erd- und Landschaftsgeschichte des Gebietes zwischen Iller und Bregenzer Ach, Hohenlohesche Buchhandlung Ferdinand Rau, 1950.
Warscher, M., Strasser, U., Kraller, G., Marke, T., Franz, H., and Kunstmann, H.: Performance of complex snow cover descriptions in a distributed hydrological model system: A case study for the high Alpine terrain of the Berchtesgaden Alps, Water Resour. Res., 49, 2619–2637, https://doi.org/10.1002/wrcr.20219, 2013.
Wendling, U. and Müller, J.: Entwicklung eines Verfahrens zur rechnerischen Abschätzung der Verdunstung im Winter, Z. Meteorol., 34, 82–85, 1984.
Zierl, B. and Bugmann, H.: Global change impacts on hydrological processes in Alpine catchments, Water Resour. Res., 41, W02028, https://doi.org/10.1029/2004WR003447, 2005.
MCM for million cubic meters