the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Technical note: Assessment of observation quality for data assimilation in flood models
Joanne A. Waller
Javier García-Pintado
David C. Mason
Sarah L. Dance
Nancy K. Nichols
The assimilation of satellite-based water level observations (WLOs) into 2-D hydrodynamic models can keep flood forecasts on track or be used for reanalysis to obtain improved assessments of previous flood footprints. In either case, satellites provide spatially dense observation fields, but with spatially correlated errors. To date, assimilation methods in flood forecasting either incorrectly neglect the spatial correlation in the observation errors or, in the best of cases, deal with it by thinning methods. These thinning methods result in a sparse set of observations whose error correlations are assumed to be negligible. Here, with a case study, we show that the assimilation diagnostics that make use of statistical averages of observation-minus-background and observation-minus-analysis residuals are useful to estimate error correlations in WLOs. The average estimated correlation length scale of 7 km is longer than the expected value of 250 m. Furthermore, the correlations do not decrease monotonically; this unexpected behaviour is shown to be the result of assimilating some anomalous observations. Accurate estimates of the observation error statistics can be used to support quality control protocols and provide insight into which observations it is most beneficial to assimilate. Therefore, the understanding gained in this paper will contribute towards the correct assimilation of denser datasets.
In data assimilation (DA), observations are combined with numerical model output, known as the background, to provide an accurate description of the current state, known as the analysis. In DA the contributions from the background and observations are weighted according to their relative uncertainty. The observation error statistics are the sum of the instrument error and representation error (Janjić et al., 2017). The error of representation arises due to the mismatch in the observation and its model equivalent, and it is often correlated and state dependent (Hodyss and Nichols, 2015; Waller et al., 2014). In DA, observation error statistics are typically assumed to be uncorrelated. The data density is reduced in order to satisfy this assumption (Lorenc, 1981). Yet having adequate estimates of these uncertainties is crucial in order to obtain an accurate analysis. Since the true state of the system is not known, the exact observation errors and their statistics can not be calculated. Instead observation uncertainties must be estimated statistically (Hollingsworth and Lönnberg, 1986; Ueno and Nakamura, 2016). Desroziers et al. (2005) provide a diagnostic to estimate observation uncertainties using the statistical average of observation-minus-background and observation-minus-analysis residuals. The diagnostic has been applied to operational numerical weather prediction (NWP) settings to estimate observation uncertainties (Cordoba et al., 2017; Stewart et al., 2014; Waller et al., 2016a, c). The use of these estimated statistics in NWP results in a more accurate analysis and improvements in objectively measured forecast skill (Bormann et al., 2016; Campbell et al., 2017; Weston et al., 2014).
The development of DA systems has largely been driven by its use in NWP, but the methodologies are applicable to any system that can be modelled and observed. There have been recent advances in real-time 2-D hydrodynamic modelling and the acquisition and processing of relevant remote sensing observations (earth observations, EOs) (Andreadis et al., 2007; Mason et al., 2010a, 2012a, 2014; Raclot, 2006; Schumann et al., 2007, 2011). Consequently, several studies have shown the benefit of applying DA to operational flood forecasting (Durand et al., 2008, 2014; García-Pintado et al., 2013, 2015; Giustarini et al., 2011; Mason et al., 2010b; Matgen et al., 2010; Montanari et al., 2009; Neal et al., 2009; Roux and Dartus, 2008). Grimaldi et al. (2016) review the potential of EOs for inundation mapping and water level estimation and their use for calibration, validation and constraint of real-time hydraulic flood forecasting models.
A predominant EO technique to obtain water level observations (WLOs) is synthetic-aperture radar (SAR). SAR provides high-resolution observations of radar backscatter which, after processing, serve to delineate the flood extent. Then, the intersection of the flood extent with a high-resolution lidar digital terrain model is used to obtain the WLOs. The resulting WLOs are discontinuous but locally dense in space; consequently, the errors in the observations may be highly correlated. However, the current practice when assimilating WLOs is to neglect the error correlations. To make the assumption of uncorrelated errors valid the current approach is to thin the data. Hence, in hydrology, one scenario that would benefit from improved understanding of the observation uncertainties is the assimilation of the satellite-derived water level observations (WLOs) for either operational flood forecast or hindcast analyses (García-Pintado et al., 2013; Mason et al., 2010a). A more detailed understanding of the observation uncertainties would be highly useful as understanding the error statistics may permit more observations to be included in the assimilation, which should allow the information from dense observation sets to be fully exploited. Additionally, accurate estimates of observation uncertainties can inform the thinning strategy and suggest which observations may benefit the assimilation most (Fowler et al., 2018). There is a clear potential to improve the flood forecast if all the SAR WLOs could be assimilated in an appropriate way.
In this article we use the diagnostic of Desroziers et al. (2005), described in Sect. 2, to estimate the observation error statistics for SAR WLOs that are assimilated using a local ensemble transform Kalman filter (LETKF) into the LISFLOOD-FP 2-D hydrodynamic model. For this study, we use a sequence of real SAR overpasses in a flood event that occurred in November 2012 in SW England. A description of the SAR WLOs and experimental design are given in Sect. 3. Results are discussed in Sect. 4. First, we estimate average WLO error statistics across the entire domain for the duration of the flood event. It will be seen later that these globally estimated error statistics show an anomalous pattern. To determine the cause of these anomalous results we consider if observations in different sub-domains have different error characteristics. We also consider if the error statistics differ for different phases of the flood event. From the results we infer that the anomalous pattern is not related to the distribution of observations over the domain but to observations during the later stages of the flood. To the best of our knowledge this is the first time that the diagnostics have been applied to estimate error statistics for hydrological data assimilation. Importantly, we show that the diagnostic of Desroziers et al. (2005) can be used to identify anomalous observation datasets that are not suitable for assimilation.
Data assimilation is a technique used to provide the best estimate, the analysis, of the current state of a dynamical system. The analysis is denoted xa ∈ . The analysis is determined by combining the background xb ∈ , a model prediction, with observations, y ∈ , weighted by their respective error statistics. Here the dimensions of the observation and model state vectors are denoted by Np and Nm, respectively. To compare observations and background it is necessary to project the background into observation space using the observation operator, → , which may be non-linear. The analysis can be used to initialize a forecast which in turn provides a background for the next assimilation.
In Desroziers et al. (2005) the analysis is calculated using
where R ∈ and B ∈ are the observation and background error covariance matrices, K is the Kalman gain matrix and H is defined as the observation operator linearized about the background state. The observation-minus-background residuals = y − ℋ(xb), also known as the innovations, are assumed to be unbiased. Hence any bias should be removed before assimilation (Dee, 2005).
The observation error covariance matrix can be estimated using the observation-minus-background, = y − ℋ(xb), and observation-minus-analysis, = y − ℋ(xa), residuals (Desroziers et al., 2005). Assuming that the observation and background errors are mutually uncorrelated, the statistical expectation of the product of the analysis and background residuals is
As the resulting matrix is estimated statistically it will not be symmetric. Therefore, it must be symmetrized before it can be used in a data assimilation scheme.
The form of the diagnostic in Eq. (2) is not suitable to calculate observation error statistics when each assimilation cycle uses different observations. Instead components of the background and analysis residuals must be paired and binned, with the binning dependent on the type of correlation being estimated. For example, when calculating spatial correlations the bins may depend on the distance between observations, whereas for temporal correlations the bins would depend on the time between observations. For each bin, β, the covariance, cov(β), is then computed individually using
where is the kth pair of elements of and in bin β, and Nβ is the number of residual pairs in bin β. It is assumed that the observation-minus-background and observation-minus-analysis residuals are unbiased, but this is not guaranteed. Hence the second term of Eq. (3) ensures that the computation of the observation error statistics is not affected by bias (Waller et al., 2016a). To calculate the spatial correlation, the covariance in each bin, cov(β), is divided by the estimated variance (the covariance at zero distance, cov(0)).
The diagnostic in Eqs. (2) and (3) only gives a correct estimate of the observation error uncertainties if the error statistics used in the assimilation are exact. Even if the assumed statistics are not exact the diagnostic can still provide useful information about the true observation error statistics (Ménard, 2016; Waller et al., 2016b). Further limitations include the use of an ergodic assumption in order to obtain sufficient samples (Todling, 2015) and the assumption that the observation operator is linear (Terasaki and Miyoshi, 2014).
One further issue is that the standard diagnostic is derived assuming that the analysis is calculated using minimum variance linear statistical estimation. If local ensemble DA is used to determine the analysis, the diagnostic does not result in a correct estimate of the observation uncertainties. However, by using a modified version of the diagnostic some of the observation error statistics may be estimated. It is possible to estimate the error correlations between two observations if the observation operator that determines the model equivalent of observation yi acts only on states that have been updated using the observation yj (Waller et al., 2017). Since we use a LETKF assimilation scheme in this study, we must take this into account when estimating observation error statistics for the WLOs.
In this article we estimate the observation error statistics for SAR WLOs that are assimilated using a LETKF into the LISFLOOD-FP 2-D hydrodynamic model. This study makes use of the observation, model and assimilation system described in García-Pintado et al. (2015). We direct the reader to this reference, and references therein (particularly Mason et al., 2012a, b), for a thorough description of the derivation of WLOs and the assimilation design. Here we summarize the methodology and provide a description of the data used specifically in this study.
3.1 Derivation of WLOs
The original observations used in the deviation of WLOs are obtained using SAR which observes the surface backscatter. In a SAR image flood water appears dark so long as the surface water turbulence is insignificant. Therefore, to obtain flood extent, the pixels in a SAR image are grouped into homogeneous regions. A mean backscatter value is calculated for each region and if this value is below a given threshold, the region is classified as flooded. The threshold is determined by using training data from “flood” and “non-flood” regions. This initial estimate of flood extent is then refined by, for example, (1) correcting for any high backscatter that is a result of vegetation either within the flooded region or at the flood edge; (2) correcting for high backscatter near flooded areas that is a result of water with a rough surface; (3) performing a “nearest neighbour” check, where any local flood height that is significantly larger than those nearby is reclassified as non-flooded.
To provide the WLOs the refined flood extent is intersected with high-resolution digital elevation model (DEM). In order to improve the accuracy of the WLOs, they are only calculated if the slope in the DEM is sufficiently shallow. A further refinement takes into account, for example, the emergent vegetation at the flood edge.
The WLO derivation process results in a large number of WLOs that exist in clusters. It is expected that many of the observations in a cluster will be highly correlated and hence not contribute independent information. At this stage in the processing, Mason et al. (2012a) thin the WLOs to reduce spatial correlation. However, we postpone this step until after the quality control procedures for the data assimilation have been performed.
3.2 Model and data assimilation
The observations are assimilated into a 75 m resolution LISFLOOD-FP flood simulation model (Bates and Roo, 2000) using a LETKF (Hunt et al., 2007). Due to the formulation with the diagnostic described in Sect. 2, the localization in the LETKF is set in standard 2-D Euclidean space rather than the physically based distance along the river channel described in García-Pintado et al. (2015), which would require a further adaptation of the diagnostic calculation. The localization radius is set using a compactly supported fifth-order piecewise rational function (Gaspari and Cohn, 1999) with length scale 20 km.
To compare the modelled field with the observed quantity it is necessary to define an observation operator that maps from model to observation space. In this study we use the “nearest wet pixel” approach described in García-Pintado et al. (2013). The mapping in the nearest wet pixel approach is dependent on the inundation status at the model location. If at an observation location the model is flooded, the model equivalent of the observation is simply the water level predicted by the model. However, if the model is dry at the observation location the model equivalent of the observation is taken to be the model water level at the wet pixel nearest to the observation location.
3.3 Quality control and data thinning
Data assimilation techniques can lose accuracy if presented with an observation that is grossly inconsistent with the model state (Vanden-Eijnden and Weare, 2013). Thus, before being assimilated, the WLOs are subjected to several quality control (QC) protocols according to the physical characteristics of the terrain and land cover. An additional background check is performed where observations that result in anomalous observation-minus-background residuals are discarded. The QC procedures result in dense cluster of discontinuous observations in which both the observations and their errors may be highly correlated. A direct assimilation of this dense dataset would lead to an analysis biased towards the observations and, for covariance-evolving methods (e.g. ensemble Kalman filters), an over-reduced posterior covariance and unstable long-term forecast/assimilation cycles. Thus, to reduce the number of correlated observations and to avoid dealing with the spatial correlation in the assimilation, the current approach is to further thin the data (as is standard in other assimilation applications such as NWP and oceanography; Dando et al., 2007; Li et al., 2010). The applied thinning, as described in Mason et al. (2012a), uses a top down clustering approach in which principal component analysis is used to select observations that have the highest information content. The spatial autocorrelation of the resulting observations is calculated, and if any significant correlation exists the thinning procedure is applied iteratively until no significant correlation remains. Typically the thinned dataset contains approximately 1 % of the pre-thinned observations. The measured standard deviation for the thinned dataset can be calculated by fitting a plane by linear regression to the WLOs. The variance of the difference between the WLO and planar surface can be used as an estimate of the observation error variance. This approach is considered adequate for this case study as the floodplain in the downstream observed areas is reasonably flat.
3.4 Potential observation error sources
In data assimilation the observation uncertainty has contributions from both measurement errors and representation errors. The representation error arises due to the difference between an actual observation and the modelled representation of an observation; this difference can be a result of the following:
-
Pre-processing/QC errors are errors introduced during the observation pre-processing or quality control procedures.
-
Observation operator errors are errors that arise due to approximations in the mapping between model and observation space.
-
Errors due to unresolved scales and processes are errors that result from the mismatch between the scales represented in the model field and the observations.
For the WLOs it is clear that a pre-processing error will exist as there is potential for errors to be introduced in the derivation of the WLOs. For example if the water surface is rough it may be assumed that the pixel is dry; as a result the flood extent would be incorrect and hence an error would be introduced in the WLO. For nearby pixels it is possible that there will be similar errors in the derivation process, thereby introducing correlated observation errors. The procedures in Mason et al. (2012a) provide an estimated standard deviation for the WLO pre-processing error and thin the data to ensure that the pre-processing error is uncorrelated. However, we note that in this study we use a denser dataset than is typically produced. Therefore, there is potential for some correlated pre-processing error to remain.
A potential source of correlated error for WLOs is the observation operator error. As described in Sect. 3.2 the observation operator uses the “nearest wet pixel” approach. For observations in locations where the model is flooded it is expected that there is minimal error in the observation operator (since the corresponding water level is predicated directly by the model). However, if the observation location does not coincide with a flooded model pixel it is necessary to find the nearest wet pixel in the model. It is possible that in locating the nearest wet pixel and extrapolating information we introduce correlated error.
The error due to unresolved scales and processes is also a possible source of observation error correlations. Although in this case the model is of relatively high resolution compared to the observation resolution, there are still scales that are unresolved. Previous studies that have considered these scale mismatch errors have found that they are typically correlated (Hodyss and Nichols, 2015; Janjić and Cohn, 2006; Waller et al., 2014).
3.5 Calculation of WLO error statistics
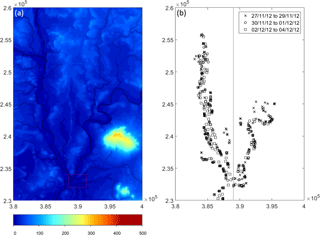
Figure 1(a) Flood model domain where the colour bar denotes the height in metres and (b) position of SAR WLOs on OSGB 1936 British National Grid projection; coordinates in metres. For (b) the line denotes the west/east domain split discussed in Sect. 4.2, crosses: 27–29 November, circles: 30 November and 1 December, squares: 2 and 4 December.
We estimate observation uncertainties for observations from a real flood event that occurred in West England on an area of the lower Severn and Avon rivers in November 2012 (Fig. 1a). The WLOs were extracted from a sequence of seven satellite SAR observations (acquired by the COSMO-SkyMed constellation) using the method described in Mason et al. (2012a). During the flood event the WLOs are available daily for the period 27 November to 4 December 2012 (with the exception of 3 December). Observations on the first day illustrate the flood levels just before the flood peak in the Severn. On 30 November the river went back in bank; however, a substantial amount of water remained on the floodplain (García-Pintado et al., 2015).
Before being assimilated, the WLOs are subject to the QC and thinning procedures described in Sect. 3.3. When used in previous studies such as García-Pintado et al. (2015) the dataset has been thinned to a separation distance of 250 m, at which the observation errors are assumed uncorrelated. However, in this article a denser observation set (although still sparse) with thinning distance of 125 m is used, in which some spatial correlation should remain. The location of the observations is plotted in Fig. 1b.
We apply the diagnostic of Desroziers et al. (2005) to the observation-minus-background and observation-minus-analysis residuals resulting from the flood assimilation. We first use all available data to calculate the average horizontal error variance and correlations. We then consider if the observations of the flood on the Severn are similar to the error statistics for the Avon. Finally we consider if the error statistics vary for different periods of the flood. For all cases the observation error correlations are calculated at a 1 km bin spacing. As we use an LETKF we must use a modified form of the diagnostic (see Sect. 2). As a result we are not able to calculate observation error correlations for observation pairs with a separation distance greater than 19 km. When evaluating the correlations we assume that they become insignificant when they drop below 0.2 (Liu and Rabier, 2002).
For this assimilation system we assume that the ensemble background error covariance matrix gives a reasonable estimate of the true background error statistics. The assumed standard deviation for the WLOs is 59 cm; this is calculated as described in Sect. 3.3. The value accounts only for the preprocessing error, and not for any error introduced by the approximations in the observation operator or scale mismatch errors and, therefore, may be an underestimate of the true error standard deviation.
As is typical for most DA systems, the observation errors are assumed uncorrelated. With these assumed error statistics the theoretical work of Waller et al. (2016b) suggests that the observation error statistics estimated using the diagnostic will have the following:
-
an underestimated standard deviation
-
an underestimated correlation length scale.
Therefore, we would expect the true standard deviations and length scales to be larger than those we estimate using the diagnostic.
4.1 Average observation error statistics
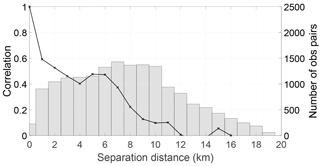
We first estimate average horizontal error covariances across the entire domain for the duration of the flood event. We plot in Fig. 2 the estimated correlation, along with the number of samples used, for the WLOs.
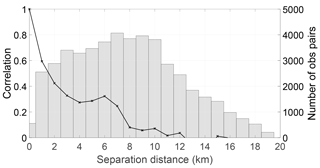
Figure 2Estimated SAR WLO error correlations (black line) and number of samples (bars) used for the calculation. Estimated error standard deviation is 54 cm.
The estimated statistics give a standard deviation of 54 cm. This is slightly lower that the assumed error standard deviation of 59 cm. Following the theory of Waller et al. (2016b) we expect the estimated standard deviation to be an underestimate of the true observation error standard deviation, and hence the results suggest that the assumed standard deviation is likely set at the correct level.
Our results show that the correlations become insignificant (< 0.2) at approximately 8 km, but there is some unexpected behaviour before 8 km. The correlations drop smoothly between 0 and 4 km then increase again up to 6 km before dropping off. This behaviour is seen for a variety of different binning widths (not shown). We investigate the cause of this “local maximum” in the estimated correlations in Sects. 4.2 and 4.3. In general we find that the correlation distance is much longer than the thinning distance of 125 m, which was chosen to try to ensure that the observation errors are uncorrelated. Furthermore, theoretical results of Waller et al. (2016b) suggest that, with this design of assimilation experiment, the correlation length scales will be underestimated.
4.2 Correlations in different parts of the domain
It is possible that the local maximum in the correlations is a result of observations on different tributaries of the river. To test this hypothesis we split the domain in two (as shown in Fig. 1): the western domain covering the river Severn and eastern domain covering the river Avon. We plot the estimated correlations, along with the number of samples used for the SAR WLOs, for the western part of the domain in Fig. 3 and for the eastern part of the domain in Fig. 4. We note that there are fewer observations in the eastern domain. This results in fewer available samples for the calculation in Eq. (3) and hence the results are subject to greater sampling error.
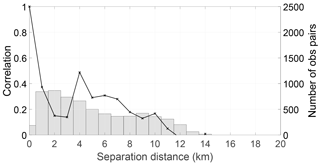
Figure 3Estimated SAR WLO error correlations (black line) and number of samples (bars) used (bin width = 1 km), west domain. Estimated error standard deviation is 58 cm.
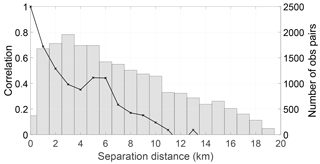
Figure 4Estimated SAR WLO error correlations (black line) and number of samples (bars) used (bin width = 1 km), east domain. Estimated error standard deviation is 43 cm.
From Figs. 3 and 4 we see that the “local maximum” in the correlations is still present in both parts of the domain. In the eastern domain it is very pronounced. This suggests that the cause of the increase in correlations between 4 and 6 km is not observations on different tributaries of the river.
4.3 Correlations at different times
We next consider if the correlation structure changes over time. We plot in Figs. 5, 6 and 7 the correlations calculated for the first three days, the second two days and the final two days respectively. At the beginning of the flood period, the observations have similar standard deviations to those estimated for the entire flood event; however, the correlation length scale is short, approximately 2 km.
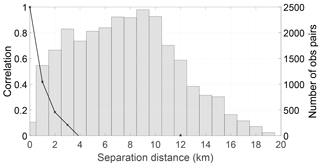
Figure 5Estimated SAR WLO error correlations (black line) and number of samples (bars) used (bin width = 1 km), 27–29 November. Estimated error standard deviation is 53 cm.
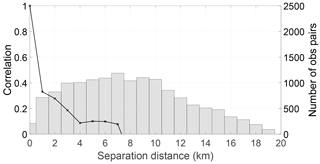
Figure 6Estimated SAR WLO error correlations (black line) and number of samples (bars) used (bin width = 1 km), 30 November and 1 December. Estimated error standard deviation is 43 cm.
During the middle of the flood event the observation error standard deviation decreases and the correlation length scale increases slightly. For the final two days the river is back in bank; for this period the standard deviation is largest, as is the correlation length scale, which is approximately 8 km. It is also in this final period where the “local maximum” appears in the correlations.
Figure 7 shows the estimated error statistics for the recession stages for the flood. During this period a high proportion of the observations were in areas which remained flooded but were disconnected from the main river flow. For this same sequence of SAR overpasses García-Pintado et al. (2015) showed that the assimilation of the last three overpasses was still able to exploit the background ensemble covariances to pass some of the information from these WLOs to the main flow. However, two effects became evident: (a) the assimilation increments were of a smaller magnitude in these last stages, and (b) the corrections to the flow in these last stages were gradually more short-lived. This was a result of the reduced information content in these WLOs regarding the inflow errors upstream, which in the end control the flood and flow evolution. Here the Desroziers et al. (2005) diagnostic has been able to identify a corresponding anomalous structure in the WLO errors at these last stages. The correlation structure shown in Fig. 7 indicates that apart from the longer correlation errors, which can be expected from the smoother flood dynamics at the end of the flood, an increase in the correlation appears at ∼ 6 km. The increasing disconnection of the WLOs in the flood plain from the main flow appears to be the cause for the local maximum in the estimated correlation structure. However, further work is required to determine why the “local maximum” in the estimated correlation function appears at 6 km.
We have shown that the Desroziers et al. (2005) diagnostic is a useful tool to identify the error covariance in WLOs from satellite SAR. Further, the diagnostic has been able, in the case study, to isolate an unexpected anomaly in the correlation structure, pointing to the applicability limits of the satellite WLOs in the flood plain in the recession stages of the flood. The diagnostic has been useful in this study for highlighting anomalous data. Given its low-cost calculation, we propose it be customarily calculated in flood forecasts and hindcast analyses to support the understanding of the observation errors and to support QC protocols for selection of adequate observations. However, due to the dependence of the observation error on the choice of observation operator and model resolution, results will differ for each individual user. Therefore, further study may be required to understand how the diagnostic results can best support QC protocols.
The data used in this study are available in García-Pintado (2018).
JW, JG-P and DM prepared the data and ran the experiments. JW and JG-P analysed the results and drafted the manuscript. DM, SD and NN contributed to the discussion and manuscript editing.
The authors declare that they have no conflict of interest.
Joanne A. Waller, Nancy K. Nichols and Sarah L. Dance were supported in part by
UK NERC grants NE/K008900/1 (FRANC), NE/N006682/1 (OSCA). Joanne A. Waller and
Sarah L. Dance received additional support from UK EPSRC grant EP/P002331/1 (DARE).
Nancy K. Nichols was also supported by the UK NERC National Centre for Earth
Observation (NCEO). Javier García-Pintado, David C. Mason and Sarah L. Dance were
supported by UK NERC grants NE/1005242/1 (DEMON) and NE/K00896X/1 (SINATRA).
The data used in this study may be obtained on request, subject to licensing
conditions, by contacting the corresponding author.
Edited by: Florian Pappenberger
Reviewed by: two anonymous referees
Andreadis, K. M., Clark, E. A., Lettenmaier, D. P., and Alsdorf, D. E.: Prospects for river discharge and depth estimation through assimilation of swath-altimetry into a raster-based hydrodynamics model, Geophys. Res. Lett., 34, L10403, https://doi.org/10.1029/2007GL029721, 2007. a
Bates, P. and Roo, A. D.: A simple raster-based model for flood inundation simulation, J. Hydrol., 236, 54–77, https://doi.org/10.1016/S0022-1694(00)00278-X, 2000. a
Bormann, N., Bonavita, M., Dragani, R., Eresmaa, R., Matricardi, M., and McNally, A.: Enhancing the impact of IASI observations through an updated observation-error covariance matrix, Q. J. Roy. Meteorol. Soc., 142, 1767–1780, https://doi.org/10.1002/qj.2774, 2016. a
Campbell, W. F., Satterfield, E. A., Ruston, B., and Baker, N. L.: Accounting for Correlated Observation Error in a Dual-Formulation 4D Variational Data Assimilation System, Mon. Weather Rev., 145, 1019–1032, https://doi.org/10.1175/MWR-D-16-0240.1, 2017. a
Cordoba, M., Dance, S., Kelly, G., Nichols, N., and Waller, J.: Diagnosing Atmospheric Motion Vector observation errors for an operational high resolution data assimilation system, Q. J. Roy. Meteorol. Soc., 143, 333–341, https://doi.org/10.1002/qj.2925, 2017. a
Dando, M., Thorpe, A., and Eyre, J.: The optimal density of atmospheric sounder observations in the Met Office NWP system, Q. J. Roy. Meteorol. Soc., 133, 1933–1943, 2007. a
Dee, D. P.: Bias and data assimilation, Q. J. Roy. Meteorol. Soc., 131, 3323–3343, https://doi.org/10.1256/qj.05.137, 2005. a
Desroziers, G., Berre, L., Chapnik, B., and Poli, P.: Diagnosis of observation, background and analysis-error statistics in observation space, Q. J. Roy. Meteorol. Soc., 131, 3385–3396, 2005. a, b, c, d, e, f, g, h
Durand, M., Andreadis, K. M., Alsdorf, D. E., Lettenmaier, D. P., Moller, D., and Wilson, M.: Estimation of bathymetric depth and slope from data assimilation of swath altimetry into a hydrodynamic model, Geophys. Res. Lett., 35, L20401, https://doi.org/10.1029/2008GL034150, 2008. a
Durand, M., Neal, J., Rodríguez, E., Andreadis, K. M., Smith, L. C., and Yoon, Y.: Estimating reach-averaged discharge for the River Severn from measurements of river water surface elevation and slope, J. Hydrol., 511, 92–104, https://doi.org/10.1016/j.jhydrol.2013.12.050, 2014. a
García-Pintado, J.: DEMON: Simulation output from ensemble assimilation of Synthetic Aperture Radar (SAR) water level observations into the Lisflood-FP flood forecast model, Centre for Environmental Data Analysis, https://doi.org/10.5285/b43ce022c8f94f79b5c3b3ede7aad975, 2018. a
Fowler, A., Dance, S., and Waller, J.: On the interaction of observation and prior error correlations in data assimilation, Q. J. Roy. Meteorol. Soc., 144, 48–62, https://doi.org/10.1002/qj.3183, 2018. a
García-Pintado, J., Neal, J. C., Mason, D. C., Dance, S. L., and Bates, P. D.: Scheduling satellite-based SAR acquisition for sequential assimilation of water level observations into flood modelling, J. Hydrol., 495, 252–266, https://doi.org/10.1016/j.jhydrol.2013.03.050, 2013. a, b, c
García-Pintado, J., Mason, D., Dance, S., Cloke, H., Neal, J., Freer, J., and Bates, P.: Satellite-supported flood forecasting in river networks: A real case study, J. Hydrol., 523, 706–724, https://doi.org/10.1016/j.jhydrol.2015.01.084, 2015. a, b, c, d, e, f
Gaspari, G. and Cohn, S. E.: Construction of correlation functions in two and three dimensions, Q. J. Roy. Meteorol. Soc., 125, 723–757, 1999. a
Giustarini, L., Matgen, P., Hostache, R., Montanari, M., Plaza, D., Pauwels, V. R. N., De Lannoy, G. J. M., De Keyser, R., Pfister, L., Hoffmann, L., and Savenije, H. H. G.: Assimilating SAR-derived water level data into a hydraulic model: a case study, Hydrol. Earth Syst. Sci., 15, 2349–2365, https://doi.org/10.5194/hess-15-2349-2011, 2011. a
Grimaldi, S., Li, Y., Pauwels, V. R. N., and Walker, J. P.: Remote Sensing-Derived Water Extent and Level to Constrain Hydraulic Flood Forecasting Models: Opportunities and Challenges, Surv. Geophys., 37, 977–1034, https://doi.org/10.1007/s10712-016-9378-y, 2016. a
Hodyss, D. and Nichols, N. K.: The error of representation: basic understanding, Tellus A, 67, 24822, https://doi.org/10.3402/tellusa.v67.24822, 2015. a, b
Hollingsworth, A. and Lönnberg, P.: The statistical structure of short-range forecast errors as determined from radiosonde data. Part I: The wind field, Tellus A, 38, 111–136, https://doi.org/10.1111/j.1600-0870.1986.tb00460.x, 1986. a
Hunt, B. R., Kostelich, E. J., and Szunyogh, I.: Efficient data assimilation for spatiotemporal chaos: A local ensemble transform Kalman filter, Physica D, 230, 112–126, https://doi.org/10.1016/j.physd.2006.11.008, 2007. a
Janjić, T. and Cohn, S. E.: Treatment of Observation Error due to Unresolved Scales in Atmospheric Data Assimilation, Mon. Weather Rev., 134, 2900–2915, 2006. a
Janjić, T., Bormann, N., Bocquet, M., Carton, J. A., Cohn, S. E., Dance, S. L., Losa, S. N., Nichols, N. K., Potthast, R., Waller, J. A., and Weston, P.: On the representation error in data assimilation, Q. J. Roy. Meteorol. Soc., https://doi.org/10.1002/qj.3130, in press, 2017. a
Li, X., Zhu, J., Xiao, Y., and Wang, R.: A Model-Based Observation-Thinning Scheme for the Assimilation of High-Resolution SST in the Shelf and Coastal Seas around China, J. Atmos. Ocean. Tech., 27, 1044–1058, https://doi.org/10.1175/2010JTECHO709.1, 2010. a
Liu, Z.-Q. and Rabier, F.: The interaction between model resolution observation resolution and observation density in data assimilation: A one dimensional study, Q. J. Roy. Meteorol. Soc., 128, 1367–1386, 2002. a
Lorenc, A. C.: A global three-dimensional multivariate statistical interpolation scheme, Mon. Weather Rev., 109, 701–721, 1981. a
Mason, D. C., Speck, R., Deveraux, B., Schumann, G., Neal, J., and Bates, P.: Flood detection in urban areas using TerraSAR-X, IEEE T. Geosci. Remote, 48, 882–894, 2010a. a, b
Mason, D. C., Schumann, G., and Bates, P. D.: Data Utilization in Flood Inundation Modelling, in: Flood Risk Science and Management, edited by: Pender, G. and Faulkner, H., Wiley-Blackwell, Chichester, 209–233, https://doi.org/10.1002/9781444324846.ch11, 2010b. a
Mason, D. C., Schumann, G. J.-P., Neal, J., Garcia-Pintado, J., and Bates, P.: Automatic near real-time selection of flood water levels from high resolution Synthetic Aperture Radar images for assimilation into hydraulic models: A case study, Remote Sens. Environ., 124, 705–716, https://doi.org/10.1016/j.rse.2012.06.017, 2012a. a, b, c, d, e, f
Mason, D. C., Davenport, I. J., Neal, J. C., Schumann, G. J. P., and Bates, P. D.: Near Real-Time Flood Detection in Urban and Rural Areas Using High-Resolution Synthetic Aperture Radar Images, IEEE T. Geosci. Remote, 50, 3041–3052, https://doi.org/10.1109/TGRS.2011.2178030, 2012b. a
Mason, D. C., Giustarini, L., Garcia-Pintado, J., and Cloke, H.: Detection of flooded urban areas in high resolution Synthetic Aperture Radar images using double scattering, Int. J. Appl. Earth Obs. Geoinf., 28, 150–159, https://doi.org/10.1016/j.jag.2013.12.002, 2014. a
Matgen, P., Montanari, M., Hostache, R., Pfister, L., Hoffmann, L., Plaza, D., Pauwels, V. R. N., De Lannoy, G. J. M., De Keyser, R., and Savenije, H. H. G.: Towards the sequential assimilation of SAR-derived water stages into hydraulic models using the Particle Filter: proof of concept, Hydrol. Earth Syst. Sci., 14, 1773–1785, https://doi.org/10.5194/hess-14-1773-2010, 2010. a
Ménard, R.: Error covariance estimation methods based on analysis residuals: theoretical foundation and convergence properties derived from simplified observation networks, Q. J. Roy. Meteorol. Soc., 142, 257–273, https://doi.org/10.1002/qj.2650, 2016. a
Montanari, M., Hostache, R., Matgen, P., Schumann, G., Pfister, L., and Hoffmann, L.: Calibration and sequential updating of a coupled hydrologic-hydraulic model using remote sensing-derived water stages, Hydrol. Earth Syst. Sci., 13, 367–380, https://doi.org/10.5194/hess-13-367-2009, 2009. a
Neal, J., Schumann, G., Bates, P., Buytaert, W., Matgen, P., and Pappenberger, F.: A data assimilation approach to discharge estimation from space, Hydrol. Process., 23, 3641–3649, 2009. a
Raclot, D.: Remote sensing of water levels on floodplains: a spatial approach guided by hydraulic functioning, Int. J. Remote Sens., 27, 2553–2574, https://doi.org/10.1080/01431160600554397, 2006. a
Roux, H. and Dartus, D.: Sensitivity Analysis and Predictive Uncertainty Using Inundation Observations for Parameter Estimation in Open-Channel Inverse Problem, J. Hydraul. Eng., 134, 541–549, https://doi.org/10.1061/(ASCE)0733-9429(2008)134:5(541), 2008. a
Schumann, G. J.-P., Hostache, R., Puech, C., Hoffmann, L., Matgen, P., Pappenberger, F., and Pfister, L.: High-Resolution 3-D Flood Information From Radar Imagery for Flood Hazard Management, IEEE T. Geosci. Remote, 45, 1715–1725, 2007. a
Schumann, G. J.-P., Neal, J. C., Mason, D. C., and Bates, P. D.: The accuracy of sequential aerial photography and SAR data for observing urban flood dynamics, a case study of the UK summer 2007 floods, Remote Sens. Environ., 115, 2536–2546, https://doi.org/10.1016/j.rse.2011.04.039, 2011. a
Stewart, L. M., Dance, S. L., Nichols, N. K., Eyre, J. R., and Cameron, J.: Estimating interchannel observation-error correlations for IASI radiance data in the Met Office system, Q. J. Roy. Meteorol. Soc., 140, 1236–1244, https://doi.org/10.1002/qj.2211, 2014. a
Terasaki, K. and Miyoshi, T.: Data Assimilation with Error-Correlated and Non-Orthogonal Observations: Experiments with the Lorenz-96 Model, SOLA, 10, 210–213, https://doi.org/10.2151/sola.2014-044, 2014. a
Todling, R.: A complementary note to `A lag-1 smoother approach to system-error estimation': the intrinsic limitations of residual diagnostics, Q. J. Roy. Meteorol. Soc., 141, 2917–2922, https://doi.org/10.1002/qj.2546, 2015. a
Ueno, G. and Nakamura, N.: Bayesian estimation of the observation-error covariance matrix in ensemble-based filters, Q. J. Roy. Meteorol. Soc., 142, 2055–2080, https://doi.org/10.1002/qj.2803, 2016. a
Vanden-Eijnden, E. and Weare, J.: Data Assimilation in the Low Noise Regime with Application to the Kuroshio, Mon. Weather Rev., 141, 1822–1841, https://doi.org/10.1175/MWR-D-12-00060.1, 2013. a
Waller, J. A., Dance, S. L., Lawless, A. S., Nichols, N. K., and Eyre, J. R.: Representativity error for temperature and humidity using the Met Office high-resolution model, Q. J. Roy. Meteorol. Soc., 140, 1189–1197, https://doi.org/10.1002/qj.2207, 2014. a, b
Waller, J. A., Ballard, S. P., Dance, S. L., Kelly, G., Nichols, N. K., and Simonin, D.: Diagnosing Horizontal and Inter-Channel Observation Error Correlations for SEVIRI Observations Using Observation-Minus-Background and Observation-Minus-Analysis Statistics, Remote Sensing, 8, 581, https://doi.org/10.3390/rs8070581, 2016a. a, b
Waller, J. A., Dance, S. L., and Nichols, N. K.: Theoretical insight into diagnosing observation error correlations using observation-minus-background and observation-minus-analysis statistics, Q. J. Roy. Meteorol. Soc., 142, 418–431, https://doi.org/10.1002/qj.2661, 2016b. a, b, c, d
Waller, J. A., Simonin, D., Dance, S. L., Nichols, N. K., and Ballard, S. P.: Diagnosing observation error correlations for Doppler radar radial winds in the Met Office UKV model using observation-minus-background and observation-minus-analysis statistics, Mon. Weather Rev., 144, 3533–3551, https://doi.org/10.1175/MWR-D-15-0340.1, 2016c. a
Waller, J. A., Dance, S. L., and Nichols, N. K.: On diagnosing observation error statistics in localized ensemble data assimilation, Q. J. Roy. Meteorol. Soc., 143, 2677–2686, https://doi.org/10.1002/qj.3117, 2017. a
Weston, P. P., Bell, W., and Eyre, J. R.: Accounting for correlated error in the assimilation of high-resolution sounder data, Q. J. Roy. Meteorol. Soc., 140, 2420–2429, https://doi.org/10.1002/qj.2306, 2014. a