the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Technical note: Pitfalls in using log-transformed flows within the KGE criterion
Guillaume Thirel
Charles Perrin
Log-transformed discharge is often used to calculate performance criteria to better focus on low flows. This prior transformation limits the heteroscedasticity of model residuals and was largely applied in criteria based on squared residuals, like the Nash–Sutcliffe efficiency (NSE). In the recent years, NSE has been shown to have mathematical limitations and the Kling–Gupta efficiency (KGE) was proposed as an alternative to provide more balance between the expected qualities of a model (namely representing the water balance, flow variability and correlation). As in the case of NSE, several authors used the KGE criterion (or its improved version KGE′) with a prior logarithmic transformation on flows. However, we show that the use of this transformation is not adapted to the case of the KGE (or KGE′) criterion and may lead to several numerical issues, potentially resulting in a biased evaluation of model performance. We present the theoretical underpinning aspects of these issues and concrete modelling examples, showing that KGE′ computed on log-transformed flows should be avoided. Alternatives are discussed.
In the context of rainfall–runoff modelling, evaluating the quality of the models' outputs is essential. Deterministic simulations are commonly evaluated using efficiency criteria such as the Nash–Sutcliffe efficiency (Nash and Sutcliffe, 1970). The choice of the criteria obviously depends on the modeller's objective. For example, one may wish to focus on the overall water balance evaluation, or more specifically on the simulation of different flow ranges – typically high, intermediate or low flows. For these different objectives, given that the model residuals are generally not homoscedastic and often depend on the flow magnitude, one common option to focus more closely on specific flow ranges is to apply various prior transformations on the simulated and observed discharge time series to distort the range of errors, which consequently changes the relative weight of different flow ranges in the criterion. This is commonly done within the NSE criterion, which has been one of the most popular criteria used in hydrological modelling in the past few decades. NSE is the distance to 1 of the ratio between the mean square error of the model and the variance of observed flows. Compared to the basic criterion computed on untransformed flows, a prior squared transformation on flows would put even more weight on high flows, and a logarithmic or inverse transformation would put more weight on low flows, while a square-root transformation would have an intermediate effect (De Vos and Rientjes, 2010; Krause et al., 2005; Oudin et al., 2006; Pushpalatha et al., 2012).
However, the Nash–Sutcliffe criterion was shown to have limitations. Indeed, using a decomposition of NSE based on the correlation, bias and ratio of variances, Gupta et al. (2009) clearly demonstrated that discharge variability is not correctly taken into account for the evaluation. Therefore, Gupta et al. (2009) proposed a new criterion, the Kling–Gupta efficiency (KGE), which was then improved into a modified criterion called KGE′ (Kling et al., 2012). KGE combines the previous components of NSE (correlation, bias, ratio of variances or coefficients of variation) in a more balanced way. It corrects the underestimation of variability and provides direct assessment of four aspects of discharge time series, namely shape, timing, water balance and variability.
Given that this criterion tends to be sensitive to large errors, some users chose to apply prior transformations on flows before computing KGE, e.g. to put more weight on low flows, as done with NSE. For example, Pechlivanidis et al. (2014) applied the logarithmic transformation to use it as a benchmark for fitting a model on low flows. Seeger and Weiler (2014) used it as an objective function. Beck et al. (2016) used the untransformed and log-transformed flows in NSE, R2 and KGE as an evaluation of different global models, and Quesada-Montano et al. (2018) also used it as an evaluation criterion of the HBV model outputs.
In this technical note we show that the use of a logarithmic transformation when computing KGE or KGE′, applied in a similar way to with NSE, introduces numerical flaws and should be avoided. After reviewing the mathematical formulation of KGE′, we expose the theoretical aspects explaining these flaws and illustrate them with modelling examples. Then we suggest alternatives to circumvent this issue. The tests will be carried out using KGE′ but they are also valid for the initial KGE formulation.
The KGE and KGE′ criteria (Gupta et al., 2009; Kling et al., 2012) are written as a linear transformation () of the Euclidian distance to an ideal value (i.e. [1,1,1]) in a three-dimensional space defined by three components of the modelling error:
in which
-
r, the Pearson correlation coefficient, evaluates the error in shape and timing between observed (Qo) and simulated (Qs) flows:
where “cov” is the covariance between observation and simulation and σ is the standard deviation, with subscripts “o” and “s” standing for observed and simulated, respectively.
-
β, the bias term, evaluates the bias between observed and simulated flows:
where μ is the mean also with subscripts “o” and “s” standing for observed and simulated, respectively.
-
α, the ratio between the simulated and observed standard deviations, evaluates the flow variability error:
-
γ, the ratio between the simulated and observed coefficients of variation (CV), also evaluates the flow variability error. These coefficients of variation are used to avoid the impact of bias on the variability indicator (Kling et al., 2012):
The KGE′ values range between −∞ and 1, as for NSE, and it is positively oriented.
3.1 Instability when the moments of log-transformed flows become close to zero
Because the three terms γ, β and r are ratios, they can become overly sensitive to the denominator values (here μo, μs, σo or σs) if they become close to zero. In this case, a small absolute variation in the moments' values can negatively impact the related ratio and thus produce very negative KGE′ values. It is generally unlikely that values of σo, σs, μs and μo so close to zero can be obtained to produce numerical instability when using untransformed flows. However, when a prior logarithmic transformation is applied, the values of μlog,o or μlog,s (more rarely σlog,o or σlog,s) computed on transformed values can become equal or close to zero (because log(1)=0). The corresponding ratios r, β or γ would therefore become very large, leading to strongly negative KGE′ values. Thus a small relative difference can lead to very different conclusions. In this case, the score value does not adequately represent the qualities of the model simulation.
3.2 Dependence on the flow unit chosen
KGE′ and NSE criteria are dimensionless. This means that using discharge values expressed in litres per second or in cubic metres per second has no impact on the criteria values. It can be easily demonstrated that γ, β and r remain identical when flow is expressed in any of these two units, since the division by 1000 necessary for the conversion is eliminated in the ratios. When using a prior logarithmic transformation, the NSE criterion is not affected because the squared differences of flows eliminates the multiplicative conversion coefficients in the mean square error (numerator) or in the variance (denominator). However, the KGE′ calculation is altered through the β ratio. Using the example of the average observed flow calculation, the conversion from cubic metres per second to litres per second gives the following:
Consequently, because the conversion term becomes additive when applying the logarithmic transformation, the β ratio value is modified. Similarly, the γ ratio is also altered. Therefore, if the logarithmic transformation is used, the KGE′ (and also the KGE) is no longer a dimensionless value. This can lead to interpretation problems.
3.3 Dependence on the constant added to avoid the zero-flow issue
When using a logarithmic (or an inverse) transformation, the case of null flows, which may exist in the case of intermittent or ephemeral streams, prevents proper calculation. To avoid this, different techniques may be set up in the case of NSE:
-
The first involves discarding the zero-flow values from the series, i.e. considering them as gaps (Nguyen and Dietrich, 2018). The drawback is that parts of the hydrographs become neglected, though they can bring important information on the processes at play.
-
The second involves adding a small constant to all flow values (Pushpalatha et al., 2012), typically a fraction of average flow. This option is widely used and Pushpalatha et al. (2012) showed that the NSE value has limited sensitivity to this constant with a logarithmic transformation as long as it is small enough compared to flow values. These authors advise a constant equal to 1∕100 of the mean observed flows. But the dependence of KGE′ on this constant has not been investigated so far.
-
The third involves using a Box–Cox transformation to reproduce the effects of the logarithmic transformation without the zero-flow issue (Box and Cox, 1964; Hogue et al., 2000; Vázquez et al., 2008).
To illustrate these numerical issues and their potential impacts, several tests were carried out in a wide range of catchments, using the GR4J rainfall–runoff model (Perrin et al., 2003).
4.1 Catchment set and data
A daily data set of 240 catchments across France (Fig. 1), set up by Ficchí et al. (2016), was used. The climate data of the SAFRAN daily reanalysis (Vidal et al., 2010) were used as input data. Precipitation and temperature were spatially aggregated in each catchment since the GR4J model is lumped. Potential evapotranspiration was calculated using a temperature-based formula (Oudin et al., 2005). Full details on this data set are available in Ficchí et al. (2016). Observed flows were retrieved for each catchment outlet from the Banque HYDRO (Leleu et al., 2014). The availability of data covers the 2005–2013 period. To avoid requiring a snow model, the catchments with less than 10 % of precipitation falling as snow were selected.
4.2 Model and calibration
The tests were performed with the daily lumped conceptual GR4J model (Perrin et al., 2003). The four parameters of the model are calibrated using the local search optimization algorithm used in Coron et al. (2017). The available records are split into a calibration (from July 2005 to June 2009) and a validation (from July 2009 to July 2013) period following a standard split-sample test procedure (Klemeš, 1986). The calibration procedure was run using the KGE′ on untransformed flows as an objective function. The performance of the model is then evaluated during the validation period using KGE′ on untransformed and log-transformed flows. The performance is also calculated using different transformations that can substitute the logarithmic transformation, namely the square-rooted flows, the inverted flows and the Box–Cox transformed flows. The NSE criterion is also calculated on log-transformed flows to be compared to KGE′ using the same transformation. The zero flows were treated following the conclusions of Pushpalatha et al. (2012), i.e. by adding to flows a constant equal to 1∕100 of the mean observed flows. The parameter of the Box–Cox transformation is fixed at the value of 0.25, as Vázquez et al. (2008) argue that it is an usual value in hydrological studies.
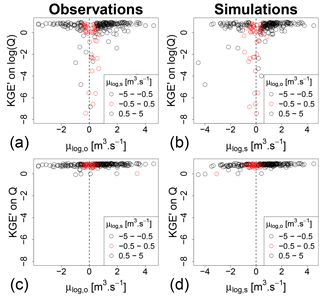
Figure 2Values of KGE′ on log-transformed flows (a, b) versus the mean of the log-transformed observed and simulated flows compared. As a benchmark, the same plots are drawn with untransformed flows (c, d). Each dot represents the performance obtained in validation for one catchment after calibration with the KGE′ on untransformed flows as an objective function. In plots (a) and (c), the axis values represent the observed log-transformed flow averages and the color represents the simulated averages, while in plots (b) and (d) it is the opposite.
5.1 Instability when the moments of log-transformed flows become close to zero
Figure 2a and b analyse the stability of the KGE′ values with log-transformed flows obtained in the validation period. The KGE′ values were plotted against the mean of the log-transformed observed (a) and simulated (b) flows. When any of these means tends to be close to zero, the KGE′ criterion exhibits unusually low values. This plot illustrates the problem identified in Sect. 3.1. These very negative values may alter model evaluation. When working on a large set of catchments, they may also bias the calculation of the mean performance over the catchment set, by heavily weighting these outlier values. Figure 2c and d shows that the catchments with negative KGE′ values in Fig. 2a and b do not seem to exhibit any specific behaviour when evaluated with the KGE′ values on untransformed flows: the criterion values are not lower in these catchments than in other catchments. Furthermore, this result can be completed by making the same plot for other transformations, giving more weight to low flows. Figure 3 shows that square-root (Fig. 3a and b) and inverse (Fig. 3c and d) transformations do not encounter the same problems as with the logarithm for catchments that have an average log-transformed flow around zero.
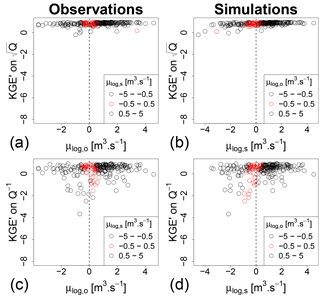
Figure 3Values of KGE′ on square-root (a, b) and inverse (c, d) transformed flows versus the mean of the log-transformed observed and simulated flows. Each dot represents the performance obtained in validation for one catchment after calibration with the KGE′ on untransformed flows as an objective function. In plots (a) and (c), the axis values represent the observed log-transformed flow averages and the color represents the simulated averages, while in plots (b) and (d) it is the opposite.
The KGE′ on log-transformed flows can also be compared to the NSE using the same transformation. Figure 4 shows that, when KGE′ is significantly lower than NSE, the average of log-transformed flows (observed or simulated) is around zero (red dots in the figure). This tends to confirm that the strongly negative KGE′ values stem more from a numerical issue than an actual problem in simulated values, because the NSE values in these catchments remain positive or around zero.
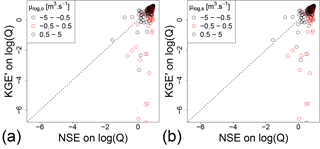
Figure 4Comparison between KGE′ and NSE values on the validation period using a calibration with KGE′ on untransformed flows as an objective function. The red dots represent the catchments where the average of log-transformed observed (a) or simulated (b) flows is around 0.
In this technical note, the impact of a near-zero standard deviation of log-transformed flows is not presented because it is rarer than near-zero mean values. The standard deviations of flows in the catchments studied are indeed all significantly higher than zero.
5.2 Dependence on the flow unit chosen
The dependence of KGE′ on log-transformed flows on the chosen flow units can easily be shown by plotting the KGE′ on log-transformed flows in cubic metres per second versus the KGE′ on log-transformed flows in litres per second. Figure 5b shows that, for the catchments tested, the values of KGE′ on log-transformed flows clearly depend on the flow unit used. A more optimistic evaluation of model performance will generally be obtained with the flows in litres per second. As a comparison, Fig. 5a shows that the KGE′ with untransformed flows is not affected by the flow unit change. This dimension dependence makes the KGE′ values based on log-transformed flows very difficult to interpret.
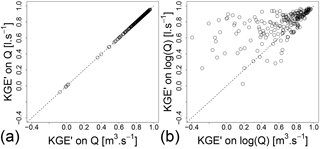
Figure 5Dependence on flow units of the KGE′ using untransformed flows (a) and log-transformed flows (b) in the 240 catchments. The parameters used for simulation evaluation were obtained by calibrating GR4J using KGE′ on untransformed flows.
The higher model performance when using litres per second than when using square metres per second can be explained analytically. Considering Eq. (7), the formula of the bias ratio in litres per second regarding the averages in metres per second is as follows:
Because log(1000) is not negligible compared to the averages, adding this constant term would artificially improve β and, by extension, the KGE′ value. The γ ratio is also affected and, due to the interactions between the standard deviation and the averages, modifies the KGE′ value differently.
5.3 Dependence on the value added to avoid the zero-flow issue
Pushpalatha et al. (2012) showed that the sensitivity of the NSE criterion on log-transformed flows to the small added constant declines when this constant decreases (from 1∕10 to 1∕100 of the mean observed flow) and becomes limited for very small values (Pushpalatha et al., 2012). We performed the same test with the KGE′ criterion and we obtained a very different result (Fig. 6). The impact on performance is erratic for different values added to flows and does not show any trend. This may be due to the numerical issues shown in Sect. 5.1. For these reasons, the impact of added values can be major and may alter the model evaluation.
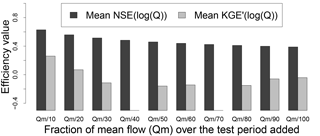
Figure 6Sensitivity of NSE and KGE′ to the fraction of average flows that is added to flows to avoid zero flows in the logarithmic transformation for 240 catchments over the validation period. This graph is inspired by Fig. 9 in Pushpalatha et al. (2012).
5.4 The case of the Box–Cox transformation
As presented in Sect. 3.3, instead of adding a small value to flows, a Box–Cox transformation can be applied to flows to mimic the logarithm transformation without the zero-flow problem. However, even though it removes the dependence of the KGE′ value to the value added to avoid zero flows, the other issues presented in the previous sections exist as for the logarithm. For catchments in which the log-transformed flows' average is close to zero, the Box–Cox transformed flows exhibit the same behaviour as with the logarithm (Fig. 7). This result is logical because the Box–Cox transformation of 1 is equal to 0, as for the logarithmic transformation.
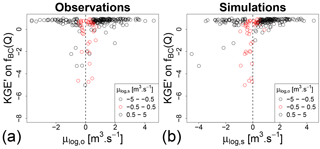
Figure 7Values of KGE′ on Box–Cox transformed flows versus the mean of the log-transformed observed (a) and simulated (b) flows. Each dot represents the performance obtained in validation for one catchment after calibration with the KGE′ on untransformed flows as an objective function. In plot (a), the axis values represent the observed log-transformed flow averages and the color represents the simulated averages, while in plot (b) it is the opposite.
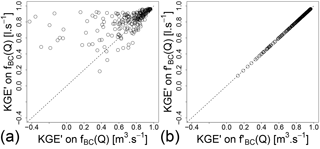
The Box–Cox transformation is also dependent on the units (Fig. 8a). However, for this last issue, a slight modification of the Box–Cox formula allows one to address this problem. The classical Box–Cox transformation can be written as follows:
in which λ is an exponent to be chosen by the user, Q is the flow value for any unit and fBC is the Box–Cox function.
Using this equation, the KGE′ on transformed flows will be unit-dependent because of the additive term 1 in the numerator. To avoid this, we can slightly modify the formula, by replacing the term 1 by a constant with a unit dependence (here we propose 1∕100 of the mean flow) and by putting it to the power λ:
Using Eq. (10), the KGE′ criterion remains dimensionless using the Box–Cox transformation (Fig. 8b).
Furthermore, because the zero of the modified Box–Cox function is not 1 any more, this transformation would reduce the issue of strongly negative values when μlog,o or μlog,s are around zero. However, there still is an issue if the average of simulated flows is around the zero of the modified Box–Cox function (i.e. if μs=(0.01μo)λ, Fig. 9). This instability occurs more rarely than for the logarithm transformation but can be more frequent if larger percentages of the average of observed flow or different λ value are used. Because this instability is due to μs (which is only in the denominator of the γ ratio in Eq. 6), it will only affect the KGE′. The KGE is not affected because an α ratio is used instead of the γ ratio (Eqs. 1 and 5).
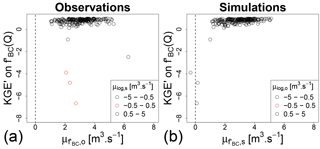
Figure 9Values of KGE′ on modified Box–Cox transformed flows (Eq. 10) versus the mean of this transformed observed (a) and simulated (b) flows. Each dot represents the performance obtained in validation for one catchment after calibration with the KGE′ on untransformed flows as an objective function. In plot (a), the axis values represent the observed transformed flow averages and the color represents the simulated averages, while in plot (b) it is the opposite.
The modified Box–Cox transformation (Eq. 10) allows unit dependence to be avoided and the instability issues due to the values of average flows to be reduced (especially when using the KGE). The behaviour of this modified transformation also remains similar to the one of the initial Box–Cox transformation except when μlog,o or μlog,s are around zero (Fig. 10).
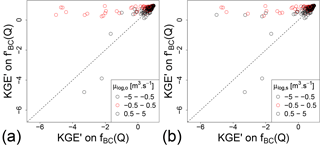
Figure 10Comparison between KGE′ values on Box–Cox and modified Box–Cox transformed flows on the validation period using a calibration with KGE′ on untransformed flows as an objective function. The red dots represent the catchments where the average of log-transformed observed (a) or simulated (b) flows is around 0.
Table 1Pros (+) and cons (−) of different flow transformations to improve consideration of low flows in KGE′. In the second column, the number of + symbols represents the intensity of the low-flow weight increase. There are parentheses around the last + for inverted root and Box–Cox transformations because the low-flow weight depends on parameters.

6.1 Log transformation should not be used in the KGE or KGE′ criterion
Given the previous results, we can argue that using log-transformed flows to calculate the KGE or the KGE′ criterion can lead to difficulties in the interpretation of criterion values. The criterion does not remain dimensionless like NSE with a prior logarithmic transformation. It also becomes overly sensitive when the log-transformed flows' average becomes close to zero, yielding potentially very negative values, or when a small constant is added to flows prior to logarithmic transformation to cope with zero flows. Because of all these issues, logarithmic transformation should be avoided when using KGE′.
6.2 Alternatives
Instead of KGE′ on log-transformed flows, several transformations can be used to calculate KGE′. The pros and cons for several transformations are summarised in Table 1. The reciprocal of root (RoR) is an example of a transformation used in the literature that is not tested in the article but leads to an increase in the weight of low flows (Chapman, 1964; Ding, 1966; Ishihara and Takagi, 1965). As stated in Ding (2018b), it can be parametrized with the value of the power in the root (). Depending on the value of N, there will be more or less weight on low flows (Ding, 2018a). The higher N is, the less the weight on low flows is. This N value can also be determined with the recession curves of observed flows. Regarding this table, the modified Box–Cox transformation (Eq. 10) seems to be the best solution but it still faces instabilities for some flow average values (for the KGE′). Thus, there is no ideal solution to avoid all problems. Modellers have to make a choice depending on their specific applications. According to the intensity of low-flow weight increase that is needed, the choice of transformation has to be adapted. Garcia et al. (2016), for example, recommend averaging two KGE′ criteria, computed on untransformed and inverted flows, into a composite criterion.
Note that many studies use NSE on log-transformed flows (Lyon et al., 2017; Nguyen and Dietrich, 2018). Fortunately, the mathematical formulation of NSE avoids all the problematic aspects identified for KGE with the logarithmic transformation. However, this may not be a sufficient argument to continue to use NSE given the issues presented by Gupta et al. (2009) and Schaefli and Gupta (2007):
-
the underestimation of variability,
-
the low weight of water balance errors for catchments with highly variable flows,
-
the poor benchmark represented by the mean flows for catchments with highly variable flows.
6.3 Final remarks
Two additional remarks should be taken into account on this topic. First, as noted by Harald Kling in a personal communication, 2018, prior transformations on flows in KGE (or in NSE) lead to a misinterpretation in the estimation of the water balance. The other components of the KGE also lose their initial physical meaning. KGE on transformed flows can give more information on low flows, but the physical interpretation of the criterion is not as simple as in the case of untransformed flows.
Secondly, even if it did not occur in our experiment, the issue described in this technical note may lead to problems during the calibration process. Indeed, it can create a strongly negative zone in the objective function hyperspace, which may negatively impact the performance of local calibration algorithms.
The daily flow data can be downloaded from the Banque HYDRO website (http://www.hydro.eaufrance.fr/, last access 29 August 2018). The climatic data from the SAFRAN reanalysis used in this paper (daily precipitation and temperature) are not freely available. The data was provided to Irstea following a convention between the two institutes. However, the analyses can be reproduced using open data and would lead to similar conclusions.
LS made the technical development and the analysis. The paper was written by him, GT and CP.
The authors declare that they have no conflict of interest.
The authors thank Météo France for providing the data used in this work. We also wish to thank Alban De Lavenne, Laure Lebecherel, Maria-Helena Ramos and Cedric Rebolho for the discussions on the different aspects of the issues using the logarithmic transformation with KGE. We thank Andrea Ficchí for his work on the database and Linda Northrup for her correction of the English language of an earlier version of the paper. Finally, we extend our thanks to Harald Kling for discussions on this issue.
We thank the topical editor, Bettina Schaefli, for her careful reading of the
paper, her suggestion on the modified Box–Cox transformation and the
following discussions. We also thank the two reviewers, Lieke Melsen and
Björn Guse, for taking the time to read our paper and for their
remarks that helped us to make the paper and the figures more
understandable. We thank Sivarajah Mylevaganam for the discussions that
helped us to be more precise in the KGE and KGE′ description. Finally, we
particularly want to thank John Ding for his suggestion to add the RoR
transformation (that we did not know about before) to the article and for the
fruitful discussions that followed.
Edited by: Bettina Schaefli
Reviewed by: Lieke Melsen and Björn Guse
Beck, H. E., van Dijk, A. I. J. M., de Roo, A., Miralles, D. G., McVicar, T. R., Schellekens, J., and Bruijnzeel, L. A.: Global-scale regionalization of hydrologic model parameters, Water Resour. Res., 52, 3599–3622, https://doi.org/10.1002/2015WR018247, 2016. a
Box, G. E. P. and Cox, D. R.: An Analysis of Transformations, J. Roy. Stat. Soc. B, 26, 211–252, 1964. a
Chapman, T. G.: Effects of groud-water storage and flow on the water balance, in: Proceedings of “Water resources, use and management”, 291–301, Australian Academy of Science, Melbourne Univ. Press, 1964. a
Coron, L., Thirel, G., Delaigue, O., Perrin, C., and Andréassian, V.: The suite of lumped GR hydrological models in an R package, Environ. Model. Softw., 94, 166–177, https://doi.org/10.1016/j.envsoft.2017.05.002, 2017. a
De Vos, N. J. and Rientjes, T. H. M.: Multi-objective performance comparison of an artificial neural network and a conceptual rainfall-runoff model, Hydrol. Sci. J., 52, 397–413, https://doi.org/10.1623/hysj.52.3.397, 2010. a
Ding, J.: Interactive comment on “Technical note: Pitfalls in using log-transformed flows within the KGE criterion” by Léonard Santos et al., Hydrol. Earth Syst. Sci. Discuss., https://doi.org/10.5194/hess-2018-298-SC2, 2018a. a
Ding, J.: Interactive comment on “Technical note: Pitfalls in using log-transformed flows within the KGE criterion” by Léonard Santos et al., Hydrol. Earth Syst. Sci. Discuss., https://doi.org/10.5194/hess-2018-298-SC5, 2018b. a
Ding, J. Y.: Discussion of “Inflow hydrograph from large unconfined aquifers” by Ibrahim, H. A. and Brutsaert, W. J., J. Irrig. Drain. Am. Soc. Civ. Eng., 92, 104–107, 1966. a
Ficchí, A., Perrin, C., and Andréassian, V.: Impact of temporal resolution of inputs on hydrological model performance: An analysis based on 2400 flood events, J. Hydrol., 538, 454–470, https://doi.org/10.1016/j.jhydrol.2016.04.016, 2016. a, b
Garcia, F., Folton, N., and Oudin, L.: Which objective function to calibrate rainfall–runoff models for low-flow index simulations?, Hydrol. Sci. J., 62, 1149–1166, https://doi.org/10.1080/02626667.2017.1308511, 2016. a
Gupta, H. V., Kling, H., Yilmaz, K. K., and Martinez, G. F.: Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling, J. Hydrol., 377, 80–91, https://doi.org/10.1016/j.jhydrol.2009.08.003, 2009. a, b, c, d
Hogue, T. S., Sorooshian, S., Gupta, H., Holz, A., and Braatz, D.: A Multistep Automatic Calibration Scheme for River Forecasting Models, J. Hydrometeorol., 1, 524–542, https://doi.org/10.1175/1525-7541(2000)001<0524:AMACSF>2.0.CO;2, 2000. a
Ishihara, T. and Takagi, F.: A study on the variation of low flow, Bulletin of the Disaster Prevention Research Institute, 15, 75–98, http://hdl.handle.net/2433/124698, 1965. a
Klemeš, V.: Operational testing of hydrological simulation models, Hydrol. Sci. J., 31, 13–24, https://doi.org/10.1080/02626668609491024, 1986. a
Kling, H., Fuchs, M., and Paulin, M.: Runoff conditions in the upper Danube basin under ensemble of climate change scenarios, J. Hydrol., 424–425, 264–277, https://doi.org/10.1016/j.jhydrol.2012.01.011, 2012. a, b, c
Krause, P., Boyle, D. P., and Bäse, F.: Comparison of different efficiency criteria for hydrological model assessment, Adv. Geosci., 5, 89–97, https://doi.org/10.5194/adgeo-5-89-2005, 2005. a
Leleu, I., Tonnelier, I., Puechberty, R., Gouin, P., Viquendi, I., Cobos, L., Foray, A., Baillon, M., and Ndima, P.-O.: Re-founding the national information system designed to manage and give access to hydrometric data, La Houille Blanche, 1, 25–32, https://doi.org/10.1051/lhb/2014004, 2014 (in French). a
Lyon, S. W., King, K., Polpanich, O., and Lacombe, G.: Assessing hydrologic changes across the Lower Mekong Basin, J. Hydrol.: Reg. Stud., 12, 303–314, https://doi.org/10.1016/j.ejrh.2017.06.007, 2017. a
Nash, J. E. and Sutcliffe, J. V.: River flow forecasting through conceptual models. Part I – A discussion of principles, J. Hydrol., 10, 282–290, https://doi.org/10.1016/0022-1694(70)90255-6, 1970. a
Nguyen, V. T. and Dietrich, J.: Modification of the SWAT model to simulate regional groundwater flow using a multicell aquifer, Hydrol. Process., 32, 939–953, https://doi.org/10.1002/hyp.11466, 2018. a, b
Oudin, L., Hervieu, F., Michel, C., Perrin, C., Andréassian, V., Anctil, F., and Loumagne, C.: Which potential evapotranspiration input for a lumped rainfall–runoff model?, J. Hydrol., 303, 290–306, https://doi.org/10.1016/j.jhydrol.2004.08.026, 2005. a
Oudin, L., Andréassian, V., Mathevet, T., Perrin, C., and Michel, C.: Dynamic averaging of rainfall-runoff model simulations from complementary model parameterizations, Water Resour. Res., 42, W07410, https://doi.org/10.1029/2005wr004636, 2006. a
Pechlivanidis, I. G., Jackson, B., McMillan, H., and Gupta, H.: Use of an entropy-based metric in multiobjective calibration to improve model performance, Water Resour. Res., 50, 8066–8083, https://doi.org/10.1002/2013WR014537, 2014. a
Perrin, C., Michel, C., and Andréassian, V.: Improvement of a parsimonious model for streamflow simulation, J. Hydrol., 279, 275–289, https://doi.org/10.1016/s0022-1694(03)00225-7, 2003. a, b
Pushpalatha, R., Perrin, C., Moine, N. L., and Andréassian, V.: A review of efficiency criteria suitable for evaluating low-flow simulations, J. Hydrol., 420–421, 171–182, https://doi.org/10.1016/j.jhydrol.2011.11.055, 2012. a, b, c, d, e, f, g
Quesada-Montano, B., Westerberg, I. K., Fuentes-Andino, D., Hidalgo, H. G., and Halldin, S.: Can climate variability information constrain a hydrological model for an ungauged Costa Rican catchment?, Hydrol. Process., 32, 830–846, https://doi.org/10.1002/hyp.11460, 2018. a
Schaefli, B. and Gupta, H. V.: Do Nash values have value?, Hydrol. Process., 21, 2075–2080, https://doi.org/10.1002/hyp.6825, 2007. a
Seeger, S. and Weiler, M.: Reevaluation of transit time distributions, mean transit times and their relation to catchment topography, Hydrol. Earth Syst. Sci., 18, 4751–4771, https://doi.org/10.5194/hess-18-4751-2014, 2014. a
Vázquez, R. F., Willems, P., and Feyen, J.: Improving the predictions of a MIKE SHE catchment-scale application by using a multi-criteria approach, Hydrol. Process., 22, 2159–2179, https://doi.org/10.1002/hyp.6815, 2008. a, b
Vidal, J.-P., Martin, E., Franchisteguy, L., Baillon, M., and Soubeyroux, J.-M.: A 50-year high-resolution atmospheric reanalysis over France with the Safran system, Int. J. Climatol., 30, 1627–1644, https://doi.org/10.1002/joc.2003, 2010. a