the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Evaluation of lacustrine groundwater discharge, hydrologic partitioning, and nutrient budgets in a proglacial lake in the Qinghai–Tibet Plateau: using 222Rn and stable isotopes
Xingxing Kuang
Jiu Jimmy Jiao
Sihai Liang
Xiaolang Zhang
Hailong Li
Proglacial lakes are good natural laboratories to investigate groundwater and glacier dynamics under current climate conditions and to explore biogeochemical cycling under pristine lake status. This study conducted a series of investigations of 222Rn, stable isotopes, nutrients, and other hydrogeochemical parameters in Ximen Co Lake, a remote proglacial lake in the east of the Qinghai–Tibet Plateau (QTP). A radon mass balance model was used to quantify the lacustrine groundwater discharge (LGD) of the lake, leading to an LGD estimate of 10.3±8.2 mm d−1. Based on the three-endmember models of stable 18O and Cl−, the hydrologic partitioning of the lake is obtained, which shows that groundwater discharge only accounts for 7.0 % of the total water input. The groundwater-derived DIN and DIP loadings constitute 42.9 % and 5.5 % of the total nutrient loading to the lakes, indicating the significance of LGD in delivering disproportionate DIN into the lake. This study presents the first attempt to evaluate the LGD and hydrologic partitioning in the glacial lake by coupling radioactive and stable isotopic approaches and the findings advance the understanding of nutrient budgets in the proglacial lakes of the QTP. The study is also instructional in revealing the hydrogeochemical processes in proglacial lakes elsewhere.
- Article
(8610 KB) -
Supplement
(179 KB) - BibTeX
- EndNote
High-altitude and high-latitude areas are intensively influenced by the melting of glaciers due to climatic warming. Of particular importance are the proglacial areas, such as proglacial lakes and moraines, because they are particularly affected by climatic-change-induced glacier retreating and thawing of permafrost (Heckmann et al., 2016; Barry, 2006; Slaymaker, 2011). The proglacial lakes are usually located close to the ice front of a glacier, ice cap, or ice sheet, with the vicinity to the ice front sometimes defined as the areas with subrecent moraines and formed by the last significant glacier advances at the end of the Little Ice Age (Heckmann et al., 2016; Barry, 2006; Slaymaker, 2011; Harris et al., 2009). These lakes are located in the transition zones from glacial to non-glacial conditions, and can serve as natural laboratories to explore hydrological processes, biogeochemical cycles, and geomorphic dynamics under current climatic conditions (Dimova et al., 2015; Heckmann et al., 2016).
The Qinghai–Tibet Plateau (QTP), the third pole of the world, serves as the water tower of most of the major rivers in Asia (Qiu, 2008). Unique landscapes such as endorheric lakes, permafrost, glaciers, and headwater fluvial networks are developed due to the intensive interaction between the atmosphere, hydrosphere, biosphere, and cryosphere (Lei et al., 2017; Zhang et al., 2017a, b; Yao et al., 2012, 2013). Distributed mountainous glaciers and lakes are the most representative landscapes and are highly sensitive to the climate changes. In the past decade, the lakes in the interior of the QTP show overall expansion with respect to an overall increase in precipitation, accelerated glacier melting, and permafrost degradation (Zhang et al., 2013, 2017a, b; Heckmann et al., 2016; Yang et al., 2014). Some recent studies have made efforts to depict the hydrologic partitioning of the majority of the lakes in the QTP based on long-term observation of climatological parameters and remote sensing approaches. However, so far a quantitative evaluation of the water balance and hydrologic partitioning, especially the groundwater component of the lakes in the QTP, has been limited due to the scarcity of observational data. Therefore, there is a great need to conduct refined and systematical field observation to provide a groundtruth dataset and tenable models to depict the water balance and hydrologic partitioning of the lakes, especially proglacial lakes in the QTP (Yang et al., 2014; Zhang et al., 2017b).
Mountainous proglacial lakes, formed by glacial erosion and filled by melting glaciers, are widely distributed in the Qinghai–Tibet Plateau (QTP), especially along the substantial glacier retreating areas of the Himalaya Mountains (MT.), Qilian MT., Tienshan MT., etc. Characterized by higher elevations, small surface areas but relatively large depths, mountainous proglacial lakes in QTP lack systematic field-based hydrological studies due to their remote locations and difficulty in conducting fieldwork (Yao et al., 2012; Farinotti et al., 2015; Bolch et al., 2012).
There has been extensive recognition of the importance of groundwater discharge to various aquatic systems for decades (Dimova and Burnett, 2011; Valiela et al., 1978; Johannes, 1980). Very recently, the topic of lacustrine groundwater discharge (LGD), which is comprehensively defined as groundwater exfiltration from lakeshore aquifers to lakes (Lewandowski et al., 2013, 2015; Rosenberry et al., 2015; Blume et al., 2013), has been introduced. LGD is analogous to submarine groundwater discharge (SGD) in coastal environments. LGD also plays a vital role in lake hydrologic partitioning, which is defined as the separation of groundwater discharge/exfiltration, riverine inflow, riverine outflow infiltration, surface evaporation, and precipitation for the hydrological cycle of the lake (Luo et al., 2017; Good et al., 2015). LGD also serves as an important component in delivering solutes to lakes since groundwater is usually concentrated in nutrients, CH4, dissolved inorganic/organic carbon (DIC/DOC), and other geochemical components (Paytan et al., 2015; Lecher et al., 2015; Belanger et al., 1985; Dimova et al., 2015). Nutrients and carbon loading from groundwater greatly influence ratios of dissolved inorganic nitrogen (DIN) to dissolved inorganic phosphate (DIP) (referred to as N:P ratios thereafter), ecosystem structure, and the primary productivity of the lake aquatic system (Nakayama and Watanabe, 2008; Belanger et al., 1985; Hagerthey and Kerfoot, 1998).
The approaches to investigate LGD include (1) direct seepage meters (Shaw and Prepas, 1990; Lee, 1977), (2) geo-tracers such as radionuclides and stable 2H and 18O isotopes (Gat, 1995; Kluge et al., 2007; Kraemer, 2005; Lazar et al., 2008), (3) heat and temperature signatures (Liu et al., 2015; Sebok et al., 2013), (4) numerical modelling (Winter, 1999; Smerdon et al., 2007; Zlotnik et al., 2009, 2010), and (5) remote sensing (Lewandowski et al., 2013; Wilson and Rocha, 2016; Anderson et al., 2013). Recently, some researchers started to investigate groundwater dynamics in periglacial and proglacial areas, mostly based on the approaches of numerical modelling (Lemieux et al., 2008a, b, c; Andermann et al., 2012; Scheidegger and Bense, 2014). However, the quantification of groundwater and surface water exchange in proglacial lakes is still challenging due to limited hydrogeological data and extreme seasonal variability of aquifer permeability (Dimova et al., 2015; Callegary et al., 2013; Xin et al., 2013).
222Rn, a naturally occurring inert gas nuclide highly concentrated in groundwater, can be more applicable in fresh aquatic systems and has been widely used as a tracer to quantify groundwater discharge in freshwater lakes (Luo et al., 2016; Corbett et al., 1997; Dimova et al., 2013, 2015; Dimova and Burnett, 2011; Kluge et al., 2007, 2012; Schmidt et al., 2010) and terrestrial rivers and streams (Burnett et al., 2010; Cook et al., 2003, 2006; Batlle-Aguilar et al., 2014). Of particular interest are investigations of temporal 222Rn distribution in lakes, since it can be used to quantify groundwater discharge and reflect the locally climatological dynamics (Dimova and Burnett, 2011; Luo et al., 2016). Temporal radon variations give high-resolution estimates of groundwater discharge to lakes over diel cycles, allowing evaluation of LGD and the associated chemical loadings. However, there has been no study of radon-based groundwater discharge in mountainous proglacial lakes, especially for those lakes in the QTP.
This study aims to investigate the groundwater–surface water interactions for the proglacial lake of Ximen Co, by estimating the LGD and evaluating the hydrologic partitioning of the lake. LGD is estimated with the 222Rn mass balance model, and the hydrologic partitioning of the lake is obtained with the three-endmember model coupling the mass balance of water, stable isotopes, and Cl−. Moreover, LGD-derived nutrients are estimated and the nutrient budgets of the lake are depicted. This study, to our knowledge, makes the first attempt to quantify the LGD, hydrologic partition, and groundwater-borne nutrients of the proglacial lake in the QTP and elsewhere via the approach of integrating multiple tracers. This study provides insights into hydrologic partitioning in a typical mountainous proglacial lake under current climate conditions and reveals groundwater-borne chemical loadings in this proglacial lake in the QTP and elsewhere.
2.1 Site descriptions
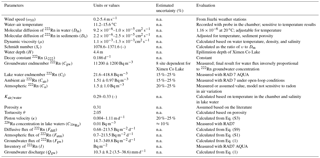
The Nianbaoyeze MT., located at the eastern margin of the QTP and being the easternmost part of NW–SW trending Bayan Har Shan, is situated at the main water divide of the upper reaches of the Yellow River and Yangtze River (Fig. 1). With a peak elevation of 5369 m, the mountain rises about 500–800 m above the surrounding peneplain and displays typical Pleistocene glacial landscapes such as moraines, U-shaped valleys, and cirques (Lehmkuhl, 1998; Schlutz and Lehmkuhl, 2009; Wischnewski et al., 2014). The present snow line is estimated to be at an elevation of 5100 m (Schlutz and Lehmkuhl, 2009). Controlled by the South Asia and East Asia monsoons, the mountain has an annual precipitation of 975 mm in the southern part and 582 mm in the northwestern part, with 80 % occurring during May and October (Yuan et al., 2014; Zhang and Mischke, 2009). The average temperature gradient is about 0.55 ∘C per 100 m, and the closest weather station, located in Jiuzhi (N: 33.424614∘, E: 101.485998∘) at the lower plains of the mountain, recorded a mean annual temperature of 0.1 ∘C. Snowfalls occur in nearly 10 months of the entire year and there is no free frost all year around (Böhner, 1996, 2006; Schlutz and Lehmkuhl, 2009). The precipitation, daily bin-averaged wind speed, and temperature in August 2015 were recorded to be 90 mm, 0.7 m s−1, and 9.5 ∘C from Jiuzhi weather station (Fig. 2). The water surface evaporation was recorded to be 1429.8 mm in 2015 from Jiuzhi weather station.
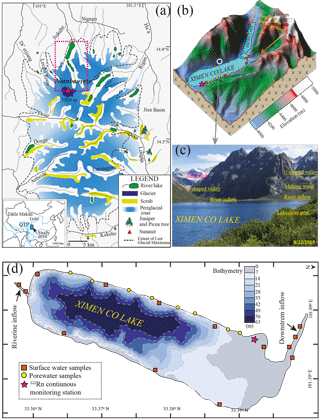
Figure 1The geological and topographic map of the Yellow River source region, Nianbaoyeze glacial mountains (a), and sampling settings of Ximen Co Lake (b), with the bathymetry map of the lake (d). (c) Photograph of Ximen Co Lake and the surrounding geomorphic settings looking in a northeasterly direction on 22 August 2015, showing the late-laying snowpack in the U-shaped valleys of the northern part of the Nianbaoyeze mountains.
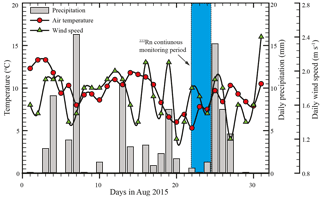
Figure 2The climatological parameters (wind speed, air temperature, and precipitation) in August 2015 recorded from Jiuzhi weather station.
Among the numerous proglacial lakes developed in the U-shaped valleys of the Nianbaoyeze MT., Ximen Co Lake is located at the northern margin of the mountain with an elevation of 4030 m a.s.l., and is well studied and easily accessible (Lehmkuhl, 1998; Zhang and Mischke, 2009; Schlutz and Lehmkuhl, 2009; Yuan et al., 2014). The lake was formed in a deep, glacially eroded basin with a catchment area of 50 km2, and has a mean and a maximum depth of 40 and 63.2 m, and a surface area of 3.6 km2. The vegetation around the lake is dominated by pine meadows with dwarf shrubs, rosette plants, and alpine cushion (Schlutz and Lehmkuhl, 2009; Zhang and Mischke, 2009; Yuan et al., 2014). Mostly recharged by the glacial and snowpack melting water and regional precipitation, the lake is stratified with an epilimnion depth of about 4.4 m in the summertime. The lake is usually covered by ice in the wintertime (Zhang and Mischke, 2009). The superficial layer within the U-shaped valley is characterized by peat, clay, and fluvial gravels with a depth of about 1–3.5 m. Discontinuous and isolated permafrost is present at the slope of the valley above an elevation of about 4150 m. The maximum frozen depth is about 1.5 m for the seasonal frozen ground around the lake. The seasonal frozen ground serves as an unconfined aquifer during the unfrozen months from July to October, and groundwater discharges into the epilimnion of the lake (Wang, 1997; Schlutz and Lehmkuhl, 2009; Zhang and Mischke, 2009).
2.2 Sampling and field analysis
The field campaign to Ximen Co Lake was conducted in August 2015, when it is warm enough to take the water samples of different origins as the studied site is seasonally frozen. A 222Rn continuous monitoring station was set up in the southeast part of the lake, where is fairly flat for setting up our tent and monitoring system. Surface water samples were collected around the lake and rivers at the upstream and downstream. Porewater samples were collected at one side of the lake as the other side is steep and rocky. The basic water quality parameters of conductivity (EC), dissolved oxygen (DO), TDS, ORP, and pH in the water were recorded with the multi-parameter meter (HANNA, Co.). Relative humidity was recorded with a portable thermo-hydrometer (KTH-2, Co.). Lake water samples were taken with a peristaltic pump into 2.5 L glass bottles for 222Rn measurement with the Big Bottle system (Durridge, Co.). Surface water samples were filtered with 0.45 µm filters (Advantec, Co.) in situ and taken into 5, 15, 15, and 50 ml Nalgene centrifugation tubes for stable isotope, major anion, cation, and nutrient analysis. Porewater samples were taken from the lakeshore aquifers with a push point sampler (M.H.E, Co.) connected to a peristaltic pump (Solinst, Co.) (Luo et al., 2014, 2016); 100 ml raw surface water or porewater was titrated with a 0.1 µM H2SO4 cartridge (Hach, Co.) in situ to measure total alkalinity (Hasler et al., 2016; White et al., 2016; Warner et al., 2013). Porewater was filtered with 0.45 µm syringe filters in situ and taken into 5, 15, 15, and 50 ml Nalgene centrifugation tubes for stable isotope, major anion, cation, and nutrient analysis; 250 ml porewater was taken for 222Rn measurement with RAD7 H2O (Durridge, Co.). Samples for major cation analysis were acidified with distilled HNO3 immediately after the sampling.
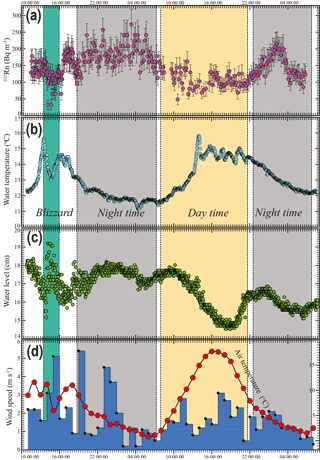
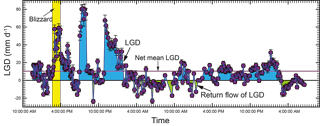
A 222Rn continuous monitoring station was set up in the northwest of the lake, close to the downstream of the lake (Fig. 1b). Lake water (about 0.5 m in depth) was pumped with a DC pump (12 V) driven by lithium batteries (100 Ah) and sprinkled into the chamber of RAD7 AQUA with a flow rate >2 L min−1, where 222Rn in water vapour was equilibrated with the air 222Rn. The vapour in the chamber was delivered into two large dry units (Drierite, Co) to remove the moisture and circulated into a RAD7 monitor, where 222Rn activities were recorded every 5 min. A temperature probe (HOBO@) was inserted into the chamber to record the temperature of the water vapour. The monitoring was performed from 11:31, 22 August to 06:30, 24 August 2015. During the period of 13:50–16:30 on 22 August, a sudden blizzard occurred, leading to an hourly precipitation of about 0.6 mm onto the lake area. Daily and hourly climatological data such as wind speed, air temperature, and precipitation were retrieved from the nearest weather station in Jiuzhi (N: 33.424614∘, E: 101.485998∘). Moreover, another RAD7 was placed at the lake shore to measure 222Rn in the ambient air around the lake. Due to extremely low activities, the monitoring period was conducted only for 4 h, and the mean activity was adopted as the background radon-222 activity to be used in the mass balance model. Water level and temperature fluctuations were recorded with a conductivity–temperature–depth diver (Schlumberger, Co.) fixed at about 20 cm below the lake surface and calibrated with local atmospheric pressure recorded by a baro-diver (Schlumberger, Co.) above the lake. To correct for dissolved 226Ra supported 222Rn, one radium sample was extracted from 100 L lake water with MnO2 fibre as described elsewhere (Luo et al., 2014; Moore, 1976).
2.3 Chemical analysis
Major ions were measured with ICS-1100 (Dionex. Co.) in the Department of Earth Sciences, University of Hong Kong. The uncertainties of the measurements are less than 5 %. Nutrients, DIN, and DIP were analysed with flow injection analysis equipped with an auto-sampler (Lachat. Co.) in the School of Biological Sciences, University of Hong Kong. Stable 18O and 2H isotopes were measured with a MOA-ICOS laser absorption spectrometer (Los Gatos Research (LGR) Triple Isotope Water Analyzer (TIWA-45EP)) at the State Key Laboratory of Marine Geology, Tongji University, Shanghai. The stable isotopic standards and the recovery test have been fully described elsewhere (Luo et al., 2017). The measurement uncertainty is better than 0.1 % for 18O and 0.5 % for 2H. 226Ra was detected with RAD7 with the method described elsewhere (Kim et al., 2001; Lee et al., 2012; Luo et al., 2018).
2.4 Radon transient model
Previous studies employed a steady-state radon-222 mass balance model to quantify LGD to lentic systems such as lakes and wetlands (Dimova and Burnett, 2011; Luo et al., 2016). This model assumes that radon inputs derived from groundwater inflow, diffusion, and river inflow are balanced by the radon losses of atmospheric evasion, decay, and river outflow. However, recent studies revealed that the steady state is mainly reached after 2–15 days of constant metrological conditions, and most lentic systems cannot be treated as steady state due to rapid radon-222 degassing to the atmosphere driven by wind-induced turbulence (Gilfedder et al., 2015; Dimova and Burnett, 2011).
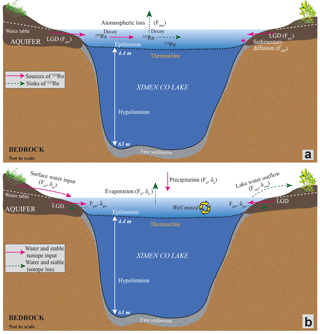
Ximen Co Lake has been demonstrated to be highly stratified, with an epilimnion of 4.4 m (Zhang and Mischke, 2009). The lake was formed by glacier erosion and the lake bed is characterized by granite bedrock with a thin sedimentary clay layer. Previous studies have indicated that sediment consisting of clay, soils, and gravels has developed on the bedrock and forms the lakeshore aquifer with a thickness of 0.7–3.3 m (Schlutz and Lehmkuhl 2009). Porewater sampled in the aquifer immediately behind the lake shore can well represent groundwater discharging into the lake, as suggested previously (Lewandowski et al., 2015; Rosenberry et al., 2015; Schafran and Driscoll, 1993). LGD has been widely considered to occur within the first few metres of the lake shore (Schafran and Driscoll, 1993; Rosenberry et al., 2015; Lee et al., 1980) and groundwater is considered to predominately discharge into the epilimnion since deep groundwater flow is highly limited by the Precambrian bedrock (Einarsdottir et al., 2017). Due to a negligible hydrological connection between the epilimnion and hypolimnion, the 222Rn mass balance model is established to quantify LGD to the epilimnion from the lake shore.
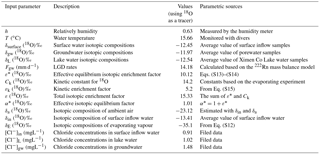
The governing equation of the radon-222 transient mass balance model within cm (where z is the depth in centimetres) can be expressed as (Gilfedder et al., 2015)
where Fgw, Fdiff, and Fatm (Bq m−2 d−1) are 222Rn loadings from LGD, water–sediment diffusion, and water–air evasion, respectively; z (m) is the lake water level depth recorded by the diver. λ222 is the decay constant of 222Rn with a value of 0.186 d−1. and λ222×Iw account for the production and decay of 222Rn (Bq m−2 d−1) in the water column, respectively. Iw and (Bq m−2) represent 222Rn and 226Ra inventories in the epilimnion, and are expressed as and , respectively, where H (m) is the depth of the epilimnion; Cw and are the 222Rn and 226Ra activity (Bq m−3), respectively.
The model is valid under the following assumptions. (1) The epilimnion is well mixed, which is the actual condition for most natural boreal and high-altitude glacial lakes (Zhang and Mischke, 2009; Åberg et al., 2010). (2) 222Rn input from riverine water inflow, and loss from the lake water outflow and infiltration into the lakeshore aquifer, are negligible compared to the groundwater-borne 222Rn, because 222Rn concentration of groundwater is 2–3 orders of magnitude larger than that of lake water (Dimova and Burnett, 2011; Dimova et al., 2013). Generally, 222Rn in the epilimnion is sourced from LGD and decay input from the parent isotope of 226Ra under secular equilibrium, and is mainly lost via atmospheric evasion and radioactive decay.
Fatm is the key sinking component of the transient model and is finally a function of wind speed and water temperature, both of which are temporal variant variables (information in the Supplement). Lake water level z is also a temporal variant variable which represents the fluctuations of water volume of the epilimnion. This equation is discretized by the forward finite difference method, and the groundwater flux at each time step can be solved as follows:
where 222Rnt+Δt and 222Rnt+Δt (Bq m−3) are the 222Rn activity at the current time step and at the previous time steps, respectively, and Δt (min) is the time step which is set to be 5 min, consistent with the 222Rn record interval. With the inverse calculation based on Eq. (2), the groundwater inflow at each time step can be obtained. However, large errors of the final LGD calculation will be induced by even a small amount of noise in the measured 222Rn data due to the term being with the measured uncertainty. To reduce the random errors of the measured 222Rn concentrations, the time window with a width of 1 h is proposed to smooth the curve (information in the Supplement).
3.1 Time series data
Figure 2 shows the basic climatological parameters of the lake catchment during the campaign month. There are discrete rainfall events occurring throughout the month with an average rainfall of 3.1 mm d−1. The temperature during the month ranges from 5.0 to 12.5 ∘C, with an average of 9.3 ∘C. The daily averaged wind speed ranges from 0.7 to 2.5 m s−1, with an average of 1.7 m s−1. 222Rn temporal distribution and other time series data are shown in Fig. 3a and listed in Table S1 in the Supplement. Generally, 222Rn concentration varies from 32.2 to 273 Bq m−3, with an average of 144.2±27.7 Bq m−3. 222Rn over the monitoring period shows a typical diel cycle, much higher at nighttime and lower in the daytime. Figure 3b–d show the time series data of temperature (5 min interval), nearshore lake water level (1 min interval), and wind speed (1 h interval). Temperature and lake water level also show typical diel cycles, but with antiphase fluctuations with each other. Temperature is higher during the daytime and lower at nighttime. However, a sudden decrease in temperature was recorded due to the sudden blizzard (Fig. 3b). Water level is higher at nighttime and lower during the daytime, with a strong fluctuation due to the turbulence caused by the blizzard (Fig. 3c). The variability might reflect the dynamics of groundwater input and surface water inflow. The air temperature of the lake area is in phase with the water temperature. Wind speed is normally higher during the daytime and lower at nighttime (Fig. 3d).
The variation of 222Rn is nearly in antiphase with the fluctuations of lake water temperature and air temperature, indicating that the dominated controlling factors of 222Rn fluctuations are water temperature and wind speed (Fig. 3a). This phenomenon is reasonable as lake water 222Rn is predominately lost via atmospheric evasion, which is the function of wind speed and water temperature (Dimova et al., 2013, 2015; Dimova and Burnett, 2011). High water temperature and wind speed lead to elevated atmospheric evasion and cause the decline of 222Rn concentration in the lake water. However, there is a sudden reduction of radon activity from 14:00 to 16:00 (GMT + 8) on 22 July 2015, when the snow event led to a sudden decrease in water temperature, increase in wind speed, and large surface water turbulence as indicated by water level fluctuations (Fig. 3a–d). 222Rn in the porewater is 2–3 orders of magnitude larger than 222Rn in the lake water, suggesting that 222Rn is an ideal tracer to estimate the LGD (Table S1). 222Rn concentrations in surface water range from 22.2 to 209 Bq m−3, with an average of 92.5 Bq m−3 (n=12), which is in the range of 222Rn continuous monitoring results, suggesting reliable 222Rn measurements (Table S2).
3.2 Geochemical results
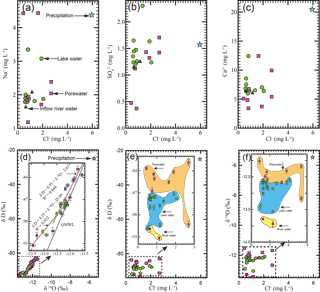
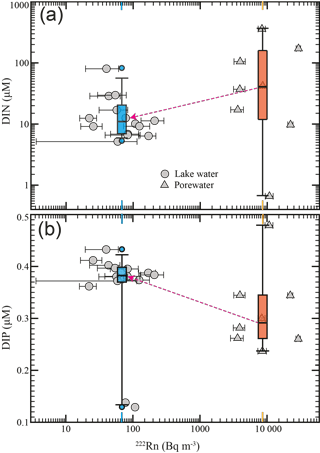
The results of major ions, nutrients, and stable isotopes in different water endmembers are shown in Figs. 4 and 5. Cl− ranges from 0.6 to 2.1 mg L−1 in the surface water (including riverine inflow water, lake water, and downstream water) and 0.4 to 2.7 mg L−1 in porewater, and has a much higher concentration of 5.9 mg L−1 in rainfall water. Na+ ranges from 1.6 to 3.4 mg L−1 in the surface water and 1.2 to 4.4 mg L−1 in porewater and has a concentration of 4.4 mg L−1 in rainfall water. ranges from 1.2 to 2.3 mg L−1 in the surface water and 0.4 to 1.7 mg L−1 in porewater, and has a significant low concentration of 0.01 mg L−1 in rainfall water. Ca2+ ranges from 3.0 to 12.4 mg L−1 in lake water and 3.4 to 12.5 mg L−1 in porewater, and has a significantly high concentration of 20.5 mg L−1 in rainfall water. Other concentrations of major ions are listed in Table S2. As shown in Fig. 4d and Table S2, δ18O in the lake water ranges from −13.06 ‰ to −12.11 ‰, with an average of −12.41 ‰ (n=7), and δ2H ranges from −91.83 ‰ to −87.47 ‰, with an average of −89.0 ‰ (n=7). δ18O in the riverine inflow water ranges from −13.44 ‰ to −13.29 ‰, with an average of −13.37 ‰ (n=2), and δ2H ranges from −93.25 ‰ to −91.92 ‰, with an average of −92.59 ‰ (n=2). δ18O in the downstream water ranges from −12.51 ‰ to −12.18 ‰, with an average of −12.35 ‰ (n=3), and δ2H ranges from −88.96 ‰ to −87.1‰, with an average of −87.98 ‰ (n=3). δ18O in the porewater ranges from −12.66 ‰ to −11.52 ‰, with an average of −11.97 ‰ (n=8), and δ2H ranges from −91.3 ‰ to −82.87 ‰, with an average of −85.5 ‰ (n=8). DIN in the surface water (including riverine inflow water, lake water, and downstream water) ranges from 6.6 to 16.9 µM, with an average of 10.3 µM, and DIP from 0.36 to 0.41 µM, with an average of 0.38 µM. DIN for the porewater ranges from 0.7 to 358.8 µM, with an average of 92.8 µM, and DIP from 0.18 to 0.44 µM, with an average of 0.31 µM (Fig. 5).
4.1 Proglacial hydrologic processes and geochemical implications
Generally, major ion concentrations in the lake water and porewater of Ximen Co Lake are significantly lower than those in major rivers, streams, and other tectonic lakes in the QTP (Yao et al., 2015; Wang et al., 2010, 2016b), and are similar to those of snow and glaciers (Liu et al., 2011), suggesting that the lake water mainly originated from glacier and snow melting. Ion concentrations in the lake and porewater of Ximen Co Lake are much lower than those of rainfall collected in Jiuzhi. This suggests that lake water is less influenced by precipitation (Fig. 4a–c). The concentrations of major ions in the porewater are high compared to the lake water, indicating weathering effects from the aquifer grains. The ratios of Ca2+ ∕ Na+ in the porewater and groundwater are >1, also suggesting influences of weathering digenesis of major ions from the seasonal frozen ground at the lakeshore aquifer (Weynell et al., 2016; Yao et al., 2015; Wang et al., 2010).
The isotopic compositions of the lake water and porewater are significantly isotopically depleted, with values close to the compositions of glaciers and surface snow in the QTP, suggesting the lake is dominantly recharged from snow and glacier melting (Cui et al., 2014; Wang et al., 2016a; Zongxing et al., 2015). The relation of δ18O versus δ2H for the lake water is , with a slope much lower than that of the global meteoric water line (GMWL) (Fig. 4d), suggesting the effects of lake surface evaporation. The relation of δ18O versus δ2H for the porewater is , overall on the GWML (Fig. 4d). Deuterium excess is defined as (Dansgaard, 1964). The value of ΔD is dependent on airmass origins, altitude effect, and the kinetic effects during evaporation (Hren et al., 2009). Global meteoric water has a ΔD of +10 ‰. In the QTP, glacier/snowpack melting water usually has a large positive ΔD, while the precipitations derived from the warm and humid summer monsoon have a lower ΔD (Ren et al., 2013, 2017). In this study, ΔD of surface water, lake, and porewater ranges from +8.5 to +11.8 ‰, close to the glacier melting water but much smaller than that of the local precipitation of +18.8 ‰. This indicates the stream and lake waters mainly originated from glacial/snowpack melting rather than precipitation (Gat, 1996; Wang et al., 2016a; Lerman et al., 1995). The slopes of δ2H versus δ18O in lake water and porewater are 4.25 and 6.93, both of which are lower than that of the GMWL due to surface evaporation. Lake water is more intensively influenced by evaporation compared to porewater. The plots of δ18O versus Cl−, and δ2H versus Cl−, are well clustered for porewater endmember (orange area), lake water endmember (blue area), riverine inflow water endmember (yellow area), and precipitation water (Fig. 4e and f), suggesting stable δ18O and δ2H isotopes and Cl− can serve as tracers to quantify the hydrologic partitioning of the lake by setting three-endmember models.
The concentrations of DIN and DIP are all within the ranges of other glacial melting water and proglacial lake water (Hawkings et al., 2016; Hodson, 2005, 2007; Hudson et al., 2000; Tockner et al., 2002). Briefly, rainfall and upstream lake water such as YN-4 have the highest DIN concentrations, indicating the glacier melting and precipitation could be important DIN sources in proglacial areas (Dubnick et al., 2017; Anderson et al., 2017). DIN in porewater is overall higher compared to the lake water, suggesting the porewater to be an effective DIN source, and DIP concentration is higher in the lake water compared to porewater, suggesting the porewater is a DIP sink (Fig. 5). The N:P ratios in the lake water and porewater are averaged to be 27.1 and 320.5, respectively, both much larger than the Redfield ratio () in water and organisms in most aquatic systems, and within the range of other proglacial lakes (Anderson et al., 2017). This also suggests that the lake water and porewater are under phosphate-limited conditions. The N:P ratio in the rainfall water is 30.4, similar to the lake water. The average N:P ratio of porewater is much higher than that of lake water, indicating DIN enrichment in the lakeshore aquifers (Fig. 5). In pristine groundwater, is the predominant form of dissolved nitrogen and is highly mobile within the oxic aquifers, leading to much higher DIN concentrations in the porewater; DIP has a high affinity with the aquifer grains, resulting in much lower DIP concentrations in the porewater (Lewandowski et al., 2015; Rosenberry et al., 2015; Slomp and Van Cappellen, 2004). Thus, analogously to surface runoff from glacier/snowpack melting, LGD can also be regarded as an important DIN source for the proglacial lakes. Because of very high DIN and N:P ratios in the porewater, a relatively small portion of LGD delivers considerable nutrients into the glacial lake, shifting the aquatic N:P ratios and affecting the proglacial aquatic ecosystem (Anderson et al., 2017).
4.2 Estimation of LGD
Figure 6a shows all the sinks and sources of radon with the epilimnion of the lake. Within the 222Rn transient mass balance model, the dominant 222Rn loss is atmospheric degassing/evasion. Generally, the 222Rn degassing rate is the function of the radon-222 concentration gradient at the water–air interface and the parameter of gas piston velocity k, which is finally the function of wind speed and water temperature (Dimova and Burnett, 2011; Gilfedder et al., 2015). To evaluate the 222Rn evasion rate, this study employs the widely used method proposed by MacIntyre et al. (1995) which is also detailed in the Supplement. Based on the field data of 222Rn concentration in the lake water, wind speed, and temperature log, the radon degassing rate is calculated in a range of 0.8 to 265.2 Bq m2 d−1, with an average of 42.0 Bq m2 d−1.
In addition to the atmospheric loss and sedimentary diffusion inputs, 222Rn is also sinked via radioactive decay, and sourced from decay of the parent isotope of 226Ra. The decay loss of 222Rn fluctuates in phase with the distribution of 222Rn concentration monitored by RAD 7 AQUA. The equations to estimate benthic fluxes are shown in the Supplement. The decay loss is calculated to be 26.4 to 223.4 Bq m−2 d−1, with an average of 118.0±22.7 Bq m−2 d−1. 226Ra concentration is 0.01 Bq m−3 for the lake water. Under secular equilibrium, the 226Ra decay input can be calculated by multiplying 226Ra concentration in the lake water by λ222 (Corbett et al., 1997; Kluge et al., 2007; Luo et al., 2016). 226Ra decay input is calculated to be 0.83 Bq m−2 d−1, which is significantly low compared to other 222Rn sources to the epilimnion.
With the obtained sinks and sources of 222Rn in the lake, and the constants given in Table 1, LGD rate can be obtained by dividing the groundwater-derived 222Rn by its concentration in the groundwater endmember. The obtained LGD rate ranges from −23.7 to 90.0 mm d−1, with an average of 10.3±8.2 mm d−1 (Fig. 7). The LGD rate range is relatively smaller than the daily lake water level variations (≈50 mm), indicating that the lake water level variation could be a combined effect of surface runoff and LGD (Hood et al., 2006). The negative values of LGD rate reflect the return groundwater flow due to infiltration into the porewater. Normally, the dominant values are positive, indicating LGD rate is significant compared to water infiltration into the lakeshore aquifer. The temporal variation of LGD rate could be attributed to the fluctuations of the hydraulic gradient in the proglacial areas (Hood et al., 2006; Levy et al., 2015). As indicated by ΔD (mostly >10) of surface water, the lake and the upstream water are considered to be mainly recharged from glacial/snowpack melting rather than other precipitations.
To assess the magnitude of uncertainty of the 222Rn transient model, the sensitivity of estimated LGD to changes in other variables is examined. A sensitivity coefficient f is proposed to evaluate this uncertainty according to Langston et al. (2013):
where ΔFLGD is the amount of change in FLGD from the original value. Δyi is the amount of change in the other variable of yi from the original value. Thus, higher f indicates a large uncertainty of the final LGD estimate. The uncertainty mainly stems from 222Rn measurements in different water endmembers, the atmospheric loss, and the water level record. The uncertainties of 222Rn measurement are about 10 % and 15 %–20 % in groundwater and lake water endmembers, respectively. The uncertainty of atmospheric loss is derived from uncertainty of 222Rn in lake water (with an uncertainty of 15 %–20 %), temperature (with an uncertainty of ≈5 %), and wind speed (with an uncertainty of ≈5 %). Thus, the final LGD estimate has an integrated uncertainty of 35 %–40 %.
4.3 Hydrologic partitioning
Compared to the groundwater labelled radionuclide of 222Rn, stable 18O ∕ 2H isotopes are advantageous in the investigation of evaporation processes due to their fractionations from water to vapour and have been widely used to investigate the hydrologic cycle of lakes in various environments (Stets et al., 2010; Gat, 1995; Gonfiantini, 1986; Gibson et al., 1993). With the field data of stable isotopic composition and Cl− concentrations in different water endmembers, groundwater input, surface water input, lake water outflow and infiltration, and evaporation can be partitioned by coupling the stable isotopic mass balance model with the Cl− mass balance model (Fig. 6b).
The model, consisting of the budgets of stable isotopes and Cl−, and water masses for the epilimnion, is used to quantify riverine inflow, lake water outflow and infiltration, and evaporation (LaBaugh et al., 1995, 1997; Gibson et al., 2016). The model is valid under the following assumptions: (1) constant density of water; (2) no long-term storage change in the reservoir; (3) well mixed for the epilimnion (Gibson, 2002; Gibson et al., 2016; Gibson and Edwards, 2002; LaBaugh et al., 1997). The above assumptions are reasonably tenable during the short monitoring period. The model can be fully expressed as
where Fin (mm d−1) is the surface water inflow to the lake; Fgw (mm d−1) is the LGD rate. Fp (mm d−1) is the mean daily rainfall rate during the sampling period. FE (mm d−1) is the lake evaporation. Fout (mm d−1) is the lake water outflow via runoff and infiltration into the lakeshore aquifer. δin, δgw, δE, and δp are the isotopic compositions of surface water inflow, LGD, and evaporative flux, respectively. The values of δin, δgw, and δp are obtained from field data and the composition of δE are calculated as shown in the Supplement. [Cl−]in, [Cl−]gw, [Cl−]L, and [Cl−]p are the chloride concentrations in the inflow water, porewater, lake water, and precipitation, respectively.
The components of the mass balance model can be obtained from the field data of isotopic composition and Cl− concentrations in different water endmembers. The average 18O composition −13.37 ‰ of riverine inflow water is taken as the value of the input parameter δin. δ18O and δ2H in the groundwater endmember and lake water endmember are calculated to be −12.41 ‰ and −87.18 ‰, respectively. δ18O and δ2H in the rainfall are measured to be −5.47 ‰ and −24.98 ‰, respectively. With the measured values of δL, h, and δin, and the estimated ε and δa, the isotopic composition of δE is calculated to be −35.11 ‰, which is in line with the results of alpine and arctic lakes elsewhere (Gibson, 2002; Gibson et al., 2016; Gibson and Edwards, 2002). The values of [Cl−]in, [Cl−]gw, and [Cl−]L are calculated to be 0.91 mg L−1, 1.48 mg L−1, and 1.02 mg L−1, respectively. All the parameters used in the model are shown in Table 2.
According to Eqs. (4)–(6), the uncertainties of calculations of Fin, Fout, and E are mainly derived from the uncertainty of FLGD and the compositions of Cl−, ΔD, and δ18O in different water endmembers as suggested in previous studies (Genereux, 1998; Klaus and McDonnell, 2013). The compositions of Cl−, ΔD, and δ18O in surface water–groundwater endmembers have an uncertainty of 5 %. The uncertainty of δE is reasonably assumed to be ≈20 %. Thus, considering the uncertainty propagation of all the above parameters, the uncertainties of Fin, Fout, and E would be scaled up to 70 %–80 % of the final estimates.
4.4 The hydrologic partitioning of the glacial lake
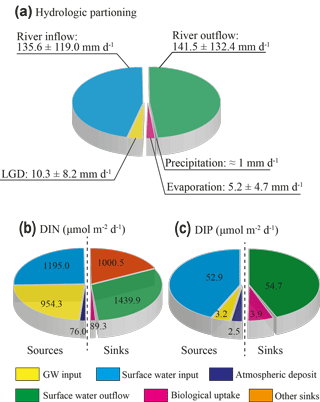
Based on the three-endmember model of 18O and Cl−, the riverine inflow rate was calculated to be 135.6±119.0 mm d−1, and the lake outflow rate is estimated to be 141.5±132.4 mm d−1; the evaporation rate is calculated to be 5.2±4.7 mm d−1. The summary of the hydrologic partitioning of the lake is shown in Fig. 8a. Generally, the proglacial lake is mostly recharged by the riverine inflow from the snowpack or the glacier melting. The groundwater discharge contributes about only 7.0 % of the total water input to the lake, indicating groundwater input does not dominate water input to the proglacial lake. The recent review of LGD rate by Rosenberry et al. (2015) suggests that the median of LGD rate in the literatures is 7.4 mm d−1 (0.05 to 133 mm d−1), which is about 2∕3 of the LGD rate in this study. This difference may be due to the hydrogeological setting of the lakeshore aquifer. This aquifer is formed by grey loam, clayey soil, and sand (Lehmkuhl, 1998; Schlutz and Lehmkuhl, 2009), which has a relatively high permeability.
Previous studies have indicated that groundwater forms a key component of proglacial hydrology (Levy et al., 2015). However, there have been limited quantitative studies of groundwater contribution to the hydrologic budget of proglacial areas. This study further summarizes the groundwater discharge studies over the glacial forefield areas. Based on long-term hydrological and climatological parameter monitoring on Nam Co Lake in the QTP, Zhou et al. (2013) estimated the LGD to be 5–8 mm d−1, which is comparable to the surface runoff input and LGD of this study. Brown et al. (2006) investigated the headwater streams in the proglacial areas of Taillon Glacier in France and found that groundwater contributes 6 %–10 % of the stream water immediately downwards of the glacier. Using the water mass balance model, Hood et al. (2006) show that groundwater inflow is substantial in the hydrologic partitioning of the proglacial Lake O'Hara in front of Opabin Glacier in Canada and comprised 30 %–74 % of the total inflow. Roy and Hayashi (2008) studied the proglacial lakes of Hungabee Lake and Opabin Lake at the glacier forefield of Opabin Glacier and found that the groundwater component is a predominant water source of the lakes and consisted of 35 %–39 % of the total water input of the lakes. Langston et al. (2013) further investigated a tarn immediately in front of Opabin Glacier and indicated the tarn is predominantly controlled by groundwater inflow/outflow, which consisted of 50 %–100 % of the total tarn volume. Magnusson et al. (2014) studied the streams in the glacier forefield of the Damma Glacier, Switzerland, and revealed that groundwater contributed only 1 %–8 % of the total surface runoff. Groundwater contribution in this study is similar to those obtained from the mountainous proglacial areas in Europe, but much lower than those obtained in the proglacial areas of polar regions. It is concluded that proglacial lakes/streams in front of mountainous glaciers are mainly recharged by surface runoff from glacier/snowpack melting. This might be due to well-developed stream networks and limited deep groundwater flow (Einarsdottir et al., 2017; Brown et al., 2006; Magnusson et al., 2014). However, proglacial tarns and lakes in the polar areas are predominantly controlled by groundwater discharge, due to less connectivity of surface runoff and high shallow and deep groundwater connectivity (Langston et al., 2013; Hood et al., 2006; Roy and Hayashi, 2008).
The evaporation constitutes a relatively small ratio (≈3.5 %) of total water losses. The annual evaporation rate was recorded to be 1429.8 mm (equivalent to 3.92 mm d−1) in 2015 by the Jiuzhi weather station, lower than the obtained evaporation in this study. This may be due to much higher evaporation in August during the monitoring period. The estimation of evaporation in this study generally represents the upper limit of the lake, as the sampling campaign was conducted during the summer time when the highest evaporation might occur. The lake surface evaporation derived from the pan evaporation in the QTP ranges from ∼700 mm yr−1 in the eastern QTP to over 1400 mm yr−1 in the interior lakes of the QTP (Zhang et al., 2007; Ma et al., 2015; Yang et al., 2014). The evaporation of this study is rather in line with the previous evaporation observation in the eastern QTP, stressing the tenability of evaporation in this study. The runoff input is the predominant recharge component (>90 %) compared to other components, with an area normalized value comparable to previous studies of runoff input in other glacial melting dominant lakes in the QTP (Zhou et al., 2013; Zhang et al., 2011; Biskop et al., 2016). The runoff input and the lake evaporation of the study area, however, are subject to high daily, seasonal, and inter-annual variability as indicated by previous studies in the QTP (Zhou et al., 2013; Lei et al., 2017; Ma et al., 2015; Lazhu et al., 2016). Therefore, further investigations of long-term and high-resolution climatological and isotopic data are required to provide precise constraints on hydrologic partitioning of the lakes in the QTP.
4.5 LGD-derived nutrient loadings, nutrient budget, and ecological implications
Compared to extensive studies of SGD-derived nutrient loadings in the past decade (Luo and Jiao, 2016; Slomp and Van Cappellen, 2004), studies of LGD-derived nutrient loadings have received limited attention, even given the fact that groundwater in lakeshore aquifers is usually concentrated in nutrients (Lewandowski et al., 2015; Rosenberry et al., 2015). Even fewer studies focus on chemical budgets in the proglacial lakes which are often difficult to access for sampling. Groundwater-borne DIN and DIP across the sediment–water interface in this study are determined with an equation coupling the advective, or LGD-derived, and diffusive solute transport (Lerman et al., 1995; Hagerthey and Kerfoot, 1998):
where is the diffusion input and vgwCj is the LGD-derived fluxes; Fj (µM m−2 d−1) is the mol flux of nutrient species j (representing DIN or DIP). n is the sediment porosity. is the molecular diffusion coefficient of nutrient species j, which is given to be m2 d−1 for DIP (Quigley and Robbins, 1986) and m2 d−1 for DIN (Li and Gregory, 1974), respectively. Cj (µM) is the concentration of nutrient species j. x (m) is the sampling depth. vgw is LGD rate estimated by the 222Rn mass balance model and has a value of 10.3±8.2 mm d−1. is the concentration gradient of nutrient species j across the water–sediment interface.
Substituting the constants and the field data of DIN and DIP into Eq. (6), LGD-derived nutrient loadings are calculated to be 954.3 and 3.2 µmol m−2 d−1 for DIN and DIP, respectively. Riverine inflow brings 1195.0 µmol m−2 d−1 DIN and 52.9 µmol m−2 d−1 DIP into the lake. Lake water outflow-derived nutrient loss is estimated to be 1439.9 and 54.7 µmol m−2 d−1 for DIN and DIP, respectively. Nutrients in the lake can also be sourced from atmospheric deposit (mostly in the form of precipitation). With the nutrient concentrations in the rainwater during the monitoring period, the wet deposit is calculated to be 76 and 2.5 µmol m−2 d−1 for DIN and DIP, respectively. The loadings of DIN to the lakes are mainly from surface runoff and LGD, which comprised 42.9 % and 53.7 % of the total DIN loadings. Groundwater-derived DIP input, however, constitutes only 6.3 % of the total DIP inputs to the lake, indicating groundwater-borne DIP is less contributive to the nutrient budget of the lake compared to DIN. Very recent studies on polar regions have indicated that the glacier/snowpack water is the main N source to the proglacial lakes (Anderson et al., 2013; Dubnick et al., 2017). However, they do not consider the contribution of groundwater-borne N, in spite of the high groundwater connectivity in the proglacial areas (Roy and Hayashi, 2008). This study stresses that groundwater-borne DIN could be comparable to the surface runoff-derived DIN.
Based on nutrient results, the lake is considered to be an oligotrophic lake, similar to other glacier melting dominant lakes in the QTP (Mitamura et al., 2003; Liu et al., 2011). Phytoplankton are good dissolved organic phosphate (DOP) recyclers and will overcome inorganic P limitation though DOP cycling in most template lakes (Hudson et al., 2000). However, this may be not applicable for the glacial melting water and the periglacial/proglacial lake water. Previous studies show that phosphate nutrients are dominated by DIP and particulate phosphate, and the DOP contributes less than 10 % of the dissolved phosphate (Cole et al., 1998; Hawkings et al., 2016; Hodson, 2007). Thus, DOP recycling is not likely to lower the N:P ratio under these conditions. Thus, the primary production (PP) is considered to be controlled by the DIP loadings. The sum of DIN and DIP inputs minus the calculated DIN and DIP outputs leads to surpluses of 785.4 and 3.9 µmol m−2 d−1 for DIN and DIP, respectively. The surpluses are expected to be consumed by the phytoplankton and converted into the PP under phosphate-limited conditions. As primary producers in the fresh lacustrine system consume the nutrient under variant N:P ratios (7.1 to 44.2, mean: 22.9) (Downing and McCauley, 1992), the biological uptake of DIN is roughly estimated to be 89.3 µM m2 d−1. Therefore, the nutrient budgets for DIN and DIP can be finally conceptualized in Fig. 8b and c.
4.6 Implications, prospects, and limitations
Mountainous proglacial lakes are readily developed in glacier forefields of the QTP and other high mountainous glacial areas such as the European Alps and Pamir in central Asia (Heckmann et al., 2016). The proglacial lakes are always trapping systems of sediment and sinks for water and chemicals originating from glacier/snowpack melting and groundwater. Analogously to cosmogenic isotopes such as 10Be serving as a tool to quantify the sediment sources, approaches integrating 222Rn and stable isotopes provide both qualitative and quantitative evaluations of groundwater contributions and hydrologic partitioning in these remote and untapped lacustrine systems. Thus, it is expected that the multiple aqueous isotopes will be considered to be effective tools to investigate the LGD and hydrologic partitioning in other proglacial lakes. This study is mainly limited by the relatively short sampling and monitoring period. As a special hydrologic regime, the lakeshore aquifers of the proglacial lakes are experiencing frozen–unfrozen transition seasonally, and the dominant recharge of glacial melting could fluctuate significantly due to air temperature variation. Therefore, future groundwater and hydrological studies can be extended to longtime sampling and monitoring of stable isotopes and 222Rn in different water endmembers to reveal the seasonal hydrological and hydrogeological dynamics and their impacts on local biogeochemical cycles and ecological systems. Special concerns would be placed on how surface–groundwater interactions and the associated biogeochemical processes respond to the seasonal frozen ground variations and glacier/snowpack melting intensity.
A 222Rn continuous monitoring is conducted at Ximen Co Lake, a proglacial lake located in the eastern QTP. A dynamic 222Rn mass balance model constrained by radium mass balance and water level fluctuation is used to quantify temporal distribution of the LGD of the lake. The obtained LGD over the monitoring time ranges from −23.7 to 80.9 mm d−1, with an average of 10.3±8.2 mm d−1. Thereafter, a three-endmember model consisting of the budgets of water, stable isotopes, and Cl− is used to depict the hydrologic partitioning of the lake. Riverine inflow, lake water outflow via surface runoff, and surface evaporation are estimated to be 135.6, 141.5, and 5.2 mm d−1, respectively. LGD-derived nutrient loading is estimated to be 785.4 and 3.2 µmol m−2 d−1 for DIN and DIP, respectively. This study also implies that LGD constitutes a relatively small portion of the proglacial hydrologic partitioning; however, it delivers nearly half of the nutrient loadings to the proglacial lake.
This study presents the first attempt to quantify LGD and the associated nutrient loadings to the proglacial lake of the QTP. To our knowledge, there is almost no study on the groundwater–lake water interaction in the high-altitude proglacial lakes in the QTP. This study demonstrates that the 222Rn-based approach can be used to investigate the groundwater dynamics in the high-altitude proglacial lakes. The method is instructional to similar studies in other proglacial lakes in the QTP and elsewhere. For a comprehensive understanding of the hydrological and biogeochemical dynamics in the QTP, interdisciplinary and multi-approach integrated studies are greatly needed. Of particular importance are the lake hydrology and groundwater–surface water interaction studies based on multiple approaches such as remote sensing products, long-term and high-resolution observation of climatological parameters, and isotopic data.
Supporting data are included as in the files of Supplement information 1 and 2. The climatological data created by the China Meteorological Administration (CMA) are purchased through its data cloud link http://www.weatherdt.com/ (CMA, 2016); any additional data may be obtained from Xin Luo (email: xinluo@hku.hk).
The supplement related to this article is available online at: https://doi.org/10.5194/hess-22-5579-2018-supplement.
JJJ and XL conceived the study. XL, XXK, XLZ and SHL conducted the fieldwork; all the authors contributed to the data interpretation and manuscript construction.
The authors declare that they have no conflict of interest.
This study was supported by grants from the National Natural Science
Foundation of China (NSFC, no. 41572208, and NSFC, 91747204), the Research
Grants Council of Hong Kong Special Administrative Region, China
(HKU17304815), and the seed fund programme granted by HKU-ZIRI. The authors
thank Buming Jiang for his kind help in the fieldwork during the campaign and
Ergang Lian for his help in stable isotope analysis. The authors thank Jessie
Lai for her help in FIA analysis in the School of Biological Sciences, HKU.
Edited
by: Bill X. Hu
Reviewed by: two anonymous referees
Åberg, J., Jansson, M., and Jonsson, A.: Importance of water temperature and thermal stratification dynamics for temporal variation of surface water CO2 in a boreal lake, J. Geophys. Res.-Biogeo., 115, 2005–2012, https://doi.org/10.1029/2009JG001085, 2010.
Andermann, C., Longuevergne, L., Bonnet, S., Crave, A., Davy, P., and Gloaguen, R.: Impact of transient groundwater storage on the discharge of Himalayan rivers, Nat. Geosci., 5, 127–132, https://doi.org/10.1038/Ngeo1356, 2012.
Anderson, L., Birks, J., Rover, J., and Guldager, N.: Controls on recent Alaskan lake changes identified from water isotopes and remote sensing, Geophys. Res. Lett., 40, 3413–3418, 2013.
Anderson, N. J., Saros, J. E., Bullard, J. E., Cahoon, S. M., McGowan, S., Bagshaw, E. A., Barry, C. D., Bindler, R., Burpee, B. T., and Carrivick, J. L.: The Arctic in the Twenty-First Century: Changing Biogeochemical Linkages across a Paraglacial Landscape of Greenland, Bioscience, 67, 118–133, 2017.
Barry, R. G.: The status of research on glaciers and global glacier recession: a review, Prog. Phys. Geog., 30, 285–306, 2006.
Batlle-Aguilar, J., Harrington, G. A., Leblanc, M., Welch, C., and Cook, P. G.: Chemistry of groundwater discharge inferred from longitudinal river sampling, Water Resour. Res., 50, 1550–1568, https://doi.org/10.1002/2013WR013591, 2014.
Belanger, T. V., Mikutel, D. F., and Churchill, P. A.: Groundwater seepage nutrient loading in a Florida Lake, Water Res., 19, 773–781, https://doi.org/10.1016/0043-1354(85)90126-5, 1985.
Biskop, S., Maussion, F., Krause, P., and Fink, M.: Differences in the water-balance components of four lakes in the southern-central Tibetan Plateau, Hydrol. Earth Syst. Sci., 20, 209–225, https://doi.org/10.5194/hess-20-209-2016, 2016.
Blume, T., Krause, S., Meinikmann, K., and Lewandowski, J.: Upscaling lacustrine groundwater discharge rates by fiber-optic distributed temperature sensing, Water Resour. Res., 49, 7929–7944, https://doi.org/10.1002/2012WR013215, 2013.
Böhner, J.: Säkulare Klimaschwankungen und rezente Klimatrends Zentral-und Hochasiens, Goltze, 101 Inst. of Geography, Göttingen, 1996.
Böhner, J.: General climatic controls and topoclimatic variations in Central and High Asia, Boreas, 35, 279–295, 2006.
Bolch, T., Kulkarni, A., Kääb, A., Huggel, C., Paul, F., Cogley, J. G., Frey, H., Kargel, J. S., Fujita, K., Scheel, M., Bajracharya, S., and Stoffel, M.: The State and Fate of Himalayan Glaciers, Science, 336, 310–314, 2012.
Brown, L. E., Hannah, D. M., Milner, A. M., Soulsby, C., Hodson, A. J., and Brewer, M. J.: Water source dynamics in a glacierized alpine river basin (TaillonGabiétous, French Pyrénées), Water Resour. Res., 42, W08404, https://doi.org/10.1029/2005WR004268, 2006.
Burnett, W. C., Peterson, R. N., Santos, I. R., and Hicks, R. W.: Use of automated radon measurements for rapid assessment of groundwater flow into Florida streams, J. Hydrol., 380, 298–304, 2010.
Callegary, J. B., Kikuchi, C. P., Koch, J. C., Lilly, M. R., and Leake, S. A.: Review: Groundwater in Alaska (USA), Hydrogeol. J., 21, 25–39, https://doi.org/10.1007/s10040-012-0940-5, 2013.
China Meteorological Administration: Climatological data, available at: http://www.weatherdt.com/, last access: 2 June 2016.
Cole, J., Nina, J., and Caraco, F.: Atmospheric exchange of carbon dioxide in a low-wind oligotrophic lake measured by the addition of SF6, Limnol. Oceanogr., 43, 647–656, 1998.
Cook, P., Lamontagne, S., Berhane, D., and Clark, J.: Quantifying groundwater discharge to Cockburn River, southeastern Australia, using dissolved gas tracers 222Rn and SF6, Water Resour. Res., 42, W10411, https://doi.org/10.1029/2006WR004921, 2006.
Cook, P. G., Favreau, G., Dighton, J. C., and Tickell, S.: Determining natural groundwater influx to a tropical river using radon, chlorofluorocarbons and ionic environmental tracers, J. Hydrol., 277, 74–88, https://doi.org/10.1016/S0022-1694(03)00087-8, 2003.
Corbett, D. R., Burnett, W. C., Cable, P. H., and Clark, S. B.: Radon tracing of groundwater input into Par Pond, Savannah River site, J. Hydrol., 203, 209–227, 1997.
Cui, X., Ren, J., Qin, X., Sun, W., Yu, G., Wang, Z., and Liu, W.: Chemical characteristics and environmental records of a snow-pit at the Glacier No. 12 in the Laohugou Valley, Qilian Mountains, J. Earth Sci., 25, 379–385, 2014.
Dansgaard, W.: Stable isotopes in precipitation, Tellus A, 16, 436–468, https://doi.org/10.3402/tellusa.v16i4.8993, 1964.
Dimova, N., Paytan, A., Kessler, J. D., Sparrow, K., Garcia-Tigreros Kodovska, F., Lecher, A. L., Murray, J., and Tulaczyk, S. M.: The current magnitude and mechanisms of groundwater discharge in the Arctic: a case study from Alaska, Environ. Sci. Technol., 49, 12036–12043, 2015.
Dimova, N. T. and Burnett, W. C.: Evaluation of groundwater discharge into small lakes based on the temporal distribution of radon-222, Limnol. Oceanogr., 56, 486–494, 2011.
Dimova, N. T., Burnett, W. C., Chanton, J. P., and Corbett, J. E.: Application of radon-222 to investigate groundwater discharge into small shallow lakes, J. Hydrol., 486, 112–122, https://doi.org/10.1016/j.jhydrol.2013.01.043, 2013.
Downing, J. A. and McCauley, E.: The nitrogen: phosphorus relationship in lakes, Limnol. Oceanogr., 37, 936–945, 1992.
Dubnick, A., Wadham, J., Tranter, M., Sharp, M., Orwin, J., Barker, J., Bagshaw, E., and Fitzsimons, S.: Trickle or treat: The dynamics of nutrient export from polar glaciers, Hydrol. Process., 31, 1776–1789, https://doi.org/10.1002/hyp.11149, 2017.
Einarsdottir, K., Wallin, M. B., and Sobek, S.: High terrestrial carbon load via groundwater to a boreal lake dominated by surface water inflow, J. Geophys. Res.-Biogeo., 122, 15–29, https://doi.org/10.1002/2016JG003495, 2017.
Farinotti, D., Longuevergne, L., Moholdt, G., Duethmann, D., Molg, T., Bolch, T., Vorogushyn, S., and Guntner, A.: Substantial glacier mass loss in the Tien Shan over the past 50 years, Nat. Gesoci., 8, 716–722, https://doi.org/10.1038/ngeo2513, 2015.
Gat, J.: Stable isotopes of fresh and saline lakes, in: Physics and chemistry of lakes, Springer, Berlin, Heidelberg, 139–165, 1995.
Gat, J.: Oxygen and hydrogen isotopes in the hydrologic cycle, Annu. Rev. Earth Pl. Sc., 24, 225–262, 1996.
Genereux, D.: Quantifying uncertainty in tracerbased hydrograph separations, Water Resour. Res., 34, 915–919, 1998.
Gibson, J., Edwards, T., Bursey, G., and Prowse, T.: Estimating evaporation using stable isotopes: quantitative results and sensitivity analysis for, Nord. Hydrol., 24, 79–94, 1993.
Gibson, J. J.: Short-term evaporation and water budget comparisons in shallow Arctic lakes using non-steady isotope mass balance, J. Hydrol., 264, 242–261, 2002.
Gibson, J. J. and Edwards, T. W. D.: Regional water balance trends and evaporation-transpiration partitioning from a stable isotope survey of lakes in northern Canada, Global Biogeochem. Cy., 16, 10-1–10-14, https://doi.org/10.1029/2001GB001839, 2002.
Gibson, J. J., Birks, S. J., and Yi, Y.: Stable isotope mass balance of lakes: a contemporary perspective, Quaternary Sci. Rev., 131, 316–328, https://doi.org/10.1016/j.quascirev.2015.04.013, 2016.
Gilfedder, B., Frei, S., Hofmann, H., and Cartwright, I.: Groundwater discharge to wetlands driven by storm and flood events: Quantification using continuous Radon-222 and electrical conductivity measurements and dynamic mass-balance modelling, Geochim. Cosmochim. Ac., 165, 161–177, 2015.
Gonfiantini, R.: Environmental isotopes in lake studies, Handbook of environmental isotope geochemistry, Elsevier Scientific Publishing Company, Cornell University, 2, 113–168, 1986.
Good, S. P., Noone, D., and Bowen, G.: Hydrologic connectivity constrains partitioning of global terrestrial water fluxes, Science, 349, 175–177, https://doi.org/10.1126/science.aaa5931, 2015.
Hagerthey, S. E. and Kerfoot, W. C.: Groundwater flow influences the biomass and nutrient ratios of epibenthic algae in a north temperate seepage lake, Limnol. Oceanogr., 43, 1227–1242, 1998.
Harris, C., Arenson, L. U., Christiansen, H. H., Etzelmüller, B., Frauenfelder, R., Gruber, S., Haeberli, W., Hauck, C., Hölzle, M., and Humlum, O.: Permafrost and climate in Europe: Monitoring and modelling thermal, geomorphological and geotechnical responses, Earth-Sci. Rev., 92, 117–171, 2009.
Hasler, C. T., Midway, S. R., Jeffrey, J. D., Tix, J. A., Sullivan, C., and Suski, C. D.: Exposure to elevated pCO2 alters post-treatment diel movement patterns of largemouth bass over short time scales, Freshwater Biol., 61, 1590–1600, https://doi.org/10.1111/fwb.12805, 2016.
Hawkings, J., Wadham, J., Tranter, M., Telling, J., Bagshaw, E., Beaton, A., Simmons, S. L., Chandler, D., Tedstone, A., and Nienow, P.: The Greenland Ice Sheet as a hot spot of phosphorus weathering and export in the Arctic, Global Biogeochem. Cy., 30, 191–210, 2016.
Heckmann, T., McColl, S., and Morche, D.: Retreating ice: research in proglacial areas matters, Earth Surf. Proc. Land., 41, 271–276, https://doi.org/10.1002/esp.3858, 2016.
Hodson, A.: Phosphorus in glacial meltwaters, Glacier Science and Environmental Change, John Wiley & Sons, New York City, 81–82, 2007.
Hodson, A., Mumford, P., Kohler, J., and Wynn, P. M.: The High Arctic glacial ecosystem: new insights from nutrient budgets, Biogeochemistry, 72, 233–256, 2005.
Hood, J. L., Roy, J. W., and Hayashi, M.: Importance of groundwater in the water balance of an alpine headwater lake, Geophys. Res. Lett., 33, L13405, https://doi.org/10.1029/2006GL026611, 2006.
Hren, M. T., Bookhagen, B., Blisniuk, P. M., Booth, A. L., and Chamberlain, C. P.: δ18O and δD of streamwaters across the Himalaya and Tibetan Plateau: Implications for moisture sources and paleoelevation reconstructions, Earth Planet. Sc. Lett., 288, 20–32, 2009.
Hudson, J. J., Taylor, W. D., and Schindler, D. W.: Phosphate concentrations in lakes, Nature, 406, 54–56, 2000.
Johannes, R. E.: The Ecological Significance of the Submarine Discharge of Groundwater, Mar. Ecol. Prog. Ser., 3, 365–373, 1980.
Kim, G., Burnett, W. C., Dulaiova, H., Swarzenski, P. W., and Moore, W. S.: Measurement of Ra-224 and Ra-226 activities in natural waters using a radon-in-air monitor, Environ. Sci. Technol., 35, 4680–4683, 2001.
Klaus, J. and McDonnell, J.: Hydrograph separation using stable isotopes: Review and evaluation, J. Hydrol., 505, 47–64, 2013.
Kluge, T., Ilmberger, J., von Rohden, C., and Aeschbach-Hertig, W.: Tracing and quantifying groundwater inflow into lakes using a simple method for radon-222 analysis, Hydrol. Earth Syst. Sci., 11, 1621–1631, https://doi.org/10.5194/hess-11-1621-2007, 2007.
Kluge, T., von Rohden, C., Sonntag, P., Lorenz, S., Wieser, M., Aeschbach-Hertig, W., and Ilmberger, J.: Localising and quantifying groundwater inflow into lakes using high-precision 222Rn profiles, J. Hydrol., 450, 70–81, 2012.
Kraemer, T. F.: Radium isotopes in Cayuga Lake, New York: Indicators of inflow and mixing processes, Limnol. Oceanogr., 50, 158–168, 2005.
LaBaugh, J. W., Rosenberry, D. O., and Winter, T. C.: Groundwater contribution to the water and chemical budgets of Williams Lake, Minnesota, 1980–1991, Can. J. Fish. Aquat. Sci., 52, 754–767, 1995.
LaBaugh, J. W., Winter, T. C., Rosenberry, D. O., Schuster, P. F., Reddy, M. M., and Aiken, G. R.: Hydrological and chemical estimates of the water balance of a closedbasin lake in north central Minnesota, Water Resour. Res., 33, 2799–2812, 1997.
Langston, G., Hayashi, M., and Roy, J. W.: Quantifying groundwater-surface water interactions in a proglacial moraine using heat and solute tracers, Water Resour. Res., 49, 5411–5426, https://doi.org/10.1002/wrcr.20372, 2013.
Lazar, B., Weinstein, Y., Paytan, A., Magal, E., Bruce, D., and Kolodny, Y.: Ra and Th adsorption coefficients in lakes – Lake Kinneret (Sea of Galilee) “natural experiment”, Geochim. Cosmochim. Ac., 72, 3446–3459, 2008.
Lazhu, Yang, K., Wang, J., Lei, Y., Chen, Y., Zhu, L., Ding, B., and Qin, J.: Quantifying evaporation and its decadal change for Lake Nam Co, central Tibetan Plateau, J. Geophys. Res.-Atmos., 121, 7578–7591, 2016.
Lecher, A. L., Kessler, J., Sparrow, K., Garcia-Tigreros Kodovska, F., Dimova, N., Murray, J., Tulaczyk, S., and Paytan, A.: Methane transport through submarine groundwater discharge to the North Pacific and Arctic Ocean at two Alaskan sites, Limnol. Oceanogr., 61, S344–355, 2015.
Lee, C. M., Jiao, J. J., Luo, X., and Moore, W. S.: Estimation of submarine groundwater discharge and associated nutrient fluxes in Tolo Harbour, Hong Kong, Sci. Total Environ., 433, 427–433, https://doi.org/10.1016/j.scitotenv.2012.06.073, 2012.
Lee, D. R.: A device for measuring seepage flux in lakes and estuaries, Limnol. Oceanogr., 22, 140–147, 1977.
Lee, D. R., Cherry, J. A., and Pickens, J. F.: Groundwater transport of a salt tracer through a sandy lakebed, Limnol. Oceanogr., 25, 45–61, 1980.
Lehmkuhl, F.: Extent and spatial distribution of Pleistocene glaciations in eastern Tibet, Quatern. Int., 45–46, 123–134, https://doi.org/10.1016/S1040-6182(97)00010-4, 1998.
Lei, Y., Yao, T., Yang, K., Sheng, Y., Kleinherenbrink, M., Yi, S., Bird, B. W., Zhang, X., Zhu, L., and Zhang, G.: Lake seasonality across the Tibetan Plateau and their varying relationship with regional mass changes and local hydrology, Geophys. Res. Lett., 44, 892–900, 2017.
Lemieux, J. M., Sudicky, E. A., Peltier, W. R., and Tarasov, L.: Dynamics of groundwater recharge and seepage over the Canadian landscape during the Wisconsinian glaciation, J. Geophys. Res.-Earth, 113, F01011, https://doi.org/10.1029/2007JF000838, 2008a.
Lemieux, J. M., Sudicky, E. A., Peltier, W. R., and Tarasov, L.: Simulating the impact of glaciations on continental groundwater flow systems: 1. Relevant processes and model formulation, J. Geophys. Res.-Earth, 113, F03017, https://doi.org/10.1029/2007JF000928, 2008b.
Lemieux, J. M., Sudicky, E. A., Peltier, W. R., and Tarasov, L.: Simulating the impact of glaciations on continental groundwater flow systems: 2. Model application to the Wisconsinian glaciation over the Canadian landscape, J. Geophys. Res.-Earth, 113, F03018, https://doi.org/10.1029/2007JF000929, 2008c.
Lerman, A., Imboden, D., and Gat, J.: Physics and chemistry of lakes, New York, Springer-Verlag, Berlin, 1995.
Levy, A., Robinson, Z., Krause, S., Waller, R., and Weatherill, J.: Longterm variability of proglacial groundwaterfed hydrological systems in an area of glacier retreat, Skeiðarársandur, Iceland, Earth Surf. Proc. Land., 40, 981–994, https://doi.org/10.1002/esp.3696, 2015.
Lewandowski, J., Meinikmann, K., Ruhtz, T., Pöschke, F., and Kirillin, G.: Localization of lacustrine groundwater discharge (LGD) by airborne measurement of thermal infrared radiation, Remote Sens. Environ., 138, 119–125, https://doi.org/10.1016/j.rse.2013.07.005, 2013.
Lewandowski, J., Meinikmann, K., Nützmann, G., and Rosenberry, D. O.: Groundwater – the disregarded component in lake water and nutrient budgets. Part 2: effects of groundwater on nutrients, Hydrol. Process., 29, 2922–2955, https://doi.org/10.1002/hyp.10384, 2015.
Li, Y. H. and Gregory, S.: Diffusion of Ions in Sea-Water and in Deep-Sea Sediments, Geochim. Cosmochim. Ac., 38, 703–714, 1974.
Liu, C., Liu, J., Wang, X. S., and Zheng, C.: Analysis of groundwater-lake interaction by distributed temperature sensing in Badain Jaran Desert, Northwest China, Hydrol. Process., 30, 1330–1341, 2015.
Liu, Y., Yao, T., Jiao, N., Tian, L., Hu, A., Yu, W., and Li, S.: Microbial diversity in the snow, a moraine lake and a stream in Himalayan glacier, Extremophiles, 15, 411–421, 2011.
Luo, X. and Jiao, J. J.: Submarine groundwater discharge and nutrient loadings in Tolo Harbor, Hong Kong using multiple geotracer-based models, and their implications of red tide outbreaks, Water Res., 102, 11–31, https://doi.org/10.1016/j.watres.2016.06.017, 2016.
Luo, X., Jiao, J. J., Moore, W., and Lee, C. M.: Submarine groundwater discharge estimation in an urbanized embayment in Hong Kong via short-lived radium isotopes and its implication of nutrient loadings and primary production, Mar. Pollut. Bull., 82, 144–154, 2014.
Luo, X., Jiao, J. J., Wang, X.-S., and Liu, K.: Temporal 222Rn distributions to reveal groundwater discharge into desert lakes: implication of water balance in the Badain Jaran Desert, China, J. Hydrol., 534, 87–103, 2016.
Luo, X., Jiao, J. J., Wang, X.-s., Liu, K., Lian, E., and Yang, S.: Groundwater discharge and hydrologic partition of the lakes in desert environment: Insights from stable 18O ∕ 2H and radium isotopes, J. Hydrol., 546, 189–203, 2017.
Luo, X., Jiao, J. J., Liu, Y., Zhang, X., Liang, W., and Tang, D.: Evaluation of Water Residence Time, Submarine Groundwater Discharge, and Maximum New Production Supported by Groundwater Borne Nutrients in a Coastal Upwelling Shelf System, J. Geophys. Res.-Oceans, 123, 631–655, 2018.
Ma, N., Zhang, Y., Szilagyi, J., Guo, Y., Zhai, J., and Gao, H.: Evaluating the complementary relationship of evapotranspiration in the alpine steppe of the Tibetan Plateau, Water Resour. Res., 51, 1069–1083, https://doi.org/10.1002/2014WR015493, 2015.
MacIntyre, S., Wannikhof, R., Chanton, J. P., Matson, P. A., and Hariss, R. C.: Biogenic Trace Gases: Measuring Emissions from Soil and Water, John Wiley & Sons, New York City, 52 pp., 1995.
Magnusson, J., Kobierska, F., Huxol, S., Hayashi, M., Jonas, T., and Kirchner, J. W.: Melt water driven stream and groundwater stage fluctuations on a glacier forefield (Dammagletscher, Switzerland), Hydrol. Process., 28, 823–836, 2014.
Mitamura, O., Seike, Y., Kondo, K., Goto, N., Anbutsu, K., Akatsuka, T., Kihira, M., Tsering, T. Q., and Nishimura, M.: First investigation of ultraoligotrophic alpine Lake Puma Yumco in the pre-Himalayas, China, Limnology, 4, 167–175, 2003.
Moore, W. S.: Sampling radium-228 in the deep ocean, Deep-Sea Res., 23, 647–651, 1976.
Nakayama, T. and Watanabe, M.: Missing role of groundwater in water and nutrient cycles in the shallow eutrophic Lake Kasumigaura, Japan, Hydrol. Process., 22, 1150–1172, 2008.
Paytan, A., Lecher, A. L., Dimova, N., Sparrow, K. J., Kodovska, F. G.-T., Murray, J., Tulaczyk, S., and Kessler, J. D.: Methane transport from the active layer to lakes in the Arctic using Toolik Lake, Alaska, as a case study, P. Natl. Acad. Sci. USA, 112, 3636–3640, 2015.
Qiu, J.: China: the third pole, Nature News, 454, 393–396, 2008.
Quigley, M. A. and Robbins, J. A.: Phosphorus release processes in nearshore southern Lake Michigan, Can. J. Fish. Aquat. Sci., 43, 1201–1207, 1986.
Ren, W., Yao, T., Yang, X., and Joswiak, D. R.: Implications of variations in δ18O and δD in precipitation at Madoi in the eastern Tibetan Plateau, Quatern. Int., 313–314, 56–61, https://doi.org/10.1016/j.quaint.2013.05.026, 2013.
Ren, W., Yao, T., Xie, S., and He, Y.: Controls on the stable isotopes in precipitation and surface waters across the southeastern Tibetan Plateau, J. Hydrol., 545, 276–287, https://doi.org/10.1016/j.jhydrol.2016.12.034, 2017.
Rosenberry, D. O., Lewandowski, J., Meinikmann, K., and Nützmann, G.: Groundwaterthe disregarded component in lake water and nutrient budgets. Part 1: effects of groundwater on hydrology, Hydrol. Process., 29, 2895–2921, 2015.
Roy, J. W. and Hayashi, M.: Groundwater exchange with two small alpine lakes in the Canadian Rockies, Hydrol. Process., 22, 2838–2846, 2008.
Schafran, G. C. and Driscoll, C. T.: Flow pathcomposition relationships for groundwater entering an acidic lake, Water Resour. Res., 29, 145–154, 1993.
Scheidegger, J. M. and Bense, V. F.: Impacts of glacially recharged groundwater flow systems on talik evolution, J. Geophys. Res.-Earth, 119, 758–778, https://doi.org/10.1002/2013JF002894, 2014.
Schlutz, F. and Lehmkuhl, F.: Holocene climatic change and the nomadic Anthropocene in Eastern Tibet: palynological and geomorphological results from the Nianbaoyeze Mountains, Quaternary Sci. Rev., 28, 1449–1471, 2009.
Schmidt, A., Gibson, J. J., Santos, I. R., Schubert, M., Tattrie, K., and Weiss, H.: The contribution of groundwater discharge to the overall water budget of two typical Boreal lakes in Alberta/Canada estimated from a radon mass balance, Hydrol. Earth Syst. Sci., 14, 79–89, https://doi.org/10.5194/hess-14-79-2010, 2010.
Sebok, E., Duque, C., Kazmierczak, J., Engesgaard, P., Nilsson, B., Karan, S., and Frandsen, M.: Highresolution distributed temperature sensing to detect seasonal groundwater discharge into Lake Væng, Denmark, Water Resour. Res., 49, 5355–5368, 2013.
Shaw, R. D. and Prepas, E. E.: Groundwater-lake interactions: I. Accuracy of seepage meter estimates of lake seepage, J. Hydrol., 119, 105–120, https://doi.org/10.1016/0022-1694(90)90037-X, 1990.
Slaymaker, O.: Criteria to distinguish between periglacial, proglacial and paraglacial environments, Quaestiones Geographicae, 30, 85–94, 2011.
Slomp, C. P. and Van Cappellen, P.: Nutrient inputs to the coastal ocean through submarine groundwater discharge: controls and potential impact, J. Hydrol., 295, 64–86, https://doi.org/10.1016/j.jhydrol.2004.02.018, 2004.
Smerdon, B., Mendoza, C., and Devito, K.: Simulations of fully coupled lakegroundwater exchange in a subhumid climate with an integrated hydrologic model, Water Resour. Res., 43, W01416, https://doi.org/10.1029/2006WR005137, 2007.
Stets, E. G., Winter, T. C., Rosenberry, D. O., and Striegl, R. G.: Quantification of surface water and groundwater flows to open and closedbasin lakes in a headwaters watershed using a descriptive oxygen stable isotope model, Water Resour. Res., 46, W03515, https://doi.org/10.1029/2009WR007793, 2010.
Tockner, K., Malard, F., Uehlinger, U., and Ward, J.: Nutrients and organic matter in a glacial river-floodplain system (Val Roseg, Switzerland), Limnol. Oceanogr., 47, 266–277, 2002.
Valiela, I., Teal, J. M., Volkmann, S., Shafer, D., and Carpenter, E. J.: Nutrient and Particulate Fluxes in a Salt-Marsh Ecosystem – Tidal Exchanges and Inputs by Precipitation and Groundwater, Limnol. Oceanogr., 23, 798–812, 1978.
Wang, C., Dong, Z., Qin, X., Zhang, J., Du, W., and Wu, J.: Glacier meltwater runoff process analysis using δD and δ18O isotope and chemistry at the remote Laohugou glacier basin in western Qilian Mountains, China, J. Geogr. Sci., 26, 722–734, 2016a.
Wang, J., Zhu, L., Wang, Y., Ju, J., Xie, M., and Daut, G.: Comparisons between the chemical compositions of lake water, inflowing river water, and lake sediment in Nam Co, central Tibetan Plateau, China and their controlling mechanisms, J. Great Lakes Res., 36, 587–595, 2010.
Wang, R., Liu, Z., Jiang, L., Yao, Z., Wang, J., and Ju, J.: Comparison of surface water chemistry and weathering effects of two lake basins in the Changtang Nature Reserve, China, J. Environ. Sci., 41, 183–194, https://doi.org/10.1016/j.jes.2015.03.016, 2016b.
Wang, S.: Frozen ground and environment in the Zoige Plateau and its surrounding mountains, Journal of Glaciology and Geocryology, 19, 39–46, 1997 (in Chinese with English abstract).
Warner, N. R., Christie, C. A., Jackson, R. B., and Vengosh, A.: Impacts of shale gas wastewater disposal on water quality in western Pennsylvania, Environ. Sci. Technol., 47, 11849–11857, 2013.
Weynell, M., Wiechert, U., and Zhang, C.: Chemical and isotopic (O, H, C) composition of surface waters in the catchment of Lake Donggi Cona (NW China) and implications for paleoenvironmental reconstructions, Chem. Geol., 435, 92–107, https://doi.org/10.1016/j.chemgeo.2016.04.012, 2016.
White, D., Lapworth, D. J., Stuart, M. E., and Williams, P. J.: Hydrochemical profiles in urban groundwater systems: New insights into contaminant sources and pathways in the subsurface from legacy and emerging contaminants, Sci. Total Environ., 562, 962–973, https://doi.org/10.1016/j.scitotenv.2016.04.054, 2016.
Wilson, J. and Rocha, C.: A combined remote sensing and multi-tracer approach for localising and assessing groundwater-lake interactions, Int. J. Appl. Earth Obs., 44, 195–204, 2016.
Winter, T. C.: Relation of streams, lakes, and wetlands to groundwater flow systems, Hydrogeol. J., 7, 28–45, 1999.
Wischnewski, J., Herzschuh, U., Rühland, K. M., Bräuning, A., Mischke, S., Smol, J. P., and Wang, L.: Recent ecological responses to climate variability and human impacts in the Nianbaoyeze Mountains (eastern Tibetan Plateau) inferred from pollen, diatom and tree-ring data, J. Paleolimnol., 51, 287–302, 2014.
Xin, W., Yongjian, D., Shiyin, L., Lianghong, J., Kunpeng, W., Zongli, J., and Wanqin, G.: Changes of glacial lakes and implications in Tian Shan, central Asia, based on remote sensing data from 1990 to 2010, Environ. Res. Lett., 8, 044052, https://doi.org/10.1088/1748-9326/8/4/044052, 2013.
Yang, K., Wu, H., Qin, J., Lin, C., Tang, W., and Chen, Y.: Recent climate changes over the Tibetan Plateau and their impacts on energy and water cycle: A review, Global Planet. Change, 112, 79–91, 2014.
Yao, T., Thompson, L., Yang, W., Yu, W., Gao, Y., Guo, X., Yang, X., Duan, K., Zhao, H., Xu, B., Pu, J., Lu, A., Xiang, Y., Kattel, D. B., and Joswiak, D.: Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings, Nat. Clim. Change, 2, 663–667, 2012.
Yao, T., MassonDelmotte, V., Gao, J., Yu, W., Yang, X., Risi, C., Sturm, C., Werner, M., Zhao, H., He, Y., Ren, W., Tian, L., Shi, C., and Hou, S.: A review of climatic controls on δ18O in precipitation over the Tibetan Plateau: Observations and simulations, Rev. Geophys., 51, 525–548, https://doi.org/10.1002/rog.20023, 2013.
Yao, Z., Wang, R., Liu, Z., Wu, S., and Jiang, L.: Spatial-temporal patterns of major ion chemistry and its controlling factors in the Manasarovar Basin, Tibet, J. Geogr. Sci., 25, 687–700, https://doi.org/10.1007/s11442-015-1196-5, 2015.
Yuan, H., Liu, E., Shen, J., Zhou, H., Geng, Q., and An, S.: Characteristics and origins of heavy metals in sediments from Ximen Co Lake during summer monsoon season, a deep lake on the eastern Tibetan Plateau, J. Geochem. Explor., 136, 76–83, https://doi.org/10.1016/j.gexplo.2013.10.008, 2014.
Zhang, B., Wu, Y., Zhu, L., Wang, J., Li, J., and Chen, D.: Estimation and trend detection of water storage at Nam Co Lake, central Tibetan Plateau, J. Hydrol., 405, 161–170, 2011.
Zhang, C. and Mischke, S.: A Lateglacial and Holocene lake record from the Nianbaoyeze Mountains and inferences of lake, glacier and climate evolution on the eastern Tibetan Plateau, Quaternary Sci. Rev., 28, 1970–1983, 2009.
Zhang, G., Yao, T., Xie, H., Kang, S., and Lei, Y.: Increased mass over the Tibetan Plateau: from lakes or glaciers?, Geophys. Res. Lett., 40, 2125–2130, 2013.
Zhang, G., Yao, T., Piao, S., Bolch, T., Xie, H., Chen, D., Gao, Y., O'Reilly, C. M., Shum, C., and Yang, K.: Extensive and drastically different alpine lake changes on Asia's high plateaus during the past four decades, Geophys. Res. Lett., 44, 252–260, 2017a.
Zhang, G., Yao, T., Shum, C., Yi, S., Yang, K., Xie, H., Feng, W., Bolch, T., Wang, L., and Behrangi, A.: Lake volume and groundwater storage variations in Tibetan Plateau's endorheic basin, Geophys. Res. Lett., 44, 5550–5560, 2017b.
Zhang, Y., Liu, C., Tang, Y., and Yang, Y.: Trends in pan evaporation and reference and actual evapotranspiration across the Tibetan Plateau, J. Geophys. Res.-Atmos., 112, D12110, https://doi.org/10.1029/2006JD008161, 2007.
Zhou, S., Kang, S., Chen, F., and Joswiak, D. R.: Water balance observations reveal significant subsurface water seepage from Lake Nam Co, south-central Tibetan Plateau, J. Hydrol., 491, 89–99, 2013.
Zlotnik, V. A., Olaguera, F., and Ong, J. B.: An approach to assessment of flow regimes of groundwater-dominated lakes in arid environments, J. Hydrol., 371, 22–30, 2009.
Zlotnik, V. A., Robinson, N. I., and Simmons, C. T.: Salinity dynamics of discharge lakes in dune environments: Conceptual model, Water Resour. Res., 46, W11548, 2010.
Zongxing, L., Qi, F., Wei, L., Tingting, W., Xiaoyan, G., Zongjie, L., Yan, G., Yanhui, P., Rui, G., and Bing, J.: The stable isotope evolution in Shiyi glacier system during the ablation period in the north of Tibetan Plateau, China, Quatern. Int., 380, 262–271, 2015.