the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Anatomy of simultaneous flood peaks at a lowland confluence
Tjitske J. Geertsema
Adriaan J. Teuling
Remko Uijlenhoet
Paul J. J. F. Torfs
Antonius J. F. Hoitink
Lowlands are vulnerable to flooding due to their mild topography in often densely populated areas with high social and economic value. Moreover, multiple physical processes coincide in lowland areas, such as those involved in river–sea interactions and in merging rivers at confluences. Simultaneous occurrence of such processes can result in amplifying or attenuating effects on water levels. Our aim is to understand the mechanisms behind simultaneous occurrence of discharge waves in a river and its lowland tributaries. Here, we introduce a new way of analyzing lowland discharge and water level dynamics, by tracing individual flood waves based on dynamic time warping. We take the confluence of the Meuse River (∼33 000 km2) with the joining tributaries of the Dommel and Aa rivers as an example, especially because the January 1995 flood at this confluence was the result of the simultaneous occurrence of discharge peaks in the main stream and the tributaries and because independent observations of water levels and discharge are available for a longer period. The analysis shows that the exact timing of the arrival of discharge peaks is of little relevance because of the long duration of the average discharge wave compared to typical time lags between peaks. The discharge waves last on average 9 days, whereas the lag time between discharge peaks in the main river and the tributaries is typically 3 days. This results in backwaters that can rise up to 1.5 m over a distance of 4 km from the confluence. Thus, local measures to reduce the impact of flooding around the confluence should account for the long duration of flood peaks in the main system.
- Article
(7161 KB) - Full-text XML
- BibTeX
- EndNote
In January 1995, water was only a few centimeters below the crest of the dikes in the lowlands of the major rivers Rhine and Meuse. This high water event created fears for major flooding across large parts of the Netherlands, causing the Dutch government to decide to evacuate more than 200 000 inhabitants from the area immediately under threat. Luckily these fears did not materialize and people could return to their homes within a few days. However, this high water event did lead to local flooding (Fig. 1). The flood occurred just upstream of the city center of 's-Hertogenbosch, where two tributaries (Dommel, DD, and Aa, AD) join and spread over a small region. This small region included an economically important European highway and could have spread over a much larger area if the duration of the overtopping had been longer (Fig. 1). The overtopping was the result of water levels rising to 4.9 m a.m.s.l. (above mean sea level) in the Dommel, indicated by the water authorities as the maximum protection level. It was concluded that the simultaneous occurrence of the discharge peaks in the Meuse River and the Dommel tributary likely caused the flooding, but no in-depth analysis of the simultaneous occurrence has been performed so far.
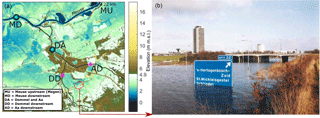
Figure 1Flood proneness near the confluence of the Meuse and the tributaries Dommel and Aa. (a) DEM of the area around the Dutch city of 's-Hertogenbosch is shown. The green and blue colors indicate areas below 4.9 m a.m.s.l. (the maximum water level in the Meuse that was reached in January 1995 and also the maximum protected flood level). These areas are, at least potentially, prone to flooding. The magenta asterisks indicate gauge stations with discharge and water level data and the cyan asterisks indicate stations with only water level data. The red circle indicates the flooded area of the European highway E25 (IJpelaar et al., 2009).
While simultaneous occurrence (coincidence) of high discharge and storm surge has been investigated (Kew et al., 2013; Klerk et al., 2015; van Den Hurk et al., 2015), only few studies have addressed the processes leading to the simultaneous occurrence of discharge peaks. In one of these studies, Pattison et al. (2014) analyzed the sensitivity of the changing hydrological response to the relative timing and succession of discharge peaks by sub-watersheds, to investigate the possibility of reducing flood risk. The cause of the relative timing and succession, however, was not considered in their analysis, making it difficult to extrapolate their findings. A key point from their analysis was that flood impacts are unpredictable when synergy occurs between two sub-watersheds. In another study by Vorogushyn and Merz (2013), it is shown that a discharge wave accelerates with river training, resulting in the simultaneous occurrence of flood peaks in the Rhine River and the Neckar tributary, which partly causes increasing Rhine flood discharges. Vorogushyn and Merz (2013) analyzed the simultaneous occurrence of discharge peaks of the Rhine and Neckar based on trend analysis, without offering details of individual discharge events, while in rain-fed systems, the variability in the hydrograph shapes of individual peak discharge events can be so large that changes in the relative timing cannot readily be translated to a change in flood risk.
Various factors contribute to the process of the simultaneous occurrence of discharge peaks at lowland confluences. These include spatial precipitation distribution, precipitation duration, length of the drainage network, the slope of the catchment area and the antecedent soil moisture. The spatiotemporal variability of precipitation is a key factor in the simultaneous occurrence of discharge peaks. Since there are no discharge peaks to coincide if there is no rain in one of the catchment areas, the spatial precipitation pattern over a larger river basin and the lowland tributary might show little correlation (Betterle et al., 2017). Precipitation events exceeding 1 day can cover more than 104 km2 (Merz and Blöschl, 2003; Skøien et al., 2003; Van de Beek et al., 2011, 2012) and may therefore be comparable for a part of the river basin, but not for the entire basin of medium-sized rivers (river lengths between 300 and 1000 km). On the other hand, the climatological precipitation maxima can be influenced by orographic effects and can therefore be relatively close to the lowland area, which after all lead to a correlated spatial precipitation distribution between both catchments. Even if the precipitation pattern were homogeneous across both catchment areas, then the shorter drainage network length of the lowland tributary should result in discharge peaks reaching the confluence before the peak in the main river (Marchi et al., 2010; Melone et al., 2002). In addition to the factors spatial precipitation pattern and drainage network length, the process of simultaneous occurrence at confluence is influenced by the duration of the discharge peaks (Meade et al., 1991). The multiple lowland tributaries can increase the duration of the discharge peaks due to the different arrival times at the main river and can therefore result in the simultaneous occurrence of the discharge peaks, as has been reported for large river basins such as the Amazon (Meade et al., 1991). This leads to the question of what the dominant factors are in medium-sized rivers and whether the event described above reflects a general pattern of the possible simultaneous occurrence of flood peaks or is simply a rare extreme event.
This study aims to increase our understanding of the simultaneous occurrence of flood peaks at confluences in lowland areas, by investigating the precipitation, discharge and water level dynamics for peak discharge events in the lower branch of the river Meuse. We will address the following research questions:
-
Under which conditions do discharge peaks coincide at the selected lowland confluences?
-
How are water level profiles in lowland tributaries affected by backwater associated with the simultaneous occurrence of flood peaks in the main river?
Peak discharge hydrographs vary in time due to heterogeneity in precipitation patterns and antecedent catchment characteristics. A single flood event may be insufficiently representative to gain generic insight into the conditions when discharge peaks coincide and what the consequences are. Here we carry out an analysis of a selection of events leading to the highest discharges, and establish the impacts on water levels. The precipitation patterns for these events provide insight into the variety of conditions that may lead to the simultaneous occurrence of discharge peaks, whereas water level analysis offers insight into the possible consequences. Obviously, extreme water levels in tributaries can lead to the inundation of larger areas when the surrounding region is flat (i.e. in lowlands).
The lowland Dommel and Meuse confluence is used as a study area for two reasons: first, because simultaneous occurrence reportedly occurred in January 1995. Second, the study area is uniquely suited to this research since routine and independent observations of water height and discharge are available at several locations in the Meuse and its tributaries. The nine highest discharge events of the Meuse between 1999 and 2015 are analyzed in detail to gain insight into the spatiotemporal precipitation and discharge patterns. For these events, the time lags between peaks in the Meuse and the Dommel and Aa are determined, as the timing indicates the potential of simultaneous occurrence of discharge peaks. We employ a method that is relatively new in hydrology to calculate time lags, dynamic time warping (DTW), which is introduced in Sect. 2 (Methods and Materials). The Meuse River basin, its tributaries and the employed discharge and precipitation data are described in more detail in the same section. Section 3 (Results) shows the precipitation patterns prior to these discharge events, and the resulting time lags between the Meuse and the tributaries Dommel and Aa for the studied discharge peaks. In addition, the effects of the simultaneous occurrence of discharge peaks on water levels in the rivers are analyzed. Finally, we will discuss our results and conclude that the exact timing of the discharge peaks is not the single and most important factor in explaining the hydrological consequences of the simultaneous occurrence of discharge peaks at lowland confluences (Sect. 4, Discussion, and Sect. 5, Conclusions).
2.1 Dynamic time warping
Dynamic time warping (DTW) is a relatively new method and has so far seen few applications in the field of hydrology (Dupas et al., 2015; Ouyang et al., 2010). The DTW method compares time series to determine, for example, the time shift or the similarity between these time series. Within hydrology, the DTW method can have great value in determining transport through the system, for example, of substances or water quantities (Dupas et al., 2015). The method can therefore be used to compare transport effects through and between catchment areas, for example, rainfall–runoff characteristics or distribution of pollution. This comparison can be performed for one discharge event or for multiple years. We have used the DTW method to determine the time lag between rainfall and runoff, and the time lag between the nine highest discharge peaks of the different catchments, namely of the Meuse and the Dommel and Aa. The advantage of DTW is that no assumptions are needed regarding the definition of a wave in discharge time series. This is in contrast to common methods based on the center of mass and the unit hydrograph. The only required input data are the discharge time series and a possible restriction of the warping path. We have used 1 week before and after the discharge peak as input signal. Considering discharge wave propagation, the time lags between stations cannot be infinite. Therefore, warping paths greater than 1 week are not used, but this warping path restriction can be increased for larger catchments. Moreover, the method has no difficulty with different diffusion effects of the discharge time series, and DTW is unique in considering the time axis to be elastic or dynamic, which is desirable to match similar shapes in different phases, such as long-wave propagation. Keogh and Ratanamahatana (2005); Kruskal and Liberman (1983) provide a detailed description of the DTW method. Below, step-by-step, we describe the essence of the method using two discharge time series as an example (Fig. 4a), xi (upstream) with i=1 … n and yj (downstream) with j=1 … m.
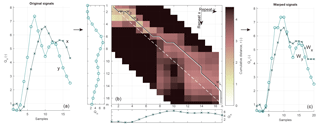
Figure 2Map of the Meuse, Dommel and Aa catchments. The locations of the main gauging stations in the Meuse are shown. Color indicates elevation, and green boxes indicate the areas over which the precipitation is assumed to be representative of the Meuse and Dommel–Aa catchments, respectively. The white box indicates the area of Fig. 1.
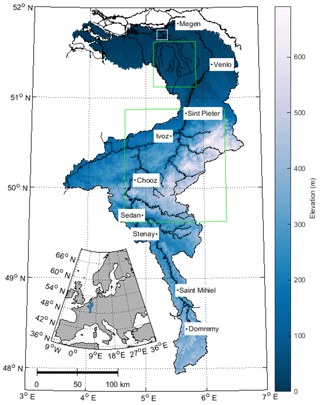
Figure 3Precipitation and discharge extremes for the Meuse. The grey lines show measurements and the black line shows the average value over the measuring period. The colors of the peaks indicate the year and the numbers the decreasing order of the maximum discharges. Note the strong seasonality in discharge, with peaks only occurring in the period November–March, whereas precipitation events occur year round.
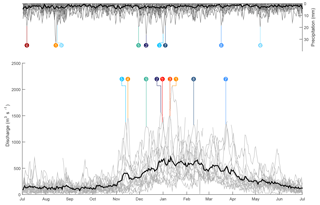
Figure 4Principle of Dynamic Time Warping. The original time series (a) were used for the cumulative distance matrix (b), which shows the cumulative distance between points in the time series on the x axis and y axis. The black line shows the warping path and the white dashed line shows the path without a time lag. The difference between the black and the white dashed line is the visualized time lags. The warping path was used to construct the warping signals (c).

Figure 5Distribution of the 5-day precipitation sum preceding the discharge peaks at Megen (MU). The red circle represents the location and the amount of the highest daily precipitation sum (mm). The numbers in the boxes show the time delay between the day with the largest precipitation sum and the discharge peak at MU (d). The flood peaks are arranged from the highest flood peak (a) to the lowest flood peak of the nine events (i).
-
Step 1: standardization.
For optimal matching of the time series, the amplitudes of x and y should be similar, which is achieved by standardizing both time series (through subtracting the mean and dividing by the standard deviation). This operation changes the hydrographs in terms of scale, but not in terms of shape, and is similar to common methods such as cluster analysis. It is also used in other hydrological studies employing DTW (Dupas et al., 2015; Ouyang et al., 2010). A property of standardization is that the Euclidean distances between two standardized time series can become equally spaced in periods without peaks, which makes the method unsuitable for DTW in these circumstances. This was prevented by limiting the analysis to the nine highest discharge peaks. The Derivative Dynamic Time Warping (DDTW) method can provide a solution to the need of standardization (Keogh and Pazzani, 2001), but the minor tidal influence at the lowland confluence makes DDTW not applicable in this case.
-
Step 2: Euclidean and cumulative distance
The Euclidean distance, d(xi, yj), between the two time series is expressed as an n-by-m matrix,
which should not be confused with the physical distance between the two stations. The distance is used to find optimal matches by minimizing the distances. The cumulative distance, r(i, j), is the sum of the distance d(i, j) of the current element and the minimum of the cumulative distances of the surrounding elements:
Figure 4b shows the x and y time series below and to the left of the figure with the cumulative distance. The cumulative distance is shown using colors, with the lighter colors showing smaller cumulative distances and the darker colors larger cumulative distances between the samples of the time series. The figure also shows that the cumulative distance increases to the end of the time series, which results from the summation of the (cumulative) distance from the smallest horizontal left, vertical up or diagonal upper left element (right-hand side of Eq. 2) In the next step, we will further explain the path of the cumulative distance. The white spaces in the figure correspond to the warping path restriction of 1 week.
-
Step 3: warping path.
The warping path, W, is a matrix that maps x to y with the lowest cumulative distance (black line in Fig. 4b) and basically reconstructs the i′s and j′s of the right-hand side of the plus in Eq. (2) (black line in Fig. 4b). The warping path in Fig. 4b thus connects the path with the lightest colors. The length of the path is not necessarily equal to the length of x or y due to the dynamic time lags, where i is not equal to j (horizontal and vertical movement of the warping path in Fig. 4b). Hence,
where Wx and Wy are the x′s and y′s, respectively, of the lowest cumulative distances with lengths, L, of max(m, . In the given example, n and m have 17 samples and L has 20 (Fig. 4a and c). The warping path is subject to the following constraints related to the dependency on the cumulative distance:
-
Boundary conditions require the warping path to start in the top left and end in the bottom right of the matrix (Fig. 4b).
-
Continuity restricts the allowable step size not to be greater than 1 relative to the previous i and j, thus moving horizontally, vertically or diagonally with steps of 1 (Fig. 4b).
-
Monotonicity forces the points in W not to go back in time (black line is only going down and/or to the left in Fig. 4b).
The boundary conditions constraint requires a start-up time before a “stable” time lag is found. We used a start-up time equal to the warping path limitation, thus 1 week. The example in Fig. 4b shows a start-up time of 1 day; therefore w1 and wL are connected to the 2nd and the 16th sample, respectively. The final result of the warping path into a time series is shown in Fig. 4c. Note that the time series before and after warping are not equal. The Wx and Wy are not used for further analysis because of the lack of physical interpretation of the time series after the warping process; instead the indices to transform x and y into Wx and Wy are used in the further analysis.
-
-
Step 4: time lag and duration of discharge peaks.
The difference between indices to transform x and y into Wx and Wy was not constant during the analyzed discharge wave, for example, due to diffusion. When a diffusive discharge wave is compared with a non-diffusive discharge wave, the slope of the rising and falling limbs differ between the two waves. This difference results in a variation of the time lag along the rising and falling limbs of the discharge waves, regardless of the time lag influenced by advection. The time lag was calculated as the modal difference between the indices to transform x and y into Wx and Wy, as the modal difference is not influenced by diffusion. Figure 4b shows the time lag by the model of (diagonal) difference between the white dashed and the warping path. The time lag at w1 is zero, at w2 one and at wL two, but the model time lag from w1 and wL is 2 days.
The duration of the discharge peaks was defined as the time the discharge is above the 5 % highest discharges over the 15 analyzed years.
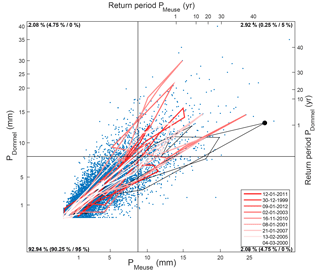
Figure 6Gumbel distribution of the precipitation in the combined Dommel and Aa catchments and the Ardennes from 1968 to 2015. The red lines shows the precipitation a week prior and a week after the analyzed discharge events in Megen, and the black line shows the precipitation 2 weeks prior to the flood event in 1995. The figure is divided in quadrants in such a way that 95 % of precipitation values for the Meuse are located on the left side of the vertical line and that 95 % of precipitation values at the Dommel are located below the horizontal line. The numbers in the corners successively indicate the percentage of samples in each quadrant and the percentages that would result from complete randomness and exact (1-to-1) correlation, which are shown in brackets.
2.2 Study area and data
2.2.1 Meuse River
The Meuse drains an area of 33 000 km2 between northern France and the Netherlands (Fig. 2) and experiences a temperate climate. The Meuse is mainly rain-fed and has an average annual discharge of 350 m3 s−1. The rain-fed flow regime is erratic and the catchment has different geological and orographic settings, causing different response times and precipitation patterns within the Meuse catchment area (Berger, 1992; Leander et al., 2005; de Wit et al., 2007). The Meuse can be divided into three parts: Meuse Lorraine, Ardennes Meuse and the lowland Meuse (de Wit et al., 2007). Meuse Lorraine has mild valley slopes and lies between two ridges. It therefore responds temperately to precipitation, which is partly retained in reservoirs. The Ardennes Meuse consists mainly of hard rock and has steep valley slopes, and as such responds in a flashy way, besides there being some retention in reservoirs. The lowland Meuse has very mild slopes and lies in deep alluvial deposits, and therefore responds slowly to precipitation. The largest amount of precipitation falls in the Ardennes and therefore contributes most to the discharge (Leander et al., 2005; Rakovec et al., 2012).
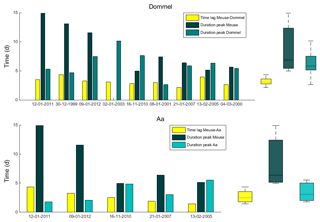
Figure 7Duration of the discharge peaks in the Meuse (MU), the Dommel (DD) and the Aa (AD) rivers and the time lag at the confluence between the Meuse and the Dommel and between the Meuse and the Aa. Box plots show the median, the 25th and 75th percentiles and the range of the durations and time lags.
2.2.2 Tributaries Dommel and Aa
The Dommel and Aa catchments represent 5 % of the Meuse catchment and flow from the Belgian Kempen region to the Dutch city of 's-Hertogenbosch (Fig. 2). The average discharges of the Dommel and the Aa are 14 and 8 m3 s−1, respectively, and their gradients are ∼75 m per 100 km. The Dommel and Aa are rain-fed and, due to the high groundwater levels, have a flashy character despite the rivers' deep alluvial basins. The Aa has been straightened and canalized in the past hundred years. The Dommel has mostly kept its natural plan form. Downstream of the confluence of the Dommel and Aa, the river is called Dieze. When the water level in the Dieze is less than 5 cm higher than the Meuse, the weir in the Dieze is closed and the water discharges through the Drongelse canal, which has a capacity of 100 m3 s−1. The aim of the river training is to prevent the Meuse from flooding areas in the Dommel and Aa catchments. Retention areas of 8.60 million m3 are used when the discharge capacity of the Drongelse canal is not sufficient in discharging the Dommel and Aa when the weir to the Meuse is closed. The weir in the Dieze was only closed for a few hours in the focus period 1999–2015, namely during the January 2011 event.
2.2.3 Discharge and precipitation data
In this study, we used hourly measured water levels and discharges of the Meuse at Megen (MU) and of the Dommel (DD) and Aa (AD) between 1999 and 2015 (Fig. 1). Flow velocities were measured every 15 min using a current meter, a FLOW 2000 measuring device. The flow velocities were converted to discharges using a known cross-sectional area. The water level differences were computed by subtracting MD from MU and DA from DD or AD (Fig. 1). The water levels in this area are controlled by weirs and dikes due to the high flood risk, but the positions of the gauging stations were chosen such that the water levels would be least influenced by the weirs.
In addition to discharge and water level data, a data set of daily precipitation for Europe was used (Haylock et al., 2008). The data set interpolates the European precipitation observations (using the European Climate Assessment Data set; https://www.ecad.eu/, last access: 14 October 2018) on a grid of 0.25∘ latitude by 0.25∘ longitude. The combined Dommel and Aa catchment areas and the Ardennes catchment area are extracted from the data set using the green boxes in Fig. 2. The precipitation sum over the catchment, thus the sum over the area of the boxes, is used in the analysis because the highest discharge and precipitation peaks will generally have the largest flood implications in the case of simultaneous occurrence. The nine highest discharge peaks at Megen (MU) were analyzed (Fig. 3). High evaporation rates in summer cause a strong seasonal discharge cycle. The highest precipitation peaks in summer will therefore be stored in the soil or evaporated, and will not result in discharge peaks. As a result, the timing of the nine highest discharge peaks does not match with the nine highest precipitation peaks in the Meuse and Dommel.
2.3 Response times and time lags
The simultaneous occurrence of discharge waves is caused by a combination of similar precipitation and discharge patterns in two catchments (Betterle et al., 2017). We first analyze the rainfall-discharge response times for the nearest gauging stations upstream of the confluences subject to study, indicated with DD, AD and MU in Fig. 1. For these stations, we calculate the time lags between peaks in rainfall and discharge using the dynamic time warping method (DTW). The time lags are calculated in days and hours for the rainfall and discharge, respectively.
Subsequently, we analyze the travel time needed for a discharge peak to move from the gauging station to the confluence, based on the celerity of the flood wave (Jansen et al., 1994). In order to be able to determine the time lag between a main river and a tributary at a confluence, the celerity from the nearest gauging station to the confluence is determined and added to the timing of the measured discharge peaks. The travel time of the discharge peak can be approximated by
where tc (s) is the travel time of a discharge peak from gauging station to confluence, s (m) the distance from gauging station to confluence, g (m s−2) the gravitational acceleration and h (m) the mean water depth during the discharge peak. We used the mean water depth to keep the travel time constant during the discharge wave. The average travel time from the gauging station to the confluence for the Meuse is 2 h. It is negligible for both the Dommel and the Aa. Hence, in order to calculate the degree of simultaneous occurrence of discharge peaks at the confluence, 2 h are subtracted from the time lag between the main river and tributary determined from the gauging stations.
Together, these two time lags serve to understand the meteorological and hydraulic conditions leading to the discharge events. In addition, the time lags between the main river and its tributaries were determined, again based on DTW.
Rainfall in the Meuse River basin is mainly concentrated in the Ardennes and surrounding area as a result of orographic effects (Fig. 5). The precipitation patterns of 5-daily precipitation sums preceding discharge peaks show that both catchments typically receive large sums, with the sums over the Ardennes part of the basin generally being larger. Even though the combined Dommel–Aa catchment and the Ardennes catchment are separated by 150 km (the green boxes in Fig. 5), daily precipitation patterns over the two catchments are spatially correlated (Fig. 6). Figure 6 shows the daily precipitation summed over the Ardennes and the Dommel–Aa catchment areas over the period of the past 45 years. As result of the multiple measurements without precipitation, the data have been transformed into a Gumbel distribution to focus on the high precipitation events. The scatter plot shows that the simultaneous occurrence of the high precipitation events in both the Meuse and the Dommel–Aa catchment areas occurs 2.9 % over the past 45 years in relation to 5 and 0.25 % in the case of complete correlation and in the case of randomness, respectively. The daily precipitation values summed over the Ardennes and the Dommel are not completely correlated due to travel times and increase or decrease of rainfall events. The lines in Fig. 6 indicate that most precipitation events do not consist of a single day event, and therefore a combination of multi-day and heavy precipitation event results in high discharge events. The highest discharge events are caused by multi-day precipitation events or by a series of precipitation events with an interval of a couple of days.
The average response times between precipitation and discharge at the three gauging stations close to the junctions subject to study are 3 days for MU (Fig. 5), 2 days for DD and 1 day for AD, with standard deviations of approximately half the average response times. These standard deviations emphasize the large variability of the events. The response times suggest that precipitation events occurring within a 2-day interval may lead to a higher probability of simultaneous occurrence of the maxima of discharge waves. Inundations with societal impacts are reported for the discharge events of 2003, 2010 and 2011 in Wallonia (Belgium) and in the southern regions of the Netherlands. The computed response time for the severe precipitation event of 2003 to a discharge peak is negative because the discharge measuring device failed and consequently leads to an incomplete discharge wave. The high discharge events show that the response time from precipitation to discharge not only depends on the intensity and duration of the precipitation event, but also on wave attenuation (Sholtes and Doyle, 2011; Turner-Gillespie et al., 2003; Woltemade and Potter, 1994) and initial conditions of the catchment before the discharge peak, such as antecedent soil moisture (Fig. 3).
Our results show that the precipitation patterns for the Dommel–Aa and Meuse catchment areas are correlated (Fig. 6), which underlines the importance of the time lags between the discharge peaks of the Meuse and the Dommel–Aa to assess the potential for the simultaneous occurrence of discharge waves. The discharge waves in the Dommel and Aa arrive at the confluence 3.2 and 2.7 days prior to the discharge wave in the Meuse, respectively (Fig. 7). The time lag of the Aa is thus half a day smaller, likely because of the shorter drainage length and the higher degree of canalization of the channels. The corresponding standard deviations are 16 h (0.67 days) for the Dommel and 28 h (1.17 days) for the Aa. Note that the discharge of the Aa has only been measured since 2004, which explains the absence of time lags prior to 2004. Figure 8 shows the average travel time of the nine highest discharge waves along the Meuse catchment. The tributaries increase the peak discharges in the Meuse, which is shown by the increasing circle sizes along the Meuse. In addition, some tributaries show similar time lags at the confluence joining the Meuse, which indicates the possible simultaneous occurrence of upstream confluences. We conclude that the average time lags between the arrival of discharge peaks from the Meuse–Dommel and Meuse–Aa confluences are larger than the average response time of discharge at the monitoring stations to precipitation events. Thus, when processes of runoff generation are fast, the simultaneous occurrence of discharge peaks is unlikely.
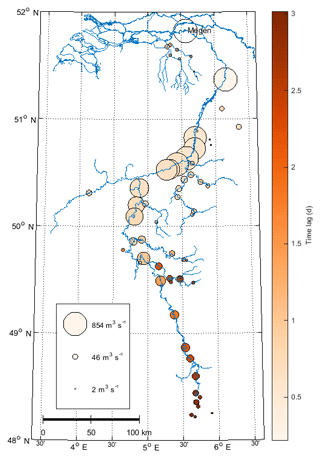
Figure 8Distribution of the average travel time of the nine highest discharge waves in the period 1999–2015, between various gauging stations along the Meuse and the confluence subject to study. The circle size indicates the 95th percentile discharge of the gauging station.
Although discharge peaks may not coincide, the question remains whether the time lag between the discharge waves is large enough to prevent the simultaneous occurrence of high discharges. Figure 9 shows the precipitation of the Meuse and the tributaries Dommel and Aa, as well as the standardized discharge waves. The colored discharge waves are the periods during which the standardized discharge exceeds the 95th percentile of the time series. Unfortunately, some data gaps (caused by measurement errors) are present in the time series during discharge waves. Despite this, it is evident that all nine highest discharge waves show color overlap and thus coincide.
The fact that the simultaneous occurrence of discharge waves takes place for all analyzed extreme events can be explained from the relatively long durations of the discharge waves. The duration of the discharge waves is 9 days on average at MU and even 13 days for the three highest discharge waves (Fig. 7). The average time lag between the discharge waves of 3 days is therefore too small to prevent simultaneous occurrence. Figure 10 shows the discharges in the Meuse and Dommel upstream of the confluence over the 15 years analyzed, with and without applying a 3-day time shift, corresponding to the left and right panels, respectively. Similar to the precipitation sum, the discharges are transformed into a Gumbel distribution to emphasize the high discharges over the low discharges. The Meuse and Dommel discharges are 2.5 % of the time both higher than 5 % of their discharge, which is between complete correlation and randomness. The Meuse and Dommel discharges are not completely correlated as a consequence of the time lag between Meuse and Dommel discharge. The application of the time shift increases, however, the correlation for the highest discharges only slightly, which is apparent from the increase of data points in the top right quadrant from 2.5 % to 2.7 %. The lines in Fig. 10 show that, besides the time shift, most of the nine events move through all quadrants, which implies that the scatter is due to the different peak duration length by, for example, the spatial rainfall distribution and the size of catchment.
From a water management perspective, it is relevant to establish the degree to which the simultaneous occurrence of discharge waves affects extreme water levels. During high discharge events the water level difference over a distance of 40 km in the Meuse between MU and MD (Fig. 1) increases by about 1.5 m (Fig. 11). Afterwards, it decreases to the water level difference typical of normal discharges (0.5 to 1 m). The water level differences in the Dommel (between DD and DA) and Aa (between AD and DA), on the other hand, decrease from about 1.5 to 0.5 m, and in some cases the difference even vanishes during peak discharges, and increases afterwards over a distance of 4 and 6 km, respectively (Fig. 11). Hence, the water level differences decrease during a discharge event in the tributaries, reflecting backwater effects of the Meuse on the tributaries, also visible in the corresponding stage–discharge relation (Fig. 12). The backwater height can reach 1.5 m over 4 km from the confluence in the Dommel and Aa tributaries.
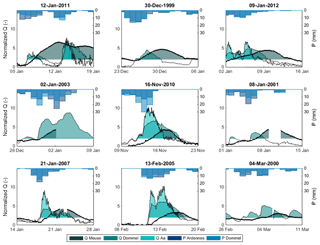
Figure 9Standardized/normalized hydrographs of the Meuse, Dommel and Aa rivers for the nine highest discharge peaks (Fig. 3). The colors indicate discharge exceeding the 95th percentile for the Meuse River (dark green), the Dommel River (lighter green) and the Aa River (light turquoise). The overlap between the colors is indicative of simultaneous occurrence. The precipitation in the catchment areas is indicated by dark blue for the Ardennes catchment and lighter blue for the Dommel–Aa catchment.
The exact time lag between discharge waves in the main river and the tributary is shown to be less relevant than the duration and magnitude of the discharge waves. The impacts of simultaneous occurrence of discharge waves depend strongly on the detailed hydrograph of the discharge wave, which may have a composite character. The probability of the simultaneous occurrence of discharge peaks, as referred to in existing studies (Vorogushyn and Merz, 2013; de Wit et al., 2007), becomes less relevant when the duration of the discharge waves becomes large compared to the time lag between the arrival of discharge waves from branches joining at a confluence. The amount of discharge before or after the peak can be relatively high, and can lead to backwater effects in the tributary similar to those generated during a true event of wave peak coincidence. The choice of an appropriate discharge threshold is critical in the analysis because it determines the portion of the discharge wave taken into consideration. The threshold here employed to isolate the nine extreme discharge events does not influence the results of the DTW method, which shows that DTW can be considered a robust tool when analyzing the interaction between discharge waves. Catchment properties and climate characteristics are known to determine the duration of discharge peaks (Gaál et al., 2012). This study adds main stream–tributary interaction as an important factor influencing the local duration of a discharge wave in lowland areas.
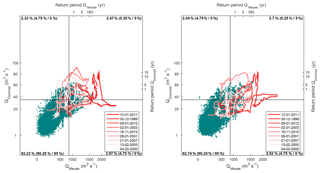
Figure 10Gumbel distribution of the discharge of the Dommel and the Meuse from 1996 to 2015. The red lines show the discharge a week prior and a week after the analyzed discharge peaks at Megen and follow a clockwise hysteresis. The discharge of the flood event of 1995 was 2.825 m3 s−1 for the Meuse and 100 m3 s−1 for the Dommel. The figure is divided in quadrants in such a way that 95 % of discharge values at the Meuse are located on the left side of the vertical line and that 95 % of discharge values at the Dommel are located below the horizontal line. The numbers in the corners successively indicate the percentage of samples in each quadrant and the percentages that would result from complete randomness and exact (1-to-1) correlation, which are shown in brackets.
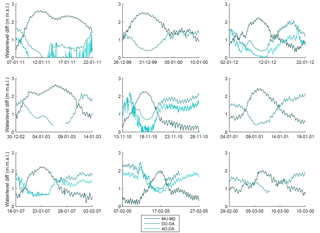
Figure 11Water level differences of the Meuse, Dommel and Aa rivers during the nine highest discharge peaks in the Meuse. Note that the water level difference of the Meuse (MU–MD) increases, while the differences of the Dommel (DD–DA) and Aa (AD–DA) decrease during the discharge peak.

Figure 12The stage–discharge relation of the Dommel River at measuring station DD (Fig. 1). Note that stage and discharge have been measured independently, and that strong nonuniqueness and hysteresis effects can be seen.
Based on our analysis and a literature review, the following conceptual framework for simultaneous occurrence emerges (Fig. 13). The time lag between discharge peaks at the confluence and the duration of the discharge waves are the most important parameters for determining whether discharge peaks coincide (given that precipitation falls over both drainage areas). Figure 13 shows the proposed conceptual framework with relations between factors influencing the time-to-peak discharge at the outlet and the duration of discharge waves. Since the time lag between the catchment is of interest for simultaneous occurrence of discharge peaks, we consider the differences of the factors influencing the time-to-peak discharge as conceptual representation of the time lag between the catchments (dashed box in Fig. 13). The time-to-peak discharge at the confluence is positively related to the drainage network length, amount of precipitation/discharge and friction and negatively related to slope and antecedent soil moisture. The slope and drainage length are the predominant factors influencing the time-to-peak discharge in catchments. The duration of the discharge wave is positively related to the number of tributaries, friction, duration of precipitation and time to discharge and is thus also related to the factors influencing time-to-peak discharge. The friction factor can occur in various forms, such as roughness in watercourse, transport through soil or river training by, e.g., weirs. Figure 13 can be used to conceptually understand the effects of other climates and catchment areas. For example, if most precipitation in the Meuse basin were concentrated further upstream (which may be expected in many other lowland areas), the difference in travel time would merely increase by about 2 days (Fig. 8). An extra travel time of 2 days would still result in the simultaneous occurrence of discharge peaks at the confluence for most of the analyzed discharge waves. Another example is the Amazon River for which simultaneous occurrence of discharge peaks is described by Meade et al. (1991). A discharge wave in the Amazon River lasts for 4 months in the wet season and coincides with discharge waves from tributaries that can peak 1 month to 2 months earlier. The simultaneous occurrence of discharge waves in the Amazon region is the result of the duration of precipitation in the Amazon area, which can also last for 4 months (Arvor et al., 2017; Buarque et al., 2011; Marengo et al., 2001). A more extensive investigation into multiple confluences and climates would have an added value in understanding simultaneous occurrence of discharge peaks, and the presented method provides a generic tool for further investigation of the influencing factors and processes.
The common practice of determining the discharge using stage–discharge relations is not applicable near confluences because one cannot account for the backwater effects apparent as hysteresis in a rating curve (Hidayat et al., 2011, 2017). Especially during the highest discharge waves, backwater effects show the most variation. For this reason, the exceedance levels of the upstream stations of the confluence cannot directly be projected to locations closer to the confluence. Establishing the exceedance levels and stage–discharge relations for regions near a confluence therefore presents challenges for water management and introduces one of the causes for spatial variation in flood risk.
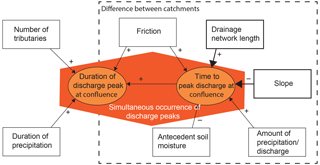
Figure 13Conceptual framework of processing controlling the simultaneous occurrence of discharge peaks at confluences. When discharge peaks coincide at confluences indicated by the orange polygon, the time to discharge plus the duration of the discharge peaks should overlap. The arrows indicate the factors influencing the time to discharge and/or duration of the discharge peak. The plus signs indicate a positive effect and the minus signs indicate a negative effect of the factors. The drainage network length and the slope have a larger influence on time to discharge than the other factors. For the time to discharge it is crucial to understand the difference between the catchment areas joining at the confluence, which is indicated by the dashed box.
The aim of the current Dutch water policy is to retain water in small catchments contributing to the main rivers, mainly to prevent drought and to improve water quality. From a flood risk perspective, water should preferably be retained for the duration of the discharge peak in the main river. An existing concern is that the current practice of water retention in the Dommel and Aa catchments increases flood risk, by enhancing the probability of coinciding flood waves. Our analysis puts the importance of the relative timing of flood waves in perspective. The average duration of extreme discharge events is 9 days in the study area, and it is not so relevant when the peaks in discharge of the Dommel and Aa occur in this period. A significant reduction in flood risk would only be achieved when the water is retained for a period covering multiple rainfall events, which is far from the present-day situation.
Extreme discharge events at the confluence of the river Meuse and two joining lowland tributaries are studied, introducing a new method of analysis based on dynamic time warping. The method offers robust means of tracing individual discharge waves in discharge time series collected throughout a catchment. The study shows that the precipitation patterns in the catchment areas are spatially correlated. Spatial correlation of the precipitation patterns is a prerequisite for simultaneous occurrence at the confluence. From a comparison of the nine highest discharge waves in the main stream and the joining lowland tributaries, it follows that the exact timing of the discharge peaks and the probability of simultaneous occurrence of discharge peaks are little relevant to flood risk. The duration of the discharge wave in the main stream is large compared to the time lags between discharge peaking in the main channel and the tributaries. Initial catchment characteristics produce ambiguous discharge responses to precipitation, such that the timing of duration and magnitude of the discharge peak relative to the precipitation is variable. When discharge waves coincide, the water level difference in the Meuse increases and the water level differences in the tributaries Dommel and Aa decrease. The decrease of water level differences indicates backwater effects in the tributaries due to simultaneous occurrence. The backwater height can increase to 1.5 m over 4 km from the confluence in the Dommel and Aa rivers. A public belief is that rapid drainage in a lowland tributary will reduce flood risk because it diminishes the likelihood of coincident discharge peaks in the main stream and the tributary. In addition, there is a concern that measures of water retention, for example, to prevent drought and to improve water quality, will increase flood risk. Our analysis puts this concern into perspective, as a systematic retention in the order of days will only marginally affect peak water levels.
The DTW code can be requested from the corresponding author and the data can be requested from the following organizations:
-
Dutch water level and discharge data are measured by Rijkswaterstaat and are available at https://www.rijkswaterstaat.nl/water/waterdata-en-waterberichtgeving/waterdata/index.aspx (Rijkswaterstaat, 2018).
-
Walloon water level and discharge data are measured by Service Publique de Wallonie (SPW) and are available at http://voies-hydrauliques.wallonie.be/opencms/opencms/fr/hydro/Archive/annuaires/index.html (Service public de Wallonie, 2018).
-
French water level and discharge data are measured by Direction Générale de la Prévention des Risques/Service des Risques Naturels et Hydrauliques (DGPR/SRNH) and are available at http://www.hydro.eaufrance.fr/ (Hydro, 2018).
-
Dommel water level and discharge data are measured by De Dommel water board and are available from the contact person Michelle Berg.
-
Aa water level and discharge data are measured by Aa en Maas water board and are available from the contact person Pim van Santen.
-
Rainfall data are collected from the E-OBS dataset and are available at http://www.ecad.eu (European Climate, 2018).
TJG, AJT, and AJFH designed the research. PJJFT introduced the DTW method and helped with the analysis. TJG performed the research, analyzed the data, and wrote the draft; all authors contributed to interpreting results, discussing findings, and improving the manuscript.
The authors declare that they have no conflict of interest.
This research is part of the research programme RiverCare, supported by the
Dutch Technology Foundation STW (currently TTW), which is part of the
Netherlands Organization for Scientific Research (NWO), and which is partly
funded by the Ministry of Economic Affairs under grant number P12-14
(Perspective Programme). The authors furthermore would like to thank the Dutch
Ministry of Infrastructure and Environment (Rijkswaterstaat), Service
Publique de Wallonie, Direction générale opérationnelle de la
Mobilité et des Voies hydrauliques, Département des Etudes et de
l'Appui à la Gestion, Direction de la Gestion hydrologique
intégrée, HYDRO Bank MEEDDAT (Direction Générale de la
Prévention des Risques/Service des Risques Naturels et
Hydrauliques)/DGPR/SRNH and Dutch water boards “De Dommel” and “Aa en Maas”
in collaboration with STOWA, Dutch Foundation of Applied Water Research, for
providing discharge and water level data. In addition, the authors
acknowledge the E-OBS dataset from the EU-FP6 project ENSEMBLES
(http://ensembles-eu.metoffice.com, last access: 24 October 2018) and the
data providers in the ECA & D project (http://www.ecad.eu, last access: 24 October 2018). Data can be
requested at the aforementioned organizations. The authors furthermore would
like to thank Michelle Berg for organizing a meeting with the water managers
to evaluate the problems together with Pim van Santen for helping out
with the datasets. The authors would also like to thank their colleagues
Lieke Melsen and Claudia Brauer for reading the first drafts.
Edited by: Fabrizio Fenicia
Reviewed by: Paul Bates and one anonymous referee
Arvor, D., Funatsu, B., Michot, V., and Dubreui, V.: Monitoring rainfall patterns in the southern amazon with PERSIANN-CDR data: Long-term characteristics and trends, Remote Sensing, 9, 889, https://doi.org/10.3390/rs9090889, 2017. a
Berger, H. E. J.: Flow forecasting for the river Meuse, TU Delft, Delft University of Technology, Delft, the Netherlands, 1992. a
Betterle, A., Schirmer, M., and Botter, G.: Characterizing the spatial correlation of daily streamflows, Water Resour. Res., 53, 1646–1663, https://doi.org/10.1002/2016WR019195, 2017. a, b
Buarque, D., De Paiva, R., Clarke, R., and Mendes, C.: A comparison of Amazon rainfall characteristics derived from TRMM, CMORPH and the Brazilian national rain gauge network, J. Geophys. Res.-Atmos., 116, D19105, https://doi.org/10.1029/2011JD016060, 2011. a
de Wit, M., Peeters, H., Gastaud, P., Dewil, P., Maeghe, K., and Baumgart, J.: Floods in the Meuse basin: Event descriptions and an international view on ongoing measures, Int. J. River Basin Manage., 5, 279–292, 2007. a, b, c
Dupas, R., Tavenard, R., Fovet, O., Gilliet, N., Grimaldi, C., and Gascuel-Odoux, C.: Identifying seasonal patterns of phosphorus storm dynamics with dynamic time warping, Water Resour. Res., 51, 8868–8882, https://doi.org/10.1002/2015WR017338, 2015. a, b, c
European Climate: Assessment & Dataset, available at: https://www.ecad.eu/, last access: 24 October 2018. a
Gaál, L., Szolgay, J., Kohnová, S., Parajka, J., Merz, R., Viglione, A., and Blöschl, G.: Flood timescales: Understanding the interplay of climate and catchment processes through comparative hydrology, Water Resour. Res., 48, W04511, https://doi.org/10.1029/2011WR011509, 2012. a
Haylock, M., Hofstra, N., Klein Tank, A., Klok, E., Jones, P., and New, M.: A European daily high-resolution gridded data set of surface temperature and precipitation for 1950–2006, J. Geophys. Res.-Atmos., 113, D20119, https://doi.org/10.1029/2008JD010201, 2008. a
Hidayat, H., Vermeulen, B., Sassi, M., Torfs, F. P., and Hoitink, A.: Discharge estimation in a backwater affected meandering river, Hydrol. Earth Syst. Sci., 15, 2717–2728, https://doi.org/10.5194/hess-15-2717-2011, 2011. a
Hidayat, H., Teuling, A. J., Vermeulen, B., Taufik, M., Kastner, K., Geertsema, T. J., Bol, D. C. C., Hoekman, D. H., Haryani, G. S., Van Lanen, H. A. J., Delinom, R. M., Dijksma, R., Anshari, G. Z., Ningsih, N. S., Uijlenhoet, R., and Hoitink, A. J. F.: Hydrology of inland tropical lowlands: the Kapuas and Mahakam wetlands, Hydrol. Earth Syst. Sci., 21, 2579–2594, https://doi.org/10.5194/hess-21-2579-2017, 2017. a
Hydro: Eaufrance, available at: http://www.hydro.eaufrance.fr/, last access: 24 October 2018. a
IJpelaar, R., Groot, S., and Van de Wouw, M.: De trits van hoogwatergolven Aa, Dommel en Maas bij 's-Hertogenbosch, H2O, 6, 33–35, 2009. a
Jansen, P., Van Bendegom, L., Van den Berg, J., De Vries, M., and Zanen, A.: Principles of river engineering: The non-tidal alluvial river, Delftse Uitgevers Maatschappij, Delft, the Netherlands, 64–65, 1994. a
Keogh, E. and Ratanamahatana, C.: Exact indexing of dynamic time warping, Knowledge Inform. Syst., 7, 358–386, https://doi.org/10.1007/s10115-004-0154-9, 2005. a
Keogh, E. J. and Pazzani, M. J.: Derivative Dynamic Time Warping, in: Sdm, vol. 1, SIAM, Chicago, IL, USA, 5–7, 2001. a
Kew, S., Selten, F., Lenderink, G., and Hazeleger, W.: The simultaneous occurrence of surge and discharge extremes for the Rhine delta, Nat. Hazards Earth Syst. Sci., 13, 2017–2029, https://doi.org/10.5194/nhess-13-2017-2013, 2013. a
Klerk, W., Winsemius, H., Van Verseveld, W., Bakker, A., and Diermanse, F.: The co-incidence of storm surges and extreme discharges within the Rhine-Meuse Delta, Environ. Res. Lett., 10, 035005, https://doi.org/10.1088/1748-9326/10/3/035005, 2015. a
Kruskal, J. and Liberman, M.: The symmetric time warping problem: from continuous to discrete, Time warps, string edits and macromolecules: The theory and practice of sequence comparison, Addison-Wesley, with a foreword by John Nerbonne, CSLI Publications, Stanford, CA, 125–161, 1983. a
Leander, R., Buishand, A., Aalders, P., and De Wit, M.: Estimation of extreme floods of the River Meuse using a stochastic weather generator and a rainfall-runoff model, Hydrolog. Sci. J., 50, 1089–1104, https://doi.org/10.1623/hysj.2005.50.6.1089, 2005. a, b
Marchi, L., Borga, M., Preciso, E., and Gaume, E.: Characterisation of selected extreme flash floods in Europe and implications for flood risk management, J. Hydrol., 394, 118–133, https://doi.org/10.1016/j.jhydrol.2010.07.017, 2010. a
Marengo, J., Liebmann, B., Kousky, V., Filizola, N., and Wainer, I.: Onset and end of the rainy season in the Brazilian Amazon Basin, J. Climate, 14, 833–852, https://doi.org/10.1175/1520-0442(2001)014<0833:OAEOTR>2.0.CO;2, 2001. a
Meade, R., Rayol, J., Da Conceicão, S., and Natividade, J.: Backwater effects in the Amazon River basin of Brazil, Environ. Geol. Water Sci., 18, 105–114, https://doi.org/10.1007/BF01704664, 1991. a, b, c
Melone, F., Corradini, C., and Singh, V.: Lag prediction in ungauged basins: An investigation through actual data of the upper Tiber River valley, Hydrol. Process., 16, 1085–1095, https://doi.org/10.1002/hyp.313, 2002. a
Merz, R. and Blöschl, G.: A process typology of regional floods, Water Resour. Res., 39, 1340, https://doi.org/10.1029/2002WR001952, 2003. a
Ouyang, R., Ren, L., Cheng, W., and Zhou, C.: Similarity search and pattern discovery in hydrological time series data mining, Hydrol. Process., 24, 1198–1210, https://doi.org/10.1002/hyp.7583, 2010. a, b
Pattison, I., Lane, S., Hardy, R., and Reaney, S.: The role of tributary relative timing and sequencing in controlling large floods, Water Resour. Res., 50, 5444–5458, https://doi.org/10.1002/2013WR014067, 2014. a
Rakovec, O., Hazenberg, P., Torfs, F. P., Weerts, A., and Uijlenhoet, R.: Generating spatial precipitation ensembles: Impact of temporal correlation structure, Hydrol. Earth Syst. Sci., 16, 3419–3434, https://doi.org/10.5194/hess-16-3419-2012, 2012. a
Rijkswaterstaat: Waterdata, available at: https://www.rijkswaterstaat.nl/water/waterdata-en-waterberichtgeving/waterdata/index.aspx, last access: 24 October 2018. a
Service public de Wallonie: Annuaires et statistiques, available at: http://voies-hydrauliques.wallonie.be/opencms/opencms/fr/hydro/Archive/annuaires/index.html, last access: 24 October 2018. a
Sholtes, J. and Doyle, M.: Effect of channel restoration on flood wave attenuation, J. Hydraul. Eng., 137, 196–208, https://doi.org/10.1061/(ASCE)HY.1943-7900.0000294, 2011. a
Skøien, J., Blöschl, G., and Western, A.: Characteristic space scales and timescales in hydrology, Water Resour. Res., 39, 1223, https://doi.org/10.1029/2002WR001736, 2003. a
Turner-Gillespie, D., Smith, J., and Bates, P.: Attenuating reaches and the regional flood response of an urbanizing drainage basin, Adv. Water Resour., 26, 673–684, https://doi.org/10.1016/S0309-1708(03)00017-4, 2003. a
Van de Beek, C. Z., Leijnse, H., Torfs, P. J. J. F., and Uijlenhoet, R.: Climatology of daily rainfall semi-variance in The Netherlands, Hydrol. Earth Syst. Sci., 15, 171–183, https://doi.org/10.5194/hess-15-171-2011, 2011. a
Van de Beek, C. Z., Leijnse, H., Torfs, P. J. J. F., and Uijlenhoet, R.: Seasonal semi-variance of Dutch rainfall at hourly to daily scales, Adv. Water Resour., 45, 76–85, https://doi.org/10.1016/j.advwatres.2012.03.023, 2012. a
van Den Hurk, B., Van Meijgaard, E., De Valk, P., Van Heeringen, K.-J., and Gooijer, J.: Analysis of a compounding surge and precipitation event in the Netherlands, Environ. Res. Lett., 10, 035001, https://doi.org/10.1088/1748-9326/10/3/035001, 2015. a
Vorogushyn, S. and Merz, B.: Flood trends along the Rhine: The role of river training, Hydrol. Earth Syst. Sci., 17, 3871–3884, https://doi.org/10.5194/hess-17-3871-2013, 2013. a, b, c
Woltemade, C. and Potter, K.: A watershed modeling analysis of fluvial geomorphologic influences on flood peak attenuation, Water Resour. Res., 30, 1933–1942, https://doi.org/10.1029/94WR00323, 1994. a





