the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Analysis of combined and isolated effects of land-use and land-cover changes and climate change on the upper Blue Nile River basin's streamflow
Dagnenet Fenta Mekonnen
Zheng Duan
Tom Rientjes
Markus Disse
Understanding responses by changes in land use and land cover (LULC) and climate over the past decades on streamflow in the upper Blue Nile River basin is important for water management and water resource planning in the Nile basin at large. This study assesses the long-term trends of rainfall and streamflow and analyses the responses of steamflow to changes in LULC and climate in the upper Blue Nile River basin. Findings of the Mann–Kendall (MK) test indicate statistically insignificant increasing trends for basin-wide annual, monthly, and long rainy-season rainfall but no trend for the daily, short rainy-season, and dry season rainfall. The Pettitt test did not detect any jump point in basin-wide rainfall series, except for daily time series rainfall. The findings of the MK test for daily, monthly, annual, and seasonal streamflow showed a statistically significant increasing trend. Landsat satellite images for 1973, 1985, 1995, and 2010 were used for LULC change-detection analysis. The LULC change-detection findings indicate increases in cultivated land and decreases in forest coverage prior to 1995, but forest area increases after 1995 with the area of cultivated land that decreased. Statistically, forest coverage changed from 17.4 % to 14.4%, by 12.2 %, and by 15.6 %, while cultivated land changed from 62.9 % to 65.6 %, by 67.5 %, and by 63.9 % from 1973 to 1985, in 1995, and in 2010, respectively. Results of hydrological modelling indicate that mean annual streamflow increased by 16.9 % between the 1970s and 2000s due to the combined effects of LULC and climate change. Findings on the effects of LULC change on only streamflow indicate that surface runoff and base flow are affected and are attributed to the 5.1 % reduction in forest coverage and a 4.6 % increase in cultivated land areas. The effects of climate change only revealed that the increased rainfall intensity and number of extreme rainfall events from 1971 to 2010 significantly affected the surface runoff and base flow. Hydrological impacts by climate change are more significant as compared to the impacts of LULC change for streamflow of the upper Blue Nile River basin.
- Article
(7611 KB) -
Supplement
(487 KB) - BibTeX
- EndNote
The Abay (upper Blue Nile) River in Ethiopia contributes more than 60 % of the water resources in the Nile River (McCartney et al., 2012). Due to the high potential of Abay river flows, the Ethiopian government has conducted a series of studies since 1964 (USBR, 1964) for supporting national development and reducing poverty (BCEOM, 1998) by increasing the number of water storage reservoirs in the upper Blue Nile River basin (UBNRB), both for irrigation and hydropower development. As a result, large-scale irrigation and hydropower projects such as the Grand Ethiopian Renaissance Dam (GERD), which will be the largest dam in Africa after completion, have been planned and realised along the main stem of the Blue Nile River. However, its hydrology exhibits high seasonal flows, as influenced by large variations in climate, altitude and topography, and land-use and land-cover (LULC) change. Over the past decades, changes in climate (e.g. Haile et al., 2017) and changes in LULC (e.g. Woldesenbet et al., 2017b) have affected the magnitude of streamflow. Effective planning, management, and the regulation of water resource development is therefore required to avert conflicts between the competing water users.
Only the understanding of the hydrological processes and sources impacting water quantity, such as LULC change and climate change, can achieve this, as they are the key driving forces that can modify the watershed's hydrology and water availability (Oki and Kanae, 2006; Woldesenbet et al., 2017b; Yin et al., 2017). LULC change can modify the rainfall path to generate basin runoff by altering critical water-balance components, such as groundwater recharge, infiltration, interception, and evaporation. McCartney et al. (2012) and Alemseged and Tom (2015) described that the UBNRB experiences significant spatial and temporal climate variability. Less than 500 mm of precipitation falls annually near the Sudanese border, whereas more than 2000 mm falls annually in some areas of the southern basin (Awulachew et al., 2009). Potential evapotranspiration (ET) also varies considerably and is strongly correlated with altitude. At annual bases, it varies from more than 2200 mm near the Sudanese border to between about 1300 and 1700 mm in the Ethiopian highlands (McCartney et al., 2012). The precipitation and ET cycles are characterised by seasonal and inter-annual variability, which affect the characteristics of the UBNRB streamflow.
A literature review shows that several sub-basin or basin level studies were conducted in the UBNRB. Most of the studies focused on the trend analysis of precipitation and streamflow (see Bewket and Sterk, 2005; Cheung et al., 2008; Conway, 2000; Gebremicael et al., 2013; Melesse et al., 2009; Rientjes et al., 2011; Seleshi and Zanke, 2004; Teferi et al., 2013; Tekleab et al., 2014; Tesemma et al., 2010), and all reported no significant trend in annual and seasonal precipitation totals within the Lake Tana sub-basin, whereas Mengistu et al. (2014) reported statistically non-significant increasing trends in annual and seasonal rainfall series, except for a short rainy season (Belg) from February to May.
Gebremicael et al. (2013) reported statistically significant increasing long-term annual streamflow (1970–2005) at the El Diem gauging station for the UBNRB's streamflow. However, Tesemma et al. (2010) reported no statistically significant trend for long-term annual streamflow (1964–2003) at the El Diem gauging station but did report a significantly increasing trend at the Bahir Dar and Kessie stations. At the sub-basin scale, Rientjes et al. (2011) reported a decreasing trend for the low flows of Gilgel Abay sub-basin (Lake Tana catchment, the Blue Nile headwaters) during the 1973–2005 period, specifically of 18.1 % and 66.6 % in the periods 1982–2000 and 2001–2005, respectively. However, the high flows for the same periods show an increase of 7.6 % and 46.6 % due to LULC change and seasonal rainfall variability.
Although progress has been made in assessing the impacts of LULC and climate change on the UBNRB's hydrology, only a few studies have endeavoured to assess the attribution of changes in the water balance to LULC change and climate change. Woldesenbet et al. (2017b), used partial-least-squares regression (PLSR) and a modelling approach based on the Soil and Water Assessment Tool (SWAT) to quantify the contributions of changes in individual LULC classes to changes in hydrological components in the Lake Tana and Beles sub-basins. Woldesenbet et al. (2017b) reported that increases in cultivated land area and decreases in woody shrub and woodland appear to be major environmental stressors affecting local water resources through, for example, increasing surface runoff and decreasing ground water contribution in both watersheds; however, the impacts of climate change were not considered. Nonetheless, proper water resource management requires an in-depth understanding of the aggregated and disaggregated effects of LULC and climate change on streamflow, and water-balance components such as the interaction between LULC, climate characteristics, and the underlying hydrological processes are complex and dynamic (Yin et al., 2017).
This study's objectives are therefore to (i) assess the long-term trend of rainfall and streamflow, (ii) analyse LULC change, and (iii) examine streamflow responses to the combined and isolated effects of LULC and climate change in the UBNRB. This is doable by combining the analysis of statistical trend tests, the change detection of LULC derived from satellite remote sensing, and hydrological modelling during the 1971–2010 period.
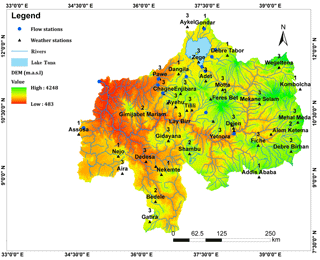
The UBNRB is located in north-western Ethiopia. Its catchment area is about 172 760 km2. Highlands, hills, valleys, and occasional rock peaks with elevations ranging from 500 to above 4000 m a.s.l. typically characterise the basin's topography (Fig. 1). According to BCEOM (1998), two-thirds of the basin lies in Ethiopia's highlands, with annual rainfall ranging from 800 to 2200 mm. The central and south-eastern areas are characterised by relatively high rainfall (1400 to 2200 mm), whereas in most of the eastern and north-western parts of the basin, rainfall is less than 1200 mm. Fenta Mekonnen and Disse (2018) showed that the UBNRB has a mean areal annual rainfall of 1452 mm and mean annual minimum and maximum temperatures of 11.4 and 24.7 ∘C, respectively.
Table 1The UBNRB's areal long-term (1971–2010) mean annual and seasonal rainfall and streamflow.
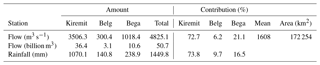
Kiremit: long rainy season, Belg: short rainy season, Bega: dry season.
The subtropical climate of the basin is affected by the movement of the intertropical convergence zone (ITCZ; Conway, 2000; Mohamed et al., 2005). NMA (2013) classified the climate in Ethiopia into three distinct seasons. The main rainy season (Kiremit) generally lasts from June to September, during which south-western winds bring rains from the Atlantic Ocean. Some 70 %–90 % of the total rainfall occurs during this season. A dry season (Bega) lasts from October to January, and the short rainy season (Belg) lasts from February to May. According to BCEOM (1998), the average annual discharge (1960 to 1992) at the Ethiopia–Sudan border (El Diem) is about 49.4 billion m3, with the low-flow month (April) equivalent to less than 2.5 % of that of the high-flow month (August). The analysis of this study revealed that the long-term (1971–2010) mean annual volume of streamflow at El Diem is 50.7 billion m3, with low streamflow volume (dry season) contributing 21.1 % and the short rainy season contributing about 6.2 %. As such, some 73 % of streamflow occurred during the rainy season (Table 1). The basin's land cover essentially follows the divide between highland and lowland. Predominantly farmlands (about 90 %), bush and shrubs cover the highlands. The lowlands, in contrast, are still largely untouched by development. As a result, woodlands, bush, and shrubs are the dominant forms of land cover (BCEOM, 1998).
In this study, non-parametric Mann–Kendall (MK; Kendall, 1975; Mann, 1945) statistics and the SWAT, developed by the Agricultural Research Service of the United States Department of Agriculture (USDA-ARS; Arnold et al., 1998), are used for statistical trend analysis and water-balance modelling, respectively. Details of both methods are available in Sect. 4. The input data sets used for the SWAT model can be categorised into those containing weather and streamflow data and spatially distributed data sets.
3.1 Weather and streamflow data
The daily weather variables used in this study for trend analysis and for driving the water-balance model are precipitation, minimum air temperature (Tmin), maximum air temperature (Tmax), relative humidity (RH), hours of sunshine (SH), and wind speed (WS). Weather data from 40 meteorological stations were obtained from the Ethiopian National Meteorological Services Agency (ENMSA) for the 1971–2010 period. Daily streamflow data for 25 gauging stations were collected from the Federal Ministry of Water, Irrigation and Electricity of Ethiopia for the same period 1971–2010. After screenings and rigorous analyses of the weather data, a considerable amount of time series data were found to be missing in most of the stations (see Table S1 in the Supplement). The occurrences of civil war and defective and outdated devices were the main causes for the missing data records. As a result, only the 15 stations (Fig. 1) in which rainfall data are relatively more complete proved to be suitable for trend analysis. Some 10 stations having complete climate variables, such as Tmax, Tmin, RH, WS, and SH, were used as input for the SWAT model (Fig. 1).
We resorted to spatial interpolation techniques, such as the inverse distance weighting (IDW) and linear regression (LR), to fill the gaps. Uhlenbrook et al. (2010) applied similar approaches or methods to the Gilgel Abbay sub-basin, which is the UBNRB's headwater. The selection and number of adjacent stations for interpolation are important for the accuracy of interpolated values. As mentioned by Woldesenbet et al. (2017a), different authors used different criteria to select neighbouring stations. Because of the relatively low number of network stations, a geographic distance of 100 km was considered for most stations when selecting neighbouring stations. If no station was located within 100 km of the target station, then the search distance was increased until at least one suitable station is reached. After the neighbouring stations were selected, the two methods (IDW and LR) were tested by means of cross-validation to fill in missing data sets. The candidate methods' performances were evaluated using the statistical metrics such as the root-mean-square error (RMSE), mean absolute error (MAE), correlation coefficient (R2), and percent bias (% bias) between observed and estimated values for the target stations. Equally weighted statistical metrics are applied to compare the performances of selected methods at target stations and to establish the ranking. A score was assigned to each candidate method according to the individual metrics. For example, the candidate achieving the smallest values of RMSE and MAE or the smallest percentage of bias received score 1, and score 2 was assigned to the one with the larger value. The final score is obtained by summing up the score pertaining to each candidate approach at each station. The method with the smallest score is the best. The monthly, seasonal, and annual weather data were aggregated from the daily time series data after filling the gaps. While filling in the missing data, uncertainty is expected due to low station density, poor correlations, and the considerable number of missing records. Similar techniques and approaches were used for the analysis and filling in of missing streamflow data records.
3.2 Spatial data
Spatially distributed data required for the SWAT model includes tabular and spatial soil data, tabular and spatial LULC information, and elevation data. A Shuttle Radar Topographic Mission digital elevation model (SRTM DEM) with a resolution of 90 m from the Consultative Group on International Agricultural Research – Consortium for Spatial Information (CGIAR-CSI; http://srtm.csi.cgiar.org/SELECTION/inputCoord.asp, last access: 21 February 2015) – was used to represent land-surface drainage patterns. Terrain characteristics, such as slope gradient and the slope length of the terrain, and stream network characteristics, such as channel slope, length, and width, were derived from the digital elevation model (DEM).
The soil map (1:5 000 000) developed by the Food and Agriculture Organization of the United Nations (FAO-UNESCO) was downloaded from http://www.fao.org/soils-portal/soil-survey/soil-maps-and-databases/faounesco-soil-map-ofthe-world/en/, last access: 4 April 2017. Soil information, such as the soil textural and physiochemical properties needed for the SWAT model, were extracted from the Harmonized World Soil Database v1.2, a database that combines existing regional and national soil information (http://www.fao.org/soils-portal/soil-survey/soil-maps-and-databases/harmonized-world-soil-databasev12/en/, last access: 4 April 2017) with information provided by the FAO-UNESCO soil map (Polanco et al., 2017).
The LULC maps were produced from satellite-remote-sensing Landsat images for 1973, 1985, 1995, and 2010 at a scale of 30 m × 30 m resolution. Detailed descriptions on image processing and classification are available under Sect. 4.2.
4.1 Trend analysis
The non-parametric Mann-Kendall (MK; Kendall, 1975; Mann, 1945) statistic is chosen to detect trends for rainfall and streamflow time series data, as it is widely used for water resource planning, design, and management (Yue and Wang, 2004). Its advantage over parametric tests such as t test is that the MK test is more suitable for non-normally distributed and missing data, which are frequently encountered in hydrological time series (Yue et al., 2004). However, the existence of positive serial correlation in time series data affects the MK test results. If serial correlation exists in time series data, the MK test rejects the null hypothesis of no trend detection more often than specified by the significance level (Von Storch, 1995).
Von Storch (1995) proposed a prewhitening technique to limit the influence of serial correlation on the MK test. The effective or equivalent sample size (ESS) method developed by Hamed and Rao (1998) has also been proposed to modify the variance. However, the study by Yue et al. (2002) reported that von Storch's prewhitening is effective only when no trend exists, and the ESS approach's rejection rate after modifying the variance is much higher than the actual (Yue et al., 2004). Yue et al. (2002) then proposed trend-free prewhitening (TFPW) prior to applying the MK trend test in order to minimise its limitation. This study therefore employed TFPW to remove the serial correlation and to detect a trend in time data series with significant serial correlation. Further details can be found in (Yue et al., 2002). All the trend results in this study have been evaluated at the 5 % level of significance to ensure the effective exploration of the trend.
4.2 Change point test
The Pettitt test is used to identify whether or not there is a point change or jump in the data series (Pettitt, 1979). This method detects one unknown change point by considering a sequence of random variables that may have a change point at N, if the Xt variable for , …, N time step has a common distribution function, F1(x), and Xt for , …; T time step has a common distribution function, F2(x), where F1(x) ≠ F2(x).
4.3 Sen's slope estimator
The trend magnitude is estimated using a non-parametric median-based slope estimator proposed by (Sen, 1968), as it is not greatly affected by gross data errors or outliers and can be computed when data are missing. The slope estimation is given by
where xj and xk are the sequential data values, and n is the number of the recorded data. , and β is considered as the median of all possible combinations of pairs for the whole data set. A positive value of β indicates an upward (increasing) trend, and a negative value indicates a downward (decreasing) trend in the time series. All MK trend tests, Pettitt change-point detections, and Sen's slope analyses were conducted using the XLSTAT add-in tool from Excel (https://www.xlstat.com).
4.4 Remote-sensing land-use and land-cover map
4.4.1 Landsat image acquisition
Landsat images from the years 1973, 1985, 1995, and 2010 were accessed from the US Geological Survey (USGS) Center for Earth Resources Observation and Science (EROS) via http://glovis.usgs.gov (last access: 29 December 2016). The Landsat images were selected based on the criteria of the acquisition period, availability, and percentage of cloud cover. Hayes and Sader (2001) recommend acquiring images from the same acquisition period to reduce the image-to-image variation caused by the sun angle, soil moisture, atmospheric condition, and vegetation-phenology differences. Cloud-free images were hence collected for the dry months of January to May. However, as the basin covers a large area, each of the LULC map's periods comprised 16 Landsat images. Accessing all the images during a dry season in a single year was therefore difficult. Hence, images were acquired ± 1 year for each time period, and some images were also acquired in the months of November and December. For example, 16 Landsat MSS image scenes were acquired in 1973 (10 images in January, four images in December and two images in November; ±1 year) and were merged to arrive at one LULC representation for selected years. Please see Table S2 in the Supplement for the details on Landsat images.
4.4.2 Preprocessing and processing images
Several standard preprocessing methods, including geometric and radiometric correction, were implemented to prepare the LULC maps from Landsat images. Although many different classification methods exist, supervised and unsupervised classifications are the two most widely used methods for land-cover classification from remote-sensing images. Hence, in this study, a hybrid supervised and unsupervised classification approach was adopted to classify the images from 2010 (LandsatTM). Iterative self-organising data analysis (ISODATA) clustering was first performed to determine the image's spectral classes or land cover classes. Polygons for all of the training samples based on the identified LULC classes were then digitised using ground truth data. The samples for each land cover type were then aggregated. Finally, a supervised classification was performed using a maximum likelihood algorithm to extract four LULC classes.
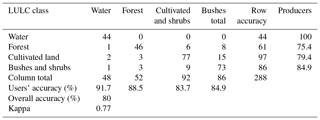
A total of 488 ground control points (GCPs) regarding land-cover types and their spatial locations were collected from field observations in March and April 2017 using a global positioning system (GPS). Reference data were collected and taken from areas where there had not been any significant land-cover change between 2017 and 2010. These areas were identified by interviewing local elderly people and were supplemented using high-resolution Google Earth images and the first author's prior knowledge. As many as 288 GCPs were used for accuracy assessment, and 200 points served as training sites to generate a signature for each land-cover type. The classifications' accuracy was assessed by computing the error matrix (also known as the confusion matrix), which compares the classification result with ground truth information as suggested by DeFries and Chan (2000). A confusion matrix lists the values for the reference data's known cover types in the columns and for the classified data in the rows (Banko, 1998), as shown in Table 5. From the confusion matrix, statistical metrics of overall accuracy, producers' accuracy, and users' accuracy are used. Another discrete multivariate technique useful in accuracy assessment is called KAPPA (Congalton, 1991). The statistical metric for KAPPA analysis is the Kappa coefficient, which is another measure of the proportion of agreement or accuracy. The Kappa coefficient is computed as
where r is the number of rows in the matrix, xii is the number of observations in row i and column i, and xi+ and x+i are the marginal totals of row i and column i, respectively. N is the total number of observations.
Once the land-cover classification of the year 2010 Landsat image had been completed and its accuracy checked, the normalised difference vegetation index (NDVI) differencing technique (Mancino et al., 2014) was applied to classify the images from 1973, 1985, and 1995. This technique was chosen to increase the accuracy of classification, as it is hard to find an accurately classified digital or analog LULC map of the study area during 1973, 1985, and 1995. The information obtained from the elders is also more subjective, and its reliability is questionable when there is a considerable time gap. We first calculated the NDVI from the Landsat MSS (1973) and three preprocessed Landsat TM images (1985, 1995, and 2010), following the general normalised difference between band TM4 and band TM3 images (Eq. 3). The resulting successive NDVI images were subtracted from each other to assess the ΔNDVI image with positive (vegetation increase), negative (vegetation cleared), and no changes at a 30 m × 30 m pixel resolution (Eqs. 4–6). The Landsat MSS 60 m × 60 m pixel-size data sets were resampled to a 30 m × 30 m pixel size using the “nearest neighbour” technique to have equal pixel sizes for the different images without altering the image data's original pixel values. This process is represented by the following:
The ΔNDVI image was then reclassified using a threshold value calculated as μ±nσ; where μ represents the ΔNDVI pixels value mean, and σ represents the standard deviation. The threshold identifies three ranges in the normal distribution: (a) the left tail (), (b) the right tail (), and (c) the central region of the normal distribution (). Pixels within the two tails of the distribution are characterised by significant land-cover changes, whereas pixels in the central region represent no change. To be more conservative, n=1 was selected for this study in order to narrow the threshold ranges for reliable classification. The standard deviation (σ) is one of the most widely applied threshold identification approaches for different natural environments based on different remotely sensed imagery (Hu et al., 2004; Jensen, 1996; Lu et al., 2004; Mancino et al., 2014; Singh, 1989), as cited by Mancino et al. (2014).
ΔNDVI pixel values (2010–1995) in the central region of the normal distribution () represent an absence of land-cover change between two different periods (i.e. 1995 and 2010); therefore, pixels from 1995 corresponding to no land-cover change can be classified as similar to the 2010 land-cover classes. Pixels with significant NDVI changes are reclassified using supervised classification, taking signatures from the already classified, no-change pixels. Likewise, 1985 and 1973 land-cover images were classified based on the classified images of 1995 and 1985, respectively. Finally, after classifying the raw Landsat images into different land-cover classes, change detection, which requires the comparison of independently produced classified images (Singb, 1989), was performed by the post-classification method. The post-classification change-detection comparison was conducted to determine changes in LULC between two independently classified maps of images from two different dates. Although this technique has some limitations, it is the most common approach, because it does not require data normalisation between two dates (Singh, 1989). This is because data from two dates are separately classified, thereby minimising the problem of normalisation for atmospheric and sensor differences between two dates.
4.5 SWAT hydrological model
The SWAT is an open-source-code, semi-distributed model with a large and growing number of model applications in a variety of studies, ranging from catchment to continental scales (Allen et al., 1998, 2012; Neitsch et al., 2002). It enables the impact of LULC change and climate change on water resources to be evaluated in a basin with varying soil, land-use, and management practices over a set period of time (Arnold et al., 2012).
In SWAT, the watershed is divided into multiple sub-basins, which are further subdivided into hydrological response units (HRUs) consisting of homogeneous land-use management, slope, and soil characteristics (Arnold et al., 1998; Arnold et al., 2012). HRUs are the smallest units of the watershed in which relevant hydrologic components, such as evapotranspiration, surface runoff and peak rate of runoff, groundwater flow, and sediment yield, can be estimated. Water balance is the driving force behind all of the processes in the SWAT calculated using Eq. (7),
where SWt is the final soil-water content (mm H2O), SWo is the initial soil-water content on day i (mm H2O), t is the time (days), Rday is the amount of precipitation on day i (mm H2O), Qs is the amount of surface runoff on day i (mm H2O), Ql is the amount of return flow on day i (mm H2O), Qb is the return flow from the shallow aquifer on day i (mm H2O), Ea is the amount of evapotranspiration from the canopy and soil surface on day i (mm H2O), Revap is the amount of water transferred from the underlying shallow aquifer reversely upward to the soil-moisture storage on day i (mm H2O) in response to water demand for evapotranspiration, and DA_recharge is the amount of water recharge to the deep aquifer on day i (mm H2O).
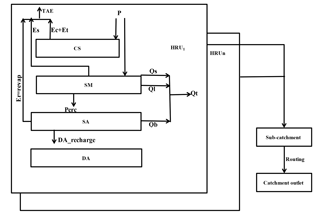
Figure 2Schematic representation of the SWAT model structure modified from Marhaento et al. (2017). P is precipitation; CS is canopy storage; TAE is total actual evapotranspiration; Ec is evaporation from the canopy surface; Es is evaporation from the soil surface; Et is transpiration from plants; Perc is percolation from the soil storage to shallow aquifer; SM is soil-moisture storage; SA is shallow aquifer; Er = Revap is evaporation from the shallow aquifer; Qt is total streamflow; DA is deep aquifer; HRU is hydrological response unit; Qb is base flow; Ql is lateral flow; and Qs is surface runoff.
Runoff is calculated separately for each HRU and routed to obtain the total streamflow for the watershed using either the soil-conservation-service (SCS) curve-number (CN) method (Mockus, 1964) or the Green–Ampt infiltration method (GAIM; Green and Ampt, 1911; see Fig. 2). However, spatial connectivity and interactions among HRUs are ignored. Instead, the cumulative output of each spatially discontinuous HRU at the sub-watershed outlet is directly routed to the channel (Pignotti et al., 2017). This lack of spatial connectivity among HRUs makes implementation and the impact analysis of spatially targeted management such as the soil-and-water conservation structure difficult to incorporate into the model. Different authors have made efforts to overcome this problem, for instance, a grid-based version of the SWAT model (Rathjens et al., 2015) or a landscape simulation on a regularised grid (Rathjens and Oppelt, 2012). Moreover, Arnold et al. (2010) and Bosch et al. (2010) further modified SWAT so that it allows landscapes to be subdivided into catenas comprising upland, hillslope, floodplain units, and flow to be routed through these catenas. However, the SWAT grid, developed to overcome this limitation, remains largely untested and computationally demanding (Rathjens et al., 2015).
Hence, the standard SWAT CN method was chosen for this study, because it was applied in many Ethiopian watersheds (Gashaw et al., 2018; Gebremicael et al., 2013; Setegn et al., 2008; Woldesenbet et al., 2017b). Furthermore, its ability to use daily input data (Arnold et al., 1998; Neitsch et al., 2011; Setegn et al., 2008) as compared to the GAIM, which requires subdaily precipitation as a model input that can be difficult to obtain in data-scarce regions like the UBNRB. This study focused on the effects of LULC change and climate change on the basin's water-balance components, which include the components of inflows, outflows, evapotranspiration, losses, and the change in storage as shown in the general water balance in Eq. (8).
where and total actual evapotranspiration TAE = , as shown in Fig. 2.
R is the amount of precipitation (mm d−1) as the main inflow, Qt is the total amount of streamflow (mm d−1) as outflow, TAE is the total actual evapotranspiration (mm d−1), Ec is evaporation from the canopy surface (mm d−1), Et is the amount of plant transpiration (mm d−1), Es is evaporation from the soil surface (mm d−1), Er or Revap is evaporation from the shallow aquifer (mm d−1; Abiodun et al., 2018), losses are the amount of water lost from the system as a recharge to the deep aquifer (DA_recharge; mm d−1), and ΔS is the change in soil-water storage (mm d−1). SWAT has four storages: canopy storage (CS), soil moisture (SM), shallow aquifer (SA), and deep aquifer (DA). Water movement from the soil-moisture storage to the shallow aquifer is due to percolation, whereas water movement from the shallow aquifer reversely upward to the soil-moisture storage is Revap, and further water movement from the shallow aquifer to the deep aquifer is recharge. For a more detailed description of the SWAT model, refer to Neitsch et al. (2011).
The SWAT model set-up and data preparation were done using the ArcSWAT2012 tool in the ArcGIS environment, whereas parameter sensitivity analysis and model calibration and validation were performed using the SWAT-CUP (Calibration and Uncertainty Procedures) interface Sequential Uncertainty Fitting (SUFI-2) algorithm (Abbaspour, 2008). During model set-up, the observed daily weather and streamflow data from the given period were divided into three different periods: the first to warm up the model, the second to calibrate it, and the third to validate it. Determining the most sensitive parameters is the first step in the model calibration and validation process using the global sensitivity analysis option (Arnold et al., 2012). The second step is to complete the calibration process, making necessary adjustments for the model's input parameters to match model output with observed data, thereby reducing the prediction uncertainty. Initial parameter estimates were taken from the default lower and upper bound values of the SWAT model database and from earlier studies in the basin, such as that of Gebremicael et al. (2013). The final step, model validation, involves running a model using parameters that were determined during the calibration process and comparing the predictions to independently observed data not used in the calibration.
Table 2Data sets of the baseline and altered periods for the SWAT simulation used to analyse the combined and isolated effect of LULC and climate change on streamflow and water-balance components.

In this study, both manual and automatic calibration strategies were applied to attain the minimum differences between observed and simulated streamflows in terms of surface flow, peak flow, and total flow, following the steps recommended by Arnold et al. (2012). For the purpose of impact analysis, we divided the simulation period 1971–2010 into four decadal periods, hereafter referred as the 1970s (1971–1980), 1980s (1981–1990), 1990s (1991–2000), and 2000s (2001–2010), as shown in Table 2. The model's performance for the streamflow was then evaluated using statistical methods (Moriasi et al., 2007) such as the Nash–Sutcliffe coefficient of efficiency (NSE), the coefficient of determination (R2), and the relative volume error (RVE %), which are shown in Eq. (9)–(11). Furthermore, graphical comparisons of the simulated and observed data, as well as water-balance checks, were used to evaluate the model's performance. This evaluation may be represented by the following:
where Qm,i is the measured streamflow in m3 s−1, are the mean values of the measured streamflow (m3 s−1), Qs,i is the simulated streamflow in m3 s−1, and are the mean values of simulated data in m3 s−1.
4.6 SWAT simulations
Three different approaches were applied for assessing the effects of LULC change and climate change on streamflow and water-balance components. The first approach is to assess the response of streamflow to the combined effects of LULC change and climate change. We followed the approach in Marhaento et al. (2017) and divided the analysis period, 1971–2010, into four periods of similar length (four decades). These are periods when land-use changes are expected to change the hydrological regime within a catchment (Marhaento et al., 2017; Yin et al., 2017). The first period, the 1970s, was regarded as the baseline period. The other periods, the 1980s, 1990s, and 2000s, were regarded as altered periods. LULC maps of 1973, 1985, 1995, and 2010 were used to represent LULC patterns during the 1970s, 1980s, 1990s, and 2000s, respectively. For analyses, the SWAT model was calibrated and validated for each respective period using the respective LULC map and weather data (Table 2). The DEM and soil data sets remained unchanged. The differences between the simulation result of the baseline and altered periods represent the combined effects of LULC and climate change on streamflow and water-balance components.
The second approach included simulations that attribute the effects from LULC changes alone. It aimed to investigate whether LULC change is the main driver for changes in water-balance components. To identify the hydrological impacts caused solely by LULC, a “fixing–changing” method was used (Marhaento et al., 2017; Woldesenbet et al., 2017b; Yan et al., 2013; Yin et al., 2017). The calibrated and validated SWAT model and its parameter settings in the baseline period were forced by weather data from the baseline period, 1973–1980, while changing only the LULC maps from 1985, 1995, and 2010, keeping the DEM and soil data constant (Hassaballah et al., 2017; Marhaento et al., 2017; Woldesenbet et al., 2017b; Yin et al., 2017). We ran the calibrated SWAT model for the baseline period (1970s) four times, only changing the LULC map for the years 1973, 1985, 1995, and 2010 and retaining the constant weather data set from the 1970s (Table 2). The third approach is similar to the second, but the simulations are attributed only for climate change. The calibrated models for the baseline period were run again four times, corresponding to the LULC periods using a unique LULC map of the year 1973 but altering the four different periods of weather data sets for their respective periods.
5.1 Trend test
5.1.1 Rainfall
The summary of the MK trend test results for the rainfall recorded at the 15 selected stations located in and around the UBNRB revealed mixed trends (increasing, decreasing, and no changes). For daily time series, the computed probability values (p values) for seven stations were greater, although for eight stations, they were less than the selected significance level (α=5 %). This means that no statistically significant trend existed in seven stations, but a monotonic trend occurred in the remaining eight. Positive trends developed only at six stations, four of which were concentrated in the northern and central highlands (Bahir Dar, Dangila, Debre Markos, and Gimijabet Mariam). The other two stations, Assosa and Angergutten, are located in the south-western and southern lowlands (see Fig. 1). The other two stations, Alem Ketema and Nejo, which are located in the east and south-west of the UBNRB, respectively, showed a decreasing trend. On a monthly basis, the MK trend test result showed that no trend existed in 11 stations, while statistically non-significant increasing trends exist in 3 stations (Dangila, Gimijabet Mariam, and Shambu) and a decreasing trend exists in Alem Ketema station. On an annual timescale, MK trend test could not find any trend in 11 stations, but did exhibit a trend in 4 stations. The Debre Markos and Shambu stations showed statistically non-significant increasing trend, while Gimijabet Mariam and Alem Ketema showed statistically significant positive trends and non-significant decreasing trends, respectively. The trend analysis result for the annual rainfall time series agrees well with a previous study by Gebremicael et al. (2013), who reported no significant annual rainfall change at eight out of nine stations during the 1973–2005 period. Hence, it is interesting to note that the timescale of analysis is a critical factor in determining the given trends.
Table 3MK and Pettitt tests for the UBNRB's rainfall and streamflow after TFPW at different timescales.
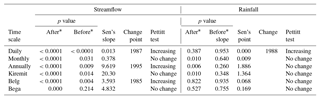
∗ Before and after TFPW; p probability at 5 % significance level.
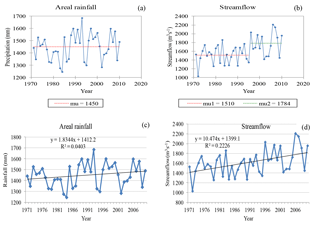
Figure 3The Pettitt homogeneity test's (a) annual rainfall, (b) annual flow of the UBNRB, (c) linear trend of mean annual rainfall, and (d) linear trend of mean annual streamflow, where mu is the mean annual precipitation (mm), mu1 is the mean annual precipitation before change (mm), and mu2 is the mean annual precipitation after change (mm).
The basin-wide areal UBNRB rainfall trend and change point analysis was again carried out on daily, monthly, seasonal, and annual timescales using the MK and Pettitt tests. We applied a widely used spatial interpolation technique, the Thiessen polygon method, to calculate basin-wide rainfall series from station data. A summary is provided in Table 3 and Fig. 3. The MK test showed increasing trends for annual, monthly, and long rainy-season rainfall series, whereas no trend for daily, short rainy, and dry season rainfall series appeared. The magnitude of trends for annual, monthly, and long rainy-season rainfall series are not statistically significant, as explained by the values of Sen's slope. However, the Pettitt test could not detect any jump point in basin-wide rainfall series except for daily time series rainfall (see Fig. S1 in the Supplement).
Previous studies (Conway, 2000; Gebremicael et al., 2013; Tesemma et al., 2010) conducted trend analyses of basin-wide rainfall and reported that no significant change in annual and seasonal rainfall series across the UBNRB exists, which contradicts the results of this study. This disagreement could be due to the number of stations and their spatial distribution across the basin, time period of the analysis, approach used to calculate basin-wide rainfall from gauging stations, and data sources. Tesemma et al. (2010) used monthly rainfall data downloaded from Global Historical Climatology Network (GHCN) database and 10 day rainfall data for the 10 selected stations obtained from the National Meteorological Service Agency of Ethiopia from 1963 to 2003. Conway (2000) also constructed basin-wide annual rainfall in the UBNRB for the 1900–1998 period from the mean of 11 gauges. Furthermore, (Conway, 2000) employed simple linear regressions over time to detect trends in annual rainfall series without removing the serial autocorrelation effects. Gebremicael et al. (2013), used only nine stations from the 1970–2005 period. However, in this study, we used daily observed rainfall data from 15 stations collected from Ethiopian Meteorological Agency from 1971 to 2010. The stations are more or less evenly distributed over the UBNRB.
5.1.2 Streamflow
The MK test's result for daily, monthly, annual, and seasonal (long and short rainy season and dry season) streamflow time series showed a positive trend, the magnitude of which is statistically significant, as summarised in Table 3. The Pettitt test also detected change points for daily, annual, and short rainy-season streamflow but did not detect change points for monthly, long, and dry season streamflow (see Figs. 3 and S2). The change point detected by the Pettitt test for annual streamflow is in 1995, whereas for daily and short rainy seasons, it is in 1985 and 1987, respectively. The result obtained from the MK test agrees well with the findings in Gebremicael et al. (2013), who reported an increasing trend in the observed annual, short, and long rain seasons' streamflow at the El Diem gauging station, but our results disagree with findings for dry-season streamflow. Furthermore, the increasing trend of long rainy-season streamflow agrees well with the result of Tesemma et al. (2010), but it disagrees with the results of short rainy season and annual flows. Tesemma et al. (2010) reported that the short rainy season and the annual flows are constant for the 1964–2003 period. This disagreement is likely attributable to the difference in analysis period, as can be seen from Fig. 3. The last 7 years, 2004–2010, had relatively higher streamflow records.
Although, the results of the MK test for annual and long rainy-season rainfall and streamflow show an increasing trend for the last 40 years in the UBNRB, the magnitude of Sen's slope for streamflow is much greater than it is for rainfall (Table 3). Moreover, short rainy-season streamflow shows a statistically significant positive increase, whereas the rainfall shows no change. The mismatch between the rainfall and the streamflow trend magnitude could be associated with evapotranspiration and could be attributable to the combined effect of LULC change, climate change, the infiltration rate due to changing soil properties, rainfall intensity, and extreme events.
5.2 LULC change analysis
According to the confusion-matrix report, with an overall accuracy of 80 %, a producer's accuracy values for all classes ranged from 75.4 % to 100 %, user's accuracy values ranged from 83.7 % to 91.7 %, and a kappa coefficient (k) of 0.77 was attained for the 2010 classified image (Table 5). Monserud (1990) suggested a kappa value of <40 % as poor, 40 %–55 % as fair, 55 %–70 % as good, 70 %–85 % as very good, and >85 % as excellent. According to these ranges, the classification in this study has very good agreement with the validation data set and meets the minimum accuracy requirements to be used for further change detection and impact analysis.

Figure 4Land-cover map of UBNRB derived from Landsat images from (a) 1973, (b) 1985, (c) 1995, and (d) 2010a (b).
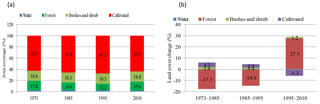
The classified images of the basin (Fig. 4) have shown different LULC proportions at four distinct time periods, as shown in Fig. 5. In 1973, cultivated land dominantly covered (62.9 %) the UBNRB, followed by bushes and shrubs (18 %), forest (17.4 %), and water (1.74 %). In 1985, cultivated land area increased to 65.6 %, followed by bushes and shrubs (18.3 %), while forest decreased to 14.4 %, and water remained unchanged at 1.7 %. In 1995, cultivated land area further increased to 67.5 %, followed by bushes and shrubs (18.5 %). Forest further decreased to 12.2 %, and water remained unchanged at 1.7 %. In 2010, cultivated land decreased to 63.9 %, bushes and shrubs increased to 18.8 %, forest increased to 15.6 %, and water remained unchanged at 1.7 %. During the entire 1973–2010 period, cultivated land, along with bushes and shrubs, remained the major proportions compared to the other LULC classes. The highest increase (2.7 %) and the largest decrease (−3.6 %) in cultivated land occurred during the 1973–1985 and 1995–2010 periods, respectively. The largest increase in bushes and shrubs was 0.3 % from 1973 to 1985, whereas the largest increase in forest coverage (3.4 %) was recorded during the 1995–2010 period. Water coverage remained unchanged from 1973 to 2010.
Although, the image classification results show very good accuracy, uncertainties in classification could be expected. First, as elsewhere in Ethiopia, LULC may change rapidly over the land surface of the basin, and image reflectance may be confusing due to the topography and variation in the image acquisition date. Landsat images were not all available for a particular year or season (as described under Sect. 4.2.1); images from different years and different seasons might harbour errors. Secondly, the workflow associated with LULC classification involves many steps and can be a source of uncertainty. The errors are observed in the classified LULC map, as shown in Fig. 4. On the western side of the map in Fig. 4a, a rectangular section with forest appears, which completely disappears in Fig. 4b. Rectangular forest cover appears in the northern part of the country in Fig. 4b, which again disappears completely in Fig. 4c. In Fig. 4d, forest cover with linear edges (north–south) appears on the map's eastern side. That being recognised, the land-cover mapping is reasonably accurate overall, providing a good base for land-cover estimation and for providing basic information for the hydrological impact analysis.
The rate of expansion of cultivated land before 1995 was higher than after 1995. Conversely, the area of the forest land decreased in 1985 and 1995 with reference to the 1973 baseline. However, after 1995, the forest's size increased again, whereas cultivated land decreased. The increased forest coverage and the decrease in cultivated land over the period 1995 to 2010 showed that the environment was recovering from the devastating drought, and forest clearing for firewood and cultivation due to population growth has been minimised. This could be due to the afforestation programme, which the Ethiopian government initiated, and to the extensive soil-and-water conservation measures carried out by the community. Since 1995, eucalyptus tree plantations expanded significantly across the country at the homestead level for firewood, construction materials, charcoal production, and income generation (Woldesenbet et al., 2017b). In summary, forest coverage decreased by 1.8 %, while both bushes and shrubs as well as cultivated land increased by 0.8 % and 1 %, respectively, from the original 1973 level to the 2010 period. This result agrees well with other studies (Gebremicael et al., 2013; Rientjes et al., 2011; Teferi et al., 2013; Woldesenbet et al., 2017b), which reported a significant conversion of natural vegetation cover into agricultural land.
5.3 SWAT model calibration and validation
The SWAT model's most sensitive parameters for simulating streamflow were identified using a global sensitivity analysis of SWAT-CUP. Their optimised values were determined by the calibration process that Arnold et al. (2012) recommended. Parameters such as the SCS curve number (CN2), base-flow alpha factor (ALPHA_BF), soil evaporation compensation factor (ESCO), threshold water depth in the shallow aquifer required for return flow to occur (GWQMN), groundwater “Revap” coefficient (GW_REVAP), and available water capacity (SOL_AWC) were found to be the most sensitive parameters for the streamflow predictions.
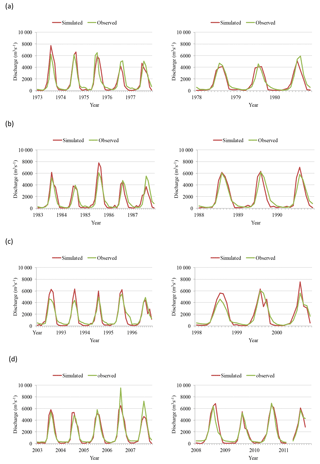
Figure 6Calibration and validation of the SWAT hydrological model (left and right, respectively) at monthly timescale: (a) 1970s, (b) 1980s, (c) 1990s, and (d) 2000s.
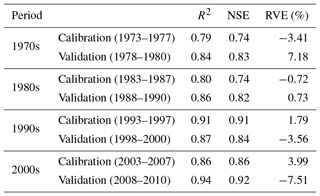
Figure 6 shows the calibration and the validation results for monthly streamflow hydrographs for each model. These results revealed that the model represents the monthly hydrographs well, as also indicated by R2, NSE, and RVE (%) statistical performance measures (Table 6). For the calibration period, the values of R2, NSE, and RVE (%) range from 0.79 to 0.91, 0.74 to 0.91, and −3.4 % to 4 %, respectively. For the validation period, they ranged from 0.84 to 0.94, 0.82 to 0.92, and −7.5 % to 7.2 %, respectively. According to the rating of Moriasi et al. (2007), the SWAT model's performance in the UBNRB can be categorised as very good, although underestimation was observed in the base-flow simulation. The optimal parameter values of the four calibrated-model runs are shown in Table 7. A change was obtained for CN2 parameter values, which can be attributed to the catchment's response behaviour. For instance, an increase in the absolute average (basin-wide) CN2 value from the 1970s to the 1980s and 1990s, from 72.9 to 74.7 and 75.6, respectively, indicates a reduction in forest coverage and an expansion of cultivated land. By contrast, a decrease in the CN2 value was attained during the period 1990s to 2000s, from 75.6 to 73.6, attributed to the increase in forest coverage and reduction in cultivated land.
5.4 Combined effects of LULC change and climate change on streamflow and water-balance components
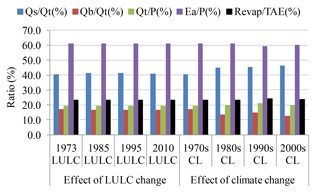
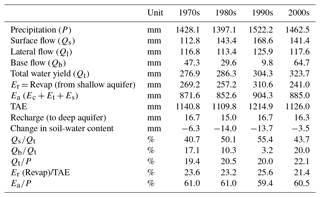
The simulation results of the four independent, decadal-time-scale calibrated and validated SWAT model runs reflect the combined effect of both LULC and climate change during the past 40 years (Table 8). From the simulation result, mean annual streamflow increased by 16.9 % between the 1970s and the 2000s, while the observed mean annual streamflow increased by 15.3 % for the same period. However, the rate of change is different in different decades. For example, it increased by 3.4 % and 9.9 % during the 1980s and 1990s, respectively, from the baseline 1970s period.
The ratio of mean annual streamflow to mean annual precipitation (Qt∕P) increased from 19.4 % to 22.1 %, while the actual evaporation to precipitation (Ea∕P) ratio decreased from 61.1 % to 60.5 % from the 1970s to 2000s. Moreover, the ratio of surface runoff to streamflow (Qs∕Qt) increased notably, from 40.7 % in the 1970s to 50.1 % and 55.4 % in the 1980s and 1990s, respectively, and it decreased to 43.7 % in the 2000s. In contrast, the base-flow-to-streamflow ratio (Qb∕Qt) notably decreased from 17.1 % in the 1970s to 10.3 % and 3.2 % during the 1980s and 1990s, respectively, but it increased to 20 % in the 2000s. The result for surface runoff agrees with findings in Gebremicael et al. (2013), but disagreement is observed for base flow. The study reported that the surface runoff (Qs) contribution to the total river discharge increased by 75 %, while the base flow (Qb) decreased by 50 % from the 1970s to 2000s.
Table 6Summary of the UBNRB's precipitation indices at decadal time series.

SDII is the ratio of total precipitation (mm) to R1 mm (days).
In general, 1.8 % forest cover loss and 1 % increased cultivated land combined with 2.2 % increased rainfall from the 1970s to the 2000s led to a 16.9 % increase in simulated streamflow. The 1990s was the period during which the greatest deforestation and expansion of cultivated land was reported; meanwhile, it was the time when the rainfall intensity and the number of rainfall events significantly increased compared to the 1970s and 1980s, as shown in Table 4. Hence, the increased mean annual streamflow could be ascribed to the combined effects of LULC and climate change. In the case of (Qs∕Qt), the increasing pattern could be ascribed to increasing rainfall intensities, the expansion of cultivated land, and the diminution of forest coverage, which might adversely affect soil and water storage and decrease rainfall infiltration, thereby increasing water yield or streamflow. In contrast, the decreasing Qb∕Qt is positively related to the increasing evapotranspiration linked to both LULC and climate factors (Table 8). This hypothesis can be explained with the change in CN2 parameter values obtained during calibration of the four SWAT model runs. The CN2 parameter value, which is a function of evapotranspiration derived from LULC, soil type, and slope, increased in the 1980s and 1990s, relative to the 1970s, and could be associated with the expansion of cultivated land and shrinkage of forest land. The increasing CN2 results reflect more surface runoff and less base flow being generated.
Table 7SWAT sensitive model parameters and their (final) calibrated values for the four model runs.
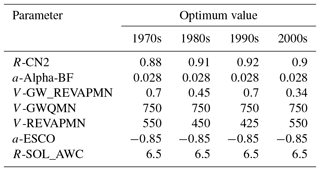
R value from the SWAT database is multiplied by a given value; V replace the initial parameter by the given value; a adding the given value to initial parameter value.
Table 8Mean annual water-balance-component analysis in the upper Blue Nile River basin, considering LULC and climate change over their respective periods. All streamflow estimates are for the El Diem station, where water yield (Qt) = and change in soil storage = -Revap-Recharge.
Another important factor contributing to decreasing surface runoff and an increasing base-flow ratio from the 1990s to the 2000s could be the establishment of soil-and-water conservation (SWC) measures. According to Haregeweyn et al. (2015), various nationwide SWC initiatives, such as Food for Work (FFW), the Managing Environmental Resources to Enable Transition (MERET) programme for more sustainable livelihoods, the Productive Safety Net Programme (PSNP), community mobilisation through free-labour days, and the National Sustainable Land Management Project (SLMP), have been undertaken since the 1980s. Haregeweyn et al. (2015) evaluated these initiatives' effectiveness and concluded that community labour mobilisation seems to be the best approach. This can reduce mean seasonal surface runoff by 40 %, with broad spatial variability ranging from 4 % in Andit Tid (north-western Ethiopia) to 62 % in Gununo (southern Ethiopia).
5.5 Effects of an isolated LULC change on streamflow and water-balance components
Yan et al. (2013) used a fixing–changing method, which was also applied in this study to identify the hydrological impacts of LULC change alone. The calibrated and validated SWAT model and its parameter settings in the baseline period was forced by weather data from the baseline 1973–1980 period, while changing only the LULC maps from 1985, 1995, and 2010, keeping the DEM and soil data constant, as suggested by Hassaballah et al. (2017). The results from Fig. 7 indicated that Qs∕Qt ratio changed from 40.7 % to 41.2 %, 41.9 %, and 40.9 % by using the LULC maps from 1973, 1985, 1995, and 2010, respectively, whereas the Qb∕Qt ratio changed from 17.1 % to 16.8 %, 16.5 %, and 16.9 %, respectively. The largest Qs∕Qt ratio (41.9 %) and the smallest Qb∕Qt ratio (16.5 %) were recorded with the 1995 LULC map. This could be attributed to the 5.1 % reduction in forest coverage and the 4.6 % increase in cultivated land with the 1995 LULC map, relative to the 1973 LULC map.
On a basin scale over a decadal time period, water gains are mainly from precipitation. The losses are mainly due to runoff and evapotranspiration (Oki et al., 2006), as the losses due to the deep percolation over the whole UBNRB are negligible (Steenhuis et al., 2009). The long-term mean annual deep percolation simulated in this study is about 16.7 mm and is constant in four decadal periods, which is about 6 % of the total water yield. With the fixing–changing approach, the change in streamflow attributable to LULC change was essentially the change in evapotranspiration between the two periods, as the amount of precipitation was constant (1970s), and the change in water storage during the two periods was similar (Yan et al., 2013). Annual Ea losses from seasonal crops are smaller than those from forests, because seasonal crops transpire during a relatively shorter time interval than perennial trees do (Yan et al., 2013). As a result, the actual mean annual Ea simulated by the SWAT model was 871.6 mm at the baseline. It decreased to 871.4 and 871 mm in 1985 and 1995, respectively, and increased to 872.1 mm in 2010. This could be due to the simultaneous expansion of cultivated land and the shrinkage in forest coverage in the 1985 and 1995 LULC maps, relative to the 1973 baseline. Furthermore, this deforestation may reduce the canopy's interception of the rainfall, decrease soil infiltration by increasing raindrop impacts, and reducing plant transpiration, which can significantly increase surface runoff, reducing base flow (Huang et al., 2013). Here, the evapotranspiration change caused by the LULC change is minimal. As a result, the change for surface runoff and base flow is not significant.
5.6 Effects of isolated climate change on streamflow and water-balance components
The impacts of climate change are analysed by running the four models using a unique LULC map from 1973 with its model parameters, while changing only the weather data sets from the 1970s, 1980s, 1990s, and 2000s. The simulated water-balance components shown in Fig. 7 indicate that the Qs∕Qt ratio increased from 40.7 % to 45.2 %, 45.6 %, and 46.2 % during the 1970s, 1980s, 1990s, and 2000s, respectively, while the Qb∕Qt ratio changed from 17.1 % to 13.5 %, 14.9 %, and 12.7 % for the same simulation periods. The decreasing Qb∕Qt ratio for the altered periods, compared to the baseline period, could be attributed to evapotranspiration changing from 872 to 854 mm, 906 mm, and 884 mm in 1970s, 1980s, 1990s, and 2000s, respectively, which can be linked to temperature and amount of rainfall. However, it is important to know the dominant rainfall–runoff process in the study area to fully understand the effect of climate change on the water-balance components.
Although no detailed research has been conducted on the upper Blue Nile River basin to investigate the runoff-generation processes, Liu et al. (2008) investigated the rainfall–runoff processes at three small watersheds located inside and around the upper Blue Nile River basin, namely Mayber, Andit Tid, and Anjeni. Their analysis showed that, unlike in temperate watersheds, in monsoonal climates, a given rainfall volume at the onset of the monsoon produces a different runoff volume than the same rainfall at the end of the monsoon. Liu et al. (2008) and Steenhuis et al. (2009) showed that the ratio of discharge to precipitation minus evapotranspiration, Q∕(P–ET), increases with cumulative precipitation from the onset of a monsoon. This suggests that saturation excess processes play an important role in watershed response.
Furthermore, the infiltration rates that Engda (2009) measured in 2008 were compared with rainfall intensities in the Maybar and Andit Tid watersheds located inside and around the UBNRB. In the Andit Tid watershed, which has an area of less than 500 ha, the measured infiltration rates at 10 locations were compared with rainfall intensities considered from the 1986–2004 period. The analysis showed that only 7.8 % of rainfall intensities were found to be higher than the lowest soil infiltration rate of 25 mm h−1. Derib (2005) performed a similar analysis in the Maybar watershed (with a catchment area of 113 ha). The infiltration rates measured from 16 measurements ranged from 19 to 600 mm h−1, with a 240 mm h−1 average and 180 mm h−1 median, whereas the average daily rainfall intensity from 1996 to 2004 was 8.5 mm h−1. Hence, he suggested from these infiltration measurements that infiltration excess runoff is not a common feature in these watersheds.
From the above discussion points, it is to be noted that surface runoff could increase with increasing total rainfall amount, regardless of rainfall intensity. However, the mean annual rainfall amount in this study decreased from the 1970s to the 1980s (1428 and 1397 mm, respectively), while the (Qs∕Qt) ratio increased from 40.7 % to 45.2 %. Similarly, the mean annual rainfall amount in the 1990s (1522 mm) was greater than the mean annual rainfall amount in the 2000s (1462 mm) while the (Qs∕Qt) increased from 45.6 % to 46.2 %. In contrast, in climate indices such as 99 % rainfall and SDII (ratio of total precipitation amount to number of days when rainfall >1 mm; R1 mm), the number of days when rainfall >20 mm (R20 mm) increases consistently from 1970 to the 2000s, as shown in Table 4. This indicates that the increasing surface runoff might be due to an increasing of number of extreme rainfall events and rainfall intensity. Although we did not use hourly rainfall data for the SWAT model, this study suggested that the excess infiltration of overland flow dominates the rainfall–runoff processes in the UBNRB, not the saturation excess of overland flow. The contradiction from the previous studies might be due either to the limitation of the SWAT CN method when applied in monsoonal climates or the overlooked tillage activities, which significantly impact the soil infiltration rate. Extensive tillage activities are carried out across the basin at the beginning of the rainy season. Soils get disturbed as a result, which can increase the infiltration rate and ultimately decrease the amount of rainfall converted to runoff.
Although the CN method is easy to use and provides acceptable results for discharge at the watershed outlet in many cases, researchers have concerns about its use in watershed models (Steenhuis et al., 1995; White et al., 2011). The SWAT CN model relies on a statistical relationship between soil-moisture condition and CN values obtained from plot data in the United States, with a temperate climate that was never tested in a monsoonal climate, exhibiting two extreme soil-moisture conditions. In monsoonal climates, long periods of rain can lead to prolonged soil saturation, whereas during the dry period, the soil dries out completely, which may not happen in temperate climates (Steenhuis et al., 2009). Hence, further research that considers biophysical activities such as tillage and the seasonal effects on soil moisture at representative watersheds of the basin is necessary to properly assess the rainfall–runoff processes.
This study's objectives were to understand the long-term variations of rainfall and streamflow in the UBNRB using statistical techniques (MK and Pettitt tests) and to assess the combined and isolated effects of climate and LULC change using a semi-distributed hydrological model (SWAT). Although the results of the MK test for annual and long rainy-season rainfall and streamflow show an increasing trend over the last 40 years, the magnitude of Sen's slope for streamflow is much larger than the Sen's slope of areal rainfall. Moreover, the short rainy-season streamflow shows a statistically significant positive increase, while the rainfall shows no change. The mismatch of trend magnitudes between rainfall and streamflow could be attributed to the combined effect of LULC and climate change, associated with decreasing actual evapotranspiration (Ea) and increasing rainfall intensity and extreme events.
LULC change detection was assessed by comparing the classified images. The result showed that the dominant process is largely the expansion of cultivated land and a decrease in forest coverage. The rate of deforestation is high during the 1973–1995 period. This is probably due to the severe drought that occurred in the mid-1980s and to a large population increase resulting from the expansion of agricultural land. On the other hand, forest coverage increased by 3.4 % during the period 1995–2010. This indicates that the environment was recovering from the devastating drought in the 1980s, regenerating the forests as the result of afforestation programme initiated by the Ethiopian government and soil-and-water conservation activities accomplished by the communities.
The SWAT model was used to analyse the combined and isolated effects of LULC and climate change on the monthly streamflow at the basin outlet (El Diem station, located on the Ethiopia–Sudan border). The result showed that the combined effects of the LULC and climate change increased the mean annual streamflow by 16.9 % from the 1970s to the 2000s. The increased mean annual streamflow could be ascribed to the combined effects of LULC and climate change. The LULC change alters the catchment responses. As a result, SWAT model parameter values could be changed. For instance, the expansion of cultivated land and the shrinkage of forest coverage from 1973 to 1995 changed the basin average CN2 parameter values from 72.9 in 1973 to 74.7 and 75.6 in 1985 and 1995, respectively. Increasing the CN2 value might increase surface runoff and decrease base flow. Similarly, the increase in rainfall intensity and extreme precipitation events led to a substantial increase in Qs∕Qt, a substantial decrease in Qb∕Qt, and, ultimately, to increases in the streamflow during the 1971–2010 simulation period.
The fixing–changing approach result using the SWAT model revealed that the isolated effect of LULC change could potentially alter the streamflow generation processes. The results of Fig. 7 show that surface runoff is increasing, while base flow is decreasing due to the expansion of cultivated land and reduction of forest coverage that reduce evapotranspiration during the periods 1985 and 1995, as compared to the baseline-period 1973 LULC map. Furthermore, the SWAT simulation results from Table 8 and Fig. 7 revealed that the Revap has been a significant contributor to the TAE in the UBNRB for the last 40 years, with a mean annual contribution ranging from 21.4 % to 25.6 %; this could be due to the large coverage of deep-rooted Eucalyptus tree species that can access the saturated zone (Neitsch et al., 2011). The Revap component of this study appears consistent with the results of Abiodun et al. (2018) and Benyon et al. (2006), who reported the annual groundwater ET contribution to total ET ranged from 13 % to 72 % and 20 %, respectively, for south-eastern Australia and the Sixth Creek catchments. However, a detailed investigation of the contribution of Revap to the total actual evapotranspiration in the study area is required, which is beyond the scope of this study. In general, a 5.1 % reduction in forest coverage and a 4.6 % increase in cultivated land led to a 9.9 % increase in mean annual streamflow from 1973 to 1995. This study provides a better understanding and substantial information about how climate and LULC change affects streamflow and water-balance components separately and jointly, which is useful for basin-wide water resource management. The SWAT simulation indicated that the impacts of climate change are more substantial than the impacts of LULC change, as shown in Fig. 7. Surface water is no longer used for agriculture and plant consumption in areas such as the UBNRB, where water-storage facilities are scarce. On the other hand, base flow provides the most reliable source of the irrigation needed to increase agricultural production. Hence, the increasing amount of surface water and diminished base flow, caused by both LULC and climate change, negatively affect socio-economic developments in the basin.
Protecting and conserving the natural forests and expanding soil-and-water conservation activities is therefore highly recommended, not only to increase the base flow available for irrigation but also to reduce soil erosion. Doing so might increase productivity and improve the livelihoods and regional-water-resource-use cooperation. However, the uncertainties of Landsat image classification and the model uncertainty of the SWAT simulation might limit this study. To improve the accuracy of LULC classification from Landsat images, further efforts, such as integrating other images with Landsat images through image-fusion techniques (Ghassemian, 2016), are required. The SWAT model does not adjust CN2 for slopes greater than 5 %. This could be significant in areas where the majority of the area has a slope greater than 5 %, such as in the UBNRB. We therefore suggest that adjusting CN2 values for slopes >5 % outside of the SWAT model might improve the results. Moreover, further research involving rainfall intensity, the infiltration rate, and the event-based analysis of hydrographs and critical evaluation of rainfall–runoff processes in the study area might overcome this study's limitations. Finally, the authors would like to point out that the impacts of current and future water resource developments should be investigated to establish comprehensive, holistic water resource management in the Nile basin.
The data can be made available upon request to the corresponding author.
The supplement related to this article is available online at: https://doi.org/10.5194/hess-22-6187-2018-supplement.
The authors declare that they have no conflict of interest.
The authors would like to thank the Ethiopian Ministry of
Water, Irrigation and Electricity and the Ethiopian National Meteorological
Services Agency for providing the streamflow and meteorological data,
respectively. The first author received financial support from the DAAD
water–food–energy NeXus project. The authors would also like to express
their gratitude to the anonymous referees and the editor, Axel
Bronstert, who gave constructive remarks and comments that enhanced the
quality of the paper.
Edited by: Axel Bronstert
Reviewed by: two anonymous referees
Abbaspour, C. K.: SWAT Calibrating and Uncertainty Programs, A User Manual. Eawag Zurich, Switzerland, 2008.
Abiodun, O. O., Guan, H., Post, V. E. A., and Batelaan, O.: Comparison of MODIS and SWAT evapotranspiration over a complex terrain at different spatial scales, Hydrol. Earth Syst. Sci., 22, 2775–2794, https://doi.org/10.5194/hess-22-2775-2018, 2018.
Alemseged, T. H. and Tom, R.: Evaluation of regional climate model simulations of rainfall over the Upper Blue Nile basin, Atmos. Res., 161, 57–64, https://doi.org/10.1016/j.atmosres.2015.03.013, 2015.
Allen, R. G., Pereira, L. S., Raes, D., and Smith, M.: Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56, FAO, Rome, 300(9), D05109, 1998.
Arnold, J. G., Srinivasan, R., Muttiah, R. S., and Williams, J. R.: Large area hydrologic modeling and assessment Part I: Model development1, Wiley Online Library, https://doi.org/10.1111/j.1752-1688.1998.tb05961.x, 1998.
Arnold, J. G., Allen, P., Volk, M., Williams, J., and Bosch, D.: Assessment of different representations of spatial variability on SWAT model performance, Trans. Asabe, 53, 1433–1443, 2010.
Arnold, J. G., Moriasi, D. N., Gassman, P. W., Abbaspour, K. C., White, M. J., Srinivasan, R., Santhi, C., Harmel, R., Van Griensven, A., and Van Liew, M. W.: SWAT: Model use, calibration, and validation, Trans. Asabe, 55, 1491–1508, 2012.
Awulachew, S. B., McCartney, M., Steenhuis, T. S., and Ahmed, A. A.: A review of hydrology, sediment and water resource use in the Blue Nile Basin, 131, IWMI, 2009.
Banko, G.: A review of assessing the accuracy of classifications of remotely sensed data and of methods including remote sensing data in forest inventory IASA Interim Report, IIASA, Laxenburg, Austria, IR-98-08, 1998.
BCEOM: Abbay river basin integrated development master plan project, phase 3 main report, Ministry of Water Resources, Addis Ababa, Ethiopia, Volume I, Main report, 1998.
Benyon, R. G., Theiveyanathan, S., and Doody, T. M.: Impacts of tree plantations on groundwater in south-eastern Australia, Aust. J. Botany, 54, 181–192, https://doi.org/10.1071/BT05046, 2006.
Bewket, W. and Sterk, G.: Dynamics in land cover and its effect on stream flow in the Chemoga watershed, Blue Nile basin, Ethiopia, Hydrol. Proc., 19, 445–458, https://doi.org/10.1002/hyp.5542, 2005.
Bosch, D., Arnold, J., Volk, M., and Allen, P.: Simulation of a low-gradient coastal plain watershed using the SWAT landscape model, Trans. Asabe, 53, 1445–1456, 2010.
Cheung, W. H., Senay, G. B., and Singh, A.: Trends and spatial distribution of annual and seasonal rainfall in Ethiopia, Int. J. Climatol., 28, 1723–1734, https://doi.org/10.1002/joc.1623, 2008.
Congalton, R. G.: A review of assessing the accuracy of classifications of remotely sensed data, Remote Sens. Environ., 37, 35–46, 1991.
Conway, D.: The climate and hydrology of the Upper Blue Nile River, The Geographical Journal, 166, 49–62, 2000.
DeFries, R. and Chan, J. C.-W.: Multiple criteria for evaluating machine learning algorithms for land cover classification from satellite data, Remote Sens. Environ., 74, 503–515, 2000.
Derib, S. D.: Rainfall-runoff processes at a hill-slope watershed: case of simple models evaluation at Kori-Sheleko Catchments of Wollo, Ethiopia, M. Sc. Thesis, 2005.
Engda, T. A.: Modeling rainfall, runoff and soil loss relationships in the northeastern highlands of Ethiopia, andit tid watershed, Citeseer, 2009.
Fenta Mekonnen, D. and Disse, M.: Analyzing the future climate change of Upper Blue Nile River basin using statistical downscaling techniques, Hydrol. Earth Syst. Sci., 22, 2391–2408, https://doi.org/10.5194/hess-22-2391-2018, 2018.
Gashaw, T., Tulu, T., Argaw, M., and Worqlul, A. W.: Modeling the hydrological impacts of land use/land cover changes in the Andassa watershed, Blue Nile Basin, Ethiopia, Sci. Total Environ., 619, 1394–1408, https://doi.org/10.1016/j.scitotenv.2017.11.191, 2018.
Gebremicael, T., Mohamed, Y., Betrie, G., van der Zaag, P., and Teferi, E.: Trend analysis of runoff and sediment fluxes in the Upper Blue Nile basin: A combined analysis of statistical tests, physically-based models and landuse maps, J. Hydrol., 482, 57–68, https://doi.org/10.1016/j.jhydrol.2012.12.023, 2013.
Ghassemian, H.: A review of remote sensing image fusion methods, Information Fusion, 32, 75–89, https://doi.org/10.1016/j.inffus.2016.03.003, 2016.
Green, W. H. and Ampt, G.: Studies on Soil Phyics, The Journal of Agricultural Science, 4, 1–24, 1911.
Haile, A. T., Akawka, A. L., Berhanu, B., and Rientjes, T.: Changes in water availability in the Upper Blue Nile basin under the representative concentration pathways scenario, Hydrol. Sci. J., 62, 2139–2149, https://doi.org/10.1080/02626667.2017.1365149, 2017.
Hamed, K. H. and Rao, A. R.: A modified Mann-Kendall trend test for autocorrelated data, J. Hydrol., 204, 182–196, 1998.
Haregeweyn, N., Tsunekawa, A., Nyssen, J., Poesen, J., Tsubo, M., Tsegaye Meshesha, D., Schütt, B., Adgo, E., and Tegegne, F.: Soil erosion and conservation in Ethiopia: a review, Prog. Phys. Geog., 39, 750–774, https://doi.org/10.1177/0309133315598725, 2015.
Hassaballah, K., Mohamed, Y., Uhlenbrook, S., and Biro, K.: Analysis of streamflow response to land use and land cover changes using satellite data and hydrological modelling: case study of Dinder and Rahad tributaries of the Blue Nile (Ethiopia-Sudan), Hydrol. Earth Syst. Sci., 21, 5217–5242, https://doi.org/10.5194/hess-21-5217-2017, 2017.
Hayes, D. J. and Sader, S. A.: Comparison of change-detection techniques for monitoring tropical forest clearing and vegetation regrowth in a time series, Photogramm. Eng. Rem. S., 67, 1067–1075, 2001.
Hu, Y., De Jong, S., and Sluiter, R.: A modeling-based threshold approach to derive change/no change information over vegetation area, Proceedings of the “12 International Conference on Geoinformatics-Geospatial Information Research: Bridging the Pacific and Atlantic”, University of Gävle (Sweden), 647–654, 2004.
Huang, J., Wu, P., and Zhao, X.: Effects of rainfall intensity, underlying surface and slope gradient on soil infiltration under simulated rainfall experiments, Catena, 104, 93–102, https://doi.org/10.1016/j.catena.2012.10.013, 2013.
Jensen, J. R.: Introductory digital image processing: a remote sensing perspective, Prentice-Hall Inc., 1996.
Kendall, M.: Rank correlation methods, 4th Edition, Charles Griffin, London, 1975.
Liu, B. M., Collick, A. S., Zeleke, G., Adgo, E., Easton, Z. M., and Steenhuis, T. S.: Rainfall-discharge relationships for a monsoonal climate in the Ethiopian highlands, Hydrol. Proc., 22, 1059–1067, 2008.
Lu, D., Mausel, P., Batistella, M., and Moran, E.: Comparison of land-cover classification methods in the Brazilian Amazon Basin, Photogramm. Eng. Rem. S., 70, 723–731, 2004.
Mancino, G., Nolè, A., Ripullone, F., and Ferrara, A.: Landsat TM imagery and NDVI differencing to detect vegetation change: assessing natural forest expansion in Basilicata, southern Italy, iForest-Biogeosciences and Forestry, 7, 75, https://doi.org/10.3832/ifor0909-007, 2014.
Mann, H. B.: Nonparametric Tests Against Trend, Econometrica, 13, 245–259, 1945.
Marhaento, H., Booij, M.J., Rientjes, T., and Hoekstra, A. Y.: Attribution of changes in the water balance of a tropical catchment to land use change using the SWAT model, Hydrol. Proc., 31, 2029–2040, https://doi.org/10.1002/hyp.11167, 2017.
McCartney, M., Alemayehu, T., Easton, Z. M., and Awulachew, S. B.: Simulating current and future water resources development in the Blue Nile River Basin, The Nile River Basin: water, agriculture, governance and livelihoods, Routledge-Earthscan, Abingdon, 269–291, 2012.
Melesse, A., Abtew, W., Dessalegne, T., and Wang, X.: Low and high flow analyses and wavelet application for characterization of the Blue Nile River system, Hydrol. Proc., 24, 241, https://doi.org/10.1002/hyp.7312, 2009.
Mengistu, D., Bewket, W., and Lal, R.: Recent spatiotemporal temperature and rainfall variability and trends over the Upper Blue Nile River Basin, Ethiopia, Int. J. Climatol., 34, 2278–2292, https://doi.org/10.1002/joc.3837, 2014.
Mockus, V.: National engineering handbook, Section 4: Hydrology, 630, 1964.
Monserud, R. A.: Methods for comparing global vegetation maps, IIASA Working Paper, IIASA, Laxenburg, Austria, WP-90-040, 1990.
Moriasi, D. N., Arnold, J. G., Van Liew, M. W., Bingner, R. L., Harmel, R. D., and Veith, T. L.: Model evaluation guidelines for systematic quantification of accuracy in watershed simulations, Trans. Asabe, 50, 885–900, 2007.
Neitsch, S., Arnold, J., Kiniry, J. R., Srinivasan, R., and Williams, J.: Soil and water assessment tool user's manual version 2000, GSWRL report, 202(02-06), 2002.
Neitsch, S. L., Arnold, J. G., Kiniry, J. R., and Williams, J. R.: Soil and water assessment tool theoretical documentation version 2009, Texas Water Resources Institute, 2011.
NMA: Annual climate buletien for the year 2013, National Meteorological Agency, Meteorological Data and Climatology Directorate, Addis Ababa, Ethiopia, available at: http://www.ethiomet.gov.et/bulletins/bulletin_viewer/bulletins/348/2013_Annual_Bulletin/en (last access: 12 March 2017), 2013.
Oki, T. and Kanae, S.: Global hydrological cycles and world water resources, science, 313, 1068–1072, https://doi.org/10.1126/science.1128845, 2006.
Pettitt, A.: A non-parametric approach to the change-point problem, Appl. Stat., 126–135, 1979.
Pignotti, G., Rathjens, H., Cibin, R., Chaubey, I., and Crawford, M.: Comparative Analysis of HRU and Grid-Based SWAT Models, Water, 9, 272, https://doi.org/10.3390/w9040272, 2017.
Polanco, E. I., Fleifle, A., Ludwig, R., and Disse, M.: Improving SWAT model performance in the upper Blue Nile Basin using meteorological data integration and subcatchment discretization, Hydrol. Earth Syst. Sci., 21, 4907–4926, https://doi.org/10.5194/hess-21-4907-2017, 2017.
Rathjens, H. and Oppelt, N.: SWATgrid: An interface for setting up SWAT in a grid-based discretization scheme, Comput. Geosci., 45, 161–167, https://doi.org/10.1016/j.cageo.2011.11.004, 2012.
Rathjens, H., Oppelt, N., Bosch, D., Arnold, J. G., and Volk, M.: Development of a grid-based version of the SWAT landscape model, Hydrol. Proc., 29, 900–914, https://doi.org/10.1002/hyp.10197, 2015.
Rientjes, T. H. M., Haile, A. T., Kebede, E., Mannaerts, C. M. M., Habib, E., and Steenhuis, T. S.: Changes in land cover, rainfall and stream flow in Upper Gilgel Abbay catchment, Blue Nile basin – Ethiopia, Hydrol. Earth Syst. Sci., 15, 1979–1989, https://doi.org/10.5194/hess-15-1979-2011, 2011.
Seleshi, Y. and Zanke, U.: Recent changes in rainfall and rainy days in Ethiopia, Int. J. Climatol., 24, 973–983, https://doi.org/10.1002/joc.1052, 2004.
Sen, P. K.: Estimates of the regression coefficient based on Kendall's tau, J. Am. Stat. Assoc., 63, 1379–1389, 1968.
Setegn, S. G., Srinivasan, R., and Dargahi, B.: Hydrological modelling in the Lake Tana Basin, Ethiopia using SWAT model, The Open Hydrol. J., 2, 49–62, 2008.
Singb, A.: Digital change detection techniques using remotely sensed data, Int. J. Remote Sens., 10, 989–1003, 1989.
Singh, A.: Review article digital change detection techniques using remotely-sensed data, Int. J. Remote Sens., 10, 989–1003, https://doi.org/10.1080/01431168908903939, 1989.
Steenhuis, T. S., Winchell, M., Rossing, J., Zollweg, J. A., and Walter, M. F.: SCS runoff equation revisited for variable-source runoff areas, Journal of Irrigation and Drainage Engineering, 121, 234–238, 1995.
Steenhuis, T. S., Collick, A. S., Easton, Z. M., Leggesse, E. S., Bayabil, H. K., White, E. D., Awulachew, S. B., Adgo, E., and Ahmed, A. A.: Predicting discharge and sediment for the Abay (Blue Nile) with a simple model, Hydrol. Proc., 23, 3728–3737, https://doi.org/10.1002/hyp.7513, 2009.
Teferi, E., Bewket, W., Uhlenbrook, S., and Wenninger, J.: Understanding recent land use and land cover dynamics in the source region of the Upper Blue Nile, Ethiopia: Spatially explicit statistical modeling of systematic transitions, Agric. Ecosyst. Environ., 165, 98–117, https://doi.org/10.1016/j.agee.2012.11.007, 2013.
Tekleab, S., Mohamed, Y., Uhlenbrook, S., and Wenninger, J.: Hydrologic responses to land cover change: the case of Jedeb mesoscale catchment, Abay/Upper Blue Nile basin, Ethiopia, Hydrol. Proc., 28, 5149–5161, https://doi.org/10.1002/hyp.9998, 2014.
Tesemma, Z. K., Mohamed, Y. A., and Steenhuis, T. S.: Trends in rainfall and runoff in the Blue Nile Basin: 1964–2003, Hydrol. Proc., 24, 3747–3758, https://doi.org/10.1002/hyp.7893, 2010.
Uhlenbrook, S., Mohamed, Y., and Gragne, A. S.: Analyzing catchment behavior through catchment modeling in the Gilgel Abay, Upper Blue Nile River Basin, Ethiopia, Hydrol. Earth Syst. Sci., 14, 2153–2165, https://doi.org/10.5194/hess-14-2153-2010, 2010.
USBR: Land and water resources of the Blue Nile basin, Ethiopia, Main report, United States Bureau of Reclamation, Washington, DC., 1964.
Von Storch, H.: Misuses of Statistical Analysis in Climate Research, Analysis of Climate Variability, Springer, 11–26, 1995.
White, E. D., Easton, Z. M., Fuka, D. R., Collick, A. S., Adgo, E., McCartney, M., Awulachew, S. B., Selassie, Y. G., and Steenhuis, T. S.: Development and application of a physically based landscape water balance in the SWAT model, Hydrol. Proc., 25, 915–925, 2011.
Woldesenbet, T. A., Elagib, N. A., Ribbe, L., and Heinrich, J.: Gap filling and homogenization of climatological datasets in the headwater region of the Upper Blue Nile Basin, Ethiopia, Int. J. Climatol., 37, 2122–2140, https://doi.org/10.1002/joc.4839, 2017a.
Woldesenbet, T. A., Elagib, N. A., Ribbe, L., and Heinrich, J.: Hydrological responses to land use/cover changes in the source region of the Upper Blue Nile Basin, Ethiopia, Sci. Total Environ., 575, 724–741, https://doi.org/10.1016/j.scitotenv.2016.09.124, 2017b.
Yan, B., Fang, N., Zhang, P., and Shi, Z.: Impacts of land use change on watershed streamflow and sediment yield: an assessment using hydrologic modelling and partial least squares regression, J. Hydrol., 484, 26–37, https://doi.org/10.1016/j.jhydrol.2013.01.008, 2013.
Yin, J., He, F., Xiong, Y. J., and Qiu, G. Y.: Effects of land use/land cover and climate changes on surface runoff in a semi-humid and semi-arid transition zone in northwest China, Hydrol. Earth Syst. Sci., 21, 183–196, https://doi.org/10.5194/hess-21-183-2017, 2017.
Yue, S., Pilon, P., Phinney, B., and Cavadias, G.: The influence of autocorrelation on the ability to detect trend in hydrological series, Hydrol. Proc., 16, 1807–1829, https://doi.org/10.1002/hyp.1095, 2002.
Yue, S. and Wang, C.: The Mann-Kendall test modified by effective sample size to detect trend in serially correlated hydrological series, Water Res. Manage., 18, 201–218, 2004.