the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Empirical and analytical methods to characterize the efficiency of floods to move sediment in a small semi-arid basin
Abdesselam Megnounif
Over a long multi-year period, flood events can be classified according to their effectiveness in moving sediments. Efficiency depends both on the magnitude and frequency with which events occur. The effective (or dominant) discharge is the water discharge which corresponds to the maximum sediment supply. If its calculation is well documented in temperate or humid climates and large basins, it is much more difficult in small and semi-arid basins in which short floods with high sediment supplies occur. Using the example of 31 years of measurements in the Wadi Sebdou (north-west Algeria), this paper compares the two main statistical approaches to calculate the effective discharge (the empirical method based on histograms of sediment supply by discharge classes and an analytical calculation based on a hydrological probability distribution and on a sediment rating curve) to a very simple proxy: the half-load discharge, i.e. the flow rate corresponding to 50 % of the cumulative sediment yield. Three types of discharge subdivisions were tested. In the empirical approach, two subdivisions provided effective discharge close to the half-load discharge. Analytical solutions based on log-normal and log-Gumbel probability distributions were assessed but they highly underestimated the effective discharge, whatever the subdivision used to adjust the flow frequency distribution. Furthermore, annual series of maximum discharge and half-load discharge enabled the return period of hydrological years with discharge higher than the effective discharge (around 2 years) to be inferred and showed that more than half of the yearly sediment supply is carried by flows higher than the effective discharge only every 7 hydrological years. This study was the first to adapt the analytical approach in a semi-arid basin and to show the potentiality and limits of each method in a such climate.
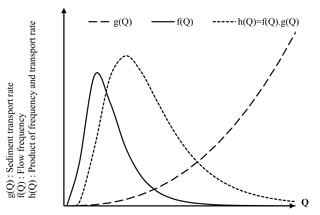
Over a long multi-year period, flood events can be classified according to their effectiveness in moving sediments. Efficiency depends both on the magnitude and frequency with which events occur. According to Wolman and Miller (1960), the efficiency can be examined through the “sediment transport effectiveness curve” h(Q) obtained by the product of the two curves f(Q)⋅g(Q), where f(Q) is the frequency distribution of water discharge, and g(Q) the rating curve estimating the suspended sediment flux Qs as a function of the water discharge (Fig. 1). Since f(Q) is a bell-shaped probability density function, often adjusted by a log-normal probability distribution, and g(Q) is a function limited in the interval [0; Qmax[, then the function h(Q) goes from 0 at very low flow rates to almost 0 at the highest flow rates through a maximum. The flow at which the function h reaches its maximum is the effective discharge, QD, in the sense of Wolman and Miller (1960). The curve h(Q) characterizes the relative geomorphic work (i.e. the amount of sediment transported) that is carried out in a basin by each flow. The effective discharge is often referred to as the dominant discharge, which has the greatest role in the formation and maintenance of river morphology, and whose knowledge is essential for stream restoration projects (Watson et al., 1999). As illustrated in Fig. 1, a large portion of sediment is conceptually transported by weak to moderate floods. Wolman and Miller (1960) confirmed this concept by comparing the frequency of flows generating suspended sediment transport in watersheds of different sizes in humid and semi-arid regions and showed that very large devastating floods which produce large amounts of sediments have, due to their scarcity, a tiny contribution over a long period compared to moderate floods with higher recurrence.
To determine the effective discharge, the empirical approach proposed by Benson and Thomas (1966) is based on the construction of a sediment supply histogram as an alternative of the sediment-transport effectiveness function, h(Q). This approach made it possible to identify the dominant class on many sites, usually from daily liquid and solid flow series in temperate environments (Andrews, 1980; Ashmore and Day, 1988; Biedenharn et al., 2001). It makes use of a subdivision of discharge into classes of equal amplitude and defined the modal class as the efficient-flow class or dominant class (Dunne and Leopold, 1978).
Alternatively, Nash (1994) proposed an analytical approach to estimate the effective discharge. He argued that for most rivers, the log-normal distribution adequately represents the flow frequency, and that sediment flow is commonly estimated from a power model, , where a and b are empirical parameters of simple regression established between the Ck and Qk class representatives (Andrews, 1980; Biedenharn et al., 2001; McKee et al., 2002; Crowder and Knapp, 2005; Bunte et al., 2014). The probability distribution of discharge and the rating curve of sediment supply provide a mathematical equation of the sediment transport efficiency curve, h(Q) (Nash, 1994; Vogel et al., 2003). The curve h has a unique maximum reached at the effective rate QD (Fig. 1), whose analytical expression is the solution of the derived function, . For more precision and in order to deal with different flow regimes, the analytical solution of the dominant discharge has been established for probability distributions other than the log-normal distribution, such as the normal, exponential or log-Pearson III distributions (Goodwin, 2004; West and Niezgoda, 2006; Quader et al., 2008; Higgins et al., 2015).
Other methods are still proposed in the literature to estimate the effective discharge. Ferro and Porto (2012), for example, associated it with the flow rate corresponding to 50 % of the cumulative sediment yield, thus taking up the concept of “half-load discharge” introduced by Vogel et al. (2003). Since flows below this threshold carry 50 % of the total sediment production and higher flow rates as much, this flow can also be called a “median water discharge in the sense of sediment yield” (). Other parameters are calculated in the literature and considered as proxies of the effective discharge, such as the bankfull discharge (Qb, the discharge which fills the channel to the level of the floodplain; see for example Andrews, 1980) or the 1.5-year flow events (Q1.5) (e.g. Crowder and Knapp, 2005; Ferro and Porto, 2012).
These approaches to analysing sediment yield are less well adapted to semi-arid environments that experience the alternation of very long periods of drought or low flows and sporadic floods. Furthermore, Colombani et al. (1984) and Castillo et al. (2003) emphasized practical difficulties in controlling flows and associated matter in small catchments (10 to 104 km2) which are subject to flash floods that carry significant sediment loads (Reid and Laronne, 1995; Alexandrov et al., 2003; Scott, 2006; Gray et al., 2015) and where accurate sediment records are frequently lacking (Milliman and Syvistki, 1992; Biedenharn et al., 2001; Gray et al., 2015). Probst and Amiotte-Suchet (1992) and Walling (2008) reported that the lack of such series is obvious on the southern Mediterranean side. Due to the paucity of accurate time series, Crowder and Knapp (2005) highlighted that the approach developed for identifying the effective discharge has not been verified in watersheds smaller than 518 km2.
In the context of current knowledge and methods, this article proposes to adapt and compare these methods to the hydrology of a small semi-arid basin on an example in northern Algeria. The application is carried out from 31 years of hydro-sedimentary measurements in the Wadi Sebdou (1973–2004), on which floods last on average 7.78 % of the time. The questions dealt with in this paper are the following:
-
How can we precondition data series in semi-arid environments?
-
What is the best subdivision of discharge classes adapted to the empirical method based on sediment yield histograms? Three types of subdivision are compared.
-
What are the analytical solutions following the Nash's (1994) method which fit statistical probability distributions to flow histograms to derive the dominant discharge? Theoretical solutions are established for two standard probability distributions (log-normal, log-Gumbel).
-
What are the different sources of errors in each approach?
-
Which lessons can we derive by comparing their results and the half-load discharge?
-
Which return periods regarding sediment supply over a long-term period can be derived from the annual series of hydrological parameters such as the annual maximum discharge and the half-load discharge?
The Maghreb is a mountainous region with young relief, characterized by many small watersheds. In these steep marl landscapes, rainfall erosivity is particularly high (Heusch, 1982; Probst and Amiotte-Suchet, 1992). Located in the north-west of Algeria, the Wadi Sebdou (or upper Tafna River) runs along 29 km (Fig. 2). The upper reaches emerge through predominantly carbonate Jurassic terrains at altitudes up to 1400 m. Then the wadi crosses the plain of Sebdou composed of Plio-Quaternary alluviums, and a valley (the gap of Tafna) made up of carbonate rocks (marl-limestone, limestone and Jurassic dolomites) (Benest, 1972; Benest and Elmi, 1969). The Wadi Sebdou flows into the Beni Bahdel reservoir, with a storage capacity of 63 million m3, impounded in 1946. The Wadi Sebdou drainage basin area is 256 km2. Steep slopes exceeding 25 % represent about 49 % of the total basin surface. The climate is semi-arid. The wet season runs from October to May. The dry season runs from June to September with low rainfall and high evapotranspiration.
Previous studies on sediment dynamics in this basin proposed syntheses on the hydro-sedimentological dynamics and budgets, or on sediment processes at the origin of hysteresis phenomena during floods, based on the detailed analysis of short-term time variations of water and sediment discharge (Megnounif et al., 2013). Additional and detailed information on morphometric, geological and land use characteristics of the basin were reported in Bouanani (2004), Megnounif et al. (2013), and Megnounif and Ghenim (2016).
Discharge and concentration data were measured at the Beni Bahdel station by the National Agency of Hydraulic Resources (locally called ANRH; Agence Nationale des Ressources Hydrauliques, 2018), in charge of gauging stations and measurements in Algeria. These data cover a 31-year period from September 1973 to August 2004. When water level is low and stable, the operator takes water samples every other day. During flood periods, sampling is intensified, up to every half-hour. During low flow period, water samples are taken every 2 weeks. At each sampling, the operator reads the water level on a limnimetric scale or on a limnigraph which is then converted into a water discharge according to a stage–discharge relationship established for the station. The suspended sediment concentration is determined from a water sample taken from the streambank, after filtration (see Megnounif et al., 2013).
3.1 Elementary contributions and budgets
The product of discharge, Q (m3 s−1), and suspended sediment concentration, C (in g L−1or kg m3), make it possible to evaluate the instantaneous sediment discharge, ( kg s−1). Between two water samples, the liquid flow, Q, and the sediment discharge QS, are assumed to vary linearly. At each flow Qi measured at time ti, there is an associated triplet (Δti, ΔRi, ΔYi):
where Δti, ΔRi and ΔYi correspond to time duration (s), elementary input in water (unit: 106 m3) and elementary sediment yield (unit: 103 t) assigned to the discharge Qi, respectively.
Over a duration T, the water supply RT and sediment yield YT are estimated by summing the elementary contributions:
Various quantiles are given using cumulative frequencies and elementary contributions assigned to ordered discharge. The quantiles QTα, QRα and QYα stand for water discharge that delimit α % of annual time, α % of the total water supply and α % of the sediment yield, respectively. For example, is the median water discharge in terms of suspended sediment production, i.e. such that 50 % of the sediment yield is carried by discharge lower than .
3.2 Effective discharge calculation using a discharge histogram
3.2.1 Basis of the empirical method
To analyse flow frequencies and associated sediment yields, the x axis (discharge) is subdivided into class intervals (or bins) Ik=[ak, ak+1[ where k=0, …, N; and . The duration, water and sediment yields attributed to the class Ik are obtained by summing time intervals (Eq. 1), water contributions (Eq. 2) and sediment yields (Eq. 3) assigned to discharge Qi within this class, as follows:
Each discharge class, Ik, is represented by a pair (Qk, Ck) where Qk is the midpoint and Ck is the mean sediment concentration calculated by the following equation:
Discharge classes are examined according to their effectiveness to produce sediments. The discharge class that carries out the highest sediment yields over an extended period is the dominant class. For simplicity, its midpoint, QD, is the effective discharge (or dominant discharge). In this article, three ways to subdivide the discharge axis are presented, applied and compared.
3.2.2 Class interval assignment
Regarding the choice of discharge classes, the procedure is empirical and varies according to the authors (Pickup and Warner, 1976; Andrews, 1980; Lenzi et al., 2006). Biedenharn et al. (2001) recommended starting by the use of 25 classes of equal lengths. If no measurement is assigned to a class interval or the mode is isolated in the last histogram class corresponding to the highest rates, the number of classes is changed. Crowder and Knapp (2005) argued that each class must contain at least one flow of a flood event. Thus, this procedure is subjective and remains dependent on the measurement protocol and the watershed configuration (Sichingabula, 1999; Goodwin, 2004). For example, Hey (1997) showed that it is necessary to increase the number of classes to 250 for a suitable representation of the distribution of the sediment yield brought by the Little Missouri River at Marmarth and Medora. Yevjevich (1972) suggested that the number of classes should be between 10 and 25, depending on the size of the sample. He proposed that the length of the class interval does not exceed s∕4, where s is the standard deviation of the series of studied liquid flows.
In this study, we propose to compare three types of subdivision of discharge classes – classes of equal length, classes of equal water supply and classes in geometric progression:
Classes of equal length. The series of ordinal discharge is subdivided into class intervals of equal size. A flow frequency and percentages of water and sediment contributions are assigned to each class interval. Various class lengths are examined and compared to that of length 1 m3 s−1.
Classes of equal water supply. Based on a physical aspect, the second subdivision ensures that classes provide the same water supply. For that, cumulative frequencies and water and sediment elementary supplies in percentage ( %, %, %) are assigned to the ordinal discharge. Class boundaries are delimited according to the cumulative water supply. For example, to get 25 classes, elementary water inputs assigned to each class must accumulate 4 % of the total water supply. At equal water yields, the efficient class is the one that carries out the most sediments.
Classes in geometric progression. Initiation of sediment motion by water depends on shear stress (Shields, 1936). In many sediment transport models, the sediment transport rate per unit channel width (qs) follows a power law as a function of excess shear stress , where τ is the shear stress per unit area and τc is the critical stress of sediment required for grain motion, k is a parameter depending on sediment particle characteristics, and n is an empirical exponent (e.g. Bagnold, 1941; van Rijn, 2005). As a result, power law models are commonly used, where sediment discharge QS or sediment concentration C evolves as a function of water discharge Q (Walling, 1977):
or, in a consistent manner,
In a stream that verifies such a relationship, the sediment discharge varies linearly against the water discharge on a logarithmic scale. For this reason, we suggest subdividing the x axis (discharge) into classes of equal lengths on a logarithmic scale. Hence, class limits (ai) are chosen so that the following is true:
Since the log function is bijective on R+ (positive real numbers), for a constant β>0, there exists α>0 such that β=log (1+α). Following this,
In this case, the length of classes is in a geometric progression of common ratio 1+α and all the class limits may be deduced from a0, according to the following:
For a small value of α, appropriately chosen, discharge within each class can be considered as equivalent to the value at the centre of the class, , since:
The sediment yield assigned to each discharge class is represented by a histogram on logarithmic scale or by a bar graph on arithmetic scale. The midpoint of the modal class interval represents the effective discharge QD.
3.2.3 Data pre-processing
In many rivers where flow variation is slow, water sampling required for solid flow measurement is not carried out daily but at monthly or weekly intervals (Horowitz, 2003). In this case, daily solid discharge is estimated by interpolation between actual measurements. On the other hand, small drainage basins (less than 1000 km2) experiencing high-intensity rainfall can generate short floods with high variation where recession sometimes lasts less than 24 h. Biedenharn et al. (2001) and Gray et al. (2015) reported that, in small basins with irregular flow, the identification of effective discharge requires a coverage of hydrometric measurements with a fine time resolution (less than 1 h). According to Simon et al. (2004), the scarcity of such records in the USA makes it difficult to identify the regional effective discharge. In such small basins, monitoring sediment concentration requires a measurement protocol with a suitable, more tightened, temporal resolution. For a small alpine catchment river, Lenzi et al. (2006) adapted the Crowder and Knapp (2005) approach to hydrometric data at 5 min intervals (the sediment concentration was deduced from water samples taken by automatic equipment at 5 min intervals).
The measurement protocol of the ANRH services is based on a predefined calendar. However, the high variability of the flows experienced by the Wadi Sebdou is such that between two consecutive measurements the difference can be significant, and one class or more may not be represented by any flow, whatever the subdivision used to discretize the flow discharge into classes. Moreover, such large differences cause an overestimate of the contributions in the sampled classes and underestimate those that are not. A preliminary data processing was thus performed in this study in order to improve the distribution of elementary inputs amongst classes. To achieve this, liquid and solid discharge is assumed to vary linearly as a function of time between two measurements. When the discrepancy between two measured discharge is large, an intermediate discharge is added at each increase of 0.2 m3 s−1. The corresponding values of time and sediment discharge are deduced using linear interpolation between measurements. The value of 0.2 m3 s−1 was chosen close to the baseflow observed in the river, Q0=0.16 m3 s−1 (Terfous et al., 2001; Megnounif et al., 2003). This preliminary data treatment allows the information amongst the classes to be better distributed and the elementary inputs to be estimated in a more continuous way. Thus, the data series on which we applied and compared methods has increased from 6947 initial measurements collected by the ANRH to 40 081 data (ti, Qi, Ci).
3.2.4 Relevance of a subdivision of discharge
The relevance of a subdivision was examined according to its ability to represent the water and sediment supplies. Three aspects were considered:
-
A subdivision was considered suitable when histograms were informative on the three variables' (frequency, water supply and sediment supply) evolution over the whole flow range, from the weakest to the strongest.
-
The water and sediment inputs assigned to each discharge class can be quantified by the “standard” elementary contributions (Eq. 5) or alternatively estimated using the midpoint discharge and the mean sediment concentration of each class (Eq. 6). Discrepancies are expressed as a percentage by the ratios τRk and τYk, such as the following:
When estimating total water and sediment supplies, discrepancies are given by the following:
A subdivision is better when it provides the smallest discrepancies according to Eqs. (13) and (14). Note that, for the same class, the differences τRk and τYk are identical. Indeed, Eqs. (6) and (13) give the following:
After simplification of the term ΔYk, we find that τYk=τRk.
-
An additional criterion was considered to determine the effective discharge from analysis. The suspended sediment concentration assigned to each class Ck may be alternatively estimated from the power model C=aQb fitted with class representatives (Qk, Ck), a and b being empirically derived regression coefficients. A subdivision is relevant when, on the one hand, the coefficient of determination and the coefficient of Nash and Sutcliffe between measured sediment loads and estimated values were close to 1, and on the other hand, the subdivision yields the smallest differences between sediment yield using Eq. (5) and its estimate using the following power model:
The total discrepancy was quantified by the following ratio:
3.3 Analytical determination of the effective discharge
Probability density functions representing flow frequencies from instantaneous values are left-skewed distributions. The most commonly used is the log-normal distribution (Wolman and Miller, 1960; Nash, 1994). However, for irregular flows such as those encountered in semi-arid environments with long periods of very little discharge, more pronounced asymmetric distributions are recommended. Hence, in addition to the log-normal distribution, the log-Gumbel distribution was examined. The theoretical density functions were fitted to the discharge frequency histogram. The dominant discharge was deduced from the analytical solution of , using the sediment rating curve C−Q fitting the pairs (Qk, Ck). Analytical solutions for the log-normal and log-Gumbel distributions are given in detail in the following subsections. The relevance of these solutions was assessed through the ability of the sediment-transport effectiveness curve to represent the sediment load histogram, globally and within class intervals.
3.3.1 Effective discharge using a log-normal distribution
The two-parameter log-normal distribution has a probability density function:
where μ and δ are the mean and standard deviation of the ln(Q) distribution. So, the sediment transport effectiveness curve can be written as follows:
The derivative of the function h is given by the following:
when , and so
The mode is the discharge value that appears most often. It is the discharge at which the probability density function has a maximum value. The analytical solution of gives:
3.3.2 Effective discharge using a log-Gumbel distribution
The two-parameter log-Gumbel distribution is defined through its probability density function:
for which the parameters, and , are issued from the method of probability-weighted moments, μ and δ being identical to the parameters of the log-normal distribution.
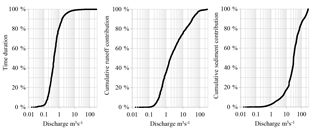
Figure 3Cumulative frequency, water and sediment inputs assigned to ordinal discharge in the Wadi Sebdou (1973–2004).
The function h is written as follows:
Its derivative h′ is written as follows:
Thus, the dominant discharge can be expressed by the following:
The solution of gives the following mode:
3.4 Half-load discharge
In their study, based on 27 stream gauge stations located in three regions of southern Italy, Ferro and Porto (2012) liken the dominant discharge to the median discharge in terms of sediment yield (); i.e. the discharge value above and below which half the long-term sediment load is transported. Vogel et al. (2003) previously introduced this parameter, which they called “half-load discharge” and distinguished from the effective discharge. The half-load discharge was determined for the Wadi Sebdou by cumulating elementary sediment contributions assigned to the ordinal discharge covering the study period 1973–2004. The obtained discharge, , was compared to the dominant discharge, QD. Its very quick and easy determination from the cumulative sediment yield curve makes it a suitable indicator for practical applications by technical staff or managers.
3.5 Return periods
The series of hydrologic data, Q, employed to estimate the recurrence interval (or return period) of an event of a given magnitude Qp, should be selected so that these values are independent and identically distributed along the considered time series. Such a series can compile any remarkable yearly discharge (e.g. average, maximum or minimum annual discharge). Each year should have a unique representative value so that the number of base values equals the number of the study years (Chow et al., 1988). The recurrence interval of an event of magnitude equal to or exceeding Qp is RI.
An effective discharge recurrence interval is traditionally derived from the probability distribution fitted to the annual maximum discharge series (Biedenharn et al., 2001; Simon et al., 2004; Crowder and Knapp, 2005; Ferro and Porto, 2012; Gao and Josefson, 2012; Bunte et al., 2014). To complete this parameter, which relies only on hydrological measurements and does not consider the associated sediment supplies, we also calculate in this study the recurrence interval of the effective discharge estimated from a probability distribution fitted to the series of annual half-load discharge and investigate its additional information.
4.1 Empirical approach: effective discharge values for various discharge subdivisions
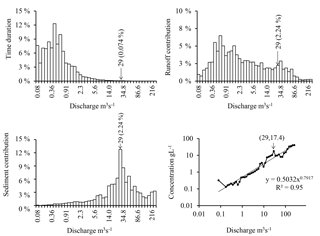
In the Wadi Sebdou, discharge is greater than m3 s−1 (see Fig. 3) during 1 % of the time each year (i.e. 87 h and 40 min), with an average sediment concentration being worth 10.3 g L−1. They represent 25.0 % of the total water input and carry 82.8 % of sediment (see Fig. 3). On the other hand, discharge is lower than 1.54 m3 s−1 () 90 % of the annual time. Their weak average concentration is 0.19 g L−1. Floods with high sediment concentration are thus rare.
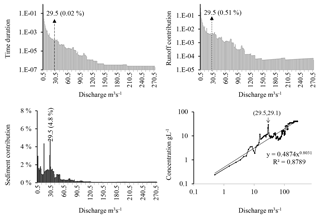
Figure 4Duration, water and sediment supplies, as well as the sediment rating curve with a subdivision into classes of equal length (1 m3 s−1).
Interquartile discharge for water supplies, [0.66; 9.68 m3 s−1[, lasts 30.3 % of the annual time and carries 15.6 % of the total sediment load with an average concentration of 0.97 g L−1. Discharge higher than m3 s−1 has an average frequency of 0.01 %, i.e. 1.3 h per year. These waters carry 16.64 % of total sediment production with an estimated average concentration of 25.9 g L−1.
The first and third quartiles for sediment production are delimited by m3 s−1 and m3 s−1. Approximately four-fifths (80.4 %) of the total volume of water flows with discharge lower than the first quartile, with an average sediment concentration being worth 0.96 g L−1. Discharge higher than the third quartile, heavily loaded with an average concentration of 15.4 g L−1, accounts for only 5.1 % of water supplies. They last 0.06 % of the annual time, i.e. 5 h per year, on average. The half-load discharge is equal to 29.8 m3 s−1, discharge equal to or higher than , and brings 12.7 % of water supply and flow in 0.24 % of the annual time (21 h) on average, with an average concentration of 1.8 g L−1. Of the 131 floods recorded during the study period, 33 had a peak flow higher than the median flow, of which 11 were multi-peaks and exceeded 26 times the value of .
4.1.1 Subdivision into classes of equal length
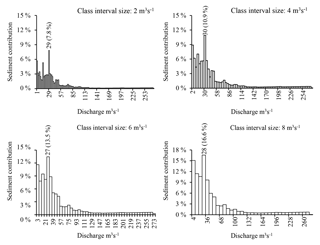
Discretization of the Wadi Sebdou discharge into classes of length equal to 1 m3 s−1 gives 273 classes. As can be seen on the histogram of sediment yields (Fig. 4), the class which induced the highest sediment contribution (the dominant class), [29; 30 m3 s−1[, brought 4.8 % of the total sediment supply. This class represents 0.51 % of the total water supply (Fig. 4) with an average concentration of 29.1 g L−1 (Table 1), for a duration of 0.02 %, i.e. about 1.5 h per year, or 0.21 % of the total flood duration, which covers on average 7.78 % of the year. The following classes, in order of efficiency to mobilize sediment, are [15; 16[, [28; 29[, [1; 2[ and [0; 1 m3 s−1[ with sediment productions of 4.35 %, 3.05 %, 2.87 % and 2.73 %, respectively. The second efficient class represents 1.16 % of the total water input and lasts 0.073 % of the time (around 6.4 h per year). The classes with low discharge, [0; 1 m3 s−1[ and [1; 2 m3 s−1[, are the most frequent; they last 81.5 % and 11.65 % of the annual time, respectively, with average water inputs of 35.49 % and 16.72 %, respectively. Every class above 38 m3 s−1 contributes a sediment load of less than 1 %. Their contribution decreases to less than 0.5 % for discharge above 53 m3 s−1 (Fig. 4).
Table 1Characteristics and performance of various subdivisions: class of dominant discharge range CDD; effective discharge; flow frequency ΔT, water supply ΔR, sediment supply ΔY and concentration C; parameters of the rating curve Ck=aQkb; discrepancies between water and sediment inputs obtained from classes and from elementary contributions.
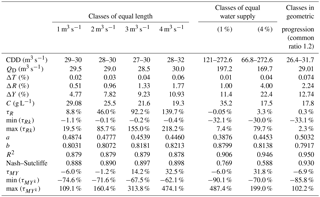
For such a subdivision, a change in class length necessarily affects the representativeness of the flow characteristics, in particular the magnitude and position of the effective discharge QD. The latter varied from 29.5 to 25 m3 s−1 when the class length increased from 1 to 10 m3 s−1, i.e. when the number of classes was reduced from 273 to 28. The contribution of the dominant class changed accordingly, from 4.8 % to 19.0 % of sediment supply, and from 0.51 % to 4.32 % of water flow. The frequency of discharge in this class changed as well, from 0.02 % to 0.17 % of the annual time.
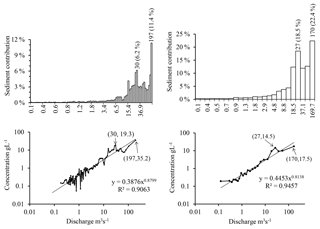
Figure 6Sediment supply per class, and sediment rating curves, for a subdivision into classes of equal water supplies of 1 % (left panels) and 4 % (right panels).
The comparison between the water and sediment inputs estimated from class representatives (Qk, Ck), on one side, and those directly calculated from elementary contributions, on the other side, shows that the subdivision into classes of length 1 m3 s−1 gives the smallest discrepancies, as calculated by Eqs. (13) and (14). Deviations increase with increasing class sizes (Table 1). Similarly, power models, C=aQb, based on class representatives (Qk, Ck) of equal lengths 1 and 2 m3 s−1 (Table 1) give the best rating curves: above 2 m3 s−1, the greater the amplitude, the higher the error in sediment production (see τMY in Table 1). Overall, with classes of equal amplitude, the informative part of histogram remains confined to low to moderate flow and decreases when the class amplitude decreases (Fig. 5). However, an excessive increase or decrease in the length class, to more than 8 m3 s−1 or less than 0.5 m3 s−1, affects the quality of information on the flow efficiency and makes the reading of histograms not very informative.
Table 2Recurrence intervals, R.I. QMAX and R.I. , of the dominant discharge QD calculated for the subdivisions into classes of equal amplitude 1 m3 s−1 and of geometric progression.

4.1.2 Subdivision into classes of equal water supply
Subdivision into classes of equal water input of 4 % results in 25 classes (Fig. 6). The choice of 4 % allows 25 classes to be obtained, as recommended by Biedenharn et al. (2001) and Crowder and Knapp (2005). The upper class concerns discharge higher than 66.8 m3 s−1 and carries the most of sediment, accounting for 22.4 % of the total annual sediment load. The frequency of concerned discharge is 0.04 %. The effective discharge, at the centre of the class, is QD=169.7 m3 s−1. The second class in terms of efficiency, [22.1; 31.6 m3 s−1[, carried 18.5 % of the total sediment flow, with a flow frequency of 0.14 %. The last five highest classes, from 15 to 273 m3 s−1, collected 20 % of water inputs and 80 % of sediment inputs.
Although this subdivision describes a physical reality, allowing a rather detailed reading of the frequency variations and water and sediment inputs at low flows, it remains basic and provides little detail on the efficiency of moderate to high flows. The difference (Eq. 13) between direct calculation of water inputs (Eqs. 2 and 4) and the one based on discharge of each class (Eq. 5), despite being low globally (3.3 %), was shown to be high for some classes (Table 1). The corresponding rating curve Ck=aQkb leads to a 32 % underestimate of the sediment load compared to the elementary contributions (Table 1). The maximum gap (199 %) was reached for the dominant class.
A calculation performed with a subdivision into 100 classes of equal water contributions of 1 % (Fig. 6) reduced the errors made on τR and τMY (Table 1). However, despite a high coefficient of determination, class-by-class differences were too high and the maximum error, obtained on the last class which is the dominant class, was around 500 %.
4.1.3 Subdivision into classes in geometric progression
The subdivision into classes of geometric progression was chosen so that from one class to another, the amplitude of the class increases by 20 %. Thus, discharge in the same class is within 10 % of the class centre. In this case, on a logarithmic scale, classes have a length equal to , and the amplitude of classes is in geometric progression of common ratio 1.2. The initial term m3 s−1 corresponds to the flow delimiting 1% of water supplies. This subdivision required 42 classes to cover the discharge of the Wadi Sebdou over 1973–2004. The class [26.4; 31.7 m3 s−1[ stands out and dominates with a relative contribution of 12.74 % of the total sediment supply (Fig. 7). Its average frequency is 0.074 % or 6.5 h per year and its water supply represents 2.24 % of the total, with an average concentration of 17.8 g L−1. Histograms (Fig. 7) allow a fairly detailed representation and reading of the flow frequency distribution and of the water and sediment supplies, as well, for the different flow regimes. In addition, the difference between water and sediment supplies estimated from class representatives and those calculated from elementary contributions is almost nil in total and is low to moderate with different classes (Table 1). The maximum error coincides with the first class, assigned to low flows.
The determination coefficient and Nash–Sutcliffe (1970) coefficient of the rating curve, Ck=aQkb, are satisfactory for the three types of subdivisions used in this study (Table 1). However, the best performances are obtained with the subdivision in geometric progression, which also allows a better quantification of the sediment supply (Table 1).
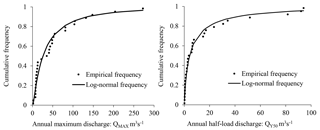
4.2 Return periods
The annual series of maximum flow rate series, QMAX, and half-load discharge, , fit log-normal distributions (Fig. 8). These two probability distributions make it possible to evaluate recurrence intervals related to QD values. The two subdivisions with very close QD values (equal classes of amplitudes 1 m3 s−1 and in geometric progression of common ratio 1.2) give similar recurrence intervals: the return periods of QD are 2.2 years for the annual series QMAX and 6.9 to 7 years for the annual series (Table 2). The difference of nearly 5 years is attributed to their different meanings. While one indicates that the effective discharge is observed at least once in a hydrological year roughly every 2 years at the gauging station, the other shows that half of the yearly sediment supply is carried by flows higher than the effective discharge only every 7 hydrological years.
4.3 Analytical determination of the effective discharge
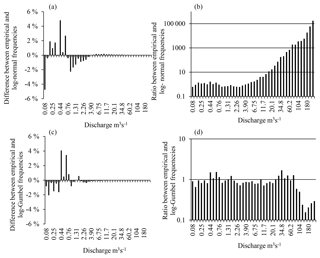
The analytical approach requires a probability density function f(Q) representing the distribution of flow frequencies as well as a curve g(Q) representing the solid discharge QS as a function of the water flow Q. The study shows that these two curves are closely related to the types of subdivisions used. For the subdivision into classes of equal amplitude 1 m3 s−1 and the one with geometric progression of common ratio 1.2, the adjustment of flow frequency distribution to the log-normal and log-Gumbel probability distributions are satisfactory (Fig. 9), with the log-Gumbel distribution showing to perform the best by a small margin. The highest difference for a class between the empirical and theoretical (log-Gumbel) frequency distributions was 4.1 % for the subdivision into classes of equal amplitudes and 4.8 % for subdivision into geometric progression. Characteristic parameters associated with the subdivision into classes of equal amplitudes and the one into geometric progression are (, δ=0.6572) and (, δ=0.9649), respectively. However, the dominant discharge obtained when the log-Gumbel distribution is considered is very low: QD=0.64 m3 s−1 for the subdivision into equal classes of amplitude 1 m3 s−1 (with b=0.8031), and QD=0.62 m3 s−1 for the subdivision into geometric progression (with b=0.7917). The use of a log-normal distribution leads to slightly higher values for QD: 0.92 m3 s−1 for the subdivision into classes of 1 m3 s−1 and 1.02 m3 s−1 for the subdivision into geometric progression, far from the dominant discharge obtained from the histograms, 29.5 and 29.01 m3 s−1 (Table 1).
5.1 Pre-processing of data of the gauging station
Half-hour sampling carried out by the ANRH is unsuitable during the Wadi Sebdou flash floods, which produce more than 80 % of the total sediment load in 1 % of the time, with an estimated average concentration of 10.3 g L−1. To overcome the presence of empty classes, Biedenharn et al. (2001), Goodwin (2004), and Crowder and Knapp (2005) propose to downgrade, subjectively, the number of classes by readjusting their amplitude to cover all classes in the information. Another alternative applied in this study is to refine the dataset, by interpolation between measurements. The refinement tested in this study has the advantage of not modifying the water and sediment budgets brought by the Wadi compared to the original series, since the interpolation is linear. The discharge step chosen for the interpolation, close to the low flow at the hydrographic station, also makes it possible to cover all classes of the different considered subdivisions and thus to make it possible to calculate the effective discharge. Note that a similar method has already been applied by Biedenharn et al. (2001) and Gray et al. (2015) to refined data from monthly steps to daily steps, and by Simon et al. (2004) and Lenzi et al. (2006) from daily and hourly measurements to a finer time step of 15 or even 5 min. In other studies, for which the frame of reference is the daily time step, instantaneous measurements are replaced by daily averages (Andrews, 1980; Nolan et al., 1987; Emmett and Wolman, 2001).
5.2 Methodology to identify the dominant class in the empirical approach
The quality of graphs and the error on water and sediment supplies made it possible to compare subdivisions and select those that are able to represent the flows and to identify the effective discharge. Several studies dedicated to dominant discharge class focused exclusively on the graphical aspect by readjusting the interval amplitude with equal classes until a dominant class appears outside the first and last classes (Benson and Thomas, 1966; Pickup and Warner, 1976; Andrews, 1980; Hey, 1997; Lenzi et al., 2006; Roy and Sinha, 2014). However, this approach remains subjective (Sichingabula, 1999; Biedenharn et al., 2001; Goodwin, 2004) and poses a dilemma. Reducing the class amplitude can make the dominant class emerge outside the two extreme classes, but this can bring up empty classes which, conversely, require the amplitude for each class that is to be covered to be increased. Where appropriate, the series is considered non-compliant with the selection criteria and does not allow the dominant class to be identified (Crowder and Knapp, 2005). To avoid such situations, Bienderhan et al. (2000) recommended the use of adequately provided datasets covering at least 10 years of measurements.
Yevjevich's (1972) proposal, based on statistical concepts, to use between 10 and 25 classes of amplitude less than s∕4, where s is the standard deviation of the flow series, is difficult to apply to the Wadi Sebdou. The standard deviation, which can be calculated from , where and Δti is the elementary time interval (Eq. 1), gives m3 s−1 for the Wadi Sebdou. Subdivision into classes of equal s∕4 amplitudes would require 355 classes to cover the range of flows. In a stream with such high flow variability, the strong flow asymmetry has a negative impact on the representativeness of flows and sediment discharge, especially for low flow classes that cover most of the water supply. This suggestion does not seem appropriate for wadis.
In this study, two types of subdivisions other than the classical subdivision with classes of equal amplitude were examined: discharge classes corresponding to equal water supply, and a geometric progression of flows. The subdivisions into classes of equal amplitude 1 m3 s−1 and the subdivision into classes with geometric progression best represented liquid and sediment supplies (Table 1) and are used to characterize the Wadi Sebdou flows. They give dominant discharge (QD=29.5 m3 s−1 and QD=29.0 m3 s−1, respectively) very close to each other and to the half-load discharge m3 s−1. This result is in perfect agreement with Vogel et al. (2003). The half-load discharge, which is simple to compute, is used by several authors (Doyle and Shields, 2008; Klonsky and Vogel, 2011; Ferro and Porto, 2012; Gray et al., 2015) and has been generalized to identify the dominant discharge conveying a variety of solid or dissolved matter (nutrients, sand, accidental pollution, etc.), especially for the study of ecological aspects and environmental management (Vogel et al., 2003; Doyle et al., 2005; Wheatcroft et al., 2010).
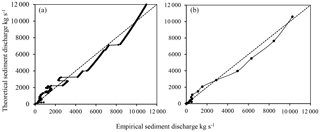
Figure 10Comparison between the analytical sediment supply by class given from the rating curve (, in ordinate) and the elementary contributions , where ΔYK (unit: 103 t) and ΔTK (unit: s) are obtained from Eq. (3) (in abscissa): for a subdivision into classes of equal amplitudes 1 m3 s−1 (a) and with a geometric progression of common ratio 1.2 (b).
5.3 Limits to the use of a rating curve Qs=g(Q) in the Wadi Sebdou
The sediment supply calculated from data (ti, Qi, Ci) (reminder: the supply is the same with the 6947 initial values as with the 40 081 values, linearly interpolated) provided a reference to evaluate the ability of a rating curve to estimate sediment discharge from water flows. This rating curve established from the series (Qk, Ck) generates errors we call hereafter “of the first type”, which we must specify. The sediment supply associated with the kth discharge class is as follows:
where Qk and ΔTK are the centre and the duration of flows corresponding to a given class.
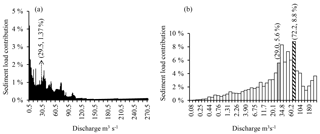
Figure 11Sediment load histogram established using the sediment rating curve: for a subdivision into classes of equal amplitudes 1 m3 s−1 (a) and with a geometric progression of common ratio 1.2 (b).
In the Wadi Sebdou, despite a correct estimate of the total sediment supply for the two subdivisions of equal amplitude 1 m3 s−1 and in geometric progression (Fig. 10, Table 1), the rating curve generates errors that induce a shift in the class of dominant discharge (Fig. 11). The subdivision into classes of equal amplitude leads to a value of effective discharge, QD=1.5 m3 s−1, which is very low in comparison with the one calculated from initial data using Eq. (5) (29.5 m3 s−1). The use of a rating curve for Qs with the subdivision in geometric progression results in an effective discharge of 72.2 m3 s−1, well above the value obtained directly (29.01 m3 s−1). These offsets are explained because the actual sediment discharge associated with each class is around the rating curve g(Qk), sometimes below or sometimes above (Figs. 4 and 7). For both subdivisions, the empirical average sediment concentration observed in the dominant class is well above the rating curve. As a result, the rating curve greatly underestimates the sediment supply in this class. Combined with the flow frequency, the supply is lowered compared to other classes where the model overestimates the average concentration.
This result may be site-specific. Indeed, sediment–discharge rating curves fail to properly reproduce the dynamics of suspended sediment flows in the Wadi Sebdou due to the hysteresis phenomena, studied in Megnounif et al. (2013). Such errors “of the first type”, high in the wadi Sebdou, may be reduced in other semiarid basins.
5.4 Limits to the application of the analytical solution in semi-arid environments
When the flow frequency is represented by a probability distribution, the sediment load histogram can be built from this distribution and the sediment rating curve. However, it should be remembered that for a continuous random variable such as water discharge, the theoretical probability at a point does not exist in the probabilistic sense, but necessarily refers to an interval. Thus, the contribution of a class, Ik, can be quantified by the following:
where Qk is the centre of the Ik interval, f is the probability density function, and T is the total duration of the study period.
Since the function f increases until the mode, Qmode, where it reaches its maximum, the dominant discharge QD is greater than Qmode by construction (Fig. 1). The difference between QD and Qmode depends on the growth of the function g and the decrease of the function f. However, for wadis, the scarcity of flood events and the dominance of low flows (80 % of flows are less than 1 m3 s−1 in the Wadi Sebdou) require the use of a probability density function with a pronounced dissymmetry where, after the mode, the decay is rapid. In this context, only the log-normal and log-Gumbel distributions have apparently shown a satisfactory fit to subdivisions in classes of equal amplitude 1 m3 s−1 and in geometric progression (Fig. 9).
However, the analysis of errors associated with the subdivision in geometric progression and the log-normal distribution (Fig. 12) shows that above 18.3 m3 s−1, the ratio actual frequency on analytical frequency is very high and varies from 11.6 to more than 105 for the log-normal distribution. Consequently, the analytic supply is minimal compared to the load calculated from elementary contributions for these flows, and the total analytical supply given by Eq. (29) underestimates by 79 % the sediment supply established by Eq. (5). With the log-Gumbel distribution, the ratio varies between 0.16 and 1.69 and the total analytical yield overestimates by 35 % the one deduced from elementary contributions (Eq. 5). The offset is also high when flows are subdivided into equal classes of amplitude 1 m3 s−1. Compared with the total analytical yield, low flow rates seem to be the most effective. The class [1, 2 m3 s−1[ dominates with a contribution of about 6 % for the log-normal distribution and 15.7 % for the log-Gumbel distribution. In this case, the total sediment load estimated from the log-normal and log-Gumbel distributions underestimates by 84 % and 66 %, respectively, the empirical load. This example shows that the product of the theoretical frequency distribution generates errors of a second type which are not taken into account in the construction of the sediment load histogram, which, as a result, poorly represents the distribution of the sediment supply (Fig. 13). This type of error may likely be frequent in semi-arid environments, since the frequency of flash floods that carry high sediment supplies is not well represented by pronounced asymmetric flow frequency distributions.
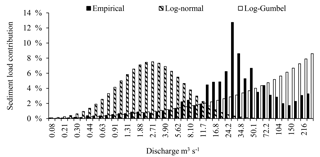
Figure 13Three sediment load histograms obtained from the dataset, from the product of the rating curve times to the log-normal distribution of discharge, and from the product of the rating curve times to the log-Gumbel distribution.
The analytical expressions giving QMode and QD (Eqs. 21, 22, 26 and 27) partly explain the low value of the dominant discharge found for the Wadi Sebdou, which is mainly dependent on the low value of the μ parameter due to the specific hydrologic regime in semi-arid environments, where the annual modulus is very low, often below 1 m3 s−1. The dominant discharge is thus very close to the mode. As a result, the analytical approach seems to be suitable only for rivers where extreme flows are less distant from the mode than on wadis.
In summary, the pronounced asymmetric probability distributions which seemed to be adapted to the Wadi Sebdou failed to reproduce good frequencies of high discharge associated with flash floods. Consequently, the empirical method by decomposition of histogram classes is the most suitable in a semi-arid environment. This had never been tested in the literature. It is an original result of this paper.
Another point deserves a remark in the calculation of the effective discharge from f and g, for the general case. Whatever the probability density function f, the sediment transport efficiency curve is given by . Thus, the effective discharge, solution of the derived function , is independent of the parameter a and depends only on the parameter b. In other words, the dominant discharge depends exclusively on characteristics of the watercourse since parameter b is commonly considered as an indicator of the erosive power of the watercourse (Leopold and Maddock, 1953; Roehl, 1962; Fleming, 1969; Gregory and Walling, 1973; Robinson, 1977; Sarma, 1986; Reid and Frostick, 1987; Iadanza and Napolitano, 2006; Yang et al., 2007). However, the suspended sediment load in rivers is strongly influenced by characteristics of the basin as well, where slope contribution to sediment supply is high (Megnounif et al., 2013), and even sometimes higher than the one of the hydrographic network (Roehl, 1962; Gregory and Walling, 1973; Duysing, 1985; Asselman, 1999). The debate on the relationship between a and b (see for example Achite and Ouillon, 2016) is still open.
Finally, it should be noted that introducing a density function necessarily gives a monomodal sediment transport efficiency curve, whereas this is not necessarily the case. Pickup and Warner (1976), Carling (1988), Phillips (2002), Lenzi et al. (2006) and Ma et al. (2010) reported the existence on some sites of a bimodal dominant flow. Hudson and Mossa (1997) pointed out that sediment load histograms present a variety of forms, including bimodal and complex forms, that differ from the unimodal form identified by Wolman and Miller (1960). In addition to the monomodal sediment load histograms, Ashmore and Day (1988) distinguished three other kinds of histograms: bimodal, multimodal and complex. Of the 55 basins studied by Nash (1994), 29 are bimodal and 9 are multimodal.
5.5 Sensitivity of the dominant class to the environment
Biedenharn et al. (2001) suggest to carefully study long (over 30 years) data series (liquid flow, sediment concentration and flow frequency) and to ensure that the hydrological regime of the watershed did not undergo a significant change in flow rates or sediment production in the long term. Change can be attributed to climate change (Zhang and Nearing, 2005; Ziadat and Taimeh, 2013; Liu et al., 2014; Achite and Ouillon, 2016) or anthropogenic actions (Cerdà, 1998a, b; Liu et al., 2014), such as intensification of agriculture (Montgomery, 2007; Lieskovský and Kenderessy, 2014), deforestation (Walling, 2006), forest fires (González-Pelayo et al., 2006; Cerdà et al., 2010) or urbanization (Graham et al., 2007; Whitney et al., 2015). In the study area, and like northern Africa and the Maghreb, there has been a continuous drought since the mid-1970s (Giorgi and Lionello, 2008; Achite and Ouillon, 2016; Zeroual et al., 2016). Overall, decreasing rainfall is more concentrated over time (Ghenim and Megnounif, 2016), which increases the susceptibility of soils to erosion (Shakesby et al., 2002; Bates et al., 2008; Vachtman et al., 2012). Megnounif and Ghenim (2016) showed that sediment production, which is increasing with increasing rainfall variability (Achite and Ouillon, 2007), increased significantly in the late 1980s, with a pivot in 1988. After 1988, the annual sediment yield was on average 7 times higher compared to the previous period (Megnounif and Ghenim, 2013).
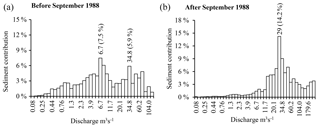
Figure 14Sediment supply by class for the subdivision in geometric progression: for 1973–1988 (a) and for 1988–2004 (b).
The application of a subdivision of discharge classes into geometric progression at the Wadi Sebdou for the two periods 1973–1988 and 1988–2004 confirmed the change in the watershed functioning, with a bimodal sediment supply distribution for the first period (Fig. 14). For 1973–1988, the class [6.1; 7.4 m3 s−1[, which includes the effective discharge QD=6.7 m3 s−1, contributed 7.5 % of the total sediment yield. These relatively frequent flows last on average 0.5 % of the annual time, i.e. 1.83 days, or 6.3 % of the annual duration of floods which, for this period, lasted 7.65 % of the annual time. The second peak was observed for Q=34.8 m3 s−1, representing the class [31.7; 38.0 m3 s−1[. Flows of this class were rare and lasted only 0.09 % of the annual time (7 h and 45 min per year), but carried 5.9 % of the total sediment yield. Over the period 1988–2004, the distribution of sediment supply became essentially monomodal (Fig. 14) with a dominant flow QD=29.0 m3 s−1. During this second period, an increasing sediment contribution was also observed at high discharge (>110 m3 s−1, up to 273 m3 s−1) that was not sampled during the period 1973–1988.
The half-load discharge in 1973–1988, (7.68 m3 s−1), was close to the dominant discharge QD (6.7 m3 s−1) and not far from the modal class [6.1; 7.4 m3 s−1[; in 1988–2003, (31.80 m3 s−1) was very close to the modal class [26.4; 31.7 m3 s−1[, whose centre was defined as the effective discharge (QD=29.0 m3 s−1). Thus, in the Sebdou Basin, the half-load discharge can be seen as a robust proxy for the effective discharge. This result warrants further study in other basins.
From a time series of flow and concentration data, a direct calculation provides estimates of water and sediment supplies by summing the elementary contributions. This gives access to seasonal or annual values, and to the analysis of their variability. Sediment dynamics can also be analysed from discharge and sediment yield histograms by water discharge classes. In the Wadi Sebdou, we have shown that an appropriate choice of subdivisions makes it possible to minimize the difference between the flows estimated and measured at less than 10 % ( % for classes of equal amplitude 1 m3 s−1, Table 1) or even less than 1 % ( % for classes in geometric progression of common ratio 1.2, Table 1). Classes thus defined make it possible to determine a dominant class in the sense of sediment yield QD (29.5 or 29 m3 s−1 according to the two classifications mentioned above), which is similar to the median flow in the sense of sediment yield (29.8 m3 s−1) in the Wadi Sebdou. Other classifications have proved to be able to estimate the effective discharge (with a lesser precision) but unable to provide good estimates of the water and sediment supplies (classes of equal amplitude greater than 1 m3 s−1), or able to estimate these supplies but unable to estimate the effective discharge (classes with equal water supplies).
The introduction of a rating curve between the Qk and Ck series considered to build the histogram induced an additional bias with respect to the direct calculation for the sedimentary yield. In the Wadi Sebdou, this bias, which depends on the choice of subdivisions, can be reduced by 6 to 7 %, as indicated by τMY (Table 1), which is acceptable with regard to either the uncertainties of measurements, or sometimes of inappropriate or insufficient sampling (Coynel et al., 2004). Previous work (Megnounif et al., 2013) has shown the importance of hysteresis phenomena on this basin, which induces a strong dispersion of instant parameter pairs (Q, C) and a bias in the estimation of supplies using a rating curve. The rating curve based on average values by flow class, of defined length in geometric progression, appreciably improves statistical performances in the computation of the sediment supply (higher value of R2, 0.95, and better Nash–Sutcliffe criterion, 0.93, compared to any other method – see Table 1). It will be interesting in future works to analyse whether this is a singular phenomenon or whether the use of a rating curve based on subdivision classes rather than on instantaneous measurements makes it possible to improve the calculation of sediment yield compared with more conventional methods.
In the Wadi Sebdou, the coupled use of a sediment rating curve and the log-normal and log-Gumbel probability distributions were most likely to reproduce the observed regime, characterized by a very weak mode. However, they failed to properly estimate the flow frequency of flash floods which are typical in semi-arid environments, and the corresponding sediment yield.
Two return periods of the effective discharge were identified: one (from the annual maximum flow rate series, QMAX) for the interval between two hydrological years with occurrence of the effective discharge, and one (from the annual half-load discharge series) for the duration between two hydrologic years for which , i.e. such than half of the sediment supply at least is carried by flows higher than the effective discharge.
Flows of the dominant class carry the most sediment in the watercourse. It should be possible to link them to major processes of erosion, transport and deposition that occur in the watershed. Lenzi et al. (2006), who have observed a bimodal sediment contribution for a mountain river in the Alps in Italy, attributed the first modal class, of low but more frequent flow, to the shaping of channel and suggested that the second-class flows, larger in magnitude but of low occurrence, would be responsible for the macroscale shape of the watercourse. In the Wadi Sebdou, we also observed a bimodal distribution. However, it is difficult to conclude because the secondary mode of distribution obtained for the first period (1973–1988) became the dominant mode of distribution later (1988–2004). The modes moved with the hydrological regime towards higher and higher sediment yields, in line with what has been observed in most watersheds studied over recent decades in the semi-arid environments of Algeria (e.g. Achite and Ouillon, 2016). Applying this method to other watersheds will undoubtedly allow us to go further in the analysis of dominant discharge and in their dynamics, in a context of global change.
Discharge and suspended sediment concentrations are available on request for scientific purposes from the National Agency of Hydraulic Resources of Algeria (locally called ANRH, http://www.anrh.dz/; Agence Nationale des Ressources Hydrauliques, 2018), from its national office in Bir Mourad Raïs, Algiers. The data can alternatively be made available upon request to the first author (megnounif_aslam@yahoo.fr).
AM and SO designed the study. AM computed and processed the results. Both authors performed all analyses, prepared the manuscript, revised it and approved the final version.
The authors declare that they have no conflict of interest.
Two anonymous reviewers are warmly thanked for their reviews and comments on
previous versions of this paper. The editor, Thomas Kjeldsen, is gratefully
acknowledged.
Edited by: Thomas Kjeldsen
Reviewed by: two anonymous referees
Achite, M. and Ouillon, S.: Suspended sediment transport in a semiarid watershed, Wadi Abd, Algeria (1973–1995), J. Hydrol., 343, 187–202, https://doi.org/10.1016/j.jhydrol.2007.06.026, 2007.
Achite, M. and Ouillon, S.: Recent changes in climate, hydrology and sediment load in the Wadi Abd, Algeria (1970–2010), Hydrol. Earth Syst. Sci., 20, 1355–1372, https://doi.org/10.5194/hess-20-1355-2016, 2016.
Agence Nationale des Ressources Hydrauliques: http://www.anrh.dz/, last access: 20 November 2018.
Alexandrov, Y., Laronne, J. B., and Reid, I.: Suspended sediment concentration and its variation with water discharge in a dryland ephemeral channel, northern Negev, Israel, J. Arid Environ., 53, 73–84, https://doi.org/10.1006/jare.2002.1020, 2003.
Andrews, E. D.: Effective and bankfull discharges of streams in the Yampa River basin, Colorado and Wyoming, J. Hydrol., 46, 311–330, https://doi.org/10.1016/0022-1694(80)90084-0, 1980.
Ashmore, P. E. and Day, T. J.: Effective discharge for suspended sediment transport in streams of the Saskatchewan River Basin, Water Resour. Res., 24, 864–870, https://doi.org/10.1029/WR024i006p00864, 1988.
Asselman, N. E. M.: Suspended sediment dynamics in a large drainage basin: the River Rhine, Hydrol. Process., 13, 1437–1450, https://doi.org/10.1002/(SICI)1099-1085(199907)13:10<1437::AID-HYP821>3.0.CO;2-J, 1999.
Bagnold, R. A.: The physics of blown sand and desert dunes, Methuen and Co, London, 1941.
Bates, B. C., Kundzewicz, Z. W., Wu S., and Palutikof, J. P. (Eds.): Climate Change and Water, Technical Paper of the Intergovernmental Panel on Climate Change, IPCC Secretariat, Geneva, 210 pp., 2008.
Benest, M.: Les formations carbonatées et les grands rythmes du Jurassique supérieur des monts de Tlemcen (Algérie), C. R. Acad. Sci. Paris Série D, 275, 1469–1471, 1972.
Benest, M. and Elmi, S.: Précisions stratigraphiques sur le Jurassique inférieur et moyen de la partie méridionale des Monts de Tlemcen (Algérie), C. R. Som. Soc. Geol. France, 8, 295–296, 1969.
Benson, M. A. and Thomas, D. M.: A definition of dominant discharge, Bull. Int. Assoc. Scient. Hydrol., 11, 76–80, 1966.
Biedenharn, D. S., Thorne, C. R., Soar, P. J., Hey, R. D., and Watson, C. C.: Effective discharge calculation guide, Int. J. Sediment Res., 16, 445–459, 2001.
Bouanani, A.: Hydrologie, transport solide et modélisation. Etude de quelques sous bassins de la Tafna (NW Algérie), PhD Thesis, Tlemcen University, Algeria, p. 250, 2004.
Bunte, K., Abt, S. R., Swingle, K. W., and Cenderelli, D. A.: Effective discharge in Rocky Mountain headwater streams, J. Hydrol., 519, 2136–2147, https://doi.org/10.1016/j.jhydrol.2014.09.080, 2014.
Carling, P. A.: The concept of dominant discharge applied to two gravel-bed streams in relation to channel stability thresholds, Earth Surf. Proc. Land., 13, 355–367, https://doi.org/10.1002/esp.3290130407, 1988.
Castillo, V. M., Gomez-Plaza, A., and Martinez-Mena, M.: The role of antecedent soil water content in the runoff response of semiarid catchments: a simulation approach, J. Hydrol., 284, 114–130, https://doi.org/10.1016/S0022-1694(03)00264-6, 2003.
Cerdà, A.: Relationships between climate and soil hydrological and erosional characteristics along climatic gradients in Mediterranean limestone areas, Geomorphology, 25, 123–134, https://doi.org/10.1016/S0169-555X(98)00033-6, 1998a.
Cerdà, A.: Effect of climate on surface flow along a climatological gradient in Israel. A field rainfall simulation approach, J. Arid Environ., 38, 145–159, https://doi.org/10.1006/jare.1997.0342, 1998b.
Cerdà, A., Lavee, H., Romero-Díaz, A., Hooke, J., and Montanarella, L.: Soil erosion and degradation in mediterranean type ecosystems, Land Degrad. Dev., 21, 71–74, https://doi.org/10.1002/ldr.968, 2010.
Chow, V. T., Maidment, D. R., and Mays, L. W.: Applied Hydrology, McGraw-Hill, New York, USA, 1988.
Colombani, J., Olivry, J. C., and Kallel, R.: Phénomènes exceptionnels d'érosion et de transport solide en Afrique aride et semi-aride, Challenges in African Hydrology and Water Ressources, IAHS Publ., 144, 295–300, 1984.
Coynel, A., Schäfer, J., Hurtrez, J. E., Dumas, J., Etcheber, H., and Blanc, G.: Sampling frequency and accuracy of SPM flux estimates in two contrasted drainage basins, Sci. Total Environ., 330, 233–247, https://doi.org/10.1016/j.scitotenv.2004.04.003, 2004.
Crowder, D. W., and Knapp, H. V.: Effective discharge recurrence intervals of Illinois streams, Geomorphology, 64, 167–184, https://doi.org/10.1016/j.geomorph.2004.06.006, 2005.
Doyle, M. W. and Shields, C. A.: An alternative measure of discharge effectiveness, Earth Surf. Proc. Land., 33, 308–316, https://doi.org/10.1002/esp.1543, 2008.
Doyle, M. W., Stanley, E. H., Strayer, D. L., Jacobson, R. B., and Schmidt, J. C.: Effective discharge analysis of ecological processes in streams, Water Resour. Res., 41, W11411, https://doi.org/10.1029/2005WR004222, 2005.
Dunne, T. and Leopold, L. B.: Water in Environmental Planning, W. H. Freeman, San Francisco, USA, 818 pp., 1978.
Duysing, J. J. H. M.: Streambank contribution to the sediment budget of forest stream, Unpubl. PhD Thesis, Lab. Phys. Geogr. Soil Sci., Univ. Amsterdam, Amsterdam, p. 190, 1985.
Emmett, W. W. and Wolman, M. G.: Effective discharge and gravel-bed rivers, Earth Surf. Proc. Land., 26, 1369–1380, https://doi.org/10.1002/esp.303, 2001.
Ferro, V. and Porto, P.: Identifying a dominant discharge for natural rivers in southern Italy, Geomorphology, 139–140, 313–321, https://doi.org/10.1016/j.geomorph.2011.10.035, 2012.
Fleming, G.: Design curves for suspended load estimation, Proc. Inst. Civ. Eng., 43, 1–9, https://doi.org/10.1680/iicep.1969.7398, 1969.
Gao, P. and Josefson, M.: Temporal variations of suspended sediment transport in Oneida Creek watershed, central New York, J. Hydrol., 426–427, 17–27, https://doi.org/10.1016/j.jhydrol.2012.01.012, 2012.
Ghenim, A. N. and Megnounif, A.: Variability and Trend of Annual Maximum Daily Rainfall in Northern Algeria, Int. J. Geophys., 2016, 6820397, https://doi.org/10.1155/2016/6820397, 2016.
Giorgi, F. and Lionello, P.: Climate change projections for the Mediterranean region, Global Planet. Change, 63, 90–104, https://doi.org/10.1016/j.gloplacha.2007.09.005, 2008.
González-Pelayo, O., Andreu, V., Campo, J., Gimeno-García, E., and Rubio, J. L.: Hydrological properties of a Mediterranean soil burned with different fire intensities, Catena, 68, 186–193, https://doi.org/10.1016/j.catena.2006.04.006, 2006.
Goodwin, P.: Analytical solutions for estimating effective discharge, J. Hydraul. Eng., 130, 729–738, https://doi.org/10.1061/(ASCE)0733-9429(2004)130:8(729), 2004.
Graham, L. P., Andréasson, J., and Carlsson, B.: Assessing climate change impacts on hydrology from an ensemble of regional climate models, model scales and linking methods – a case study on the Lule River basin, Climatic Change, 81, 293–307, https://doi.org/10.1007/s10584-006-9215-2, 2007.
Gray, A. B., Pasternack, G. B., Watson, E. B., Warrick, J. A., and Goñi, M. A.: Effects of antecedent hydrologic conditions, time dependence, and climate cycles on the suspended sediment load of the Salinas River, California, J. Hydrol., 525, 632–649, https://doi.org/10.1016/j.jhydrol.2015.04.025, 2015.
Gregory, K. J. and Walling, D. E.: Drainage Basin Form and Process, Edward Arnold, London, p. 458, 1973.
Heusch, B.: Etude de l'érosion et des transports solides en zone semi-aride, Recherche bibliographique sur l'Afrique du Nord, Projet RAB/80/04/PNUD, PNUD, Geneva, Switzerland, 1–83, 1982.
Hey, R. D.: Channel Response and Channel Forming Discharge, Final Report, US Army Corps of Engineers, R&D6871EN-01, European Research Office, London, UK, p. 108, 1997.
Higgins, A., Restrepo, J. C., Ortiz, J. C., Pierini, J., and Otero, L.: Suspended sediment transport in the Magdalena River (Colombia, south America): Hydrologic regime, rating Parameters and effective discharge variability, Int. J. Sediment Res., 31, 25–35, https://doi.org/10.1016/j.ijsrc.2015.04.003, 2015.
Horowitz, A. J.: An evaluation of sediment rating curves for estimating suspended sediment concentrations for subsequent flux calculations, Hydrol. Process., 17, 3387–3409, https://doi.org/10.1002/hyp.1299, 2003.
Hudson, P. F. and Mossa, J.: Suspended sediment transport effectiveness of three large impounded rivers, US Gulf Coast Plain. Environ. Geol., 32, 263–273, https://doi.org/10.1007/s002540050216, 1997.
Iadanza, C. and Napolitano, F.: Sediment transport time series in the Tiber River, Phys. Chem. Earth, 31, 1212–1227, https://doi.org/10.1016/j.pce.2006.05.005, 2006.
Klonsky, L. and Vogel, R. M.: Effective Measures of “Effective” Discharge, J. Geol., 119, 1–14, https://doi.org/10.1086/657258, 2011.
Lenzi, M. A., Mao, L., and Comiti, F.: Effective discharge for sediment transport in a mountain river: Computational approaches and geomorphic effectiveness, J. Hydrol., 326, 257–276, https://doi.org/10.1016/j.jhydrol.2005.10.031, 2006.
Leopold, L. B. and Maddock Jr., T.: The Hydraulic Geometry of Stream Channels and Some Physiographic Implications, Professional Paper 252, US Geological Survey, Washington, D.C., p. 56, available at: https://pubs.usgs.gov/pp/0252/report.pdf (last access: 20 November 2018), 1953.
Lieskovský, J. and Kenderessy, P.: Modelling the effect of vegetation cover and different tillage practices on soil erosion in vineyards: a case study en Vráble (Slovakia) using WATEM/SEDEM, Land Degrad. Dev., 25, 288–296, https://doi.org/10.1002/ldr.2162.2014, 2014.
Liu, Z., Yao, Z., Huang, H., Wu, S., and Liu, G.: Land use and climate changes and their impacts in the Yarlung Zangbo river basin, China, Land Degrad. Dev., 25, 203–215, https://doi.org/10.1002/ldr.1159, 2014.
Ma, Y. X., Huang, H. Q., Xu, J. X., Brierley, G. J., and Yao, Z. J.: Variability of effective discharge for suspended sediment transport in a large semi-arid river basin, J. Hydrol., 388, 357–369, https://doi.org/10.1016/j.jhydrol.2010.05.014, 2010.
McKee, L. J., Hossain, S., and Eyre, B. D.: Magnitude-frequency analysis of suspended sediment loads in the subtropical Richmond River basin, northern New South Wales, Australia, IAHR Publ., 276, 289–296, 2002.
Megnounif, A. and Ghenim, A. N.: Influence des fluctuations hydropluviométriques sur la production des sédiments: Cas du bassin de la haute Tafna, Rev. Sci. Eau, 26, 53–62, https://doi.org/10.7202/1014919ar, 2013.
Megnounif, A. and Ghenim, A. N.: Rainfall irregularity and its impact on the sediment yield in Wadi Sebdou watershed, Algeria, Arab. J. Geosci., 9, 267, https://doi.org/10.1007/s12517-015-2280-y, 2016.
Megnounif, A., Terfous, A., and Bouanani, A.: Production and transport of suspended sediment transport in the Upper-Tafna river basin (North West Algeria), Rev. Sci. Eau, 16, 369–380, 2003.
Megnounif, A., Terfous, A., and Ouillon, S.: A graphical method to study suspended sediment dynamics during flood events in the Wadi Sebdou, NW Algeria (1973–2004), J. Hydrol., 497, 24–36, https://doi.org/10.1016/j.jhydrol.2013.05.029, 2013.
Milliman, J. D. and Syvitski, J. P. M.: Geomorphic/tectonic control of sediment discharge to the ocean: the importance of small mountainous rivers, J. Geol., 100, 325–344, https://doi.org/10.1086/629606, 1992.
Montgomery, D. R.: Soil erosion and agricultural sustainability, P. Natl. Acad. Sci. USA, 4, 268–272, https://doi.org/10.1073/pnas.0611508104, 2007.
Nash, D. B.: Effective sediment-transporting discharge from magnitude-frequency analysis, J. Geol., 102, 79–95, https://doi.org/10.1086/629649, 1994.
Nash, J. E. and Sutcliffe, J. V.: River flow forecasting through conceptual models, Part I – A discussion of principles, J. Hydrol., 10, 282–290, https://doi.org/10.1016/0022-1694(70)90255-6, 1970.
Nolan, K. M., Lisle, T. E., and Kelsey, H. M.: Bankfull discharge and sediment transport in northwestern California. Erosion and sedimentation in the Pacific Rim, IAHS Publ., 165, 439–449, 1987.
Phillips, J. D.: Geomorphic impacts of flash flooding in a forested headwater basin, J. Hydrol., 269, 236–250, https://doi.org/10.1016/S0022-1694(02)00280-9, 2002.
Pickup, G. and Warner, R. F.: Effects of hydrologic regime on magnitude and frequency of dominant discharge, J. Hydrol., 29, 51–75, https://doi.org/10.1016/0022-1694(76)90005-6, 1976.
Probst, J. L. and Amiotte-Suchet, P. A.: Fluvial suspended sediment transport and mechanical erosion in the Maghreb (North Africa), Hydrolog. Sci. J., 37, 621–637, https://doi.org/10.1080/02626669209492628, 1992.
Quader, A., Guo, Y., and Stedinger, J. R.: Analytical estimation of effective discharge for small southern Ontario streams, Can. J. Civ. Eng., 35, 1414–1426, https://doi.org/10.1139/L08-088, 2008.
Reid, I. and Frostick, L. E.: Discussion of conceptual models of sediment transport in streams, in: Sediment transport in gravel-bed rivers, edited by: Thorne, C. R., Bathurst, J. C., and Hey, R. D., Wiley, New York, 410–411, 1987.
Reid, I. and Laronne, J. B.: Bed load sediment transport in an ephemeral stream and a comparison with seasonal and perennial counterparts, Water Resour. Res., 31, 773–781, https://doi.org/10.1029/94WR02233, 1995.
Robinson, A. R.: Relationships between soil erosion and sediment delivery. Erosion and Solid Matter Transport in Inland Waters, IAHS Bull., 122, 159–167, 1977.
Roehl, J. W.: Sediment source areas, delivery ratios, and influencing morphological factors, IAHS Publ., 59, 202–213, 1962.
Roy, N. G. and Sinha, R.: Effective discharge for suspended sediment transport of the Ganga River and its geomorphic implication, Geomorphology, 227, 18–30, https://doi.org/10.1016/j.geomorph.2014.04.029, 2014.
Sarma, J. N.: Sediment transport in the Burhi Dihing River, India, in: Drainage basin sediment delivery, edited by: Hadley, R. F., IAHS Publ., 159, 199–215, 1986.
Scott, S.: Predicting sediment transport dynamics in ephemeral channels: a review of literature. ERDC/CHL CHETN-VII-6, US Army Engineer Research and Development Center, Vicksburg, available at: http://chl.erdc.usace.army.mil/chetn (last access: 19 November 2018), 2006.
Shakesby, R. A., Coelho, C. O. A., Schnabel, S., Keizer, J. J., Clarke, M. A., Lavado Contador, J. F., Walsh, R. P. D., Ferreira, A. J. D., and Doerr, S. H.: A ranking methodology for assessing relative erosion risk and its application to dehesas and montados in Spain and Portugal, Land Degrad. Dev., 13, 129–140, https://doi.org/10.1002/ldr.488, 2002.
Shields, A.: Anwendung der Ähnlichkeitsmechnik und der Turbulenz Firschung auf die geschiebebewegung Mitt, Heft 26, Der Preuss. Versuchsamst. für Wasserbau und Schiffbau, Berlin, Deutschland, 1936.
Sichingabula, H. M.: Magnitude-frequency characteristics of effective discharge for suspended sediment transport, Fraser River, British Columbia, Canada, Hydrol. Process., 13, 1361–1380, https://doi.org/10.1002/(SICI)1099-1085(19990630)13:9<1361::AID-HYP808>3.0.CO;2-H, 1999.
Simon, A., Dickerson, W., and Heins, A.: Suspended-sediment transport rates at the 1.5-year recurrence interval for ecoregions of the United States: transport conditions at the bankfull and effective discharge, Geomorphology, 58, 243–262, https://doi.org/10.1016/j.geomorph.2003.07.003, 2004.
Terfous, A., Megnounif, A., and Bouanani, A.: Etude du transport solide en suspension dans l'Oued Mouilah (Nord-Ouest Algérien), Revue Sciences de l'Eau, 14, 173–185, 2001.
Vachtman, D., Sandler, A., Herut, B., and Greenbaum, N.: Dynamics of suspended sediment delivery to the Eastern Mediterranean continental shelf, Hydrol. Process., 27, 1105–1116, https://doi.org/10.1002/hyp.9265, 2012.
van Rijn, L. C.: Principles of sediment transport in rivers, estuaries and coastal seas, Aqua Publications, Amsterdam, the Netherlands, 2005.
Vogel, R. M., Stedinger, J. R., and Hooper, R. P.: Discharge indices for water quality loads, Water Resour. Res., 39, 1273, https://doi.org/10.1029/2002WR001872, 2003.
Walling, D. E.: Derivation of erosion and sediment yield parameters in areas with deficient data reconnaissance measurements, Hydrological Sciences – Bulletin des Sciences Hydrologiques, XXII, 4 12/197, 517–520, 1977.
Walling, D. E.: Human impact on land–ocean sediment transfer by the world's rivers, Geomorphology, 79, 192–216, https://doi.org/10.1016/j.geomorph.2006.06.019, 2006.
Walling, D. E.: The impact of global change on erosion and sediment dynamics: current progress and future challenges, UNESCO-IHP International Sediment Initiative (ISI) paper, available at: http://unesdoc.unesco.org/images/0018/001850/185078E.pdf (last access: 19 November 2018), 2008.
Watson, C. C., Biedenharn, D. S., and Thorne, C. R. (Eds.): Demonstration Erosion Control: Design Manual. Engineer Research and Development Center, US Army Corps of Engineering, Engineer Research and Development Center, Vicksburg, MS, 274 pp., 1999.
West, T. S. and Niezgoda, S. L.: Estimating a stream restoration design discharge, in: Proceedings of the World Environmental and Water Resource Congress: Examining the Confluence of Environmental and Water Concerns, ASCE, 21–25 May 2006, Omaha, Nebraska, 2006.
Wheatcroft, R. A., Goñi, M. A., Hatten, J. A., Pasternack, G. B., and Warrick, J. A.: The role of effective discharge in the ocean delivery of particulate organic carbon by small, mountainous river systems, Limnol. Oceanogr., 55, 161–171, https://doi.org/10.4319/lo.2010.55.1.0161, 2010.
Whitney, J. W., Glancy, P. A., Buckingham, S. E., and Ehrenberg, A. C.: Effects of rapid urbanization on streamflow, erosion, and sedimentation in a desert stream in the American Southwest, Anthropocene, 10, 29–42, https://doi.org/10.1016/j.ancene.2015.09.002, 2015.
Wolman, M. G. and Miller, J. P.: Magnitude and frequency of forces in geomorphic processes, J. Geol., 68, 54–74, 1960.
Yang, G. F., Chen, Z. Y., Yu, F. L., Wang, Z. H., and Zhao, Y. W.: Sediment rating parameters and their implications: Yangtze River, China, Geomorphology, 85, 166–175, https://doi.org/10.1016/j.geomorph.2006.03.016, 2007.
Yevjevich, V.: Probability and Statistics in Hydrology, Water Resources Publications, Fort Collins, USA, Colorado, 302 pp., 1972.
Zeroual, A., Assani, A. A., and Meddi, M.: Combined analysis of temperature and rainfall variability as they relate to climate indices in Northern Algeria over the 1972–2013 period, Hydrol. Res., 48, 584–595, https://doi.org/10.2166/nh.2016.244, 2016.
Zhang, X. C. and Nearing, M. A.: Impact of climate change on soil erosion, runoff, and wheat productivity in central Oklahoma, Catena, 61, 185–195, https://doi.org/10.1016/j.catena.2005.03.009, 2005.
Ziadat, F. M. and Taimeh, A. Y.: Effect of rainfall intensity, slope and land use and antecedent soil moisture on soil erosion in an arid environment, Land Degrad. Dev., 24, 582–590, https://doi.org/10.1002/ldr.2239, 2013.
half-load discharge, was compared to analytical values based on statistics and rating curves. Return periods were also explained.