the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Incorporating the logistic regression into a decision-centric assessment of climate change impacts on a complex river system
Daeha Kim
Jong Ahn Chun
Si Jung Choi
Climate change is a global stressor that can undermine water management policies developed with the assumption of stationary climate. While the response-surface-based assessments provided a new paradigm for formulating actionable adaptive solutions, the uncertainty associated with the stress tests poses challenges. To address the risks of unsatisfactory performances in a climate domain, this study proposed the incorporation of the logistic regression into a decision-centric framework. The proposed approach replaces the “response surfaces” of the performance metrics typically used for the decision-scaling framework with the “logistic surfaces” that describes the risk of system failures against predefined performance thresholds. As a case study, water supply and environmental reliabilities were assessed within the eco-engineering decision-scaling framework for a complex river basin in South Korea. Results showed that human-demand-only operations in the river basin could result in the water deficiency at a location requiring environmental flows. To reduce the environmental risks, the stakeholders could accept increasing risks of unsatisfactory water supply performance at the sub-basins with small water demands. This study suggests that the logistic surfaces could provide a computational efficiency to measure system robustness to climatic changes from multiple perspectives together with the risk information for decision-making processes.
Climate change is a global stressor that poses prodigious challenges to long-term management of water resources. While water infrastructures have been constructed across the globe to sustain human livelihood and activities, those assets have been traditionally managed by heuristic operation policies developed under the assumption of stationary climate (Cosgrove and Loucks, 2015; Cully et al., 2016). However, probabilistic behaviors of hydrological processes can be significantly altered by the warming atmosphere; therefore, the heuristic policies are expected to become increasingly vulnerable (Brown et al., 2015; Georgakakos et al., 2012).
When formulating management solutions to non-stationary climate for a water system, an essential step is to assess impacts of climate change on its performance. An established method for the impact assessment was to investigate outputs of relevant system models forced by projections of the general circulation models (GCMs) under hypothetical greenhouse gas (GHG) emission scenarios (e.g., Xu et al., 2015; Eum and Simonovic, 2010). This type of assessments takes the “predict-then-act” paradigm for which the first prerequisite is sufficiently reliable predictions. The GCM projections, however, are often biased by inappropriate model formulations and/or imperfectly understood physical processes (Stevens and Bony, 2013; Deser et al., 2012; Dufresne and Bony, 2008; Stainforth et al., 2005). Thus, they may contain unacceptable risk costs for policymakers (Brown et al., 2012), hindering utilization of GCM-led strategies (Weaver et al., 2013; Brown and Wilby, 2012).
To overcome the weakness of GCM-driven assessments in practical decision support, alternative frameworks within the “robust decision” paradigm have emerged (e.g., Hadka et al., 2015; Whateley et al., 2014; Lampert and Groves, 2010). These decision-centric approaches seek robust solutions that can minimize adverse effects of climatic stresses on given hydrological systems. Examples include the decision scaling (Brown et al., 2012), the dynamic adaptive policy pathways (Haasnoot et al., 2013), the real option analysis (Woodward et al., 2014), the info-gap decision theory (Korteling et al., 2013), and the robust decision-making (Lampert and Groves, 2010), among others. Whereas the predict-then-act paradigm focuses on the most likely future conditions that can maximize expected utility, the decision-centric approaches pay attention to sensitivity (or vulnerability) of system performance to climatic stressors (Weaver et al., 2013; Brown et al., 2012). This paradigm accepts the irreducible uncertainty in climate predictions as an inevitable part of long-term planning and guides decision makers toward low-regret strategies for sustainable system performance under non-stationary climate.
Among the decision-centric frameworks, the assessments based on the response functions of system performance have provided convenience in defining decision thresholds at which adaptation actions are required (e.g., Kim et al., 2018; Steinschneider et al., 2015a; Turner et al., 2014; Whateley et al., 2014; Brown et al., 2012; Prudhomme et al., 2010). They developed the relationships between system performances and climatic stressors (hereafter referred to as the response surfaces) via stress tests. Then, GCM projections were employed to indicate future system performance on the response surfaces. The response-surface-based methods have been refined to consider spatially varying system performance (e.g., Schlef et al., 2018) and multiple management objectives within a hydrological system (e.g., Culley et al., 2016). They allowed efficient evaluation of climate change risks by simply comparing the performance metrics indicated by a collection of GCMs against predefined thresholds.
Nonetheless, uncertainty of the response surfaces cannot be neglected due to assumptions and simplifications associated with the stress tests. Kim et al. (2018), for instance, showed how climate change risks could be underestimated if a modeling scale was inappropriately chosen. Kay et al. (2014) emphasized the importance of uncertainty allowances being used alongside the response surfaces. Moreover, Steinschneider et al. (2015b) suggested that hydrological modeling and climatic variability may introduce uncertainty in the response surfaces as much as GCM projections. The prior studies imply that over-reliance on the response surfaces of general performance metrics may misguide users to inappropriate and/or untimely adaptation policies. Importantly, the response surfaces have usually been developed with climatic shifts defined by long-term changes in statistical moments of weather observations (e.g., Poff et al., 2016; Steinschneider et al., 2015a; Whateley et al., 2014; Turner et al., 2014), even though they might insufficiently explain variation in the chosen performance indicators. Whateley and Brown (2016) found that the performance variation in a water supply system can be attributed significantly to the internal climate variability over a time horizon of policy planning. In other words, even if a projected climatic shift indicates a satisfactory performance on the response surface, the system of interest could still be subject to a considerable risk of unsatisfactory performance.
Due to the associated uncertainty, the response surface of general system performance needs to be treated in a probabilistic manner. A possible approach is to gauge the uncertainty via the Monte Carlo sampling of system performances per climate stress (e.g., Steinschneider et al., 2015b; Whateley and Brown, 2016). However, if a complex system model is employed with a large combination of climate stressors, this stochastic sampling approach would require expensive computational costs, even with modern computing power (Whateley et al., 2016). To explore the effect of internal climate variability with the exhaustive Monte Carlo sampling, the computational burden for the stress test would be multiplied many times.
In this work, therefore, an efficient approach was proposed to evaluate the risks of system failures within a decision-centric framework. We simply incorporated the logistic regression into typical stress tests for the response-surface-based assessments. This study shows that the response surface can be simply converted into a probabilistic domain by categorizing the performance samples from the stress tests against a threshold. As a case study, we provided here a slightly modified version of the eco-engineering decision-scaling framework (Poff et al., 2016) to explore the probabilities of system failures varying across a complex river system with two contrasting management purposes.
2.1 Eco-engineering decision-scaling framework
The eco-engineering decision-scaling (EEDS) framework (Poff et al., 2016) expanded the decision scaling (Brown et al., 2012) to consider stakeholders' multifaceted interests in the response surfaces. Five iterative steps are required for this framework. Step 1 is to identify possible management options (e.g., upgrading operations and/or structural investments), to select indicators of ecological and engineering performances (e.g., water supply reliability and ecological vulnerability), and to define user-specific thresholds under which the system performs unacceptably. Step 2 is to build system models for the hypothetical stress tests. For water resource management, the system models may include a runoff model and a water allocation model. By exposing the system models to a wide range of hypothetical climatic stressors, ecological and engineering performances can be evaluated. In step 3, the response surfaces of engineering and ecological performances are developed with outcomes of the stress tests. For vulnerability analysis, the predefined thresholds are imposed on the response surfaces. Step 4 is to evaluate the management options with the size of the climatic zones satisfying the performance thresholds. In step 5, preferred decisions for the management options can be made, or, if necessary, the assessment from step 1 to 4 can be repeated with new management options and/or different criteria.
In the EEDS framework, the key information would be the size of the climate zone mutually satisfying the engineering and ecological thresholds since it measures overall system robustness to climate stresses. Decision makers may prefer management options that can widen the mutual climate zone, if they are socio-economically viable. However, the system robustness is not the only criterion for selecting management options. In decision-making processes, questions can be raised such as “what if future climates will not fall within the mutual climate zone?” and “how much do risks of system failures still exist within the climate zone that expects satisfactory performances?” Those questions can be answered by incorporating the logistic regression and a collection of GCM projections into the EEDS framework.
2.2 Incorporating the logistic regression into the stress tests
The stress tests in step 3 for the EEDS framework are intended to find expected performances per given climate exposure. By comparing the obtained performances against a predefined threshold, the climate exposures applied to the stress tests can be categorized into binary outcomes (i.e., 1 for satisfactory performances and 0 for other cases). With no need for the homogeneity and normality assumptions, the logistic regression model allows the explanation of occurrences of the satisfactory performances with the sigmoid function of the climate exposures (xi):
where π is the probability of satisfactory performance and βi is the regression coefficients. Thus, 1−π becomes the probability of unsatisfactory performance.
When two explanatory variables are chosen for xi (e.g., changes in mean annual precipitation and temperature), it is possible to develop a two-dimensional surface to describe variation in π within a climate domain. Hereafter, the surface of π will be referred to as the logistic surface. In this study, the logistic surfaces were used for the steps 3 and 4 of the EEDS framework in lieu of the response surfaces. The following example shows how to assess the risk of system failures together with robustness to climate stresses for a complex water system.
3.1 Study area
The case study area is the Geum River basin located in the western–central part of South Korea with a total area of 9915 km2 (Fig. 1). The mean and the highest elevations in the river basin are 85 m and 1596 m a.s.l. (above sea level), respectively. The mean basin slope is 16.7 %. The total length of the main channel is approximately 402 km. The river basin has a semi-humid climate with monsoonal summer seasons. Wet air masses moving from the North Pacific usually make for hot and humid summer seasons, whereas winter seasons are dry and cold due to the Siberian high pressure. Approximately 60 %–70 % of annual precipitation falls in June to September (KMA, 2011); thus, rivers flow across the basin peaks in the middle of summer monsoon seasons. Snowmelt runoff minimally contributes to streamflow variations due to small winter precipitation (Bae et al., 2008).
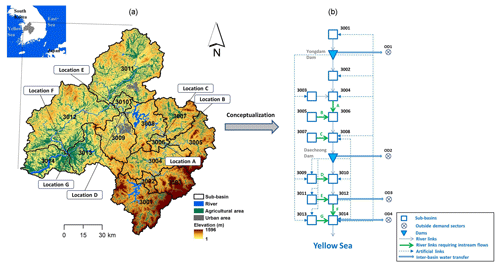
Figure 1Layout of the Geum River basins (a) and the simplified node-and-link network for modeling water allocations (b).
The Geum River basin is officially divided into 14 sub-basins for administrative purposes along the geomorphological boundaries. The sub-basin areas vary between 120 and 1856 km2, with an average of 708 km2. 60 % of the entire river basin is covered by forests, while agricultural areas account for 18 %. The forest covers and agricultural lands within the 14 sub-basins occupy 33 %–83 % and 4.6–42 %, respectively. The sub-basins with relatively large agricultural lands tend to have small forest covers. The urban areas are 5.3 % of the river basin in total. According to the Korea Forest Service (http://forest.go.kr, last access: 11 October 2017), the soils across the Geum River basin have moderate to high infiltration capacity, implying that sub-surface runoff generations are dominant.
Human intervention affects the flow regimes in the Geum River basin. The main channel is regulated by two large dams serially connected for water supplies and flood controls. The Yongdam Dam located in the upper river basin has an effective storage capacity of 809 Mm3, while the Daecheong Dam at the middle of the main channel has a larger capacity of 1040 Mm3. Water storage in both dams is delivered to several sub-basins through water distribution systems developed for municipal and industrial (M & I) water demands, making non-geomorphological human-made connectivity between the sub-basins. The two large dams supply water to the demand sectors in outsides of the river basin through the distribution systems; hence, inter-basin water transfers may conflict with water demands within the river basin. During monsoon seasons, the Yongdam and Daecheong dams should reduce their storage limits by 137 and 250 Mm3 for flood control, respectively. In addition, many small-sized local reservoirs are widespread across the river basin to sustain irrigated agriculture (mostly for planting paddy rice). Though 95 % of the small reservoirs have minimal storage capacities below 1 Mm3, their gross capacity is more than 320 Mm3 and thus considerably alters natural flow regimes. The total storage capacities of the agricultural reservoirs in the 14 sub-basins are from 1.1 to 100.9 Mm3, with a median value of 12.5 Mm3. In each sub-basin, natural river flows and water transferred from the storage facilities (i.e., the agricultural reservoirs and dams) are consumed for agricultural, municipal, and industrial purposes. The water diverted for the M & I demands could return to the rivers, becoming available water for lower demand sectors.
For water allocation modeling, we simplified the complex river system with a node-and-link network shown in Fig. 1. Each sub-basin was conceptualized as a node with natural water availability (i.e., natural runoff), storage capacity (i.e., water storage in the agricultural reservoirs), and water demands (i.e., agricultural and M & I water uses). The sub-basin nodes were connected by the stream links (the continuous lines). The two large dams were represented by the nodes only having storage capacities and were located between the two adjacent sub-basins accordingly. The outside water demand sectors were represented by nodes with no natural flows and zero storage capacities. The human-made connections between the dams and the sub-basins were conceptualized by separate links (the dashed lines) with conveyance limits.
3.2 Data collections
3.2.1 Climate and water demand data
We collected daily precipitation and maximum and minimum temperatures over South Korea at 3 km grid resolution for 1973–2015. The grid data were produced by interpolating synoptic observations at 60 stations in the automated surface observing system (ASOS) operated by the Korea Meteorological Administration. The point weather data were spatially interpolated by the parameter-elevation regressions on independent slopes model (PRISM; Daly et al., 2008), and overestimated values were smoothed by the inverse distance method. Jung and Eum (2015) found improved performance of the combined method in South Korea via comparative evaluations to the original PRISM. For the case study, the collected grid data were spatially aggregated with the sub-basin boundaries. The aggregated daily precipitation and temperature were perturbed by a stochastic weather generator for the stress tests and were then used to generate streamflow at the sub-basin nodes. According to the grid data, the mean annual precipitation and temperature over the Geum River basin for 1976–1995 were 1245 mm and 11.7 ∘C, respectively. They have risen to 1325 mm (+6.4 %) and 12.2 ∘C (+0.5 ∘C) during 1996–2015, providing an indication that atmospheric water supply and demand gradually increase over time within the river basin.
Table 1Annual agricultural and M & I demands per demand node, and the minimum instream flows from the sub-basins corresponding to the seven locations.
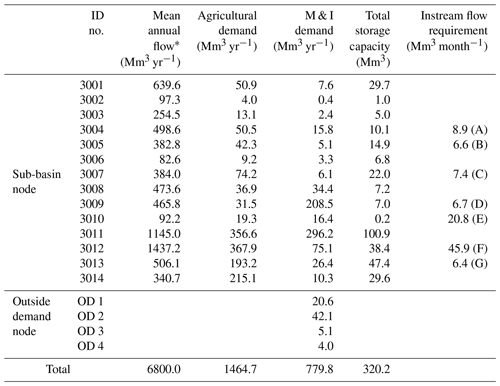
* Natural runoff averaged over 20-year rainfall–runoff simulations with stochastic weather series containing zero climatic perturbations (ΔPavg=0 %, ΔPcv=0 %, and ΔTavg=0 %) relative to 1996–2015. The letters A to G in the brackets are the corresponding instream flow locations.
The water demands for 2030 were taken as the reference demands to evaluate water allocation performance across the river basin. In South Korea, government-driven national water resources plans are legally developed for sustainable resource management for every 20-year period. The water resources plan for 2020 was first established in 2000 including water demand projections up to 2020 (MOCT, 2000) and has been revised three times to consider hydrologic and socio-economic changes since the initial version (MOCT, 2006; MLTM, 2011; MOLIT, 2016). In the third version of the water resources plan for 2020 (MOLIT, 2016), the water demands across South Korea were re-projected up to 2030. By an electronic correspondence (requested on 26 September 2017), we obtained the demand data projected to 2030 given at 10-day intervals for the sub-basins and the two outside nodes directly linked to sub-basins from the team leading the national water plan at the Korea Institute of Civil Engineering and Building Technology. Among the three demand scenarios (high, medium, and low) given in MOLIT (2016), we chose the high-demand scenario from a conservative perspective. More details about the demand projections are available in MOLIT (2016). For simplicity, the M & I demands at the two outside nodes connected with the two dams were estimated by the water transfer records.
In addition, we collected the information of the minimum flow rates required for ecosystem sustainability, namely “instream flows” (Jowett, 1997), at seven locations within the river basin. The instream flows are determined by the experts' investigations into water quality and ecological conditions in the vicinity of major rivers in South Korea and are officially announced by the Ministry of Environment and the Ministry of Land, Infrastructure, and Transport (MOLIT, 2016). Though the human water demands (i.e., agricultural and M & I uses) are the first priority of the local and regional authorities (MOLIT, 2016), they are recommended for considering the instream flows for environmental sustainability. Table 1 summarizes the agricultural and M & I demands for the year of 2030 and the instream flow requirements. For water allocation modeling, the demand data at 10-day intervals were aggregated into monthly values.
3.2.2 Bias-corrected GCM projections
Daily precipitation and temperature projections of 25 GCMs (Table A1) were collected from the archive of the Coupled Model Intercomparison Project Phase 5 (Taylor et al., 2012). Two representative concentration pathways (RCPs), RCP4.5 and RCP8.5, were selected to assess the water supply capacity of the river basin for the upcoming 20-year period of 2020–2039. RCP4.5 and RCP8.5 were used frequently as scenarios of stabilized and increasing greenhouse gas concentrations in climate change studies (e.g., Yan et al., 2015; Zhang et al., 2016; Moursi et al., 2017).
The 50 GCM projections (i.e., 25 GCMs × 2 RCPs) were bias corrected by the de-trended quantile mapping (DQM; Bürger et al., 2013; Eum and Cannon, 2017) that can preserve raw climate change signals given by GCMs. The DQM removes the long-term mean change in projected values first. After applying the ordinary quantile mapping (QM; e.g., Hwang and Graham, 2013) to the de-trended values, the removed trend is reintroduced to the bias-corrected projections. The de-trending procedure may prevent the exaggeration of raw climate change signals, which is a typical drawback of the ordinary QM. More details about DQM and related bias-correction methods are available in Bürger et al. (2013), Cannon et al. (2015), and Eum and Cannon (2017). To correct the 50 GCM projections toward the spatial averaged precipitation and temperatures over the Geum River basin, 1976–2005 and 2006–2099 were set as the reference and the projection periods, respectively.
3.3 Stress tests for water allocation performances
The stress tests were conducted for optimal water allocations in the node-and-link system. The 14 sub-basins are forced by atmospheric drivers (i.e., precipitation and temperature) to generate natural streamflow. The generated streamflows are regulated to meet the water demands and instream flow requirements. The operations should be constrained by geomorphological and management conditions. We used a conceptual runoff model and an optimization model for evaluating water supply and ecological performances with stochastic weather series perturbed by hypothetical climate stresses.
3.3.1 Generating climate-stress-induced weather series
The stochastic weather generator (WG) by Steinschneider and Brown (2013) was employed to produce plausible daily precipitation and temperature sequences with climatic perturbations (i.e., generating climate stresses). Several bottom-up assessments successfully used this model to evaluate performance of hydrologic systems under varying climate stresses (e.g., Whateley et al., 2014; Steinschneider et al., 2015b). The semi-parametric WG combines two stochastic models. The wavelet autoregressive model proposed by Kwon et al. (2007) first generates annual precipitation series spatially averaged within a region of interest for a desired length (20 years in this study). The wavelet components of the annual precipitation series are extended by the autoregressive model to embed the low-frequency structure inherent in observations. Then, daily weather series conditioned by the random annual precipitation are simulated by the Markovian bootstrap resampler of Apipattanavis et al. (2007). In this process, the daily observations are resampled by the k-nearest-neighbor scheme and the precipitation occurrence series generated by the standard Markovian process (e.g., Wilks, 1998). The weather data at multiple locations within the region of interest are sampled together for spatial coherence. For the final step, the mean and variance of stochastic precipitation series are adjusted by the ordinary QM to impose climatic perturbations stresses. The temperature series are simply perturbed by adding a temperature differential. Further in-depth details about the stochastic WG are found in Steinschneider and Brown (2013).
Using the stochastic WG, we generated 539 sets of 20-year-long precipitation and temperature time series perturbed by a combination of three climatic stresses for each set. Since each weather series was newly generated, the 539 stochastic series contain different internal variations. The 539 perturbations were 11 changes in the average of daily precipitation, 7 changes in the coefficient of variance (CV) of daily precipitation, and seven increases in the mean temperature over the 20-year time horizons. The perturbations of mean precipitation were from −60 % to +40 % at 10 % increments relative to the observations for 1973–2015, while the CV changes were from −40 % to +80 % at 20 % increments. The temperature perturbations were from +0 to +6 ∘C at 1 ∘C increments. The 539 () sets of climate-stress-induced weather series were input to a rainfall–runoff model to quantify natural water flows at the sub-basins. To develop the logistic response surfaces, each weather series generated by the WG was represented with the mean annual precipitation (Pavg), the CV of daily precipitation (Pcv), and the mean annual temperature (Tavg) over the 20-year time horizon.
3.3.2 Simulating natural runoff at the sub-basin nodes
A simple rainfall–runoff model, GR4J (Perrin et al., 2003), was used to simulate natural flows at the sub-basins nodes. GR4J has been frequently employed in many studies under diverse climates, such as parameter regionalization (e.g., Oudin et al., 2010), predicting flow durations (e.g., Zhang et al., 2015), and low flow estimations (e.g. Demirel et al., 2015), among many others. GR4J uses four conceptual parameters to describe functional behaviors of a watershed in response to lumped precipitation and potential evapotranspiration (PET) inputs. The parameters implicitly explain soil water storage, groundwater exchange, routing storage, and excess runoff generations within a watershed. The parsimonious structure of GR4J poses a relatively small equifinality problem in parameter calibration and regionalization (Oudin et al., 2008; Perrin et al., 2010). Perrin et al. (2003) provides the computation procedures in detail.
In the case study, a proximity-based regionalization was applied for parameter identification because almost no natural streamflow observations are available at the outlets of the sub-basins. The operational inflow records at the Yongdam Dam were the only applicable observations for parameter calibration at the sub-basin 3001. For the other sub-basins, the parameter sets were transferred from neighboring watersheds assessed in Kim et al. (2017). Kim et al. (2017) comparatively assessed performance of the proximity-based parameter transfer in comparison to several alternative methods, concluding that spatial proximity captured functional similarity well between 45 gauged watersheds in South Korea. The mean Nash–Sutcliffe efficiency (NSE) was 0.53, with a standard deviation of 0.41, when transferring the parameter sets of five neighboring catchments calibrated with observed hydrographs (Kim et al., 2017). Hence, for the 13 sub-basins from 3002 to 3014, natural flows were simulated with the transferred parameter sets from five nearby gauged watersheds, while flows at the sub-basin 3001 were generated by the parameters calibrated against the inflow data. The five runoff simulations were averaged for the sub-basins in which the regionalization scheme was used. The parameter set calibrated against the inflow records for the sub-basin 3001 yielded a NSE value of 0.62 for 2007–2015. The daily natural flows simulated by GR4J with the 539 climate-altered versions of the stochastic weather simulations were temporally aggregated at monthly values for water allocation modeling.
3.3.3 Water allocation modeling
The total water availability in the river basin during a certain month is water storage in the dams and reservoirs at the end of the previous month plus the natural flows at the sub-basins in the current month. Some of the available water is again kept in the storage facilities for supplying water in upcoming months. Thus, operators' decisions on water storage in each month recursively affect supply performance in the river basin through a 20-year period. A monthly sequential optimization model was used to determine amounts of the water storage and consumption at each sub-basin. The operators could minimize the water deficiency during a current month, while the water storage needs to be maximized for water supplies in upcoming months. We assumed that the two conflicting objectives are equally important for the operators. Hence, the objective function for determining water supplies and storage at the nodes for a particular month was
where Di is the total demand, Si is the total supply, Vi is the water storage, and Ci is the storage capacity (Ci) at node i. SAi and SMi are agricultural, and M & I water supplied for agricultural (DAi) and M & I demands (DMi) at node i. The total water demand at each node (Di) is the sum of agricultural demand (DAi) and M & I demand (DMi). Likewise, the water supply at each node is divided into agricultural supply (SAi) and M & I supply (SMi).
The monthly optimizations were subject to constraints. The water supply (Si) to a demand node was limited by water availability, which is the sum of natural flow at the node in the current month, flows from other nodes via the stream and the human-made links in the current month, and water storage at the node in the previous month. Water surplus at the nodes was not allowed (i.e., Si≤Di). The water remaining after supplies and storage at a sub-basin node should be discharged from the node through the channel network. The water storage at each node is constrained by its storage capacity (Vi≤Ci). The water transfers through the human-made links were only supplied for M & I demands of destination nodes and were limited by the conveyance capacity (40 Mm3 month−1). The agricultural and M & I demands were of equal priority in optimizations.
With 20-year-long natural flows per climatic perturbation, we determined SAi, SMi, and Vi month by month using the global optimization tool “fmincon” in the Matlab software. Since Vi values determined for a month become water availability for the next month, optimizations for 240 months interact sequentially. To consider the return flows, we followed the assumptions in the water plan for 2020 (MOLIT, 2016). Simply put, 65 % of the M & I water use at each node was assumed to return and become available water for following nodes, while no return flows after agricultural uses were considered in the water plan due to high water use efficiency.
3.3.4 Evaluating water supply and ecological performances
Using the optimized SAi, SMi, and Vi values, water supply performances at the demand nodes were measured for the given 20-year-long stress-imposed weather series. For each sub-basin node, we measured the water supply reliability (ρs,i) defined as the probability of satisfactory supply against 99 % of the monthly demands:
The amount of water passing through the seven locations with the instream flow requirements can be also calculated using the decision variables and the natural flows. The environmental reliability at an instream flow location j (ρe,j) was evaluated by the following:
where Fj and Fmin,j are the flow passing location j and the instream flows required for ecosystem sustainability at the location, respectively.
In total, water reliabilities at the 14 demand nodes (14 sub-basins) and the seven locations requiring instream flows were evaluated for each climatic perturbation. These 21 sets of performance indicators were used to develop the logistic response functions for each sub-basin node and instream flow location with corresponding climate stress. To develop the logistic surfaces, we assumed that the stakeholder-driven thresholds for ρs,i and ρe,j were 0.95 and 0.70, respectively. The 539 sets of Pavg, Pcv, and Tavg that represent the perturbed weather series were categorized into zero and one against the two thresholds for the logistic regressions.
4.1 Water supply performance at the sub-basins
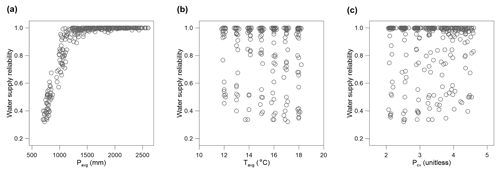
The stress tests that forced the system models (i.e., GR4J and the optimization model) with the perturbed weather series produced 539 sets of reliabilities for each sub-basin and each location of instream flow. Figure 2 displays the scatter plots between water supply reliability (ρs) at the sub-basin 3001 and corresponding changes in Pavg, Pcv, and Tavg relative to 1996–2015. We preliminarily checked statistical significance of the explanatory variables using the multiple linear regressions. The changes in Pavg and Tavg were of very high significance to variation in the ρs values (p values < 10−16), whereas the change in Pcv was insignificant (p value = 0.744). This indicates that the water supply reliability is generally determined by variations of the mean precipitation and temperature for a 20-year period. Though higher precipitation variability (Pcv) could generate more direct runoff across the river basin, storage capacities of the agricultural reservoirs and dams seem to nullify the impacts of Pcv changes on the variation in water supply reliability. The preliminary regression analysis led us to a hypothesis that changes in Pavg and Tavg could sufficiently capture the variation in water supply reliabilities across the river basin.
Figure 3a illustrates the multiple regression function between the ρs values and changes in Pavg and Tavg (the coefficient of determination is 0.93) on which the collection of 50 GCM projections was overlaid. Most of the 50 GCMs expected that ρs at the sub-basin 3001 would be greater than 0.95 for 2020–2039. This type of response surfaces between expected performance and hypothetical climatic stresses have been commonly used in the decision-centric assessments (e.g., Brown et al., 2012; Whateley et al., 2014; Turner et al., 2014). Figure 3c indicates that ρs at the sub-basin 3001 could be less than 0.95 if Pavg decreases by approximately 30 %. The ρs values varied significantly even with zero decrease in Pavg, indicating that there might be the risk of unsatisfactory supply performance even with no changes in Pavg.
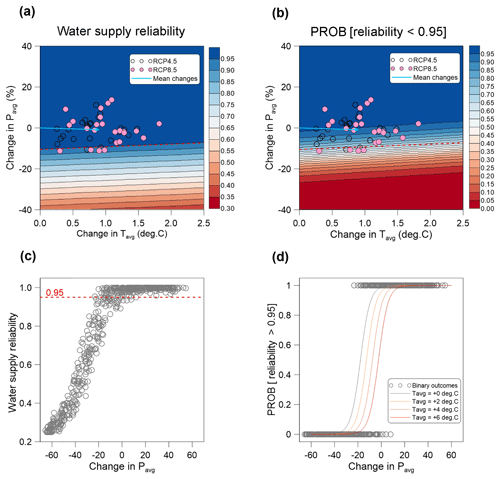
Figure 3(a) Response surface of ρs at the sub-basin 3011, and (b) logistic response surface of the probability of ρs>0.95. (c) The scatter plot between ρs and change in Pavg; (d) the binary outcomes against the threshold of ρs>0.95 and the sigmoid functions for the probability of ρs>0.95. The empty and filled circles overlaid on (a) and (b) are the 50 GCM projections for 2020–2039. The dashed lines in (a) and (b) are the climatic bounds for the climatic threshold of ρs=0.95. PROB stands for probability.
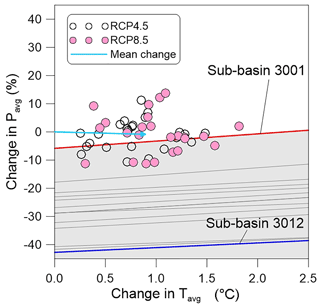
The risk of ρs<0.95 could be evaluated by the logistic surface shown in Fig. 3b. The sigmoid functions fitted to the binary outcomes categorized against the threshold of ρs>0.95 (Fig. 3d) could provide approximate probabilities of ρs>0.95 (hereafter referred to as πs95) at the sub-basin 3001. πs95 declined with rising temperatures, since water availability was reduced by evaporation losses. The πs95 values indicated by the 50 GCMs ranged between 74 % and 99 % for 2020–2039. It should be noted that the climatic bound for ρs=0.95 (dashed lines in Fig. 3a and b) has the risk of ρs<0.95 as much as 40 %–60 % on the logistic surfaces. It seems that considerable risks of unsatisfactory performances still exist on the zone of satisfactory performance in Fig. 3a.
Likewise, we fitted the sigmoid functions to the binary outcomes against the threshold of ρs>0.95 for the other sub-basins. Figure 4 displays the climatic bounds at which πs95=95 % for each sub-basin. The sub-basin 3001 was of the highest bound among the 14 sub-basins, indicating that the uppermost sub-basin is the most vulnerable to changes in Pavg and Tavg. 15 GCMs were located below the climate boundary of the sub-basin 3001. On the contrary, the boundary of the sub-basin 3012 was the lowest. For every GCM projection, πs95 at the sub-basin 3012 was larger than 99 %. The sub-basins with limited connections to the upper sub-basins tend to have higher climatic bounds of πs95=95 %. The lower sub-basins receiving streamflow generated by the upper sub-basins are likely to withstand stronger climate stresses, even though they have relatively large agricultural demands.
4.2 Environmental reliability against the instream flow requirements
We compared the modeled flows at the seven locations of instream flow against the minimum requirements and evaluated the environmental reliabilities (i.e., ρe) at each location. Figure 5 shows the box plots of ρe values at the seven locations in response to the 539 climate perturbations. While ρe values at all the locations decreased as climate became drier, the location E was the most vulnerable. Even with no changes in Pavg and Tavg, the outflows from the sub-basin 3011 were often less than the minimum requirement, implying that ecosystems near the location E might be currently undermined by the large agricultural and M & I demands in the sub-basin 3011. If Pavg decreased by 20 % and Tavg rose by 3 ∘C, ρe at the location E would fall below 0.5. In contrast, streamflow at the location D perfectly satisfied the instream flow requirement under the same stress. Despite the second-largest M & I demands in the sub-basin 3009, water transfers from the two large dams could deliver sufficient water supplies. 65 % of the water supplies for M & I demand were supposed to return to the stream network and became streamflow to meet the instream flow requirement at the location D. Although both sub-basins 3009 and 3011 had limited geomorphological connectivity to the upper sub-basins, their demand components and linkages to the two large dams made the significant difference between their ρe values.
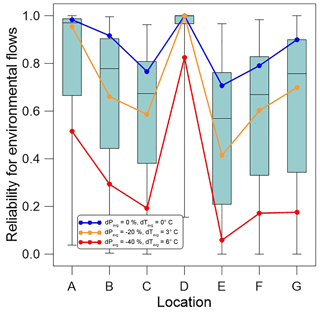
Figure 5Reliability against the instream flow requirements at the seven locations obtained from the 539 sequential optimizations with stress-induced weather series. The blue, grey, and red lines connect the reliabilities at the seven locations under the three representative climatic stresses.
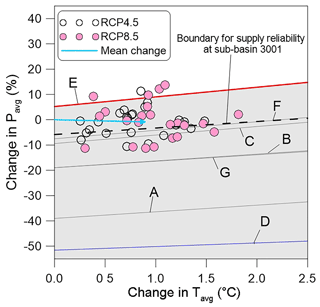
We developed the logistic response surfaces with binary outcomes against the threshold of ρe>0.70 at which the instream flow requirement at the location E was satisfied in the optimization model under no climate stresses (i.e., no changes in Pavg and Tavg relative to 1996–2015); Fig. 6 displays the climatic bounds at which the probability of ρe>0.70 (hereafter referred to as πe70) is 95 % for all the locations requiring instream flow. As expected, the bound for the location E was the highest, and the climate zone for πe70>95 % sensitively declines with rising Tavg. The bound for πs95=95 % at the sub-basin 3001 (black dashed line) was below the bounds for the locations E. The human-demand-only operations would increase the risks of ecosystem degradation near the locations E if climate becomes drier. The environmental risks at the locations E seem to be more sensitive to rising Tavg than the water supply risk at the sub-basin 3001. Only 5 out of the 50 GCMs for 2020–2039 (10 %) indicate πe70>95 % at the location E.
4.3 Consideration of the instream flow into water management
From the assessments with the logistic surfaces and the GCM projections, the environmental risk at the location E was likely to become an issue for 2020–2039. As an adaptation strategy, the instream flow could be considered in water management to be balanced between water supply and environmental risks. We modeled this management option by including the instream flow requirement at the location E in the objective function of the water allocation model as
where Qmin,E and QE are the instream flow requirement and flow at the location E, respectively. w is a weight representing relative importance of the instream flow in water management. While the instream flow requirement at the location E could be treated as a constraint for optimizations, this approach may lead to no optimal solutions under severe climate stresses. Hence, it would be better to consider the instream flow requirement in the objective function for the stress tests.

Figure 7The logistic regression models for πs95 at the sub-basin 3002 (a, c) and πe70 at the location E (b, d) under the human-demand-only operation (a, b), and the operation considering human demands and instream flow together (c, d).
Through trial and error experiments with the 539 climate perturbations, we found that ρe at the location E could considerably increase with a tiny w value. The sequential optimizations with w=0.01 allowed us to have a fairly improved ρe value at the location E. However, we found that the improved ecological reliability at the location E was from substantial reduction in water supply reliability at the sub-basin 3002. Figure 7 illustrates the logistic models for water supply at the sub-basin 3002 and the instream flow requirement at the location E under the two operation options applied to the case study. The first operation only considered the given agricultural and M & I demands (O1), whereas the deficit against the instream flow requirement was considered in the second option (O2). By changing the operation objective from O1 to O2, the risk of ρe<0.95 at the sub-basin substantially increased at the sub-basin 3002. The risk of unsatisfactory water supply was found even with increasing Pavg under O2. Indeed, the water supply performance became much more sensitive to Tavg changes. Conversely, the risk of unsatisfactory ecological reliability at the location E substantially declined. This is because the optimization model could not increase discharge from the sub-basin 3011 for the instream flow requirement due to the high agricultural demands. Instead, the model forced an increase in outflows from the Yongdam Dam to meet the agricultural demands at the sub-basins 3012 and 3014 and the instream flow at the location E. It was inevitable to have deficient water supplies in the sub-basin 3002 with relatively small demands, even under optimized water allocations. In other words, minimizing the total water deficiency of the entire basin may force the local water deficit in the sub-basin 3002.
4.4 Validating the logistic models and assessing the management options with the EEDS framework
Since the sigmoid function is hypothetical, the logistic surfaces need to be validated to ensure their predictive performance. As an interval validation (i.e., reusing the 539 sets of performance samples for validation), the logistic models were evaluated with the bootstrap prognoses (Harrell et al., 1996). To measure the “optimism” of each logistic model, we used the Nagelkerke pseudo-R2 (Nagelkerke, 1991; hereafter simply R2) as the metric of predictive performance. The optimism of a regression model can be evaluated with performance differences between the original model and the models developed by bootstrap samples (with replacements). Hence, it indicates a potential performance loss when applying new samples to the original model. Together with the regression results, Table 2 summarizes the optimism estimated from 2000 bootstrap models. Most of the logistic models showed 0.9 or higher R2 values, and the highest optimism was only 0.80 %. The internal validation implies that predictive performance of the logistic models seems acceptably high and robust. As an external validation (i.e., validation with out-of-sample data), we conducted additional stress tests of the river system with three arbitrary perturbations of (−37.1 %, +2.5 ∘C), (−27.7 %, +1.3 ∘C) and (−13.6 %, +0.6 ∘C) for both Pavg and Tavg. The change in Pcv was fixed at a random value of +21 % because it was insignificant to the regression models. Then, 100 sets of 20-year-long weather series were generated for each perturbation using the stochastic WG, and the system models were forced by the generated weather series. By counting the cases satisfying ρs>0.95 or ρe>0.70 among the 100 simulations, the πs95 and πe70 estimates at the sub-basins and the instream flow locations were obtained for each perturbation. Figure 8 compares the πs95 and πe70 estimates from the stress tests against those estimated by the logistic models for the sub-basins and the instream flow locations. The probability estimates from the two methods seem to agree approximately. The median and the highest differences between the two estimates were 0.004 and 0.15, respectively.
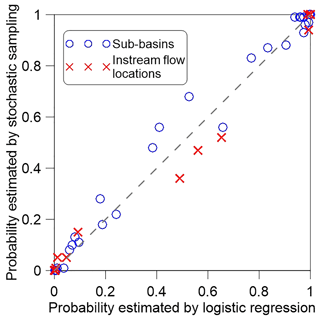
Figure 81:1 plots between the probability estimates from the stochastic sampling and those from the logistic regressions for the case study. The probabilities of satisfactory performance at the 14 sub-basins and the seven instream flow locations were estimated by the 100 Monte Carlo simulations for each climatic perturbation. The number of points for comparison to the logistic models becomes 63 (3 (perturbations) × 21 (locations) = 63.)

Figure 9Climatic bounds for πs95=95 % (a, d) and πe70=95 % (b, e), and the bound mutually satisfying both criteria (c, f) under the human-demand-only operations (a–c) in comparison to the operations considering the instream flows at the location E (d–f). The empty and filled circles are the 50 GCM projections for 2020–2039.
The internal and external validations led us to believe that the logistic surfaces could be acceptable for impact assessments using the bias-corrected GCM projections. By overlapping the logistic models, we could assess the two operation options applied in the case study for all the sub-basins and the instream flow locations simultaneously (Fig. 9). For the assessment, we used the boundaries of πs95=95 % and πe70=95 %. With the logistic surfaces, the system robustness to climate change could be measured in the same manner proposed in the original EEDS framework (Poff et al., 2016). Comparing Fig. 9b and e indicates that considering the instream flow in the objective function significantly lowered the climatic bound of πe70=95 % at the location E, thereby widening the climatic zone within which all the locations mutually satisfy πe70>95 %. However, in the trade-off, the bound of πs95=95 % for the sub-basin 3002 moved upward, narrowing the climatic zone mutually satisfying πs95>95 % for all the demand nodes. Overall, the climatic zone mutually satisfying πs95>95 % and πe70>95 % for all the sub-basins and instream flow locations was expected to decrease when the instream flow requirement at the location E was considered. Based on the reduced mutual climate zone, considering the environmental requirement in operations would slightly decrease overall system robustness to climate stresses.
In summary, water supply reliabilities at the sub-basins 3001 and 3002 would be the most vulnerable to climate stresses. The highest environmental risks from climate change would be found at the locations E in terms of the instream flow requirements. To reduce the environmental risk at the location E, fairly increasing risks of ρs≤0.95 at the sub-basin 3002 should be accepted. Only 4 out of the 50 GCMs indicated πs95>0.95.
5.1 Use of the logistic surfaces for the EEDS framework
The response surfaces allowed users to estimate expected performances of hydrologic systems in response to climate stressors, providing convenience in promptly evaluating many GCM projections (e.g., Turner et al., 2014; Brown et al., 2012; Prudhomme et al., 2010). Nevertheless, they could provide insufficient probabilistic information needed for decision-making processes. A possible approach for evaluating the risk of unsatisfactory performances was to count the GCM projections satisfying a predefined threshold (e.g., Moursi et al., 2017; Brown et al., 2012). However, the GCM counts are highly dependent on the size of the GCM collections. Even in the case that all the GCMs in users' hands fall within the favorable climate zone on the response surfaces, it does not guarantee that future system performance will be satisfactory at 100 % confidence.
The logistic response surface could supplement this weakness of the ordinary response surfaces. It enables the direct evaluation of the risk of system failures from a single climate projection. The probability estimates from the logistic surfaces can play a role in risk-based decision-making, particularly when an adaptive solution is targeted at a particular climate prediction (e.g., resizing infrastructures for a reference climate condition). The logistic surface developed for the adaptive solution may directly provide the risk of system failures under the climate prediction. Since it requires no more than a simple conversion of the sampled performance metrics, the logistic regression allows a probabilistic evaluation of system performance in a very efficient manner. If a complex hydrologic system is assessed within the bottom-up framework, a typical approach such as an exhaustive Monte Carlo sampling may not be preferred for uncertainty analysis due to expensive computational costs. In such a case, the logistic surfaces may become an alternative for simply assessing the associated risks.
The external validation of the logistic models (Fig. 8) implies that the effect of interval climatic variability might be measured in a collective manner, despite the varying climatic perturbations of the weather series. Even though the perturbations were different, the same probabilistic structure would be inherent in all the generated weather series. This might allow the logistic models to collectively capture the effect of internal climate variability from the 539 weather series having different climate alterations. Thus, uncertainty associated with the stress tests could be in part gauged with the simple regression approach. However, this also implies that the external validation might be imperfect, and hence a more rigorous stress test and validation would be necessary to improve reliability of the response-surface-based assessment. Given the large uncertainty associated with climatic variability, a single stochastic structure might be insufficient for developing and validating the logistic and response surfaces. If affordable, multiple WGs should be employed with a large number of stochastic generations.
The EEDS framework (Poff et al., 2016) integrates the responsive behaviors of multiple performance metrics into a single climate space. By measuring the size of the climate zone mutually satisfying the multiple criteria, decision makers can perceive the robustness of system performance with conflicting interests. The decision makers may select solutions that can widen the mutual climate zone for robust adaptations to climate change. Poff et al. (2016) provided a prominent example that assessed adaptation costs and potential environmental risks with this framework in order to find the most robust strategies in a dam site to climate change. In this study, we showed the advantage of this framework to explore performances at many subcomponents of a large system in a single climate domain.
One difference between this study and Poff et al. (2016) is that we used the logistic climate bounds to measure the size of the mutual climate zone satisfying the multiple probabilistic thresholds. Since the original EEDS framework was focused on expected performances, a question can be raised as to “what if no climate projections fall within the mutual climate zone?” In this case, stakeholders may perceive unacceptable risks even though an adaptive solution can enlarge the mutual climate zone for multiple criteria. By its nature, the EEDS considering multiple criteria should have a narrower acceptable climate zone than single-criterion assessments. If the logistic response surfaces were employed instead, users can simultaneously measure how much system robustness can be obtained from an adaptive solution and how much the risks of unsatisfactory performances are indicated by climate projections. They may be necessary information for decision-making processes.
5.2 Limitations
There are several caveats in the case study. First, the monthly operations to balance between water scarcity and storage might be only a part of operators' interests. The stakeholders in practice may have conflicting interests (e.g., reducing flood risks vs. increasing water storage) rather than taking actions toward the single objective. Thus, this study should be deemed a special case focused on the maximum supply reliability under the given operational objectives. A validated simulation model for water allocation will be needed for a more realistic application.
Second, it was unavoidable for us to use many simplifications and assumptions for modeling optimal water managements in the study river basin with complicated features (e.g., monthly dam operations and simple temperature perturbations). Given the substantial uncertainty sources associated with system models, the risks of system failures might be greater than our assessments. The logistic surfaces in this work would only consider the impacts of internal climatic variability on system performances.
5.3 Conclusions
In this study, we proposed incorporating the logistic regression into a decision-centric framework for probabilistic impact assessments. The proposed approach requires no more stress tests than typical response-surface-based assessments, albeit some validation is needed. Thus, it may be an efficient method to support risk-based decision-making processes. The following conclusions are worth emphasizing:
-
The logistic surfaces can provide convenience in exploring potential risks of system failures when a predefined threshold is available, while the response surface can show system performance. On the logistic surfaces, the risk of system failures could be directly indicated by individual GCMs.
-
Within the eco-engineering decision-scaling framework, the logistic surfaces can be flexibly used to evaluate robustness of hydrological systems to climate stressors. Multi-faceted stakeholder interests can be considered in a domain of probability.
-
The case study for the Geum River basin in South Korea provides an assessment in which the human-demand-only operations would make the ecosystems increasingly vulnerable. To consider the instream flow requirement in operations for 2020–2039, risks of insufficient water supply should increase at the upper sub-basins with small water demands.
The data required to reproduce the results are available upon request from the authors (d.kim@apcc21.org, sjchoi@kict.re.kr).
DK provided the main idea for this work and drafted the manuscript. DK, JAC, and SC designed the case study and participated in discussion of the results. All the authors contributed to revision of the paper.
The authors declare that they have no conflict of interest.
This study was supported by the APEC Climate Center. We give special thanks
for the water demand data provided by the team leading the national
water resource plan at the Korea Institute of Civil Engineering and
Building Technology. The GCMs downscaled by Hyung-Il Eum at Alberta
Environment and Parks are greatly appreciated.
Edited by: Graham Jewitt
Reviewed by: two anonymous referees
Apipattanavis, S., Podesta, G., Rajagopalan, B., and Katz, R. W.: A semiparametric multivariate and multisite weather generator, Water Resour. Res., 43, W11401, https://doi.org/10.1029/2006WR005714, 2007.
Bae, D.-H., Jung, I.-W., and Chang, H: Long-term trend of precipitation and runoff in Korean river basins, Hydrol. Process., 22, 2644–2656, 2008.
Brown, C., and Wilby, R. L.: An alternate approach to assessing climate risks, Eos Trans. AGU, 93, 401, 2012.
Brown, C., Ghile, Y., Laverty, M., and Li, K.: Decision scaling: linking bottom-up vulnerability analysis with climate projections in the water sector, Water Resour. Res., 48, W09537, https://doi.org/10.1029/2011WR011212, 2012.
Brown, C. M., Lund, J. R., Cai, X., Reed, P. M., Zagona, E. A., Ostfeld, A., Hall, J., Characklis, G. W., Yu, W., and Brekke, L.: The future of water resources systems analysis: Toward a scientific framework for sustainable water management, Water Resour. Res., 51, 6110–6124, https://doi.org/10.1002/2015WR017114, 2015.
Bürger, G., Sobie, S. R., Cannon, A. J., Werner, A. T., and Murdock, T. Q.: Downscaling extremes: an intercomparison of multiple methods for future climate, J. Climate, 26, 3429–3449, https://doi.org/10.1175/JCLI-D-12-00249.1, 2013.
Cannon, A. J., Sobie, S. R., and Murdock, T. Q.: Bias correction of GCM precipitation by quantile mapping: How well do methods preserve changes in quantiles and extremes?, J. Climate, 28, 6938–6959, 2015.
Cosgrove, W. J. and Loucks, D. P.: Water management: Current and future challenges and research directions, Water Resour. Res., 51, 4823–4839, https://doi.org/10.1002/2014WR016869, 2015.
Culley, S., Noble, S., Yates, A., Timbs, M., Westra, S., Maier, H. R., Giuliani, M., and Castelletti, A.: A bottom-up approach to identifying the maximum operational adaptive capacity of water resource systems to a changing climate, Water Resour. Res., 52, 6751–6768, https://doi.org/10.1002/2015WR018253, 2016.
Daly, C., Halbleib, M., Smith, J. I., Gibson, W. P., Doggett, M. K., Taylor, G. H., Curtis, J., and Pasteris, P. P.: Physiographically sensitive mapping of climatological temperature and precipitation across the conterminous United States, Int. J. Climatol., 28, 2031–2064, https://doi.org/10.1002/joc.1688, 2008.
Demirel, M. C., Booij, M. J., and Hoekstra, A. Y.: The skill of seasonal ensemble low-flow forecasts in the Moselle River for three different hydrological models, Hydrol. Earth Syst. Sci., 19, 275–291, https://doi.org/10.5194/hess-19-275-2015, 2015.
Deser, C., Phillips, A., Bourdette, V., and Teng, H.: Uncertainty in climate change projections: the role of internal variability, Clim. Dynam., 38, 527–546, https://doi.org/10.1007/s00382-010-0977-x, 2012.
Dufresne, J.-L. and Bony, S.: An assessment of the primary sources of spread of global warming estimates from coupled atmosphere-ocean models, J. Climate, 21, 5135–5144, 2008.
Eum, H.-I. and Cannon, A. J.: Intercomparison of projected changes in climate extremes for South Korea: Application of trend preserving statistical downscaling methods to the CMIP5 ensemble, Int. J. Climatol., 37, 3381–3397, 2017.
Eum, H.-I. and Simonovic, S. P.: Integrated reservoir management system for adaptation to climate change: The Nakdong River Basin in Korea, Water Resour. Manage., 24, 3397–3417, 2010.
Georgakakos, A. P., Yao, H., Kistenmacher, M., Georgakakos, K. P., Graham, N. E., Cheng, F.-Y., Spencer, C., and Shamir, E.: Value of adaptive water resources management in Northern California under climatic variability and change: Reservoir management, J. Hydrol., 412–413, 34–46, https://doi.org/10.1016/j.jhydrol.2011.04.038, 2012.
Haasnoot, M., Kwakkel, J. H., Walker, W. E., and ter Maat, J.: Dynamic adaptive policy pathways: A method for crafting robust decisions for a deeply uncertain world, Global Environ. Change, 23, 485–498, 2013.
Hadka, D., Herman, J., Reed, P., and Keller, K.: An open source framework for many-objective robust decision making, Environ. Model. Softw., 74, 114–129, 2015.
Harrell, F. E., Lee, K. L., and Mark, D. B.: Multivariate prognostic models: issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors, Statist. Med., 15, 361–387, https://doi.org/10.1002/(SICI)1097-0258(19960229)15:4<361::AID-SIM168>3.0.CO;2-4, 1996.
Hwang, S. and Graham, W. D.: Development and comparative evaluation of a stochastic analog method to downscale daily GCM precipitation, Hydrol. Earth Syst. Sci., 17, 4481–4502, https://doi.org/10.5194/hess-17-4481-2013, 2013.
Jowett, I. G.: Instream flow methods: a comparison of approaches, Regul. Rivers: Res. Mgmt., 13, 115–127, 1997.
Jung, Y. and Eum, H.-I.: Application of a statistical interpolation method to correct extreme values in high-resolution gridded climate variables, J. Clim. Change Res., 6, 331–334, 2015.
Kay, A. L., Crooks, S. M., and Reynard, N. S.: Using response surfaces to estimate impacts of climate change on flood peaks: assessment of uncertainty, Hydrol. Process., 28, 5273–5287, https://doi.org/10.1002/hyp.10000, 2014.
Kim, D., Jung, I. W., and Chun, J. A.: A comparative assessment of rainfall–runoff modelling against regional flow duration curves for ungauged catchments, Hydrol. Earth Syst. Sci., 21, 5647–5661, https://doi.org/10.5194/hess-21-5647-2017, 2017.
Kim, D., Chun, J. A., and Aikins, C. M.: An hourly-scale scenario-neutral flood risk assessment in a mesoscale catchment under climate change, Hydrol. Process., 32, 3416–3430, https://doi.org/10.1002/hyp.13273, 2018.
KMA – Korean Meteorological Administration: Climatological normals of Korea (1981–2010), Publ. 11-1360000-000077-14, Korea Meteorological Administration, 678 pp., available at: http://www.kma.go.kr/down/Climatological_2010.pdf (last access: 12 October 2017), 2011.
Korteling, B., Dessai, S., and Kapelan, Z.: Using information-gap decision theory for water resources planning under Severe Uncertainty, Water Resour. Manage., 27, 1149–1172, https://doi.org/10.1007/s11269-012-0164-4, 2013.
Kwon, H.-H., Lall, U., and Khalil, A. F.: Stochastic simulation model for nonstationary time series using an autoregressive wavelet decomposition: Applications to rainfall and temperature, Water Resour. Res., 43, W05407, https://doi.org/10.1029/2006WR005258, 2007.
Lampert, R. J. and Groves, D. G.: Identifying and evaluating robust adaptive policy responses to climate change for water management agencies in the American west, Technol. Forecast. Soc. Change, 77, 960–974, 2010.
MLTM – Ministry of Land, Transport and Maritime Affairs: National Water Resources Plan (2011–2020), Daejeon, South Korea, 2011.
MOCT – Ministry of Construction and Transportation: National Water Resources Plan (Water Vision 2020), Daejeon, South Korea, 2000.
MOCT – Ministry of Construction and Transportation: National Water Resources Plan (2006–2020), Daejeon, South Korea, 2006.
MOLIT – Ministry of Land, Infrastructure and Transport: National Water Resources Plan (2001–2020) – 3rd revision (2016–2020), Daejeon, South Korea, 2016.
Moursi, H., Kim, D., and Kaluarachchi, J. J.: A probabilistic assessment of agricultural waer scarcity in a semi-arid and snowmelt-dominated river basin under climate change, Agr. Water Manage., 193, 142–152, 2017.
Nagelkerke, N. J. D.: A note on a general definition of the coefficient of determination, Biometrika, 78, 691–692, 1991.
Oudin, L., Andréassian, V., Perrin, C., Michel, C., and Le Moine, N.: Spatial proximity, physical similarity, regression and ungaged catchments: a comparison between of regionalization approaches based on 913 French catchments, Water Resour. Res., 44, W03413, https://doi.org/10.1029/2007WR006240, 2008.
Oudin, L., Kay, A., Andréassian, V., and Perrin, C.: Are seemingly physically similar catchments truly hydrologically similar?, Water Resour. Res., 46, W11558, https://doi.org/10.1029/2009WR008887, 2010.
Perrin, C., Michel, C., and Andréassian, V.: Improvement of a parsimonious model for streamflow simulation, J. Hydrol., 279, 275–289, 2003.
Perrin, C., Oudin, L., Andreassian, V., Rojas-Serna, C., Michel, C., and Mathevet, T.: Impact of limited streamflow data on the efficiency and the parameters of rainfall-runoff models, Hydrolog. Sci. J., 52, 131–151, https://doi.org/10.1623/hysj.52.1.131, 2010.
Poff, N. L., Brown, C. M., Grantham, T. E., Matthews, J. H., Palmer, M. A., Spence, C. M., Wilby, R. L., Haasnoot, M., Mendoza, G. F., Dominique, K. C., and Baeza, A.: Sustainable water management under future uncertainty with eco-engineering decision making, Nat. Clim. Change, 6, 25–34, https://doi.org/10.1038/nclimate2765, 2016.
Prudhomme, C., Wilby, R. L., Crooks, S., Kay, A. L., and Reynard, N. S.: Scenario-neutral approach to climate change impact studies: Application to flood risk, J. Hydrol., 390, 198–209, https://doi.org/10.1016/j.jhydrol.2010.06.043, 2010.
Schlef, K. E., Steinschneider, S., and Brown, C. M.: Spatiotemporal impacts of climate and demand on water supply in the Apalachicola-Chattahoochee-Flint Basin, J. Water Resour. Plan. Manage., 144, 05017020, https://doi.org/10.1061/(ASCE)WR.1943-5452.0000865, 2017.
Stainforth, D. A., Aina, T., Christensen, C., Collins, M., Faull, N., Frame, D. J., Kettleborough, J. A., Knight, S., Martin, A., Murphy, J. M., Piani, C., Sexton, D., Smith, L. A., Spicer, R. A., Thorpe, A. J., and Allen, M. R.: Uncertainty in predictions of the climate response to rising levels of greenhouse gases, Nature, 433, 403–406, 2005.
Steinschneider, S. and Brown, C: A semiparametric multivariate, multisite weather generator with low-frequency variability for use in climate risk assessments, Water Resour. Res., 49, 7205–7220, https://doi.org/10.1002/wrcr.20528, 2013.
Steinschneider, S., McCrary, R., Wi, S., Mulligan, K., Mearns, L. O., and Brown, C.: Expanded decision-scaling framework to select robust long-term water-system plans under hydroclimatic uncertainties, J. Water Resour. Plan. Manage., 141, 04015023-1, https://doi.org/10.1061/(ASCE)WR.1943-5452.0000536, 2015a.
Steinschneider, S., Wi, S., and Brown, C.: The integrated effects of climate and hydrologic uncertainty on future flood risk assessments, Hydrol. Process., 29, 2823–2839, https://doi.org/10.1002/hyp.10409, 2015b.
Stevens, B. and Bony, S.: What are climate models missing?, Science, 340, 1053–1054, 2013.
Taylor, K. E., Stouffer, R. J., and Meehl, G. A.: An overview of CMIP5 and the experiment design, B. Am. Meteorol. Soc., 93, 485–498, https://doi.org/10.1175/BAMS-D-11-00094.1, 2012.
Turner, S. W. D., Marlow, D., Ekström, M., Rhodes, B. G., Kularathna, U., and Jeffrey, P. J.: Linking climate projections to performance: A yield-based decision scaling assessment of a large urban water resources system, Water Resour. Res., 50, 3553–3567, https://doi.org/10.1002/2013WR015156, 2014.
Weaver, C. P., Lempert, R. J., Brown, C., Hall, J. A., Revell, D., and Sarewitz, D.: Improving the contribution of climate model information to decision making: the value and demands of robust decision frameworks, WIREs Clim. Change, 4, 39–60, https://doi.org/10.1002/wcc.202, 2013.
Whateley, S. and Brown, C.: Assessing the relative effects of emissions, climate means, and variability on large water supply systems, Geophys. Res. Lett., 43, 11329–11338, https://doi.org/10.1002/2016GL070241, 2016.
Whateley, S., Steinschneider, S., and Brown, C.: A climate change range-based method for estimating robustness for water resources supply, Water Resour. Res., 50, 8944–8961, https://doi.org/10.1002/2014WR015956, 2014.
Whateley, S., Steinschneider, S., and Brown, C.: Selecting stochastic climate realizations to efficiently explore a wide range of climate risk to water resource systems, J. Water Resour. Plan. Manage., 142, 06016002, https://doi.org/10.1061/(ASCE)WR.1943-5452.0000631, 2016.
Wilks, D.: Multisite generalization of a daily stochastic precipitation generation model, J. Hydrol., 210, 178–191, 1998.
Woodward, M., Kapelan, Z., and Gouldby, B.: Adaptive flood risk management under climate change uncertainty using real options and optimization, Risk Anal., 34, 75–92, https://doi.org/10.1111/risa.12088, 2014.
Xu, W., Zhao, J., Zhao, T., and Wang, Z: Adaptive reservoir operation model incorporating nonstationary inflow prediction, J. Water Resour. Plan. Manage., 141, 04014099, https://doi.org/10.1061/(ASCE)WR.1943-5452.0000502, 2015.
Yan, D., Werners, S. E., Ludwig, F., and Huang, H. Q.: Hydrological response to climate change: the Pearl River, China under different RCP scenarios, J. Hydrol. Reg. Stud., 4, 228–245, 2015.
Zhang, Y., Vaze, J., Chiew, F. H. S., and Li, M.: Comparing flow duration curve and rainfall-runoff modelling for predicting daily runoff in ungauged catchments, J. Hydrol., 525, 72–86, 2015.
Zhang, Y., You, Q., Chen, C., and Ge, J.: Impacts of climate change on streamflows under RCP scenarios. A case study in Xin River Basin, China, Atmos. Res. 178, 521–534, 2016.