the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Future projections of temperature and mixing regime of European temperate lakes
Wim Thiery
Georgiy Kirillin
The physical response of lakes to climate warming is regionally variable and highly dependent on individual lake characteristics, making generalizations about their development difficult. To qualify the role of individual lake characteristics in their response to regionally homogeneous warming, we simulated temperature, ice cover, and mixing in four intensively studied German lakes of varying morphology and mixing regime with a one-dimensional lake model. We forced the model with an ensemble of 12 climate projections (RCP4.5) up to 2100. The lakes were projected to warm at 0.10–0.11 ∘C decade−1, which is 75 %–90 % of the projected air temperature trend. In simulations, surface temperatures increased strongly in winter and spring, but little or not at all in summer and autumn. Mean bottom temperatures were projected to increase in all lakes, with steeper trends in winter and in shallower lakes. Modelled ice thaw and summer stratification advanced by 1.5–2.2 and 1.4–1.8 days decade−1 respectively, whereas autumn turnover and winter freeze timing was less sensitive. The projected summer mixed-layer depth was unaffected by warming but sensitive to changes in water transparency. By mid-century, the frequency of ice and stratification-free winters was projected to increase by about 20 %, making ice cover rare and shifting the two deeper dimictic lakes to a predominantly monomictic regime. The polymictic lake was unlikely to become dimictic by the end of the century. A sensitivity analysis predicted that decreasing transparency would dampen the effect of warming on mean temperature but amplify its effect on stratification. However, this interaction was only predicted to occur in clear lakes, and not in the study lakes at their historical transparency. Not only lake morphology, but also mixing regime determines how heat is stored and ultimately how lakes respond to climate warming. Seasonal differences in climate warming rates are thus important and require more attention.
Most lakes in the world tend to warm due to climate change, though the response of lakes to climate change varies among different regions and different lake types (O'Reilly et al., 2015). Warming alters lake mixing characteristics and has consequences for lake ecology, metabolism, and biogeochemistry, yet the broader impacts of lake warming remain unclear.
Recent studies highlighted that lakes respond quite individually to climate change. Although surface water temperature (Ts) is perhaps the most predictable indicator of warming (Adrian et al., 2009), trends in Ts remain highly variable at a global scale (O'Reilly et al., 2015). Deep water temperatures respond less predictably to warming and have been observed to increase, decrease, or not change with increasing air temperature (Dokulil et al., 2006; Ficker et al., 2017; Kirillin et al., 2013, 2017; Richardson et al., 2017; Winslow et al., 2017). Stratification strength and duration generally increase due to warming (Butcher et al., 2015; Kirillin, 2010), but patterns of change may have little regional coherence and cannot be reliably inferred from surface water trends (Read et al., 2014). We know even less about how warming influences the mixed-layer depth, which is important for instance for light availability for primary production.
To better understand the sources of this variability, research has focused on identifying which characteristics modulate how lakes and particularly lake stratification respond to warming. Recently, a series of modelling studies reported the variable regional responses of lakes to projected climate change in the near future (e.g. Boike et al., 2015; Butcher et al., 2015; Dibike et al., 2011; Ladwig et al., 2018; Magee and Wu, 2017; Prats et al., 2018; Woolway et al., 2017). Such regional studies typically focus on the role of lake-specific factors, such as lake size, morphometry, and water quality in long-term lake trends due to local warming. A consistent research extension in this direction could embrace upscaling to worldwide lake trends in combination with evaluating different global change scenarios and (or) different lake models. Complementary to this “extensive” approach, lake modelling is an efficient tool for generalizing regional studies via “intensive” understanding of the energy transport between different temporal scales, which finally produces the integrated effect of slow atmospheric warming on lake dynamics. In this regard, the seasonal variations deserve special attention because they represent the most energetic part of the entire spectrum both in lakes and in the atmospheric boundary layer. High amplitudes of the seasonal variations involve the formation of density stratification and ice cover. These processes are, in turn, governed by different sets of physical forces at different stages of the seasonal cycle, ensuring a highly non-linear lake response to atmospheric forcing on longer timescales. In freshwater lakes, the non-linear effects of seasonality get stronger as the seasonal temperature amplitudes increase relative to the maximum density value of freshwater (∼4 ∘C) and to the freezing point of 0 ∘C. Hence, geographically, seasonality is the strongest in lakes at mid-latitudes, being damped towards tropical and polar regions.
Seasonal stratification and ice cover prevent certain water layers from interacting directly with the atmosphere for certain periods of the year, so it follows that the mixing regime should mediate the effect of increasing air temperature on lakes. Major seasonal stratification patterns in freshwater lakes include dimictic (with lake stratification destroyed twice a year, when lake temperatures cross the maximum density value) and monomictic (with stratification destroyed once a year, when surface temperatures decrease to the maximum density value, but do not reach the freezing point, so that no stable winter stratification forms), as well as polymictic (in lakes too shallow for a stable stratification to form) and oligomictic (in lakes too deep for stratification to be destroyed). The fact that climate warming is likely to shift the mixing regime of some lakes to the right along the polymictic–dimictic–monomictic–oligomictic continuum (Kirillin, 2010; Livingstone, 2008; Shimoda et al., 2011) makes understanding the role of the mixing regime all the more important. Still, seasonal warming patterns and their role in mediation of the long-term changes remain comparatively unexplored (Winslow et al., 2017).
Lake morphology has been identified as a key factor affecting the seasonal mixing regime (Kraemer et al., 2015; Magee and Wu, 2017) but it cannot explain all the observed variance in lake stratification or temperature (Kraemer et al., 2015; O'Reilly et al., 2015). Besides morphology, the mixing regime depends on climate and water transparency (Kirillin and Shatwell, 2016) and therefore integrates many of the factors that determine how lakes react to climate change. Transparency influences the vertical temperature distribution by determining how far solar radiation can penetrate into the water column. Low transparency generally leads to stronger vertical temperature gradients and stratification, a shallower mixed-layer depth, and lower deep water and whole-lake temperatures (Hocking and Straskraba, 1999; Persson and Jones, 2008; Thiery et al., 2014a; Yan, 1983). Decreasing transparency (dimming) has been shown to buffer or even potentially reverse climate-induced trends in mean lake temperature (Rose et al., 2016). However, the opposite is true for stratification, where warming and dimming effects amplify to increase thermal gradients (Kirillin, 2010). The pattern becomes even more complicated with seasonal variations of the effect of transparency on stratification as well as transparency itself (Rinke et al., 2010; Shatwell et al., 2016). A major factor determining water transparency is the trophic level, which can also experience long-term variations due to changing nutrient supply. Thus, the sensitivity of warming to transparency warrants more investigation.
The present study was designed to analyse the effects of seasonality on the response of northern temperate lakes to projected future warming. We project future changes in thermal characteristics and mixing regime of four temperate lakes with a thermodynamic model forced by an ensemble of climate projections based on a moderate warming scenario, the Representative Concentration Pathway 4.5 (RCP4.5). To differentiate the potential effect of mixing regime on lake response, we simulate two shallow and two deep lakes, where each pair is similar in terms of morphology but different in terms of transparency and/or mixing regime. The four lakes are located within a distance of ≤150 km from each other; hence differences in their response to climate change are conditioned predominantly by lake properties. The aim of our study is to better understand the internal physical mechanisms determining the response of lakes to a future warmer climate by interaction of vertical mixing, ice formation, and water transparency.
2.1 Study sites
We consider four lakes located in north-eastern Germany in a temperate continental climate (Fig. 1). Stechlinsee (53.15∘ N, 13.03∘ E) and Arendsee (52.89∘ N, 11.48∘ E) are deep dimictic groundwater-fed lakes of similar area and depth. Stechlinsee is oligo-mesotrophic and one of the clearest lakes in the region, whereas Arendsee is eutrophic and turbid (Table 1). Müggelsee (52.44∘ N, 13.65∘ E) is a eutrophic, polymictic lake and Heiligensee (52.61∘ N, 13.22∘ E) is a hypertrophic, dimictic lake. Both are shallow lakes and located in Berlin.
2.2 Lake data
Long-term water temperature measurements were available at weekly intervals and 0.5 m depth increments for Müggelsee, in bi-weekly to monthly intervals at 1 m depth increments for Heiligensee, and in weekly to monthly intervals at varying depth increments in both Stechlinsee and Arendsee. In addition, hourly water temperature profiles were available for Müggelsee since 2004. The thermodynamic model was calibrated with long-term temperature measurements from 1979 to 2014 (Müggelsee), 1979 to 2001 (Heiligensee), 1991 to 2014 (Stechlinsee), and 1979 to 2010 (Arendsee). Stratification duration measurements in Müggelsee were only based on the high-frequency temperature measurements from 2004 to 2014. Secchi depths (hsecchi) were measured with a standard 20 cm disk at weekly to monthly intervals since at least 1979 in all lakes. Light extinction (γ) in Müggelsee, Heiligensee, and Stechlinsee was calculated using the Lambert–Beer law from simultaneous light measurements at different depths (generally 0.5 m apart) recorded with spherical sensors (Licor, Nebraska). Using regression, we related light extinction to parallel measurements of Secchi depth using the relationship (Poole and Atkins, 1929). We determined the constant c to be 2.05±0.04 (mean ± SE, n=300) for Müggelsee, 2.13±0.10 (n=52) for Heiligensee (Shatwell et al., 2016), and 2.33±0.08 (n=57) for Stechlinsee. In the absence of direct measurements in Arendsee, light extinction was estimated from Secchi depth measurements as , where the constant c=2.17 was simply the mean of the estimates from the other three lakes.
2.3 Modelling
Modelling was performed with the lake temperature and mixing model FLake (Kirillin et al., 2011; Mironov, 2008) – a bulk model of the lake thermal regime specifically designed to parameterize inland waters in climate models and numerical weather prediction systems. FLake is based on a two-layer parametric representation of the vertical temperature structure. The upper layer is treated as well-mixed and vertically homogeneous. The structure of the lower stably stratified layer, the lake thermocline, is parameterized using a self-similar representation of the temperature profile. The same self-similarity concept is used to describe the temperature structure of the thermally active upper layer of the bottom sediments (Golosov and Kirillin, 2010) and the ice cover (Mironov et al., 2012). The depth of the mixed layer is computed from the prognostic entrainment equation in convective conditions, and from the diagnostic equilibrium boundary-layer depth formulation in conditions of wind mixing against the stabilizing surface buoyancy flux. The integrated approach implemented in FLake allowed high computational efficiency to be combined with a realistic representation of the major physics behind turbulent and diffusive heat exchange in the stratified water column and similar skill compared to other lake models (e.g. Stepanenko et al., 2013, 2014; Thiery et al., 2014b). As a result, FLake is widely used for representing lakes in land schemes of regional and global climate models, being implemented, for example, in the surface schemes of the Weather Research and Forecasting model (WRF, Mallard et al., 2014), Consortium for Small-scale Modelling (COSMO; Mironov et al., 2010), HTESSEL (European Centre for Medium-Range Weather Forecasts, ECMWF; Dutra et al., 2010), SURFEX (Meteo France; Salgado and Le Moigne, 2010), and JULES (UK Met Office; Rooney and Jones, 2010). Thanks to its robustness and computational efficiency, FLake has become the standard choice in climate studies involving the feedbacks between inland waters and the atmosphere and is used operationally in the NWP models of the German Weather Service (DWD), the ECMWF, the UK Met Office, the Swedish Meteorological and Hydrological Institute (SMHI), the Finnish Meteorological Institute (FMI), and others.
FLake is a process-based model with a high level of parameterization, which includes several empirical constants estimated from independent observational and numerical data. The model parameterizations have proven reliable in application to lakes of different morphometry and climatic conditions (Docquier et al., 2016; Kirillin, 2010; Kirillin et al., 2013, 2017; Martynov et al., 2010; Shatwell et al., 2016; Thiery et al., 2014a, 2015, 2016), so that FLake does not normally require re-tuning for a specific lake. Minor model adjustments were performed based on observations. The adjustments refer to two model parameters, each of them encompassing multiple effects of lake-specific mechanisms on the thermal stratification.
The first parameter is the rate of change of the self-similar temperature profile shape under the surface mixed layer ϑ(ζ). It is assumed to vary with time, so that the integral shape factor fluctuates between the two asymptotic bounds and with a characteristic timescale t∗ as
The parameterization incorporates mixing in the lower stratified layer (hypolimnion) by intermittent shear turbulence and breaking internal waves. The timescale t∗ is parameterized as a function of the thickness of the hypolimnion, the strength of stratification across it, and the rate of mixing at the top of the thermocline (see Mironov, 2008, for details). Observational data on temporal variations of Cϑ in several lakes demonstrated that t∗ tends to vary among them depending on lake depth (Kirillin, unpublished data). This parameter was increased from 0.04 to 0.22 for the shallow Müggelsee, in order to mimic the additional vertical mixing produced by the flow of the River Spree through the lake, which is not explicitly accounted for by one-dimensional modelling. The second parameter is the rate of change of the wind-mixed layer depth, which is assumed in the model to relax exponentially to the equilibrium depth determined following Zilitinkevich and Mironov (1996). The parameter is suggested to have the order of magnitude 10−2 (Mironov 2008) and was set to 0.025 for all lakes based on observed mixed-layer dynamics.
2.4 Climate warming scenarios
FLake was forced with an ensemble of continuous 21st century climate projections from the Coordinated Regional climate Downscaling Experiment for Europe (EURO-CORDEX; Kotlarski et al., 2014). The climate projections were based on an intermediate greenhouse gas concentration trajectory (RCP4.5), representing a moderate climate warming scenario with an end-of-century, top-of-the-atmosphere radiative forcing of 4.5 W m−2 compared to the pre-industrial period (IPCC, 2014). The ensemble was assembled from different downscaled global climate models (MPI-ESM-LR, EC-EARTH, CanESM2, CNRM-CM5, CSIRO-Mk3-6-0, GFDL-ESM2M, MIROC5, NorESM1-M) each providing lateral boundary conditions to the RCA4 regional climate model. In addition, the MPI-ESM-LR global climate model (GCM) was downscaled by the CCLM4-8-17 and REMO2009 regional climate models, and the EC-EARTH GCM was downscaled by HIRHAM5 and RACMO22E, yielding an ensemble of 12 climate projections (2006–2100) for each lake. The dispersion of mean monthly and annual air temperature in the ensemble is quite comparable to that of both the ERA-Interim reanalysis dataset and the observed data from a nearby weather station (Fig. 2). The ensemble tended to slightly underestimate the frequency of extremely warm months in the upper 10th percentile (Fig. 2a) but not the frequency of warm years (Fig. 2b). All simulations were performed at a horizontal resolution of atmospheric forcing data of 0.44∘. For the analysis we selected the model pixel containing the lake under consideration.
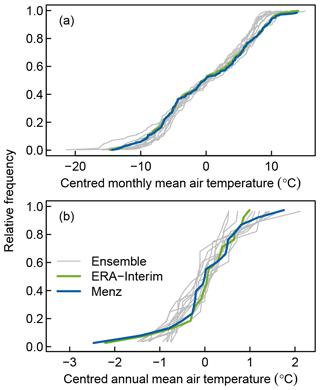
Figure 2Cumulative distribution function of centred monthly (a) and annual mean air temperature (b), based on data from 1991 to 2010. The grey lines show the 12 historical scenarios in the ensemble, the green line shows ERA-Interim reanalysis data, and the blue line shows the observed data from the Menz weather station. All data are for the closest pixel or weather station to Stechlinsee.
2.5 Temporal downscaling of meteorology
The FLake forcing variables included solar radiation (IR), near-surface air temperature (Ta), 10 m wind speed (U10), specific humidity (ea), and cloud fraction (N). These variables were available at daily resolution in the climate projections and were downscaled for model simulations to 6-hourly resolution with the same daily mean to account for diurnal forcing. Solar radiation and wind speed were downscaled assuming a sine course during the day, with a constant minimum value during the night, according to the model:
where p is the solar radiation or wind speed as a function of time of day (t, in hours); pmin and pmax are the night-time minimum and daytime maximum values, respectively; trise and tset are the times of sunrise and sunset, respectively; lag is the time lag of the maximum value behind solar noon (halfway between trise and tset); and m is a shape constant. The constant m was empirically determined to be 1.3 based on high-resolution weather data (1 November 1991 to 24 August 2004) from the Menz weather station 5 km from Lake Stechlin (Fig. 1). Sunrise and sunset times were determined at the coordinates of each study lake on each day of the year with a NOAA algorithm using the R package maptools (Bivand and Lewin-Koh, 2016). The daily mean is given by
For solar radiation, lag =0 and pmin=0. For wind speed, lag =1 h based on empirical observations and pmin is non-zero. Accordingly, the daily course of solar radiation p for a prescribed daily mean from the climate projections is given by calculating pmax with Eq. (3) and substituting it into Eq. (2). For wind speed, the daily course is defined from the daily mean given the daily amplitude pmax−pmin, which was empirically estimated from the Menz weather data and varied seasonally. Random Gaussian noise was added to wind speeds with the same variability (variance proportional to mean) as observed in the Menz station. This method accurately reproduced the complexity of the observed wind speed dynamics: It produced realistic behaviour of day-to-day wind speed (Fig. 3a), as well as the diurnal variation of mean wind speed and associated variance (Fig. 3b, c), and also the seasonal change of this diurnal variation (Fig. 3b, c), while still preserving the given daily mean wind speeds. Sub-daily air temperatures were interpolated between a daytime maximum assumed at 14:00 LT and night-time minimum assumed at 02:00 LT using a cubic spline, where the daily temperature amplitude ΔTa (K) was estimated from the daily mean temperature (∘C) using the empirical relationship based on the Menz data. Sub-daily humidity and cloud fraction were linearly interpolated between the daily mean values.

Figure 3Comparison of disaggregated and observed sub-daily wind speeds at the Menz weather station (5 km from Stechlinsee): sample of observed hourly wind data from 1998 and the disaggregated wind speeds generated from the corresponding daily means (a); hourly mean and standard deviation of observed (circles, shaded area) and disaggregated wind speeds (solid and dashed lines) in February (b) and July (c).
2.6 Extinction scenarios
We performed lake model simulations with different scenarios of seasonal extinction, which in these lakes is primarily determined by phytoplankton chlorophyll (Shatwell et al., 2016). Here the thermodynamic model was modified to account for seasonally variable extinction, following a typical bimodal pattern according to the Plankton Ecology Group (PEG) model (Sommer et al., 1986, 2012), as described in detail in Shatwell et al. (2016). A base seasonal extinction pattern was derived from long-term observations of extinction and/or Secchi depth in each study lake, preserving important seasonal characteristics including long-term annual mean extinction (see Table 1), minimum extinction, and timing and magnitude of the spring and summer blooms (Fig. 4). The spring and summer blooms were described by Weibull and Gauss curves, respectively.
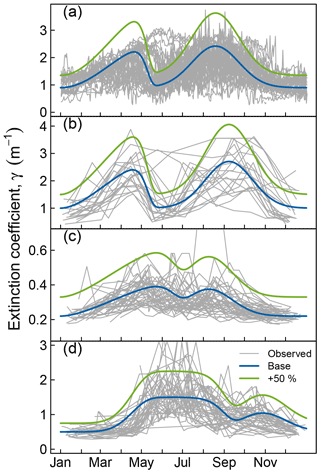
Figure 4Seasonal course of extinction (γ) in Müggelsee (a), Heiligensee (b), Stechlinsee (c), and Arendsee (d). Grey lines show superimposed observed extinction during individual years, thick blue lines show the idealized seasonal course of extinction used in model simulations with FLake (base scenario). Green lines show base extinction increased by 50 %. Panels (a) and (b) modified from Shatwell et al. (2016).
Using these base extinction patterns as the control scenario, we simulated the hydrodynamics of the four lakes for the period 2006–2100 forced by the climate projection ensemble. To test the sensitivity of lake warming response to water clarity, we then repeated these simulations with a modified mean extinction coefficient. The mean extinction coefficient was varied by scaling the whole seasonal extinction pattern, affecting mean, minimum, and peak extinction equally. A principal component analysis on long-term extinction coefficient measurements in Müggelsee and Heiligensee showed that this method best represented the natural variation in the seasonality of extinction (Shatwell et al., 2016).
2.7 Model set-up and calibration
FLake was configured for each lake by setting mean lake depth and fetch, the temperature at the bottom of the thermally active sediment layer (set to the historical long-term mean water temperature at the lake bottom), and the extinction coefficient as described above. The model was manually calibrated for each lake by adjusting t∗ with a constant. Additionally, in the case of shallow Müggelsee, the rate of change of the mixed-layer depth due to wind forcing was changed to account for the additional vertical mixing produced by the riverine throughflow (see Sect. 2.3 for details). Hindcast simulations were forced with meteorology from ERA-Interim gridded reanalyses produced by the European Centre for Medium-Range Weather Forecasts (Dee et al., 2011). Using this meteorological forcing as a basis for the model calibration was preferred over using (i) in situ meteorology, as the future projections are obtained by forcing FLake with a gridded simulation product rather than in situ information, and (ii) the EURO-CORDEX reanalysis downscaling simulations, as calibrated model parameters would in that case differ between model projections. For consistency the ERA-Interim-driven simulations were downscaled from daily means to sub-daily values using the same procedure as for the climate projections described above. Using a model calibrated on a different dataset (ERA-Interim) than the climate projections can introduce bias into the results. Thus we reran the model calibrated on ERA-Interim data with forcing from the historical hindcasts of each of the 12 GCM–RCM combinations in the ensemble. The mean bias of each variable forced by the ensemble hindcast barely differed from the bias obtained using ERA-Interim forcing. In fact, the ensemble showed on average a smaller absolute bias in bottom temperature, mixed-layer depth, stratification duration and stratification onset timing and a slightly greater bias only in surface temperature and stratification breakdown timing. Therefore, our simulations are largely unaffected by bias.
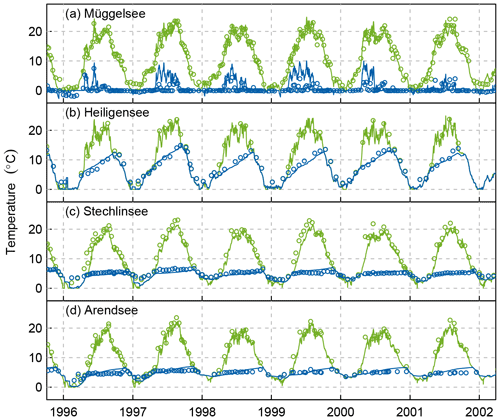
Figure 5Comparison of modelled (lines) and observed temperatures (points) in Müggelsee (a), Heiligensee (b), Stechlinsee (c), and Arendsee (d). Green lines and symbols show surface temperatures, blue lines and symbols show bottom temperatures (b–d) or surface–bottom temperature differences (a).
Precipitation, including snow cover on ice, was not included in modelling. There are several indications suggesting that including the snow as model input would not improve the predictive value of the model outcomes. Firstly, the current version of FLake treats the thermal regime under ice in a simplified way, without taking into account the shortwave radiation penetrating into the water column under the ice cover. Therefore including the insulating effect of snow on the radiation flux would not substantially change the mixing physics of the ice-covered period. Secondly, in temperate regions, the relatively short ice-covered periods on lakes are weakly affected by the snow cover compared to, for example, boreal and arctic lakes. This fact was also supported by the study of the FLake performance for the ice modelling on Lake Müggelsee (Bernhardt et al., 2012). Moreover, we did not account for changes in inflow because our focus was on lake–atmosphere interactions. Instead we assessed the sensitivity of the lakes to a change in transparency, which can be expected if warming alters runoff as well as nutrient and carbon export.
Model performance was assessed by comparing the modelled and observed surface temperature (Ts), bottom temperature (Tb), and, for the seasonally stratified lakes (Heiligensee, Stechlinsee, and Arendsee), the mean summer mixed-layer depth (hmix) and timing and duration of seasonal stratification. Here we assessed model performance using temperature profiles in the period from 1979 to 2014 in Müggelsee (measured weekly, and from 2004 to 2014 hourly), from 1979 to 2001 in Heiligensee (monthly), from 1991 to 2012 in Stechlinsee (weekly to monthly), and from 1979 to 2010 in Arendsee (weekly to monthly). As different measures of goodness of fit, we examined model bias (Eq. 4), centred root mean square error (RMSEc, Eq. 5), normalized root mean square error (RMSEn, Eq. 6), and normalized standard deviation (σnorm, Eq. 7), where mi and oi are the modelled and observed values, respectively, and () and () are their means:
2.8 Data handling and statistics
Ts was calculated from field data as the mean temperature in the 0–1 m layer. Tb was calculated as the mean temperature at the mean depth of each lake. Stratification was inferred when the absolute difference between Ts and Tb exceeded 0.5 ∘C. The lake was assumed to be mixed when it was not stratified. The duration of seasonal stratification was defined as the length of the longest uninterrupted stratification period each season. Similarly, the duration of overturn was defined as the length of the longest uninterrupted period of mixing in each season following the main stratification events. Winter was defined as January to March, spring as April to June, summer as July to September, and autumn as October to December. Trends were assessed using linear regression over time. Differences between transparency treatments were assessed by comparing decadal means of a particular variable for each climate projection in the ensemble, yielding 12 means per decade over 9 decades from 2010 to 2100. Comparisons were made using ANCOVA with decade as the covariate. Normality of residuals was assessed with quantile–quantile plots, homogeneity of variance with plots of residuals versus fitted values, and outliers with plots of Cook's distances. Increasing variance with the mean was resolved by log transformation. Ice-cover duration was extended by 1 day to avoid zero values before log transformation. Outliers with a Cook's distance > 1 were excluded from statistical analyses. Small deviations from normality were tolerated. All statistical analyses were performed with R version 3.3.0 (R Core Team, 2016).

Figure 6Projected changes in over-lake near-surface air temperature under RCP4.5. Lines show decadal means over all climate projections and all four locations.
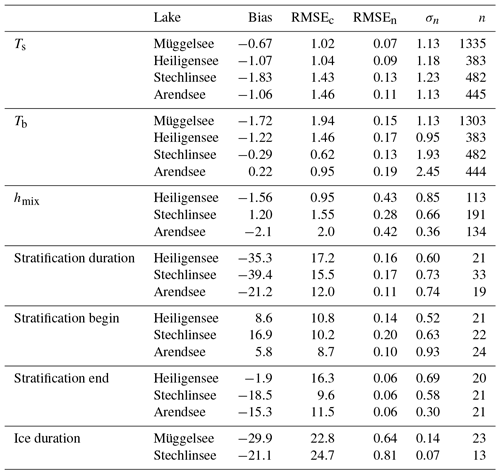
Table 2Goodness-of-fit statistics of the four study lakes. Stratification statistics not shown for polymictic Müggelsee.
3.1 Model validation
The thermodynamic model forced by the ERA-Interim reanalysis data performed well at reproducing the observed thermodynamic characteristics of the study lakes (Fig. 5). The model predicted water temperature with good precision as evident in RMSEc values generally less than 1.5 ∘C for surface and bottom temperatures (Table 2). The model also reproduced observed temperature variability well with σn close to 1, except in bottom temperatures of the two deep lakes Stechlinsee and Arendsee, which are quite invariant with a standard deviation of 0.86 and 0.99 ∘C respectively. However, the model had a systematic tendency to underestimate Ts in all lakes by 0.7–1.8 ∘C. The model also adequately reproduced the stratification characteristics of the three seasonally stratified lakes with a centred error of 1–2 m for hmix and about 2–3 weeks for stratification duration, noting that the sampling interval (and thus measurement error) for stratification duration was generally 4 weeks. The model systematically underestimated the stratification duration by about 1 month, probably because the surface temperatures were also underestimated.
3.2 Meteorology trends
Air temperatures in the RCP4.5 forcing ensemble increased on average by 0.16 ∘C per decade over all lakes. These increases were strongest in winter and spring (0.23–0.30 ∘C decade−1) and weakest in summer (0.04 ∘C decade−1, Fig. 6). Mean annual radiation decreased in the ensemble by 0.29 W m−2 decade−1. The overall decrease was unevenly distributed seasonally, with a strong decrease projected for summer (1.65–1.70 W m−2 decade−1) but an increase projected for winter (1.1 W m−2 decade−1). Annual mean water vapour pressure was projected to increase by 0.1 Pa decade−1 with stronger increases in winter and spring than in summer and autumn. The projected changes in wind speed were negligible.
3.3 Lake response to warming
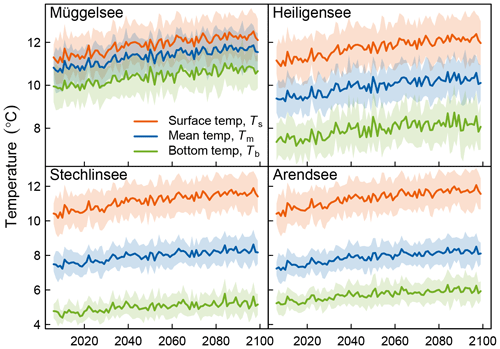
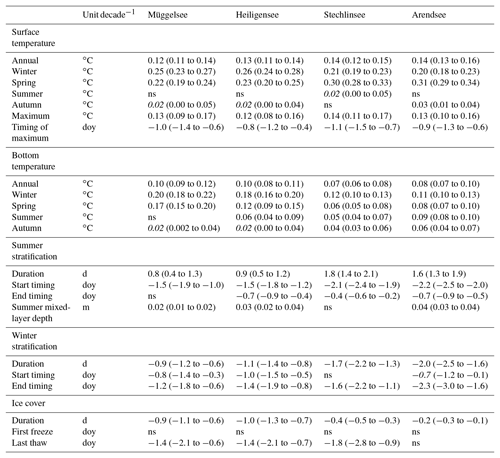
In model runs with the historical, baseline extinction, these projected climate trends resulted in an increase in annual surface water temperatures (higher rates of increase in deeper lakes) in all lakes for the simulation period 2006–2100 (Fig. 7, Table 3). Bottom temperatures increased in all lakes, with faster warming rates projected in the two shallower lakes Müggelsee and Heiligensee. Accordingly, mean lake temperatures increased in all lakes at 0.10–0.11 ∘C decade−1.
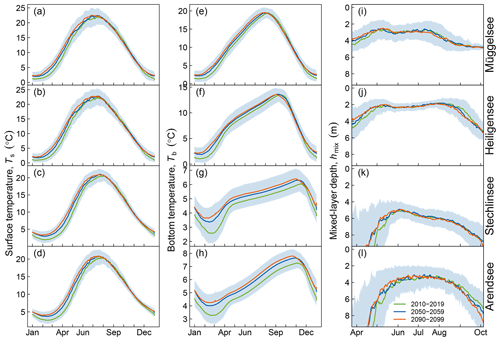
Figure 8Modelled seasonal cycle of surface (a–d) and bottom temperature (e–h) and mixed-layer depth (i–l) in Müggelsee (a, e, i), Heiligensee (b, f, j), Stechlinsee (c, g, k), and Arendsee (d, h, l). Lines indicate decadal means and shading denotes 1 standard deviation each side of the mean.
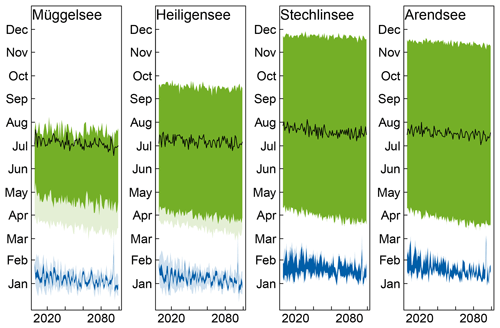
Figure 9Projected trends in stratification in the four study lakes. Green shading shows summer stratification, blue shows winter stratification. Lighter shading indicates intermittent stratification. The black line shows the timing of maximum surface temperature. The model was forced with the baseline (historical) transparency.
Ts increased most rapidly during the winter in the two shallower lakes and during spring in the two deeper lakes. On the other hand, mean summer Ts increased only marginally in Stechlinsee (0.02 ∘C decade−1) and not at all in the other lakes (Fig. 8). Tb increased most rapidly in winter. Moreover, the higher Tb in April and May, when stratification typically began, persisted until the end of stratification (September in Heiligensee and November–December in deeper Stechlinsee and Arendsee; Fig. 8). Accordingly, deep water warmed faster than surface water during summer (and autumn in the deep lakes), which led to a lower vertical temperature gradient in summer, and consequently weaker stratification. Furthermore, annual maximum surface temperature increased and occurred earlier in summer (Fig. 9, Table 3).
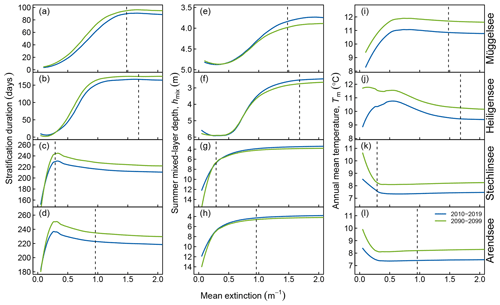
Figure 10Interacting effects of extinction and warming on stratification duration (a–d), mean mixed-layer depth in summer (e–h), and annual mean temperature (i–l) in Müggelsee (a, e, i), Heiligensee (b, f, j), Stechlinsee (c, g, k), and Arendsee (d, h, l). Lines have been loess-smoothed and show ensemble means for the decades 2010–2019 (blue) and 2090–2099 (green) as a function of extinction. Black vertical dashed lines show the long-term measured extinction in each lake.
Winter and spring warming caused stratification to begin earlier in all lakes in the model simulations (Fig. 9). This was also reflected in a shallower mean hmix during spring in the deep lakes Stechlinsee and Arendsee. The end of stratification also advanced slightly due to the slightly smaller vertical temperature gradients in summer, but not as rapidly as stratification onset, so that overall stratification duration increased. Mean summer hmix increased in three lakes by less than 0.05 m decade−1, which is practically negligible. Winter stratification and ice cover were more intermittent in the two shallow lakes than in the two deeper lakes. Winter and spring warming mainly caused winter stratification and ice cover to end earlier, reducing the overall duration (Fig. 9). Interestingly, most of the changes in winter stratification and ice cover were projected to occur in the first half of the 21st century, with little change in the second half.
The projected increase in stratification duration was insufficient to cause Müggelsee to stratify continuously from spring to the end of summer (median duration in the decade 2090–2099: 102 days) and thus shift from a polymictic to a dimictic regime. On the other hand, the deeper dimictic lakes Stechlinsee and Arendsee were projected to be at the transition to a monomictic regime by the middle of the 21st century. In the decade 2050–2059, the model projected that Stechlinsee and Arendsee would have no winter stratification in 33 % and 55 % of winters and be ice-free in 76 % and 93 % of winters, respectively. By comparison, in the decade 2010–2019, Stechlinsee and Arendsee were projected to have no winter stratification in 13 % and 24 % of winters and be ice-free in 58 % and 75 % of winters, respectively. The mean winter bottom temperature in the decade 2090–2099 was projected to be 3.96±0.93 ∘C in Stechlinsee (compared to 3.03±0.79 ∘C in 2010–2019) and 4.48±0.93 ∘C in Arendsee (compared to 3.62±0.73 ∘C in 2010–2019).
Annual mean whole-lake water temperature correlated with annual mean air temperature. At any given annual mean air temperature, Müggelsee was warmest, followed by Heiligensee, Stechlinsee, and Arendsee. Moreover, at a given annual mean air temperature, all lakes were colder following winters with ice cover than without ice cover, where the temperature differences increased with mean lake depth.
3.4 Interaction between warming and transparency
To investigate the sensitivity of different lake types to a change in transparency combined with warming, we modelled the projected warming effects (2006–2100) in the given lakes with mean extinction ranging from extremely clear (γ=0.05 m−1) to extremely turbid (γ=3 m−1). The effect of transparency and its interactions with warming were highly non-linear and the responses were very sensitive to lake type. There were transparency ranges where transparency had a very large effect on thermal structure, and ranges where it had little effect at all. In general, changes in transparency had a strong effect on stratification duration and vertical temperature structure at intermediate extinction (ca. 0.4–1.1 m−1) in the moderately shallow lakes Müggelsee and Heiligensee (Fig. 10a, b) and at very low extinction (< 0.3 m−1) in the deep lakes Stechlinsee and Arendsee (Fig. 10c, d). Outside these ranges, changes in extinction had a much smaller effect: at extinctions above about 1.1 m−1 in the two shallower lakes (or > 0.3 m−1 in Stechlinsee) a further increase in extinction no longer increased stratification duration, but rather decreased it gradually due to a very gradual increase in summer bottom temperatures. Accordingly, at extinction values higher than the historical means in the four study lakes (vertical dashed lines in Fig. 10; see also Table 1), the trends in stratification duration due to warming were stable and relatively insensitive to changes in transparency. Thus, an increase in extinction combined with warming is unlikely to push Müggelsee from a polymictic to a dimictic regime. However, the simulations also suggested that clearer shallow lakes, which are close to the transition between polymictic and dimictic regimes, can potentially switch mixing regimes because interactions between warming and dimming are stronger. Altogether, the model suggested that changes in stratification duration due to changes in transparency can be expected at optically normalized depths γ×hmean < 5 to 8 (Fig. 11). Figure 11 was derived for the period 2090–2099. Although stratification duration increased over time as indicated in Table 3, the relative dependence on extinction was similar during the whole period covered in the ensemble.
The model predicted that an increase in extinction in the four study lakes above their historical values would not influence whole-lake warming rates (Tm) induced by climate change (Fig. 10i–l). However, the model did suggest that there would be an interaction between warming and dimming at extinctions considerably lower than the historical extinction values observed in these lakes. In the deep lakes, dimming was predicted to decrease Tm at extinctions below about 0.3 m−1 (Fig. 10c, d). According to simulations, increasing extinction from 0.1 to 0.3 m−1 would approximately cancel out the expected effect on Tm of 90 years of climate warming. The shallower lakes behaved differently to the deep lakes at low extinction. In Müggelsee, Tm increased with increasing extinction up to about 0.5 m−1 (Fig. 10a). In Heiligensee the model suggested a strong interaction between warming and dimming up to an extinction of about 0.5 m−1, where dimming would decrease Tm in the warmer climate at the end of the 21st century but increase Tm in the cooler climate of today (Fig. 10b).
Whereas the model predicted that warming would have a small (deepening) effect on mixed-layer depth, it predicted that an increase in extinction would have a stronger (shoaling) effect (Fig. 10e–h). Again, a change in extinction would have a much stronger effect on the mixed-layer depth at intermediate extinctions in the shallower lakes and at a low extinction in the deep lakes.
4.1 Warming trends
Our projections suggest that surface waters in all modelled lakes will warm at about 75 %–90 % of the rate of air temperature increase, with surface temperatures in the deeper lakes increasing faster than the shallower lakes. This is similar to other modelling studies based on climate projections, which found warming rates of 70 %–85 % of air temperature trends (Butcher et al., 2015; Schmid et al., 2014). The relatively uniform results obtained from climate and lake modelling studies are not entirely consistent with empirical evidence, which shows that warming rates of surface water relative to air can be more variable (O'Reilly et al., 2015; Torbick et al., 2016).

Figure 11Stratification duration vs. optically normalized depth (mean extinction (γ, m−1) × mean depth (hmean, m), dimensionless) in lakes Müggelsee, Heiligensee, Stechlinsee, and Arendsee. The curves are loess-smoothed and are based on ensemble simulations with the baseline extinction in each lake for the 2090–2099 period.
4.2 Influence of seasonality and stratification
We found that seasonality of warming played an important role and we concur with Winslow et al. (2017) that summer lake warming rates are not representative of warming in other seasons. In fact, our projections suggest that the study lakes will warm predominantly in winter and spring, and only marginally in summer and autumn. These seasonal patterns largely reflect the seasonality of air temperature trends in the warming ensemble. The model may have slightly underestimated the increase in summer peak temperatures and occurrence of extended stratification during heatwaves in polymictic Müggelsee because the ensemble tended to slightly underestimate the frequency of extremely warm months. The leftward seasonal skew of surface water temperature increase towards spring and our estimates that the summer maximum temperature should occur increasingly earlier in the year imply that the number of days per year when the surface temperature exceeds a certain threshold will increase. Accordingly, although summer warming was slow, the length of the bathing season will likely increase and along with it both the recreational value and the recreational pressure on lakes.
Stratification and ice cover restrict vertical heat transport and thus influence heat storage in lakes. Therefore they should modulate how lakes respond to warming. This was evident in our simulations because, at the same annual mean air temperature, lakes were colder in years with ice cover (dimictic regime) than in years without ice (monomictic regime). This can be explained in part by the thermal inertia from the previous season (Crossman et al., 2016), and in part due to altered heat accumulation in deep water during mixing preceding summer stratification. The latter was demonstrated by the relatively steep trends in bottom temperature during winter simulated in the four study lakes. These effects were also observed empirically in Stechlinsee, which was thermally polluted by a nuclear power plant, preventing ice cover and shifting the mixing regime from dimictic to monomictic (Kirillin et al., 2013). Here the waste heat input during winter mixing was stored in deep water until the following winter and increased the mean lake temperature, whereas the waste heat input during stratification was confined to the surface layer and quickly lost to the atmosphere. The effect of summer stratification on heat transport and storage explains why the simulated mean lake temperature increased faster in the polymictic lake Müggelsee than in seasonally stratified Heiligensee, although these lakes have very similar mean depths. We conclude that not just morphology, but also mixing regime modulates how lakes respond to climate warming. Moreover, we conclude that seasonal differences in climate warming rates combined with the strongly non-linear sensitivity of lakes to monthly temperature changes determine how lakes react to warming overall.
4.3 Mixing regime shifts
The comparatively rapid increase in winter air temperature was projected to strongly affect ice cover and winter stratification, and push the two deeper dimictic lakes (Stechlinsee and Arendsee) towards a monomictic regime. Such shifts have been projected as a consequence of climate warming for temperate stratified lakes (Ficker et al., 2017; Kirillin, 2010; Livingstone, 2008). Both of these lakes switched regularly between monomixis and dimixis and the climate-induced transition between regimes is projected to be gradual. In particular the slightly deeper Arendsee will rarely be ice covered in the coming decades and will experience a predominantly monomictic regime and mean winter bottom temperatures generally above 4 ∘C. Our finding that almost all of the change in winter stratification and ice cover will occur in the first half of the 21st century is in part because the winter air temperature in the ensemble is projected to increase twice as fast then as in the second half of the 21st century, and also because of the highly non-linear response of ice cover to air temperature changes. Our model projections suggested that lake depth was the most important factor regulating ice cover duration, as expected (Kirillin et al., 2012). Moreover, the timing of ice-off was more sensitive to warming than ice-on, which concurs with several studies (Benson et al., 2012; Crossman et al., 2016; Vavrus et al., 1996). The sensitivity analysis suggested that transparency would not influence ice cover in the modelled lakes but may have an effect in extremely clear lakes. Other modelling studies suggested that transparency can affect the timing of ice-on (Heiskanen et al., 2015) but may have little effect on ice-off timing (Fang and Stefan, 2009). The disappearance of ice will increase evaporation rates, as well as the exchange of heat and gases with the atmosphere.
According to our simulations, summer stratification duration in Müggelsee is likely to increase, but not enough to switch the lake from a polymictic to a dimictic regime within the current century. An increase in the frequency of stratification events is likely to increase the occurrence of nuisance cyanobacterial blooms and influence nutrient cycles, as was already demonstrated in this lake (Wagner and Adrian, 2009). The warming effect on stratification duration and mixed-layer depth was relatively small in comparison with the potential effect of a change in transparency (Fig. 10a, e). Thus, lakes at the transition between polymictic and dimictic regimes may shift more due to changes in transparency or water level than due to warming alone.
4.4 Mixed-layer depth
An important question that has not been conclusively answered is how climate change will affect the mixed-layer depth. Our simulations suggested that climate warming would increase the mixed-layer depth in stratified lakes, but the projected increase of less than 0.05 m decade−1 should be considered negligible. Other lake model simulations have also predicted that the mixed layer will deepen with warming (Missaghi et al., 2017). In contrast, ocean models have consistently projected a shoaling of the mixed layer (Capotondi et al., 2012; Jang et al., 2011; Sen Gupta et al., 2009) but empirical evidence does not confirm this (Somavilla et al., 2017). In lakes, empirical data show that the mixed layer can deepen (Flaim et al., 2016; Kraemer et al., 2015), remain relatively constant (Ficker et al., 2017; Kirillin et al., 2013), or possibly shoal (Saros et al., 2016) as a result of warming. In our simulations, the mixed-layer depth was much more sensitive to transparency than warming, which concurs with empirical data (Flaim et al., 2016; Saros et al., 2016). We conclude that there is little physical evidence that climate warming causes the mixed layer to become shallower and suggest that observed changes in mixed-layer depth may be more due to changes in transparency or wind speed.
4.5 Transparency – warming interactions
A major finding of our study was that interactions between global warming and changes in transparency are highly non-linear. Thus, we confirm our initial hypothesis that warming and dimming act in synergy to increase stratification duration but oppose each other to stabilize mean lake temperature. However, we add that this only applies within certain extinction ranges which vary with lake mixing regime. In general, interactions between a change in transparency and warming occurred at very low to moderate extinction. The reason for the non-linearity is probably the extent to which transparency influences the mixed-layer depth and the extent to which the mixed layer interacts with the lake bottom. Transparency is the major determinant of mixed-layer depth in small, wind-sheltered lakes but its effect diminishes with increasing lake size and wind speed (Kirillin and Shatwell, 2016).
According to the sensitivity analysis, a change in transparency was projected to affect mean lake temperature most strongly at very high transparency, where the nature of the effect depended on the lake mixing regime. At high transparency (low extinction coefficient), dimming increased lake temperature in the polymictic Müggelsee because increased absorption of radiation affected the whole water column (Fig. 10). On the other hand, dimming decreased lake temperature in the stratified lakes Arendsee and Stechlinsee because less radiation reached the deep waters. Heiligensee was the most sensitive because dimming was projected to alter the mixing regime from polymictic to stratified. We assume that the interesting behaviour of Heiligensee in Fig. 10j is probably due to how the mixed layer (if present) interacts with the lake bottom, making the heat budget of this lake especially sensitive to the mixing regime. Although the model suggested that a change in transparency would have strong effects on lake thermal properties, the four lakes we simulated were predicted to be too turbid in their present state to be substantially influenced by a further decrease in transparency. This may be because shallower lakes are naturally more turbid than deep lakes, so that lakes in which a substantial amount of incoming radiation is able to reach large areas of the lake bottom are rare. Very shallow lakes where radiation can reach most of the lake bottom tend to be dominated by macrophytes, which themselves strongly alter stratification and mixing conditions (Vilas et al., 2017). Transparency is affected by anthropogenic activities (Jeppesen et al., 2005) and also climate change (Larsen et al., 2011), so investigations into how lakes respond to global warming should consider these complex interactions.
4.6 Model reliability
The model errors in this study were relatively small compared to other studies (for discussion and comparison see Shatwell et al., 2016), providing confidence in the results. There were, however, some systematic errors, which we attempted to alleviate by focusing on comparative analyses, such as trends. Our finding that mean bottom water temperatures in summer should increase under higher extinction in the stratified lakes was unexpected according to empirical evidence (Snucins and Gunn, 2000). The reason for this result in the simulations was apparently diurnal heating and cooling cycles, which increased the downward transport of heat into the hypolimnion during summer because this effect was present when the model time step was decreased from 6 to 3 h, but it disappeared when the time step was increased to 1 day (results not shown). A comparison with empirical data suggests that this effect was probably overestimated by the model because a decrease in transparency with a weaker spring clear-water phase caused an increase in summer surface–bottom temperature differences in lakes Müggelsee and Heiligensee (Shatwell et al., 2016). Additional error can arise through bias in the forcing meteorological data but we found that the mean bias in key variables obtained from the ensemble forcing did not differ from the bias of the model calibrated with ERA-Interim reanalysis data. Another source of error can be incorrect representation of dispersion in the forcing ensemble. However, here we found that the dispersion of air temperature was quite similar to the dispersion in measured meteorological data and the ERA-Interim reanalysis. The slight underestimation of extremely warm periods in the ensemble may also cause a slight underestimation in our results of peak summer temperatures in all lakes and of the frequency of extended stratification events during heatwaves in polymictic Müggelsee. This should not influence our overall conclusions.
Altogether our study suggests that warming over the next century will gradually shift many temperate dimictic lakes towards a predominantly monomictic regime, particularly since projected warming rates were highest in winter and spring, with deeper lakes shifting before shallower ones. On the other hand, shifts from polymixis to dimixis are more likely to occur due to a change in transparency or depth than due to climate warming alone. Dimming trends can buffer lake warming trends but amplify increases in stratification duration. However, this effect will probably be limited to relatively clear lakes, particularly those at the transition between polymictic and stratified regimes. Lake mixing regime is an important modulator of climate change impacts on lakes and it is necessary to understand how the seasonality of warming interacts with stratification and ice cover to interpret differences in lake warming trends.
The source code of the model FLake is freely (MIT license) available online at http://www.lakemodel.net (FLake Core Team, 2019). The observational data are stored in the database IGBFRED (https://fred.igb-berlin.de, Leibniz-Institute of Freshwater Ecology and Inland Fisheries, 2019) subject to the data policy of the Leibniz-Institute of Freshwater Ecology and Inland Fisheries (IGB). Regional climate projections from the EURO-CORDEX are publicly available through the Earth System Grid Federation (ESGF; https://esgf-data.dkrz.de, EURO-CORDEX Consortium, 2019). The raw output of the lake modelling is available from the corresponding author by request.
GK conceived the study and modified the model with TS. WT provided the climate projections. TS performed the simulations and analysed the results. All authors contributed to interpreting the results. TS wrote the paper with contributions from GK and WT.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Modelling lakes in the climate system (GMD/HESS inter-journal SI)”. It is a result of the 5th workshop on “Parameterization of Lakes in Numerical Weather Prediction and Climate Modelling”, Berlin, Germany, 16–19 October 2017.
We are grateful to the World Climate Research Programme (WRCP) for
initiating and coordinating the CORDEX-Africa initiative, to the modelling
centres for making their downscaling results publicly available through
ESGF, and to the European Centre for Medium-Range Weather
Forecasts (ECMWF) for providing access to ERA-Interim. We thank the
Leibniz-Institute of Freshwater Ecology and Inland Fisheries for providing
long-term lake data. We also thank the German Meteorological Service (DWD)
for providing high-resolution weather data and some temperature data for
Stechlinsee. Tom Shatwell and Georgiy Kirillin were funded by a German Research Foundation grant (DFG
no. KI-853/7-1). Georgiy Kirillin was additionally supported by the DFG project IceBound
(KI-853/11-1). Wim Thiery was supported by an ETH Zurich postdoctoral fellowship
(Fel-45 15-1).
The article processing charges for this open-access
publication were covered by a Research
Centre of the Helmholtz Association.
This paper was edited by Miguel Potes and reviewed by two anonymous referees.
Adrian, R., O'Reilly, C. M., Zagarese, H., Baines, S. B., Hessen, D. O., Keller, W., Livingstone, D. M., Sommaruga, R., Straile, D., Van Donk, E., Weyhenmeyer, G. A., and Winder, M.: Lakes as sentinels of climate change, Limnol. Oceanogr., 54, 2283–2297, https://doi.org/10.4319/lo.2009.54.6_part_2.2283, 2009.
Benson, B. J., Magnuson, J. J., Jensen, O. P., Card, V. M., Hodgkins, G., Korhonen, J., Livingstone, D. M., Stewart, K. M., Weyhenmeyer, G. A., and Granin, N. G.: Extreme events, trends, and variability in Northern Hemisphere lake-ice phenology (1855–2005), Clim. Change, 112, 299–323, https://doi.org/10.1007/s10584-011-0212-8, 2012.
Bernhardt, J., Engelhardt, C., Kirillin, G., and Matschullat, J.: Lake ice phenology in Berlin-Brandenburg from 1947–2007: observations and model hindcasts, Clim. Change, 112, 791–817, https://doi.org/10.1007/s10584-011-0248-9, 2012.
Bivand, R. and Lewin-Koh, N.: maptools: Tools for Reading and Handling Spatial Objects, 2016.
Boike, J., Georgi, C., Kirilin, G., Muster, S., Abramova, K., Fedorova, I., Chetverova, A., Grigoriev, M., Bornemann, N., and Langer, M.: Thermal processes of thermokarst lakes in the continuous permafrost zone of northern Siberia – observations and modeling (Lena River Delta, Siberia), Biogeosciences, 12, 5941–5965, https://doi.org/10.5194/bg-12-5941-2015, 2015.
Butcher, J. B., Nover, D., Johnson, T. E., and Clark, C. M.: Sensitivity of lake thermal and mixing dynamics to climate change, Clim. Change, 129, 295–305, https://doi.org/10.1007/s10584-015-1326-1, 2015.
Capotondi, A., Alexander, M. A., Bond, N. A., Curchitser, E. N., and Scott, J. D.: Enhanced upper ocean stratification with climate change in the CMIP3 models, J. Geophys. Res.-Oceans, 117, C04031, https://doi.org/10.1029/2011JC007409, 2012.
Crossman, J., Eimers, M. C., Kerr, J. G., and Yao, H.: Sensitivity of physical lake processes to climate change within a large Precambrian Shield catchment, Hydrol. Process., 30, 4353–4366, https://doi.org/10.1002/hyp.10915, 2016.
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J. J., Park, B. K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J. N., and Vitart, F.: The ERA-Interim reanalysis: configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011.
Dibike, Y., Prowse, T., Saloranta, T., and Ahmed, R.: Response of Northern Hemisphere lake-ice cover and lake-water thermal structure patterns to a changing climate, Hydrol. Process., 25, 2942–2953, https://doi.org/10.1002/hyp.8068, 2011.
Docquier, D., Thiery, W., Lhermitte, S., and van Lipzig, N.: Multi-year wind dynamics around Lake Tanganyika, Clim. Dynam., 47, 3191–3202, https://doi.org/10.1007/s00382-016-3020-z, 2016.
Dokulil, M. T., Jagsch, A., George, G. D., Anneville, O., Jankowski, T., Wahl, B., Lenhart, B., Blenckner, T., and Teubner, K.: Twenty years of spatially coherent deepwater warming in lakes across Europe related to the North Atlantic Oscillation, Limnol. Oceanogr., 51, 2787–2793, https://doi.org/10.4319/lo.2006.51.6.2787, 2006.
Dutra, E., Balsamo, G., Viterbo, P., Miranda, P. M. A., Beljaars, A., Schar, C., and Elder, K.: An Improved Snow Scheme for the ECMWF Land Surface Model: Description and Offline Validation, J. Hydrometeorol., 11, 899–916, https://doi.org/10.1175/2010jhm1249.1, 2010.
EURO-CORDEX consortium: Regional Climate Projections, available at: https://esgf-data.dkrz.de, last access: 13 March 2019.
Fang, X. and Stefan, H. G.: Simulations of climate effects on water temperature, dissolved oxygen, and ice and snow covers in lakes of the contiguous United States under past and future climate scenarios, Limnol. Oceanogr., 54, 2359–2370, https://doi.org/10.4319/lo.2009.54.6_part_2.2359, 2009.
Ficker, H., Luger, M., and Gassner, H.: From dimictic to monomictic: Empirical evidence of thermal regime transitions in three deep alpine lakes in Austria induced by climate change, Freshwater Biol., 62, 1335–1345, https://doi.org/10.1111/fwb.12946, 2017.
FLake Core Team: The FLake (Fluxes in Lakes) model, available at: http://www.lakemodel.net, last access: 13 March 2019.
Flaim, G., Eccel, E., Zeileis, A., Toller, G., Cerasino, L., and Obertegger, U.: Effects of re-oligotrophication and climate change on lake thermal structure, Freshwater Biol., 61, 1802–1814, https://doi.org/10.1111/fwb.12819, 2016.
Golosov, S. and Kirillin, G.: A parameterized model of heat storage by lake sediments, Environ. Model. Software, 25, 793–801, https://doi.org/10.1016/j.envsoft.2010.01.002, 2010.
Heiskanen, J. J., Mammarella, I., Ojala, A., Stepanenko, V., Erkkilä, K.-M., Miettinen, H., Sandström, H., Eugster, W., Leppäranta, M., Järvinen, H., Vesala, T., and Nordbo, A.: Effects of water clarity on lake stratification and lake-atmosphere heat exchange, J. Geophys. Res.-Atmos., 120, 7412–7428, https://doi.org/10.1002/2014JD022938, 2015.
Hocking, G. C. and Straskraba, M.: The effect of light extinction on thermal stratification in reservoirs and lakes, Int. Rev. Hydrobiol., 84, 535–556, https://doi.org/10.1002/iroh.199900046, 1999.
IPCC: Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Core Writing Team, Pachauri, R. K., and Meyerm, L. A., IPCC, Geneva, Switzerland, 151 pp., 2014.
Jang, C. J., Park, J., Park, T., and Yoo, S.: Response of the ocean mixed layer depth to global warming and its impact on primary production: a case for the North Pacific Ocean, ICES J. Mar. Sci., 68, 996–1007, https://doi.org/10.1093/icesjms/fsr064, 2011.
Jeppesen, E., Sondergaard, M., Jensen, J. P., Havens, K. E., Anneville, O., Carvalho, L., Coveney, M. F., Deneke, R., Dokulil, M. T., Foy, B., Gerdeaux, D., Hampton, S. E., Hilt, S., Kangur, K., Köhler, J., Lammens, E., Lauridsen, T. L., Manca, M., Miracle, M. R., Moss, B., Noges, P., Persson, G., Phillips, G., Portielje, R., Schelske, C. L., Straile, D., Tatrai, I., Willen, E., and Winder, M.: Lake responses to reduced nutrient loading – an analysis of contemporary long-term data from 35 case studies, Freshwater Biol., 50, 1747–1771, https://doi.org/10.1111/j.1365-2427.2005.01415.x, 2005.
Kirillin, G.: Modeling the impact of global warming on water temperature and seasonal mixing regimes in small temperate lakes, Boreal Environ. Res., 15, 279–293, 2010.
Kirillin, G. and Shatwell, T.: Generalized scaling of seasonal thermal stratification in lakes, Earth-Sci. Rev., 161, 179–190, https://doi.org/10.1016/j.earscirev.2016.08.008, 2016.
Kirillin, G., Hochschild, J., Mironov, D., Terzhevik, A., Golosov, S., and Nutzmann, G.: FLake-Global: Online lake model with worldwide coverage, Environ. Model. Software, 26, 683–684, https://doi.org/10.1016/j.envsoft.2010.12.004, 2011.
Kirillin, G., Lepparanta, M., Terzhevik, A., Granin, N., Bernhardt, J., Engelhardt, C., Efremova, T., Golosov, S., Palshin, N., Sherstyankin, P., Zdorovennova, G., and Zdorovennov, R.: Physics of seasonally ice-covered lakes: a review, Aquat. Sci., 74, 659–682, https://doi.org/10.1007/s00027-012-0279-y, 2012.
Kirillin, G., Shatwell, T., and Kasprzak, P.: Consequences of thermal pollution from a nuclear plant on lake temperature and mixing regime, J. Hydrol., 496, 47–56, https://doi.org/10.1016/j.jhydrol.2013.05.023, 2013.
Kirillin, G., Wen, L., and Shatwell, T.: Seasonal thermal regime and climatic trends in lakes of the Tibetan highlands, Hydrol. Earth Syst. Sci., 21, 1895–1909, https://doi.org/10.5194/hess-21-1895-2017, 2017.
Kotlarski, S., Keuler, K., Christensen, O. B., Colette, A., Déqué, M., Gobiet, A., Goergen, K., Jacob, D., Lüthi, D., van Meijgaard, E., Nikulin, G., Schär, C., Teichmann, C., Vautard, R., Warrach-Sagi, K., and Wulfmeyer, V.: Regional climate modeling on European scales: a joint standard evaluation of the EURO-CORDEX RCM ensemble, Geosci. Model Dev., 7, 1297–1333, https://doi.org/10.5194/gmd-7-1297-2014, 2014.
Kraemer, B. M., Anneville, O., Chandra, S., Dix, M., Kuusisto, E., Livingstone, D. M., Rimmer, A., Schladow, S. G., Silow, E., Sitoki, L. M., Tamatamah, R., Vadeboncoeur, Y., and McIntyre, P. B.: Morphometry and average temperature affect lake stratification responses to climate change, Geophys. Res. Lett., 42, 4981–4988, https://doi.org/10.1002/2015gl064097, 2015.
Ladwig, R., Furusato, E., Kirillin, G., Hinkelmann, R., and Hupfer, M.: Climate Change Demands Adaptive Management of Urban Lakes: Model-Based Assessment of Management Scenarios for Lake Tegel (Berlin, Germany), Water, 10, 186, https://doi.org/10.3390/w10020186, 2018.
Larsen, S., Andersen, T. O. M., and Hessen, D. O.: Climate change predicted to cause severe increase of organic carbon in lakes, Glob. Change Biol., 17, 1186–1192, https://doi.org/10.1111/j.1365-2486.2010.02257.x, 2011.
Leibniz-Institute of Freshwater Ecology and Inland Fisheries (IGB): FRED – Freshwater Research and Environmental Database, available at: https://fred.igb-berlin.de, last access: 13 March 2019.
Livingstone, D. M.: A change of climate provokes a change of paradigm: taking leave of two tacit assumptions about physical lake forcing, Int. Rev. Hydrobiol., 93, 404–414, https://doi.org/10.1002/iroh.200811061, 2008.
Magee, M. R. and Wu, C. H.: Response of water temperatures and stratification to changing climate in three lakes with different morphometry, Hydrol. Earth Syst. Sci., 21, 6253–6274, https://doi.org/10.5194/hess-21-6253-2017, 2017.
Mallard, M. S., Nolte, C. G., Bullock, O. R., Spero, T. L., and Gula, J.: Using a coupled lake model with WRF for dynamical downscaling, J. Geophys. Res.-Atmos., 119, 7193–7208, https://doi.org/10.1002/2014JD021785, 2014.
Martynov, A., Sushama, L., and Laprise, R.: Simulation of temperate freezing lakes by one-dimensional lake models: performance assessment for interactive coupling with regional climate models, Boreal Environ. Res., 15, 143–164, 2010.
Mironov, D.: Parameterization of lakes in numerical weather prediction, Description of a lake model, Deutscher Wetterdienst, Offenbach am Main, Germany, 2008.
Mironov, D., Heise, E., Kourzeneva, E., Ritter, B., Schneider, N., and Terzhevik, A.: Implementation of the lake parameterisation scheme FLake into the numerical weather prediction model COSMO, Boreal Environ. Res., 15, 218–230, 2010.
Mironov, D., Ritter, B., Schulz, J.-P., Buchhold, M., Lange, M., and MacHulskaya, E.: Parameterisation of sea and lake ice in numerical weather prediction models of the German Weather Service, Tellus A, 64, 17330, https://doi.org/10.3402/tellusa.v64i0.17330, 2012.
Missaghi, S., Hondzo, M., and Herb, W.: Prediction of lake water temperature, dissolved oxygen, and fish habitat under changing climate, Clim. Change, 141, 747–757, https://doi.org/10.1007/s10584-017-1916-1, 2017.
O'Reilly, C. M., Sharma, S., Gray, D. K., Hampton, S. E., Read, J. S., Rowley, R. J., Schneider, P., Lenters, J. D., McIntyre, P. B., Kraemer, B. M., Weyhenmeyer, G. A., Straile, D., Dong, B., Adrian, R., Allan, M. G., Anneville, O., Arvola, L., Austin, J., Bailey, J. L., Baron, J. S., Brookes, J. D., de Eyto, E., Dokulil, M. T., Hamilton, D. P., Havens, K., Hetherington, A. L., Higgins, S. N., Hook, S., Izmest'eva, L. R., Joehnk, K. D., Kangur, K., Kasprzak, P., Kumagai, M., Kuusisto, E., Leshkevich, G., Livingstone, D. M., MacIntyre, S., May, L., Melack, J. M., Mueller-Navarra, D. C., Naumenko, M., Noges, P., Noges, T., North, R. P., Plisnier, P.-D., Rigosi, A., Rimmer, A., Rogora, M., Rudstam, L. G., Rusak, J. A., Salmaso, N., Samal, N. R., Schindler, D. E., Schladow, S. G., Schmid, M., Schmidt, S. R., Silow, E., Soylu, M. E., Teubner, K., Verburg, P., Voutilainen, A., Watkinson, A., Williamson, C. E., and Zhang, G.: Rapid and highly variable warming of lake surface waters around the globe, Geophys. Res. Lett., 42, 10773–10781, https://doi.org/10.1002/2015GL066235, 2015.
Persson, I. and Jones, I. D.: The effect of water colour on lake hydrodynamics: a modelling study, Freshwater Biol., 53, 2345–2355, https://doi.org/10.1111/j.1365-2427.2008.02049.x, 2008.
Poole, H. H. and Atkins, W. R. G.: Photo-electric measurements of submarine illumination throughout the year, J. Mar. Biol. Assoc. UK, 16, 297–324, https://doi.org/10.1017/S0025315400029829, 1929.
Prats, J., Salençon, M.-J., Gant, M., and Danis, P.-A.: Simulation of the hydrodynamic behaviour of a Mediterranean reservoir under different climate change and management scenarios, J. Limnol., 77, 62–81, https://doi.org/10.4081/jlimnol.2017.1567, 2018.
R Core Team: R: A language and environment for statistical computing, R Foundation for Statistical Computing, Vienna, Austria, 2016.
Read, J. S., Winslow, L. A., Hansen, G. J. A., Van den Hoek, J., Hanson, P. C., Bruce, L. C., and Markfort, C. D.: Simulating 2368 temperate lakes reveals weak coherence in stratification phenology, Ecol. Model., 291, 142–150, https://doi.org/10.1016/j.ecolmodel.2014.07.029, 2014.
Richardson, D., Melles, S., Pilla, R., Hetherington, A., Knoll, L., Williamson, C., Kraemer, B., Jackson, J., Long, E., Moore, K., Rudstam, L., Rusak, J., Saros, J., Sharma, S., Strock, K., Weathers, K., and Wigdahl-Perry, C.: Transparency, Geomorphology and Mixing Regime Explain Variability in Trends in Lake Temperature and Stratification across Northeastern North America (1975–2014), Water-Sui, 9, 442, https://doi.org/10.3390/w9060442, 2017.
Rinke, K., Yeates, P., and Rothhaupt, K. O.: A simulation study of the feedback of phytoplankton on thermal structure via light extinction, Freshwater Biol., 55, 1674–1693, https://doi.org/10.1111/j.1365-2427.2010.02401.x, 2010.
Rooney, G. G. and Jones, I. D.: Coupling the 1-D lake model FLake to the community land-surface model JULES, Boreal Environ. Res., 15, 501–512, 2010.
Rose, K. C., Winslow, L. A., Read, J. S., and Hansen, G. J. A.: Climate-induced warming of lakes can be either amplified or suppressed by trends in water clarity, Limnol. Oceanogr., 1, 44–53, https://doi.org/10.1002/lol2.10027, 2016.
Salgado, R. and Le Moigne, P.: Coupling of the FLake model to the Surfex externalized surface model, Boreal Environ. Res., 15, 231–244, 2010.
Saros, J. E., Northington, R. M., Osburn, C. L., Burpee, B. T., and Anderson, N. J.: Thermal stratification in small arctic lakes of southwest Greenland affected by water transparency and epilimnetic temperatures, Limnol. Oceanogr., 61, 1530–1542, https://doi.org/10.1002/lno.10314, 2016.
Schmid, M., Hunziker, S., and Wuest, A.: Lake surface temperatures in a changing climate: a global sensitivity analysis, Clim. Change, 124, 301–315, https://doi.org/10.1007/s10584-014-1087-2, 2014.
Sen Gupta, A., Santoso, A., Taschetto, A. S., Ummenhofer, C. C., Trevena, J., and England, M. H.: Projected Changes to the Southern Hemisphere Ocean and Sea Ice in the IPCC AR4 Climate Models, J. Climate, 22, 3047–3078, https://doi.org/10.1175/2008jcli2827.1, 2009.
Shatwell, T., Adrian, R., and Kirillin, G.: Planktonic events may cause polymictic-dimictic regime shifts in temperate lakes, Sci. Rep. UK, 6, 24361, https://doi.org/10.1038/srep24361, 2016.
Shimoda, Y., Azim, M. E., Perhar, G., Ramin, M., Kenney, M. A., Sadraddini, S., Gudimov, A., and Arhonditsis, G. B.: Our current understanding of lake ecosystem response to climate change: What have we really learned from the north temperate deep lakes?, J. Great Lakes Res., 37, 173–193, https://doi.org/10.1016/j.jglr.2010.10.004, 2011.
Snucins, E. and Gunn, J.: Interannual variation in the thermal structure of clear and colored lakes, Limnol. Oceanogr., 45, 1639–1646, https://doi.org/10.4319/lo.2000.45.7.1639, 2000.
Somavilla, R., González-Pola, C., and Fernández-Diaz, J.: The warmer the ocean surface, the shallower the mixed layer. How much of this is true?, J. Geophys. Res.-Oceans, 122, 7698–7716, https://doi.org/10.1002/2017JC013125, 2017.
Sommer, U., Gliwicz, Z. M., Lampert, W., and Duncan, A.: The PEG model of seasonal succession of planktonic events in fresh waters, Arch. Hydrobiol., 106, 433–471, 1986.
Sommer, U., Adrian, R., De Senerpont Domis, L., Elser, J. J., Gaedke, U., Ibelings, B., Jeppesen, E., Lürling, M., Molinero, J. C., Mooij, W. M., van Donk, E., and Winder, M.: Beyond the Plankton Ecology Group (PEG) model: Mechanisms driving plankton succession, Annu. Rev. Ecol. Evol. S., 43, 429–448, https://doi.org/10.1146/annurev-ecolsys-110411-160251, 2012.
Stepanenko, V. M., Martynov, A., Jöhnk, K. D., Subin, Z. M., Perroud, M., Fang, X., Beyrich, F., Mironov, D., and Goyette, S.: A one-dimensional model intercomparison study of thermal regime of a shallow, turbid midlatitude lake, Geosci. Model Dev., 6, 1337–1352, https://doi.org/10.5194/gmd-6-1337-2013, 2013.
Stepanenko, V., Jöhnk, K. D., Machulskaya, E., Perroud, M., Subin, Z., Nordbo, A., Mammarella, I., and Mironov, D.: Simulation of surface energy fluxes and stratification of a small boreal lake by a set of one-dimensional models, Tellus A, 66, 21389, https://doi.org/10.3402/tellusa.v66.21389, 2014.
Thiery, W., Martynov, A., Darchambeau, F., Descy, J.-P., Plisnier, P.-D., Sushama, L., and van Lipzig, N. P. M.: Understanding the performance of the FLake model over two African Great Lakes, Geosci. Model Dev., 7, 317–337, https://doi.org/10.5194/gmd-7-317-2014, 2014a.
Thiery, W., Stepanenko, V. M., Fang, X., Jöhnk, K. D., Li, Z. S., Martynov, A., Perroud, M., Subin, Z. M., Darchambeau, F., Mironov, D., and Van Lipzig, N. P. M.: LakeMIP Kivu: evaluating the representation of a large, deep tropical lake by a set of one-dimensional lake models, Tellus Ser. A-Dyn. Meteorol. Oceanol., 66, https://doi.org/10.3402/tellusa.v66.21390, 2014b.
Thiery, W., Davin, E. L., Panitz, H. J., Demuzere, M., Lhermitte, S., and van Lipzig, N.: The Impact of the African Great Lakes on the Regional Climate, J. Climate, 28, 4061–4085, https://doi.org/10.1175/Jcli-D-14-00565.1, 2015.
Thiery, W., Davin, E. L., Seneviratne, S. I., Bedka, K., Lhermitte, S., and van Lipzig, N. P. M.: Hazardous thunderstorm intensification over Lake Victoria, Nat. Commun., 7, 12786, https://doi.org/10.1038/ncomms12786, 2016.
Torbick, N., Ziniti, B., Wu, S., and Linder, E.: Spatiotemporal Lake Skin Summer Temperature Trends in the Northeast United States, Earth Interact., 20, 1–21, https://doi.org/10.1175/ei-d-16-0015.1, 2016.
Vavrus, S. J., Wynne, R. H., and Foley, J. A.: Measuring the sensitivity of southern Wisconsin lake ice to climate variations and lake depth using a numerical model, Limnol. Oceanogr., 41, 822–831, https://doi.org/10.4319/lo.1996.41.5.0822, 1996.
Vilas, M. P., Marti, C. L., Adams, M. P., Oldham, C. E., and Hipsey, M. R.: Invasive Macrophytes Control the Spatial and Temporal Patterns of Temperature and Dissolved Oxygen in a Shallow Lake: A Proposed Feedback Mechanism of Macrophyte Loss, Front. Plant Sci., 8, 2097, https://doi.org/10.3389/fpls.2017.02097, 2017.
Wagner, C. and Adrian, R.: Cyanobacteria dominance: Quantifying the effects of climate change, Limnol. Oceanogr., 54, 2460–2468, https://doi.org/10.4319/lo.2009.54.6_part_2.2460, 2009.
Winslow, L. A., Read, J. S., Hansen, G. J. A., Rose, K. C., and Robertson, D. M.: Seasonality of change: Summer warming rates do not fully represent effects of climate change on lake temperatures, Limnol. Oceanogr., 62, 2168–2178, https://doi.org/10.1002/lno.10557, 2017.
Woolway, R. I., Meinson, P., Nõges, P., Jones, I. D., and Laas, A.: Atmospheric stilling leads to prolonged thermal stratification in a large shallow polymictic lake, Clim. Change, 141, 759–773, https://doi.org/10.1007/s10584-017-1909-0, 2017.
Yan, N. D.: Effects of changes in pH on transparency and thermal regimes of Lohi Lake, near Sudbury, Ontario, Can. J. Fish. Aquat. Sci., 40, 621–626, https://doi.org/10.1139/f83-081, 1983.
Zilitinkevich, S. and Mironov, D. V.: A multi-limit formulation for the equilibrium depth of a stably stratified boundary layer, Bound.-Lay. Meteorol., 81, 325–351, https://doi.org/10.1007/Bf02430334, 1996.