the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Stochastic reconstruction of spatio-temporal rainfall patterns by inverse hydrologic modelling
Jens Grundmann
Sebastian Hörning
András Bárdossy
Knowledge of spatio-temporal rainfall patterns is required as input for distributed hydrologic models used for tasks such as flood runoff estimation and modelling. Normally, these patterns are generated from point observations on the ground using spatial interpolation methods. However, such methods fail in reproducing the true spatio-temporal rainfall pattern, especially in data-scarce regions with poorly gauged catchments, or for highly dynamic, small-scale rainstorms which are not well recorded by existing monitoring networks. Consequently, uncertainties arise in distributed rainfall–runoff modelling if poorly identified spatio-temporal rainfall patterns are used, since the amount of rainfall received by a catchment as well as the dynamics of the runoff generation of flood waves is underestimated. To address this problem we propose an inverse hydrologic modelling approach for stochastic reconstruction of spatio-temporal rainfall patterns. The methodology combines the stochastic random field simulator Random Mixing and a distributed rainfall–runoff model in a Monte Carlo framework. The simulated spatio-temporal rainfall patterns are conditioned on point rainfall data from ground-based monitoring networks and the observed hydrograph at the catchment outlet and aim to explain measured data at best. Since we infer a three-dimensional input variable from an integral catchment response, several candidates for spatio-temporal rainfall patterns are feasible and allow for an analysis of their uncertainty. The methodology is tested on a synthetic rainfall–runoff event on sub-daily time steps and spatial resolution of 1 km2 for a catchment partly covered by rainfall. A set of plausible spatio-temporal rainfall patterns can be obtained by applying this inverse approach. Furthermore, results of a real-world study for a flash flood event in a mountainous arid region are presented. They underline that knowledge about the spatio-temporal rainfall pattern is crucial for flash flood modelling even in small catchments and arid and semiarid environments.
- Article
(4063 KB) -
Supplement
(134 KB) - BibTeX
- EndNote
The importance of spatio-temporal rainfall patterns for rainfall–runoff (RR) estimation and modelling is well known in hydrology and has been addressed by several simulation studies, especially since distributed hydrologic models have become available. Many of those studies demonstrated the effect of resulting runoff responses for different spatial rainfall patterns (Beven and Hornberger, 1982; Morin et al., 2006; Nicotina et al., 2008; Obled et al., 1994) or addressed the errors in runoff prediction and the difficulties in parameterisation and calibration of hydrologic models if the spatially distribution of rainfall is not well known (Andreassian et al., 2001; Chaubey et al., 1999; Lopes, 1996; Troutman, 1983). As a consequence, studies were performed to investigate configurations of rainfall monitoring networks (Faures et al., 1995) and rainfall errors and uncertainties for hydrologic modelling (McMillan et al., 2011; Renard et al., 2011).
In general, rainfall monitoring networks based on point observations on the ground (station data) require interpolation methods to obtain spatio-temporal rainfall fields usable for distributed hydrologic modelling. Traditional interpolation methods fail in reproducing the true spatio-temporal rainfall pattern, especially for (i) data-scarce regions with poorly gauged catchments and low network density; (ii) highly dynamic, small-scale rainstorms which are not well recorded by existing monitoring networks; and (iii) catchments which are partly covered by rainfall. Consequently, uncertainties are associated with poorly identified spatio-temporal rainfall patterns in distributed rainfall–runoff-modelling since the amount of rainfall received by a catchment as well as the dynamics of runoff generation processes are typically underestimated by current methods.
The effects of poorly estimated spatio-temporal rainfall fields are visible in particular for semiarid and arid regions, where rainstorms show a great variability in space and time and the density of ground-based monitoring networks is sparse compared to other regions (Pilgrim et al., 1988). Based on an analysis of 36 events in a mountainous region of Oman, McIntyre et al. (2007) show a wide range of event-based runoff coefficients, which underlines that achieving reliable runoff predictions by using hydrologic models in those regions is extremely challenging. This is supported by several simulation studies (Al-Qurashi et al., 2008; Bahat et al., 2009), who address the uncertainties in model parameterisation due to uncertain rainfall input. In this context Gunkel and Lange (2012) report that reliable model parameter estimation was only possible by using rainfall radar. However, this information is not available everywhere.
To address the inherent uncertainties described above, stochastic rainfall generators are used intensively to create spatio-temporal rainfall inputs for distributed hydrologic models to transform rainfall into runoff. A large amount of literature exists describing different approaches for space–time simulation of rainfall fields, including multi-site temporal simulation frameworks (Wilks, 1998), approaches based on the theory of random fields (Bell, 1987; Pegram and Clothier, 2001), or approaches based on the theory of point processes and its generalisation, which includes the popular turning-band method (Mantoglou and Wilson, 1982). Enhancements were made in order to portray different rainstorm patterns and distinct properties of rainfall fields, like spatial covariance structure, space–time anomaly, and intermittency (see Leblois and Creutin, 2013; Paschalis et al., 2013; Peleg et al., 2017).
Applications of spatio-temporal rainfall simulations together with hydrologic models are straightforward Monte Carlo types, where a large number of potential rainfall fields are generated driven by stochastic properties of observed rainstorms or longer time series. These fields are used as inputs for distributed hydrologic model simulations to investigate the impact of certain aspects of rainfall like uncertainty in measured rain depth, spatial variability, etc., on simulated catchment responses. Rainfall simulation applications are performed in unconditional mode (reproducing rain field statistics only) or conditional mode, where observations (e.g. from rain gauges) are reproduced too. The latter are commonly used for investigating the effect of spatial variability using fixed total precipitation and variations in spatial patterns (Casper et al., 2009; Krajewski et al., 1991; Paschalis et al., 2014; Shah et al., 1996). However, stochastic rainfall simulations in combination with distributed hydrologic modelling can be computationally demanding and can fail at matching the observed streamflow if rainfall fields are conditioned on rainfall point observations only.
On the other hand, inverse hydrologic modelling approaches have been developed to estimate rainfall time series based on observed streamflow data. Those approaches require either an inversion of the underlying mathematical equations for the non-linear transfer function (Kirchner, 2009; Kretzschmar et al., 2014) or an application of the hydrologic model in a Bayesian inference scheme (Del Giudice et al., 2016; Kavetski et al., 2006). Up to now, both approaches deliver time series of catchment-averaged rainfall only, which gives no idea about the spatial extent and distribution of rainfall. This is particularly important when considering events such as localised rainstorms, which might be underestimated and not accurately portrayed.
The goal here is an event-based reconstruction of spatio-temporal rainfall patterns which best explains measured point rainfall data and catchment runoff response. For that we looked for potential candidates for rainfall fields for sub-daily time steps and spatial resolution of 1 km2 which, to our knowledge has not been done so far. To achieve this task, we combined stochastic rainfall simulations and distributed hydrologic modelling in an inverse modelling approach, where spatio-temporal rainfall patterns are conditioned on rainfall point observations and observed runoff. The methodology of the inverse hydrologic modelling approach consists of the stochastic random field simulator Random Mixing and a distributed rainfall–runoff model in a Monte Carlo framework. Until now, Random Mixing, developed by Bárdossy and Hörning (2016b) for solving inverse groundwater modelling problems, has been used by Haese et al. (2017) for reconstruction and interpolation of precipitation fields using different data sources for rainfall.
After this introduction the methods are described in Sect. 2. It gives an overview of the methodology and further details for the applied rainfall–runoff model, the Random Mixing and its application for rainfall fields. Section 3 aims to test the methodology. A synthetic test site is introduced which is used to demonstrate and discuss (i) the limits of common hydrologic modelling approaches (using rainfall interpolation) and (ii) the shortcomings of rainfall simulations which are not conditioned on the observed runoff. In contrast, the functionality of the inverse hydrologic modelling approach is illustrated and discussed. In Sect. 4, the inverse hydrologic modelling approach is applied for real-world data by an example of an arid mountainous catchment in Oman. The test site is introduced and results are shown and discussed. Finally, summary and conclusions are given in Sect. 5.
2.1 General approach
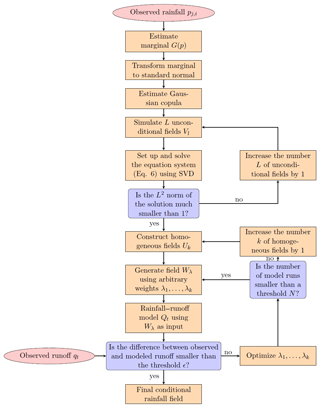
The methodology described here can be characterized as an inverse hydrologic modelling approach. It aims to infer potential candidates for the unknown spatio-temporal rainfall patterns from runoff observations at the catchment outlet, known parameterisation of the rainfall–runoff model, and rain gauge observations. The approach combines a grid-based spatially distributed rainfall–runoff model and a conditional random field simulation technique called Random Mixing (Bárdossy and Hörning, 2016a, b). Random Mixing is used to simulate a conditional rainfall field which honours the observed rainfall values as well as their spatial and temporal variability. Afterwards, an optimisation is performed to additionally condition the rainfall field on the observed runoff. Therefore, the initial field is used as input to the rainfall–runoff model. The deviation between the simulated runoff and the observed runoff is evaluated based on the model efficiency (NSE) defined by Nash and Sutcliffe (1970). To minimise this deviation the rainfall field is mixed with another random field which exhibits certain properties such that the mixture honours the observed rainfall values and their spatio-temporal variability. This procedure is repeated until a satisfying solution, i.e. a conditional rainfall field that achieves a reasonable NSE, is found. To enable a reasonable uncertainty estimation the procedure is repeated until a predefined number of potential candidates has been found. In the following, rainfall is used interchangeably with precipitation.
2.2 Rainfall runoff model
A simple spatially distributed rainfall–runoff model is used as transfer function to portray the non-linear transformation of spatially distributed rainfall into runoff at catchment outlets. The model is dedicated to describe rainfall–runoff processes in arid mountainous regions, which are mostly based on infiltration excess and Hortonian overland flow. The model is working on regular grid cells in event-based modes. It is parsimonious in the number of parameters, considers transmission losses but has no base flow component. Pre-state information at the beginning of an event is neglected since runoff processes mostly start under dry conditions (Pilgrim et al., 1988).
More specifically, only simple approaches known from hydrologic textbooks for the simulation of single rainfall–runoff events (no long-term water balance) are used (Dyck and Peschke, 1983). Effective precipitation Pe(x, t) with location x∈D and time t∈T is calculated by an initial and constant rate loss model applied on each grid cell which is affected by rainfall. The initial loss Ia(x) represents interception and depression storage. If the accumulated precipitation exceeds Ia(x) surface runoff may occur, which is reduced by the constant rate fc(x) throughout an event to consider infiltration. The calculated effective precipitation (or surface runoff) is transferred to the next river channel section considering translation and attenuation processes. Translation is accounted for with a grid-based travel-time function to include the effects of surface slope and roughness. Attenuation is accounted for with a single linear storage unit with recession constant fr(x). Both approaches are applied on grid cells affected by effective precipitation only to fully support spatial distributed calculations corresponding to the spatial extent of the rain field. The properties of several landscape units are addressed by different parameter sets (for ) following the concept of hydrogeological response units (Gerner, 2013) (since hydrologic processes are mostly driven by hydrogeology in these regions). Runoff is routed to the catchment outlet by a simple lag model in combination with a constant rate (ft) loss model to portray transmission losses along the stream channel. The RR model is applied on an hourly time step on regular grids cells of 1 km by 1 km. Parameters are assumed to be known and fixed during the inverse modelling procedure. The RR model is linked to Random Mixing directly and named with the working title NAMarid.
2.3 Random Mixing for inverse hydrologic modelling
Random Mixing is a geostatistical simulation approach. It uses copulas as spatial random functions (Bárdossy, 2006) and represents an extension to the gradual deformation approach (Hu, 2000). In the following a brief description of the Random Mixing algorithm is presented. A detailed explanation can be found in Hörning (2016).
The goal of the inverse hydrologic modelling approach presented herein is to find a conditional precipitation field P(x, t) with location x∈D and time t∈T which reproduces the observed spatial and temporal variability and marginal distribution of P. This field should also honour precipitation observations at locations xj and times ti:
Note that P denotes a spatial field and p denotes a precipitation value within that field. Furthermore, the solution of a rainfall–runoff model using the field P as input variable should approximately honour the observed runoff:
where Qt denotes the rainfall–runoff model and qt represents the observed runoff values at time step t. Note that Qt(P) represents a non-linear function of the field P.
In order to find such a precipitation field P which fulfills the conditions given in Eqs. (1) and (2), Random Mixing can be applied. Figure 1 shows a flowchart of the corresponding procedure.
Using the given observations pj, i, a marginal distribution G(p) has to be fitted to them. Note that in general any type of distribution function (e.g. parametric, non-parametric, and combinations of distributions) can be used. For the applications presented herein the selected marginal distribution consists of two parts: the discrete probability of zero precipitation and an exponential distribution for the wet precipitation observations. It is defined as follows:
with p denoting precipitation values, p0 is the discrete probability of zero precipitation and λ denotes the parameter of the exponential distribution. Thus the parameters that need to be estimated are p0 and λ. Then, using the fitted marginal distribution the observed precipitation values are transformed to standard normal:
where Φ−1 denotes the univariate inverse standard normal distribution. Note that zero precipitation observations are not transformed to the same value, but they are considered as inequality constraints as described in Eq. (4). Thus the spatio-temporal dependence structure of the variable is taken into account as described in Hörning (2016). Further note that the transformation of the marginal distribution described in Eq. (4) can be reversed via the following:
where G−1 denotes the inverse marginal distribution of P and Φ denotes the univariate standard normal distribution. Also, note that W denotes the transformed spatial field while w denotes a transformed observed value within that field. Note that in this approach we assume that the precipitation distribution is the same for each location x and each time-step t. One could use a location and/or time-specific distribution to take spatial or temporal non-stationarity into account; however, this requires a relatively large amount of precipitation observations and/or additional information.
As a next step we assume that the field W is normal, and thus its spatio-temporal dependence is described by the normal copula with correlation matrix Γc. In general copulas are multivariate distribution functions defined on the unit hypercube with uniform univariate marginals. They are used to describe the dependence between random variables independently of their marginal distributions. The normal copula can be derived from a multivariate standard normal distribution (see Bárdossy and Hörning, 2016b, for details). It enables modelling of a Gaussian spatio-temporal dependence structure with arbitrary marginal distribution. Note that its correlation matrix Γc has to be assessed from the available observations. If no zero observations are present the maximum likelihood estimation procedure described in Li (2010) can be applied to estimate the copula parameters. If zero values are present a modified maximum likelihood approach has to be used (Bárdossy, 2011). It uses a combination of three different cases (wet–wet pairs, wet–dry pairs, dry–dry pairs of observations) for the estimation of the copula parameters.
As a next step, unconditional standard normal random fields Vl with are simulated such that they all share the same spatio-temporal dependence structure which is described by Γc of the fitted normal copula. Such fields can for example be simulated using fast Fourier transformation for regular grids (Ravalec et al., 2000; Wood, 1995; Wood and Chan, 1994) or turning-band simulation (Journel, 1974). Here we used the spectral representation method introduced by Shinozuka and Deodatis (1991, 1996). Using the fields Vl, the system of linear equations
is set up. Note that αl denotes the weights of the linear combination, is the transformed precipitation values and Vl(xj, ti) is the values of the random fields at the observation locations. Using singular value decomposition (SVD) (Golub and Kahan, 1965) to solve this equation system leads to a minimum L2 norm solution. In order to obtain a smooth, low-variance field a L2 norm is required. If no such solution is found, an additional field VL+1 is created, added to the system of linear equation and the system is solved again. Note that with increasing degrees of freedom (i.e. more fields) the L2 norm of the solution decreases.
Once a solution with an acceptable L2 norm, i.e. is found the resulting field is defined as follows:
where M denotes the number of additional fields added to the equation system. Note that W* fulfills the conditions defined in Eq. (1); however, it does not fulfill Eq. (2) and it does not represent the correct spatio-temporal dependence structure.
The next step is to simulate fields Uk with which fulfill the homogeneous conditions, i.e. . Further all fields Uk need to share the same spatio-temporal dependence structure, again described by Γc. Such fields can be generated in a similar way to W* (see Hörning, 2016 for details). The advantage of these fields Uk is that they form a vector space (they are closed for multiplication and addition), thus
where λk denotes arbitrary weights and k(λ) denotes a scaling factor results in a field Wλ, which also fulfills the conditions prescribed in Eq. (1). The scaling factor is defined as:
It ensures that Wλ exhibits the correct spatio-temporal dependence structure. Thus, transforming Wλ back to P using Eq. (5) will result in a precipitation field which has the correct spatio-temporal dependence structure and marginal distribution, and honours the precipitation observations.
To also honour the observed runoff defined in Eq. (2) an optimisation problem can be formulated:
which minimizes the difference between the modelled and observed runoff by optimising the weights λk. As these weights are arbitrary they can be changed without violating any of the already fulfilled conditions; thus they can be optimized without any further constraints. If for a given set of fields and weights and after a certain number of iterations N no suitable solution is found, the number K of fields Uk can be increased and the optimisation is repeated. A suitable solution is found when the deviation between simulated and observed runoff is smaller than the criterion of acceptance ε (here, 1−NSE is used). If a suitable solution is found the whole procedure can be restarted using new random fields Vl. Thus multiple solutions can be obtained enabling uncertainty quantification of spatio-temporal rainfall fields.
3.1 Synthetic test site
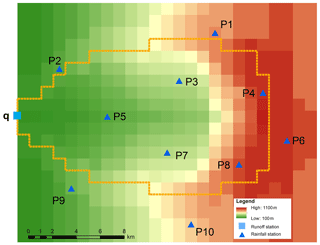
To test the ability of the methodology a synthetic example was designed. The example consists of a synthetic catchment partly covered by rainfall. The synthetic catchment has a size of 211 km2 with elevations ranging between 100 and 1100 m a.s.l. and homogeneous landscape properties (Fig. 2). A synthetic rainfall event of 6 h duration with an hourly time step and a maximum spatial extension of 118 km2 on a regular grid of 1 km by 1 km cell size is used. Rainfall amounts above 20 mm event−1 cover an area of 25 km2 with maximum rainfall of 36 mm event−1 and maximum intensity of 12 mm h−1 (see Figs. 3 and S1 in the Supplement). Based on this known spatio-temporal rainfall input pattern and RR model parameterisation the catchment response at the surface outlet was simulated and designated as the known “observed” runoff qt (see Fig. 6, blue graph).
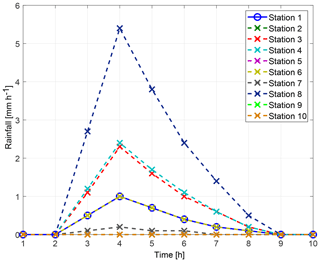
Furthermore, 10 different cells were selected from the spatio-temporal rainfall patterns to represent virtual monitoring stations of rainfall. They were chosen in a way that the centre of the event is not recorded. They are designated as the known “observed” rainfall P(xj, ti) at J monitoring stations for T time steps and provide the data basis for interpolation, conditional simulation, and inverse modelling of spatio-temporal rainfall patterns. Figure 4 shows their course in time. Note that virtual monitoring stations 2, 5, 9, and 10 measure 0 mm h−1 rainfall only. Based on these observations the fitted parameters for the marginal distribution (Eq. 3) are p0=0.36 and λ=0.48. The fitted copula for the dependency structure in space and time is a Gaussian copula with an exponential correlation function with a range of 2.5 km in space and a range of 1.5 h in time. In comparison, using the full synthetic dataset a range of 4.5 km in space and a range of 2.5 h in time are estimated.
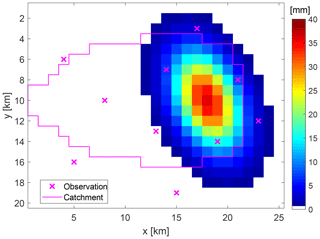
Figure 3Rainfall amounts of the synthetic rainfall event. Virtual monitoring stations are marked by crosses.
3.2 Results and discussion
3.2.1 Common hydrologic modelling approach
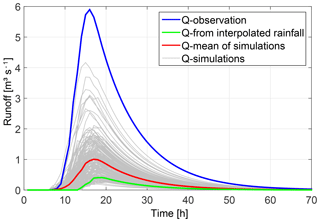
At first, hourly rainfall data from virtual monitoring stations were used to interpolate the spatio-temporal rainfall patterns on a regular grid of 1 km by 1 km cell size by using the inverse distance method, which is quite common in hydrologic modelling. Afterwards, the response of the synthetic catchment was calculated by the RR model. Figure 5 shows the interpolated pattern of the event-based rainfall amounts as the sum over single time steps. The pattern looks quite smooth and has only minor similarities with the true pattern in Fig. 3. The maximum rainfall amount per event is equal to the maximum of the observation at virtual station number 8 with 16.2 mm event−1. Therefore, the extension of a rainfall centre over 20 mm event−1 cannot be estimated. Due to low rainfall intensities, the simulated response of the RR model shows a significant underestimation of the observed runoff, with an NSE value of −0.28 (see Fig. 6, green graph).
3.2.2 Performance of conditional rainfall simulations
The Random Mixing approach was used to simulate 200 different spatio-temporal rainfall patterns conditioned on the virtual rainfall monitoring stations only. Resulting runoff simulations are displayed in Fig. 6. They show a wide range of hydrographs with peak values between 0.19 m2 s−1 and 4.17 m3 s−1 and NSE values between −0.37 and 0.89. Compared to the runoff observation, the timing of peaks is acceptable, but the peak values are underestimated. Only four hydrographs have NSE values higher than 0.7. The corresponding spatial event-based rainfall amounts for the top three runoff simulations regarding the NSE values (a: 0.89, b: 0.78, c: 0.73) is shown in Fig. 7. Their rainfall amounts range between 27.8 and 28.7 mm event−1, with a spatial extent of 9 to 11 km2 of rainfall above 20 mm event−1 and a maximum intensity 10.5 to 15.1 mm h−1. Compared to the observation (Fig. 3), the spatial patterns look similar, at least regarding the spatial location of the event, and cover the maximum intensity. But the rainfall amounts per event as well as their spatial extent is too low. As a consequence, none of the simulated spatio-temporal rainfall fields conditioned at the virtual rainfall monitoring stations only are able to match the observed peak value in resulting runoff.
3.2.3 Inverse hydrologic modelling approach
The inverse modelling approach was used to simulate 107 different spatio-temporal rainfall patterns which are conditioned on the virtual rainfall and runoff monitoring stations, and runoff simulation results better than NSE values of 0.7. Afterwards a refinement was carried out by selecting only those simulations with nearly identical runoff simulation results compared to observations. These simulations are characterized by NSE values larger than 0.995. Figure 8 shows the performance of the 20 selected realisations by grey graphs that show only minor deviations during the flood peak range compared to the observation (blue graph). Associated rainfall patterns are displayed in Fig. 9 for six selected realisations by their spatial rainfall amounts per event. Compared to the true spatial pattern (see Fig. 3) none of them reproduce the true pattern exactly, but all of them locate the centre of the event in the same region as the true pattern. This shows that by additional conditioning of spatio-temporal rainfall patterns on runoff observation and consideration of catchment's drainage characteristic represented by the RR model, the rainfall event can be localised and reconstructed in its spatial extent as well as in its course in time (see also Fig. S1). Most probably, if we would sample a large number of rainfall fields conditioned on rainfall observation only, we would find a realisation which matches the runoff observation too. Due to additional conditioning on runoff we find these realisations faster.
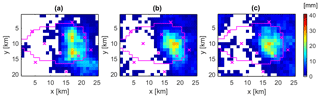
Figure 7Event-based rainfall patterns conditioned at rainfall point observations only for the top three runoff simulations in Fig. 6.
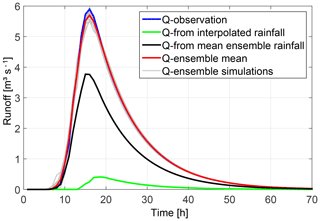
Figure 8 Comparison of hydrographs for the synthetic catchment shown by the observed runoff (blue) and rainfall–runoff simulation results based on interpolated rainfall patterns (green), a simulated ensemble of spatio-temporal rainfall patterns conditioned at rainfall and runoff observations (grey) and their mean value (red), and mean ensemble rainfall patterns (black).
However, the inference of a three-dimensional input variable by using an integral output response results in a set or ensemble of different solutions. Rainfall amounts of the selected 20 realisations above 20 mm event−1 cover an area of 13 to 25 km2 with maximum rainfall of 26.7 to 40.4 mm event−1 and maximum intensities of 10.7 to 17.1 mm h−1. The event-based areal precipitation of the catchment ranges between 98.2 % and 114.7 % of the observation (see Fig. 3). Figure 9 presents spatial rainfall amounts per event for (a) the realisation with the smallest area above 20 mm event−1 and smallest intensity, (b) the realisation with the largest area above 20 mm event−1, (c) the realisation with the highest intensity and rainfall amount per event, (d) the realisation with the best NSE value in resulting runoff, and (e)–(f) realisations with similar event statistics like the true spatio-temporal rainfall pattern. Compared to the observed pattern (see Fig. 3), the different realisations match the spatial location as well as the shape of the observed pattern very well. However, the spatial patterns of the realisations are not such smooth and symmetric like the constructed synthetic observation. Furthermore, the realisations show some scattered low rainfall amounts, which are not of importance for the hydrograph simulation, since they are addressed by the initial and constant rate losses of the RR model.
Deriving an average rainfall pattern by calculation of the mean value per grid cell over all realisations of the ensemble for each time step, a smoother pattern is obtained, which looks more similar to the true one but has smaller rainfall intensities. Using this mean ensemble pattern for calculating the runoff response leads to an underestimation of the observed hydrograph as shown by the black hydrograph in Fig. 8. Therefore, the ensemble mean of the hydrographs (red line in Fig. 8) is a better representative for the sample than the mean ensemble rainfall pattern.
In addition, data of the virtual monitoring stations (the observation) have been always reproduced and are equal for each rainfall simulation. This means that each realisation reproduces the point observation of rainfall without any uncertainty. Only the grid points between the observation differ within the three-dimensional rainfall field and contain the stochasticity given by rainfall simulations conditioned on the observed values. In this context, the ensemble can be used as a partial descriptor of the total uncertainty. It describes the remaining uncertainty of precipitation if all available data are exploited under the assumption of error-free measurements, reliable statistical rainfall models, and known hydrologic model parameters.
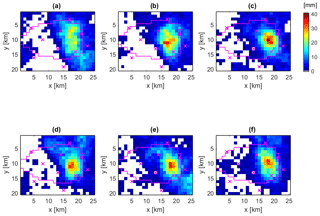
Figure 9Selected realisations of spatial rainfall amounts per event with similar performance in resulting runoff, obtained by the inverse modelling approach for simulating spatio-temporal rainfall pattern: (a) realisation with the smallest area above 20 mm event−1 and smallest intensity, (b) realisation with the largest area above 20 mm event−1 (c) realisation with the highest intensity and rainfall amount per event, (d) realisation with the best NSE value in resulting runoff, and (e)–(f) realisations with similar event statistics to the true spatio-temporal rainfall pattern.
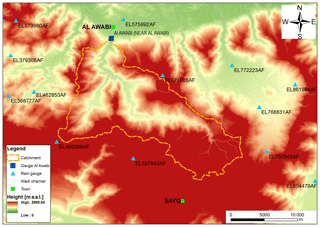
4.1 Arid catchment test site
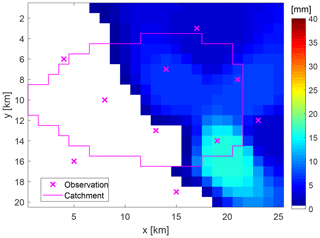
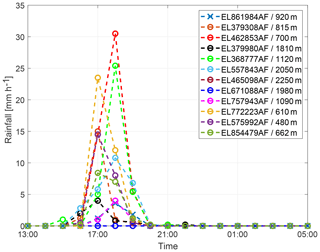
The real-world example is taken from the upper Wadi Bani Kharus in the northern part of the Sultanate of Oman. It is the starting point for the present study and part of our multi-year research on hydrologic processes in this region. The headwater under consideration is the catchment of the streamflow gauging station of Al Awabi, with an area of 257 km2, located in the Hadjar mountain range with heights ranging from 600 m a.s.l. to more than 2500 m a.s.l. The geology of the area is dominated by the Hadjar group, which consists of limestone and dolomite. The steep terrain consists mainly of rocks. Soils are negligible. However, larger units of alluvial depositions in the valleys are important for hydrologic processes, an issue which is addressed through spatial differences in RR model parameters. Vegetation is sparse and mostly cultivated in mountain oases. Annual rainfall can reach more than 300 mm year−1, showing a huge variability between consecutive years. Analysis of measured runoff data over a period of 24 years shows that runoff occurred on average only on 18 days year−1. Figure 10 displays the available monitoring network for sub-daily data. Runoff is measured in 5 to 10 min temporal resolution. Rainfall measurements vary from 1 min to 1 h. Therefore, a temporal resolution of 1 h was chosen for the event under investigation in this study. Figure 11 shows the measurements of the rainfall gauging stations and their altitudes for the rainstorm from 12 February 1999. Most of the rain was recorded on stations with lower altitudes located in the north-west and south-eastern part of the catchment. Rainfall interpolation was performed by the inverse distance method, since there was no dependency of rainfall from altitude identifiable for this single heavy rainfall event. Parameters for the inverse modelling approach are p0=0.17 and λ=0.14 for the marginal distribution (Eq. 3). The fitted copula for the dependency structure in space and time is a Gaussian copula with an exponential correlation function with a range of 10 km in space and a range of 1 h in time.
4.2 Results and discussion
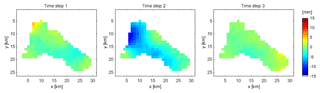
The real-world data example was performed for the runoff event from 12 February 1999 with an effective rainfall duration of 3 h. The simulated runoff for the interpolated rainfall pattern shows an underestimation of the peak discharge as well as a time shift of the peak arrival time compared to the observation (Fig. 12). Applying the inverse approach by conditioning spatio-temporal rainfall patterns on rainfall and runoff observations, an ensemble of 58 different hydrographs is obtained after refinement, with NSE values larger than 0.9. As shown in Fig. 12, all of these hydrographs (grey graphs) represent the observation well and overcome the time shift. To explain this behaviour, differential maps are calculated which show the difference between the simulated and the interpolated rainfall pattern for each time step (Fig. 13; see also Fig. S2 for comparison of event-based spatial rainfall amounts). It is easy to see that the inverse approach allows for a shift of the centre of the rainfall event from time step 1 to time step 2 and towards the catchment outlet. This results in a faster response of the catchment by its runoff compared to the interpolated rainfall pattern. In general, the obtained ensemble of spatio-temporal rainfall patterns is able to explain the observed runoff without discrepancy in rainfall measurements. Similar to the synthetic example, the ensemble mean hydrograph (Fig. 12, red graph) is a better representative for the sample than the hydrograph based on the mean ensemble rainfall spatio-temporal pattern (black graph).
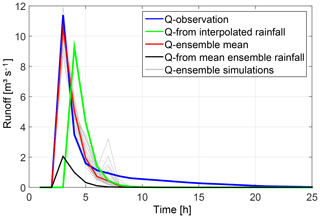
Figure 12 Comparison of hydrographs for the real-world catchment shown by the observed runoff (blue) and rainfall–runoff simulation results based on interpolated rainfall patterns (green), a simulated ensemble of spatio-temporal rainfall patterns conditioned at rainfall and runoff observations (grey) and their mean value (red), and mean ensemble rainfall patterns (black).
An inverse hydrologic modelling approach for simulating spatio-temporal rainfall patterns is presented in this paper. The approach combines the conditional random field simulator Random Mixing and a spatial distributed RR model in a joint Monte Carlo framework. It allows for obtaining reasonable spatio-temporal rainfall patterns conditioned on point rainfall and runoff observations. This has been demonstrated by a synthetic data example as well as a real-world data example for single rainstorms and catchments which are partly covered by rainfall.
The proposed framework was compared to the methods of rainfall interpolation and conditional rainfall simulation. Reconstruction of event-based spatio-temporal rainfall patterns has been feasible by the inverse approach, if runoff observation and catchment's spatial drainage characteristic represented by the RR model with spatial distributed travel times of overland flow are considered. As shown by the synthetic example, the rainfall pattern obtained by interpolation did not match the observed rainfall field and runoff. If rain gauge observations do not portray the rain field adequately, a “good” interpolation result in the least-square sense is not a solution of the problem. This is the case in particular for small scale rainstorms with high spatio-temporal rainfall variability and/or rainfall data scarcity due to insufficient monitoring network density. By rainfall simulations conditioned on rain gauge observation only, reasonable spatio-temporal rainfall fields are obtained, but with a wide spread in resulting runoff hydrographs. A large number of simulated rainfall fields is required to find those realisations which match the observed runoff, since the amount of possible conditioned rainfall fields is much higher than the amount of rainfall fields matching point observation and runoff. By applying optimisation, rainfall fields are conditioned on discharge too, and appropriate candidates for spatio-temporal rainfall patterns can be identified more reliably, faster, and with reduced uncertainty.
The inference of a three-dimensional input variable by using an integral output response results in a set of possible solutions in terms of spatio-temporal rainfall patterns. This ensemble is obtained by repetitive execution of the optimisation step within the Monte Carlo loop. It can be considered as a descriptor of the partial uncertainty resulting from spatio-temporal rainfall pattern estimates (under the assumption of error-free measurements, reliable statistical rainfall models, and known hydrologic model parameters). Realisations of the ensemble vary in rainfall amounts, intensities, and spatial extent of the event, but they reproduce the point rainfall observation exactly and yield to similar runoff hydrographs. This allows for deeper insights in hydrologic model and catchment behaviour and gives valuable information for the reanalysis of rainfall–runoff events, since rainstorm configurations leading to similar flood responses become visible. As shown in the example, operating with an ensemble mean is less successful in matching the runoff observation compared to an application of the whole ensemble due to smoothing effects.
The approach is also applicable under data-scarce situations as demonstrated by a real-world data example. Here, the flexibility of the approach becomes visible, since simulated rainfall patterns also allow for overcoming a shift in the timing of runoff. Therefore, the approach can be considered as a reanalysis tool for rainfall–runoff events, especially in regions where runoff generation and formation are based on surface flow processes (Hortonian runoff) and in catchments with wide ranges in arrival times at catchment outlets such as mountainous regions or distinct drainage structures, e.g. urban and peri-urban regions.
Nevertheless, further research and investigations are required. Examples presented in this paper are based on an hourly time resolution and 1 km2 grid size in space. In particular, for rainstorms in small fast-responding catchments, finer resolutions in space and time are required. Here the limits of the approach in the number of time steps and grid cells need to be explored. Another point is the required amount and quality of observation data as well as statistical model selection to obtain space–time rain fields. Both impact the simulation of rainfall amounts and of patterns by the derived spatial and temporal dependence structure. In these examples Gaussian copulas are used, which might be not a good estimator for the spatial dependency in any case of heavy rainfall.
The proposed framework is a first step that only aims at reconstructing spatio-temporal rainfall patterns under the assumption of fixed hydrologic model structure and parameters. Certainly, hydrologic model uncertainty is of importance. But instead of changing the model to fit the observed discharge, we estimate rainfall fields which fit the model and the discharge by doing reverse hydrology. As such plausible rainfall fields can be identified, the corresponding model and the rainfall field is plausible. Thus, the framework can be applied to proof hypothesis about hydrologic model selection or to explain extraordinary rainfall–runoff events by using a well calibrated, spatial distributed hydrologic model for the catchment of interest. In this context, further research is dedicated to providing a common interface within the Monte Carlo framework to exchange the hydrologic model and allow for broader use within the community. Also, further sources of uncertainties (e.g. model parameters, observations) need to be considered to contribute for the solution of the hydrologic modelling uncertainty puzzle.
All data (except for confidential data) can be requested via email (jens.grundmann@tu-dresden.de).
The supplement related to this article is available online at: https://doi.org/10.5194/hess-23-225-2019-supplement.
JG and AB conceived and designed the study. JG and SH performed the analysis and wrote the paper. AB contributed to the interpretation of the results and commented on the paper.
The authors declare that they have no conflict of interest.
The corresponding author wishes to thank the Ministry of Regional Municipalities
and Water Resources of the Sultanate of Oman for providing the data
for the real case study and supporting the joint Omani–German IWRM-APPM
initiative. Research for this paper was partly supported by the German
Research Foundation (Deutsche Forschungsgemeinschaft, no. 403207337,
BA 1150/24-1) and partly by the Energi Simulation Program. Furthermore,
we acknowledge support by the Open Access Publication Funds of the
SLUB/TU Dresden.
Edited by: Nadav Peleg
Reviewed by: two anonymous referees
Al-Qurashi, A., McIntyre, N., Wheater, H., and Unkrich, C.: Application of the Kineros2 rainfall-runoff model to an arid catchment in Oman, J. Hydrol., 355, 91–105, https://doi.org/10.1016/j.jhydrol.2008.03.022, 2008. a
Andreassian, V., Perrin, C., Michel, C., Usart-Sanchez, I., and Lavabre, J.: Impact of imperfect rainfall knowledge on the efficiency and the parameters of watershed models, J. Hydrol., 250, 206–223, https://doi.org/10.1016/S0022-1694(01)00437-1, 2001. a
Bahat, Y., Grodek, T., Lekach, J., and Morin, E.: Rainfall-runoff modeling in a small hyper-arid catchment, J. Hydrol., 373, 204–217, https://doi.org/10.1016/j.jhydrol.2009.04.026, 2009. a
Bárdossy, A.: Copula-based geostatistical models for groundwater quality parameters, Water Resour. Res., 42, W11416, https://doi.org/10.1029/2005WR004754, 2006. a
Bárdossy, A.: Interpolation of groundwater quality parameters with some values below the detection limit, Hydrol. Earth Syst. Sci., 15, 2763–2775, https://doi.org/10.5194/hess-15-2763-2011, 2011. a
Bárdossy, A. and Hörning, S.: Random Mixing: An Approach to Inverse Modeling for Groundwater Flow and Transport Problems, Transport Porous Med., 114, 241–259, https://doi.org/10.1007/s11242-015-0608-4, 2016a. a
Bárdossy, A. and Hörning, S.: Gaussian and non-Gaussian inverse modeling of groundwater flow using copulas and random mixing, Water Resour. Res., 52, 4504–4526, https://doi.org/10.1002/2014WR016820, 2016b. a, b, c
Bell, T. L.: A space-time stochastic model of rainfall for satellite remote-sensing studies, J. Geophys. Res.-Atmos., 92, 9631–9643, https://doi.org/10.1029/JD092iD08p09631, 1987. a
Beven, K. and Hornberger, G.: Assessing the effect of spatial pattern of precipitation in modeling stream-flow hydrographs, Water Resour. Bull., 18, 823–829, 1982. a
Casper, M. C., Herbst, M., Grundmann, J., Buchholz, O., and Bliefernicht, J.: Influence of rainfall variability on the simulation of extreme runoff in small catchments, Hydrol. Wasserbewirts., 53, 134–139, 2009. a
Chaubey, I., Haan, C., Grunwald, S., and Salisbury, J.: Uncertainty in the model parameters due to spatial variability of rainfall, J. Hydrol., 220, 48–61, https://doi.org/10.1016/S0022-1694(99)00063-3, 1999. a
Del Giudice, D., Albert, C., Rieckermann, J., and Reichert, P.: Describing the catchment-averaged precipitation as a stochastic process improves parameter and input estimation, Water Resour. Res., 52, 3162–3186, https://doi.org/10.1002/2015WR017871, 2016. a
Dyck, S. and Peschke, G.: Grundlagen der Hydrologie, Verlag für Bauwesen Berlin, 1983. a
Faures, J., Goodrich, D., Woolhiser, D., and Sorooshian, S.: Impact of small-scale spatial rainfall variability on runoff modeling, J. Hydrol., 173, 309–326, https://doi.org/10.1016/0022-1694(95)02704-S, 1995. a
Gerner, A.: A novel strategy for estimating groundwater recharge in arid mountain regions and its application to parts of the Jebel Akhdar Mountains (Sultanate of Oman), PhD thesis, Technische Universität Dresden, 2013. a
Golub, G. and Kahan, W.: Calculating the Singular Values and Pseudo-Inverse of a Matrix, J. Soc. Ind. Appl. Math., 2, 205–224, 1965. a
Gunkel, A. and Lange, J.: New Insights Into The Natural Variability of Water Resources in The Lower Jordan River Basin, Water Resour. Manage., 26, 963–980, https://doi.org/10.1007/s11269-011-9903-1, 2012. a
Haese, B., Horning, S., Chwala, C., Bardossy, A., Schalge, B., and Kunstmann, H.: Stochastic Reconstruction and Interpolation of Precipitation Fields Using Combined Information of Commercial Microwave Links and Rain Gauges, Water Resour. Res., 53, 10740–10756, 2017. a
Hörning, S.: Process-oriented modeling of spatial random fields using copulas, Eigenverlag des Instituts für Wasser- und Umweltsystemmodellierung der Universität Stuttgart, 2016. a, b, c
Hu, L.: Gradual deformation and iterative calibration of Gaussian-related stochastic models, Math Geol., 32, 87–108, 2000. a
Journel, A.: Geostatistics for conditional simulation of ore bodies, Econ. Geol., 69, 673–687, 1974. a
Kavetski, D., Kuczera, G., and Franks, S.: Bayesian analysis of input uncertainty in hydrological modeling: 1. Theory, Water Resour. Res., 42, W03407, https://doi.org/10.1029/2005WR004368, 2006. a
Kirchner, J. W.: Catchments as simple dynamical systems: Catchment characterization, rainfall-runoff modeling, and doing hydrology backward, Water Resour. Res., 45, W02429, https://doi.org/10.1029/2008WR006912, 2009. a
Krajewski, W. F., Lakshmi, V., Georgakakos, K. P., and Jain, S. C.: A Monte Carlo Study of rainfall sampling effect on a distributed catchment model, Water Resour. Res., 27, 119–128, https://doi.org/10.1029/90WR01977, 1991. a
Kretzschmar, A., Tych, W., and Chappell, N. A.: Reversing hydrology: Estimation of sub-hourly rainfall time-series from streamflow, Environ. Modell. Softw., 60, 290–301, https://doi.org/10.1016/j.envsoft.2014.06.017, 2014. a
Leblois, E. and Creutin, J.-D.: Space-time simulation of intermittent rainfall with prescribed advection field: Adaptation of the turning band method, Water Resour. Res., 49, 3375–3387, https://doi.org/10.1002/wrcr.20190, 2013. a
Le Ravalec, M., Noetinger, B., and Hu, L. Y.: The FFT Moving Average (FFT-MA) Generator: An Efficient Numerical Method for Generating and Conditioning Gaussian Simulations, Math. Geol., 32, 701–723, 2000. a
Li, J.: Application of Copulas as a New Geostatistical Tool, Eigenverlag des Instituts für Wasser- und Umweltsystemmodellierung der Universität Stuttgart, 2010. a
Lopes, V.: On the effect of uncertainty in spatial distribution of rainfall on catchment modelling, Catena, 28, 107–119, https://doi.org/10.1016/S0341-8162(96)00030-6, 1996. a
Mantoglou, A. and Wilson, J.: The Turning Bands Method for simulation of random fields using line generation by a spectral method, Water Resour. Res., 18, 1379–1394, https://doi.org/10.1029/WR018i005p01379, 1982. a
McIntyre, N., Al-Qurashi, A., and Wheater, H.: Regression analysis of rainfall-runoff data from an arid catchment in Oman, Hydrolog. Sci. J., 52, 1103–1118, International Conference on Future of Drylands, Tunis, Tunisia, June 2006, https://doi.org/10.1623/hysj.52.6.1103, 2007. a
McMillan, H., Jackson, B., Clark, M., Kavetski, D., and Woods, R.: Rainfall uncertainty in hydrological modelling: An evaluation of multiplicative error models, J. Hydrol., 400, 83–94, https://doi.org/10.1016/j.jhydrol.2011.01.026, 2011. a
Morin, E., Goodrich, D., Maddox, R., Gao, X., Gupta, H., and Sorooshian, S.: Spatial patterns in thunderstorm rainfall events and their coupling with watershed hydrological response, Adv. Water Resour., 29, 843–860, https://doi.org/10.1016/j.advwatres.2005.07.014, 2006. a
Nash, J. and Sutcliffe, J.: River flow forecasting through conceptual models part I – A discussion of principles, J. Hydrol., 10, 282–290, https://doi.org/10.1016/0022-1694(70)90255-6, 1970. a
Nicotina, L., Celegon, E. A., Rinaldo, A., and Marani, M.: On the impact of rainfall patterns on the hydrologic response, Water Resour. Res., 44, W12401, https://doi.org/10.1029/2007WR006654, 2008. a
Obled, C., Wendling, J., and Beven, K.: The sensitivity of hydrological models to spatial rainfall patterns – an evaluation using observed data, J. Hydrol., 159, 305–333, https://doi.org/10.1016/0022-1694(94)90263-1, 1994. a
Paschalis, A., Molnar, P., Fatichi, S., and Burlando, P.: A stochastic model for high-resolution space-time precipitation simulation, Water Resour. Res., 49, 8400–8417, https://doi.org/10.1002/2013WR014437, 2013. a
Paschalis, A., Fatichi, S., Molnar, P., Rimkus, S., and Burlando, P.: On the effects of small scale space-time variability of rainfall on basin flood response, J. Hydrol., 514, 313–327, https://doi.org/10.1016/j.jhydrol.2014.04.014, 2014. a
Pegram, G. and Clothier, A.: High resolution space-time modelling of rainfall: the “String of Beads” model, J. Hydrol., 241, 26–41, https://doi.org/10.1016/S0022-1694(00)00373-5, 2001. a
Peleg, N., Fatichi, S., Paschalis, A., Molnar, P., and Burlando, P.: An advanced stochastic weather generator for simulating 2-D high-resolution climate variables, J. Adv. Model. Earth Sy., 9, 1595–1627, https://doi.org/10.1002/2016MS000854, 2017. a
Pilgrim, D., Chapman, T., and Doran, D.: Problems of rainfall-runoff modeling in arid and semiarid regions, Hydrolog. Sci. J., 33, 379–400, https://doi.org/10.1080/02626668809491261, 1988. a, b
Renard, B., Kavetski, D., Leblois, E., Thyer, M., Kuczera, G., and Franks, S. W.: Toward a reliable decomposition of predictive uncertainty in hydrological modeling: Characterizing rainfall errors using conditional simulation, Water Resour. Res., 47, W11516, https://doi.org/10.1029/2011WR010643, 2011. a
Shah, S., O'Connell, P., and Hosking, J.: Modelling the effects of spatial variability in rainfall on catchment response. 2. Experiments with distributed and lumped models, J. Hydrol., 175, 89–111, https://doi.org/10.1016/S0022-1694(96)80007-2, 1996. a
Shinozuka, M. and Deodatis, G.: Simulation of stochastic processes by spectral representation, Appl. Mech. Rev., 44, 191–204, https://doi.org/10.1115/1.3119501, 1991. a
Shinozuka, M. and Deodatis, G.: Simulation of multi-dimensional Gaussian stochastic fields by spectral representation, Appl. Mech. Rev., 49, 29–53, https://doi.org/10.1115/1.3101883, 1996. a
Troutman, B.: Runoff prediction errors and bias in parameter-estimation induced by spatial variability of precipitation, Water Resour. Res., 19, 791–810, https://doi.org/10.1029/WR019i003p00791, 1983. a
Wilks, D.: Multisite generalization of a daily stochastic precipitation generation model, J. Hydrol., 210, 178–191, https://doi.org/10.1016/S0022-1694(98)00186-3, 1998. a
Wood, A.: When is a truncated covariance function on the line a covariance function on the circle?, Stat. Probabil. Lett., 24, 157–164, 1995. a
Wood, A. and Chan, G.: Simulation of stationary Gaussian process in [0,1]d, J. Comput. Graph. Stat., 3, 409–432, 1994. a