the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Using MODIS estimates of fractional snow cover area to improve streamflow forecasts in interior Alaska
Jessica E. Cherry
Ben Balk
Scott Lindsey
Remotely sensed snow cover observations provide an opportunity to improve operational snowmelt and streamflow forecasting in remote regions. This is particularly true in Alaska, where remote basins and a spatially and temporally sparse gaging network plague efforts to understand and forecast the hydrology of subarctic boreal basins and where climate change is leading to rapid shifts in basin function. In this study, the operational framework employed by the United States (US) National Weather Service, including the Alaska Pacific River Forecast Center, is adapted to integrate Moderate Resolution Imaging Spectroradiometer (MODIS) remotely sensed observations of fractional snow cover area (fSCA) to determine if these data improve streamflow forecasts in interior Alaska river basins. Two versions of MODIS fSCA are tested against a base case extent of snow cover derived by aerial depletion curves: the MODIS 10A1 (MOD10A1) and the MODIS Snow Cover Area and Grain size (MODSCAG) product over the period 2000–2010. Observed runoff is compared to simulated runoff to calibrate both iterations of the model. MODIS-forced simulations have improved snow depletion timing compared with snow telemetry sites in the basins, with discernable increases in skill for the streamflow simulations. The MODSCAG fSCA version provides moderate increases in skill but is similar to the MOD10A1 results. The basins with the largest improvement in streamflow simulations have the sparsest streamflow observations. Considering the numerous low-quality gages (discontinuous, short, or unreliable) and ungauged systems throughout the high-latitude regions of the globe, this result is valuable and indicates the utility of the MODIS fSCA data in these regions. Additionally, while improvements in predicted discharge values are subtle, the snow model better represents the physical conditions of the snowpack and therefore provides more robust simulations, which are consistent with the US National Weather Service's move toward a physically based National Water Model. Physically based models may also be more capable of adapting to changing climates than statistical models corrected to past regimes. This work provides direction for both the Alaska Pacific River Forecast Center and other forecast centers across the US to implement remote-sensing observations within their operational framework, to refine the representation of snow, and to improve streamflow forecasting skill in basins with few or poor-quality observations.
- Article
(5068 KB) -
Supplement
(1140 KB) - BibTeX
- EndNote
Arctic climate change is rapidly transforming the north with a myriad of impacts on the hydrologic realm, which has important implications for the largest biome on Earth, the boreal forest. For the northernmost United States (US) state, Alaska, climate change has affected the hydrology, ecology, and society in significant ways (Euskirchen et al., 2009; Hinzman et al., 2005, 2013; Wrona et al., 2016). Alaska has warmed more than 2 times the rate of the rest of the US since the 1950s (Karl et al., 2009). Interior boreal Alaska has warmed the most of all regions in the state, increasing by 4 ∘C in winter and 1.9 ∘C annually from 1949 to 2011 (Stewart et al., 2013). Snowpack extents in Alaska have decreased over time by 18 % (1966–2012) due to an earlier snow melt, while snowpack duration has also decreased (SWIPA, 2012). Changes in temperature and snow are also affecting frozen ground and leading to permafrost thaw – the temperature of the permafrost near Fairbanks, Alaska, has risen by 2–4 ∘C from 1930 to 2003 (Slater and Lawrence, 2013; Koven et al., 2013). Rivers in Alaska have been observed to be changing as a result of an intensified or stronger hydrologic cycle that could lead to an increase in peak flows in the North American high latitudes (Cohen et al., 2012; Huntington, 2006; Rawlins et al., 2010; Serreze et al., 2011). Riverine breakup dates have been noted to be occurring earlier (Cooley and Pavelsky, 2016; Lesack et al., 2014; Muhammed et al., 2016). Extreme events are also changing; annual maximum streamflow trends indicate that Alaskan riverine systems are experiencing streamflow declines, while minimum flow trends are largely increasing (Bennett et al., 2015). All of these shifts are leading to increased streamflow variability (Stuefer et al., 2017), which has strong impacts on the infrastructure and economy of Alaska, and the Arctic as a whole (Instanes et al., 2016), leading to a substantial task in terms of observing, understanding, mitigating, and adapting to these effects. The Far North (Arctic and subarctic) is also rapidly developing its hydroelectric water resources, unlike the contiguous US, and needs accurate decision support for managing this infrastructure (Cherry et al., 2017; Sturm et al., 2017).
A challenge for scientists attempting to accurately represent the impacts of climate change on the Alaskan hydrosphere is the vast territory, complex landscape, and sparse observational network. Alaskan hydrologic systems suffer from large uncertainties in various data inputs, and thus require care when attempting to simulate hydrologic water balance components with skill. For example, precipitation measurements are of very poor quality in winter (Cherry et al., 2005, 2007; Groisman et al., 2014) and river stage and discharge measurements by automated gages do not read accurately when ice is present in the river. Reducing these uncertainties is important, as they will reduce the value of model output (Magnusson et al., 2015; Slater et al., 2013; Clark et al., 2017) and the results cannot provide actionable guidance on water resource management (Stocker et al., 2013). In addition, the variability in landscape (i.e., forest cover, topography, discontinuous permafrost) and climate across Alaska requires robust modeling techniques to account for potential climate-driven shifts. This adaptable approach is increasingly important as the National Oceanic and Atmospheric Administration (NOAA) National Weather Service (NWS) develops the National Water Model (NWM) framework, a multi-scale water prediction model in operations over the contiguous US (NOAA, 2017). Temperature index models, based on the most reliable climate forcing, are often presumed to perform better than other models for regions with highly variable landscapes and a sparse network (Hock, 2003; Stahl et al., 2006). Alternatively, a skillfully calibrated conceptual model may provide a better representation of hydrologic responses because the underlying model is reliant upon parameterizations rather than observations that lack spatial and temporal consistency (Franz et al., 2008; Reed et al., 2004).
To deal with the inoperability of stream gages during breakup and in situ snow observations, one technique is to use remotely sensed snow cover areal extent (fSCA) to supplement point observations such as temperature, precipitation, and streamflow commonly used both as model inputs and for model calibration and validation (Parajka and Blöschl, 2008). There are two main ways that these data have been used to date: to either directly insert a time series of fSCA data into the model (McGuire et al., 2006; Rodell et al., 2004) or use complex assimilation procedures to filter the snow series and merge it with observational data (Andreadis and Lettenmaier, 2006; Sun et al., 2004; Zaitchik and Rodell, 2009). There is a concern that direct insertion methods are ineffective at improving streamflow models and do not perform better than uninformed models because melt can occur before snow cover drops below 100 % (Clark et al., 2006). In addition, the melt season duration is often short, transitioning rapidly from snow covered to snow free, although this is largely basin dependent (Clark et al., 2006). Assimilation approaches have yet to be integrated into operational models, in part because of the limited research showing the impacts of assimilation on the hydrologic forecast. Other studies have found calibrating models based solely on fSCA values may not improve skill in estimating discharge, and the improvements for in-catchment distributed fSCA estimates do not always result in improved discharge simulation (Franz and Karsten, 2013; Duethmann et al., 2014). However, Liu et al. (2013), Thirel et al. (2013), and Déry et al. (2005) found marked improvements in land surface model output for basins in Alaska when MODIS data were applied.
One approach to improve streamflow forecasts under climate change is to utilize newly developed frameworks to ingest remotely sensed data on snow cover area into streamflow models. These newer tools have been adopted by the NWS's River Forecast Centers (RFCs) and offer an opportunity for more advanced streamflow forecasting techniques, including ensemble prediction using variable input and/or forcing data. The Community Hydrologic Prediction System (CHPS), brought online in 2012 by the Alaska Pacific River Forecast Center (APRFC), is a test case for this approach. The modeling framework, developed on the Delft-FEWS software platform (Werner et al., 2011), can run many different types of models, but in its current state implements the conceptual Sacramento Soil Moisture Accounting System (SAC-SMA) rainfall–runoff model (Burnash et al., 1973), with snowpack input from the SNOW-17 snow model (Anderson, 2006).
The objective of this paper is to adapt the CHPS operational forecasting modeling framework to ingest Moderate Resolution Imaging Spectroradiometer (MODIS) remotely sensed fSCA data for improved streamflow modeling of the interior boreal forest region of Alaska within sparsely and poorly observed river basins that are experiencing shifts associated with a changing climate. We replace the standard areal depletion curve used in SNOW-17 with preprocessed MODIS fSCA grids for snow depletion. Two different versions of MODIS are applied: the MOD10A1 fractional fSCA product, which is the standard MODIS global snow cover product (Hall et al., 2002), and the MOD-Snow Covered Area and Grain size (MODSCAG) fractional fSCA product, which is a regional product (Painter et al., 2009). The SNOW-17 manual calibration using all model parameters is evaluated, including a tolerance parameter controlling snow cover updates (snow cover tolerance, SCTOL), to simulate a mixed method between direct insertion and more complex data assimilation. Preprocessing, model frameworks, and use of existing parameterizations are thus offered as a means of incorporating remotely sensed information into operational models that can be utilized out of the box by the NWS RFCs. The paper also examines issues around the use of MODIS fSCA in high-latitude boreal forest basins, the interpolation of missing data, and the improvement of streamflow estimates by calibrating model parameters used in streamflow forecasting systems across the US (Woo et al., 2008; Prowse et al., 2016).
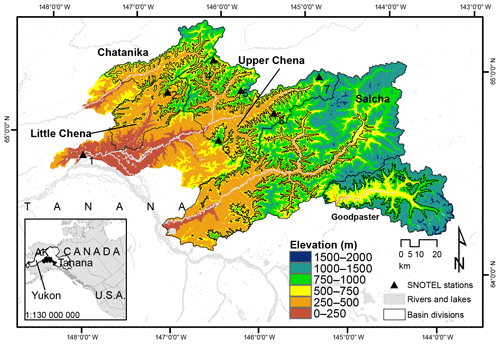
Table 1Sub-basin characteristics, including name, sub-basin ID, sub-basin unit, area, elevation mean (range), average monthly temperature, T, for January (July), average seasonal total precipitation for winter (November–February) (spring, March–June), annual average daily discharge Q, slope basin units (lower, N is north and S is south*), and land cover (based on majority cover values*). T, P, and Q calculated from the 2000–2010 water years.
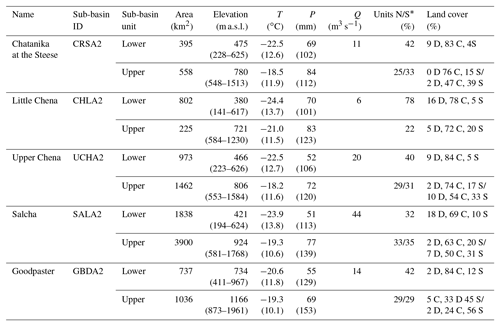
* Only upper units are divided into N and S units. Note: D: deciduous; C: coniferous; S: shrubs.
2.1 Study area
This study was carried out in five adjoining headwater sub-basins of the Tanana River, which is a sub-basin of the Yukon River basin (Fig. 1). The sub-basins include the Chatanika, Upper Chena, Little Chena, Salcha, and Goodpaster basins. The Chatanika River basin (64∘50′37′′ N, 147∘43′23′′ W; Fig. 1) is approximately 950 km2 in size and is oriented predominantly east to west. Only the area upstream of the Caribou–Poker creek confluence is considered in this study. The Chatanika was gaged from 1987 to 2007 but the records are highly discontinuous. The Upper Chena River basin is approximately 2440 km2 and has gage records from 1967 to present. This portion of the basin contains high elevation peaks and rocky outcrops where snow can persist late into the melt season. The Little Chena is 1030 km2 and contains the highest proportion of lowlands relative to the other basins; it has been gaged since 1966 to present. The Salcha River basin is a large 5740 km2 basin with its gage at the Salchaket Bridge and has the longest historical record of all rivers in this region (1948 to present). The Goodpaster basin is located east of the Salcha and is 1770 km2 in size. It has the highest proportion of its basin above 600 m in elevation and has been gaged since 1997 to present. Upper basins are split into sub-basin units with north- and south-facing aspects, with the exception of the Little Chena. There are minor urban and agriculture developments throughout the region, including the town of Fairbanks, which is located downstream of the Little Chena gage on the main stem of the Chena River. These minor developments have little or no bearing on the hydrologic response of the headwater systems of Chena basins we examine here. More information on the basins is provided in Table 1.
2.2 Data
The MODIS satellite product (Terra MOD10A1, version 5) provides daily 500 m resolution fractional snow cover area (fSCA) data. It was downloaded from the National Snow and Ice Data Center (Hall and Riggs, 2007; Hall et al., 2006; Riggs et al., 2006) for 2000–2010, and we used the MODIS Re-projection Tool (MRT, USGS, 2011) to preprocess imagery into an Alaska equal-area conic projected GeoTIFF of fractional fSCA for each sub-basin, which assisted us to correct, in part, the viewing geometry and other issues related to projections of the original MODIS data and the influence these projections have on the MODIS data for Alaska (Dwyer and Schmidt, 2006; Tan et al., 2006). MODSCAG data products were obtained from the NASA Jet Propulsion Laboratory's Snow Data System Portal (https://snow.jpl.nasa.gov/, last access: 7 May 2019) for the area of interest and preprocessed into projected GeoTIFFs to match the spatial properties of the MOD10A1 data. We interpolated cloud- and error-free pixels using a nearest-neighbor approach; only fSCA data from 0 % to 100 % for 1 October to 30 June are ingested into CHPS. Further information on the MODIS data products applied in this study are provided in the Supplement (Supplement Sect. S1.1).
Both MOD10A1 and MODSCAG fractional products require correction to adjust the values of fSCA estimates (Raleigh et al., 2013; Rittger et al., 2013), which do not account for the snow that is blocked from the sensor view. For the MOD10A1 fSCA product, this calculation is based on the viewable gap fraction, or the amount of snow-covered ground between trees that the sensor can see (Liu et al., 2004). This technique, while widely applied, assumes that the viewable gap fraction remains constant through the snowmelt season, which is incorrect as the viewable gap fraction can vary based on a complex number of factors, including forest canopy density, age and class, zenith angle of the sensor, solar zenith angles, topography, and snow loading (Kane et al., 2008; Liu et al., 2008; Molotch and Margulis, 2008; Raleigh et al., 2013; Rittger et al., 2013). To account for some of these issues, rather than applying a forest cover product to correct the product itself, the MOD10A1 data are used (Durand et al., 2008). All 2000–2013 1 to 15 March MOD10A1 pixels across interior Alaska are differenced from 100, and then a composite average of all days (n=207) is calculated. While in southeast Alaska some melt may have occurred during this time, the interior Alaska fSCA should still be at 100 % snow covered across most of the region. To account for bare ground regions such as open, wind-blown rocky faces, values less than 20 % fSCA are removed from the correction. The standard division by viewable gap fraction, where Fveg is the tree cover percentage, SCAfadj (henceforth referred to simply as fSCA) is the fSCA adjusted for canopy cover, and SCAf is the unadjusted SCA data (Eq. 1).
This formulation is applied as a static adjustment to each SCA pixel in all days and years. For MODSCAG, the daily vegetation fractional product provided with the data product is utilized, resulting in a dynamic adjustment for each SCA pixel in all days and years. In both cases, the results are constrained to 100 % fSCA when exceeded. We did not include any cloud corrections or additional interpolation methods (Dozier et al., 2008; Morriss et al., 2016).
Table 2SNOTEL stations, map identification, length of record, and observed average snow water equivalent (SWE) used for validation of modeled SWE results. Average April SWE is calculated for the entire period of record.

Mean areal values of temperature and precipitation at 6 h increments are obtained for each sub-basin from the APRFC for the time period 1969 to 2012; only the 1999–2010 data are utilized in this study. River discharge at each gage is based on the US Geological Survey (USGS) gaging record database. The exception to this is the Chatanika River basin, where observed discharge is generated based on once-a-day stage readings from a Cooperative Network observer. These daily stage readings are converted to mean daily discharge using the APRFC's rating curve for the river. Aspect and elevation were calculated using the 30 m US Geological Survey's National Elevation Dataset (NED), updated for the region in 2012 (Gesch et al., 2002). Seven snow telemetry (SNOTEL) sites are utilized to compare simulated snow water equivalent (SWE) with observed data (Table 2, NRCS 2013). SNOTEL SWE is downloaded from the National Resource Conservation Service (NRCS) snow pillow data repository (https://www.wcc.nrcs.usda.gov/legacy/ftp/cdbs/snotel/cards/alaska/, last access: 7 May 2019).
Potential evapotranspiration (PET) estimates are provided by the APRFC based on an assessment of historical potential evapotranspiration from pan evaporation data and Thornthwaite estimates (Anderson, 2006). These data are used to develop a general linear relationship between PET and elevation to estimate average monthly PET values for a generic low-elevation site. The APRFC uses the low-elevation PET values to derive monthly estimates for the mean elevation of each sub-basin as a coefficient, C (Eq. 2).
where elevation represents elevation (m). For example, if the catchment mean elevation is 716 m, the coefficient is 0.75. Finally, a monthly PET adjustment factor is applied to account for vegetation changes during the year. The result is an evapotranspiration demand estimate that is used in the SAC-SMA model, described in the next section.
2.3 Models
The SNOW-17 and the SAC-SMA models are run by the APRFC in an operational framework referred to as CHPS. CHPS is built upon the Delft Flood Early Warning System (FEWS), developed by Deltares (Werner at al., 2013). The CHPS system is briefly described in Sect. S1.2.
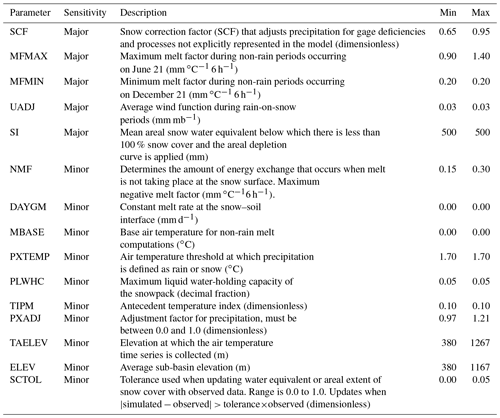
Table 3SNOW-17 model parameters. Sensitivity indicates whether a parameter has a major or minor influence on model output. Minimum (Min) and maximum (Max) parameter values used in the model simulations. When min and max values are the same the parameter did not vary.
2.3.1 SNOW-17
The SNOW-17 snow model is a single-layer snow model that calculates snow accumulation and ablation using empirical formulae to estimate heat and liquid water storage, liquid water throughflow, and snowmelt (Anderson, 1976). The model is designed for river forecasting and has been used operationally by the NWS RFCs since the mid-1970s. The only input requirements for SNOW-17 are temperature and precipitation (winds are accounted for but not input as observations), at the model time step (6 h). There are 12 parameters in the SNOW-17 model, including the areal snow depletion curve; sensitive or “major” parameters control the model outputs while less sensitive or “minor” parameters have little impact on the model output (Table 3; He et al., 2011).
SNOW-17 determines the division between rain and snow using the rain–snow elevation (RSNWELEV) module. RSNWELEV uses a defined lapse rate (6 ∘C 1000 m−1) to represent the saturated adiabatic lapse rate, which is commonly applied to determine the air temperature threshold that results in rain turning to snow (PXTEMP; Table 3; Anderson, 2002; Clark et al., 2011). This temperature threshold is related to an elevation and is passed to SNOW-17; the percent area above and below that elevation is determined from a defined area elevation curve. Multiplying these percentages by the precipitation thus defines the proportion of precipitation falling as snow or rain in the basin. Non-rain snowmelt (mm) is determined from air temperature minus the baseline temperature at which melt occurs (MBASE; set to 0 ∘C), weighted by a seasonably variable melt factor that is calculated using an oscillating sine curve that varies between the minimum (MFMIN) and maximum (MFMAX) melt factors for 21 December and 21 June (mm ∘C−1 6 h−1). These values are adjusted for latitudes above 54∘ N to account for low radiation input, a paucity of days when temperatures rise above freezing, and rapid changes in melt rates during spring and fall (Anderson, 2006). A fixed lapse rate is applied to mean air temperature within the lumped basins for the elevation at which the air temperature time series is collected (TAELEV), in the case when TAELEV differs from basin mean elevation. This fixed lapse rate can be configured in the SNOW-17 model using parameters that define the lapse rate at time of maximum or minimum temperature.
A simplified energy balance method is used to calculate melt from rain on snow using the following assumptions; the Stefan–Boltzmann constant is used to estimate incoming longwave radiation, negligible shortwave radiation, and 90 % relative humidity, and wind speed is accounted for by adjusting for the average value of the wind during rain-on-snow events using the parameter UADJ (mm hPa−1 6 h−1). Heat content within the snowpack is calculated based on a gradient between air temperature and the near-surface snowpack temperature index to determine the heat flow direction when melt is not occurring. Depending on the near-surface snowpack temperature index, more or less weight is assigned to temperatures from previous time intervals to represent deeper or shallower snowpack temperatures.
The snow heat deficit is either negative or positive; the rate of heat loss or gain is based on the amount of energy exchange that occurs when melt is not taking place at the snow surface (negative melt factor; NMF; mm ∘C−1 6 h−1), which is weighted by MFMAX to account for seasonal variations in pack heat translation. Heat can also be translated from the ground to the snow using a parameter that controls the daily melt volume at the interface between snow and soil, and is assumed to occur continuously through the snow season (DAYGM). When the snowpack is at peak water-holding capacity (PLWHC) and is isothermal at 0 ∘C, the snow is ripe and any excess water entering the snow will flow through it as outflow. Water movement through a ripe pack is attenuated or lagged based on the empirical formula derived from lysimeter studies (Anderson, 2006).
2.3.2 fSCA in SNOW-17
SNOW-17 uses an areal depletion curve (ADC) to represent the snow cover area; the ADC is used to calculate the area of the basin over which surface melt, changes in heat storage, ground melt, and rainfall on bare ground occur (Anderson, 2002; Fig. 7.4.3). The ADC not only represents areal extent of snow cover, but also accounts for slope, aspect, and differences in vegetative cover (i.e., open versus closed sites; Anderson, 2002; Fig. 7.4.3). In the baseline model simulation, the areal extent of snow cover was calculated from a lookup table (Anderson, 2002; Fig. 8) that defines the ADC and relates it to the ratio of SWE to either (a) the maximum value of SWE that occurred during snow accumulation or (b) a parameter (SI) that represents the areal SWE at which 100 % snow cover exists (referred to as the areal index). The ADC in the baseline model simulation is applied as follows: when snow accumulates, the snow cover is set to 100 %, and it stays at this value until it falls below SI or the maximum SWE value, whichever is smaller. If new snow totaling greater than 0.2 mm h−1 falls onto bare ground, 100 % snow cover is assumed until 25 % of the new snow has melted. For Alaska, several different ADC configurations are used depending on whether slopes are south versus north facing, or in upper- versus lower-elevation basins. The basins in this study used the same ADC for upper south, upper north, and lower sub-basin units since they have similar orientations within a similar geographic region. Only the Little Chena uses a different ADC for its upper basin, as no north–south aspect split is used in this basin. For all other model simulations, the ADC was replaced by areal extent of snow cover derived from the two MODIS fSCA data sets (Fig. 2). Other parameter settings used to alter the impact of the MODIS fSCA data in SNOW-17 are described in Sect. S1.3.
2.3.3 SAC-SMA
The SAC-SMA model is a conceptual rainfall–runoff model that simulates streamflow from observed input precipitation and PET (Burnash et al., 1973). SAC-SMA has been widely applied by the NWS to estimate streamflow runoff in basins across the US. The model moves water into either an upper or lower storage zone that conceptually represent soil interception or deep groundwater storage. Interception water in the upper zone flows to the lower zones via downward percolation, or it can run off directly or via interflow when the upper zone layers become saturated and the precipitation rate exceeds downward percolation. Lower zone water can be held in tension storage and contribute to baseflow runoff slowly over time, or can run off more quickly over shorter durations. Drainage from the upper and lower zones follows gravity drainage and is governed in part by both water delivery from the upper zone and soil moisture in the lower zone. Tension water is driven by potential evapotranspiration and diffusion, with a fraction of the lower zone unavailable for potential evapotranspiration as it is considered below the rooting zone.
A unit hydrograph model is used to adjust runoff timing for each lumped basin in the SAC-SMA model. Each sub-basin has its own unit hydrograph to translate the runoff through the channel system to the gage location. Simple routines sum the unit hydrograph outputs to calculate simulated streamflow at the basin outlet. While downstream basins incorporate routing models to move water from upstream to downstream basins, this study focuses on headwater basins so no routing models are needed.
2.4 Calibration
Several calibration procedures were undertaken for this project: the baseline calibration and the two MODIS data set calibrations. The baseline calibration effort updated the SAC-SMA–SNOW-17 model parameters to the 2000–2010 years used in this study, as they had previously been adjusted by APRFC to 1970–2003 historical data. The two MODIS manual calibrations used the updated baseline to adjust parameters and generate statistics. Calibration entailed using both visualizations of streamflow hydrographs from 2006 to 2010 and monthly statistics from the entire period of record for ultimate parameter selection.
To calibrate the MODIS model output, a simple approach is taken to minimize the terms required for calibration. This ensures that it was (a) easy to replicate the model adjustments to the MODIS fSCA data and (b) solely focused on the snow parameterization, as adjustments to the SAC-SMA parameters resulted in only minor improvements to model calibration statistics during the spring ice breakup period. Also, priority was placed on adjusting the empirical parameters towards a physically based realization using basin and sub-basin unit properties, including the topographic aspects and the observed melt trajectory impacted by the MODIS fSCA data. To complete this simple, physically realistic calibration approach only the parameters MFMAX and TAELEV were adjusted. Further details of the calibration efforts are described in Sect. S1.4.
2.5 Validation
For validation purposes, statistics from 2000 to 2005 are provided for all basins except the Chatanika. The Chatanika basin was calibrated from 2000 to 2004 and validated from 2005 to 2010 to make use of the better data quality and availability during the first 5 years of the study. Statistics used to evaluate model success are based on five main objective functions and monthly average daily model output. The first two of these criteria are standard in NWS RFC calibration approaches and are provided in the CHPS statistical output. These statistics were used for evaluation during the calibration: total volume bias as a percent (PBIAS, %) and the correlation coefficient (R, unitless). Three additional objectives were added for further validation of the results, Nash–Sutcliffe efficiency (NSE, unitless), the mean absolute error (MAE, m3 s−1), and the root-mean-squared error (RMSE, m3 s−1). Statistics were run only for April, May, and June to focus on the changes to the snowmelt season; March is not included because generally river ice melts and breaks up in interior Alaska in March; thus any differences in statistics would be indicative of changing winter conditions rather than changes in spring snowmelt timing or volume.
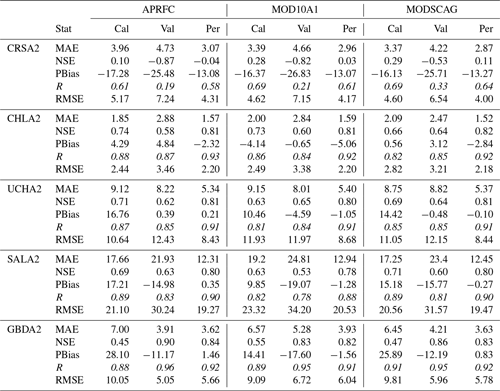
Table 4April–May–June monthly calibration (Cal), validation (Val), and the period of record (Per., 1999–2010) statistics (MAE: mean absolute error (m3 s−1); NSE: Nash–Sutcliffe efficiency (unitless); PBIAS: flow bias (%); R: correlation coefficient (unitless); and RMSE: root-mean-squared error (m3 s−1)) for APRFC, MOD10A1, and MODSCAG modeled discharge for all basins. Statistically significant (p value < 0.05) R values are shown in italics. Note that the calibration and validation years are not the same for all catchments.
3.1 Baseline model results
The APRFC SAC-SMA–SNOW-17 baseline model estimates of streamflow in the Alaskan interior river basins for the 11-year period of record indicate that these basins are captured with skill (Table 4). The Chatanika basin is problematic given the limited quality and quantity of the observed streamflow data, as noted in the statistics below for each objective function. For all of the five basins analyzed, the daily average bias for the period of record is ±3 % or less. Daily correlation coefficients (R, unitless) are equal to or greater than 0.84 and higher for the four basins with quality observed data, while the Chatanika basin is 0.70. NSE (unitless) daily values are also above 0.60 for all basins except the Chatanika, which is 0.18 due to the noise in the observed data values. Daily mean absolute error statistics are below 10 m3 s−1 for all basins except the Salcha, which is 15.89 m3 s−1 owing to its long discharge record. RMSE ranges from 3.5 m3 s−1 (Chatanika) to 33 m3 s−1 (Salcha). Across all basins, fSCA is variable by elevation zones and years (Fig. 3). Upper-elevation areas tend to have 100 % fSCA, while middle to lower areas often begin the year with 75 % fSCA or less. The very lowest-elevation zone appears to have slightly higher fSCA values than two adjacent higher-elevation zones (Fig. 3). Some years have a markedly late melt out, with high variability across all elevation bins. Lower-elevation zones tend to melt out in early April, while the upper regions of the basins hold snowpack weeks or months into the subarctic spring (Fig. 3).
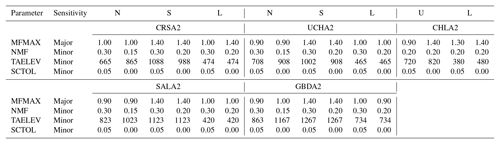
Table 5SNOW-17 parameters for the MOD10A1 calibration. North (N), south (S), upper (U), and lower (L) sub-basins are described. For each sub-basin, the first column indicates the parameter value in the APRFC calibration and the second column indicates the parameter value used in the MODIS calibration. Bold values indicate where the MODIS value differs from the APRFC value.
3.2 SAC-SMA model MODIS calibrations
Calibrated SNOW-17 parameters for the APRFC and MOD10A1 simulations resulted in increased MFMAX for the north-facing aspect in two sub-basin units and increased TAELEV for the north slopes (Table 5) compared to the baseline APRFC SAC-SMA–SNOW-17 simulation. In some sub-basin units, TAELEV was set to be equal for the north and south slopes. MFMAX for the Chatanika's lowland sub-basin increased and TAELEV at the north sub-basin was increased, while TAELEV was decreased for the south sub-basin unit. MFMAX in the Upper Chena north was unchanged and TAELEV was equalized for both south and north sub-basin units. The Little Chena sub-basin parameters were altered by setting MFMAX equal to its maximum recommended value for forested regions (1.4; Anderson, 2002; Table 7-4-1) for the upper and lower sub-basins and by increasing TAELEV 100 m greater than the elevation for both sub-basins. TAELEV for Salcha and Goodpaster were differenced by 100 m for the north and south sub-basin units, and the northern sub-basin MFMAX for Goodpaster was increased slightly. Goodpaster's lower basin MFMAX was reduced by a small amount. Although these changes may appear minor, MFMAX is highly sensitive during the melt season and therefore these changes have a substantial effect on the MODIS fSCA forced snowmelt trajectory at these sites (Anderson, 2006).
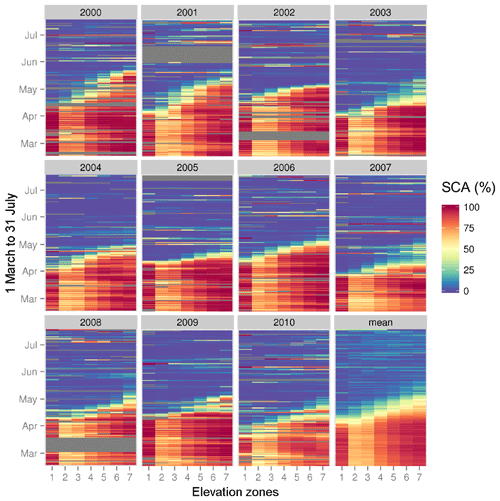
Figure 3Snow cover area (%) based on MOD10A1 SCA average across all watersheds divided into elevation zones. The years 2000 to 2010 are shown, with the mean of all years in the final panel. Elevation zones are 1=100–200 m, 1–6, progressing in 200 m increments from 200 to 1200 m, 7=1200–2000 m. Grey areas indicate dates when there is no SCA information (i.e., cloud cover, missing sensor data).
Table 6SNOW-17 parameters for the MODSCAG calibration. North (N), south (S), and lower (L) sub-basins are described. For each sub-basin, the first column indicates the parameter value in the APRFC calibration and the second column indicates the parameter value used in the MODIS calibration. Bolded values indicate where the MODIS value differs from the APRFC value.
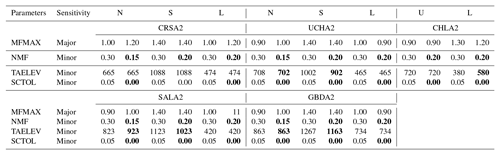
In the MODSCAG simulations, values for MFMAX were increased slightly for the north sub-basin units for all basins. TAELEV values were adjusted slightly in Upper Chena, Salcha, and Little Chena basins (Table 6), but were not altered from the baseline run in Chatanika. In the Goodpaster basin, the TAELEV value for the south sub-basin unit was decreased. NMF was altered slightly for both MODIS simulations to account for different snow densities and thermal conductivities of snow on south and lowland sites versus north aspects. Snow density (gm cm−3) is generally low in interior Alaska river basins; based on analysis of field data from the Caribou Poker Creek basin, snow density on the sites is approximately 0.20 gm cm−3and is slightly higher on the southern sites compared to the north site. The northern-facing slopes were therefore given the NMF value of 0.15 mm ∘C−1 6 h−1, which Anderson (2002) indicates is a “reasonable” value of NMF. The south and lowland sites, which have generally warmer temperatures and more dense snow, were assigned the NMF value of 0.2 mm ∘C−1 6 h−1. For these simulations, SCTOL is set to 0 for all basins to ensure that the MODIS data are utilized 100 % of the time.
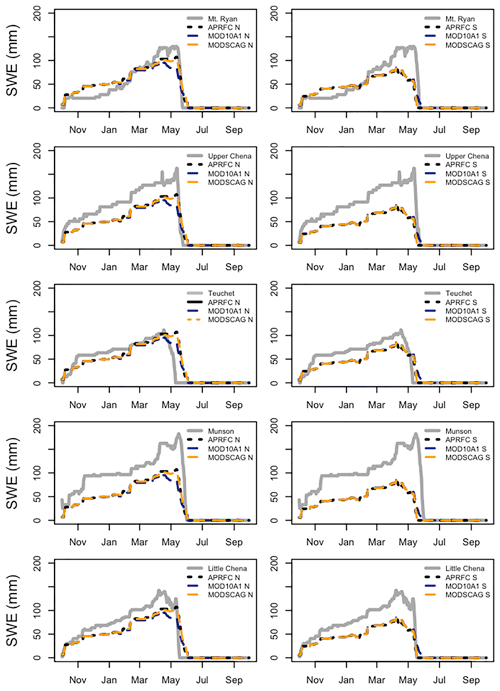
Figure 4Simulated SWE (mm) versus SNOTEL SWE (grey line) for APRFC (solid black line), MOD10A1 (blue dashed line), and MODSCAG (orange dotted line) for October 2000 to September 2001. The Upper Chena River basin north slope is shown in the left panels, and the south slope is shown in the right panels.
3.3 fSCA and SWE
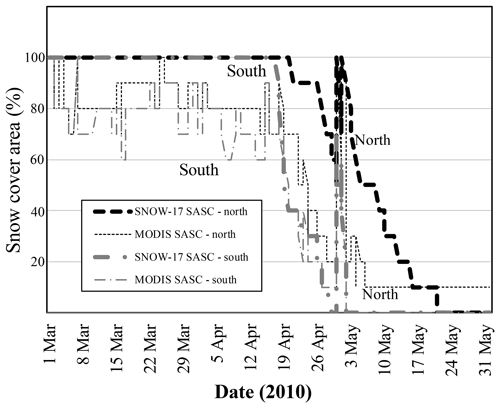
Compared to the APRFC simulations, the MODIS simulations have less snow cover on the north-facing slopes and more on the south-facing slopes (Fig. 4; the average Upper Chena River basin unit results for 2001 plotted against the SNOTEL stations are shown as an example). Differences between the two simulations become discernable in late January as a result of the different calibrations of the SNOW-17 model in the basins (Fig. 4), with larger differences at the north sub-basin units compared to the south sub-basin unit. As soon as the MOD10A1 fSCA begins to alter the weighting factors for outflow from the snow, differences between the SWE generated by APRFC and MODIS simulations are observed. The greatest differences between the model simulations occur during the melt season. All model simulations peak in early April and start a downward melt trajectory, reflecting melt patterns at the upper-elevation SNOTEL sites: Mt. Ryan, Munson, and Upper Chena. The APRFC and MOD10A1 runs melt out later than the MODSCAG fSCA north unit and the MODSCAG estimates are closer to the APRFC simulations in volume, although all simulations terminate on the same approximate day for the northern sub-basins.
The SNOTEL sites are mostly located at upper elevations (Mt. Ryan, 850 m; Munson, 940 m) compared to the SNOW-17's ∼800 m elevation parameter and thus illustrate conditions exhibited at high-elevation northern sites in the basin. Mt. Ryan, in particular, does not build a snowpack early in the season, perhaps owing to its open, mountainous, and presumably windy environment. The SNOW-17 model is run over a lumped area so there is a mix of site conditions that act to smooth and reduce the volume of SWE; hence the comparison between SNOTEL SWE and SNOW-17 modeled SWE is inherently qualitative as opposed to quantitative (Molotch and Bales, 2005). The lower-elevation SNOTEL sites, Teuchet and Little Chena, show earlier melt out than is seen in either the model output or the MODIS data sets. There is stronger coherence in the response of the northern sites as opposed to the southern sites. In the south sub-basin units, the MODIS simulations melt out later, with MODSCAG again having the latest melt, similar in timing to the high-elevation stations.
The areal extent of snow cover varies across the basins in both simulations. The preprocessed gridded MOD10A1 fSCA illustrated for 15 May 2001 is shown in Fig. 5a and the MODSCAG fSCA is shown in Fig. 5b for the basins. The high-elevation snowpack (blue) is present within the upper basin regions but the pack is largely gone in the valleys and lower basin reaches. This translates into the lumped average fSCA estimates shown in Fig. 5c and d, which illustrate how CHPS ingests and converts the gridded MODIS fSCA for the sub-basin units. North and south sub-basin units are differentiated in the upper sub-basin units (see Table 1) but not at other locations because both aspects have begun to melt by this date (as opposed to early in the melt period when the south slopes would have comparatively less fSCA than the north slopes). MODSCAG has less cloud cover interaction in this scene (Fig. 5b) and this results in slightly higher values of fSCA (Fig. 5d).
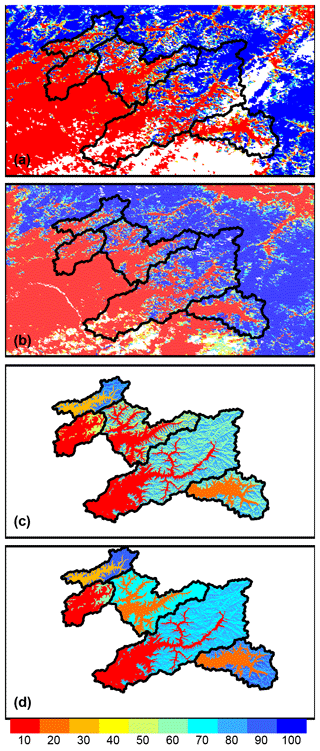
Figure 5Study area snow cover area in the CHPS model framework for (a) MOD10A1 and (b) MODSCAG, where white is either missing or cloud covered, and elevation-averaged (lumped by elevation) snow cover extent based on (c) MOD10A1 and (d) MODSCAG. Values range from 10 % to 100 % snow cover. All panels show results for 15 May 2001.
SWE estimates for MOD10A1 (Fig. 6a), MODSCAG (Fig. 6b), and the difference between the MODIS (both versions) and APRFC runs (Fig. 6c and d) is shown for 15 May 2001. Sub-basin units can be clearly differentiated in these plots, which illustrate the range of SWE values from 0 to 25 mm in the lowland regions to 125 mm in the upper headwaters. The MODSCAG data have an average fSCA value of 0.51 (51 %) and SWE is 45 mm, whereas the MOD10A1 has an average of 0.45 (45 %) fSCA and an average of 54 mm SWE, very small differences overall although sub-basin to sub-basin the variation between the products is notable. The difference plots highlight the fact that MODIS tends to have lower SWE values compared to the APRFC SNOW-17 model simulations on the north-facing slopes and higher values on the south-facing slopes. The APRFC tends to have lower SWE estimates for the lowland regions, although this is more true for MOD10A1 than MODSCAG (Fig. 6c, d).
3.4 Streamflow estimates
Calibration and validation results are provided for April–May–June (Table 4) for the MODIS and APRFC simulations. For MODIS data, many statistics are similar or nearly identical to the APRFC run with slight declines in model performance and some gains (Chatanika; Little Chena), particularly for the analysis focused on the whole period of record (Table 4). NSE statistics are particularly poor for all simulations in the Chatanika basin, where the lack of continuous and high-quality observations hampers calibration efforts. The MOD10A1 data improve streamflow simulations in the Chatanika and Goodpaster systems during the calibration period, while they perform similarly or slightly worse during the validation and period of record in most of the basins except the Chatanika. The MODSCAG run exhibits better performance compared to the APRFC run during the calibration periods in the Chatanika, Salcha, and Goodpaster basins, while the validation period statistics showed improvement for the Chatanika, Little Chena, and Upper Chena basins. Overall, improvements in skill are observed for the MODIS simulations in the Chatanika and Goodpaster basins, the validation period for Upper Chena, and the calibration period for Goodpaster (Table 4).
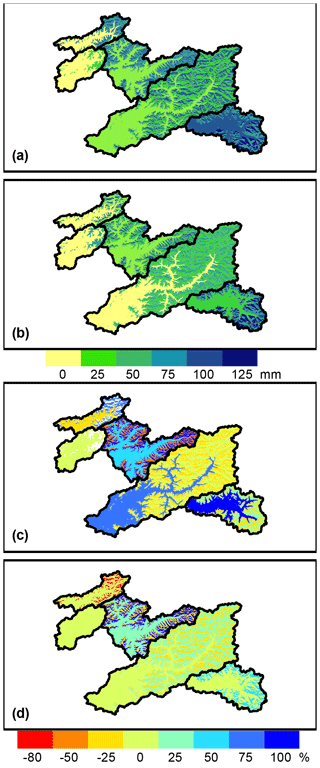
Figure 6Study area basin SWE (mm) estimates in CHPS model framework for (a) MOD10A1 and (b) MODSCAG and the percentage difference between both SWE estimates and the APRFC run (for positive values, MODIS is higher, for negative values, APRFC is higher; c and d). All panels show results for 15 May 2001.
The calibration, validation, and whole period of record results illustrate that for the poorly performing basins, MODSCAG (and MODSCAG with SCTOL =0.25) tends to do slightly better versus APRFC in the calibration/validation time where improvements are also made for MOD10A1, while both MODIS versions perform nearly identically over the 11-year period (Fig. 7). This can also be observed from the analysis presented in Fig. 8 for all five basins. Figure 8 illustrates that the MODSCAG results tend to follow more closely (and are hence more constrained) with the APRFC results, while the MOD10A1 product has more scatter. However, the differences from observations are similar between the two products.
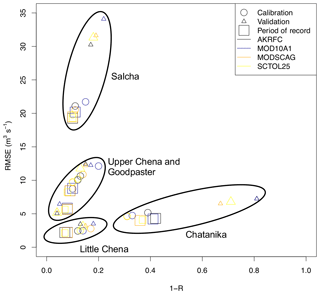
Figure 7Monthly RMSE (m3 s−1) plotted against 1−R for calibration (open circles), validation (open triangles), and period of record (open squares). Values are given for each of the five basins. Black: APRFC; blue: MOD10A1; orange: MODSCAG; and yellow: MODSCAG with SCTOL = 0.25. Results cluster by basin, as indicated by the oval groupings on the plot.
Average (2000–2011) streamflow for each basin in Fig. 9 illustrates the variations between simulated specific discharge (m2 s−1 km−1) plotted against observed specific discharge at the streamflow gages; results for each year and basin are provided in the Supplement. Streamflow is shown as specific discharge (weighted by area) for ease of comparison. Only March to June results are shown in Fig. 9; in March the basins have not begun to melt and the hydrograph depicts baseflow contributions in the systems. The active period begins in late March to early April and the differences between the two estimates of streamflow persist until June, after which point streamflow responses to rainfall input are essentially the same. Statistics for the April–May–June calibration, validation, and the period of record in Table 4 illustrate that the Upper Chena River basin shows improvement compared to the APRFC run during the early melt period, while the later period is overpredicted by the MODSCAG. For Chatanika, the simulated MODIS simulations are of greater magnitude (Fig. 9) and have earlier timing compared to the APRFC simulated flows. In the Little Chena River basin, MODIS-simulated discharge overall fits better than the APRFC, which over-simulates streamflow on average, and both products perform similarly well. Streamflow simulations for the Upper Chena, Salcha, and Goodpaster systems match observations more closely, on average. This also is clear from the averages across basins and years; the MODSCAG simulations match observed streamflow, while the MOD10A1 product underestimates runoff during the mid-May to early June period (Fig. 9, last panel). The year-to-year variability illustrates similar results to the long-term averages for each basin (Supplement).
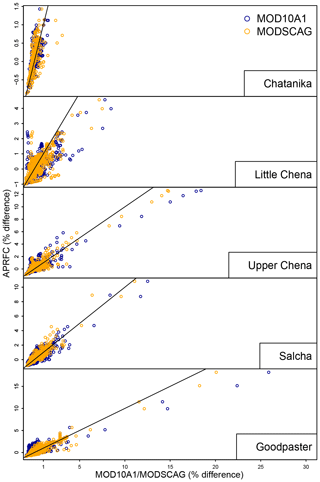
Figure 8Percent difference between observed streamflow and that modeled using APRFC plotted against modeled MOD10A1 (blue) and MODSCAG (orange) for March–June from 2000 to 2010. The APRFC percent difference (y axis) is plotted against the MOD10A1 and MODSCAG percent differences (x axis). The 1:1 line is illustrated on the plots for reference.
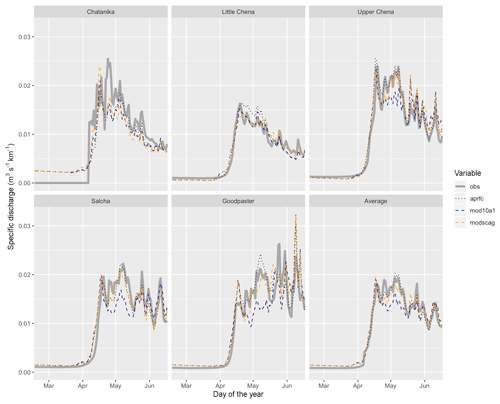
Figure 9Upper Chena River basin streamflow: observed (grey line), simulated with APRFC (black dotted line), simulated with MOD10A1 (blue dashed line), and simulated with MODSCAG (orange dashed line) for all years (2000–2010, 15th of the month shown on x axis). Streamflow is shown as specific discharge, with discharge divided by area of the basins (km). The mean of all stations is shown in the final panel.
3.5 Other integration methods
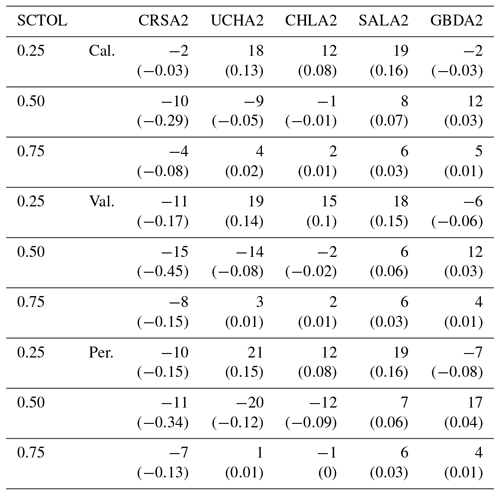
Two methods were applied to integrate the MODIS data into CHPS. One method involved interpolating between missing data values, changing the number of interpolated days from 1 to 11 to investigate how changing the value impacted model results. Generally, the number of days of interpolation had little impact, but the longer interpolation period results produced slightly higher correlations and improved streamflow estimation. We also investigated the response to altering model parameter SCTOL, which can be used by forecasters to combine the strength of the ADC and the MODIS data and is similar to partial rule-based direct insertion approach; however the parameter can be altered without any additional changes to the CHPS model framework. Table 7 illustrates the results of setting the SCTOL parameter to 0.25, 0.50, and 0.75 for the MODSCAG run only, while holding the rest of the parameters constant. No recalibration is performed. NSE and R statistics increase during the calibration period, and MAE and RMSE remain similar on average, but the range of responses across the basins decreases for SCTOL =0.50. Interestingly, Chatanika, which has the largest improvement based on the differences between APRFC and MODIS simulations, does not benefit from model integration, owing to the low skill within the APRFC model version (Table 7). However, for the remaining basins strong improvements are apparent for higher values of SCTOL during the calibration period (Upper Chena, Little Chena, and Salcha), validation, and period of record (Upper Chena, Little Chena). Diminishing returns occur at a threshold between 0.25 and 0.50 SCTOL for most basins; however, Goodpaster improves at 0.50 but not 0.75. This suggests that the SCTOL parameter should be uniquely applied depending on the basin.
Results illustrate that streamflow in interior Alaska can be simulated with skill using conceptual, semi-lumped hydrologic models, even without the use of gridded observations of MODIS fSCA. However, if the initial streamflow observations are of poor quality (i.e., Chatanika River basin), applying gridded observations of MODIS fSCA in the models will generate streamflow estimates as good as or better than estimates based on SNOW-17's areal depletion curve. However, as the climate shifts, conceptual, semi-lumped models may not be representative of process changes that will likely occur as the Arctic warms (Clark et al., 2017). As fully process-based models are challenging to run in Arctic environments, where high-quality data are temporally and spatially sparse, using conceptual models parameterized with as many observations as possible represents a bridge between the fully process-based models and conceptual approaches to hydrologic modeling.
However, we found there to be major challenges in obtaining improvements in simulated streamflow discharge values when introducing additional observed data sets and their associated uncertainties into models. This result was also found in work performed in the American River basin where the California Nevada RFC lumped model provided the most accurate representation of snow cover area (Franz and Karsten, 2013). As indicated by Franz and Karsten (2013), although the gridded representation of fSCA is improved in their distributed version of SNOW-17, the streamflow simulations and associated statistics did not reflect this improvement. In addition, they found that discharge values had lower skill when estimates of snow cover are included in the calibration even though it is hypothesized that the process representation is improved, which is a finding of a number of other research studies focusing on this topic (Parajka and Blöschl, 2008; Udnæs et al., 2007). These findings are also true for Alaskan interior boreal basins, highlighting the importance of performing this work in remote areas and under monitored systems that are changing quickly due to climate shifts and increased occurrences of extreme events (Bennett and Walsh, 2015; Bennett et al., 2015).
The goal of this work was, in part, to undertake a simple application of inserting preprocessed MODIS fSCA into the CHPS operational framework to simulate streamflow across basins in interior Alaska. The preprocessing of MODIS data for insertion into the model, which included the MOD10A1 and MODSCAG data products, along with the CHPS areal averaging, eliminated some of the issues related to cloud cover and missing data, as noted in results provided in Liu et al. (2013), who assimilated Air Force Weather Agency–National Aeronautics and Space Administration Snow Algorithm (ANSA) fSCA data for similar stations in the region. For example, the findings in Liu et al. (2013) for the best case indicate NSE improvement for Salcha, Little Chena, and Chena at Fairbanks of 0.30, 0.31, and 0.06. Our study reports comparable NSE improvement values for some stations (Chatanika and Goodpaster) for the months impacted by the adjustments, although the Salcha and Little Chena system differences are closer to those values reported for the raw MODIS data in the study of Liu et al. (2013). The averaging approach and use of newly developed tools (ANSA, MODSCAG) applied in both studies appear to produce results slightly superior to those of MOD10A1. Further analysis is required to determine if cloud correction processes, such as those applied in the ANSA study, would act to reduce the impact of pixel shifting that is likely a major problem in Alaska (Arsenault et al., 2014) and improve streamflow estimates further. Both studies indicate improved representation of internal snowpack and improvements in streamflow estimates for some basins for these new iterations of the MODIS data.
Differences in the streamflow improvements provided by Liu et al. (2013) for the Salcha and Little Chena basin highlight some important variations between the two studies that should be considered. The first is that, as noted by the authors, the model-simulated streamflow estimates are biased and thus the improvements reported in the paper are still poor representations of the streamflow (Liu et al., 2013). The question then remains that if a model result without updated observations is already skillful, how much better can the model be with added information (which carries its own uncertainty with it)? Perhaps the differences between the distributed model in Liu et al. (2013) versus the lumped models used in this study are adding a buffer to the data improvements in the case of this study, and limiting the amount of difference or improvement that MODIS fSCA insertion can provide. Snow cover data appear to be improved at interior Alaska locations within the model when compared to five different SNOTEL stations (Fig. 5), particularly for the melt timing. However, the discharge values improved moderately given MODIS input over the different periods analyzed, and in particular smaller changes are noted over the entire period of record (Table 4, Figs. 8, 9). For the Chatanika basin, with limited observed data and poorer streamflow simulations however, the improvements are similar to those shown in the Liu study (Liu et al., 2013). These results suggest that skill can be added by introducing new observations when the models are performing poorly due to inadequate or low-quality records. Considering that there are numerous incomplete and low-quality gages throughout the high-latitude regions of the globe, this result is valuable and indicates the utility of the MODIS fSCA data in this regard.
Calibrations performed on the SAC-SMA model were limited in nature and targeted specifically at two parameters exhibiting the most influence on improving discharge estimates during the melt season: MFMAX and TAELEV. These parameters control the air temperature and impact snow cover depletion by either increasing or retaining melt. Previously, the APRFC parameters were set to lower MFMAX values. The TAELEV parameter was not equal to the true elevation (ELEV) and set to different values for north and south aspects. For north-facing upper elevations, TAELEV was less than ELEV so temperatures were lapsed upward to simulate the slower melt rates and cooler conditions. For south-facing aspects, TAELEV was set to greater than ELEV, so temperatures were lapsed downward to simulate increased melt from solar influence. Our updated parameterization using the MODIS data required an upward adjustment of these values because the areal depletion curve is no longer controlling the melt rate. Thus, fSCA present on northern, upper-elevation slopes in the late spring must have higher melt rates applied to melt the snow with the correct timing. The primary reason that the areal depletion curves in SNOW-17 differ from one that would be derived from actual measurements of fSCA is that melt rates decline as fSCA declines because the remaining snow is usually found in locations where snow melts at a slower rate, such as under canopies or on north-facing slopes (Anderson, 2006).
Adjustments to MFMAX across the north sub-basin units suggest that the modified areal depletion curves within SNOW-17 underestimate snow-covered area. At many of the sites, particularly when using the MODSCAG product, MFMAX for the northern sites had to be increased. This suggests that the APRFC run uses a lower value that attempts to account for cooler temperatures on the northern slopes by retaining the snow on these slopes for longer, thus slowing runoff (Franz and Karsten, 2013). By more accurately representing conditions in the north sub-basin units, the MODIS simulations required an increase in the snowmelt factor to allow for initiation of the melt on these slopes. MFMAX represents the dependency between the melt factor to account for a constant fSCA curve used in the model and the ability of the “standard” fSCA curves used in the APRFC SNOW-17 to replicate the conditions of the melt properties within the basins (Shamir and Georgakakos, 2007). As noted in Shamir and Georgakakos (2007), there is considerable inter-annual variability in snow cover depletion and this variability is not represented when the standard APRFC model is applied. Therefore, by improving the internal physical processes in the model, the snowmelt timing should improve. However, this might not translate into improved discharge estimates because precipitation and temperature inputs could still be incorrect, and errors in forcing data that generate incorrect water equivalents for snow carry larger uncertainty bounds than that which can be addressed by changing the weighting factors and timing of snowmelt by adjusting fSCA, as undertaken in this study.
For the MOD10A1 calibration, fewer parameters were adjusted compared to the MODSCAG simulations. The end result is that the MODSCAG data have improved streamflow simulations compared to the MOD10A1 result. The model parameters require greater adjustment for MODSCAG simulations as a result of the variability between the two data sets compared to the APRFC baseline simulations. The MODSCAG data have a different melt trajectory for northern slopes and hold snow for longer on the south-facing slopes of the Upper Chena River basin, while the MOD10A1 acts similarly to the APRFC melt trajectory for SWE data (Fig. 4). This region is known to have variable melt timing based on south-facing slopes; therefore the north and south slopes should be differentiated to reflect the physical processes occurring on the warmer south-facing slopes compared to the cold and often permafrost-dominated north-facing slopes (Jones and Rinehart, 2010). Although MODSCAG improvement is noted for the Chatanika and Goodpaster basins in the streamflow statistics, the results for both MODIS versions are overall very similar in this region (Fig. 8). This may be due to the different canopy adjustments applied to the data sets or because of the lack of a spectral end member for the boreal forest in MODSCAG (Painter et al., 2009). Regardless, it is not clear that one of these data sets is markedly improving streamflow estimates and it is possible that both approaches could be considerably useful as additional observations of fSCA estimates for the region.
Two other means by which the CHPS framework can be altered to improve streamflow estimates are explored in this work. The interpolation over MODIS missing days can be altered easily in CHPS; however this had only a small effect on the streamflow results. The SCTOL, which allows for interaction between the model and the observed MODIS fSCA data, had an effect on streamflow and therefore may be a useful technique for the RFCs to apply during recalibration efforts to observed snow cover data. An advantage was noted between the MODSCAG with an SCTOL setting greater than to 0.25. However, the basins with the strongest improvement (Chatanika) over the APRFC simulation did not improve using an SCTOL greater than zero, which was because the baseline model performed so poorly given the weakness of the underlying observed discharge data. Therefore, the RFCs may wish to selectively apply this parameter when basins have reliable observed information and the MODIS data can be utilized partially in conjunction with the model ADC and partially on the MODIS fSCA observations.
Although complex tools and distributed models are available from the research community and in the CHPS to integrate observed snow cover area data, the RFCs across the US are not, as of writing this paper, using these features in their operational river forecasting to estimate floods and droughts. This study focuses on developing tools that can, with a minor amount of testing, be brought into the RFC's CHPS modeling framework and used to improve physical estimates of fSCA across basins of interest. The method integrates information such as MODIS remotely sensed snow cover into the model framework using a simple calibration approach for the SNOW-17 model, and also provides some input regarding expected improvements and other possible parameters that may be introduced to enrich forecasting and simulation of streamflow. Our recommendation is to incorporate MODIS data as an interim step. However, in the long run the RFCs should begin to use more complex models and data assimilation tools as the move towards the National Water Model proceeds.
In this work, we answer several outstanding questions regarding the application of MODIS data in the RFC models. Basins with poor-quality streamflow observations benefited from the use of the MODIS fSCA but improvements are also made to the internal snow timing estimates, observed in both the validation against SNOTEL data and also through the calibration that corrected the model parameters to better reflect the physical differences altering processes occurring on north- and south-facing slopes. Overall, minor differences were observed between MOD10A1 and MODSCAG data; however the MODSCAG data provided improvement over MOD10A1 in average streamflow simulations across all basins. We observed limited impact of changing the interpolation length between missing days, although adjustments based on altering the interaction between the model and the observed MODIS fSCA data did alter streamflow and therefore are useful during recalibration efforts.
The utility of the MODIS data in CHPS goes beyond improvements to the streamflow; these tools can be used for a number of internal checks for SWE and fSCA that are currently under way, such as the ingestion of data for ensemble forecasts (NWS, 2012). This study opens the door for insertion of parameters via assimilation alongside developments such as physically based model usage.
The observations of rapid change in the Arctic highlight important alterations to hydrological regimes in the subarctic interior boreal forest of Alaska. These observed, rapid changes and future anticipated alterations introduce a pressing need in Alaska to further understand the anticipated changes through modeling of major climate drivers of streamflow. The sparse observational network in Alaska, along with the magnitude and rate of change, necessitates the use of robust modeling tools to examine these changes and their impacts on hydrology. However, due to the limited high-quality observations, and our lack of understanding of Arctic hydrologic processes, process-based modeling approaches are limited in this environment. Therefore, we must apply available conceptual models with calibrations informed by observations, including remote sensing tools of SWE and fSCA to examine these effects. In this way, we will be able to define and quantify increasing impacts associated with these changes that lead to multi-scale risk to hydro-ecological systems, not only to the local and state resources, but also regionally and globally.
MODIS MOD10A data set is available for download through https://doi.org/10.5067/MODIS/MOD10A1.006 (Hall and Riggs, 2016). MODSCAG data are available via https://snow.jpl.nasa.gov/portal/ (Painter et al., 2009). USGS river gauge data are available for download from https://waterdata.usgs.gov/nwis/rt (USGS, 2019). SNOTEL SWE data are available from https://www.wcc.nrcs.usda.gov/snow/snotel-wereports.html (NRCS, 2019) Mean areal temperature and precipitation 6-hourly data used to run SACSMA/SNOW17 are available via the authors at the Alaska Pacific River Forecast Center.
The supplement related to this article is available online at: https://doi.org/10.5194/hess-23-2439-2019-supplement.
All authors were involved in the conception, and development of workflow. KB and BB responsible for development of software manipulation of CHPS modeling framework. KB and JEC responsible for writing. KB, JEC, and SL contributed to editing process through various stages of the manuscript development.
The authors declare that they have no conflict of interest.
Katrina E. Bennett acknowledges support for this work from the Alaska Climate Science Center, the Natural Science and Engineering Research Council of Canada, and the DOE Office of Science, Biological and Environmental Research program, Next Generation Ecosystem Experiment, NGEE-Arctic project. Katrina E. Bennett, Ben Balk, and Jessica E. Cherry acknowledge support from the GOES-R High Latitude Proving Ground award NA08OAR432075. Thank you to Sarah Boon for reviewing an earlier version of this work. The authors thank the Alaska Pacific River Forecast Center staff for their collaborative efforts and the Arctic Region Supercomputer Center for the use of their supercomputer.
This paper was edited by Shraddhanand Shukla and reviewed by Stephen Déry, Edward Bair, and one anonymous referee.
Arsenault, K. R., Houser, P. R., and De Lannoy, G. J.: Evaluation of the MODIS snow cover fraction product, Hydrol. Process., 28, 980–998, 2014.
Anderson, E. A.: A point energy and mass balance model of a snow cover, NOAA Tech. Rep. NWS 19, Office of Hydrology, National Weather Service, Silver Spring, MD, 150 pp., 1976.
Anderson, E. A.: Calibration of conceptual hydrologic models for use in river forecasting, Office of Hydrologic Development, US National Weather Service, Silver Spring, MD, 372 pp., available at: https://www.nws.noaa.gov/oh/hrl/modelcalibration/1. Calibration Process/1_Anderson_CalbManual.pdf (last access: 8 May 2019), 2002.
Anderson, E. A.: Snow Accumulation and Ablation Model – SNOW-17, Nat. Weather Serv. NOAA, 44 pp., available at: http://www.nws.noaa.gov/oh/hrl/nwsrfs/users_manual/part2/_pdf/22snow17.pdf (last access: 17 August 2018), 2006.
Andreadis, K. M. and Lettenmaier, D. P.: Assimilating remotely sensed snow observations into a macroscale hydrology model, Adv. Water Res., 29, 872–886, https://doi.org/10.1016/j.advwatres.2005.08.004, 2006.
Bennett, K. E. and Walsh, J.: Spatial and temporal changes in indices of extreme precipitation and temperature for Alaska, Int. J. Climatol., 35, 1434–1452, https://doi.org/10.1002/joc.4067, 2015.
Bennett, K. E., Cannon, A. J., and Hinzman, L.: Historical trends and extremes in boreal Alaska river basins, J. Hydrol., 527, 590–607, https://doi.org/10.1016/j.jhydrol.2015.04.065, 2015.
Burnash, R. J. E., Ferral, R. L., and McGuire, R. A.: A generalized streamflow simulation system, Joint Federal-State River Forecast Center, Sacramento, CA, 204 pp., 1973.
Cherry, J. E., Tremblay, L. B., Déry, S. J., and Stieglitz, M.:. Reconstructing solid precipitation from snow depth measurements and a land surface model, Water Resour. Res., 41, 1–15, https://doi.org/10.1029/2005WR003965, 2005.
Cherry, J. E., Tremblay, L. B., Stieglitz, M., Gong, G., and Déry, S. J.: Development of the pan-arctic snowfall reconstruction: new land-based solid precipitation estimates for 1940-99, J. Hydrometeorol., 8, 1243–1263, https://doi.org/10.1175/2007JHM765.1, 2007.
Cherry, J. E., Knapp, C., Trainor, S., Ray, A. J., Tedesche, M., and Walker, S.: Planning for climate change impacts on hydropower in the Far North, Hydrol. Earth Syst. Sci., 21, 133–151, https://doi.org/10.5194/hess-21-133-2017, 2017.
Clark, M. P., Slater, A. G., Barrett, A. P., Hay, L. E., McCabe, G. J., Rajagopalan, B., and Leavesley, G. H.: Assimilation of snow covered area information into hydrologic and land-surface models, Adv. Water Res., 29, 1209–1221, https://doi.org/10.1016/j.advwatres.2005.10.001, 2006.
Clark, M. P., Hendrikx, J., Slater, A. G., Kavetski, D., Anderson, B., Cullen, N. J., Kerr, T., Hreinsson, E. Ö., and Woods, R. A: Representing spatial variability of snow water equivalent in hydrologic and land-surface models: A review, Water Resour. Res., 47, 1–23, https://doi.org/10.1029/2011WR010745, 2011.
Clark, M. P., Bierkens, M. F. P., Samaniego, L., Woods, R. A., Uijlenhoet, R., Bennett, K. E., Pauwels, V. R. N., Cai, X., Wood, A. W., and Peters-Lidard, C. D.: The evolution of process-based hydrologic models: historical challenges and the collective quest for physical realism, Hydrol. Earth Syst. Sci., 21, 3427–3440, https://doi.org/10.5194/hess-21-3427-2017, 2017.
Cohen, J. L., Furtado, J. C., Barlow, M. A., Alexeev, V. A., and Cherry, J. E.: Arctic warming, increasing snow cover and widespread boreal winter cooling, Environ. Res. Lett., 7, 014007, https://doi.org/10.1088/1748-9326/7/1/014007, 2012.
Cooley, S. W. and Pavelsky, T. M.: Spatial and temporal patterns in Arctic river ice breakup revealed by automated ice detection from MODIS imagery, Remote Sens. Environ., 175, 310–322, https://doi.org/10.1016/j.rse.2016.01.004, 2016.
Déry, S. J., Salomonson, V. V., Stieglitz, M., Hall, D. K., and Appel, I.: An approach to using snow areal depletion curves inferred from MODIS and its application to land surface modelling in Alaska, Hydrol. Process., 19, 2755–2774, https://doi.org/10.1002/hyp.5784, 2005.
Dozier, J., Painter, T. H., Rittger, K., and Frew, J. E.: Time-space continuity of daily maps of fractional snow cover and albedo from MODIS, Adv. Water Res., 31, 1515–1526, https://doi.org/10.1016/j.advwatres.2008.08.011, 2008.
Duethmann, D., Peters, J., Blume, T., Vorogushyn, S., and Güntner, A.: The value of satellite-derived snow cover images for calibrating a hydrological model in snow-dominated catchments in Central Asia, Water Resour. Res., 50, 2002–2021, https://doi.org/10.1002/2013WR014382. 2014.
Durand, M., Molotch, N. P., and Margulis, S. A.: Merging complementary remote sensing datasets in the context of snow water equivalent reconstruction, Remote Sens. Environ., 112, 1212–1225, https://doi.org/10.1016/j.rse.2007.08.010, 2008.
Dwyer, J. and Schmidt, G.: The MODIS reprojection tool, in: Earth Science Satellite Remote Sensing, Springer, Berlin, Heidelberg, Germany, 162–177, 2006.
Euskirchen, E., McGuire, A., Chapin III, F., Yi, S., and Thompson, C.: Changes in vegetation in northern Alaska under scenarios of climate change, 2003–2100: implications for climate feedbacks, Ecol. Appl., 19, 1022–1043, https://doi.org/10.1890/08-0806.1, 2009.
Franz, K. J. and Karsten, L. R.: Calibration of a distributed snow model using MODIS snow covered area data, J. Hydrol., 494, 160–175, https://doi.org/10.1016/j.jhydrol.2013.04.026, 2013.
Franz, K. J., Hogue, T. S., and Sorooshian, S.: Operational snow modeling: Addressing the challenges of an energy balance model for National Weather Service forecasts, J. Hydrol., 360, 48–66, https://doi.org/10.1016/j.jhydrol.2008.07.013, 2008.
Gesch, D., Oimoen, M., Greenlee, S., Nelson, C., Steuck, M., and Tyler, D.: The National Elevation Dataset, Photogramm. Eng. Rem. S., 68, 5–11, 2002.
Groisman, P. Y., Bogdanova, E., Alexeev, V., Cherry, J., and Bulygina, O.: Impact of snowfall measurement deficiencies on quantification of precipitation and its trends over northern Eurasia, Ice Snow, 54, 29–43, https://doi.org/10.15356/2076-6734-2014-2-29-43, 2014.
Hall, D. K. and Riggs, G. A.: Accuracy assessment of the MODIS snow product, Hydrol. Process., 21, 1534–1547, https://doi.org/10.1002/hyp.6715, 2007.
Hall, D. K. and Riggs, G. A.: MODIS/Terra Snow Cover Daily L3 Global 500m SIN Grid, Version 6, Snow Cover, Boulder, Colorado USA, NASA National Snow and Ice Data Center Distributed Active Archive Center, https://doi.org/10.5067/MODIS/MOD10A1.006, 2016.
Hall, D. K., Riggs, G. A., Salomonson, V. V., DiGirolamo, N. E., and Bayr, K. J.: MODIS snow-cover products, Remote Sens. Environ., 83, 181–194, https://doi.org/10.1016/S0034-4257(02)00095-0, 2002.
Hall, D. K., Riggs, G. A., and Salomonson, V. V.: MODIS/Terra Snow Cover Daily L3 Global 500m Grid V005, 2000-Daily Updates, National Snow and Ice Data Center, Boulder, Colorado USA, 2006.
He, M., Hogue, T. S., Franz, K. J., Margulis, S. A., and Vrugt, J. A.: Characterizing parameter sensitivity and uncertainty for a snow model across hydroclimatic regimes, Adv. Water Res., 34, 114–127, https://doi.org/10.1016/j.advwatres.2010.10.002, 2011.
Hinzman, L. D., Bettez, N. D., Bolton, W. R., Chapin, F. S., Dyurgerov, M. B., Fastie, C. L., Griffith, B., Hollister, R. D., Hope, A., Huntinton, H. P., Jensen, A. M., Jia, G. J., Jorgenson, T., Kane, D. L., Klein, D. R., Kofinas, G., Lynch, A. H., Lloyd, A. H., McGuire, A. D., Nelson, F. E., Oechel, W. C., Osterkamp, T. E., Racine, C. H., Romanovsky, V. E., Stone, R. S., Stow, D. A., Sturm, M. D., Walker, D. A., Webber, P. J., Welker, J. M., Winker, K. S., and Yoshikawa, K.: Evidence and implications of recent climate change in northern Alaska and other Arctic regions, Climate Change, 72, 251–298, https://doi.org/10.1007/s10584-005-5352-2, 2005.
Hinzman, L. D., Deal, C. J., McGuire, A. D., Mernild, S. H., Polyakov, I. V., and Walsh, J. E.: Trajectory of the Arctic as an integrated system, Ecol. Appl., 23, 1837–1868, https://doi.org/10.1890/11-1498.1, 2013.
Hock, R.: Temperature index melt modelling in mountain areas, J. Hydrol., 282, 104–115, https://doi.org/10.1016/S0022-1694(03)00257-9, 2003.
Huntington, T. G.: Evidence for intensification of the global water cycle: review and synthesis, J. Hydrol., 319, 83–95, https://doi.org/10.1016/j.jhydrol.2005.07.003, 2006.
Instanes, A., Kokorev, V., Janowicz, R., Bruland, O., Sand, K., and Prowse, T.: Changes to freshwater systems affecting Arctic infrastructure and natural resources, J. Geophys. Res.-Biogeo., 121, 567–585, https://doi.org/10.1002/2015JG003125, 2016.
Jones, J. B. and Rinehart, A. J.: The long-term response of stream flow to climatic warming in headwater streams of interior Alaska, Can. J. Forest Res., 40, 1210–1218, 2010.
Kane, V. R., Gillespie, A. R., McGaughey, R., Lutz, J. A., Ceder, K., and Franklin, J. F.: Interpretation and topographic compensation of conifer canopy self-shadowing, Remote Sens. Environ., 112, 3820–3832, https://doi.org/10.1016/j.rse.2008.06.001, 2008.
Karl, T. R., Melillo, J. M., Peterson, T. C., and Hassol, S. J. (Eds.): Global climate change impacts in the United States, Cambridge University Press, 2009.
Koven C. D., Riley W. J., and Stern, A.: Analysis of permafrost thermal dynamics and response to climate change in the CMIP5 Earth system models, J. Climate, 26, 1877–900, https://doi.org/10.1175/JCLI-D-12-00228.1, 2013.
Lesack, L. F. W., Marsh, P., Hicks, F. E., and Forbes, D. L.: Local spring warming drives earlier river-ice breakup in a large Arctic delta, Geophys. Res. Lett., 41, 1560–1567, https://doi.org/10.1002/2013GL058761, 2014.
Liu, J., Melloh, R. A., Woodcock, C. E., Davis, R. E., and Ochs, E. S.: The effect of viewing geometry and topography on viewable gap fractions through forest canopies, Hydrol. Process., 18, 3595–3607, https://doi.org/10.1002/hyp.5802, 2004.
Liu, J., Woodcock, C. E., Melloh, R. A., Davis, R. E., McKenzie, C., and Painter, T. H.: Modeling the view angle dependence of gap fractions in forest canopies: Implications for mapping fractional snow cover using optical remote sensing, J. Hydrometeorol., 9, 1005–1019, https://doi.org/10.1175/2008JHM866.1, 2008.
Liu, Y., Peters-Lidard, C. D., Kumar, S., Foster, J. L., Shaw, M., Tian, Y., and Fall, G. M.: Assimilating satellite-based snow depth and snow cover products for improving snow predictions in Alaska, Adv. Water Res., 54, 208–227, https://doi.org/10.1016/j.advwatres.2013.02.005, 2013.
Magnusson, J., Wever, N., Essery, R., Helbig, N., Winstral, A., and Jonas, T.: Evaluating snow models with varying process representations for hydrological applications, Water Resour. Res., 51, 2707–2723, https://doi.org/10.1002/2014WR016498, 2015.
McGuire, M., Wood, A. W., Hamlet, A. F., and Lettenmaier, D. P.: Use of satellite data for streamflow and reservoir storage forecasts in the Snake River Basin, J. Water Resour. Plan. Man., 132, 97–1109, https://doi.org/10.1061/(ASCE)0733-9496(2006)132:2(97), 2006.
Molotch, N. P. and Bales, R. C.: Scaling snow observation from the point to the grid element: Implications for observation network design, Water Resour. Res., 41, 1–16, https://doi.org/10.1029/2005WR004229, 2005.
Molotch, N. P. and Margulis, S. A.: Estimating the distribution of snow water equivalent using remotely sensed snow cover data and a spatially distributed snowmelt model: A multi-resolution, multi-sensor comparison, Adv. Water Res., 31, 1503–1514, https://doi.org/10.1016/j.advwatres.2008.07.017, 2008.
Morriss, B. F., Ochs, E., Deeb, E. J., Newman, S. D., Daly, S. F., and Gagnon, J. J.: Persistence-based temporal filtering for MODIS snow products, Remote Sens. Environ., 175, 130–137, https://doi.org/10.1016/j.rse.2015.12.030, 2016.
Muhammad, P., Duguay, C., and Kang, K.-K.: Monitoring ice break-up on the Mackenzie River using MODIS data, The Cryosphere, 10, 569–584, https://doi.org/10.5194/tc-10-569-2016, 2016.
National Resources Conservation Service: Snow Water Equivalent (SWE) and Snow Depth Products, https://www.wcc.nrcs.usda.gov/snow/snotel-wereports.html, last access 16 May 2019.
NOAA: NOAA National Water Model: Improving NOAA's Water Prediction Services, 2 pp., available at: https://water.noaa.gov/documents/wrn-national-water-model.pdf (last access: 1 December 2018), 2017.
NWS: Overview of the Hydrologic Ensemble Forecast Service (HEFS), Office of Hydrologic Development, 34 pp., available at: http://www.nws.noaa.gov/os/water/RFC_support/HEFS_doc/HEFS_Overview_0.1.2.pdf (last access: 1 December 2018), 2012.
Painter, T. H., Rittger, K., McKenzie, C., Slaughter, P., Davis, R. E., and Dozier, J.: Retrieval of subpixel snow covered area, grain size, and albedo from MODIS, Remote Sens. Environ., 113, 868–879, https://doi.org/10.1016/j.rse.2009.01.001, 2009.
Parajka, J. and Blöschl, G.: The value of MODIS snow cover data in validating and calibrating conceptual hydrologic models, J. Hydrol., 358, 240–258, https://doi.org/10.1016/j.jhydrol.2008.06.006, 2008.
Prowse, T., Bring, A., Mård, J., Carmack, E., Holland, M., Instanes, A., Vihma, T., and Wrona, F.: Arctic Freshwater Synthesis: Summary of key emerging issues, J. Geophys. Res.-Biogeo., 120, 1887–1893, https://doi.org/10.1002/2015JG003128, 2015.
Rawlins, M. A., Steele, M., Holland, M. M., Adam, J. C., Cherry, J. E., Francis, J. A., Groisman, P. Y., Hinzman, L. D., Huntington, T. G., Kane, D. L., Kimball, J. S., Kwok, R., Lammers, R. B., Lee, C. M., Lettenmaier, D. P., McDonald, K. C., Podest, E., Pundsack, J. W., Rudels, B., Serreze, M. C., Shiklomanov, A., Skagseth, Ø., Troy, T. J., Vörösmarty, C. J., Wensnahan, M., Wood, E. F., Woodgate, R., Yang, D., Zhang, K., and Zhang, T.: Analysis of the Arctic System for Freshwater Cycle Intensification: Observations and Expectations, J. Climate, 23, 5715–5737, https://doi.org/10.1175/2010JCLI3421.1, 2010.
Raleigh, M. S., Rittger, K., Moore, C. E., Henn, B., Lutz, J. A., and Lundquist, J. D.: Ground-based testing of MODIS fractional snow cover in subalpine meadows and forests of the Sierra Nevada, Remote Sens. Environ., 128, 44–57, https://doi.org/10.1016/j.rse.2012.09.016, 2013.
Reed, S., Koren, V., Smith, M., Zhang, Z., Moreda, F., and Seo, D.-J.: Overall distributed model intercomparison project results, J. Hydrol., 298, 27–60, https://doi.org/10.1016/j.jhydrol.2004.03.031, 2004.
Riggs, G. A., Hall, D. K., and Salomonson, V. V.: MODIS Snow Products User Guide to Collection 5, 80 pp., available at: https://modis-snow-ice.gsfc.nasa.gov/?c=userguides (last access: 1 December 2018), 2006.
Rittger, K., Painter, T. H., and Dozier, J.: Assessment of methods for mapping snow cover from MODIS, Adv. Water Res., 51, 367–380, https://doi.org/10.1016/j.advwatres.2012.03.002, 2013.
Rodell, M., Houser, P., Jambor, U., Gottschalck, J., Mitchell, K., Meng, C.-J., Arsenault, K., Cosgrove, B., Radakovich, J., Bosilovich, M., Entin, J. K., Walker, J. P., Lohmann, D., and Toll, D.: The global land data assimilation system, B. Am. Meteorol. Soc., 85, 381–394, https://doi.org/10.1175/BAMS-85-3-381, 2004.
Serreze, M. C. and Barry, R. G.: Processes and impacts of Arctic amplification: A research synthesis, Global Planet. Change, 77, 85–96, https://doi.org/10.1016/j.gloplacha.2011.03.004, 2011.
Shamir, E. and Georgakakos, K. P.: Estimating snow depletion curves for American River basins using distributed snow modeling, J. Hydrol., 334, 162–173, https://doi.org/10.1016/j.jhydrol.2006.10.007, 2007.
Slater, A. G. and Lawrence, D. M., Diagnosing present and future permafrost from climate models, J. Climate, 26, 5608–5623, https://doi.org/10.1175/JCLI-D-12-00341.1, 2013.
Stahl, K., Moore, R. D., Floyer, J. A., Asplin, M. G., and McKendry, I. G.: Comparison of approaches for spatial interpolation of daily air temperature in a large region with complex topography and highly variable station density, Agr. Forest Meteorol., 139, 224–236, https://doi.org/10.1016/j.agrformet.2006.07.004, 2006.
Stewart, B. C., Kunkel, K. E., Stevens, L. E., and Sun, L.: Regional climate trends and scenarios for the U.S. National Climate Assessment, Part 7. Climate of Alaska, NOAA technical Report NESDIS 142–147, 60 pp., 2013.
Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M.: Climate Change 2013: The physical science basis, Intergovernmental Panel on Climate Change, Working Group I Contribution to the IPCC Fifth Assessment Report (AR5), Cambridge Univ Press, New York, available at: https://www.ipcc.ch/report/ar5/wg1/ (last access: 1 December 2018), 2013.
Stuefer, S. L., Arp, C. D., Kane, D. L., and Liljedahl, A. K.: Recent extreme runoff observations from Coastal Arctic watersheds in Alaska, Water Resour. Res., 53, 9145–9163, https://doi.org/10.1002/2017WR020567, 2017.
Sturm, M., Goldstein, M. A., and Parr, C.: Water and life from snow: A trillion dollar science question, Water Resour. Res., 53, 3534–3544, https://doi.org/10.1002/2017WR020840, 2017.
Sun, C., Walker, J. P., and Houser, P. R.: A methodology for snow data assimilation in a land surface model, J. Geophys. Res.-Atmos., 109, D08108, https://doi.org/10.1029/2003JD003765 2004.
Tan, B., Woodcock, C. E., Hu, J., Zhang, P., Ozdogan, M., Huang, D., Yang, W., Knyazikhin, Y., and Myneni, R. B.: The impact of gridding artifacts on the local spatial properties of MODIS data: Implications for validation, compositing, and band-to-band registration across resolutions, Remote Sens. Environ., 105, 98–114, https://doi.org/10.1016/j.rse.2006.06.008, 2006.
Thirel, G., Salamon, P., Burek, P., and Kalas, M.: Assimilation of MODIS snow cover area data in a distributed hydrological model using the particle filter, Remote Sens., 5, 5825–5850, https://doi.org/10.3390/rs5115825, 2013.
U.S. Geological Survey: National Water Information System data available on the World Wide Web (USGS Water Data for the Nation), https://waterdata.usgs.gov/nwis/rt, last access: 16 May 2019.
Udnæs, H., Alfnes, E., and Andreassen, L. M.: Improving runoff modelling using satellite-derived snow covered area?, Hydrol. Res., 38, 21–32, https://doi.org/10.2166/nh.2007.032, 2007.
Werner, M., Schellekens, J., Gijsbers, P., Van Dijk, M., Van den Akker, O., and Heynert, K.: The Delft-FEWS flow forecasting system, Environ. Model. Softw., 40, 65–77, https://doi.org/10.1016/j.envsoft.2012.07.010 2013.
Woo, M. K., Thorne, R., Szeto, K., and Yang, D.: Streamflow hydrology in the boreal region under the influences of climate and human interference, Philos. T. R. Soc. B, 363, 2249–2258, https://doi.org/10.1098/rstb.2007.2197, 2008.
Wrona, F. J., Johansson, M., Culp, J. M., Jenkins, A., Mård, J., Myers-Smith, I. H., Prowse, T. D., Vincent, W. F., and Wookey, P. A.: Transitions in Arctic ecosystems: Ecological implications of a changing hydrological regime, J. Geophys. Res.-Biogeo., 121, 650–674, https://doi.org/10.1002/2015JG003133, 2016.
Zaitchik, B. and Rodell, M.: Forward-looking assimilation of MODIS-derived snow-covered area into a land surface model, J. Hydrometeorol., 10, 130–148, https://doi.org/10.1175/2008JHM1042.1, 2009.