the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The 18O ecohydrology of a grassland ecosystem – predictions and observations
Regina T. Hirl
Hans Schnyder
Ulrike Ostler
Rudi Schäufele
Inga Schleip
Sylvia H. Vetter
Karl Auerswald
Juan C. Baca Cabrera
Lisa Wingate
Margaret M. Barbour
Jérôme Ogée
The oxygen isotope composition (δ18O) of leaf water (δ18Oleaf) is an important determinant of environmental and physiological information found in biological archives, but the system-scale understanding of the propagation of the δ18O of rain through soil and xylem water to δ18Oleaf has not been verified for grassland. Here we report a unique and comprehensive dataset of fortnightly δ18O observations in soil, stem and leaf waters made over seven growing seasons in a temperate, drought-prone, mixed-species grassland. Using the ecohydrology part of a physically based, 18O-enabled soil–plant–atmosphere transfer model (MuSICA), we evaluated our ability to predict the dynamics of δ18O in soil water, the depth of water uptake, and the effects of soil and atmospheric moisture on 18O enrichment of leaf water (Δ18Oleaf) in this ecosystem. The model accurately predicted the δ18O dynamics of the different ecosystem water pools, suggesting that the model generated realistic predictions of the vertical distribution of soil water and root water uptake dynamics. Observations and model predictions indicated that water uptake occurred predominantly from shallow (<20 cm) soil depths throughout dry and wet periods in all years, presumably due (at least in part) to the effects of high grazing pressure on root system turnover and placement. Δ18Oleaf responded to both soil and atmospheric moisture contents and was best described in terms of constant proportions of unenriched and evaporatively enriched water (two-pool model). The good agreement between model predictions and observations is remarkable as model parameters describing the relevant physical features or functional relationships of soil and vegetation were held constant with one single value for the entire mixed-species ecosystem.
- Article
(3505 KB) -
Supplement
(2248 KB) - BibTeX
- EndNote
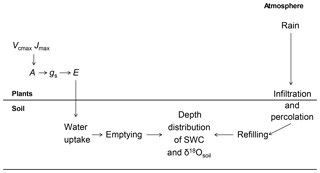
The stable oxygen isotope composition (δ18O) of meteoric water varies greatly in space and time. Meteoric waters impart their isotopic signal (δ18Orain) to that of soil water (δ18Osoil), changing it as a function of refilling, exchange and percolation processes throughout the soil profile. The oxygen isotope composition of leaf water (δ18Oleaf) differs from that of the water taken up from the soil, as leaf water becomes 18O-enriched due to evaporative effects and morpho-physiological controls (Barbour, 2007). As a consequence, δ18Oleaf carries important environmental and physiological information that is imprinted on photosynthetic products and archived in long-lived cellular compounds such as cellulose in tree rings (Farquhar et al., 2007; Barbour, 2007; Treydte et al., 2014; Lehmann et al., 2018). The δ18O of leaf water also imprints the oxygen isotope compositions of atmospheric CO2 and molecular oxygen, a property that can be used to estimate regional- and global-scale land primary productivity from seasonal to millennium timescales (Dole et al., 1954; Farquhar et al., 1993; Bender et al., 1994; Luz and Barkan, 2011; Wingate et al., 2009; Welp et al., 2011). A quantitative understanding of the hydrological and plant morpho-physiological mechanisms controlling δ18Oleaf is therefore fundamental to biological, Earth and environmental science disciplines (Barbour, 2007). This science, which explores relationships between the spatio-temporal dynamics of water in the soil–vegetation–atmosphere system with help of the dynamics of δ18O of water in the different components of the system, may be termed 18O ecohydrology.
Studies that deal with the δ18O in water and biomass compartments of grassland, the largest terrestrial biome after forest, are sparse (e.g. Flanagan and Farquhar, 2014; Webb and Longstaffe, 2003, 2006; Ramirez et al., 2009; Riley et al., 2002, 2003). To our knowledge, simultaneous observations of seasonal variations of the isotopic composition of the different water pools in a temperate grassland ecosystem over multiple years have not been reported so far. Only datasets covering short periods (e.g. Lai et al., 2008; Leng et al., 2013) or one single vegetation period (e.g. Wen et al., 2012) have been reported. In addition, our system-scale understanding of the propagation of the rainwater δ18O signal through soil water and plant xylem water to the leaf water has as yet not been verified for grassland. As a consequence, our quantitative knowledge of the drivers of δ18Oleaf in grassland ecosystems is limited.
The isotopic composition of the water taken up by plants (henceforth termed δ18Ostem) can vary over time through changes in the depth of soil water uptake by roots or direct changes in soil water isotopic composition. For example, summer rains in continental Europe are usually isotopically distinct (18O-enriched) relative to winter precipitation, generating intra-annual variations of δ18Osoil with soil depth. Apart from the temporal distribution of rainfall amounts and associated δ18Orain, the relationship between δ18Orain and δ18Ostem is affected by soil properties (that determine water storage, transport and mixing of rainwater with water stored at depth in the soil profile), the depth distribution of roots and their specific activities, and atmospheric conditions and vegetation properties (that determine transpiration as well as soil evaporation and associated enrichment of δ18Osoil near the soil surface). Assuming that root water uptake proceeds without 18O discrimination (Dawson et al., 2002), the comparison of δ18Osoil and δ18Ostem can help identify the depth of root water uptake (e.g. Durand et al., 2007) and how it changes during drought (e.g. Hoekstra et al., 2014; Nippert and Knapp, 2007a). So far, studies on potential shifts of root water uptake depth in C3 grassland communities during drought were mainly conducted using rainout shelters and comparing the water uptake depth in droughted and control plots (Hoekstra et al., 2014; Prechsl et al., 2015). Thus it is still unclear how edaphic drought arising under natural conditions modifies the root water uptake depth in C3 grassland communities over time, especially at a multi-seasonal timescale.
The mechanisms driving the isotopic enrichment of leaf water can be studied separately from those driving changes in δ18Ostem by expressing the isotopic composition of leaf water as enrichment above δ18Ostem; i.e. if the δ18O of water entering the leaf is the same as that taken up by the root system as a whole. The process of evaporative enrichment was first modelled by Craig and Gordon (1965) for open water bodies and adapted to leaves by Dongmann et al. (1974). Many authors have since noted a discrepancy between the 18O enrichment at the evaporative sites predicted by the Craig–Gordon model (Δ18Oe) and leaf water enrichment (Δ18Oleaf) (Cernusak et al., 2016). This discrepancy has been interpreted conceptually with two different models called the two-pool model (Leaney et al., 1985; Yakir et al., 1994) and the Péclet model (Farquhar and Lloyd, 1993; Farquhar et al., 2007). In the two-pool model, leaf water is assumed compartmentalised between evaporatively 18O-enriched water (supposed to represent mainly mesophyll cells) and unenriched water (supposed to represent veins and associated ground tissues). In the so-called Péclet model, the mixing of water isotopes within the leaf lamina is assumed incomplete because of a limited back diffusion of heavy water from the evaporative sites to the remaining leaf lamina as a result of the high tortuosity of the path of water within the mesophyll. This incomplete mixing is characterised by a Péclet number p, defined as the ratio of advection to back diffusion (Farquhar and Lloyd, 1993; Cuntz et al., 2007). The two models predict a different effect of transpiration rate on the proportional difference (φ) between the 18O enrichment predicted by the Craig–Gordon model and the observed 18O enrichment of leaf water: (Song et al., 2013; Cernusak et al., 2016). Because Δ18Oleaf, rather than Δ18Oe, imprints sugars (Barbour et al., 2000; Cernusak et al., 2003) and ultimately organic matter (Barbour and Farquar, 2000; Helliker and Ehleringer, 2002; Barbour, 2007), the choice of the model relating Δ18Oleaf and Δ18Oe has important implications. The Péclet model predicts an increase in φ with leaf transpiration while in the two-pool model φ does not respond to transpiration and is expected to be constant, at least on short (hourly to daily) timescales. Thus far, experimental and empirical studies on a large range of plant species have provided mixed results on these two alternative models of Δ18Oleaf, with some studies supporting the two-pool model and others the Péclet model (e.g. Barbour et al., 2000, 2004; Loucos et al., 2015; Song et al., 2015; Cernusak et al., 2016). The question as to which model is more appropriate for predicting the Δ18O of canopy-scale leaf water is particularly relevant for the modelling of Δ18Oleaf, and ultimately δ18Oleaf, at larger temporal and spatial scales.
In general, Δ18Oleaf responds strongly to changes in atmospheric humidity or the isotope composition of water vapour (e.g. Farquhar et al., 2007) and to changes in stomatal conductance (Wang and Yakir, 1995; Barbour and Farquhar, 2000; Helliker and Ehleringer, 2000; Xiao et al., 2012). However, it is generally not known whether edaphic drought, via its effect on stomatal conductance, indirectly affects the relative humidity response of leaf water enrichment. To our knowledge, the only study that reports a distinct effect of edaphic drought on Δ18Oleaf is that of Ferrio et al. (2012) on Vitis vinifera. Based on their results, and theoretical considerations regarding the effect of soil water availability on leaf stomatal closure and energy budget and associated 18O fractionation, one would expect a positive effect of edaphic drought on leaf water enrichment. Yet, whether or not drought exerts a measurable effect on Δ18Oleaf of grasslands, often found in climates with sporadic or prolonged drought periods, is not known.
The interpretation of the isotopic composition of water from samples collected in natural ecosystems is complicated by the fact that multiple environmental as well as site or plant morpho-physiological factors vary simultaneously, causing difficulties in disentangling the effect of different parameters on the water isotope composition. Hence, process-based ecosystem-scale models are key to aiding the interpretation of the water isotope signals in response to environmental and morphological parameters (e.g. Riley et al., 2003). Here we evaluate our system-scale ecohydrological understanding of the propagation of the δ18O signal of rainwater through soil water pools, root water uptake and 18O enrichment of leaf water in a drought-prone grassland ecosystem. For this, we systematically trace, predict and validate δ18Osoil, δ18Ostem and Δ18Oleaf and evaluate their sensitivity to input parameters. Specifically, we ask the following: what is the plant community's depth of root water uptake and does it shift in response to soil water scarcity? Is the two-pool model or the Péclet model more appropriate for describing Δ18Oleaf at the canopy scale? Does Δ18Oleaf respond to edaphic drought in grasslands? And, more generally, what is the sensitivity of soil, stem and leaf water δ18O to changes in soil and vegetation parameters that are suspected to alter ecosystem water dynamics? To explore these questions we compared predictions from the 18O-enabled soil–plant–atmosphere transfer model MuSICA (Ogée et al., 2003; Wingate et al., 2010; Gangi et al., 2015) with those observed in a unique, multi-annual dataset (7 years) of growing season (April to November), fortnightly samplings and δ18O analysis of soil water (at 7 and 20 cm depth), stem and midday leaf water, and atmospheric water vapour, along with rainfall amount and δ18Orain data. The experimental site (Schnyder et al., 2006) was an intensively grazed Lolio-Cynosuretum (Williams and Varley, 1967; Klapp, 1965) community with Lolium perenne, Poa pratensis, Dactylis glomerata, Phleum pratense, Taraxacum officinale and Trifolium repens as the main species. Vegetation samples were taken as mixed-species samples, as described below.
2.1 Study site
The study was performed inside pasture paddock no. 8 of the Grünschwaige Grassland Research Station near Freising, Germany (Schnyder et al., 2006). Mean annual air temperature from 2006 to 2012 was 9.3 ∘C, and mean annual precipitation was 743 mm, as measured at the Munich airport meteorological station 3 km from the field site. The soil is a Mollic Fluvisol, with a shallow topsoil of low water holding capacity (66 mm plant-available field capacity) overlying coarse calcareous gravel. The depth to the groundwater table is around 1.5 m.
During the main vegetation period (mid-April to beginning of November) the paddock was grazed continuously by Limousin suckler cows (Schnyder et al., 2006). Animal stocking density was adjusted periodically to maintain a constant sward height of about 7 cm. This management system aimed at maintaining a constant sward state by continuously balancing pasture grass production and consumption by the grazing cattle.
2.2 Sampling
Precipitation water was collected following events during the vegetation periods of 2007 to 2012 and during winter 2007/2008 (see Methods S1 in the Supplement). Leaf, stem, soil, groundwater and atmospheric moisture samples were collected on non-rainy days, between 11:00 and 16:00 CEST (Central European Summer Time). Sampling occurred at approximately fortnightly intervals during the vegetation periods from April 2006 to September 2012. Samples were collected at random locations in an area of about 1 ha in the vicinity of an eddy flux tower installed near the centre of the paddock. On each date, two replicate samples of leaf, (pseudo-)stem and soil were collected. Soil samples were taken at two depths (7 and 20 cm) using an auger. Leaf and stem samples were obtained as mixed-species collections of the co-dominant species: four C3 grasses (Lolium perenne, Poa pratensis, Phleum pratense, Dactylis glomerata), one rosette dicot (Taraxacum officinale) and one legume (Trifolium repens). Each leaf sample included all leaf blades, including the exposed part of the growing leaf but excluding senescing leaves (cf. Fig. 1 of Liu et al., 2017) from two vegetative tillers of D. glomerata and 16 vegetative tillers of L. perenne, P. pratensis and P. pratense, one half of a leaf blade of T. officinale (with the latter severed along, but not including, the midvein) and two trifoliate leaves of T. repens. This protocol ensured collection of the entire within-leaf evaporative 18O gradient of all sampled leaf blade tissue of the different species. Stem (xylem) samples comprised the midvein of T. officinale, the petioles of the two T. repens leaves and the basal part of the vegetative grass tillers, except for the outermost part that was removed as it could have been subject to evaporative enrichment (cf. pseudo-stem in Fig. 1 of Liu et al., 2017).
Atmospheric moisture was collected by pumping ambient air through a glass coil immersed in a dry ice–ethanol mixture at a flow rate of 1 L min−1 over periods of 2–6 h around noon. Groundwater was sampled from a well located at about 100 m upstream of the ground water flow beneath paddock no. 8.
All plant and soil samples were immediately transferred to 12 mL Exetainer vials (Labco, High Wycombe, UK), sealed and covered with Parafilm. All samples were stored in a freezer at approx. −18 ∘C until water extraction. Water was extracted for 2 h using a cryogenic vacuum distillation apparatus with sample vials placed in a water bath with a temperature set to 80 ∘C (Liu et al., 2016).
2.3 Isotope analysis
Oxygen isotope composition was expressed in per mil (‰) deviation relative to a standard:
where Rsample and Rstandard are the 18O∕16O ratios of the sample and the V-SMOW standard (Vienna Standard Mean Ocean Water). Samples collected between 2007 and 2012 were analysed by cavity ring-down spectroscopy using previously described procedures (Liu et al., 2016). Water samples collected in 2006 were analysed with an IsoPrime isotope ratio mass spectrometer interfaced with a multi-flow equilibration unit (both GVI, Manchester, UK). Each sample was measured against a laboratory standard gas, which was previously calibrated against secondary isotope standards (V-SMOW, V-SLAP and V-GISP). Heavy and light laboratory water standards, which spanned the range of δ18O values in the dataset, were analysed every five samples. Analytical uncertainty was 0.2 ‰. δ18O measurements obtained by cavity ring-down spectroscopy were linearly related to those obtained by isotope ratio mass spectrometry (n=176; R2=0.99). In a previous study, we found no difference between the results from spectroscopy-based and pyrolysis-based measurements performed using a TC/EA HTC coupled to an isotope ratio mass spectrometer (see Liu et al., 2017).
2.4 MuSICA modelling
The isotope-enabled soil–plant–atmosphere model MuSICA (Ogée et al., 2003, 2009; Wingate et al., 2010; Gangi et al., 2015) was parameterised for the studied grassland based on data collected at the site or taken from the literature (for details and parameter values, see below and Methods S2 and Table S1).
The model was validated with latent energy flux (LE) data obtained from an eddy covariance station (EC) at the site. According to that comparison (Fig. S1), MuSICA estimates were unbiased (LEMuSICA=0.997LEEC; R2=0.59). Further, we compared MuSICA predictions of total plant-available soil water (PAW, mm) in the entire topsoil with PAW modelling and data for the same site presented in Schnyder et al. (2006). For the 2007–2012 data, this yielded the relationship .
Although the MuSICA model is capable of simulating δ2H of water pools in the soil–plant system, we excluded those data in the paper, as (1) we are primarily interested in the processes leading up to the δ18O of cellulose, (2) we had noticed discrepancies in the model–data agreement for 2H∕1H indicating fractionation (including a surface effect on 2H∕1H of soil water at the experimental site; Chen et al., 2016) that are currently not accounted for in the model, and (3) we did not want to overload the paper with extra figures and discussion. Issues of 2H∕1H fractionation of water including data from this experimental site will be addressed in a separate paper.
2.4.1 Meteorological forcing and isoforcing
MuSICA was forced by half-hourly values of meteorological data and δ18O of water vapour (δ18Ovapour) and rainwater (δ18Orain). Wind speed, precipitation, air temperature, relative humidity and air pressure data were obtained from the Munich airport meteorological station, located at about 3 km south of the experimental site. Radiation was calculated as the mean of two weather stations located 10 km west and 12 km east of the experimental site. CO2 concentration was measured at the site by an open-path infrared CO2∕H2O gas analyser (LI-7500, LI-COR, Lincoln, USA). For δ18Ovapour and δ18Orain, observations at the experimental site were used whenever available. Otherwise δ18Ovapour and δ18Orain estimates were obtained from globally gridded reconstructions derived from the isotope-enabled, nudged atmospheric general circulation model IsoGSM (Yoshimura et al., 2011). The IsoGSM-predicted δ18Ovapour and δ18Orain at the grid point relevant to our site were first corrected for their offset with observed data, as predictions were found to be more enriched by 2 ‰ and 1.3 ‰ on average compared to the δ18Ovapour and δ18Orain measured at the site (Figs. S2–S4).
2.4.2 Soil parameters
Soil structural properties (proportion of quartz and organic matter) as well as hydraulic characteristics (water retention and hydraulic conductivity) were determined on soil core samples taken at the site (Methods S2 and Fig. S5). In MuSICA, the δ18O of soil water is predicted based on liquid- and vapour-phase water isotope transport in the soil column and evaporative enrichment during soil evaporation. MuSICA allows two alternative formulations of the liquid water and water vapour effective diffusivities through the soil matrix. In the first formulation, these effective soil diffusivities increase linearly with the soil volumetric content of the liquid or vapour phase (Penman, 1940), while in the other formulation, proposed by Moldrup et al. (2003), the influence of the pore-size distribution parameter and the total soil porosity is also taken into account. Here, we explore the consequences of using either the Penman or Moldrup soil diffusivity formulation on the prediction of the δ18O of soil, xylem and leaf waters.
2.4.3 Canopy and gas exchange parameters
Grassland vegetation at the experimental site was parameterised in terms of canopy structure, the gas exchange properties of leaves, and root distribution and hydraulic properties (Table S1). In theory, MuSICA could account for species mixtures and competition for water and light, but this would require parameters for every single species. As the mixed-species samples were dominated by L. perenne and P. pratensis with closely similar morpho-physiology, we treated the vegetation sample as one plant type, described with one parameter set (Table S1).
The mean leaf area index (LAI; 2.6±0.7 m2 m−2) and the mean leaf zenithal angle (LZA; , corresponding to a leaf inclination index (LII) close to zero, typical of a spherical leaf angle distribution) were estimated from compressed sward height measurements made throughout the 2005 to 2012 grazing seasons (n=74 dates with a total of more than 7000 measurements) and calibration functions obtained from parallel measurements of compressed sward height, uncompressed sward height (estimated with a ruler), LAI and leaf zenithal angle (both determined with a LAI-2000, LI-COR, Nebraska, USA) at the site. The vertical distribution of leaf area in the canopy was described based on Wohlfahrt et al. (2003) (Fig. S6). In the standard parameterisation, LAI and LII were set as constants, in agreement with the constant sward state imposed by management practices (see above). In the sensitivity analyses, we also tested the effect of observed variations of sward height, LAI and LII on modelled δ18O of the different water compartments.
Leaf turnover is generally high in grassland (Chapman and Lemaire, 1996), including at our experimental site (Schleip et al., 2013). Thus, the co-dominant species (L. perenne, P. pratensis, T. officinale and T. repens) had a short and very similar mean leaf life span of ∼460 growing degree days (GDD, with a base temperature of 4 ∘C) throughout the vegetation period (Schleip et al., 2013). As leaf turnover is high, the photosynthetic characteristics of leaves were set constant in the standard parameterisation. Leaf photosynthesis was modelled according to the Farquhar–von Caemmerer–Berry model (Farquhar et al., 1980). Values for the maximum rate of carboxylation (Vcmax), the light-saturated potential rate of electron transport (Jmax) and other photosynthetic parameters were all taken from literature (Table S1). Leaf respiration rate was estimated from measurements made in the dark at the site (Ostler et al., personal communication, 2018) and was assumed to be partly inhibited during the day (e.g. Atkin et al., 1997).
Under well-watered conditions, stomatal conductance for water vapour (gs) was simulated according to the Ball–Woodrow–Berry (BWB) model (Ball et al., 1987). This model has two parameters: mgs, a species-specific non-dimensional parameter that determines the composite sensitivity of gs to net CO2 assimilation and to relative humidity and CO2 concentration at the leaf surface; and g0, the basal (or minimal) stomatal conductance. Uncertainties exist regarding the slope parameter mgs and the intercept g0 (Miner et al., 2017, and references therein). Values for mgs reported by Wohlfahrt et al. (1998) for 13 grassland species from differently managed sites ranged between 6.9 and 24.7, and values for the intercept g0 (termed gmin in their work) ranged between 12 and 193 mmol m−2 s−1. Likewise, a considerable range of night-time stomatal conductance (gnight) has been reported for C3 grasses: from 60 to 140 mmol m−2 s−1 (Ogle et al., 2012; Press et al., 1993; Snyder et al., 2003). Here, gnight (together with leaf water content W; see below) was manually adjusted by fitting MuSICA to diurnal measurements of leaf water δ18O (Fig. S7). In the standard simulation, we used mgs=10, a commonly used value for C3 vegetation (see Miner et al., 2017); g0=10 mmol m−2 s−1; and gnight=30 mmol m−2 s−1. Although the diurnal pattern of δ18Oleaf (Fig. S7) indicated some nocturnal stomatal conductance, the model generally predicted very low night-time transpiration, in agreement with the eddy flux data (Fig. S1) and the generally high nocturnal relative humidity. Finally, we tested the sensitivity of model predictions to variations of mgs and g0 (see below).
The effect of edaphic drought on gs was considered by scaling mgs and g0 with a function of predawn leaf water potential (Nikolov et al., 1995). This adds two extra model parameters whose values were sourced from the literature (Table S1) and results in a 50 % reduction of mgs and g0 at −1.5 MPa.
Characteristic dimensions of leaves and shoots for the calculation of boundary-layer conductance were estimated based on measurements on individual grass tillers. The width and length (0.1 and 7 cm, respectively) of the leaf blade of a 7 cm tall grass tiller were taken as minimum and maximum values for the leaf dimensions, and the average leaf dimension was estimated as the square root of the area of such a leaf blade (0.8 cm). Values for minimum, maximum and average shoot dimensions were taken from sward height measurements (see above). The shelter factor was varied between 1 and 3.5 (Monteith and Unsworth, 1990), with very little consequences on the results. Parameter values for leaf optical properties, rain interception and wind attenuation were taken from the literature (Table S1).
In the model, total rooting depth was equated with topsoil depth (37 cm), as in Schnyder et al. (2006). The vertical distribution of fine roots in the soil column was assumed to follow a beta distribution (e.g. Sadri et al., 2018) with a maximum at 7 cm belowground (Fig. S8). The total amount of roots (g m−2 of soil) was obtained from soil core sampling. The proportion of live roots was derived from a 14 d long dynamic 13CO2∕12CO2 labelling experiment at the same site (Gamnitzer et al., 2009; Schleip, 2013; Ostler et al., 2016; Ostler et al., personal communication, 2018). Root mass data were converted to root lengths by assuming a specific root length of 100 m g−1 (Picon-Cochard et al., 2012). Mean fine root radius was set to 0.15 mm (Picon-Cochard et al., 2012) and root xylem radial hydraulic resistance to 1.0×1012 s m−1.
2.4.4 Oxygen isotope composition of water pools
The steady-state 18O enrichment of leaf water at the evaporative site (Δ18Oe, ss) was calculated as (Farquhar and Lloyd, 1993; Farquhar and Cernusak, 2005)
where h is the air relative humidity, normalised at leaf temperature (estimated from the leaf energy budget); Δ18Ov represents the isotopic composition of atmospheric water vapour, expressed above that of xylem water; α+ is the isotope fractionation during liquid–vapour equilibrium at leaf temperature (Majoube, 1971); and αk is the kinetic isotope fractionation during water vapour diffusion through stomata and leaf boundary layer. αk was estimated at half-hourly time steps from stomatal and boundary-layer conductances for water vapour (gs and gb):
Equation (3) uses the kinetic fractionation factor during molecular diffusion (28 ‰) reported by Merlivat (1978) and assumes laminar diffusion through the leaf boundary layer (Farquhar et al., 2007).
We modelled leaf water isotope enrichment at isotopic steady state (Δ18Oleaf, ss) using the two approaches introduced earlier. In the two-pool simulation, we used a constant value for φ of 0.39, which was chosen such that the observed Δ18Oleaf was on average predicted without bias. In the sensitivity analysis, φ was varied between −0.20 and 0.50 based on the range of values reported previously for a variety of grass species (Helliker and Ehleringer, 2000; Gan et al., 2003; see Sect. 4.3). In the Péclet simulation, Δ18Oleaf, ss was related to Δ18Oe, ss using the Péclet number, as described by Farquhar and Lloyd (1993):
with p the Péclet number. The latter is calculated as , where L (m) is the effective path length, E (mol m−2 s−1) is the leaf transpiration rate, C=55 500 mol m−3 is the molar density of liquid water and D (m2 s−1) is the diffusivity of in liquid water (Farquhar and Lloyd, 1993; Cuntz et al., 2007). In line with the original notion of the Péclet model, one single value of L was applied to the dataset, which was again adjusted such that Δ18Oleaf was predicted without bias.
Two supplementary experiments were also conducted to directly test the relevance of the Péclet effect in the co-dominant pasture species L. perenne and D. glomerata. These are described in the Supplement.
As leaf water is not in isotopic steady state for extended periods of the day (Fig. S9), an equation for non-steady-state enrichment of leaf water was used in addition to Eqs. (2)–(4). Using isotopic mass balance of leaf water and assuming that Eq. (4) holds true also in the non-steady state (Farquhar and Cernusak, 2005), the time evolution of Δ18Oleaf was modelled as (see also Farquhar et al., 2007)
where W (mol m−2) denotes leaf water content, expressed on a leaf area basis.
A 27 h time series of community-scale δ18Oleaf observed at the site in August 2005 (Fig. S7) was used to fine-tune the parameters controlling leaf water enrichment in MuSICA (leaf water content and night-time and minimum stomatal conductance) within the range of values expected for temperate grasslands (for parameter values see Table S1). Because MuSICA predicts different leaf-level variables (e.g. gs, gb, h, E, Δ18Oleaf, ss) for sunlit, shaded, wet or dry leaves at different levels within the canopy, water-volume-weighted canopy averages of δ18Oleaf and Δ18Oleaf were first calculated at every time step before performing comparisons with observed data.
2.5 Sensitivity analysis
A sensitivity analysis was conducted in order to quantify the responsiveness of predicted midday δ18O of leaf, stem and soil water to plant morpho-physiological parameters that were expected to affect those predictions based on theoretical considerations and/or observed parameter variation at the site. As the leaf water enrichment submodels are embedded in the process-based model MuSICA, the effect of parameters not included in the leaf water δ18O models per se could be evaluated. Based on the ceteris paribus principle, the sensitivity was tested by varying one parameter while keeping all other parameters the same as in the standard MuSICA parameter set (Table S1). For a sensitivity run, the parameter was not decoupled from the equations in MuSICA; hence changing one parameter value at the same time affected all equations containing this parameter and all dependent variables. Parameter effects (sensitivities) were quantified by two variables: (1) the mean sensitivity relative to the reference run, obtained as the mean differences from the reference run as (, with δsens, i the δ18O of a given water compartment (leaf, stem, or soil at 7 or 20 cm depth) in a sensitivity run and δref, i that in the reference run, for a day i; and (2) the standard deviation of the sensitivity, obtained from the differences between δsens, i and δref, i. The latter illustrated how strongly the effect of a parameter varied between sampling days and hence how strongly it depended on the conditions encountered on one specific day. Thus, the sensitivity variables reported if changes in parameter values caused systematic/general effects (shown by the mean sensitivity), or cancelling effects (shown by the standard deviations of the sensitivity), or combinations, or lack of the two.
The high and low parameter values for the sensitivity analyses were chosen according to the range observed for grasses or grassland species, as reported in the literature or observed at the site (see Supplement). Values for individual parameters of the sensitivity analysis were set at −0.20 and 0.50 for φ, 1 or 12 mol m−2 for leaf water content (W), 7 or 25 for the slope of the BWB model (mgs), 0 or 193 mmol m−2 s−1 for the intercept of the BWB model (g0), 0.6 or 3.8 m2 m−2 for leaf area index (LAI), 3.6 or 11.7 cm for canopy height (hcanopy), 20 or 140 µmol m−2 s−1 for the maximum rate of carboxylation at 25 ∘C (Vcmax), 32 or 224 µmol m−2 s−1 for potential rate of electron transport at 25 ∘C (Jmax), and 0.08 or 0.265 m for the mean of the vertical root distribution (μroot). Vcmax and Jmax were altered in tandem to keep the ratio Jmax∕Vcmax at 1.6 (Medlyn et al., 2002), the same as in the standard simulation (Table S1). Apart from those plant morpho-physiological parameters, the effect of alternative submodels for the liquid and vapour effective diffusivity in the soil was tested by replacing the Moldrup formulation by the Penman one. In addition, we investigated the effect of using uncorrected IsoGSM-predicted δ18Orain and δ18Ovapour data instead of local isotopic data (gap-filled with offset-corrected IsoGSM data; see Sect. 2.4.1) for the isoforcing of MuSICA. This served to illustrate the usefulness of having local rainwater δ18O data.
2.6 Statistics
For comparison of predicted and observed data, we calculated the mean bias error (, where is the mean predicted value and the mean observed value) between observed and predicted δ18O (or Δ18O), the mean absolute error (), where Pi is the predicted and Oi is the observed value at time i, and n is the number of values; Willmott and Matsuura, 2005), and R2 values.
Simple and multiple linear regression analyses and Student t tests were performed in R, version 3.4.2 (R Core Team, 2017), and RStudio, version 1.1.383 (RStudio Team, 2017).
3.1 Rainfall, δ18O of precipitation and vapour
Growing season rainfall amounts and distribution differed between years, with total precipitation in the main growing period (May to August) varying between 321 mm (2006) and 514 mm (2010) (Fig. 1a). The mean δ18Orain signal tended to increase in the first half of the vegetation period and decrease later in the season (Fig. 1b). However, individual rain events sometimes differed markedly from the mean pattern, with excursions of up to +4.5 ‰ and −6.2 ‰ relative to the mean of the same month (Fig. 1b). The δ18Ovapour signal followed similar mean trends (Fig. 1c) and exhibited a significant correlation (P<0.001) with the δ18O of the previous rain event.
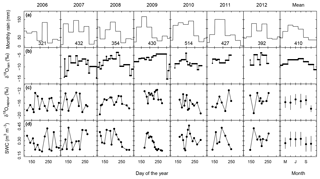
Figure 1Multi-seasonal (2006–2012) and average patterns of monthly rainfall sums (a), δ18O of rain (δ18Orain) (b), δ18O of atmospheric vapour (δ18Ovapour) (c), and volumetric soil water content (SWC, m3 water m−3 soil) at 7 cm depth as predicted by the standard MuSICA simulation (d). Permanent wilting point: 0.19 SWC; field capacity: 0.49 SWC. δ18Ovapour refers to measurements at the experimental site during the vegetation and soil sampling. δ18Orain was determined following individual rains during the vegetation periods of 2007 to 2012. Rainfall data were taken from the DWD weather station of Munich airport, located at the same altitude ∼3 km south of the experimental site. The rainfall amount in the main growing period of each year (May to August) is given at the bottom of each panel in (a). Groundwater, at ∼1.5 m below the soil surface, had an average δ18O of 10.0 ‰ (±0.4 ‰ SD).
3.2 Soil water
The observed δ18Osoil was generally more enriched at 7 cm than at 20 cm belowground (Table 1; Fig. 2a, b). This relative enrichment with shallower depth was particularly large in the first half of the vegetation period and averaged 1.7 ‰ in the entire dataset. The total observed range of δ18Osoil differed somewhat between the two depths and was 7.8 ‰ at 7 cm, i.e. 16 % greater than at 20 cm (Table 1).
Table 1Minimum, maximum, mean and range for the observed δ18O of grassland ecosystem water pools (soil water at 20 and 7 cm depth, and stem and bulk leaf water) and 18O enrichment of leaf water (Δ18O). Samples were collected at approximately fortnightly intervals during the vegetation periods of 2006–2012.
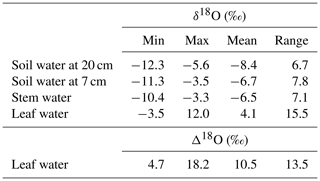
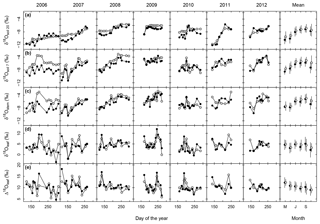
Figure 2Multi-seasonal (2006–2012) and monthly average variation of δ18O in grassland ecosystem water pools: soil water at 20 (a) and 7 cm depth (b), stem (c) and leaf water (d), and 18O enrichment (Δ18O) of leaf water (e), as observed (closed symbols) or predicted by the standard MuSICA simulations including a two-pool leaf water model (light grey). The parameters for the standard MuSICA simulations are given in the Supplement (Table S1). The error bar in the monthly mean data displays the standard deviation.
In most years, δ18Osoil followed the rain pattern and increased during the course of the vegetation period at both depths (Fig. 2a, b). This increase was generally more pronounced at 7 cm than at 20 cm. Overall, the seasonal patterns of δ18Osoil were quite dynamic, with considerable differences between individual years.
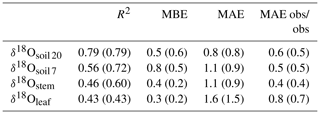
MuSICA simulations with the standard parameterisation (Table S1) predicted the multi-seasonal dynamics of δ18Osoil well (Fig. 2a, b) except in 2006 when local data of δ18Orain were not available for the isoforcing (Fig. 1b) and δ18Orain data were taken from the global atmospheric model IsoGSM, once corrected for the mean model–data offset (Figs. S2–S4). The seasonal trends and monthly fluctuations of observed δ18Osoil were reproduced with relatively small error (MAE of 1.1 ‰ and 0.8 ‰ at 7 and 20 cm, respectively). Also, the bias was small as MuSICA overestimated δ18Osoil by 0.8 ‰ and 0.5 ‰ at 7 and 20 cm, respectively.
Volumetric soil water content (SWC) predicted by MuSICA using the standard parameterisation (Table S1) exhibited strong seasonal and inter-annual variations. With SWC values (in m3 m−3) expected to vary between 0.19 (permanent wilting point) and 0.46 (field capacity), a SWC of less than 0.25 at 7 cm belowground corresponds to <25 % of the maximum plant-available water at this depth and is therefore a good indicator of edaphic drought. Each year, soil moisture at 7 cm fell below this threshold, but with a timing that differed from one year to the next (Fig. 1d).
3.3 Stem water
Observed δ18Ostem generally matched and followed that of δ18Osoil at 7 cm, independently of SWC, season and year (Figs. 2b, c, 3a and S10). Conversely, the relationship between δ18Ostem and δ18Osoil at 20 cm was generally weak, exhibiting large scatter and a significant offset between δ18Ostem and δ18Osoil at 20 cm for most of the data (Fig. 3c). Remarkably, for 90 % of all days on which the soil was classified as “dry” (predicted SWC<0.25), δ18Ostem was still closer to δ18Osoil at 7 cm than to δ18Osoil at 20 cm.
Barnard et al. (2006) showed that the δ18O of (pseudo-)stem water in grasses is very close to that of the water taken up by the root systems of grasses (see also Liu et al., 2017), meaning that root water uptake operates without 18O isotope fractionation. MuSICA simulations were based on this assumption and reproduced very similar relationships between δ18Ostem and δ18Osoil to those observed at both depths, with similar R2, MBE and MAE (Figs. 2–3), thus showing a close agreement between observed and predicted data. Importantly, the close correspondence of δ18Ostem with δ18Osoil at 7 cm depth was not affected by changes in SWC predicted by MuSICA (Fig. 3). Again, the strongest disagreement between predicted and observed δ18Ostem occurred in 2006 (Fig. 2c), when observations of local δ18Orain were unavailable.
3.4 Leaf water
Midday leaf water δ18O (δ18Oleaf) exhibited by far the greatest observed δ18O variations in the entire dataset (Table 1). Also, δ18Oleaf was unique in the way that it did not exhibit a general trend during the vegetation period (P=0.5; right panel in Fig. 2d). As on average δ18Ostem increased over the vegetation period while δ18Oleaf did not, Δ18Oleaf exhibited a significant decreasing trend over the vegetation period, with a decrease of 0.5 ‰ per month (P=0.01; right panel in Fig. 2e), in parallel with the increasing trend of relative humidity over the growing season (data not shown). Conspicuous short-term, parallel increases/anomalies of δ18Oleaf and Δ18Oleaf (i.e. changes in δ18Oleaf largely independent of variations of δ18Ostem) occurred occasionally in different years, e.g. in spring of 2008, late spring and early fall of 2009, and early summer of 2010.
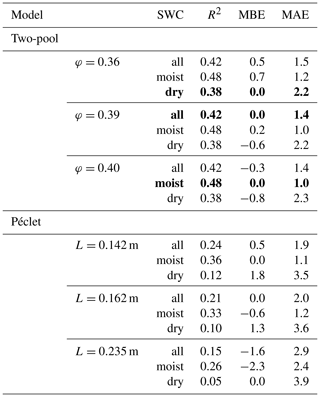
Predictions of Δ18Oleaf with MuSICA agreed best with observations using the two-pool model with φ=0.39 (R2=0.42; Table 2) in the standard MuSICA parameterisation. This result was robust for different soil water conditions. Unbiased predictions of Δ18Oleaf were best obtained by decreasing φ by 0.03 (i.e. setting φ to 0.36) under dry soil conditions (SWC<0.25) and increasing it by 0.01 (i.e. setting φ to 0.40) under moist soil conditions (SWC≥0.25), but this was an insignificant adjustment that did not change the overall coefficient of determination between observed and predicted Δ18Oleaf.
Table 2R2, mean bias error (MBE) and mean absolute error (MAE) for the comparison between predicted and observed δ18Oleaf, δ18Ostem and δ18Osoil at 7 cm (δ18Osoil 7) or 20 cm depth (δ18Osoil 20). Predictions were made with the standard MuSICA parameterisation given in Table S1. Values in parentheses exclude the data from year 2006. The last column presents the MAE between the replicate samples collected on the different dates. MBE and MAE values are given in per mil (‰).
The agreement between observed and predicted Δ18Oleaf was always weaker when using the Péclet model. Fixing the effective path length (L) at a certain value led to predictions that were systematically biased for either dry or moist soil conditions (Table 3). Unbiased predictions of Δ18Oleaf in conditions of different SWC were only obtained when increasing L (from 0.162 to 0.235 m) for dry soil conditions and decreasing L for moist soil conditions (from 0.162 to 0.142 m).
MuSICA predictions of δ18Oleaf and Δ18Oleaf obtained with the standard parameterisation agreed well with observations at all timescales (Figs. 2d, e, S7 and S9), with low or no bias (MBE of 0.3 ‰ and 0.0 ‰, respectively) and a MAE for δ18Oleaf of 1.6 ‰, i.e. 10 % of the total variation of δ18Oleaf in the entire dataset (Tables 1, 2). Also, the relationship between modelled transpiration rate and the proportional difference between the observed Δ18Oleaf and Δ18O predicted by the Craig–Gordon model (Fig. S11) was non-significant, revealing no evidence of a Péclet effect. This was also true when investigating that relationship with a subset of the data that included only the leaves that exhibited near-steady-state 18O enrichment. This subset was estimated using model output to identify the times when near-steady-state conditions were most likely and included about half of the data (results not shown).
Table 3R2, mean bias error (MBE) and mean absolute error (MAE) for the comparison between predicted and observed Δ18Oleaf obtained with different values of the proportion of unenriched leaf water (φ) in the two-pool model or effective path lengths (L) in the Péclet model for the prediction of Δ18Oleaf. Best predictions are highlighted in bold print. The agreement between predictions and observations was tested for the entire dataset (n=83) or the moist (SWC≥0.25; n=57) or dry soil subsets (SWC<0.25; n=26). The standard MuSICA parameterisation used a constant φ=0.39 for all conditions in all years. MBE and MAE values are given in per mil (‰).
3.5 Relationships between soil and atmosphere water status, transpiration, canopy conductance and 18O enrichment of bulk leaf water
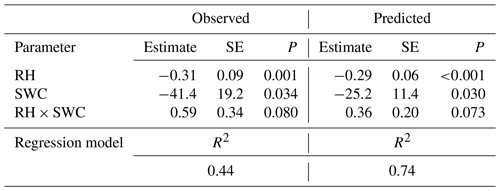
Multiple regression analysis demonstrated significant effects of air relative humidity (P<0.01) and SWC (P<0.05) on both observed and predicted Δ18Oleaf (Table 4). Δ18Oleaf increased with decreasing air relative humidity and SWC (Figs. 4a, b and 5a, b). The interaction effect of air relative humidity and SWC was close to significant for both observed (P=0.080) and predicted (P=0.073) Δ18Oleaf (Table 4). The effect of dry soil conditions on Δ18Oleaf was most evident at low air humidity (Figs. 4a, b and 5a, b) and was connected with a decrease in canopy conductance (gcanopy) (Fig. 5c).

Figure 3Correspondence between the δ18O of stem water and soil water at 7 cm (observed, a; and predicted, b) and at 20 cm depth (observed, c; and predicted, d). Colour strength indicates soil water content at 7 cm depth as predicted by MuSICA with standard parameterisation: light blue, dry soils; dark blue, soils near field capacity (for colour coding to SWC scale, see Fig. 4). The R2, MBE and MAE for the relationship between δ18Ostem and the δ18Osoil at 7 cm depth were 0.69, 0.2 ‰ and 0.7 ‰ for the observed data (a) and 0.65, −0.2 ‰ and 0.7 ‰ for the predicted data (b). Conversely, the R2, MBE and MAE values for the relationship between δ18Ostem and the δ18Osoil at 20 cm depth were 0.34, 1.9 ‰ and 2.1 ‰ for the observed data (a) and 0.17, 1.8 ‰ and 1.9 ‰ for the predicted data (b). The straight lines represent the 1:1 relationship.

Figure 4Relationship between relative humidity of air (RH) and observed Δ18Oleaf (a) and predicted Δ18Oleaf (b), and modelled response of transpiration to observed vapour pressure deficit (VPD) (c). Strength of blue colour from light to dark indicates the soil water content (SWC) at 7 cm depth as predicted by MuSICA with standard parameterisation. Permanent wilting point: 0.19 SWC; field capacity: 0.49 SWC. Predicted Δ18Oleaf data and transpiration rates were obtained with MuSICA in standard parameterisation and a two-pool leaf water model. Multiple regression analysis revealed effects of both RH and SWC on Δ18Oleaf (see Table 4).
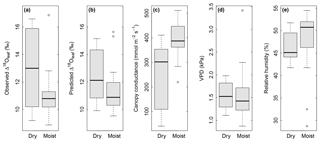
Figure 5Box plots showing the effect of soil water content (“dry” in comparison with “moist”) on observed Δ18Oleaf (a), predicted Δ18Oleaf (b), and modelled canopy conductance, gcanopy (c), under conditions of low air relative humidity (<55 % RH). Differences between dry and moist soil conditions were significant at P=0.03 (a), 0.06 (b) and 0.003 (c). At the same time, observed air VPD (d) and relative humidity (e) did not differ between dry and moist soil for the displayed subset (RH<55 %). Dry soil was defined as <0.25 SWC (n=12) and moist soil as ≥0.25 SWC (n=29) at 7 cm depth. With a permanent wilting point of 0.19 SWC and a field capacity of 0.49, a SWC<0.25 corresponded to less than 25 % of the maximum plant-available water at 7 cm.
Table 4Results of a multiple regression analysis of the effects of relative humidity (RH) and soil water content (SWC) on 18O enrichment of leaf water as observed and as predicted by MuSICA with standard parameterisation. SE, standard error; P, significance level.
The modelled dependence of transpiration on air VPD (vapour pressure deficit, the climatic driver of transpiration) was strongly modified by SWC (Fig. 4c). High air VPD drove high transpiration rates only under wet soil conditions (SWC≥0.25).
3.6 Sensitivity analysis
Increasing (decreasing) the proportion of unenriched leaf water (φ) and leaf water content (W) led to a strong reduction (increase) in δ18Oleaf (Fig. 6a, b). These changes in leaf-level parameters had no effect on δ18Osoil or δ18Ostem. Alterations of stomatal responsiveness (mgs), minimum conductance (g0), LAI or maximum carboxylation (Vcmax) and electron transport (Jmax) rates had similar directional effects (reflected by the mean sensitivity in relation to the standard simulation) on predicted δ18O of soil, stem and leaf water. However, the strength of the effects differed for the different ecosystem water pools (Fig. 6). Stronger effects were found on δ18Oleaf and δ18Osoil at 20 cm, compared to δ18Ostem or δ18Osoil at 7 cm that tended to vary in close harmony. Generally, a change in the parameter value caused an opposite change in the predicted δ18O of a given pool. Moreover, these parameters caused strong cancelling effects, evidenced by large standard deviations of the sensitivity, particularly for δ18Oleaf. The sensitivity of δ18Osoil to plant morpho-physiological parameters was related to the effect of those parameters on plant transpiration rate (not shown), which in turn altered the residence time of soil water at the lower depth. For example, lower Vcmax and Jmax values, not accompanied by a change in stomatal responsiveness mgs, implied a decrease in transpiration rate and consequent increase in the percolation of growing season rain water to the lower part of the soil profile (Figs. 7a and 8). In comparison, the 18O-depleted (winter) signal persisted longer in the lower profile at intermediate (Fig. 7b) or high (Fig. 7c) Vcmax and Jmax, as linked higher transpiration rates caused greater drying of the topsoil and reduced replenishment of deeper soil layers by summer rainfall.
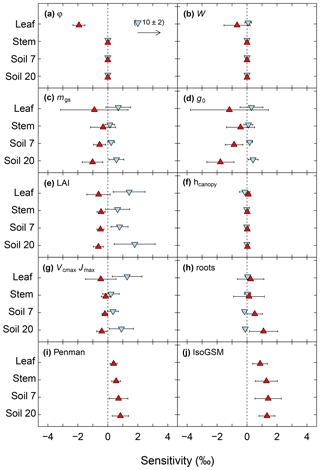
Figure 6Sensitivity of modelled midday δ18O of leaf, stem and soil water at 7 and 20 cm depth to various parameters of the MuSICA model. The sensitivity was tested by varying one parameter while keeping all other parameters the same as in the standard MuSICA parameter set (Table S1), as detailed in 2.5. Sensitivity (parameter effect) was quantified by two variables: the mean (or average) sensitivity (in ‰) resulting from the change in a parameter value relative to the reference run, and the standard deviation of the sensitivity which captures the variability of the response to a parameter change for the different sampling times (displayed by error bars). Strong averaging (cancelling) effects resulting from the change in a parameter value are revealed by large standard deviations of sensitivities. Note that the sensitivity analysis revealed four different combinations of parameter effects: (1) strong mean sensitivities without cancelling effects, (2) strong mean sensitivities superposed with strong cancelling effects, (3) small mean sensitivities resulting from strong cancelling effects or (4) absence of sensitivities unrelated to cancelling effects. Parameter identity is given in the upper left corner of each panel. In (a) to (h), blue down-pointing triangles refer to the low parameter value and red up-pointing triangles to the high parameter value of a sensitivity run, based on the range of values observed at the site or – where such values were missing – the range of reported values for grasses or grassland in literature (see Sect. 2). In (i) the Moldrup submodel for the water vapour effective diffusivity in the soil was replaced by the Penman model. In (j) we used IsoGSM-predicted δ18Orain and δ18Ovapour data instead of locally determined δ18Orain and δ18Ovapour data for the isoforcing of MuSICA. Note that the low parameter value for Péclet number (a) predicted a far greater deviation of δ18Oleaf than any other parameter.
Apart from LAI, other shoot characteristics, such as canopy height (Fig. 6f), leaf inclination, shoot shelter factor, leaf size and shoot size (not shown), had a very small or no effect on predicted δ18Oleaf, δ18Ostem and δ18Osoil.
The formulation of the water vapour diffusivity through the soil matrix (Fig. 6i) and the average rooting depth (Fig. 6h) affected δ18Osoil (and more strongly so at the lower depth), while the effect on δ18Ostem and δ18Oleaf was much weaker. Not accounting for the pore-size soil particle distribution parameter in the soil diffusivity formulation caused a greater overestimation of δ18Osoil, especially at 20 cm belowground where the MBE reached 1.3 ‰, compared to 0.5 ‰ in the standard run. Shifting the root distribution closer to the soil surface had little effect on δ18Osoil at both depths. Conversely, shifting it towards greater depth (Fig. S8) led to an overestimation of δ18Osoil, especially at 20 cm (Fig. 6h), and increased MAE in the relationship between δ18Ostem and δ18Osoil at both soil depths (not shown).
We also tested the effect of the choice of the water isotope forcing of MuSICA (δ18Orain and δ18Ovapour). In general, the agreement between predicted and observed ecosystem water pool δ18O was much better when MuSICA was forced using locally measured δ18Orain and δ18Ovapour data (Fig. 6j). The MBE for the δ18O of the different water pools was 3.1 to 6.7-fold greater when using the IsoGSM-based isotope forcing, and the MAE was 1.5 to 2.6-fold higher.
4.1 Model realism
An isotope-enabled, process-based soil–plant–atmosphere model, MuSICA, generated realistic predictions of multi-seasonal dynamics of δ18O in soil, (pseudo-)stem and midday leaf water, as well as of the 18O enrichment of leaf water in a drought-prone temperate grassland ecosystem. Throughout the vegetation periods of seven consecutive years (1) model bias (MBE) was low, (2) the range of δ18O variations of the different ecosystem water pools was similar in the predictions and observations, and (3) prediction error (MAE) was less than 15 % of the total observed range of δ18O in the different ecosystem water pools and about twice the size of the MAE for the duplicate samples of the different pools. The relationships between observed Δ18Oleaf and variables related to the water cycle such as SWC, air relative humidity, transpiration and canopy conductance were well captured by the model. Although MuSICA is a detailed and locally parameterised model, this general agreement between model predictions and observations is remarkable given that model parameters describing the relevant physical features or functional relationships of soil and vegetation were held constant with one single value for the entire mixed-species ecosystem. This is a striking outcome given that predicted δ18O were found to be sensitive to several (but not all) plant morpho-physiological parameters (Fig. 6). The greater scatter in the observed relationship between Δ18Oleaf and relative humidity compared to predictions (Fig. 4) likely resulted partly from sampling effects and error. Sampling effects could include small-scale spatial variation of soil properties, or spatio-temporal variation of LAI, nutrient levels and root distribution, a regular feature of grazed grassland (e.g. Schnyder et al., 2006, 2010). Also, Webb and Longstaffe (2003) observed differences of several per mil in δ18Osoil in the top 5 cm over distances of about 10 m in a sand dune grassland. Such spatial variations would inherently cause greater scatter in the observations compared to the model predictions.
Prediction of δ18Ostem at a given point in time is a real challenge, as δ18Ostem is influenced by numerous factors, including the temporal distribution of rainfall amounts and its associated isotopic composition, transport and mixing of rainwater with soil water, the depth distribution of root water uptake in the soil, and soil evaporation. These ecohydrological processes are described explicitly in MuSICA, and agreement between observations and predictions of δ18Ostem and δ18Osoil at 7 and 20 cm depth indicates that MuSICA is capable of simulating these ecohydrological processes including 18O of the different water pools. The ability of the model to generate realistic predictions of the δ18O dynamics at different depths in the soil (within the zone of most active root water uptake and just below that zone) suggests strongly that the ensemble of parameters dictating the spatio-temporal dynamics of soil water contents (including emptying and refilling dynamics) was described well in the model. That interpretation was also supported by the sensitivity analysis. Importantly, a better agreement between predicted and observed δ18Osoil at 7 cm and δ18Ostem was obtained when the δ18O of meteoric water was taken from local measurements rather than given by the isotope-enabled atmospheric model IsoGSM (Fig. 6j). This result is not surprising given the significant spatial and temporal variation of rainfall at weekly and sub-kilometre scales (Fiener and Auerswald, 2009) and the comparatively large grid size of the IsoGSM model simulations (ca. 200 km ×200 km). Our model sensitivity analysis also revealed a better predictive power of the soil diffusivity formulation proposed by Moldrup et al. (2003) over that proposed by Penman (1940) to reproduce the observed isotopic composition of all the ecosystem water pools (Fig. 6i). This superiority was likely related to the effect of accounting for the soil-pore-size distribution parameter for describing the effective liquid water and water vapour diffusivity through the soil matrix and estimating this parameter from the soil water retention curve parameters measured at the site.
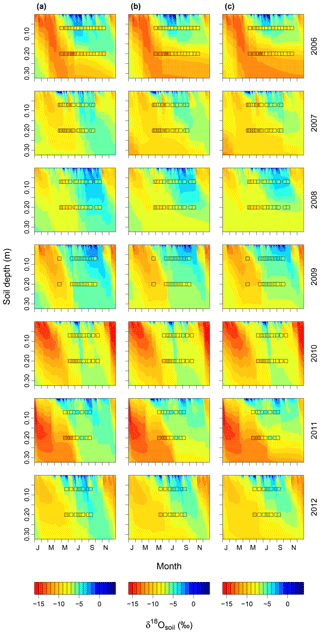
Figure 7Soil water δ18O dynamics predicted for the studied period (2006–2012) with (a) low, (b) intermediate, and (c) high Vcmax and Jmax. Values for low and high parameter values are given in the materials and methods. Observed values for δ18Osoil at 7 and 20 cm are displayed by squares. The same colour scheme is used for predicted and observed values and for each year and scenario. The abbreviations on the x axes indicate the months.
4.2 Xylem water originates from shallow soil depths independently of season and soil water content
The comparison of observed δ18Ostem and δ18Osoil (Fig. 3a) strongly suggested that root water uptake occurred mainly at shallow depths (<20 cm) throughout the vegetation periods, largely independently of changes in SWC. This interpretation of observed data was based on comparison of δ18Ostem and δ18Osoil at two depths (7 and 20 cm) only, which provides limited spatial resolution and cannot inform precisely on the depth of root water uptake (Rothfuss and Javaux, 2017; Brinkmann et al., 2018). Such information can be improved by a locally parameterised, physically based, 18O-enabled ecohydrological model, as shown here. For instance, the standard MuSICA runs (Fig. 3b) indicated near-monotonous increases in δ18Osoil between 20 and 7 cm depth, matching well the observations in the majority of sampling dates (Fig. S13). Further, the simulations predicted a mean (uptake-weighted) depth of root water uptake above 15 cm in 90 % of all sampling dates, independently of SWC and observations of δ18Osoil (Figs. S12 and S13). Support came also from the MuSICA sensitivity analysis (Fig. 6h), showing that δ18Ostem was well predicted by the model only when root length density was maximum at shallow soil depth. The potential range of rooting depths is large in grassland, depending on site, species, climatic and management effects (Schenk and Jackson, 2002; Klapp, 1971). So, why would root water uptake be constrained to shallow depths in this drought-prone permanent grassland system? Several factors likely contributed: (1) the shallow topsoil overlying calcareous gravel (Schnyder et al., 2006); (2) the rapid shoot and root biomass turnover, which is associated with high phytomer dynamics leading to short leaf and root lifespan in intensively managed grassland (Schleip et al., 2013; Yang et al., 1998; Auerswald and Schnyder, 2009; Robin et al., 2010); (3) the high rates of shoot tissue (mainly leaves) losses that elicit a priority for assimilate (including reserve) allocation to shoot regeneration at the expense of the root system (e.g. Bazot et al., 2005); and (4) predominant placement of the root system near the soil surface dictated by the high need for nutrient interception and uptake (e.g. from excreta deposits), to compensate for the high rates of nutrient losses due to grazing (Lemaire et al., 2000). Importantly, (5) in a relatively high number of cases, the model predicted situations in which rainfall recharged mainly the topsoil, while SWC at depths >20 cm remained low (e.g. June–end of year 2006, April–October 2007, or May–end of year 2008; Fig. S12; see also below). Principally, however, factors (2)–(4) alone can explain why shallow rooting depth is a typical feature of intensively grazed grasslands (Troughton, 1957; Klapp, 1971). Also, Prechsl et al. (2015) did not find an increasingly deeper root water uptake upon soil drying in an alpine and a lowland grassland system in Switzerland. Similarly, grasses continued to rely on water in the uppermost soil layer during soil water scarcity in a mesic Savanna in South Africa, in which C4 grasses were growing together with saplings and trees (Kulmatiski and Beard, 2013), and in a tallgrass prairie in the US dominated by C4 grasses and C3 shrubs and forbs (Nippert and Knapp, 2007a, b).
Predictions of δ18Osoil, particularly below the main zone of most water uptake, at 20 cm, were influenced markedly by estimates of LAI and by changes in Vcmax, Jmax, and stomatal conductance responsiveness (mgs) or minimal value (g0). This resulted from the effect of those parameters on total canopy transpiration, which in turn altered the dynamics of soil water and hence of the mixing of 18O-depleted winter and 18O-enriched summer precipitation with soil water at different depths. For instance, an increase in transpiration rate caused by a high mgs led to a decrease in δ18Osoil at 20 cm during the course of the growing season and a growing divergence between observations and predictions, particularly in years with low growing season precipitation (data not shown). This was likely caused by the fact that 18O-enriched summer rain mainly recharged the upper soil layer in this scenario, as this had been desiccated extensively because of the higher transpiration resulting from the higher mgs. So, summer rains would contribute less to wetting of the lower profile. Conversely, if mgs was set to a low value, predicted δ18Osoil at 20 cm increased throughout the vegetation period. According to the same mechanism, the effect of mgs on δ18Osoil was negligible when growing season rainfall was high in 2010. The effects of changing Vcmax and Jmax, LAI and minimum conductance on predicted δ18Osoil at 20 cm were very similar to mgs, suggesting that these parameters acted via the same mechanism, that is canopy conductance for water vapour that is controlled largely by the (integrated) stomatal conductance of all leaves within the canopy. Thus, the effect of Vcmax and Jmax was likely indirect, resulting from altered assimilation rates impacting stomatal conductance.
4.3 Evidence for a two-pool model of leaf water 18O enrichment
The Δ18Oleaf data were well predicted with a two-pool model and a constant fraction of unenriched water in bulk leaf water (φ≈0.39). This model was valid for a wide range of atmospheric and soil water conditions in seven consecutive growing seasons. Inclusion of a Péclet effect reduced the closeness of fit between measured and modelled Δ18Oleaf under all environmental conditions. We did not know if putative between-species differences in leaf water dynamics and associated 18O enrichment, or any other morpho-physiological effects for example associated with leaf ageing, could have led to a missing correlation between the proportional difference between measured leaf water 18O enrichment and that predicted by the Craig–Gordon model () and transpiration rate. For these reasons, we explored this question with separate studies of L. perenne and D. glomerata, two species that also formed part of the present grazed grassland ecosystem. Again, these studies found no evidence for a Péclet effect and supported the two-pool model, as there was no relationship between the proportional difference between measured leaf water enrichment and that predicted by the Craig–Gordon model () and transpiration rate in either L. perenne plants grown in a controlled environment at different relative humidities and water availabilities, or D. glomerata leaves measured using an online transpiration isotope method (Notes S2 and Figs. S14, S15). A two-pool model was also suggested by the diurnal time courses of δ18Oleaf in this grassland (Fig. S7) and in a broadleaf and a coniferous tree species (Bögelein et al., 2017).
When interpreted with the Péclet model, the two-pool model implies a constant Péclet number and inverse variation of transpiration rate and effective path length (L). Dynamic changes in L in response to varying transpiration have been noted before, mainly in controlled conditions, and interpreted in terms of changing contributions of different paths (symplastic, apoplastic and transcellular) of water movements to the stomatal pore (Barbour and Farquhar, 2003; Kahmen et al., 2008; Song et al., 2013; Loucos et al., 2015; Cernusak et al., 2016). Increases in L in response to drought, as suggested in this work, have also been observed previously in Vitis vinifera by Ferrio et al. (2012) and were connected with variations in leaf lamina hydraulic conductance.
In principle, failure to detect a Péclet effect could be related to the presence of major veins and associated ground tissue of the grass leaves (Holloway-Phillips et al., 2016) or errors associated with non-steady-state effects on 18O enrichment of bulk leaf water (Cernusak et al., 2016). However, MuSICA predictions of Δ18Oleaf did account for non-steady-state effects and were generally consistent with observed Δ18Oleaf. The φ value used in our simulations is in the upper range of φ values reported for grasses. Liu et al. (2017) observed species-specific φ values ranging from −0.05 to 0.43 in two C3 and three C4 grasses, with no obvious effect of vapour pressure deficit on φ. Gan et al. (2003) presented φ values between ca. 0.16 and 0.41 in maize, with lower values coming from leaves with the midvein removed. Considering a similar effect of vein removal would move our observed φ to about 0.2. Such a value of φ for grasses is very similar to the mean φ reported for a wide range of non-grass species by Cernusak et al. (2016).
4.4 Atmospheric and edaphic effects on the 18O enrichment of leaf water
The strong response of Δ18Oleaf to air relative humidity has been observed and discussed previously (e.g. Farquhar et al., 2007; Cernusak et al., 2016), in addition to soil moisture (Ferrio et al., 2012). We are not aware of a previous study that disentangled the separate effects of atmospheric and soil humidity on Δ18Oleaf, either in field or controlled conditions. Notably, the responses observed in our work were corroborated by theoretical predictions as implemented in MuSICA. Modelled transpiration rate and stomatal conductance were greatly reduced under dry soil conditions, leading to higher kinetic fractionation αk (Eq. 3) but lower α+ (Majoube, 1971) and relative humidity h, because of the warmer leaf temperatures. The net effect was a greater Δ18Oleaf predicted by MuSICA under dry soil conditions, in agreement with observations. This demonstrated that other vegetation parameters that affected the 18O enrichment in our sensitivity analysis (e.g. the unenriched fraction φ or the effective mixing length L, leaf water content W or LAI), but were not considered drought-sensitive, did not seem to be the main drivers of the enhancement of Δ18Oleaf during edaphic drought.
The data collected in this study are available upon request to the authors.
The supplement related to this article is available online at: https://doi.org/10.5194/hess-23-2581-2019-supplement.
JO, RTH and HS designed the study. RTH analysed the data and performed the modelling with guidance by JO. IS and UO designed the sampling scheme and setup, tested the water extraction unit and performed the diurnal water sampling. RS performed the isotope analysis. SHV analysed the eddy flux data. MMB performed the supplementary controlled environment experiments. RTH and HS wrote the paper. All authors contributed to the discussion and revision.
The authors declare that they have no conflict of interest.
We thank Erna Eschenbach†, Angela Ernst-Schwärzli, Anja Schmidt, Monika Michler, Hans Vogl, Richard Wenzel and Lenka Plavcová for technical assistance; Kei Yoshimura for sharing the IsoGSM δ18Orain and δ18Ovapour data; Wolfgang Durner and Alina Miller for providing soil data; and Iris Köhler for previous discussion. The authors thank Matthias Beyer and a second anonymous reviewer for the detailed comments and recommendations that helped us to improve this paper.
This research has been supported by the Deutsche Forschungsgemeinschaft (grant no. SCHN 557/9-1),
the Agence Nationale de la Recherche (grant no. ANR-13-BS06-0005), and the European Commission (grant no. SOLCA 338264).
This work was supported by the German Research Foundation (DFG) and the Technical University of Munich (TUM) in the framework of the Open Access Publishing Program.
This paper was edited by Christine Stumpp and reviewed by Matthias Beyer and one anonymous referee.
Atkin, O. K., Westbeek, M., Cambridge, M. L., Lambers, H., and Pons, T. L.: Leaf respiration in light and darkness (a comparison of slow- and fast-growing Poa species), Plant Physiol., 113, 961–965, https://doi.org/10.1104/pp.113.3.961, 1997.
Auerswald, K. and Schnyder, H.: Böden als Grünlandstandorte, in: Handbuch der Bodenkunde, 31. Erg.-Lfg., edited by: Blume, H.-P., Felix-Henningsen, P., Fischer, W. R., Frede, H.-G., Horn, R., and Stahr, K., Wiley-VCH, Weinheim, Germany, 1–15, https://doi.org/10.1002/9783527678495.hbbk2009003, 2009.
Ball, J. T., Woodrow, I. E., and Berry, J. A.: A Model Predicting Stomatal Conductance and its Contribution to the Control of Photosynthesis Under Different Environmental Conditions, in: Progress in photosynthesis research (vol. 4), edited by: Biggins, J., Martinus Nijhoff Publishers, Dordrecht, the Netherlands, 221–224, https://doi.org/10.1007/978-94-017-0519-6_48, 1987.
Barbour, M. M.: Stable oxygen isotope composition of plant tissue: a review, Funct. Plant Biol., 34, 83–94, https://doi.org/10.1071/FP06228, 2007.
Barbour, M. M. and Farquhar, G. D.: Relative humidity- and ABA-induced variation in carbon and oxygen isotope ratios of cotton leaves, Plant Cell Environ., 23, 473–485, https://doi.org/10.1046/j.1365-3040.2000.00575.x, 2000.
Barbour, M. M. and Farquhar, G. D.: Do pathways of water movement and leaf anatomical dimensions allow development of gradients in between veins and the sites of evaporation within leaves?, Plant Cell Environ., 27, 107–121, https://doi.org/10.1046/j.0016-8025.2003.01132.x, 2003.
Barbour, M. M., Schurr, U., Henry, B. K., Wong, S. C., and Farquhar, G. D.: Variation in the oxygen isotope ratios of phloem sap sucrose from castor bean. Evidence in support of the Péclet effect, Plant Physiol., 123, 671–679, https://doi.org/10.1104/pp.123.2.671, 2000.
Barbour, M. M., Roden, J. S., Farquhar, G. D., and Ehleringer, J. R.: Expressing leaf water and cellulose oxygen isotope ratios as enrichment above source water reveals evidence of a Péclet effect, Oecologia, 138, 426–435, https://doi.org/10.1007/s00442-003-1449-3, 2004.
Barnard, R. L., de Bello, F., Gilgen, A. K., and Buchmann, N.: The δ18O of root crown water best reflects source water δ18O in different types of herbaceous species, Rapid Commun. Mass Sp., 20, 3799–3802, https://doi.org/10.1002/rcm.2778, 2006.
Bazot, S., Mikola, J., Nguyen, C., and Robin, C.: Defoliation-induced changes in carbon allocation and root soluble carbon concentration in field-grown Lolium perenne plants: do they affect carbon availability, microbes and animal trophic groups in soil?, Funct. Ecol., 19, 886–896, https://doi.org/10.1111/j.1365-2435.2005.01037.x, 2005.
Bender, M., Sowers, T., and Labeyrie, L.: The Dole effect and its variations during the last 130,000 years as measured in the Vostok ice core, Global Biogeochem. Cy., 8, 363–376, https://doi.org/10.1029/94GB00724, 1994.
Bögelein, R., Thomas, F. M., and Kahmen, A.: Leaf water 18O and 2H enrichment along vertical canopy profiles in a broadleaved and a conifer forest tree, Plant Cell Environ., 40, 1086–1103, https://doi.org/10.1111/pce.12895, 2017.
Brinkmann, N., Seeger, S., Weiler, M., Buchmann, N., Eugster, W., and Kahmen, A.: Employing stable isotopes to determine the residence times of soil water and the temporal origin of water taken up by Fagus sylvatica and Picea abies in a temperate forest, New Phytol., 219, 1300–1313, https://doi.org/10.1111/nph.15255, 2018.
Cernusak, L. A., Wong, S. C., and Farquhar, G. D.: Oxygen isotope composition of phloem sap in relation to leaf water in Ricinus communis, Funct. Plant Biol., 30, 1059–1070, https://doi.org/10.1071/FP03137, 2003.
Cernusak, L. A., Barbour, M. M., Arndt, S. K., Cheesman, A. W., English, N. B., Feild, T. S., Helliker, B. R., Holloway-Phillips, M. M., Holtum, J. A. M., Kahmen, A., McInerney, F. A., Munksgaard, N. C., Simonin, K. A., Song, X., Stuart-Williams, H., West, J. B., and Farquhar, G. D.: Stable isotopes in leaf water of terrestrial plants, Plant Cell Environ., 39, 1087–1102, https://doi.org/10.1111/pce.12703, 2016.
Chapman, D. and Lemaire, G.: Tissue Flows in Grazed Plant Communities, in: The Ecology and Management of Grazing Systems, edited by: Hodgson, J. and Illius, A. W., CAB International, Guilford, 3–36, 1996.
Chen, G., Auerswald, K., and Schnyder, H.: 2H and 18O depletion of water close to organic surfaces, Biogeosciences, 13, 3175–3186, https://doi.org/10.5194/bg-13-3175-2016, 2016.
Craig, H. and Gordon, L. I.: Deuterium and oxygen-18 variations in the ocean and the marine atmosphere, in: Stable Isotopes in Oceanographic Studies and Paleotemperatures, edited by: Tongiorgi, E., Spoleto, Consiglio Nazionale Delle Ricerche, Laboratorio di Geologia Nucleare, Pisa, Italy, 9–130, 1965.
Cuntz, M., Ogée, J., Farquhar, G. D., Peylin, P., and Cernusak, L. A.: Modelling advection and diffusion of water isotopologues in leaves, Plant Cell Environ., 30, 892–909, https://doi.org/10.1111/j.1365-3040.2007.01676.x, 2007.
Dawson, T. E., Mambelli, S., Plamboeck, A. H., Templer, P. H., and Tu, K. P.: Stable Isotopes in Plant Ecology, Annu. Rev. Ecol. Syst., 33, 507–559, https://doi.org/10.1146/annurev.ecolsys.33.020602.095451, 2002.
Dole, M., Lane, G. A., Rudd, D. P., and Zaukelies, D. A.: Isotopic composition of atmospheric oxygen and nitrogen, Geochim. Cosmochim. Ac., 6, 65–78, https://doi.org/10.1016/0016-7037(54)90016-2, 1954.
Dongmann, G., Nürnberg, H. W., Förstel, H., and Wagener, K.: On the enrichment of in the leaves of transpiring plants, Radiat. Environ. Bioph., 11, 41–52, https://doi.org/10.1007/BF01323099, 1974.
Durand, J. L., Bariac, T., Ghesquière, M., Biron, P., Richard, P., Humphreys, M., and Zwierzykovski, Z.: Ranking of the depth of water extraction by individual grass plants, using natural 18O isotope abundance, Environ. Exp. Bot., 60, 137–144, https://doi.org/10.1016/j.envexpbot.2006.09.004, 2007.
Farquhar, G. D. and Lloyd, J.: Carbon and oxygen isotope effects in the exchange of carbon dioxide between terrestrial plants and the atmosphere, in: Stable isotopes and plant carbon-water relations, edited by: Ehleringer, J. R., Hall, A. E., and Farquhar, G. D., Academic Press, San Diego, California, USA, 47–70, https://doi.org/10.1016/B978-0-08-091801-3.50011-8, 1993.
Farquhar, G. D. and Cernusak, L. A.: On the isotopic composition of leaf water in the non-steady state, Funct. Plant Biol., 32, 293–303, https://doi.org/10.1071/FP04232, 2005.
Farquhar, G. D., von Caemmerer, S., and Berry, J. A.: A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species, Planta, 149, 78–90, https://doi.org/10.1007/BF00386231, 1980.
Farquhar, G. D., Lloyd, J., Taylor, J. A., Flanagan, L. B., Syvertsen, J. P., Hubick, K. T., Wong, S. C., and Ehleringer, J. R.: Vegetation effects on the isotope composition of oxygen in atmospheric CO2, Nature, 363, 439–443, https://doi.org/10.1038/363439a0, 1993.
Farquhar, G. D., Cernusak, L. A., and Barnes, B.: Heavy water fractionation during transpiration, Plant Physiol., 143, 11–18, https://doi.org/10.1104/pp.106.093278, 2007.
Ferrio, J. P., Pou, A., Florez-Sarasa, I., Gessler, A., Kodama, N., Flexas, J., and Ribas-Carbo, M.: The Péclet effect on leaf water enrichment correlates with leaf hydraulic conductance and mesophyll conductance for CO2, Plant Cell Environ., 35, 611–625, https://doi.org/10.1111/j.1365-3040.2011.02440.x, 2012.
Fiener, P. and Auerswald, K.: Spatial variability of rainfall on a sub-kilometre scale, Earth Surf. Proc. Land., 34, 848–859, https://doi.org/10.1002/esp.1779, 2009.
Flanagan, L. B. and Farquhar, G. D.: Variation in the carbon and oxygen isotope composition of plant biomass and its relationship to water-use efficiency at the leaf- and ecosystem-scales in a northern Great Plains grassland, Plant Cell Environ., 37, 425–438, https://doi.org/10.1111/pce.12165, 2014.
Gamnitzer, U., Schäufele, R., and Schnyder, H.: Observing 13C labelling kinetics in CO2 respired by a temperate grassland ecosystem, New Phytol., 184, 376–386, https://doi.org/10.1111/j.1469-8137.2009.02963.x, 2009.
Gan, K. S., Wong, S. C., Yong, J. W. H., and Farquhar, G. D.: Evaluation of models of leaf water 18O enrichment using measurements of spatial patterns of vein xylem water, leaf water and dry matter in maize leaves, Plant Cell Environ., 26, 1479–1495, https://doi.org/10.1046/j.1365-3040.2003.01070.x, 2003.
Gangi, L., Rothfuss, Y., Ogée, J., Wingate, L., Vereecken, H., and Brüggemann, N.: A new method for in situ measurements of oxygen isotopologues of soil water and carbon dioxide with high time resolution, Vadose Zone J., 1–14, https://doi.org/10.2136/vzj2014.11.0169, 2015.
Helliker, B. R. and Ehleringer, J. R.: Establishing a grassland signature in veins: 18O in the leaf water of C3 and C4 grasses, P. Natl. Acad. Sci. USA, 97, 7894–7898, https://doi.org/10.1073/pnas.97.14.7894, 2000.
Helliker, B. R. and Ehleringer, J. R.: Differential 18O enrichment of leaf cellulose in C3 versus C4 grasses, Funct. Plant Biol., 29, 435–442, https://doi.org/10.1071/PP01122, 2002.
Hoekstra, N. J., Finn, J. A., Hofer, D., and Lüscher, A.: The effect of drought and interspecific interactions on depth of water uptake in deep- and shallow-rooting grassland species as determined by δ18O natural abundance, Biogeosciences, 11, 4493–4506, https://doi.org/10.5194/bg-11-4493-2014, 2014.
Holloway-Phillips, M., Cernusak, L. A., Barbour, M., Song, X., Cheesman, A., Munksgaard, N., Stuart-Williams, H., and Farquhar, G. D.: Leaf vein fraction influences the Péclet effect and 18O enrichment in leaf water, Plant Cell Environ., 39, 2414–2427, https://doi.org/10.1111/pce.12792, 2016.
Kahmen, A., Simonin, K., Tu, K. P., Merchant, A., Callister, A., Siegwolf, R., Dawson, T. E., and Arndt, S. K.: Effects of environmental parameters, leaf physiological properties and leaf water relations on leaf water δ18O enrichment in different Eucalyptus species, Plant Cell Environ., 31, 738–751, https://doi.org/10.1111/j.1365-3040.2008.01784.x, 2008.
Klapp, E.: Grünlandvegetation und Standort, Parey, Berlin, 1965.
Klapp, E.: Wiesen und Weiden, Paul Parey, Berlin, Germany, 1971.
Kulmatiski, A. and Beard, K. H.: Root niche partitioning among grasses, saplings, and trees measured using a tracer technique, Oecologia, 171, 25–37, https://doi.org/10.1007/s00442-012-2390-0, 2013.
Lai, C. T., Ometto, J. P. H. B., Berry, J. A., Martinelli, L. A., Domingues, T. F., and Ehleringer, J. R.: Life form-specific variations in leaf water oxygen-18 enrichment in Amazonian vegetation, Oecologia, 157, 197–210, https://doi.org/10.1007/s00442-008-1071-5, 2008.
Leaney, F., Osmond, C., Allison, G., and Ziegler, H.: Hydrogen-isotope composition of leaf water in C3 and C4 plants: its relationship to the hydrogen isotope composition of dry matter, Planta, 164, 215–220, https://doi.org/10.1007/BF00396084, 1985.
Lehmann, M. M., Goldsmith, G. R., Schmid, L., Gessler, A., Saurer, M., and Siegwolf, R. T. W.: The effect of 18O-labelled water vapour on the oxygen isotope ratio of water and assimilates in plants at high humidity, New Phytol., 217, 105–116, https://doi.org/10.1111/nph.14788, 2018.
Lemaire, G., Hodgson, J., de Moraes, A., and Nabinger, C.: Grassland Ecophysiology and Grazing Ecology, CABI Publishing, Wallingford, UK, 2000.
Leng, X., Cui, J., Zhang, S., Zhang, W., Liu, Y., Liu, S., and An, S.: Differential water uptake among plant species in humid alpine meadows, J. Veg. Sci., 24, 138–147, https://doi.org/10.1111/j.1654-1103.2012.01439.x, 2013.
Liu, H. T., Gong, X. Y., Schäufele, R., Yang, F., Hirl, R. T., Schmidt, A., and Schnyder, H.: Nitrogen fertilization and δ18O of CO2 have no effect on 18O-enrichment of leaf water and cellulose in Cleistogenes squarrosa (C4) – is VPD the sole control?, Plant Cell Environ., 39, 2701–2712, https://doi.org/10.1111/pce.12824, 2016.
Liu, H. T., Schäufele, R., Gong, X. Y., and Schnyder, H.: The δ18O and δ2H of water in the leaf growth-and-differentiation zone of grasses is close to source water in both humid and dry atmospheres, New Phytol., 214, 1423–1431, https://doi.org/10.1111/nph.14549, 2017.
Loucos, K. E., Simonin, K. A., Song, X., and Barbour, M. M.: Observed relationships between leaf Péclet effective length and leaf hydraulic conductance reflect assumptions in Craig-Gordon model calculations, Tree Physiol., 35, 16–26, https://doi.org/10.1093/treephys/tpu110, 2015.
Luz, B. and Barkan, E.: The isotopic composition of atmospheric oxygen, Global Biogeochem. Cy., 25, GB3001, https://doi.org/10.1029/2010GB003883, 2011.
Majoube, M.: Fractionnement en oxygène 18 et en deuterium entre l'eau et sa vapeur, J. Chim. Phys., 68, 1423–1436, https://doi.org/10.1051/jcp/1971681423, 1971.
Medlyn, B. E., Dreyer, E., Ellsworth, D., Forstreuter, M., Harley, P. C., Kirschbaum, M. U. F., Le Roux, X., Montpied, P., Strassemeyer, J., Walcroft, A., Wang, K., and Loustau, D.: Temperature response of parameters of a biochemically based model of photosynthesis. II. A review of experimental data, Plant Cell Environ., 25, 1167–1179, https://doi.org/10.1046/j.1365-3040.2002.00891.x, 2002.
Merlivat, L.: Molecular diffusivities of , HD16O, and in gases, J. Chem. Phys., 69, 2864–2871, https://doi.org/10.1063/1.436884, 1978.
Miner, G. L., Bauerle, W. L., and Baldocchi, D. D.: Estimating the sensitivity of stomatal conductance to photosynthesis: a review, Plant Cell Environ., 40, 1214–1238, https://doi.org/10.1111/pce.12871, 2017.
Moldrup, P., Olesen, T., Komatsu, T., Yoshikawa, S., Schjønning, P., and Rolston, D. E.: Modeling diffusion and reaction in soils: X. A unifying model for solute and gas diffusivity in unsaturated soil, Soil Sci., 168, 321–337, https://doi.org/10.1097/01.ss.0000070907.55992.3c, 2003.
Monteith, J. L. and Unsworth, M. H.: Principles of Environmental Physics, second edition, Elsevier, Amsterdam, the Netherlands, 1990.
Nikolov, N., Massman, W., and Schoettle, A.: Coupling biochemical and biophysical processes at the leaf level: an equilibrium photosynthesis model for leaves of C3 plants, Ecol. Model., 80, 205–235, https://doi.org/10.1016/0304-3800(94)00072-P, 1995.
Nippert, J. B. and Knapp, A. K.: Linking water uptake with rooting patterns in grassland species, Oecologia, 153, 261–272, https://doi.org/10.1007/s00442-007-0745-8, 2007a.
Nippert, J. B. and Knapp, A. K.: Soil water partitioning contributes to species coexistence in tallgrass prairie, Oikos, 116, 1017–1029, https://doi.org/10.1111/j.0030-1299.2007.15630.x, 2007b.
Ogée, J., Brunet, Y., Loustau, D., Berbigier, P., and Delzon, S.: MuSICA, a CO2, water and energy multilayer, multileaf pine forest model: evaluation from hourly to yearly time scales and sensitivity analysis, Glob. Change Biol., 9, 697–717, https://doi.org/10.1046/j.1365-2486.2003.00628.x, 2003.
Ogée, J., Barbour, M. M., Wingate, L., Bert, D., Bosc, A., Stievenard, M., Lambrot, C., Pierre, M., Bariac, T., Loustau, D., and Dewar, R. C.: A single-substrate model to interpret intra-annual stable isotope signals in tree-ring cellulose, Plant Cell Environ., 32, 1071–1090, https://doi.org/10.1111/j.1365-3040.2009.01989.x, 2009.
Ogle, K., Lucas, R. W., Bentley, L. P., Cable, J. M., Barron-Gafford, G. A., Griffith, A., Ignace, D., Jenerette, G. D., Tyler, A., Huxman, T. E., Loik, M. E., Smith, S. D., and Tissue, D. T.: Differential daytime and night–time stomatal behavior in plants from North American deserts, New Phytol., 194, 464–476, https://doi.org/10.1111/j.1469-8137.2012.04068.x, 2012.
Ostler, U., Schleip, I., Lattanzi, F. A., and Schnyder, H.: Carbon dynamics in aboveground biomass of co-dominant plant species in a temperate grassland ecosystem: same or different?, New Phytol., 210, 471–484, https://doi.org/10.1111/nph.13800, 2016.
Penman, H. L.: Gas and vapour movements in soil: I. The diffusion of vapours through porous solids, J. Agr. Sci., 30, 437–462, https://doi.org/10.1017/S0021859600048164, 1940.
Picon-Cochard, C., Pilon, R., Tarroux, E., Pagès, L., Robertson, J., and Dawson, L.: Effect of species, root branching order and season on the root traits of 13 perennial grass species, Plant Soil, 353, 47–57, https://doi.org/10.1007/s11104-011-1007-4, 2012.
Prechsl, U. E., Burri, S., Gilgen, A. K., Kahmen, A., and Buchmann, N.: No shift to a deeper water uptake depth in response to summer drought of two lowland and sub-alpine C3-grasslands in Switzerland, Oecologia, 177, 97–111, https://doi.org/10.1007/s00442-014-3092-6, 2015.
Press, M. C., Parsons, A. N., Mackay, A. W., Vincent, C. A., Cochrane, V., and Seel, W. E.: Gas exchange characteristics and nitrogen relations of two Mediterranean root hemiparasites: Bartsia trixago and Parentucellia viscosa, Oecologia, 95, 145–151, https://doi.org/10.1007/BF00649518, 1993.
Ramirez, D. A., Querejeta, J. I., and Bellot, J.: Bulk leaf δ18O and δ13C reflect the intensity of intraspecific competition for water in a semi-arid tussock grassland, Plant Cell Environ., 32, 1346–1356, https://doi.org/10.1111/j.1365-3040.2009.02002.x, 2009.
R Core Team: R: A language and environment for statistical computing version 3.4.2, R Foundation for Statistical Computing, Vienna, Austria, available at: https://www.R-project.org/, last access: 19 October 2017.
Riley, W. J., Still, C. J., Torn, M. S., and Berry, J. A.: A mechanistic model of and C18OO fluxes between ecosystems and the atmosphere: Model description and sensitivity analyses, Global Biogeochem. Cy., 16, 1095–1109, https://doi.org/10.1029/2002GB001878, 2002.
Riley, W. J., Still, C. J., Helliker, B. R., Ribas-Carbo, M., and Berry, J. A.: 18O composition of CO2 and H2O ecosystem pools and fluxes in a tallgrass prairie: Simulations and comparisons to measurements, Glob. Change Biol., 9, 1567–1581, https://doi.org/10.1046/j.1365-2486.2003.00680.x, 2003.
Robin, A. H. K., Matthew, C., and Crush, J. R.: Time course of root initiation and development in perennial ryegrass – a new perspective, Pr. N. Z. Grassl. Assoc., 72, 233–240, 2010.
Rothfuss, Y. and Javaux, M.: Reviews and syntheses: Isotopic approaches to quantify root water uptake: a review and comparison of methods, Biogeosciences, 14, 2199–2224, https://doi.org/10.5194/bg-14-2199-2017, 2017.
RStudio Team: RStudio: Integrated Development for R version 1.1.383, RStudio, Inc., Boston, MA, available at: http://www.rstudio.com/, last access: 19 October 2017.
Sadri, S., Wood, E. F., and Pan, M.: Developing a drought-monitoring index for the contiguous US using SMAP, Hydrol. Earth Syst. Sci., 22, 6611–6626, https://doi.org/10.5194/hess-22-6611-2018, 2018.
Schenk, H. J. and Jackson, R. B.: Rooting depths, lateral root spreads and below-ground/above-ground allometries of plants in water-limited ecosystems, J. Ecol., 90, 480–494, https://doi.org/10.1046/j.1365-2745.2002.00682.x, 2002.
Schleip, I.: Carbon residence time in above-ground and below-ground biomass of a grazed grassland community, PhD thesis, Technical University of Munich, Munich, Germany, 2013.
Schleip, I., Lattanzi, F. A., and Schnyder, H.: Common leaf life span of co-dominant species in a continuously grazed temperate pasture, Basic Appl. Ecol., 14, 54–63, https://doi.org/10.1016/j.baae.2012.11.004, 2013.
Schnyder, H., Schwertl, M., Auerswald, K., and Schäufele, R.: Hair of grazing cattle provides an integrated measure of the effects of site conditions and interannual weather variability on δ13C of temperate humid grassland, Glob. Change Biol., 12, 1315–1329, https://doi.org/10.1111/j.1365-2486.2006.01169.x, 2006.
Schnyder, H., Locher, F., and Auerswald, K.: Nutrient redistribution by grazing cattle drives patterns of topsoil N and P stocks in a low-input pasture ecosystem, Nutr. Cycl. Agroecosys., 88, 183–195, https://doi.org/10.1007/s10705-009-9334-z, 2010.
Snyder, K. A., Richards, J. H., and Donovan, L. A.: Night-time conductance in C3 and C4 species: do plants lose water at night?, J. Exp. Bot., 54, 861–865, https://doi.org/10.1093/jxb/erg082, 2003.
Song, X., Barbour, M. M., Farquhar, G. D., Vann, D. R., and Helliker, B. R.: Transpiration rate relates to within- and across-species variations in effective pathlength in a leaf water model of oxygen isotope enrichment, Plant Cell Environ., 36, 1338–1351, https://doi.org/10.1111/pce.12063, 2013.
Song, X., Loucos, K. E., Simonin, K. A., Farquhar, G. D., and Barbour, M. M.: Measurements of transpiration isotopologues and leaf water to assess enrichment models in cotton, New Phytol., 206, 637–646, https://doi.org/10.1111/nph.13296, 2015.
Treydte, K., Boda, S., Pannatier, E. G., Fonti, P., Frank, D., Ullrich, B., Saurer, M., Siegwolf, R., Battipaglia, G., Werner, W., and Gessler, A.: Seasonal transfer of oxygen isotopes from precipitation and soil to the tree ring: source water versus needle water enrichment, New Phytol., 202, 772–783, https://doi.org/10.1111/nph.12741, 2014.
Troughton, A.: The Underground Organs of Herbage Grasses, Bulletin No. 44, Commonwealth Bureau of Pastures and Field Crops, Wallingford, UK, 1957.
Wang, X. F. and Yakir, D.: Temporal and spatial variations in the oxygen-18 content of leaf water in different plant species, Plant Cell Environ., 18, 1377–1385, https://doi.org/10.1111/j.1365-3040.1995.tb00198.x, 1995.
Webb, E. A. and Longstaffe, F. J.: The relationship between phytolith- and plant-water δ18O values in grasses, Geochim. Cosmochim. Ac., 67, 1437–1449, https://doi.org/10.1016/S0016-7037(02)01300-5, 2003.
Webb, E. A. and Longstaffe, F. J.: Identifying the δ18O signature of precipitation in grass cellulose and phytoliths: refining the paleoclimate model, Geochim. Cosmochim. Ac., 70, 2417–2426, https://doi.org/10.1016/j.gca.2006.02.024, 2006.
Welp, L. R., Keeling, R. F., Meijer, H. A. J., Bollenbacher, A. F., Piper, S. C., Yoshimura, K., Francey, R. J., Allison, C. E., and Wahlen, M.: Interannual variability in the oxygen isotopes of atmospheric CO2 driven by El Niño, Nature, 477, 579–582, https://doi.org/10.1038/nature10421, 2011.
Wen, X. F., Lee, X., Sun, X. M., Wang, J. L., Hu, Z. M., Li, S. G., and Yu, G. R.: Dew water isotopic ratios and their relationships to ecosystem water pools and fluxes in a cropland and a grassland in China, Oecologia, 168, 549–561, https://doi.org/10.1007/s00442-011-2091-0, 2012.
Williams, J. T. and Varley, Y. W.: Phytosociological studies of some British grasslands. I. Upland pastures in Northern England, Vegetatio, 15, 169–189, https://doi.org/10.1007/BF01963747, 1967.
Willmott, C. J. and Matsuura, K.: Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance, Clim. Res., 30, 79–82, https://doi.org/10.3354/cr030079, 2005.
Wingate, L., Ogée, J., Cuntz, M., Genty, B., Reiter, I., Seibt, U., Yakir, D., Maseyk, K., Pendall, E. G., Barbour, M. M., Mortazavi, B., Burlett, R., Peylin, P., Miller, J., Mencuccini, M., Shim, J. H., Hunt, J., and Grace, J: The impact of soil microorganisms on the global budget of δ18O in atmospheric CO2, P. Natl. Acad. Sci. USA, 106, 22411–22415, https://doi.org/10.1073/pnas.0905210106, 2009.
Wingate, L., Ogée, J., Burlett, R., Bosc, A., Devaux, M., Grace, J., Loustau, D., and Gessler, A.: Photosynthetic carbon isotope discrimination and its relationship to the carbon isotope signals of stem, soil and ecosystem respiration, New Phytol., 188, 576–589, https://doi.org/10.1111/j.1469-8137.2010.03384.x, 2010.
Wohlfahrt, G., Bahn, M., Horak, I., Tappeiner, U., and Cernusca, A.: A nitrogen sensitive model of leaf carbon dioxide and water vapour gas exchange: application to 13 key species from differently managed mountain grassland ecosystems, Ecol. Model., 113, 179–199, https://doi.org/10.1016/S0304-3800(98)00143-4, 1998.
Wohlfahrt, G., Bahn, M., Newesely, C., Sapinsky, S., Tappeiner, U., and Cernusca, A.: Canopy structure versus physiology effects on net photosynthesis of mountain grasslands differing in land use, Ecol. Model., 170, 407–426, https://doi.org/10.1016/S0304-3800(03)00242-4, 2003.
Xiao, W., Lee, X., Wen, X., Sun, X., and Zhang, S.: Modeling biophysical controls on canopy foliage water 18O-enrichment in wheat and corn, Glob. Change Biol., 18, 1769–1780, https://doi.org/10.1111/j.1365-2486.2012.02648.x, 2012.
Yakir, D., Berry, J. A., Giles, L., and Osmond, C. B.: Isotopic heterogeneity of water in transpiring leaves: identification of the component that controls the δ18O of atmospheric O2 and CO2, Plant Cell Environ., 17, 73–80, https://doi.org/10.1111/j.1365-3040.1994.tb00267.x, 1994.
Yang, J. Z., Matthew, C., and Rowland, R. E.: Tiller axis observations for perennial ryegrass (Lolium perenne) and tall fescue (Festuca arundinacea): number of active phytomers, probability of tiller appearance, and frequency of root appearance per phytomere for three cutting heights, New Zeal. J. Agr. Res., 41, 11–17, https://doi.org/10.1080/00288233.1998.9513283, 1998.
Yoshimura, K., Frankenberg, C., Lee, J., Kanamitsu, M., Worden, J., and Rockmann, T.: Comparison of an isotopic atmospheric general circulation model with new quasi-global satellite measurements of water vapor isotopologues, J. Geophys. Res.-Atmos., 116, D19118, https://doi.org/10.1029/2011JD016035, 2011.