the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Assessing the added value of the Intermediate Complexity Atmospheric Research (ICAR) model for precipitation in complex topography
Marlis Hofer
Fabien Maussion
Ethan Gutmann
Alexander Gohm
Mathias W. Rotach
The coarse grid spacing of global circulation models necessitates the application of downscaling techniques to investigate the local impact of a changing global climate. Difficulties arise for data-sparse regions in complex topography, as they are computationally demanding for dynamic downscaling and often not suitable for statistical downscaling due to the lack of high-quality observational data. The Intermediate Complexity Atmospheric Research (ICAR) model is a physics-based model that can be applied without relying on measurements for training and is computationally more efficient than dynamic downscaling models. This study presents the first in-depth evaluation of multiyear precipitation time series generated with ICAR on a 4×4 km2 grid for the South Island of New Zealand for an 11-year period, ranging from 2007 to 2017. It focuses on complex topography and evaluates ICAR at 16 weather stations, 11 of which are situated in the Southern Alps between 700 and (m m.s.l refers to meters above mean sea level). ICAR is assessed with standard skill scores, and the effect of model top elevation, topography, season, atmospheric background state and synoptic weather patterns on these scores are investigated. The results show a strong dependence of ICAR skill on the choice of the model top elevation, with the highest scores obtained for 4 km above topography. Furthermore, ICAR is found to provide added value over its ERA-Interim reanalysis forcing data set for alpine weather stations, improving the median of mean squared errors (MSEs) by 30 % and up to 53 %. It performs similarly during all seasons with a MSE minimum during winter, while flow linearity and atmospheric stability are found to increase skill scores. ICAR scores are highest during weather patterns associated with flow perpendicular to the Southern Alps and lowest for flow parallel to the alpine range. While measured precipitation is underestimated by ICAR, these results show the skill of ICAR in a real-world application, and may be improved upon by further observational calibration or bias correction techniques. Based on these findings ICAR shows the potential to generate downscaled fields for long-term impact studies in data-sparse regions with complex topography.
- Article
(4455 KB) -
Supplement
(1619 KB) - BibTeX
- EndNote
Global circulation models (GCM) generate atmospheric data sets on spatiotemporal grids that, especially in complex topography, are too coarse to investigate the local impact of a changing global climate. To bridge the gap between local and GCM scales, a variety of downscaling methods and techniques exist (Christensen et al., 2007), which are roughly characterizable as dynamic downscaling (e.g., Hill, 1968; Rasmussen et al., 2014), statistical downscaling (e.g., Klein et al., 1959; Benestad et al., 2008) or intermediate complexity downscaling (e.g., Sarker, 1966; Smith and Barstad, 2004; Gutmann et al., 2016).
While dynamic downscaling results in a self-consistent set of atmospheric fields, the computational cost required for the fine spatial and temporal grid spacing is high, especially for long-term simulations or sensitivity studies. The drawback of statistical downscaling is the associated requirement of high-quality measurements for model training, rendering it less applicable to data-sparse regions. Even more problematic, as soon as observation-based training or calibration is applied, the assumption of stationarity is introduced for statistical downscaling, which may not hold under a changing climate (Maraun, 2013; Gutmann et al., 2012). Therefore, overall, both classes are not ideally suited for the long-term study of the regional effects of a changing global climate. These problems are particularly amplified in glacierized areas, which are often located in hard-to-access, remote regions and complex topography. For such regions weather station deployment and maintenance is often impractical or too expensive, resulting in a scarcity of continuous measurements and the inapplicability of statistical downscaling approaches. In the case of dynamic downscaling the correct representation of the influence of complex topography on local weather and climate leads to a high computational cost. This cost is further increased by the long response times of glaciers to climatic changes, which are in the order of several decades (Raper and Braithwaite, 2009). Therefore, process-based glacier models require long-term information about the state of the atmosphere above the glacier to investigate the impact of a changing global climate.
The Intermediate Complexity Atmospheric Research (ICAR) model (Gutmann et al., 2016) offers a computationally frugal and physics-based alternative that does not rely on measurements, with linear mountain wave theory as its theoretical foundation. In comparison to other downscaling approaches of intermediate complexity (e.g., Sarker, 1966; Rhea, 1977; Smith and Barstad, 2004; Georgakakos et al., 2005), ICAR is a more general atmospheric model that requires fewer simplifying assumptions about the state of the atmosphere, such as spatial and temporal homogeneity of the background flow. Furthermore, in contrast to the linear theory of orography precipitation (LOP; Smith and Barstad, 2004), ICAR considers a detailed vertical structure of the atmosphere and employs a complex microphysics scheme as opposed to the characteristic timescales for cloud water conversion and hydrometeor fallout of the LOP. With regards to dynamical downscaling, in particular the Weather Research and Forecasting model, Gutmann et al. (2016) showed that ICAR may reduce the required computational time for one simulated year for a domain in the western USA by a factor of at least 140.
At the time of writing, ICAR has been evaluated in an idealized hill experiment, as well as by comparing monthly precipitation fields generated by ICAR for Colorado, USA, with WRF output and an observation-based gridded data set (Gutmann et al., 2016). Furthermore, ICAR was employed to generate downscaled atmospheric fields as input for a glacier mass balance model to simulate meltwater runoff in the western Himalayas (Engelhardt et al., 2017). Recently Bernhardt et al. (2018) applied ICAR to investigate differences in precipitation patterns and amounts for a domain in the European Alps, emerging from the choice of the microphysics scheme and associated parameters. However, Gutmann et al. (2016) evaluated ICAR for season totals and based on 1 year of precipitation data, whereas Bernhardt et al. (2018) only investigated a 7 month period.
This study conducts the first multiyear evaluation of ICAR, and compares ICAR precipitation fields to data from individual weather stations in different terrains. As a starting point for investigating the added value of ICAR, New Zealand is chosen. Here the precipitation regime is strongly orographically influenced by the Southern Alps (Sturman and Wanner, 2001). The island is isolated from major land masses and moist air from the surrounding ocean is advected toward the orographic ridge of the Southern Alps at a predominantly right angle. Measurements from 16 weather stations within the study domain, 11 of which are alpine stations located in complex topography, are used to quantify added value with regards to ERA-Interim interpolated to station location. Furthermore the model performance is diagnosed with respect to season, background atmospheric state and synoptic weather patterns. Average and seasonal precipitation patterns are compared to an operational gridded rainfall data set. Additionally, the influence of the choice of the model top height onto the downscaled results is discussed.
2.1 Overview
ICAR (Gutmann et al., 2016) is a 3-D atmospheric model based on linear mountain wave theory. As input, ICAR requires a digital elevation model and a forcing data set with 4-D atmospheric variables generated by, for instance, a coupled atmosphere–ocean general circulation model or an atmospheric reanalysis such as ERA-Interim. The forcing data set should contain at least the horizontal wind components, pressure, temperature and water vapor mixing ratio, with the possibility to additionally include hydrometeor fields, incoming long- and short-wave radiation or the skin temperature of water bodies. ICAR employs linear mountain wave theory to calculate the wind field from the topography information and the horizontal wind components to avoid a numerical solution of the Navier–Stokes equations of motion – the core of dynamical downscaling models. With this wind field, ICAR advects atmospheric quantities, such as temperature and moisture as supplied by the forcing data set at the domain boundaries. In its standard setup ICAR applies the Thompson microphysical scheme (Thompson et al., 2008), a double-moment scheme in cloud ice and rain and a single-moment scheme for the remaining quantities to compute the mixing ratios of water vapor, cloud water, rain, cloud ice, graupel and snow.
The classic approach of linear mountain wave theory predicts the wind field based on the topography and the background state of the atmosphere (Sawyer, 1962; Smith, 1979). With the background state known, its perturbation due to topography is given by a set of analytical equations (Barstad and Grønås, 2006). However, linear theory does not take interactions among waves or waves and turbulence into account, nor does it account for transient and nonlinear phenomena such as time-varying wave amplitudes, gravity wave breaking or low-level blocking and flow splitting. A basic discussion of the limitations implicit to these assumptions can be found in Nappo (2012). In ICAR, the atmospheric background state is given by the forcing data set. This yields a time sequence of steady-state wind fields between which ICAR interpolates linearly. A detailed description of the model is given in Gutmann et al. (2016).
To avoid unstable atmospheric conditions present in the forcing data set or caused by the microphysics, ICAR enforces stability by ignoring imaginary values of the Brunt–Väisälä frequency and substituting them with a minimum positive value of . In the version of ICAR employed in this study, the reflection of mountain waves at the interface of atmospheric layers is neglected.
2.2 Model setup
ICAR can be run without relying on measurements for observation-based calibrations. Therefore, it is of particular interest for data-absent, mountainous or glacierized regions (e.g., Pepin et al., 2015). This study aims at quantifying a baseline performance of ICAR with default settings as it would be applied for a region where no observations are available. For individual sites, improvement is then possible by performing data-based calibration, as routinely performed in regional climate-model-based downscaling. However, the model top of ICAR could not be adopted from default settings (Horak et al., 2019), see Sect. 2.3. The ICAR configuration used in this study (configuration file available as download, see Horak et al., 2019) employs the wind field computation process as described in Sect. 2.1 and by Gutmann et al. (2016), an upwind advection scheme to transport quantities within the wind field and the Thompson microphysics scheme. Coupling between the surface and the atmosphere is neglected, i.e., no turbulent surface fluxes of heat, moisture or momentum are considered. Atmospheric fields were downscaled to a 4×4 km2 horizontal grid and to an hourly time step.
2.3 Model top
For dynamic downscaling models the position of the model top is a critical parameter. In principal, a higher model top implies a more faithful representation of atmospheric processes and physics that, in turn, leads to an increased computational cost, whereas a lower setting has the opposite effect. In light of these requirements, the ICAR default setting of 5.7 km above topography as used in Gutmann et al. (2016) is comparatively low. Preliminary studies indicated that for a model top at 5.7 km only a small added value can be obtained for the South Island of New Zealand. Additionally, these preliminary studies showed that different choices for the model top elevation influenced the precipitation patterns and amounts throughout the study domain, leading to significant changes in model skill. Therefore, a sensitivity analysis was conducted to identify the optimal elevation of the model top for this study.
2.4 Digital elevation model
The model domain in this study, as depicted in Fig. 1, encompasses the entire South Island of New Zealand and a small section of the North Island. The digital elevation model (DEM) employed was upscaled from the ETOPO1 Ice (Amante and Eakins, 2009) DEM to 4×4 km2, corresponding to 205×225 grid points. As peaks represented by only one grid point increase the wave energy in the high-frequency part of the spectrum, leading to unphysical atmospheric perturbations, the topography was smoothed by a 3×3 moving window algorithm (Guo and Chen, 1994, p. 34). A similar type of smoothing, which is common when using the weather research and forecasting pre-processing system, was performed in previous studies employing ICAR (Gutmann et al., 2016; Engelhardt et al., 2017).
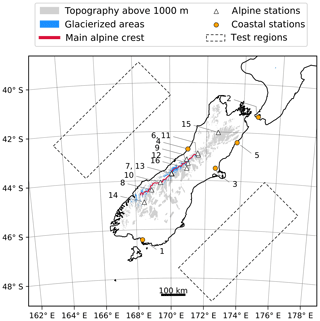
Figure 1The South Island of New Zealand. Shown are the coast (black line), the topography above an elevation of (gray shading), glacierized areas (blue shading), the approximate location of the main alpine crest (red line) and the location of test regions (dashed outlines) northwest and southeast of the mainland used to determine flow linearity. The alpine weather stations considered in the evaluation of this study are indicated by white triangles, whereas coastal weather stations are represented by orange disks. The numbers next to the markers are ordered from lowest to highest weather station elevation and may be used to look up additional information for each station in Table 1.
2.5 Forcing data and reference
In this study, ERA-Interim reanalysis data (ERAI; Dee et al., 2011) are used as the forcing data set for ICAR. Reanalysis data are obtained from computationally expensive state-of-the-art general circulation model re-forecasts constrained by quality-controlled observations with a variational data assimilation procedure. Therefore, reanalysis data are of a particular relevance for data-scarce high mountain regions around the globe, where the application of solely interpolation-based gridded historical data sets is problematic. ERAI employs a horizontal grid spacing of (globally), corresponding to approximately 81×110 km2 within the study domain, and extends to the 0.1 hPa pressure level in the vertical. The assembled ICAR forcing file contains ERAI zonal and meridional winds (U and V, respectively), potential temperature (Θ), pressure (p), specific humidity (qv), cloud liquid water mixing ratio( qc), cloud ice water mixing ratio (qi) and surface pressure (p0) at each 6 h forcing time step and every grid point within the domain.
ERA-Interim reanalysis data were also used as ICAR forcing in the study of Bernhardt et al. (2018). Bernhardt et al. (2018), however, evaluated only the precipitation sum over a 7 month period. They emphasized the importance of mountain weather station networks with respect to allowing for a more detailed evaluation of ICAR. Gutmann et al. (2016) used the North American Regional Reanalysis (NARR), which has a 32 km grid spacing (Mesinger et al., 2006). Engelhardt et al. (2017) used output from the Norwegian Earth System Model (NorESM), downscaled to a grid spacing of 25 km by the regional climate model REMO, as ICAR input for a simulation period from 2006 to 2099. In this study, ERAI are preferred over regional reanalysis data sets due to their global availability and, thus, more widespread applicability.
2.6 Convective precipitation
The ICAR configuration for this study, as described in Sect. 2.2, is able to model orographic precipitation and, at least in part, precipitation driven by the synoptic scale. To account for convective precipitation, convective precipitation from ERAI (field name: cp; parameter ID: 143), PCP, is resampled to the ICAR time step, bilinearly interpolated in space to the sites of interest and then added to the ICAR precipitation time series PI:
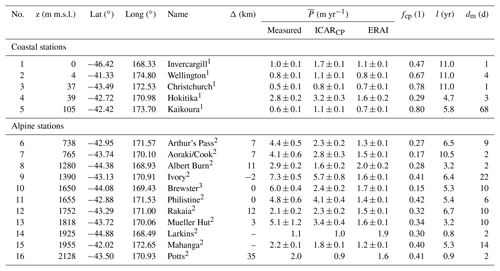
where in the following the P(t) time series is referred to as ICARCP, and PI(t) is referred to as ICAR. This is a common technique that allows for the inclusion of types of precipitation not accounted for by the downscaling model (e.g., Jarosch et al., 2012; Weidemann et al., 2013; Paeth et al., 2017; Roth et al., 2018). Table 1 shows the mean annual precipitation at each site for ICARCP and ERAI, as well as the ratio of ERAI convective precipitation to ERAI total precipitation.
3.1 Overview
This study focuses on the Southern Alps of New Zealand located in the southwestern Pacific Ocean. The Southern Alps are oriented southwest–northeast and run almost parallel to the western coast of the South Island. They are approximately 800 km long and 60 km wide, extend across a latitude range from 41 to 46 ∘ S and consist of a series of ranges and basins (Barrell et al., 2011). Of the 3144 glaciers in New Zealand with a surface area larger than 0.01km2, all except 18 lie within the Southern Alps (Chinn, 2001). The domain and glacierized areas are depicted in Fig. 1.
Table 1List of weather stations used in this study sorted by their elevation. The table lists the station number (No.), elevation (z), latitude (Lat), longitude (Long), name, average distance downwind of the main crest of the Southern Alps (Δ) based on westerly and northwesterly flow, mean annual precipitation () with the standard deviation both calculated for the years when data were available at the respective weather station, fraction of convective precipitation in ERAI annual sum fcp, length of the time series (l) and number of days removed due to missing entries or failed quality checks (dm). The superscript following the station name indicates the data provider: NCD (1), NIWA (2) and University of Otago (3). Precipitation data for Larkins and Potts were linearly extrapolated to a full year. Δ was not considered for coastal weathers stations, and no values were assigned for Mahanga and Larkins as they lie north and south, respectively, of the main alpine crest.
New Zealand's climate is characterized as humid and maritime with prevailing westerly winds. The average precipitation patterns are influenced by the Southern Alps, which act as a topographic barrier for these moist winds (Chinn, 2001). The resulting orographically influenced precipitation regime is characterized by a precipitation maximum of up to 14 m yr−1 on the western flanks close to the main divide of the Southern Alps. Along the west coast, 5 m yr−1 of precipitation is observed on average, whereas the plains east of the main divide receive less than 1 m yr−1 (Griffiths and McSaveney, 1983; Henderson and Thompson, 1999). Additionally, the strong westerly winds in the Southern Alps may lead to significant spillover, distributing precipitation to leeward slopes (Chater and Sturman, 1998).
3.2 Observational data
Precipitation time series from the weather stations in complex topography were supplied by the National Institute of Water and Atmospheric Research of New Zealand (NIWA) and the University of Otago, New Zealand (Cullen and Conway, 2015). At coastal weather stations, records from the New Zealand National Climate Database (NCD, https://cliflo.niwa.co.nz, last access: 18 June 2019) were employed. The individual time series extend over an 11-year period, with the shortest time series covering 0.8 years and the longest 11 years. Details concerning the weather stations, accumulated annual precipitation and time series length are listed in Table 1. Furthermore, Table 1 includes an average downwind distance Δ from the main alpine crest of the Southern Alps. It is calculated with regards to westerly and northwesterly flow – the wind directions associated with the largest mean precipitation.
Different instruments were employed to measure rainfall at the weather stations in the study region. At Christchurch, Invercargill and Kaikoura precipitation measurements were carried out with a tipping-bucket rain gauge, while different gauges were employed at the remaining coastal stations: a standard rain gauge at Hokitika and a drop gauge at Wellington. Precipitation at Mount Brewster was measured with a tipping-bucket rain gauge, and data post-processing is described in detail by Cullen and Conway (2015). Cullen and Conway (2015) identified the period for reliable precipitation data at the site as extending approximately from the end of December until the end of April; during this period the data were adjusted for gauge undercatch. Outside of this period, Cullen and Conway applied a scaling function to extrapolate from rain gauge data at a site 30 km southwest of Brewster Glacier at (meters above mean sea level). Precipitation at the alpine NIWA stations was measured with tipping-bucket rain gauges. Heating systems were not installed, however, a wind shield was in place at Mueller Hut. The raw data available from the NCD are provided by the Meteorological Service of New Zealand, the NIWA and, in three cases, unidentified observing authorities. For this study, all NIWA and NCD input data were subject to basic plausibility checks. They identified and flagged data points exceeding 20 standard deviations from the mean, data points with negative values, or data points with excessive temporal persistence. Marked entries were then manually reviewed and removed from the data set if physically unreasonable values were found. The quality-controlled data were then used for further processing and resampled to daily accumulated precipitation P24 h. Days that had gaps in their original time series were not considered for further analysis. The number of missing days is documented in Table 1.
To compare simulated precipitation patterns across the South Island of New Zealand to an observational data set, the NIWA virtual climate station gridded daily rainfall product (VCSR; Tait and Turner, 2005) is employed. The VCSR is an observation-based data set interpolated to a horizontal grid spacing of 3′ or approximately 5 km. It scales rainfall at high elevations and remote locations using data from mesoscale model simulations. While the VCSR does not necessarily represent the actual distribution of precipitation (Tait et al., 2012), and may miss precipitation events (Tait and Turner, 2005), it serves as an approximation of an observational gridded data set and is based on observations and expert judgment.
4.1 Evaluation strategy
In this study, ICARCP time series (see Sect. 2.6) are evaluated in terms of the added value over total precipitation from the ERAI reanalysis. Added value in this context is used as in the investigation of regional climate-model-based downscaling, where it is defined as the comparative performance of the regional climate model output to the global driving data (e.g., Di Luca et al., 2015). Similar studies with a focus on quantifying the added value over the driving input have been performed for full dynamic downscaling (for a review see Torma et al., 2015). This way, our study serves as a guide regarding the conditions under which ICAR can add value over ERAI (if it can at all) with a particular focus on complex terrain. The aim is not a downscaling method intercomparison (e.g., ICAR versus WRF; Gutmann et al., 2016).
The available data are grouped by selected criteria that are expected to affect the added value, in particular the topographic complexity, seasons, flow linearity and the synoptic situation. Flow linearity is characterized by the inverse nondimensional mountain height, which in the following is referred to as Froude number, calculated for test volumes upstream of the weather stations. The synoptic situation is determined by weather patterns as employed in an operational weather pattern classification scheme.
4.2 Skill scores and significance test
Mainly two scores are employed to quantify the added value of ICARCP over ERAI: the MSE-based (MSE: mean squared error) skill score SSMSE and the Heidke skill score HSS. The MSE-based skill score (Wilks, 2011b, chap. 8) is given by
where MSE is the MSE of ICARCP P24 h, and MSEr is the MSE of P24 h of the reference model (here, ERAI). This way, SSMSE can be interpreted as the percentage improvement (reduction of error) due to ICARCP relative to ERAI.The contingency-table-based Heidke Skill score (HSS; Wilks, 2011b, chap. 8) is used to analyze events that are characterized by either their occurrence or absence, such as, P24 h exceeding a given threshold, or whether the tested model is able to correctly diagnose the occurrences in comparison to a reference model. Thresholds investigated in this study are 1, 25 and 50 mm for 24 h accumulated precipitation. The HSS is defined as
where r is the proportion correct of ICARCP, and rr is the proportion correct of the ERAI reference model. The proportion correct is given by , with . In this context a is the number of times the event was forecast and observed to occur (hits) b is the number of events that were forecast but not observed (false hits), c is the number of events that were not forecast but observed (false alarm or missed event), d is the number of times an event was neither forecast nor observed (correct misses) and n is the total number of cases.
The scores defined by Eqs. (2) and (3) both yield values in the interval and condense the information regarding whether the tested model performs better with respect to a skill measure than a reference model into one number. A model exactly reproducing the measurements corresponds to a score of one, a score of zero is achieved if the model performs equally as well as the reference model, and lower scores are found if the model is outperformed by the reference model.
Moving block bootstrap (MBB) is employed to determine the significance of the skill scores (Wilks, 2011a, chap. 5). The procedure is similar to ordinary bootstrapping with the distinction that, instead of n individual observations, blocks of length L are resampled. For the time series considered in this study values of L range between one and nine, with the autocorrelation structure of the time series preserved within each block, and different blocks independent of each other. Each skill score is recalculated for 10 000 MBBs of the original data, yielding a sampling distribution of the respective score. If the fifth percentile of this distribution is positive, the score obtained from the original time series is considered significant.
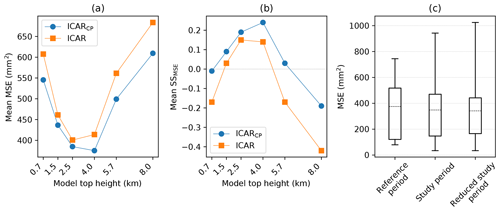
Figure 2The average (a) and MSE (b) SSMSE of ICAR and ICARCP time series from simulations for the reference period from 2014 to 2015 at alpine weather stations as a function of the chosen model top (in kilometers above topography). Connecting lines serve as guides for the eye. Panel (c) shows the distribution of skill scores for simulations with a model top set 4.0km above topography at alpine weather stations for the reference period (2014–2015), the full study period (2007–2017) and the reduced study period, where the reference period has been removed from the data set (2007–2013 and 2016–2017). The lower boundary of each box indicates the 25th percentile, the upper boundary the 75th percentile and the dashed horizontal line the mean. Whiskers show the minimum and maximum values of the data set.
4.3 Model top sensitivity study
The results of a sensitivity study used to determine the optimal position of the model top by varying the number of vertical model levels are summarized in Fig. 2. Simulations for six different model top elevations were run for a 2-year reference period (2014–2015) and the MSE was calculated for the ICAR and ICARCP time series at all alpine weather stations. The reference period was chosen as the time slice when a maximum of observational data was available, with measured time series for 9 out of 11 alpine weather stations (except for Potts and Larkins) being available during this period. The model top setting yielding the lowest average MSE for the alpine stations was considered optimal.
The lowest average MSE for ICAR was found for a model top elevation of 2.5 km above topography, whereas for ICARCP the minimum was at 4.0 km, see Fig. 2a. Setting the model top higher or lower quickly deteriorates model performance for ICAR and ICARCP alike. Furthermore, the sensitivity analysis indicates that the majority of skill is already present in the ICAR time series. Nonetheless, the inclusion of ERAI convective precipitation, as described in Sect. 2.6, results in an additional reduction in the MSE for the ICARCP time series at all simulated model top settings. The results are similar when, instead of the mean MSE, the mean SSMSE is investigated (see Fig. 2b). The mean skill maxima for ICAR and ICARCP are again found at 2.5 and 4.0 km, respectively, with ICARCP achieving the highest mean skill of 0.24. Therefore, all following analyses, unless stated otherwise, focus on the ICARCP time series obtained with a model top set to 4.0 km above topography.
The mean MSE over all alpine weather stations is almost constant when calculated either for the reference period (2014–2015), the full study period (2007–2017) or the reduced study period, where the reference period is excluded from the time series (2007–2013 and 2015–2017), see Fig. 2c. This result indicates that the reference period is representative of the full study period.
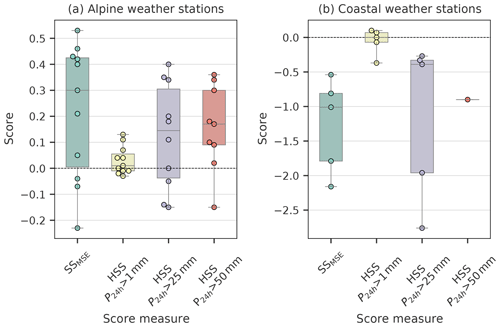
Figure 3Box and whisker plots of all assessed skill scores (x axis) obtained for ICARCP with ERAI as a reference. All skill scores were calculated using the entire P24 h time series available at each weather station for (a) alpine weather stations and (b) coastal weather stations. The lower boundary of the box indicates the 25th percentile, the upper boundary the 75th percentile and the horizontal line the median. Whiskers show the minimum and maximum values of the data set. The circles show the individual values of each skill measure for all stations.
4.4 Overall performance of ICAR for alpine and coastal weather stations
The performance of ICARCP at individual stations is presented in Table 2 and summarized in Fig. 3. For the alpine weather stations, values of SSMSE calculated across the entire period for which data are available (see Table 1 for details) indicate a median SSMSE of 0.3, equivalent to a median reduction of error of 30 % relative to ERAI for locations in complex alpine topography. Six of the eleven alpine stations have significant scores above zero, three are negative. Regarding the topographic situation (see Fig. 1), six alpine weather stations are downwind of the main alpine ridge, with respect to the predominant wind directions. The results indicate a negative correlation between SSMSE and the average distance downwind to the main alpine crest (Δ), with the weather stations farthest leeward (Albert Burn, Rakaia and Potts) exhibiting, apart from Mahanga, the lowest scores observed. No Δ value was assigned to Mahanga as it is located to the north of the alpine crest and situated approximately 80 km downwind from the coast. The topography to its west and northwest to the coast is constituted by scattered mountain ranges with elevations between 1000 and 1800m.
Table 2Time series characteristics for all of the weather stations, as well as a detailed overview of performance metrics for both ICARCP and ERAI obtained for each individual site. Empty cells indicate that less than 10 days were available for the calculation of the corresponding score. An asterisk (*) preceding a positive score denotes that the score is not significant with regards to the criteria laid out in Sect. 4.2.
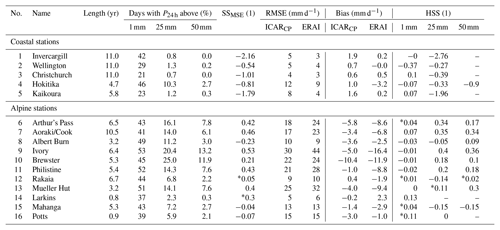
In terms of HSS at alpine stations, median scores above 0.14 are found for the P24 h thresholds 25 and 50 mm, respectively, see Fig. 3b. The only weather stations with comparatively large negative scores are Mahanga and Rakaia, the former of which is located downstream of mountainous terrain and the latter of which is the second farthest downwind of the main alpine crest. For days with P24 h exceeding 1mm, significant added value of ICARCP over ERAI is only found at 2 of the 11 locations. The fact that only small negative scores are found and the median score is 0.01 for all alpine stations indicates that ICARCP performs very similarly to ERAI at this threshold, and that ICARCP does not improve on modeling the frequency of precipitation. Table 2 contains additional information about the relative abundance of threshold exceedances at each weather station.
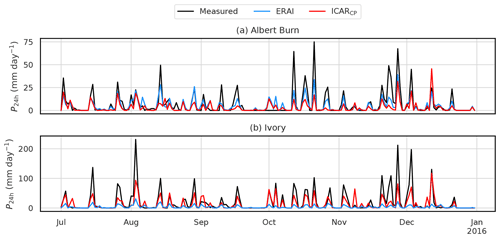
Figure 4Observed and simulated example time series of P24 h during the second half of 2015 at (a) Albert Burn and (b) Ivory. At these sites the respective lowest and highest SSMSE were achieved, during 2015: SSMSE was −0.39 for Albert Burn and 0.58 for Ivory. The sites are 210 km apart and are located at elevations of 1280 and , respectively. While Albert Burn lies approximately 11 km downstream of the main alpine ridge, Ivory is located 1 km upstream relative to the predominant westerlies and northwesterlies.
A direct comparison of measured and simulated P24 h time series at the Albert Burn and Ivory alpine stations is shown in Fig. 4. These two sites were selected as the SSMSE was lowest at Albert Burn and highest at Ivory among all alpine stations for the entire period. During 2015 (second half shown) the skill difference is largest, with SSMSE values of −0.39 and 0.58, respectively. The two weather stations are separated by a distance of about 210 km and are at a similar elevation, with Albert Burn at and Ivory at . However, Albert Burn is located 11 km downstream of the main alpine ridge, whereas Ivory lies approximately 2 km upstream of it according to the definition in Sect. 3.2. At both sites ICAR reproduces the features of the measured precipitation time series, but in the case of Albert Burn it underestimates measured precipitation amounts by almost 50 % on average; furthermore, at Ivory, where ICAR performs best in terms of SSMSE, precipitation is still underestimated by approximately 22 %.
For the coastal weather stations, figure 3b shows that no added value could be found as quantified by SSMSE and HSS for the thresholds P24 h>25 and P24 h>50 mm. Slightly positive values of HSS at P24 h>1 mm were only found for the Christchurch and Kaikoura sites, both of which are located along the east coast of the South Island of New Zealand. As ICAR is based on linear mountain wave theory, this result is expected: improvements for P24 h are mainly deemed to manifest themselves in complex topography. Hence, in the following only stations in complex topography are considered.
4.5 Seasonal variations of ICAR performance
Simulations with ICAR show the seasonal variation of precipitation across the South Island. Figure 5 illustrates the 10-year mean daily precipitation and seasonal differences to it as computed using four different methods: the observation-based and expert-judgment-based VCSR, ICAR, ICARCP and ERAI. For the weather station data in this study, skill measures were calculated for each season individually and are shown in Fig. 6.
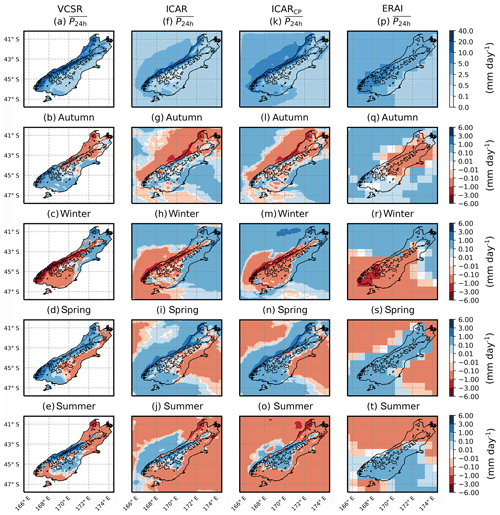
Figure 5The top four panels show patterns of P24 h averaged over 2007–2016 for VCSR (left), ICAR (second column), ICARCP (third column) and ERAI (right) over the South Island of New Zealand and surrounding ocean. Rows two to five show seasonal deviations of the all-year average patterns, for autumn (MAM, second row), winter (JJA, third row), spring (SON, fourth row) and summer (DJF, bottom). Each panel shows the coastline and the contour line of the topography. High-resolution plots are available in Horak et al. (2019).
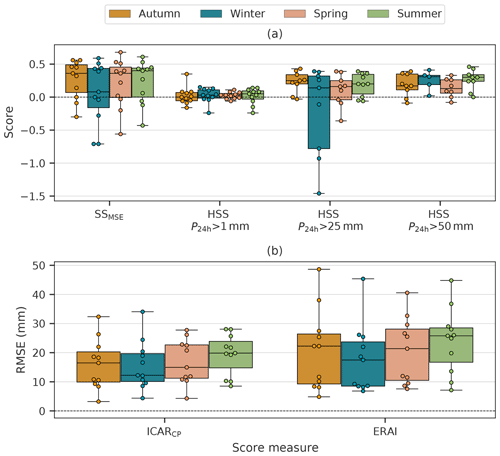
Figure 6Panel (a) shows values of SSMSE and HSS (from left to right) for all seasons (colors of the boxes) and panel (b) the root mean squared errors (RMSE) of ICARCP and ERAI for all alpine stations. Each box and whisker plot is associated with a season (indicated by box color) and a skill measure (x axis). The lower boundary of each boxplot indicates the 25th percentile, its upper boundary denotes the 75th percentile and the black line is the median. Whiskers show the minimum and maximum values of the data set. Circles on top of the boxes show the individual values of each skill measure for all stations. At some weather stations no days with P24 h>25 or P24 h>50 mm were observed or simulated during certain seasons, and, thus, no HSS scores could be calculated.
Overall, the average precipitation pattern of VCSR (Fig. 5a) is best captured by ICARCP (Fig. 5k). While ICAR and ICARCP patterns are very similar, the former is, when compared to VCSR, too dry to the east of the Southern Alps, particularly between approximately 44 and 45 ∘ S. However, VCSR indicates larger amounts of precipitation, along the southwest and west coast of the South Island, which are underestimated by ICAR and ICARCP. Furthermore VCSR shows a precipitation maximum in the Southern Alps between 43 and 44 ∘ S of approximately 20 to 40 mm d−1. While this maximum is found in ICAR and ICARCP patterns, it is confined to a smaller area and shifted westward, located along the contour line in Figs. 5f and k. Nonetheless, the characteristics of the west–east precipitation profile observed on the South Island of New Zealand (e.g., Henderson and Thompson, 1999) are captured by ICAR and ICARCP. This is, to some extent, also the case for ERAI (Fig. 5p), albeit with much lower maxima and flatter west–east gradients. While above the ocean no data are available for the VCSR, the results clearly show that ICAR is able to generate precipitation with seasonal variation above the ocean where no topography is present (Fig. 5f–j).
The seasonal variations of precipitation patterns as derived from the VCSR data set (Fig. 5b–e) are best reproduced by ICARCP (Fig. 5l–o). However, the improvements over the corresponding ICAR patterns (Fig. 5g–j) are small and the remainder of this paragraph applies to ICAR and ICARCP alike. When comparing VCSR and ICARCP the similarities are largest for winter (JJA, Fig. 5c, m) and summer (DJF, Fig. 5e, o). The differences increase for the remaining seasons, with the Southern Alps being particularly affected. For autumn (MAM), VCSR shows the precipitation as below average (Fig. 5b), whereas ICARCP indicates above average precipitation (Fig. 5l). For spring (SON), in contrast, VCSR shows an increase in precipitation throughout the Southern Alps (Fig. 5d), whereas ICARCP shows the central part of the Southern Alps as drier than average (Fig. 5n). ERAI, in comparison to VCSR, lacks the fine grid spacing needed to resolve local effects of the topography. However, the patterns roughly capture the seasonal variations of precipitation across the South Island, although at a much lower magnitude (Fig. 5q–t).
Seasonal averages of daily accumulated precipitation derived from measurements at the alpine weather stations show winter as the driest season, summer as the wettest and the transitional seasons in between (see Fig. S1 in the Supplement). values as simulated by ICARCP also correctly show winter as the driest season, autumn in between and summer as the wettest season, with spring being as wet as summer in ICARCP. However, values derived from ICARCP underestimate seasonal averages derived from measurements by up to 37 %. ERAI, in comparison, is not able to reproduce this pattern in the seasonal averages derived from measurements at all. Here, spring is the wettest season and autumn is the driest.
Added value of ICARCP in terms of SSMSE is found for spring, summer and autumn with median values greater than 0.36. For a model based on linear theory, better performance may be expected during the winter half of the year, when convective available potential energy is lower and convective events are rarer. This is not reflected in the median of SSMSE for winter, which is the lowest of all seasons with 0.08 and has the largest spread of values (see Fig. 6a). However, the seasonal variation of the root mean squared error (RMSE) for ICARCP shows a minimum during the winter season, see Fig. 6b. This is also the case for ERAI, resulting in the lowest RMSE values of ERAI during winter compared with the other seasons. As the RMSE decrease during winter is larger for ERAI than it is for ICARCP, this results in a correspondingly lower value of SSMSE in comparison to the other seasons. For HSS the 1mm threshold shows almost no seasonal variation with low median scores of less than 0.05 during all seasons. At the higher thresholds the pattern is different. For P24 h>25 mm the highest scores are found during autumn and summer with the lowest scores during the remaining seasons. At P24 h>50 mm the seasonal variation is stronger and shows less spread among the stations, with the highest median score during winter and summer and the lowest scores during the transitional seasons. While ICAR most consistently provides added value at higher thresholds, site specific improvements are even observed at P24 h>1mm.
4.6 Sensitivity of ICAR performance to upstream flow linearity
As a model that is based on linear theory, ICAR is expected to perform best in cases where linear theory is a valid approximation of the atmospheric flow at the sites of interest. An indicator of whether this is the case or not is the nondimensional mountain height (e.g., Smith, 1980), hereafter referred to as the Froude number F:
where Un denotes the horizontal wind speed perpendicular to the Southern Alps, N is the Brunt–Väisälä frequency and H is an assumed homogenous ridge height of 1500 m, characterizing the Southern Alps. Values of F equal to or larger than unity indicate linear flow, whereas values of F closer to zero point towards nonlinearity (Smith, 1980).
In order to derive Un and N, two volumes upstream of the west and east coast were defined, from which the properties of the flow at an angle of to the Southern Alps were extracted from ERAI daily averages. They are located 200 km northwest and southeast of the west and east coast of the South Island, respectively, to minimize the effect of the ERAI topography on the flow. Each volume is oriented parallel to the corresponding coast and is about 200 km wide, 500 km long and 1500 m high, with each containing 22 ERAI grid points. For northwesterly flow, properties were extracted from the volume to the northwest of the western coast, and for southeasterlies properties were extracted from the volume southeast of the eastern coast.
Following the approach of Reinecke and Durran (2008), the Brunt–Väisälä frequency and wind speed perpendicular to the Southern Alps were calculated using the averaging method for each ERAI grid point in the volumes:
where and are the averages of the Brunt–Väisälä frequency and the wind speed perpendicular to the Southern Alps, respectively, weighted by the thickness of the vertical levels. For a relative humidity (RH) below 90 % the dry Brunt–Väisälä frequency was employed in Eq. (5), whereas for RH values larger than or equal to 90 % the moist Brunt–Väisälä frequency Nm (Emanuel, 1994) was used:
Here g is the acceleration due to gravity; T is the temperature; θ is the potential temperature; θe is the equivalent potential temperature; Γm is the saturated adiabatic lapse rate; cp and cl are the specific heats at constant pressure of dry air and liquid water, respectively; qs is the saturation mixing ratio; ql is the liquid water mixing ratio; and the total water content is calculated as .
F was then calculated from the weighted averages of and at all grid points showing stable atmospheric conditions. The imaginary part of the weighted average of the Brunt–Väisälä frequency, , was used as an indicator of whether the atmosphere at an ERAI grid point was stably stratified. For below a threshold κ the stratification was considered stable, whereas larger or equal to κ was classified as near-stable. The nomenclature ”near-stable” is chosen over ”unstable” as vertical potential temperature profiles indicated that the nonzero imaginary part of in the large majority of cases was caused by a thin unstable layer close to the ocean surface, which was not representative of the conditions above and had a negligible effect on flow linearity. To investigate the dependence of the results on the threshold choice, the value of κ is varied between and in steps of . If more than half of the grid points in an upstream volume showed near-stable conditions, flow for this day was classified accordingly. Otherwise the day was marked as having stable atmospheric flow with an average Froude number . Days when the volume to the northwest and the volume to the southeast both showed flow towards the Southern Alps were excluded from the analysis. This procedure allowed for the remaining days in the 11-year study period to be categorized into days when atmospheric conditions upstream of the weather stations were either (i) near-stable (), (ii) stable with flow of low linearity () or (iii) stable with highly linear flow (). All data from alpine weather stations were then grouped by these categories and skill scores were calculated to analyze ICAR performance with regard to the atmospheric background state.
Table 3Skill measures calculated for the three categories of atmospheric flow (near-stable, stable with and stable with ), and the number of days pertaining to each category in percent as a function of κ. An asterisk preceding a score indicates that it was found to be nonsignificant by applying the criteria defined in Sect. 4.2.
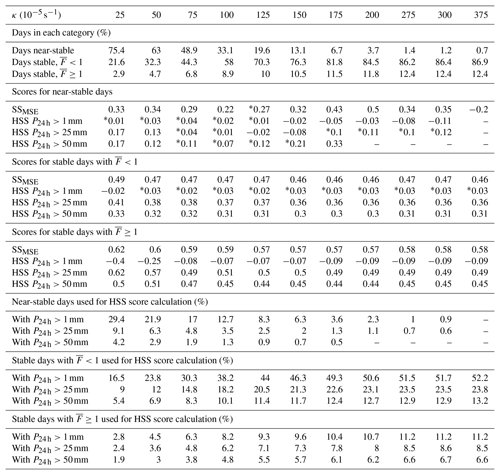
Of the 4018 d in the 11-year study period, 1847 fulfill the criteria stated above. A detailed overview of the distribution of these days among the three categories as a function of κ is given in Table 3. The results from Table 3, which are also summarized in Fig. 7, show that stable atmospheric conditions and Froude numbers larger than or equal to unity lead to an increase in median scores for sites in complex topography. This behavior is observed for SSMSE, where the score median increases from 0.33 to 0.58, and for P24 h>25 and P24 h>50 mm in the case of HSS. For P24 h>1 mm the maximum median score is found for stable conditions and , with the regime even yielding a negative median score. Notably the analysis shows that ICARCP not only provides added value over ERAI during stable days with high flow linearity, but also during near-stable days and stable days with low flow linearity.

Figure 7Dependence of SSMSE and HSS at alpine stations on atmospheric stability and the Froude number regime, calculated for all available data for each value of κ (see Table 3). SSMSE is shown in (a) in addition to HSS for the (b) P24 h>1 mm, (c) P24 h>25 mm and (d) P24 h>50 mm thresholds. The x axis indicates atmospheric stability and the Froude number regime. The lower boundary of each boxplot indicates the 25th percentile, the upper boundary denotes the 75th percentile and the black line is the median. Whiskers show the minimum and maximum values of the data set.
4.7 Weather-pattern-based evaluation of ICAR
Kidson (1994a) developed a daily weather pattern classification scheme for New Zealand based on 24 h mean sea-level pressure fields. For the underlying cluster analysis, Kidson (1994a) employed the NCEP/NCAR 40-year reanalysis data set (Kalnay et al., 1996) between January 1958 and June 1997. This analysis yielded 12 synoptic weather patterns (Kidson, 2000) associated with three regimes: “trough”, “zonal” and “blocking”. The trough regime is characterized by troughs crossing New Zealand and above average precipitation countrywide; the zonal regime is characterized by strong zonal flow to the south and highs to the north with milder conditions in the south; and the blocking regime displays highs in the south leading to a dryer southwest but wetter northeast. On average about 38 % of days are classified as belonging to the trough regime, 25 % to the zonal regime and 37 % to the blocking regime. Figure S2 gives an overview of the 12 synoptic weather patterns defined for New Zealand and the associated regime. An operational pattern-classification of each day since 1948 is available from the National Institute of Water and Atmospheric Research of New Zealand (NIWA).
Furthermore, these weather patterns have been linked to deviations of quantities, such as precipitation, from the climatological mean (Kidson, 1994b, 2000). For instance, during the HW pattern precipitation is below average at all weather stations, whereas during the TNW, T, HE and W patterns, when westerlies and northwesterlies dominate and orographic lifting in the Southern Alps is favored, precipitation at all alpine weather stations is above average (see, for example, Sect. 4.8). This allows for the investigation of whether a downscaling model is able to represent these departures correctly, offering a link between the synoptic situation and local weather anomalies.
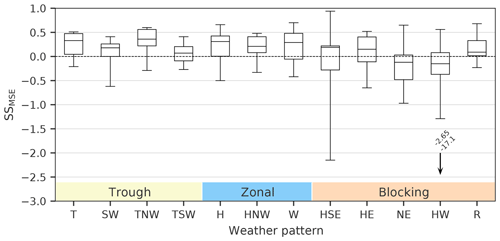
Figure 8Box and whisker plot of SSMSE calculated for all alpine weather stations as a function of the synoptic weather pattern (x axis; Kidson, 2000). The regime associated with each weather pattern is indicated by the colored shading in the lower part of the plot. The lower bound of each box marks the 25th percentile of the data, the upper bound marks the 75th and the black horizontal line is the median. The whiskers indicate the minimum and maximum values in the data set, except for the HW pattern where two data points outside the plot limit are indicated by an arrow and their corresponding values are noted above.
Figure 8 shows a distinct dependence of SSMSE on the synoptic weather pattern. Highest median scores with values above 0.29 in terms of SSMSE are achieved for the TNW, T, H and W weather patterns. Three of these patterns (TNW, T and W) are associated with distinct westerly and northwesterly flow, facilitating orographic lifting along the Southern Alps. However, the HE pattern, for which similar conditions may be expected, only yields a median SSMSE of 0.15. This comparatively low median value is due to very low scores found for the Potts, Rakaia and Mahanga weather stations. Rakaia and Potts are farthest downwind of the main alpine ridge and Mahanga is the weather station farthest downwind of the coast with approximately 80 km of mountainous terrain in between, where downwind is as defined in Sect. 3.2. Particularly low median scores are found for the HW and NE patterns, where flow parallel to the Southern Alps dominates. Consistent with the results from Sect. 3, no added value of ICARCP over ERAI was found in terms of HSS for P24 h>1mm, even though there is a small variation with weather pattern (not shown). For the higher thresholds, not enough data were available to calculate HSS for every weather pattern.
4.8 Weather-pattern-based variations of precipitation
Kidson (1994b) noted that the local climate in New Zealand shows variability as a function of the synoptic weather patterns. In this section, the capability of ICAR to capture the average 24 h accumulated precipitation amount at each weather station (ws) calculated for each of the weather patterns (wp) is investigated. To this end, averages of P24 h simulated by ICAR and ERAI are calculated individually for each weather pattern and each of the weather stations and compared to the observations. Figure 9 shows measured and modeled values of for the Ivory weather station. It is located at an elevation of and lies approximately 2 km upstream of the main alpine ridge with respect to westerly and northwesterly flow (see Sect. 3.2). Ivory is strongly affected by precipitation caused by orographic lifting, leading to local precipitation maxima during the T, TNW, W and HE patterns. Furthermore, at Ivory, the behavior found in the measurements is correctly reproduced by ICARCP and ERAI. The absolute amounts of precipitation are, although underestimated, better modeled by ICARCP. To analyze how well the simulated values of correlate with measurements, the coefficient of determination weighted by weather pattern frequency, r2, (Wilks, 2011b, chap. 5) between the observed and modeled values of are calculated for all weather stations and are shown in Fig. S3a. To investigate the added value of ICARCP over ERAI in modeling measured amounts of , SSMSE is calculated and the results are summarized in Fig. S3b.
With the exception of the Potts weather station, ICARCP is able to represent the fluctuation of as a function of weather pattern, with an r2 value higher than 0.9 (see Fig. S3a). ICARCP shows clear improvement over ERAI at 5 of the 11 weather stations, a similar performance to ERAI at 4 of the stations and a worse performance at 2 stations. Particularly noteworthy is the underperformance compared with ERAI at the Potts alpine weather station and, far less pronounced, at the Larkins weather station. Both stations are located downstream of the main alpine ridge, but only at Potts does ICARCP not correctly anticipate decreased precipitation during the HW and TSW patterns, as well as an increase in precipitation during the W pattern (Fig. S6j).

Figure 9 as a function of weather pattern (wp) and weather station (ws) at the Ivory weather station for measurements (black pentagons), ICAR simulations (orange disks) and the ERAI reanalysis (blue squares). Ivory is situated at an elevation of and, on average, approximately 2 km upstream of the main alpine ridge with regard to northwesterlies and westerlies. The connecting lines serve as guides for the eye.
Generally ICARCP is able to model measured amounts of well at all other alpine weather stations (see Fig. S3b) with a median SSMSE of 0.74, except for Albert Burn and Potts. At Albert Burn it underestimates measured and ERAI modeled values of during all patterns (Fig. S6a). Albert Burn is located approximately 11 km downwind of the main alpine ridge with respect to westerlies and northwesterlies. The lowest score is found at the Potts alpine weather station.
The model top leading to the smallest average MSE of ICARCP over all alpine weather stations was determined with a sensitivity study at 4 km above topography. At alpine sites in complex topography ICARCP was then able to reduce mean squared errors in comparison to its ERAI forcing data set by up to 53 % and 30 % on median. While ICARCP modeled the occurrence of days with a maximum accumulated precipitation of 1 mm as well as ERAI, significant improvements were found for P24 h>25 and P24 h>50 mm. Overall the mean daily precipitation pattern produced by ICARCP was found to be in agreement with the pattern derived from the VCSR observation-based gridded data set, with the seasonal variation being mostly captured by ICARCP. The results indicate that ICARCP performs best during stable atmospheric conditions with highly linear flow; however, added value over ERAI is also found for stable days with low flow linearity and near-stable days. A clear dependence of skill on the synoptic situation was found, with weather patterns associated with cross-alpine flow leading to higher scores than weather patterns with flow parallel to the alpine range.
ICAR was found to perform better for upstream flows with Froude numbers larger than unity. This result is not unexpected, as linear theory is the theoretical foundation for ICAR. Therefore, flows of higher linearity lead to increased SSMSE and HSS for thresholds of 25 and 50 mm. These results hold even if the method for classifying near-stable or stable days is changed. For instance, using as the classification criterion for near-stable days and for stable days leads to similar results (see Fig. S4). For SSMSE (see Fig. 7a) the spread of scores derived from varying κ for near-stable days is large enough to include the median score of the stable days with . Nonetheless, this is only true for , in all other cases stable days with always score higher than near stable days. Stable days with , in comparison, always achieve a higher score than the other two categories. A potential issue with the methodology is the small number of cases in the stable regime with compared with the two other classes (see Table 3). However, on stable days with is 3–7 times as high as during the other two classes (see Fig. S5). Therefore, while comparably small in number, stable days with contribute above-average amounts of precipitation to the climatology, highlighting the importance of the improvement in skill for this category.
Negative values of SSMSE were found for the Albert Burn, Mahanga and Potts alpine weather stations, whereas nonsignificant positive scores were found at Rakaia and Larkins. The time series of Potts and Larkins are the shortest of all weather stations, spanning 0.9 and 0.8 years, respectively, which potentially contributed to the negative or nonsignificant positive scores, respectively. Furthermore, Potts is the weather station with the largest difference between weather station elevation and ICAR grid cell elevation, with the ICAR grid cell located 741 m lower. While the aforementioned issues may deteriorate scores at individual stations, it is also possible that the downwind distribution of moisture by ICAR differs from expectations. This is indicated by a slight negative correlation of the score value with the average distance downwind from the main alpine crest (as defined in Sect. 3.2) which is found for SSMSE and HSS at the 25 and 50 mm thresholds. The correlation is strongest for SSMSE with a value of −0.65 and weakest for the HSS with P24 h>50 mm with a value of −0.50. Mahanga and Larkins are the weather stations farthest downwind from the coast, with mountainous topography located in between. Albert Burn, Rakaia and Potts are the weather stations farthest downwind of the main alpine crest. A potential cause for the observed negative correlation is the fact that the reflection of mountain waves at the interfaces between atmospheric layers can impact the distribution of orographic precipitation (Barstad and Schüller, 2011). Siler and Durran (2015) found, for instance, that wave reflection at the tropopause may either strengthen or weaken low-level windward ascent, which in turn affects the amount and distribution of orographic precipitation. The outcome was found to depend on the ratio of the tropopause height to the vertical wavelength of the mountain waves. As ICAR currently does not account for wave reflection, its implementation could therefore lead to improvements in this regard.
The mean SSMSE of ICARCP at alpine weather stations is 0.3. While ICARCP provides added value over ERAI it also systematically underestimates precipitation at all alpine weather stations except for Rakaia (see Tables 1 and 2). This underestimation increases with higher model top settings and is independent of the average distance of the site upwind or downwind from the main alpine ridge (with respect to northwesterlies and westerlies). Different issues may contribute to this underestimation.
- i.
ERAI is potentially too dry in the study region and therefore not enough moisture is advected across the boundary of the nested ICAR domain.
- ii.
As the coupling between surface and atmosphere is neglected in the ICAR setup employed for this study, parts of the ocean within the ICAR domain cannot contribute moisture to the airflow upwind of the South Island of New Zealand.
- iii.
Nonlinear amplification of waves could amplify updrafts in comparison to updrafts predicted by linear theory, increasing orographic precipitation correspondingly.
- iv.
The low model top setting at 4 km above topography, determined as optimal by a sensitivity study, may largely eliminate the potential seeder–feeder interaction between synoptic clouds and orographically lifted moist air. This effect is expected to play a crucial role for the formation of heavy rainfall on the South Island of New Zealand (Purdy and Austin, 2003). While increasing the model top is an apparent solution to this issue, the sensitivity study in Sect. 4.3 showed that this does not lead to a decrease in the MSE of ICAR or ICARCP (Fig. 2a), nor does it increase model skill at alpine weather stations (Fig. 2b).
- v.
Convergences and divergences in the ERAI data set influence updrafts and downdrafts in the ICAR wind field, leading, for instance, to synoptic precipitation in ICAR; however, these divergences may also dampen the updrafts calculated with linear theory, thereby reducing the precipitation computed by ICAR.
- vi.
The reflection of mountain waves is neglected by the version of ICAR used in this study. However, Siler and Durran (2015) showed that the reflection of mountain waves has a significant impact on the amount and distribution of precipitation.
Further studies are needed to quantify the influence of issues (i)–(vi) and identify their relevance for the observed underestimation. A possible ad hoc solution to the underestimation is the application of a bias-correction field estimated from a regional climate model to the ICAR precipitation fields (e.g., Engelhardt et al., 2017).
While the relative variability of average daily precipitation amounts related to synoptic weather patterns, , showed a comparable reproduction quality by both ICARCP and ERAI (see Fig. S3a), absolute amounts of are largely underestimated by ERAI (up to on average 17 mm). This underestimation is far less pronounced in ICAR_CP, resulting in a median SSMSE of 0.74 when modeling (see Fig. S3b).
Precipitation measurements, particularly those in complex topography, are associated with uncertainties. Different factors such as wetting, wind, freezing or equipment failure in harsh conditions (Henderson and Thompson, 1999) may introduce errors, such as undercatch, into the results. Wind has been recognized as the main cause of undercatch (e.g., Groisman and Legates, 1995; Yang et al., 1999; Yang and Ohata, 2001), and particularly affects alpine weather stations. The effect is most pronounced for large, solid precipitation and increases with latitude and elevation (Goodison et al., 1989; Groisman and Legates, 1995). Cullen and Conway (2015), for instance, estimated the undercatch at Mount Brewster during summer to be 25 %, whereas Kerr et al. (2011) listed annual undercatch at alpine sites in the Southern Alps as up to 20 %. However, the impact of undercatch on the results presented here is expected to be small, as these errors have an adverse effect not only on the performance of ICARCP but also on the ERAI reference model.
In this study, the chosen reference period (2014–2015) overlaps with the study period (2007–2017). While ICAR is computationally more efficient than dynamic downscaling, performing, for instance, leave-p-out cross-validation would require extensive computational resources. However, the results suggest that the reference period is representative of the full study period with regards to the presented calibration method: for simulations with the model top set at 4 km, the mean MSE over all alpine weather stations of ICAR shows only little variation depending on whether the MSE is calculated for the reference period, the study period or the study period excluding the reference period (see Fig. 2c). Furthermore, the variation between the mean MSEs for simulations with different model top settings (Fig. 2b) is larger than the variation between different evaluation periods (Fig. 2c).
The sensitivity studies leading to the choice of the model top at 4 km have shown that the model top elevation greatly influences precipitation amounts and, in turn, the mean squared errors obtained, see Fig. 2. It is not immediately obvious though why precipitation amounts decrease (not shown) and the MSEs deteriorates for higher model tops. Potential reasons are the influences of divergences in the forcing wind field on the ICAR wind field or numerical artifacts arising from the treatment of the model top in ICAR. However, further research is necessary to develop a better understanding of this issue and its causes. Subsequently, future studies could focus on finding a method that allows for the estimation of the model top elevation best suited for a domain without relying on measurements, as well as on investigating the influence of the choice of the forcing data type (i.e., global or regional reanalyzes, GCMs and weather forecast models) and the spatial grid resolution thereof on ICAR dynamics and skill.
In the analysis presented, standard verification scores based on point matches between model and observation were employed (see Sect. 4.2). Nonetheless, these verification scores are susceptible to small spatial shifts in the ICARCP precipitation field that cannot be produced by the coarse-scale reference model. Therefore, this effect may potentially over-penalize ICARCP in comparison to the much coarser ERAI field (Theis et al., 2005; Ebert, 2008). An over-penalization of ICAR compared with ERAI is suggested by the precipitation pattern comparisons shown in Fig. 5. Here the VCSR observation-based gridded data set and ICARCP are generally in good agreement, with ICARCP reproducing most seasonal variations. As noted in Sect. 4.5, for instance, a precipitation maximum in the VCSR pattern (Fig. 5a) that is located within the Southern Alps is shifted westward in the ICARCP pattern (Fig. 5k) and is, due the coarser grid-spacing, not present in ERAI at all (Fig. 5p). A variety of methods have been proposed to overcome this problem, and future evaluations of ICAR generated atmospheric fields could incorporate these methods in their evaluation procedures (e.g., Ebert, 2009).
In this study, simulations with ICAR were found to provide added value over ERA-Interim for 24 h accumulated precipitation on the South Island of New Zealand for alpine weather stations. In contrast to the almost consistently positive results found for the alpine weather stations, ICAR provides no added value over ERA-Interim for coastal weather stations. A comparison of average and seasonal precipitation patterns of an operational gridded rainfall data set with ICAR showed good agreement. Grouping the available data according to Froude number revealed that stable atmospheric conditions with a higher degree of flow linearity lead to higher skill scores, and that ICAR provides added value over ERA-Interim even for days with near-stable conditions and stable days with lower flow linearity. A grouping according to the synoptic situation showed that values of SSMSE are generally high for weather patterns associated with flow approximately perpendicular to the alpine range and lowest for weather patterns exhibiting flow parallel to the Southern Alps. While ICAR in principle does not require observations to be calibrated, the model top for this study was determined with a sensitivity analysis. All other settings could be adopted from default. With the adjusted model top, however, consistent added value for stations in complex topography was found, with a reduction of the median error by 30 %. Clear improvement may be expected on further site-specific calibration to observations as routinely performed in regional climate-model-based downscaling. Further research on how ICAR fields are influenced by the forcing data set will be necessary.
The data sets, ICAR configuration, DEM and forcing files that the results presented in this paper are based on are available from a Zenodo repository (Horak et al., 2019, https://doi.org/10.5281/zenodo.1135131). Due to licensing restrictions VCSR data are not included in the repository.
The supplement related to this article is available online at: https://doi.org/10.5194/hess-23-2715-2019-supplement.
JH carried out the investigation, formal analysis, validation, visualization and writing (original draft, review and editing). Conceptualization of the paper was a joint effort from all authors, as were the discussion and development of the methods presented. EG provided support for ICAR as well as computational resources. Funding acquisition and project administration were carried out by MH.
The authors declare that they have no conflict of interest.
The computational results were achieved with high-performance computing support from Cheyenne (https://doi.org/10.5065/D6RX99HX), provided by NCAR's Computational and Information Systems Laboratory, sponsored by the National Science Foundation, and with the HPC infrastructure LEO of the University of Innsbruck. The National Center for Atmospheric Research is sponsored by the US National Science Foundation. Furthermore the authors thank the National Institute of Water and Atmospheric Research, New Zealand, and in particular Christian Zammit, for providing support, the weather pattern classifications, the VCSR gridded rainfall data set and the data from the weather stations as specified in Table 1. Research on Brewster Glacier is supported by the Department of Geography, the University of Otago, New Zealand; the National Institute of Water and Atmospheric Research (Climate Present and Past CLC01202); and the Department of Conservation under concession OT-32299-OTH.
The following open-source libraries were employed to perform the data processing and analysis presented in this study: numpy (van der Walt et al., 2011), pandas (McKinney, 2010), xarray (Hoyer and Hamman, 2017), matplotlib (Hunter, 2007), cartopy (Met Office, 2010) and salem (Maussion et al., 2019).
This research has been supported by the Austrian Science Fund (grant no. 28006-N32).
This paper was edited by Nadav Peleg and reviewed by David Leutwyler and three anonymous referees.
Amante, C. and Eakins, B. W.: ETOPO1 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis, US Department of Commerce, National Oceanic and Atmospheric Administration, National Environmental Satellite, Data, and Information Service, National Geophysical Data Center, Marine Geology and Geophysics Division Colorado, 2009. a
Barrell, D., Andersen, B., and Denton, G.: Glacial Geomorphology of the Central South Island, New Zealand, GNS Science Monograph, GNS Science, 2011. a
Barstad, I. and Grønås, S.: Dynamical structures for southwesterly airflow over southern Norway: the role of dissipation, Tellus A, 58, 2–18, https://doi.org/10.1111/j.1600-0870.2006.00152.x, 2006. a
Barstad, I. and Schüller, F.: An Extension of Smith's Linear Theory of Orographic Precipitation: Introduction of Vertical Layers*, J. Atmos. Sci., 68, 2695–2709, https://doi.org/10.1175/JAS-D-10-05016.1, 2011. a
Benestad, R. E., Hanssen-Bauer, I., and Chen, D.: Empirical-Statistical Downscaling, World Scientific, p. 22, https://doi.org/10.1142/6908, 2008. a
Bernhardt, M., Härer, S., Feigl, M., and Schulz, K.: Der Wert Alpiner Forschungseinzugsgebiete im Bereich der Fernerkundung, der Schneedeckenmodellierung und der lokalen Klimamodellierung, Österreichische Wasser- und Abfallwirtschaft, https://doi.org/10.1007/s00506-018-0510-8, 2018. a, b, c, d
Chater, A. M. and Sturman, A. P.: Atmospheric Conditions Influencing the Spillover of Rainfall to Lee of the Southern Alps, New Zealand, International J. Climatol., 18, 77–92, https://doi.org/10.1002/(SICI)1097-0088(199801)18:1<77::AID-JOC218>3.0.CO;2-M, 1998. a
Chinn, T.: Distribution of the Glacial Water Resources of New Zealand, J. Hydrol. (New Zealand), 40, 139–187, 2001. a, b
Christensen, J. H., Hewitson, B., Busuioc, A., Chen, A., Gao, X., Held, I., Jones, R., Kolli, R. K., Kwon, W.-T., Laprise, R., Rueda, M., Mearns, V., Menéndez, L., G, C., Räisänen, J., Rinke, A., Sarr, A., and Whetton, P.: Regional Climate Projections, in: Climate Change 2007: The Physical Science Basis, Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K. B., Tignor, M., and Miller, H. L., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2007. a
Cullen, N. J. and Conway, J. P.: A 22 Month Record of Surface Meteorology and Energy Balance from the Ablation Zone of Brewster Glacier, New Zealand, J. Glaciol., 61, 931–946, https://doi.org/10.3189/2015JoG15J004, 2015. a, b, c, d, e
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hølm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J., Park, B., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J., and Vitart, F.: The ERA-Interim reanalysis: Configuration and performance of the data assimilation system, Q. J. Roy. Meteorol. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011. a
Di Luca, A., de Elía, R., and Laprise, R.: Challenges in the quest for added value of regional climate dynamical downscaling, Current Climate Change Reports, 1, 10–21, https://doi.org/10.1007/s40641-015-0003-9, 2015. a
Ebert, E. E.: Fuzzy verification of high-resolution gridded forecasts: a review and proposed framework, Meteorol. Appl., 15, 51–64, 2008. a
Ebert, E. E.: Neighborhood Verification: A Strategy for Rewarding Close Forecasts, Weather Forecast., 24, 1498–1510, https://doi.org/10.1175/2009WAF2222251.1, 2009. a
Emanuel, K. A.: Atmospheric Convection, Oxford University Press, New York, 1994. a
Engelhardt, M., Leclercq, P., Eidhammer, T., Kumar, P., Landgren, O., and Rasmussen, R.: Meltwater runoff in a changing climate (1951–2099) at Chhota Shigri Glacier, Western Himalaya, Northern India, Ann. Glaciol., 58, 1–12, https://doi.org/10.1017/aog.2017.13, 2017. a, b, c, d
Georgakakos, K., Graham, N., Carpenter, T., and Yao, H.: Integrating climate-hydrology forecasts and multi-objective reservoir management for northern California, EOS T. Am. Geophys. Un., 86, 122–127, https://doi.org/10.1029/2005EO120002, 2005. a
Goodison, B., Sevruk, B., and Klemm, S.: WMO solid precipitation measurement intercomparison: Objectives, methodology, analysis, Atmos. Depos, 179, 57–64, 1989. a
Griffiths, G. A. and McSaveney, M.: Distribution of mean annual precipitation across some steepland regions of New Zealand, New Zeal. J. Sci., 26, 197–209, 1983. a
Groisman, P. Y. and Legates, D. R.: Documenting and detecting long-term precipitation trends: Where we are and what should be done, Climatic Change, 31, 601–622, https://doi.org/10.1007/BF01095163, 1995. a, b
Guo, Y. and Chen, S.: Terrain and land use for the fifth-generation Penn State/NCAR Mesoscale Modeling System (MM5): Program TERRAIN, Tech. rep., NCAR, https://doi.org/10.5065/D68C9T67, 1994. a
Gutmann, E., Barstad, I., Clark, M., Arnold, J., and Rasmussen, R.: The Intermediate Complexity Atmospheric Research Model (ICAR), J. Hydrometeorol., 17, 957–973, https://doi.org/10.1175/JHM-D-15-0155.1, 2016. a, b, c, d, e, f, g, h, i, j, k, l
Gutmann, E. D., Rasmussen, R. M., Liu, C., Ikeda, K., Gochis, D. J., Clark, M. P., Dudhia, J., and Thompson, G.: A Comparison of Statistical and Dynamical Downscaling of Winter Precipitation over Complex Terrain, J. Climate, 25, 262–281, https://doi.org/10.1175/2011JCLI4109.1, 2012. a
Henderson, R. and Thompson, S.: Extreme rainfalls in the Southern Alps of New Zealand, J. Hydrol. (New Zealand), 38, 309–330, 1999. a, b, c
Hill, G.: Grid telescoping in numerical weather prediction, J. Appl. Meteorol., 7, 29–38, https://doi.org/10.1175/1520-0450(1968)007<0029:GTINWP>2.0.CO;2, 1968. a
Horak, J., Hofer, M., Maussion, F., Gutmann, E., Gohm, A., and Rotach, M. W.: Dataset – Assessing the Added Value of the Intermediate Complexity Atmospheric Research Model (ICAR) for Precipitation in Complex Topography, https://doi.org/10.5281/zenodo.1135131, 2019. a, b, c, d
Hoyer, S. and Hamman, J.: xarray: ND labeled Arrays and Datasets in Python, Journal of Open Research Software, 5, p. 10, https://doi.org/10.5334/jors.148, 2017. a
Hunter, J. D.: Matplotlib: A 2D Graphics Environment, Comput. Sci. Eng., 9, 90–95, https://doi.org/10.1109/MCSE.2007.55, 2007. a
Jarosch, A. H., Anslow, F. S., and Clarke, G. K.: High-resolution precipitation and temperature downscaling for glacier models, Clim. Dynam., 38, 391–409, 2012. a
Kalnay, E., Kanamitsu, M., Kistler, R., Collins, W., Deaven, D., Gandin, L., Iredell, M., Saha, S., White, G., Woollen, J., Zhu, Y., Chelliah, M., Ebisuzaki, W., Higgins, W., Janowiak, J., Mo, K. C., Ropelewski, C., Wang, J., Leetmaa, A., Reynolds, R., Jenne, R., and Joseph, D.: The NCEP/NCAR 40-year reanalysis project, B. Am. Meteorol. Soc., 77, 437–471, https://doi.org/10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2, 1996. a
Kerr, T., Owens, I., and Henderson, R.: The precipitation distribution in the Lake Pukaki Catchment, J. Hydrol. (New Zealand), 50, 361–382, 2011. a
Kidson, J. W.: An automated procedure for the identification of synoptic types applied to the New Zealand region, Int. J. Climatol., 14, 711–721, https://doi.org/10.1002/joc.3370140702, 1994a. a, b
Kidson, J. W.: Relationship of New Zealand daily and monthly weather patterns to synoptic weather types, Int. J. Climatol., 14, 723–737, https://doi.org/10.1002/joc.3370140703, 1994b. a, b
Kidson, J. W.: An analysis of New Zealand synoptic types and their use in defining weather regimes, Int. J. Climatol., 20, 299–316, https://doi.org/10.1002/(SICI)1097-0088(20000315)20:3<299::AID-JOC474>3.0.CO;2-B, 2000. a, b, c
Klein, W. H., Lewis, B. M., and Enger, I.: Objective Prediction of Five-Day Mean Temperatures During Winter, J. Meteorol., 16, 672–682, https://doi.org/10.1175/1520-0469(1959)016<0672:OPOFDM>2.0.CO;2, 1959. a
Maraun, D.: Bias correction, quantile mapping, and downscaling: Revisiting the inflation issue, J. Climate, 26, 2137–2143, https://doi.org/10.1175/JCLI-D-12-00821.1, 2013. a
Maussion, F., Siller, M., Rothenberg, D., Roth, T., Dusch, M., and Landmann, J.: fmaussion/salem: v0. 2.4, Zenodo, https://doi.org/10.5281/zenodo.2605265, 2019. a
McKinney, W.: Data structures for statistical computing in python, in: Proceedings of the 9th Python in Science Conference, vol. 445, 51–56, Austin, TX, 2010. a
Mesinger, F., DiMego, G., Kalnay, E., Mitchell, K., Shafran, P. C., Ebisuzaki, W., Jović, D., Woollen, J., Rogers, E., Berbery, E. H., Ek, M. B., Fan, Y., Grumbine, R., Higgins, W., Li, H., Lin, Y., Manikin, G., Parrish, D., and Shi, W.: North American regional reanalysis, B. Am. Meteorol. Soc., 87, 343–360, https://doi.org/10.1175/BAMS-87-3-343, 2006. a
Met Office: Cartopy: a cartographic python library with a Matplotlib interface, Exeter, Devon, available at: http://scitools.org.uk/cartopy (last access: 18 June 2019), 2010. a
Nappo, C. J.: The Linear Theory, in: An Introduction to Atmospheric Gravity Waves, edited by: Nappo, C. J., vol. 102 of International Geophysics, 29–56, Academic Press, https://doi.org/10.1016/B978-0-12-385223-6.00002-1, 2012. a
Paeth, H., Pollinger, F., Mächel, H., Figura, C., Wahl, S., Ohlwein, C., and Hense, A.: An efficient model approach for very high resolution orographic precipitation, Q. J.e Royal Meteor. Soc., 143, 2221–2234, https://doi.org/10.1002/qj.3080, 2017. a
Pepin, N., Bradley, R. S., Diaz, H. F., Baraer, M., Caceres, E. B., Forsythe, N., Fowler, H., Greenwood, G., Hashmi, M. Z., Liu, X. D., Miller, J. R., Ning, L., Ohmura, A., Palazzi, E., Rangwala, I., Schöner, W., Severskiy, I., Shahgedanova, M., Wang, M. B., Williamson, S. N., and Yang, D. Q.: Elevation-dependent warming in mountain regions of the world, Nat. Clim. Change, 5, 424–430, https://doi.org/10.1038/nclimate2563, 2015. a
Purdy, J. and Austin, G.: The role of synoptic cloud in orographic rainfall in the Southern Alps of New Zealand, Meteorol. Appl., 10, 355–365, https://doi.org/10.1017/S1350482703001087, 2003. a
Raper, S. C. B. and Braithwaite, R. J.: Glacier volume response time and its links to climate and topography based on a conceptual model of glacier hypsometry, The Cryosphere, 3, 183–194, https://doi.org/10.5194/tc-3-183-2009, 2009. a
Rasmussen, R., Ikeda, K., Liu, C., Gochis, D., Clark, M., Dai, A., Gutmann, E., Dudhia, J., Chen, F., Barlage, M., Yates, D., and Zhang, G.: Climate change impacts on the water balance of the Colorado headwaters: high-resolution regional climate model simulations, J. Hydrometeorol., 15, 1091–1116, https://doi.org/10.1175/JHM-D-13-0118.1, 2014. a
Reinecke, P. A. and Durran, D. R.: Estimating topographic blocking using a Froude number when the static stability is nonuniform, J. Atmos. Sci., 65, 1035–1048, https://doi.org/10.1175/2007JAS2100.1, 2008. a
Rhea, J. O.: Orographic Precipitation Model for Hydrometeorological Use, PhD thesis, Colorado State University, Fort Collins, Colorado, USA, 1977. a
Roth, A., Hock, R., Schuler, T. V., Bieniek, P. A., Pelto, M., and Aschwanden, A.: Modeling winter precipitation over the Juneau Icefield, Alaska, using a linear model of orographic precipitation, Front. Earth Sci., 6, 20, https://doi.org/10.3389/feart.2018.00020, 2018. a
Sarker, R.: A dynamical model of orographic rainfall, Mon. Weather Rev., 94, 555–572, https://doi.org/10.1175/1520-0493(1966)094<0555:ADMOOR>2.3.CO;2, 1966. a, b
Sawyer, J.: Gravity waves in the atmosphere as a three-dimensional problem, Q. J. Roy. Meteor. Soc., 88, 412–425, https://doi.org/10.1002/qj.49708837805, 1962. a
Siler, N. and Durran, D.: Assessing the Impact of the Tropopause on Mountain Waves and Orographic Precipitation Using Linear Theory and Numerical Simulations, J. Atmos. Sci., 72, 803–820, https://doi.org/10.1175/JAS-D-14-0200.1, 2015. a, b
Smith, R. B.: The influence of mountains on the atmosphere, Adv. Geophys., 21, 87–230, https://doi.org/10.1016/S0065-2687(08)60262-9, 1979. a
Smith, R. B.: Linear theory of stratified hydrostatic flow past an isolated mountain, Tellus, 32, 348–364, https://doi.org/10.3402/tellusa.v32i4.10590, 1980. a, b
Smith, R. B. and Barstad, I.: A Linear Theory of Orographic Precipitation, J. Atmos. Sci., 61, 1377–1391, 2004. a, b, c
Sturman, A. and Wanner, H.: A comparative review of the weather and climate of the Southern Alps of New Zealand and the European Alps, Mt. Res. Dev., 21, 359–369, 2001. a
Tait, A. and Turner, R.: Generating multiyear gridded daily rainfall over New Zealand, J. Appl. Meteorol., 44, 1315–1323, https://doi.org/10.1175/JAM2279.1, 2005. a, b
Tait, A., Sturman, J., and Clark, M.: An assessment of the accuracy of interpolated daily rainfall for New Zealand, J. Hydrol. (New Zealand), 51, 25–44, 2012. a
Theis, S. E., Hense, A., and Damrath, U.: Probabilistic precipitation forecasts from a deterministic model: a pragmatic approach, Meteorol. Appl., 12, 257–268, https://doi.org/10.1017/S1350482705001763, 2005. a
Thompson, G., Field, P. R., Rasmussen, R. M., and Hall, W. D.: Explicit forecasts of winter precipitation using an improved bulk microphysics scheme. Part II: Implementation of a new snow parameterization, Mon. Weather Rev., 136, 5095–5115, https://doi.org/10.1175/2008MWR2387.1, 2008. a
Torma, C., Giogi, F., and Coppola, E.: Added value of regional climate modeling over areas characterized by complex terrain—Precipitation over the Alps, J. Geophys. Res.-Atmos., 120, 3957–3972, https://doi.org/10.1002/2014JD022781, 2015. a
van der Walt, S., Colbert, S. C., and Varoquaux, G.: The NumPy Array: A Structure for Efficient Numerical Computation, Comput. Sci. Eng., 13, 22–30, https://doi.org/10.1109/MCSE.2011.37, 2011. a
Weidemann, S., Sauter, T., Schneider, L., and Schneider, C.: Impact of two conceptual precipitation downscaling schemes on mass-balance modeling of Gran Campo Nevado ice cap, Patagonia, J. Glaciol., 59, 1106–1116, https://doi.org/10.3189/2013JoG13J046, 2013. a
Wilks, D.: Chap. 5 – Frequentist Statistical Inference, in: Statistical Methods in the Atmospheric Sciences, edited by: Wilks, D. S., vol. 100 of International Geophysics, 133–186, Academic Press, https://doi.org/10.1016/B978-0-12-385022-5.00005-1, 2011a. a
Wilks, D. S.: Statistical Methods in the Atmospheric Sciences, vol. 100 of International Geophysics, Academic Press, 2011b. a, b, c
Yang, D. and Ohata, T.: A bias-corrected Siberian regional precipitation climatology, J. Hydrometeorol., 2, 122–139, https://doi.org/10.1175/1525-7541(2001)002<0122:ABCSRP>2.0.CO;2, 2001. a
Yang, D., Ishida, S., Goodison, B. E., and Gunther, T.: Bias correction of daily precipitation measurements for Greenland, J. Geophys. Res.-Atmos., 104, 6171–6181, https://doi.org/10.1029/1998JD200110, 1999. a





