the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Improving soil moisture and runoff simulations at 3 km over Europe using land surface data assimilation
Wolfgang Kurtz
Carsten Montzka
Wendy Sharples
Klaus Goergen
Jessica Keune
Huilin Gao
Anne Springer
Harrie-Jan Hendricks Franssen
Stefan Kollet
Accurate and reliable hydrologic simulations are important for many applications such as water resources management, future water availability projections and predictions of extreme events. However, the accuracy of water balance estimates is limited by the lack of large-scale observations, model simulation uncertainties and biases related to errors in model structure and uncertain inputs (e.g., hydrologic parameters and atmospheric forcings). The availability of long-term and global remotely sensed soil moisture offers the opportunity to improve model estimates through data assimilation with complete spatiotemporal coverage. In this study, we assimilated the European Space Agency (ESA) Climate Change Initiative (CCI) derived soil moisture (SM) information to improve the estimation of continental-scale soil moisture and runoff. The assimilation experiment was conducted over a time period 2000–2006 with the Community Land Model, version 3.5 (CLM3.5), integrated with the Parallel Data Assimilation Framework (PDAF) at a spatial resolution of 0.0275∘ (∼3 km) over Europe. The model was forced with the high-resolution reanalysis COSMO-REA6 from the Hans Ertel Centre for Weather Research (HErZ). The performance of assimilation was assessed against open-loop model simulations and cross-validated with independent ESA CCI-derived soil moisture (CCI-SM) and gridded runoff observations. Our results showed improved estimates of soil moisture, particularly in the summer and autumn seasons when cross-validated with independent CCI-SM observations. The assimilation experiment results also showed overall improvements in runoff, although some regions were degraded, especially in central Europe. The results demonstrated the potential of assimilating satellite soil moisture observations to produce downscaled and improved high-resolution soil moisture and runoff simulations at the continental scale, which is useful for water resources assessment and monitoring.
- Article
(14621 KB) -
Supplement
(1410 KB) - BibTeX
- EndNote
Soil moisture (SM) is a key variable of the hydrologic cycle, playing an important role in major processes related to infiltration and runoff generation, root water uptake and plant transpiration, and evaporation (Vereecken et al., 2016). Thus, soil moisture strongly influences the partitioning of incoming radiative energy into latent and sensible heat and significantly affects the land surface energy and water budgets. Consequently, accurate estimates of large-scale SM are needed for detection of long-term trends in hydrological states and fluxes, for example in the context of a land surface reanalysis; hydrologic predictions such as discharge forecasts for large river basins (Western et al., 2004) and water resource management and planning (e.g., groundwater recharge, mitigation of droughts) (Andreasen et al., 2013; Dobriyal et al., 2012; Sridhar et al., 2008), identifying regions susceptible to extreme events such as droughts and floods (Seneviratne et al., 2010), lower boundary conditions for numerical weather predictions (Drusch, 2007), and irrigation management and agriculture practices (Bolten et al., 2010; Shock et al., 1998). At continental spatial scales and inter-annual timescales, SM typically exhibits large variability (Brocca et al., 2010), depending on rainfall distribution, topography, soil physical properties, vegetation characteristics and human impacts such as irrigation. Monitoring this variability is a major challenge due to the scarcity of in situ SM observations networks. Recent advancements in satellite-based sensors offer great potential to monitor SM over large scales for continental water resources assessment, particularly in areas where ground observation networks are sparse (Mohanty et al., 2013). Conventionally, satellite observations have been used in global water balance studies to provide information on the water cycle components, such as precipitation, evapotranspiration (ET), soil moisture, water storage and runoff (Kiehl and Trenberth, 1997; Running et al., 2004; Trenberth et al., 2007; Vinukollu et al., 2011). However, sparse data coverage in satellite observations limits their ability to provide spatially and temporally consistent time series of water balance estimates.
Another approach to facilitate studies at a regional to global scale is to estimate water budget components using land surface models forced with precipitation and other atmospheric data – such as the Community Land Model (CLM) (Lawrence et al., 2011), the Variable Infiltration Capacity (VIC) model (Liang et al., 1994, 1996), or the Joint UK Land Environment Simulator (JULES) (Best et al., 2011; Clark et al., 2011). Simulated soil moisture distributions from the land surface models provide spatially and temporally continuous information, yet their accuracy is limited by model deficiencies and uncertainties in both model parameters and atmospheric forcing variables (Chen et al., 2013; Draper et al., 2009). Therefore these uncertainties need to be characterized in hydrologic predictions, in order to provide useful hydrologic data and information for water resource management. In order to improve model predictions and simultaneously honor observation and model uncertainties, remotely sensed soil moisture has been merged with model predication using data assimilation (DA) (Chen et al., 2013; De Lannoy and Reichle, 2016; Kumar et al., 2008; Lahoz and De Lannoy, 2014; Lievens et al., 2016; Liu and Gupta, 2007; Moradkhani et al., 2005; Nie et al., 2011). Using DA approaches, previous studies also investigated the impact of uncertainties in both parameters and state variables of a hydrologic model based on a joint state–parameter estimation approach (Cammalleri and Ciraolo, 2012; DeChant and Moradkhani, 2012; Gharamti et al., 2015; Liu et al., 2016; Pathiraja et al., 2016; Rafieeinasab et al., 2014; Xie and Zhang, 2010). For example, Han et al. (2014) evaluated the joint state and parameter estimation method at catchment scale for the coupled CLM and Community Microwave Emission Model (CMEM) (De Rosnay et al., 2009) through assimilation of synthetic microwave brightness temperature data. Similarly, Samuel et al. (2014) studied the ensemble-based DA with dual state–parameter estimation to evaluate the streamflow forecast and variations in soil moisture. However, many of these studies mainly focused on using data assimilation approaches for improved predictions at the watershed scales. Fewer studies demonstrated the potential of assimilating satellite observations into land surface models to improve soil moisture and runoff estimates at regional and global scales (e.g., Crow and Ryu, 2009; De Lannoy and Reichle, 2016; Lievens et al., 2015; Liu and Mishra, 2017; López López et al., 2016; Pan et al., 2008; Rains et al., 2017; Reichle and Koster, 2005; Renzullo et al., 2014). For instance, Rains et al. (2017) assimilated SMOS data into CLM over Australia for drought monitoring purposes. Similarly, Liu and Mishra (2017) also assimilated satellite SM data at the global scale to evaluate the performance of the community land surface model (CLM4.5) in simulating hydrologic fluxes such as SM, ET and runoff at 0.5∘ (∼50 km) spatial resolution. They found that assimilating satellite SM data into the CLM4.5 model improved the soil moisture simulations, which also led to better representation of other hydro-meteorological variables in the model, such as ET and runoff. At the continental scale, several studies have explored the role of soil moisture assimilation over Europe, in different modeling frameworks (e.g., Albergel et al., 2017; Brocca et al., 2010; De Rosnay et al., 2013; Draper et al., 2009; Ni-Meister et al., 2006). Using NASA's global catchment land surface model (CLSM), Ni-Meister et al. (2006) improved simulated soil moisture over small Eurasian catchments through assimilation of near-surface soil moisture derived from the Scanning Multichannel Microwave Radiometer (SMMR). Using an extended Kalman filter (EKF), Draper et al. (2009) demonstrated the usefulness of assimilating near-surface soil moisture observations from the C-band Advanced Microwave Scanning Radiometer (AMSR-E) in the land surface model ISBA (Interactions between Soil, Biosphere and Atmosphere) at 9 km resolution over continental Europe. More recently, Albergel et al. (2017) showed the potential of using the satellite-derived soil moisture data from the European Space Agency (ESA) Climate Change Initiative (CCI) over Europe and the Mediterranean to sequentially assimilate soil moisture and leaf-area index product into the ISBA land surface model at 0.5∘ (∼50 km) resolution. They found significant improvements in the surface soil moisture but little improvement in discharge estimates when compared to the open-loop (i.e., no assimilation) simulations.
In these global- to regional-scale studies, despite these important advancements, the data assimilation systems were employed at fairly coarse spatial resolution (i.e., at 50 to 25 km scale), which is too coarse to provide locally relevant information (Bierkens et al., 2015; Wood et al., 2011). For example, predicting water cycle processes for scientific and applied assessment of the terrestrial water cycle requires a high-resolution modeling framework on the order of 100–101 km horizontal grid spacing. While most of the global remote sensing observations are available at relatively low resolution (i.e., at 50 to 25 km scale), data assimilation systems can be used as an effective downscaling tool by merging the remote sensing information in space and time with high-resolution models. In turn, data assimilation frameworks that include higher resolution meteorological, land cover, and soil texture information can be used to constrain coarse-resolution remotely sensed soil moisture observations. However, in both cases, the spatial mismatch between coarse-resolution satellite data and high-resolution hydrologic models constitutes a great challenge. To address this issue, the scale disparity between observations and modeling approaches needs to be taken into account either in the data assimilation algorithm (De Lannoy et al., 2012; Sahoo et al., 2013) or through preprocessing of satellite products to match the model resolution (Merlin et al., 2013; Verhoest et al., 2015). Another challenge is the availability of computational resources, because the computational burden can increase nonlinearly with increasing model resolution, but could also increase linearly with an increasing number of ensembles in the data assimilation system and with the increasing complexity of simulated processes.
In this work, we assimilated the coarse-resolution ESA CCI-SM data over Europe from January 2000 to December 2006 into the 3 km high-resolution CLM using a joint state and parameter estimation approach and evaluate its impacts both on surface soil moisture and on other hydrologic variables such as surface and subsurface runoff. A number of soil moisture retrievals from other missions such as the Soil Moisture and Ocean Salinity (SMOS, launched in 2009) (Kerr et al., 2001; Mecklenburg et al., 2016) and Soil Moisture Active Passive (SMAP, launched in 2015) (Entekhabi et al., 2010) missions have been used in assimilation studies (e.g., Lievens et al., 2015, 2016). These recent high-resolution data products are only available for less than 10 years and cannot be used to apply soil moisture information in a land surface reanalysis for extended time periods. Recently, a number of studies highlighted the quality and stability of the ESA CCI product (e.g., Dorigo et al., 2017; McNally et al., 2016; Wagner et al., 2012) and its potential use in data assimilation studies (Albergel et al., 2013, 2017; Liu et al., 2018). We selected ESA CCI-SM data because of their availability at longer timescales, which also provides a basis for evaluating the feasibility of deriving a land surface reanalysis, conditioned to satellite information, for Europe over longer timescales, and allows the potential impact of assimilating longer-term soil moisture observations on hydrologic simulations to be assessed.
The main goal of this study is twofold. Firstly, it investigates the value of coarse-resolution remotely sensed soil moisture data in improving soil moisture and runoff modeling and to provide higher-spatial-resolution and downscaled estimates of the surface soil moisture profile and hydrological fluxes with complete spatiotemporal coverage over Europe. Secondly, it aims at exploring the potential of long-term remotely sensed products such as ESA CCI-SM for downscaling of soil moisture to high spatial resolution at the continental scale via data assimilation. In this study, the analysis also focused on the performance of the Community Land Model (v3.5) to simulate surface and subsurface runoff as a result of assimilation updates restricted to soil moisture for upper soil layers. In addition, the study also interrogates whether assimilation of satellite-derived surface soil moisture will improve the skill of the simulated discharge, in gauged and ungauged regions. Therefore, assimilating satellite-derived information into land surface models may have an important added value for regions where in situ measurements are not available.
In order to obtain the assimilated product of near-surface soil moisture, we used CLM3.5 coupled to the Parallel Data Assimilation Framework (PDAF) library (Nerger and Hiller, 2013). PDAF is computationally efficient due to its parallelization of data assimilation routines and in-memory exchange of data. Therefore, PDAF is suitable for applications at large spatial scales and high resolution over longer time periods. The coupled CLM-PDAF setup and the experimental design are described in Sect. 2. The results, including model validation and analysis of simulated soil moisture and runoff, are documented in Sect. 3, while the discussion and conclusions are presented in Sects. 4 and 5, respectively.
2.1 Model description
In this study, the CLM3.5 (Oleson et al., 2004) was applied to represent land surface processes such as soil moisture evolution, evaporation from soil and vegetation, transpiration and interception of precipitation by vegetation canopy, throughfall and infiltration, and surface and subsurface runoff and snow. Specifically, runoff is parameterized using a simple TOPMODEL-based scheme (SIMTOP; Niu et al., 2005). Soil water is calculated by solving the one-dimensional Richards equation (Zeng and Decker, 2009). An operational groundwater table depth and recharge to groundwater from the soil column is updated dynamically using the algorithm described in Niu et al. (2007). The snow model in CLM explicitly simulates multilayer snow depending on the total snow depth, and includes processes such as snowmelt, surface frost and sublimation, liquid water retention, and thawing–freezing processes (Dai et al., 2003; Dickinson et al., 2006; Stöckli et al., 2008). Total runoff is calculated as the sum of the subsurface runoff, surface runoff and runoff generated from lakes, glaciers, and wetlands (Oleson et al., 2004).
CLM3.5 has been widely applied at continental and global scales to understand how land processes and anthropogenic impacts affect climate (e.g., Dickinson et al., 2006). The CLM parameterizes most of the land surface processes (such as infiltration, evaporation, surface runoff, subsurface drainage, canopy and snow processes) using the water and energy balance equations. CLM3.5 offers significant improvements in estimating the components of the terrestrial water cycle compared to earlier versions (Oleson et al., 2008), including improvements in soil water availability and resistance terms to reduce the soil evaporation which was overestimated in earlier versions (Niu et al., 2005; Oleson et al., 2008; Yang and Niu, 2003). Compared to CLM3.0, Oleson et al. (2008) showed that CLM3.5 exhibits more realistic partitioning of ET into its components (i.e., transpiration, ground evaporation and canopy evaporation), which resulted in overall improvements in the representation of the annual cycle of total water storage. Previous studies also showed that CLM3.5 produces too-high soil moisture with too-low variability compared to root zone soil moisture modeled by later CLM versions (4.0 and 4.5) (e.g., Lawrence et al., 2011; Niu et al., 2011). In order to reduce these biases, Li and Ma (2015) introduced a factor to describe soil porosity and increase recharge water from the soil column to the aquifer in the newer CLM, leading to improved estimates of soil moisture and biogeochemical processes. However, Lawrence et al. (2011) showed that the differences between CLM3.5 and new versions of CLM with respect to soil moisture variability remained small when compared to observations.
In addition, CLM3.5 is designed for coupling with climate models and is also part of the fully coupled Terrestrial Systems Model Platform (TerrSysMP; Shrestha et al., 2014) that simulates the full terrestrial hydrologic cycle including feedbacks between atmosphere, land-surface and subsurface compartments of the water cycle. Moreover, the CLM can efficiently run for large model domains and at high spatial resolution. Since we performed our simulations at high spatial resolution and at continental scale, we selected the TerrSysMP–PDAF modeling framework (Kurtz et al., 2016), which is designed for high-performance computing infrastructures and can efficiently cope with the high computational burden of ensemble-based data assimilation. Kurtz et al. (2016) showed the efficient use of parallel computational resources by TerrSysMP–PDAF, which is needed to simulate predicted states and fluxes over large spatial domains and long simulations. In this study, we used the CLM–PDAF setup, in which PDAF is coupled with the stand-alone CLM3.5 for soil moisture assimilation. Readers are referred to Kurtz et al. (2016) for technical descriptions of coupling and model performance.
2.2 Data assimilation framework
The Parallel Data Assimilation Framework (Nerger and Hiller, 2013) was used to assimilate satellite soil moisture into CLM3.5. PDAF provides data assimilation methods such as the ensemble Kalman filter (EnKF) (Burgers et al., 1998; Evensen, 2003) and the local ensemble transform Kalman filter (LETKF) (Hunt et al., 2007). In this study, the EnKF algorithm was used for data assimilation, which is a relatively efficient and robust technique for assimilating satellite data into land surface models (e.g., Brocca et al., 2012; Crow et al., 2017; Draper et al., 2011; Matgen et al., 2012; Mohanty et al., 2013; Pauwels et al., 2001, 2002). It uses ensembles of model simulations to approximate the model state and parameter error covariance matrix in order to optimally merge model predictions with observations.
In this study, the joint state parameter update of soil moisture and soil texture in CLM with the EnKF was used:
where the state variable soil moisture is a vector containing soil moisture values within a soil layer for each grid cell and can be described with a nonlinear model (CLM in our case) operator ft(⋅) at time step t for realization i using the forcing data q and model parameter p.
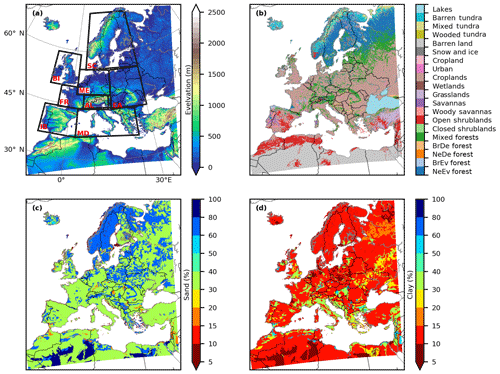
Figure 1Model surface input data: (a) USGS GMTED2010 DEM, (b) dominant land use type based on MODIS data, (c) percentage of sand content, and (d) percentage of clay content based on global FAO soil database. The inner boxes in (a) show the boundaries of the PRUDENCE regions (FR: France, ME: Mid-Europe, SC: Scandinavia, EA: eastern Europe, MD: Mediterranean, IP: Iberian Peninsula, BI: the British Isles, AL: Alpine region; Christensen and Christensen, 2007).
The state–parameter vector xi for realization i was calculated using the perturbed soil texture (% sand and % clay) and perturbed precipitation as follows:
The EnKF then calculates the ensemble of updated state–parameter vector at daily time step t of the model-estimated state–parameter variable xt for each ensemble member i, as follows:
where yt is the perturbed observation vector and ϵ is a perturbation vector of the measurement error with values drawn from a normal distribution with a mean of zero and a standard deviation corresponding to the assigned measurement error of 0.02 m3 m−3 for soil moisture and H is the measurement operator. K is the Kalman gain matrix defined as follows:
where is the transpose matrix of the measurement operator at time t, Rt is the measurement error matrix, which is defined a priori based on the expected measurement error of the ESA CCI soil moisture product. Pt is the state error covariance matrix of the model predictions calculated as follows:
where is the vector which contains the ensemble average soil moisture contents for the different grid cells and N is the number of ensemble members.
In the DA scheme, the updated states (soil moisture) were kept in reasonable physical ranges (between residual soil moisture and porosity) to yield physically meaningful estimates of soil moisture water content, energy fluxes and the water budget. For the soil moisture update, the values of the updated soil moisture were restricted to values between zero and saturated soil water content. For the soil texture update, a value of 1 % was assigned to sand and clay percentages in case the updated values are less than zero. In case the updated sum of the sand and clay are greater than 100 %, the values were constrained to the normalized sum of updated soil and clay percentages. Other soil parameters such as the soil hydraulic and thermal parameters were adjusted after the soil texture update using pedotransfer functions.
2.3 Data
2.3.1 Land surface data and atmospheric forcing
The land surface static input data used in this study consisted of topography, soil properties, plant functional types and physiological vegetation parameters (Fig. 1). Digital elevation model (DEM) data were acquired from the 1 km × 1 km Global Multi-resolution Terrain Elevation Data 2010 (GMTED2010) (Danielson and Gesch, 2011) as shown in Fig. 1a. In CLM, each grid cell consists of five land units (i.e., vegetation, wetland, lakes, glaciers and urban) covering a certain percentage of the total grid cell area. The vegetation land unit is further subdivided into plant functional types (PFTs) defined by fractional areas with respect to the entire grid cell (Bonan et al., 2002). In the current study, the land cover information for each PFT was based on the Moderate Resolution Imaging Spectroradiometer (MODIS) MCD12Q1 (version 5) land cover product (Friedl et al., 2002), which contains a classification of the dominant land cover (Fig. 1b). The dominant land cover information from MODIS was first aggregated to the model resolution, calculating the percentage of all 500 m pixels per 3 km grid cell. The aggregated land cover information was then transferred to the CLM-prescribed PFTs on the basis of WorldClim climate data (Hijmans et al., 2005).
Monthly leaf area index (LAI) values for each PFT were computed based on the 1 km Global Land Surface Satellite (GLASS) LAI product (1981–2012). GLASS contains of 1 km × 1 km global maps of LAI provided every 8 days. The product was derived from time series of MODIS (MOD09A1) and AVHRR reflectance data using a general regression neural network method (Xiao et al., 2014). To derive a monthly climatology over the assimilation period (2000–2006), the 1 km 8-day improved GLASS LAI for each year was used to calculate a mean monthly LAI that was then aggregated to the model resolution. The monthly LAI values for each PFT were then determined by mapping the 3 km pixels to the 3 km aggregated PFT values within each grid cell. This approach provides spatially distributed and temporally continuous LAI data within each PFT for the considered time period of 2000–2006. To account for annual variability in LAI, yearly model runs were performed where the LAI information was updated at the start of each year run. It should be noted that CLM3.5 only allows monthly average LAI values for each PFT to be specified.
Additional properties of each of the subgrid land fractions, such as the stem area index and the monthly heights of each PFT, were calculated based on the global CLM3.5 surface dataset (Oleson et al., 2008). To provide soil texture data in the model (Fig. 1c and d), sand and clay percentages were prescribed based on pedotransfer functions (Schaap and Leij, 1998, for 19 soil classes derived from the FAO/UNESCO Digital Soil Map of the World; Batjes, 1997).
For the time period of 2000–2006, the high-resolution atmospheric reanalysis COSMO-REA6 dataset (Bollmeyer et al., 2015) from the Hans Ertel Centre for Weather Research (HErZ; Simmer et al., 2016) was used as the atmospheric forcing for CLM3.5. We preferred to use this data over other datasets, because of its high spatial resolution in comparison to other commonly used forcing datasets such as the European gridded dataset (E-OBS) (Haylock et al., 2008) and Interim ECMWF Reanalysis (ERA-Interim; Dee et al., 2011) at 25 and 80 km resolution, respectively. We used data from 2000–2006 which were available at the beginning of this study. The COSMO-REA6 is only now publicly available for a longer time period of 1995–2015. The essential meteorological variables applied in this study, such as barometric pressure, precipitation, wind speed, specific humidity, near-surface air temperature, downward shortwave radiation and downward longwave radiation were downloaded from the German Weather Service (DWD; ftp://ftp-cdc.dwd.de/pub/REA/, last access: 15 September 2017). The COSMO-REA6 reanalysis is based on the COSMO model and available at 0.055∘ (∼6 km) covering the European CORDEX domain (Gutowski Jr. et al., 2016). COSMO-REA6 was produced through the assimilation of observational meteorological data using the existing nudging scheme in COSMO with boundary conditions from ERA-Interim data. Bollmeyer et al. (2015) compared the COSMO-REA6 precipitation data with the precipitation data from the Global Precipitation Climatology Centre and showed that COSMO-REA6 performed well compared to observations, with small underestimations of precipitation in central and southern Europe and overestimation of precipitation in Scandinavia, Russia and along the Norwegian coast. Additionally, Springer et al. (2017) assessed the closure of the water budget in the 6 km COSMO-REA6 and compared to global reanalyses (ERA-Interim) and Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2) for major European river basins. Springer et al. (2017) found that the COSMO-REA6 closes the water budget within the error estimates whereas the global reanalyses underestimate the precipitation-minus-evapotranspiration surplus in most river basins. A more comprehensive assessment of the precipitation of the HErZ reanalysis can be found in Wahl et al. (2017), albeit based on the 2 km data product, only available for central Europe.
2.3.2 ESA CCI microwave soil moisture
The ESA CCI program provides daily soil moisture (CCI-SM) at 0.25∘ spatial resolution for approximately the top few millimeters to centimeters of soil from 1978 to 2016. The daily CCI-SM product (v03.2) is produced at 0.25∘ spatial resolution from the microwave retrieved surface soil moisture data and is merged from multiple sensors (Dorigo et al., 2017; Liu et al., 2011, 2012; Wagner et al., 2012; http://www.esa-oilmoisture-cci.org, last access: 23 March 2017). For the study period of 2000 to 2006, the CCI-SM data are based on passive microwave observations (i.e., DMSP SSM/I, TRMM TMI, Aqua AMSR-E and Coriolis WindSat; Owe et al., 2008), whereas the active data products are based on observations from the C-band scatterometers on board the ERS-1 and ERS-2 (Bartalis et al., 2007; Wagner et al., 2013) satellites. In this product, the absolute soil moisture was re-scaled against the 0.25∘ land surface modeling soil moisture (GLDAS-NOAH, Rodell et al., 2004) using cumulative density function matching. The soil-type-specific hydraulic parameters in Noah are obtained from the pedotransfer function provided in Cosby et al. (1984), which was also adopted by CLM. The underlying soil classification in our setup is based on data from the FAO soil map (Batjes, 1997), which was the basis for the GLDAS-derived soil parameters used in GLDAS-Noah and employed to derive the ESA CCI-SM product (e.g., Dorigo et al., 2012). The setup and the parameterizations of Noah and our CLM should hence be fairly consistent.
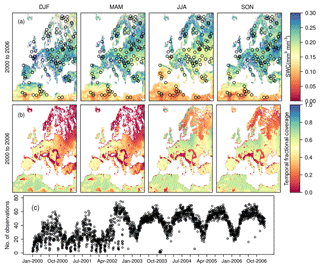
Figure 2Satellite ESA CCI soil moisture data resampled to 3 km resolution for the time period of 2000 to 2006 over EU-CORDEX. (a) Temporally averaged soil moisture content for different seasons, (b) fraction of days that soil moisture observations were reported during different seasons, and (c) number of selected observations with valid data for the respective day over the 2000–2006 period, used for assimilating soil moisture in the data assimilation experiment. Black circles in (a) indicate the location of grid cells selected for data assimilation.
In this study, we used the merged product of active and passive soil moisture data which showed better accuracy than either the passive or active data alone (Liu et al., 2011). To match the spatial resolution of our CLM3.5 setup, the original SM values were re-sampled and re-gridded to 0.0275∘ using the first-order conservative interpolation method (Jones, 1999), which is based on the ratio of source cell area overlapped with the corresponding destination cell area. The conservative regridding scheme preserves the physical flux fields between the source and destination grid. The CCI-SM dataset showed large data gaps over the European continent during the four seasons – December–February (DJF; winter), March–May (MAM; spring), June–August (JJA; summer) and September–November (SON; autumn); (Fig. 2b). According to Fig. 2b, the temporal coverage (i.e., the ratio between the number of days and the total number of days in a season) was generally low during the winter and spring seasons, ranging from less than 30 % (Scandinavian regions) to about 60 % in southern Europe. SM observations showed the highest temporal coverage during the summer and autumn. Due to the sparseness of the SM data at daily temporal resolution, 100 grid cells were randomly selected covering the complete model domain (Fig. 2a). The satellite CCI-SM daily soil moisture data at these locations were assimilated. However, the number of observations for each day ranged between 2 and 75 depending on the availability of the daily CCI-SM data. As shown in Fig. 2c, there is a higher level of noise in the CCI-SM data for the first two years (2000 and 2001), probably related to the absence of data from other sensors like AMSRE-E and Windsat in those first two years. Moreover, the availability of selected observations was lower during winter and spring, while summer soil moisture was well covered during years 2003 to 2006. This seasonal difference in data availability is related to the occurrence of soil freezing events and snow cover.
Furthermore, in land surface modeling systematic differences between the model climatology and the observation data climatology are commonly corrected before assimilation, to ensure that data assimilation is applied under conditions of no systematic bias. Previous studies used different procedures to correct for biases, such as the estimation of a single constant bias value, seasonal dependent bias or CDF matching (e.g., Drusch et al., 2005; Reichle and Koster, 2004). The procedure has some important limitations: (i) the polynomial fit during CDF matching cannot provide perfect agreement because the introduced noise changes the random difference between both datasets, (ii) the bias is only partially corrected or overcorrected; (iii) the bias in the DA-procedure is not assigned to the model or measurement data, but after the assimilation it is implicitly assumed that the systematic bias is related to the bias in the measurements (model states are not corrected for a systematic bias). A priori bias correction is a specific approach taken in land surface data assimilation in case of large mismatches between modeled and measured values, for example, when the observations are located outside of the ensemble spread. We argue that for this dataset, we see systematic biases between model and data, yet these are small enough. In addition, data assimilation is able to remove biases besides the random component. A further argument for not following this approach was that spatial patterns could be altered and thereby some of the independent information provided by the satellite may be removed. We, therefore, did not perform any bias correction of the ESA CCI-SM data by rescaling of the observations to model climatology, to retain as much of the independent satellite information as possible.
2.3.3 Observational gridded monthly runoff
In order to evaluate the potential of improving runoff estimates by assimilating soil moisture observations, the nonrouted observational gridded monthly runoff data from Gudmundsson and Seneviratne (2016) (E-RUN version 1.1) were used as independent dataset. The E-RUN product provides monthly pan-European runoff estimates from 1950 to 2015 at 0.5∘ (∼50 km) resolution. The monthly runoff rates were generated using a collection of streamflow observations from small catchments combined with gridded precipitation and temperature data using a machine learning approach (Gudmundsson and Seneviratne, 2016). Monthly runoff was estimated using a regression model, which was trained with a subset of observed runoff rates and E-OBS precipitation and temperature. The fitted model was subsequently applied to all grid cells of the E-OBS data to derive pan-European estimates of monthly runoff (Gudmundsson and Seneviratne, 2016). Using this cross-validation method, Gudmundsson and Seneviratne (2016) reported higher accuracy in central and western Europe, while accuracy was lower in other regions due to low density of available stations. For model validation, we preferred to use this dataset over the discharge observations at different gauge stations, because the nonrouted gridded runoff product has the distinct advantage of evaluating the impact of soil moisture assimilation on runoff at every grid cell within a spatial domain. Using gridded runoff is also useful to evaluate model structure errors in the representation of runoff generation in the model. In addition, in the CLM3.5, the river routing module is implemented at 0.5∘ where the discretization of river routing elements is based on a grid method in which the grid for river routing is independent of the grid for runoff simulation. Therefore, a coarse spatial resolution river network can lead to unrealistic flow accumulation, and an adequate validation of the results is not possible. However, our comparison of aggregated runoff using E-RUN data for a few watersheds with monthly discharge observed at stations and obtained from the GRDC (Global Runoff Data Center, 2011) in Europe showed a good agreement with observed discharge (Fig. S1 in the Supplement). In the current study, the half-degree monthly runoff rates were resampled and re-gridded to 0.0275∘ using the first-order conservative interpolation method for comparison with the CLM3.5 simulated total runoff.
2.4 CLM-PDAF experimental design and analyses
The joint state and parameter assimilation experiments were performed for the time period of January 2000 to December 2006. The model spinup was performed by simulating the time period of 2000–2006 5 times in order to obtain equilibrium initial state variables. The initial state variables from the spin-up were then used as initial condition for the ensemble runs as described below. In this study, we implemented CLM3.5 for the EURO-CORDEX domain with a spatial resolution of 0.0275∘ (3 km), inscribed into the official EUR-11 grid. The model was run with 1 h time step and the time window for soil moisture updates was set to 1 day. In this study, we assumed a spatially uniform observational error of 0.02 mm3 mm−3 for CCI-SM in the CLM-PDAF setup.
The outputs of a land surface model are sensitive to both atmospheric forcings and soil characteristics. To account for uncertainties in atmospheric forcing and soil texture, precipitation and soil texture (% sand and % clay) were perturbed in this study (Figs. S2 and S3). Log-normally distributed, spatially homogeneous and temporally uncorrelated multiplicative perturbations were added to precipitation. The mean and standard deviation of the applied perturbation factors for precipitation were equal to 0.1 and 0.15, respectively. Sand and clay content were perturbed with random noise drawn from spatially uniform distribution (±10 %). In order to avoid unphysical values of the soil parameters, the sum of the sand and clay content were constrained to have a value not larger than 100 %. The initial ensemble size was set to 20 for the precipitation and soil texture in the assimilation experiment to update the volumetric soil water content (SWC) of the top soil layer (∼2 cm). Previous studies (e.g., De Lannoy et al., 2012; Kumar et al., 2008; Pan and Wood, 2010; Yin et al., 2015) showed that the performance of EnKF relies on the ensemble size. For example, Yin et al. (2015) indicated that when the ensemble size is close to 12, it may lead to an efficient DA updating process, while Pan and Wood (2010) suggested 20 ensemble members. Our initial investigation showed slightly improved correlation (R2) between simulated and CCI-SM soil moisture for 20 ensemble members compared to 12 ensemble members (as shown in Fig. S4). In addition to ensemble size, systematic biases can also be attributed to erroneous model parameter values, which is one of the main sources of error and uncertainty in land surface model predictions. To account for biases in soil parameters, the joint state and parameter assimilation framework was used to estimate the model states and model parameters jointly by updating the soil water content and soil texture properties such as % sand and % clay. Although this approach has also significant limitations, related to the fact that we do not know well enough the relative importance of systematic model errors and systematic errors in the measurement data, an advantage is that we correct for possible systematic model bias by modifying soil texture parameters.
Our main experiment consisted of two CLM-PDAF simulations: (a) an open-loop simulation (no data assimilation, CLM-OL) and (b) an ensemble simulation with data assimilation of ESA CCI-SM data (CLM-DA) at 100 random locations (Fig. 2a). We evaluated the results of both simulations by a cross-validation with ESA CCI-SM data that were not assimilated. The soil moisture validation of the CLM-DA and CLM-OL simulations used all the available CCI-SM data in the time period of 2000 to 2006. This approach not only allowed us to independently cross-validate the SM values over grid cells that were not used in the data assimilation, but also to produce updated soil moisture contents at other locations (at the European scale), based on spatial correlations, and to investigate its impacts on runoff characterization and whether soil moisture characterization between measurement locations could also be improved. For SM comparison, the average of simulated SWC in the top two layers (i.e., at 0.007 and 0.03 m depth) was used. Additionally, the monthly runoff dataset E-RUN as described in Sect. 2.3 was used to validate runoff as simulated by CLM-OL and CLM-DA.
To assess the skill of the assimilation experiments, statistical evaluation including mean absolute error (MAE), the root mean square error (RMSE), percentage bias (PBIAS) and correlation coefficient (R) were used as validation measures. For runoff validation, Nash–Sutcliffe coefficient of efficiency (NSE) and Kling–Gupta efficiency (KGE) indices were also used, which are typically used to evaluate model performance for runoff and river flow. These measures are expressed as follows.
where “cc” is the Pearson correlation coefficient calculated as follows:
where n is the total number of time steps; Yi and Yobs,i represent the simulated ensemble mean and observation values at time step i, respectively, and μsim and μobs represent mean values, while σsim and σobs represent standard deviation for the simulated and observed data for the whole modeled time period. For NSE and KGE in Eqs. (10) and (11), a value equal to 1 represents perfect agreement between simulated and observed runoff, while a value less than 0 indicates that the observed mean is a better predictor than the model.
In addition to these measures, a normalized error reduction index (NER) was also used to evaluate the improvement of the data assimilation approach. NER is calculated as follows:
where EDA and EOL represent the data assimilation and open-loop model runs. E in Eq. (13) represents the statistical error index for both RMSE and MAE in this study. NER values range between negative infinity and 100 %. Positive NER values indicate improvement as a result of data assimilation relative to open loop, while NER < 0 indicates a degradation in assimilation results.
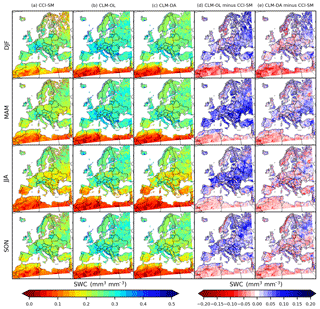
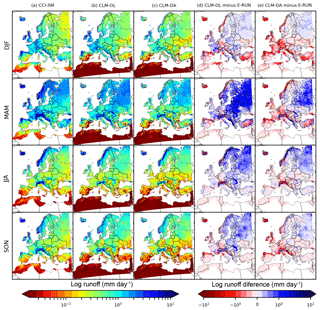
Figure 3Temporally averaged soil moisture (mm3 mm−3) content over the 2000–2006 period for (a) CCI-SM, (b) CLM-OL and (c) CLM-DA, and the difference between (d) CLM-OL and CCI-SM and (e) CLM-DA and CCI-SM for DJF (December, January and February), MAM (March, April and May), JJA (June, July and August) and SON (September, October and November) seasons.
In this section, the impact of assimilating the ESA CCI-SM data at selected locations into CLM3.5 using the joint state–parameter estimation on the terrestrial hydrologic cycle was analyzed, focusing on soil moisture and runoff. The results were presented for the complete EURO-CORDEX domain and for eight predefined analysis regions from the “Prediction of Regional scenarios and Uncertainties for Defining European Climate change risks and Effects” (PRUDENCE) project (Christensen and Christensen, 2007) as shown in Fig. 1a. We referred to these regions as the “PRUDENCE” regions.
Table 1Difference in CLM-OL and CLM-DA simulated mean seasonal SWC (mm3 mm−3) with CCI-SM data for all PRUDENCE regions and all seasons, i.e., winter (DJF), spring (MAM), summer (JJA) and autumn (SON).
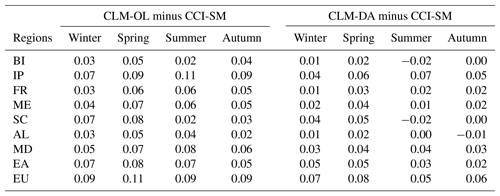
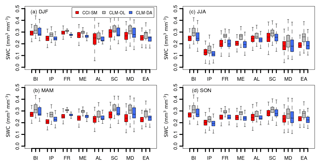
Figure 4Box plots showing the spread of seasonally averaged soil water content (mm3 mm−3) over the 2000–2006 time period and in the PRUDENCE regions for (a) DJF, (b) MAM, (c) JJA and (d) SON seasons. The box plots illustrate the spatial distribution of SWC with quartiles, median and extreme values marked by solid lines.
3.1 Impacts of assimilation on soil moisture
3.1.1 Regional and seasonal mean comparison
Figure 3 showed a comparison of the seasonal mean volumetric SWC (mm3 mm−3) in the upper soil layer from the CLM3.5 experiments (CLM-OL, CLM-DA) with the seasonal mean of satellite CCI-SM data. The CLM-OL simulation exhibited slightly higher SWC in all seasons over most parts of Europe (Fig. 3b) compared to the CLM-DA simulations (Fig. 3c). The difference between CLM-OL and CCI-SM were larger than the difference between CLM-DA and CCI-SM, which indicates that assimilation of CCI-SM minimizes the overestimation of SWC in CLM-OL. Overall, the mean difference between measured and simulated SWC was reduced from 0.11 cm3 cm−3 (CLM-OL) to 0.06 mm3 mm−3 (CLM-DA) over most parts of Europe (Table 1). This illustrated the efficiency of CCI-SM assimilation to improve simulated SWC by CLM. Seasonally, the upper soil layer SWC difference between CLM-OL and CCI-SM was larger for the spring season than for other seasons, and this overestimation was reduced in CLM-DA (i.e., from 0.11 to 0.08 mm3 mm−3; Table 1). CCI-SM assimilation also improved SWC characterization in other seasons, with the differences between CCI-SM and CLM-OL for winter, summer and autumn seasons being around 0.09 mm3 mm−3 and differences between CCI-SM and CLM-DA in these seasons being reduced to a magnitude lower than 0.05 mm3 mm−3.
Table 2Evaluation performance criteria for comparing CLM-OL and CLM-DA with CCI-SM (spatially averaged SWC of surface layer for the EU and PRUDENCE regions).
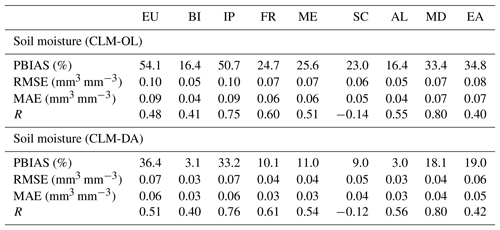
Figure 4 showed the comparison of 2000–2006 temporally averaged SM estimated by CLM-OL and CLM-DA with the CCI-SM dataset over PRUDENCE regions. Generally, CLM-OL overestimated the SWC values for all subregions and in all seasons. However, using data assimilation, this overestimation was reduced consistently in all subregions, as can be seen from the CLM-DA results. Noticeably, assimilation also helped to reduce the spatial variability, as indicated by the narrow spread of CLM-DA estimated SWC quartiles compared to CLM-OL in Fig. 4. Validating the simulations with CCI-SM data, the improvements of the CLM-DA varied within PRUDENCE regions and seasons. Improvements were more prominent for the British Isles, France and central Europe (for all seasons), while for other regions SWC was slightly overestimated in spring (Fig. 4b) and underestimated in summer and autumn (Fig. 4c and d). The underestimation of SWC was particularly pronounced over the Iberian Peninsula and Scandinavia regions in the summer (Fig. 4c).
The goodness of fit values, including PBIAS, RMSE MAE and correlation coefficient (R), between simulated SWC according to CLM-OL or CLM-DA and CCI-SM (for the surface layer) are provided in Table 2. These statistical measures were calculated over the PRUDENCE region and for each season on the basis of cross-validation with CCI-SM data that were not used in the data assimilation in order to independently evaluate the impact of data assimilation on improving soil moisture characterization. Note that for calculating these statistics, model data were only used for the days when satellite data were available. CLM-OL showed higher PBIAS, RMSE and MAE values and lower R values than CLM-DA with CCI-SM assimilation over the EU and all PRUDENCE regions (Table 2). However, the CLM-DA simulations compared well with the CCI-SM data based on the decreased PBIAS, RMSE and/or MAE values combined with a slightly improved R values over these regions.
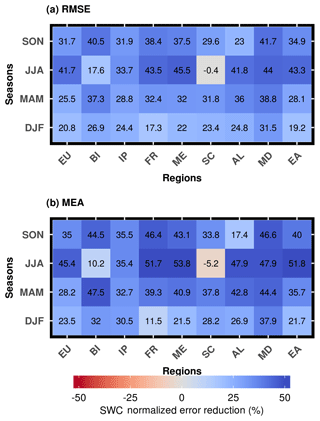
Figure 5Normalized error reduction (NER) index of (a) RMSE and (b) MEA for daily soil water content over different seasons and PRUDENCE regions using CLM-OL and CLM-DA simulations over the years 2000–2006.
In order to validate the skill of CLM-DA relative to CLM-OL, the NER index was applied to show the improvement with CCI-SM data assimilation in terms of RMSE and MAE using daily values of surface layer SWC for each PRUDENCE region and each season, as shown in Fig. 5. As described in Sect. 2.4, the positive NER signals indicate improvements while the negative NER signal presents degradations in the assimilation performance. The NER of RMSE (Fig. 5a) and MEA (Fig. 5b) were mostly positive over most regions, indicating improvements in surface SWC estimates through assimilation of CCI-SM data. Negative NER values (for both RMSE and MAE) were found over Scandinavia, reflecting a negative impact of CCI-SM data assimilation on SWC characterization. This might be because of uncertainties related to assimilated CCI-SM over this region due to the limited amount of data because of longer winters with frozen or snow cover conditions or larger measurement errors as indicated by Dorigo et al. (2017). CLM-DA showed higher positive NER values in the summer and autumn seasons, and lower NER values in the winter season, related to comparatively small SWC improvements (Fig. 5a and b).
3.1.2 Daily validation
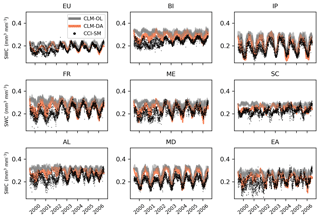
The long-term (January 2000 to December 2006) daily SM averaged over PRUDENCE regions in Europe, as simulated by CLM-OL and CLM-DA and observed by CCI-SM, are shown in Fig. 6. The assimilated CCI-SM data improved the simulations of daily surface soil moisture in CLM-DA. The daily soil moisture patterns simulated by CLM-DA compared well with the CCI-SM observations, with peaks and troughs generally coinciding for all regions and over the European domain except for the years 2000 and 2001. The CCI-SM observations showed increased variability and drier soil moisture values for the years 2000 and 2001 compared to the full period. This can be explained by the strong contribution of the X-band passive microwave data of SSM/I and TRMM to the final CCI-SM product. Wang (1987) showed that X-band data have a shallow soil penetration depth of a few millimeters and are sensitive to vegetation cover. After implementing the C-band radiometer data of AMSR-E in 2002 and Windsat in 2003 into CCI-SM, noise level and bias were reduced (Dorigo et al., 2017). Regionally, the daily soil moisture values estimated by the CLM-DA showed a slightly better agreement with the CCI-SM data for western European regions (i.e., Iberian Peninsula, France and Mid-Europe, defined in Fig. 1) than the Scandinavian, Alpine, Mediterranean and eastern European regions, where the winter season bias was more pronounced. The overall small improvements in surface soil moisture as a result of data assimilation in these regions might be due to the limited amount of CCI-SM data in the winter season (Fig. 2b), dense vegetation, frozen soil (e.g., in the Scandinavian regions) and/or CLM3.5 model errors related to simulating soil moisture in colder regions (Oleson et al., 2008; Zeng and Decker, 2009). Additionally, the magnitudes of the bias and variance of the CCI-SM observational error could be important. As indicated by Dorigo et al. (2017), the CCI-SM error variance is low where the satellite track density increases and the error variance is high in areas with more data gaps. Note that the setup of CLM-DA in this study assumed a spatially uniform observational error for CCI-SM.
3.2 Impact of soil moisture assimilation on runoff
The nonrouted gridded runoff observation data from the E-RUN product were used to evaluate simulated surface and subsurface runoff estimates. In order to compare with E-RUN runoff data, the total runoff was calculated as the sum of the surface and subsurface runoff for each grid cell. Figure 7 showed runoff estimates of the two experiments, i.e., CLM-OL and CLM-DA, compared to the E-RUN data. CLM-OL simulated higher magnitudes of runoff (on average 1.16 mm day−1) over most parts of Europe compared to CLM-DA (on average 0.76 mm day−1) in all seasons. Compared to CLM-OL (Fig. 7b), regional runoff patterns simulated by CLM-DA (Fig. 7c) compared better with runoff observations (Fig. 7a). The increasing difference in runoff between E-RUN and CLM-OL simulations was more pronounced in spring and summer seasons (Fig. 7d). CLM-DA reduced this bias over most areas with respect to the E-RUN runoff data (Fig. 7e), but underestimated runoff in winter and spring, particularly in central Europe. Overall, the difference in runoff between CLM-OL and E-RUN was, on average, 0.44 mm day−1 over Europe, which decreased to 0.03 mm day−1 (Table 3). At the seasonal scale, however, the difference in winter runoff between CLM-DA and E-RUN was −0.63 mm day−1 and higher than the differences between CLM-OL and E-RUN (on average −0.15 mm day−1). Compared to the open loop, the deviation in other seasons' runoff in CLM-DA was reduced with respect to E-RUN over most part of Europe with the exception of the Scandinavian and Alpine regions, where negative differences became larger in all seasons (Table 3).
Table 3Monthly mean bias (CLM minus E-RUN) in mean seasonal runoff (mm day−1) for CLM-OL and CLM-DA for all PRUDENCE regions and all seasons, i.e., winter (DJF), spring (MAM), summer (JJA) and autumn (SON).
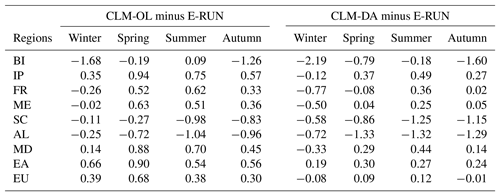
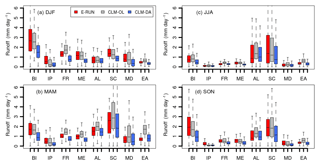
Figure 8Box plots of temporally averaged runoff (mm day−1) over the years 2000–2006 for all PRUDENCE region and seasons, i.e., (a) DJF, (b) MAM, (c) JJA and (d) SON. The box plots indicate the spatial distribution of monthly averaged runoff over each region.
The temporally averaged runoff for all grid cells over all PRUDENCE regions for both CLM-OL and CLM-DA experiments and comparison with E-RUN observation data is presented in the box plots in Fig. 8. The box plots reflect the distribution of runoff in which quartile and median are marked by solid lines. In comparison with the E-RUN data in the winter season, the CLM-DA simulations underestimated runoff over most regions, while open-loop simulations showed better agreement with E-RUN runoff over most of the grid cells (Fig. 8a). However, the overestimation of runoff in CLM-OL was more obvious in the spring season over all regions (Fig. 8b), while assimilating CCI-SM data minimized this overestimation but introduced a dry bias as suggested by lower values for CLM-DA runoff with respect to CLM-OL and E-RUN observations. This underestimation of runoff as a result of soil moisture assimilation was more pronounced over the British Isles in all seasons and over Scandinavia in summer and autumn seasons (Fig. 8c and d).
Table 4Evaluation performance criteria for comparing CLM-OL and CLM-DA with E-RUN (spatially averaged runoff, EU and PRUDENCE regions).
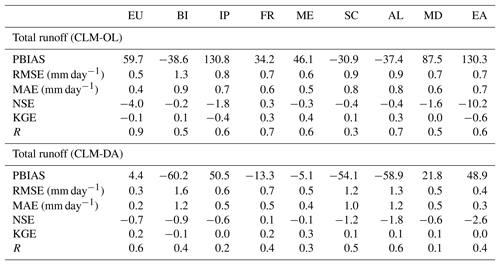
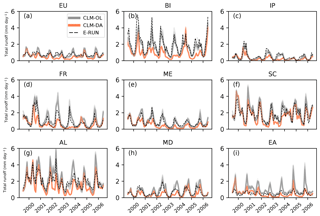
Figure 9Monthly time series of runoff from CLM-DA and CLM-OL simulation and compared with E-RUN runoff observation data for the years 2000–2006 over Europe and PRUDENCE regions. The orange and grey lines are the CLM-DA and CLM-OL for 20 ensemble members, respectively.
The time series of monthly runoff, as illustrated in Fig. 9, showed that CLM-OL compared well with runoff observations over the British Isles, Iberian Peninsula, France and the Mid-Europe regions, but overestimated the magnitude of runoff in the Mediterranean, Scandinavian, Alpine and eastern European regions. When compared to open loop, CLM-DA performed better than CLM-OL (compared to E-RUN) in Mid-Europe, Scandinavia, the Alpine region and eastern Europe in capturing peaks and low runoff, while in other regions such as the British Isles, Iberian Peninsula, France and the Mediterranean, peak runoff in winter was underestimated whereas low runoff in summer was in correspondence with observed monthly runoff data. The uncertain performance of soil moisture assimilation on peak runoff simulations is mainly due to the relatively weak dependence of runoff generation on antecedent soil moisture, because during high flow periods, the soil moisture is nearly saturated and the runoff is largely controlled by precipitation. These results are consistent with those of previous research; for example the studies of Albergel et al. (2017) and Liu et al. (2018) showed that assimilating ESA CCI satellite-derived soil moisture data into the land surface models improved the surface soil moisture but caused little improvement in discharge compared to the open-loop simulations.
In terms of statistical measures, the runoff simulation based on CLM-OL showed higher PBIAS than CLM-DA over EU and most PRUDENCE regions, except the British Isles, Scandinavia and the Alpine regions, where higher negative percentage biases were observed for CLM-DA, with magnitudes of −60 %, −54 % and −58 % bias in runoff, respectively (Table 4). Additionally, the NSE and KGE values over these regions showed low positive to negative values for the CLM-DA scenario. This indicated poor performance of the CLM in simulating runoff in spite of soil moisture assimilation. To better illustrate the impact of assimilating soil moisture on model estimates of runoff, the NER index of both RMSE and MAE showed positive values for the Iberian Peninsula, France, the Mediterranean and eastern Europe, indicating improvements in runoff (Fig. 10). However, negative signals in NER were observed in winter for all regions except in eastern Europe. Negative NER values were mainly located over the British Isles, Scandinavia and the Alpine region in all seasons. The negative impact of ESA CCI SM assimilation on runoff simulation over Scandinavia and the Alpine regions is probably related to their large proportions of the dense forest and complex topography. Both dense forest coverage and complex topography reduce the data quality of remotely sensed SM retrievals, thus impeding its performance in DA.
This study demonstrated that the assimilation of coarse-scale satellite CCI soil moisture data is beneficial and improves the high-resolution CLM simulations of soil moisture and runoff over a large spatial domain. This study also highlighted the added value of merging coarse-resolution satellite observations through data assimilation with a land surface model to generate higher spatial resolution, downscaled estimates of the surface soil moisture profile with complete spatiotemporal coverage and with a higher accuracy than that of the open-loop model estimates. To the best of our knowledge, this is the first study to provide a downscaled daily soil moisture product over 7 years and at 3 km resolution over Europe.
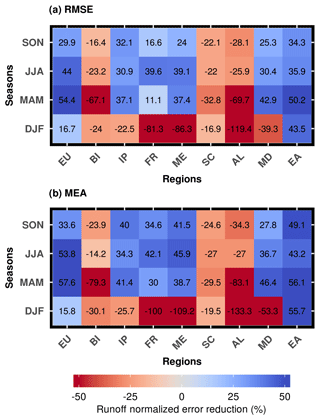
Figure 10Normalized error reduction (NER) index of (a) RMSE and (b) MEA for runoff over different seasons and PRUDENCE regions using CLM-OL and CLM-DA simulations over the years 2000–2006.
An important challenge in the assimilation was the difference in spatial resolution between CCI-SM data and model states. In this study, the coarser resolution CCI-SM data were rescaled to the model resolution (3 km). To examine whether the rescaling of the ESA CCI SM data to model resolution may introduce biases in the data, we compared the original 0.25∘ against 0.0275∘ ESA CCI soil moisture. Only small differences between the two resolutions were visible, particularly for the time period of 2003–2006 (Fig. S5). We found some differences in the first two years (2000 and 2001) and in the regions where the temporal coverage of the ESA CCI data is less than 30 %. However, for the time period and regions with a good coverage of ESA CCI soil moisture data, the differences in the resolution were not significant. A further possibility is the multiscale assimilation of the CCI-SM data, which would allow various model grid cells covered by a satellite observation to be updated (Montzka et al., 2012). In multiscale assimilation, the average soil moisture content for the group of grid cells covered by the satellite measurement is compared with the satellite-based soil moisture content, which may result in slightly improved CLM simulation results, but was beyond the scope of this study. In addition to discrepancies at the spatial scale, uncertainties in soil moisture estimations may result from data gaps in satellite soil moisture retrievals, which are limited in regions of pronounced topography or standing water, areas of dense vegetation, frozen soil and snow-covered areas. Additionally, CCI-SM is a merged product from a variety of sensors, leading to inconsistencies due to differences in viewing angles, sensor characteristics and soil moisture retrieval algorithms (Dorigo et al., 2017). In future, more observations are needed to independently validate model and assimilation experiments. In this work, the CCI-SM dataset was also used for verification over grid cells that were not used in the data assimilation. However, it would be preferable to validate with another independent dataset at the continental scale. The problem is that at the model grid scale only very limited independent (in situ) soil moisture data are available. Furthermore, it can be difficult to compare the point-based observation with the average value of coarse-resolution model grid cell.
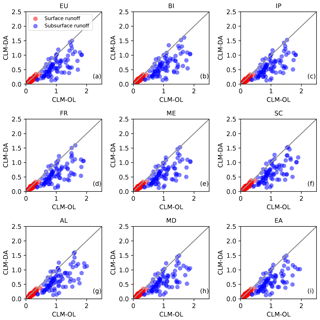
Figure 11Comparison of spatially averaged monthly simulated runoff components (surface and subsurface runoff) between CLM-OL and CLM-DA over Europe and PRUDENCE regions for the time period of 2000–2006. Grey line represents 1:1 line.
Another challenge to implement the integrated hydrologic and data assimilation framework at 3 km resolution was the high computational cost associated with the EnKF, which relies on an ensemble of realizations to estimate model uncertainty. We evaluated the impact of the number of ensemble members (i.e., 12 and 20) on the performance of EnKF by comparing the surface soil layer SWC simulated by CLM-DA for one test year (i.e., 2006). While some improvements were observed in the simulated soil moisture when using 20 instead of 12 ensemble members, in general the simulated soil moisture from the DA runs with 12 and 20 ensemble members are quite close to the observed values (Fig. S5). It should be noted that using an increased number of ensembles is a big challenge for such a large-scale high-resolution model because of the memory and storage requirements, and to a lesser degree also because of the computational burden. For example, one year of model runs with 20 ensemble members required 680 GB of computer storage per output variable (i.e., the equivalent of 5 TB of storage for 7 years of simulations per variable at daily timescale) and resulted in the use of 76 800 CPU core hours (compare to 46 000 core hours with 12 ensemble members).
The assimilation framework used in this study explicitly accounted for uncertainty in the model forcing data (e.g., precipitation) and soil texture properties (% sand and % clay) and used the joint state and parameter estimation to reduce parameter uncertainty. While parameter updating is expected to correct part of the systematic model bias, there is a possibility that other water balance terms like evapotranspiration and also runoff may be degraded through data assimilation to compensate for model structural and/or input data errors. To investigate this, we evaluated the modeled total runoff (surface and subsurface) with nonrouted gridded runoff observations. While we found overall improvement in percent bias over the EU-CORDEX domain (i.e., from 60 % to 4 % over Europe; Table 4) and smaller improvements over different PRUDENCE regions after the assimilation, there was some degradation of runoff estimates after soil moisture assimilation (Fig. 10) for many regions. The differences in runoff between CLM-DA and CLM-OL were small, since the fluxes were often reproduced reasonably well in CLM-OL, with an average correlation of 0.9 over the EU-CORDEX domain (Table 3). The degradation in runoff over some regions and overall marginal improvements might be due to several factors, including a lack of analysis updates of water flux terms, model structure error (e.g., weak coupling of runoff processes with water table dynamics and soil water storage) and observation errors in the monthly data evaluation. From a comparison of individual components of total runoff between CLM-OL and CLM-DA, we found that the assimilation of soil moisture into CLM has greater impacts on subsurface runoff than on surface runoff (Fig. 11). As shown in Fig. 11, assimilation of CCI-SM data resulted in an underestimation of subsurface runoff over all regions, but has less impact on the surface runoff. This underestimation might be related to the CLM limitations in correctly representing processes controlling the partitioning of subsurface and surface flow in the model and/or to the exponential form of runoff parameterization. For example in the CLM, the overall saturation status of the soil column is the controlling factor for both surface and subsurface runoff generation. Thus any changes in the surface layer soil moisture will also have more profound effects on the subsurface flow. In addition, the surface runoff generation is based on the assumption of saturation excess runoff, meaning that the water table needs to intersect the surface before the surface runoff is generated. This assumption is problematic at the large spatial scales, especially in arid and semiarid regions. In dry regions, assimilation of soil moisture data may result in reduction of soil moisture values close to the residual water content values, which may lead to small surface runoff generation. For example, Sheng et al. (2017) also found that CLM exhibited limitations in water-limited areas where surface runoff is determined by groundwater dynamics and identified the saturation excess surface runoff assumption as the main cause of these limitations. Additionally, the assumption of topographically controlled surface runoff generation in the CLM is problematic in areas with flat topography, thick soils or deep groundwater (Li et al., 2011). Another reason may be uncertainties in E-RUN runoff data used in this study, which were derived from gridded atmospheric variables and flow observations at coarser resolution (0.5∘ × 0.5∘ grid resolution). In the future, additional observational data need to be explored in assimilation experiments.
This study only considered uncertainty with respect to soil texture parameters, while other soil and ecosystem parameters were assumed to be deterministic. In data assimilation, it is preferable to account for additional model parameter uncertainties that show a high sensitivity towards runoff. Alternatively, prior model calibration can be considered to constrain model parameters better and reduce systematic biases and uncertainties in CLM3.5 before the assimilation framework is applied. For the improvement of hydrologic predictions, joint assimilation of additional datasets such as river discharge and snow data may also be considered in future research.
A soil moisture data assimilation framework at the continental scale was applied to generate daily soil moisture and runoff estimates as part of a terrestrial system monitoring framework for Europe at 3 km resolution for the years 2000 to 2006. An ensemble was generated by perturbing precipitation and soil texture properties. These ensembles were used as input in the CLM-PDAF data assimilation framework (Kurtz et al., 2016) and used to assimilate CCI-SM soil moisture data. The impact of satellite soil moisture assimilation on daily soil moisture and monthly runoff was evaluated and cross-validated with CCI-SM data and gridded runoff from E-RUN observations at regional and seasonal scales. Using this high-resolution CLM-PDAF setup, the conclusions of this study are as follows:
-
Assimilation of satellite SM improved the soil moisture simulations over most parts of Europe relative to open-loop simulations. Open-loop simulations overestimated SM in most parts of Europe and in all seasons. For the study domain, on average, the RMSE for near-surface SWC was reduced from 0.10 mm3 mm−3 in the open-loop simulations to 0.07 mm3 mm−3 with SM assimilation.
-
Regionally, significant improvements were achieved for soil moisture across most regions, except over Scandinavia. The low performance of CLM-DA in these regions might be due to the lack of data in space and time, as caused by satellite track changes, radio-frequency interference, dense vegetation, snow and frozen soil limiting the assimilation of soil moisture data in land surface process simulations. Analogously, CLM-DA performed poorly for years 2000 and 2001, which appears to be related to large data gaps and higher noise levels in the CCI-SM satellite data in these years. This indicates the suitability of ESA CCI-SM for data assimilation studies from 2002 onwards, whereas the accuracy and noise level of earlier data are not appropriate for this purpose.
-
At the seasonal timescale, the CLM-DA simulations performed better in the summer and autumn seasons than in the winter and spring seasons. This might be again related to large data gaps in the winter season or model limitations to correctly represent complex cold region processes such as frozen soil.
-
The assimilation of CCI-SM data into CLM3.5 led to an overall marginal improvement in the simulated total runoff over Europe. Improvements in runoff were more prominent over the Iberian Peninsula, the Mediterranean and eastern Europe, where CLM-DA, on average, minimized the difference to E-RUN from 0.65, 0.54 and 0.66 mm day−1 to 0.25, 0.14 and 0.25 mm day−1, respectively (Table 3). The improvements over other regions, such as the British Isles, France, Mid-Europe, Scandinavia and the Alpine region, were comparatively small. These findings indicated the potential of satellite soil moisture assimilation in CLM3.5 to improve other terrestrial components of the water cycle as a basis for more accurate water balance analyses.
The results from this study are not only useful as a standalone high-resolution reanalysis product over Europe, but can also be used as an independent dataset for validation of other land surface models. In this study, the soil moisture estimates, with improved spatial resolution obtained via data assimilation, offer a new product for monitoring soil water content and have distinct benefits over the original CCI-SM data. In addition, by selecting the ESA CCI soil moisture product for assimilation, the potential impact of the long term soil moisture observations on hydrologic simulations can be assessed for climate change studies. Recently, with the availability of COSMO-REA6, the time period can be extended to 2000–2015 in future studies using the proposed methodology to derive a land surface reanalysis at 3 km resolution for continental Europe. Moreover, CLM3.5 is also part of the fully coupled Terrestrial Systems Model Platform (TerrSysMP) (Gasper et al., 2014; Keune et al., 2016; Shrestha et al., 2014) that simulates the full terrestrial hydrologic cycle including feedbacks between atmosphere, land-surface and subsurface compartments of the water cycle. The impact of satellite soil moisture assimilation on other water cycle variables across the soil–vegetation–atmosphere system using TerrSysMP and its effects on the accuracy of model simulations at the continental scale remains to be explored.
The data used in this study can be provided to the readers upon request to the corresponding author.
The supplement related to this article is available online at: https://doi.org/10.5194/hess-23-277-2019-supplement.
BSN and WK designed the experiment and BSN performed the simulations and analysis and wrote the paper. CM provided the satellite data. WS and KG helped with high-performance computing and data preparations. JK provided the modeling setup. JK, HG and AS contributed to the interpretation of the results and helped to draft the paper. H-JHF provided guidance and reviewed and revised the model formulations and the paper. SK supervised the project and provided guidance to the interpretation of the results. All authors provided critical feedback and helped shape the research, analysis and manuscript.
The authors declare that they have no conflict of interest.
The authors gratefully acknowledge the computing time granted by the
JARA-HPC Vergabegremium on the supercomputer JURECA at Forschungszentrum
Jülich. This work was supported by the Energy oriented Centre of
Excellence (EoCoE), grant agreement number 676629, funded within the
Horizon2020 framework of the European Union. Carsten Montzka was funded by BELSPO
(Belgian Science Policy Office) in the framework of the STEREO III
programme HYDRAS+ (SR/00/302) and the ERA-PLANET/GEOEssential project
(Horizon2020, grant agreement number 689443). Wolfgang Kurtz was supported by
SFB-TR32 “Patterns in soil–vegetation–atmosphere systems: monitoring,
modeling and data assimilation” funded by the German Science Foundation (DFG).
We thank the anonymous reviewers and the editor for their constructive comments
and suggestions that helped us to improve the paper significantly.
The article processing charges for this open-access
publication
were covered by a Research
Centre of the Helmholtz Association.
Edited by: Alberto Guadagnini
Reviewed by: three anonymous referees
Albergel, C., Dorigo, W., Balsamo, G., Muñoz-Sabater, J., de Rosnay, P., Isaksen, L., Brocca, L., de Jeu, R., and Wagner, W.: Monitoring multi-decadal satellite earth observation of soil moisture products through land surface reanalyses, Remote Sens. Environ., 138, 77–89, https://doi.org/10.1016/j.rse.2013.07.009, 2013.
Albergel, C., Munier, S., Leroux, D. J., Dewaele, H., Fairbairn, D., Barbu, A. L., Gelati, E., Dorigo, W., Faroux, S., Meurey, C., Le Moigne, P., Decharme, B., Mahfouf, J.-F., and Calvet, J.-C.: Sequential assimilation of satellite-derived vegetation and soil moisture products using SURFEX_v8.0: LDAS-Monde assessment over the Euro-Mediterranean area, Geosci. Model Dev., 10, 3889–3912, https://doi.org/10.5194/gmd-10-3889-2017, 2017.
Andreasen, M., Andreasen, L. A., Jensen, K. H., Sonnenborg, T. O., and Bircher, S.: Estimation of regional groundwater recharge using data from a distributed soil moisture network, Vadose Zone J., 12, 3, https://doi.org/10.2136/vzj2013.01.0035, 2013.
Bartalis, Z., Wagner, W., Naeimi, V., Hasenauer, S., Scipal, K., Bonekamp, H., Figa, J., and Anderson, C.: Initial soil moisture retrievals from the METOP-A Advanced Scatterometer (ASCAT), Geophys. Res. Lett., 34, L20401, https://doi.org/10.1029/2007gl031088, 2007.
Batjes, N. H.: A world dataset of derived soil properties by FAO–UNESCO soil unit for global modelling, Soil Use Manage., 13, 9–16, 1997.
Best, M. J., Pryor, M., Clark, D. B., Rooney, G. G., Essery, R. L. H., Ménard, C. B., Edwards, J. M., Hendry, M. A., Porson, A., Gedney, N., Mercado, L. M., Sitch, S., Blyth, E., Boucher, O., Cox, P. M., Grimmond, C. S. B., and Harding, R. J.: The Joint UK Land Environment Simulator (JULES), model description – Part 1: Energy and water fluxes, Geosci. Model Dev., 4, 677–699, https://doi.org/10.5194/gmd-4-677-2011, 2011.
Bierkens, M. F., Bell, V. A., Burek, P., Chaney, N., Condon, L. E., David, C. H., de Roo, A., Döll, P., Drost, N., and Famiglietti, J. S.: Hyper-resolution global hydrological modelling: what is next? “Everywhere and locally relevant”, Hydrol. Process., 29, 310–320, 2015.
Bollmeyer, C., Keller, J. D., Ohlwein, C., Wahl, S., Crewell, S., Friederichs, P., Hense, A., Keune, J., Kneifel, S., and Pscheidt, I.: Towards a high-resolution regional reanalysis for the European CORDEX domain, Q. J. Roy. Meteorol. Soc., 141, 1–15, 2015.
Bolten, J. D., Crow, W. T., Zhan, X., Jackson, T. J., and Reynolds, C. A.: Evaluating the utility of remotely sensed soil moisture retrievals for operational agricultural drought monitoring, IEEE J. Select. Top. Appl. Earth Obs. Remote Sens., 3, 57–66, 2010.
Bonan, G. B., Oleson, K. W., Vertenstein, M., Levis, S., Zeng, X., Dai, Y., Dickinson, R. E., and Yang, Z.-L.: The land surface climatology of the Community Land Model coupled to the NCAR Community Climate Model, J. Climate, 15, 3123–3149, 2002.
Brocca, L., Melone, F., Moramarco, T., and Morbidelli, R.: Spatial-temporal variability of soil moisture and its estimation across scales, Water Resour. Res., 46, W02516, https://doi.org/10.1029/2009wr008016, 2010.
Brocca, L., Moramarco, T., Melone, F., Wagner, W., Hasenauer, S., and Hahn, S.: Assimilation of surface-and root-zone ASCAT soil moisture products into rainfall–runoff modeling, IEEE T. Geosci. Remote, 50, 2542–2555, 2012.
Burgers, G., van Leeuwen, J. P., and Evensen, G.: Analysis scheme in the ensemble Kalman filter, Mon. Weather Rev., 126, 1719–1724, 1998.
Cammalleri, C. and Ciraolo, G.: State and parameter update in a coupled energy/hydrologic balance model using ensemble Kalman filtering, J. Hydrol., 416, 171–181, 2012.
Chen, H., Yang, D., Hong, Y., Gourley, J. J., and Zhang, Y.: Hydrological data assimilation with the Ensemble Square-Root-Filter: Use of streamflow observations to update model states for real-time flash flood forecasting, Adv. Water Resour., 59, 209–220, https://doi.org/10.1016/j.advwatres.2013.06.010, 2013.
Christensen, J. H. and Christensen, O. B.: A summary of the PRUDENCE model projections of changes in European climate by the end of this century, Climatic Change, 81, 7–30, https://doi.org/10.1007/s10584-006-9210-7, 2007.
Clark, D. B., Mercado, L. M., Sitch, S., Jones, C. D., Gedney, N., Best, M. J., Pryor, M., Rooney, G. G., Essery, R. L. H., Blyth, E., Boucher, O., Harding, R. J., Huntingford, C., and Cox, P. M.: The Joint UK Land Environment Simulator (JULES), model description – Part 2: Carbon fluxes and vegetation dynamics, Geosci. Model Dev., 4, 701–722, https://doi.org/10.5194/gmd-4-701-2011, 2011.
Cosby, B. J., Hornberger, G. M., Clapp, R. B., and Ginn, T. R.: A statistical exploration of the relationships of soil moisture characteristics to the physical properties of soils, Water Resour. Res., 20, 682–690, 1984.
Crow, W. T. and Ryu, D.: A new data assimilation approach for improving runoff prediction using remotely-sensed soil moisture retrievals, Hydrol. Earth Syst. Sci., 13, 1–16, https://doi.org/10.5194/hess-13-1-2009, 2009.
Crow, W. T., Chen, F., Reichle, R. H., and Liu, Q.: L band microwave remote sensing and land data assimilation improve the representation of prestorm soil moisture conditions for hydrologic forecasting, Geophys. Res. Lett., 44, 5495–5503, 2017.
Dai, Y., Zeng, X., Dickinson, R. E., Baker, I., Bonan, G. B., Bosilovich, M. G., Denning, A. S., Dirmeyer, P. A., Houser, P. R., and Niu, G.: The common land model, B. Am. Meteorol. Soc., 84, 1013–1024, 2003.
Danielson, J. J. and Gesch, D. B.: Global multi-resolution terrain elevation data 2010 (GMTED2010), US Geological Survey, https://doi.org/10.3133/ofr20111073, 2011.
DeChant, C. M. and Moradkhani, H.: Examining the effectiveness and robustness of sequential data assimilation methods for quantification of uncertainty in hydrologic forecasting, Water Resour. Res., 48, 1–15, https://doi.org/10.1029/2011wr011011, 2012.
Dee, D. P., Uppala, S. M., Simmons, A., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M., Balsamo, G., Bauer, D. P, Bechtold, P., Beljaars, A. C., van de Berg, M. L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J.-J. Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Vitart, F.: The ERA-Interim reanalysis: Configuration and performance of the data assimilation system, Q. J. Roy. Meteorol. Soc., 137, 553–597, 2011.
De Lannoy, G. J. and Reichle, R. H.: Global assimilation of multiangle and multipolarization SMOS brightness temperature observations into the GEOS-5 catchment land surface model for soil moisture estimation, J. Hydrometeorol., 17, 669–691, 2016.
De Lannoy, G. J., Reichle, R. H., Arsenault, K. R., Houser, P. R., Kumar, S., Verhoest, N. E., and Pauwels, V. R.: Multiscale assimilation of Advanced Microwave Scanning Radiometer – EOS snow water equivalent and Moderate Resolution Imaging Spectroradiometer snow cover fraction observations in northern Colorado, Water Resour. Res., 48, W01522, https://doi.org/10.1029/2011wr010588, 2012.
De Rosnay, P., Drusch, M., Boone, A., Balsamo, G., Decharme, B., Harris, P., Kerr, Y., Pellarin, T., Polcher, J., and Wigneron, J.-P.: AMMA land surface model intercomparison experiment coupled to the community microwave emission model: ALMIP-MEM, J. Geophys. Res.-Atmos., 114, D05108, https://doi.org/10.1029/2008jd010724, 2009.
De Rosnay, P., Drusch, M., Vasiljevic, D., Balsamo, G., Albergel, C., and Isaksen, L.: A simplified Extended Kalman Filter for the global operational soil moisture analysis at ECMWF, Q. J. Roy. Meteorol. Soc., 139, 1199–1213, 2013.
Dickinson, R. E., Oleson, K. W., Bonan, G., Hoffman, F., Thornton, P., Vertenstein, M., Yang, Z.-L., and Zeng, X.: The Community Land Model and its climate statistics as a component of the Community Climate System Model, J. Climate, 19, 2302–2324, 2006.
Dobriyal, P., Qureshi, A., Badola, R., and Hussain, S. A.: A review of the methods available for estimating soil moisture and its implications for water resource management, J. Hydrol., 458, 110–117, 2012.
Dorigo, W., de Jeu, R., Chung, D., Parinussa, R., Liu, Y., Wagner, W., and Fernández-Prieto, D.: Evaluating global trends (1988–2010) in harmonized multi-satellite surface soil moisture, Geophys. Res. Lett., 39, L18405, https://doi.org/10.1029/2012gl052988, 2012.
Dorigo, W., Wagner, W., Albergel, C., Albrecht, F., Balsamo, G., Brocca, L., Chung, D., Ertl, M., Forkel, M., and Gruber, A.: ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions, Remote Sens. Environ., 203, 185–215, 2017.
Draper, C., Mahfouf, J.-F., and Walker, J.: An EKF assimilation of AMSR-E soil moisture into the ISBA land surface scheme, J. Geophys. Res.-Atmos., 114, D20104, https://doi.org/10.1029/2008JD011650, 2009.
Draper, C., Mahfouf, J.-F., Calvet, J.-C., Martin, E., and Wagner, W.: Assimilation of ASCAT near-surface soil moisture into the SIM hydrological model over France, Hydrol. Earth Syst. Sci., 15, 3829–3841, https://doi.org/10.5194/hess-15-3829-2011, 2011.
Drusch, M.: Initializing numerical weather prediction models with satellite-derived surface soil moisture: Data assimilation experiments with ECMWF's Integrated Forecast System and the TMI soil moisture data set, J. Geophys. Res.-Atmos., 112, D03102, https://doi.org/10.1029/2006jd007478, 2007.
Drusch, M., Wood, E., and Gao, H.: Observation operators for the direct assimilation of TRMM microwave imager retrieved soil moisture, Geophys. Res. Lett., 32, L15403, https://doi.org/10.1029/2005gl023623, 2005.
Entekhabi, D., Njoku, E. G., O'Neill, P. E., Kellogg, K. H., Crow, W. T., Edelstein, W. N., Entin, J. K., Goodman, S. D., Jackson, T. J., Johnson, J., Kimball, J., Piepmeier, J. R., Koster, R. D., Martin, N., McDonald, K. C., Moghaddam, M., Moran, S., Reichle, R., Shi, J. C., Spencer, M. W., Thurman, S. W., Tsang, L., and Van Zyl, J.: The soil moisture active passive (SMAP) mission, Proc. IEEE, 98, 704–716, 2010.
Evensen, G.: The ensemble Kalman filter: Theoretical formulation and practical implementation, Ocean Dynam., 53, 343–367, 2003.
Friedl, M. A., McIver, D. K., Hodges, J. C., Zhang, X. Y., Muchoney, D., Strahler, A. H., Woodcock, C. E., Gopal, S., Schneider, A., and Cooper, A.: Global land cover mapping from MODIS: algorithms and early results, Remote Sens. Environ., 83, 287–302, 2002.
Gasper, F., Goergen, K., Shrestha, P., Sulis, M., Rihani, J., Geimer, M., and Kollet, S.: Implementation and scaling of the fully coupled Terrestrial Systems Modeling Platform (TerrSysMP v1.0) in a massively parallel supercomputing environment – a case study on JUQUEEN (IBM Blue Gene/Q), Geosci. Model Dev., 7, 2531–2543, https://doi.org/10.5194/gmd-7-2531-2014, 2014.
Gharamti, M. E., Ait-El-Fquih, B., and Hoteit, I.: An iterative ensemble Kalman filter with one-step-ahead smoothing for state-parameters estimation of contaminant transport models, J. Hydrol., 527, 442–457, 2015.
Global Runoff Data Center: Long-term mean monthly discharges and annual characteristics of GRDC stations, Technical Report, The Federal Institute of Hydrology, Koblenz, Germany, 2011.
Gudmundsson, L. and Seneviratne, S. I.: Observation-based gridded runoff estimates for Europe (E-RUN version 1.1), Earth Syst. Sci. Data, 8, 279–295, https://doi.org/10.5194/essd-8-279-2016, 2016.
Gutowski Jr., W. J., Giorgi, F., Timbal, B., Frigon, A., Jacob, D., Kang, H.-S., Raghavan, K., Lee, B., Lennard, C., Nikulin, G., O'Rourke, E., Rixen, M., Solman, S., Stephenson, T., and Tangang, F.: WCRP COordinated Regional Downscaling EXperiment (CORDEX): a diagnostic MIP for CMIP6, Geosci. Model Dev., 9, 4087–4095, https://doi.org/10.5194/gmd-9-4087-2016, 2016.
Han, X., Franssen, H.-J. H., Montzka, C., and Vereecken, H.: Soil moisture and soil properties estimation in the Community Land Model with synthetic brightness temperature observations, Water Resour. Res., 50, 6081–6105, 2014.
Haylock, M. R., Hofstra, N., Tank, A. K., Klok, E. J., Jones, P. D., and New, M.: A European daily high-resolution gridded data set of surface temperature and precipitation for 1950–2006, J. Geophys. Res.-Atmos., 113, D20119, https://doi.org/10.1029/2008jd010201, 2008.
Hijmans, R., Cameron, S., Parra, J., Jones, P., Jarvis, A., and Richardson, K.: WorldClim, version 1.3, University of California, Berkeley, 2005.
Hunt, B. R., Kostelich, E. J., and Szunyogh, I.: Efficient data assimilation for spatiotemporal chaos: A local ensemble transform Kalman filter, Physica D, 230, 112–126, 2007.
Jones, P. W.: First-and second-order conservative remapping schemes for grids in spherical coordinates, Mon. Weather Rev., 127, 2204–2210, 1999.
Kerr, Y. H., Waldteufel, P., Wigneron, J.-P., Martinuzzi, J., Font, J., and Berger, M.: Soil moisture retrieval from space: The Soil Moisture and Ocean Salinity (SMOS) mission, IEEE T. Geosci. Remote, 39, 1729–1735, 2001.
Keune, J., Gasper, F., Goergen, K., Hense, A., Shrestha, P., Sulis, M., and Kollet, S.: Studying the influence of groundwater representations on land surface–atmosphere feedbacks during the European heat wave in 2003, J. Geophys. Res.-Atmos., 121, 13301–13325, https://doi.org/10.1002/2016jd025426, 2016.
Kiehl, J. T. and Trenberth, K. E.: Earth's annual global mean energy budget, B. Am. Meteorol. Soc., 78, 197–208, 1997.
Kumar, S. V., Reichle, R. H., Peters-Lidard, C. D., Koster, R. D., Zhan, X., Crow, W. T., Eylander, J. B., and Houser, P. R.: A land surface data assimilation framework using the land information system: Description and applications, Adv. Water Resour., 31, 1419–1432, 2008.
Kurtz, W., He, G., Kollet, S. J., Maxwell, R. M., Vereecken, H., and Hendricks Franssen, H.-J.: TerrSysMP-PDAF (version 1.0): a modular high-performance data assimilation framework for an integrated land surface–subsurface model, Geosci. Model Dev., 9, 1341–1360, https://doi.org/10.5194/gmd-9-1341-2016, 2016.
Lahoz, W. A. and De Lannoy, G. J.: Closing the gaps in our knowledge of the hydrological cycle over land: Conceptual problems, Surv. Geophys., 35, 623–660, 2014.
Lawrence, D. M., Oleson, K. W., Flanner, M. G., Thornton, P. E., Swenson, S. C., Lawrence, P. J., Zeng, X., Yang, Z.-L., Levis, S., Sakaguchi, K., Bonan, G. B., and Slater, A. G.: Parameterization improvements and functional and structural advances in version 4 of the Community Land Model, J. Adv. Model. Earth Syst., 3, 1, https://doi.org/10.1029/2011ms00045, 2011.
Li, H., Huang, M., Wigmosta, M. S., Ke, Y., Coleman, A. M., Leung, L. R., Wang, A., and Ricciuto, D. M.: Evaluating runoff simulations from the Community Land Model 4.0 using observations from flux towers and a mountainous watershed, J. Geophys. Res.-Atmos., 116, D24120, https://doi.org/10.1029/2011jd016276, 2011.
Li, M. and Ma, Z.: Soil moisture drought detection and multi-temporal variability across China, Sci. China Earth Sci., 58, 1798–1813, 2015.
Liang, X., Lettenmaier, D. P., Wood, E. F., and Burges, S. J.: A simple hydrologically based model of land surface water and energy fluxes for general circulation models, J. Geophys. Res.-Atmos., 99, 14415–14428, 1994.
Liang, X., Wood, E. F., and Lettenmaier, D. P.: Surface soil moisture parameterization of the VIC-2L model: Evaluation and modification, Global Planet. Change, 13, 195–206, 1996.
Lievens, H., Tomer, S. K., Al Bitar, A., De Lannoy, G. J., Drusch, M., Dumedah, G., Franssen, H.-J. H., Kerr, Y. H., Martens, B., and Pan, M.: SMOS soil moisture assimilation for improved hydrologic simulation in the Murray Darling Basin, Australia, Remote Sens. Environ., 168, 146–162, 2015.
Lievens, H., De Lannoy, G. J. M., Al Bitar, A., Drusch, M., Dumedah, G., Hendricks Franssen, H.-J., Kerr, Y. H., Tomer, S. K., Martens, B., Merlin, O., Pan, M., Roundy, J. K., Vereecken, H., Walker, J. P., Wood, E. F., Verhoest, N. E. C., and Pauwels, V. R. N.: Assimilation of SMOS soil moisture and brightness temperature products into a land surface model, Remote Sens. Environ., 180, 292–304, 2016.
Liu, D. and Mishra, A. K.: Performance of AMSR_E soil moisture data assimilation in CLM4.5 model for monitoring hydrologic fluxes at global scale, J. Hydrol., 547, 67–79, 2017.
Liu, D., Mishra, A. K., and Yu, Z.: Evaluating uncertainties in multi-layer soil moisture estimation with support vector machines and ensemble Kalman filtering, J. Hydrol., 538, 243–255, 2016.
Liu, Y. and Gupta, H. V.: Uncertainty in hydrologic modeling: Toward an integrated data assimilation framework, Water Resour. Res., 43, W07401, https://doi.org/10.1029/2006wr005756, 2007.
Liu, Y., Wang, W., and Liu, Y.: ESA CCI Soil Moisture Assimilation in SWAT for Improved Hydrological Simulation in Upper Huai River Basin, Adv. Meteorol., 2018, 1–13, https://doi.org/10.1155/2018/7301314, 2018.
Liu, Y. Y., Parinussa, R. M., Dorigo, W. A., De Jeu, R. A. M., Wagner, W., van Dijk, A. I. J. M., McCabe, M. F., and Evans, J. P.: Developing an improved soil moisture dataset by blending passive and active microwave satellite-based retrievals, Hydrol. Earth Syst. Sci., 15, 425–436, https://doi.org/10.5194/hess-15-425-2011, 2011.
Liu, Y. Y., Dorigo, W. A., Parinussa, R. M., de Jeu, R. A., Wagner, W., McCabe, M. F., Evans, J. P., and Van Dijk, A.: Trend-preserving blending of passive and active microwave soil moisture retrievals, Remote Sens. Environ., 123, 280–297, 2012.
López López, P., Wanders, N., Schellekens, J., Renzullo, L. J., Sutanudjaja, E. H., and Bierkens, M. F. P.: Improved large-scale hydrological modelling through the assimilation of streamflow and downscaled satellite soil moisture observations, Hydrol. Earth Syst. Sci., 20, 3059–3076, https://doi.org/10.5194/hess-20-3059-2016, 2016.
Matgen, P., Fenicia, F., Heitz, S., Plaza, D., de Keyser, R., Pauwels, V. R., Wagner, W., and Savenije, H.: Can ASCAT-derived soil wetness indices reduce predictive uncertainty in well-gauged areas? A comparison with in situ observed soil moisture in an assimilation application, Adv. Water Resour., 44, 49–65, 2012.
McNally, A., Shukla, S., Arsenault, K. R., Wang, S., Peters-Lidard, C. D., and Verdin, J. P.: Evaluating ESA CCI soil moisture in East Africa, Int. J. Appl. Earth Obs. Geoinform., 48, 96–109, 2016.
Mecklenburg, S., Drusch, M., Kaleschke, L., Rodriguez-Fernandez, N., Reul, N., Kerr, Y., Font, J., Martin-Neira, M., Oliva, R., Daganzo-Eusebio, E., Grant, J. P., Sabia, R., Macelloni, G., Rautiainen, K., Fauste, J., de Rosnay, P., Munoz-Sabater, J., Verhoest, N., Lievens, H., Delwart, S., Crapolicchio, R., de la Fuente, A., and Kornberg, M.: ESA's Soil Moisture and Ocean Salinity mission: From science to operational applications, Remote Sens. Environ., 180, 3–18, https://doi.org/10.1016/j.rse.2015.12.025, 2016.
Merlin, O., Escorihuela, M. J., Mayoral, M. A., Hagolle, O., Al Bitar, A., and Kerr, Y.: Self-calibrated evaporation-based disaggregation of SMOS soil moisture: An evaluation study at 3 km and 100 m resolution in Catalunya, Spain, Remote Sens. Environ., 130, 25–38, 2013.
Mohanty, B. P., Cosh, M., Lakshmi, V., and Montzka, C.: Remote sensing for vadose zone hydrology – a synthesis from the vantage point, Vadose Zone J., 12, 3, https://doi.org/10.2136/vzj2013.07.012, 2013.
Montzka, C., Pauwels, V., Franssen, H.-J. H., Han, X., and Vereecken, H.: Multivariate and multiscale data assimilation in terrestrial systems: A review, Sensors, 12, 16291–16333, 2012.
Moradkhani, H., Sorooshian, S., Gupta, H. V., and Houser, P. R.: Dual state–parameter estimation of hydrological models using ensemble Kalman filter, Adv. Water Resour., 28, 135–147, 2005.
Nerger, L. and Hiller, W.: Software for ensemble-based data assimilation systems – Implementation strategies and scalability, Comput. Geosci., 55, 110–118, 2013.
Nie, S., Zhu, J., and Luo, Y.: Simultaneous estimation of land surface scheme states and parameters using the ensemble Kalman filter: identical twin experiments, Hydrol. Earth Syst. Sci., 15, 2437–2457, https://doi.org/10.5194/hess-15-2437-2011, 2011.
Ni-Meister, W., Houser, P. R., and Walker, J. P.: Soil moisture initialization for climate prediction: Assimilation of scanning multifrequency microwave radiometer soil moisture data into a land surface model, J. Geophys. Res.-Atmos., 111, D20102, https://doi.org/10.1029/2006jd007190, 2006.
Niu, G.-Y., Yang, Z.-L., Dickinson, R. E., and Gulden, L. E.: A simple TOPMODEL-based runoff parameterization (SIMTOP) for use in global climate models, J. Geophys. Res.-Atmos., 110, D21106, https://doi.org/10.1029/2005jd006111, 2005.
Niu, G.-Y., Yang, Z.-L., Dickinson, R. E., Gulden, L. E., and Su, H.: Development of a simple groundwater model for use in climate models and evaluation with Gravity Recovery and Climate Experiment data, J. Geophys. Res.-Atmos., 112, D07103, https://doi.org/10.1029/2006jd007522, 2007.
Niu, G.-Y., Yang, Z.-L., Mitchell, K. E., Chen, F., Ek, M. B., Barlage, M., Kumar, A., Manning, K., Niyogi, D., Rosero, E., Tewari, M., and Xia, Y.: The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements, J. Geophys. Res.-Atmos., 116, D12109, https://doi.org/10.1029/2010jd015139, 2011.
Oleson, K. W., Dai, Y., Bonan, G., Bosilovich, M., Dickinson, R., Dirmeyer, P., Hoffman, F., Houser, P., Levis, S., and Niu, G. Y.: Technical description of the community land model (CLM), NCAR Technical Note NCAR/TN−461+STR, National Center for Atmospheric Research, Boulder, CO, 2004.
Oleson, K. W., Niu, G.-Y., Yang, Z.-L., Lawrence, D. M., Thornton, P. E., Lawrence, P. J., Stöckli, R., Dickinson, R. E., Bonan, G. B., and Levis, S.: Improvements to the Community Land Model and their impact on the hydrological cycle, J. Geophys. Res.-Biogeo., 113, G01021, https://doi.org/10.1029/2007jg000563, 2008.
Owe, M., de Jeu, R., and Holmes, T.: Multisensor historical climatology of satellite-derived global land surface moisture, J. Geophys. Res.-Earth, 113, F01002, https://doi.org/10.1029/2007jf000769, 2008.
Pan, M. and Wood, E. F.: Impact of accuracy, spatial availability, and revisit time of satellite-derived surface soil moisture in a multiscale ensemble data assimilation system, IEEE Select. Top. Appl. Earth Obs. Remote Sens., 3, 49–56, 2010.
Pan, M., Wood, E. F., Wójcik, R., and McCabe, M. F.: Estimation of regional terrestrial water cycle using multi-sensor remote sensing observations and data assimilation, Remote Sens. Environ., 112, 1282–1294, 2008.
Pathiraja, S., Marshall, L., Sharma, A., and Moradkhani, H.: Detecting non-stationary hydrologic model parameters in a paired catchment system using data assimilation, Adv. Water Resour., 94, 103–119, 2016.
Pauwels, V. R., Hoeben, R., Verhoest, N. E., and De Troch, F. P.: The importance of the spatial patterns of remotely sensed soil moisture in the improvement of discharge predictions for small-scale basins through data assimilation, J. Hydrol., 251, 88–102, 2001.
Pauwels, V. R., Hoeben, R., Verhoest, N. E., De Troch, F. P., and Troch, P. A.: Improvement of TOPLATS-based discharge predictions through assimilation of ERS-based remotely sensed soil moisture values, Hydrol. Process., 16, 995–1013, 2002.
Rafieeinasab, A., Seo, D.-J., Lee, H., and Kim, S.: Comparative evaluation of maximum likelihood ensemble filter and ensemble Kalman filter for real-time assimilation of streamflow data into operational hydrologic models, J. Hydrol., 519, 2663–2675, 2014.
Rains, D., Han, X., Lievens, H., Montzka, C., and Verhoest, N. E. C.: SMOS brightness temperature assimilation into the Community Land Model, Hydrol. Earth Syst. Sci., 21, 5929–5951, https://doi.org/10.5194/hess-21-5929-2017, 2017.
Reichle, R. H. and Koster, R. D.: Bias reduction in short records of satellite soil moisture, Geophys. Res. Lett., 31, L19501, https://doi.org/10.1029/2004gl020938, 2004.
Reichle, R. H. and Koster, R. D.: Global assimilation of satellite surface soil moisture retrievals into the NASA Catchment land surface model, Geophys. Res. Lett., 32, L02404, https://doi.org/10.1029/2004gl021700, 2005.
Renzullo, L. J., Van Dijk, A., Perraud, J.-M., Collins, D., Henderson, B., Jin, H., Smith, A. B., and McJannet, D. L.: Continental satellite soil moisture data assimilation improves root-zone moisture analysis for water resources assessment, J. Hydrol., 519, 2747–2762, 2014.
Rodell, M., Houser, P. R., Jambor, U. E. A., Gottschalck, J., Mitchell, K., Meng, C.-J., Arsenault, K., Cosgrove, B., Radakovich, J., and Bosilovich, M.: The global land data assimilation system, B. Am. Meteorol. Soc., 85, 381–394, 2004.
Running, S. W., Nemani, R. R., Heinsch, F. A., Zhao, M., Reeves, M., and Hashimoto, H.: A continuous satellite-derived measure of global terrestrial primary production, AIBS Bull., 54, 547–560, 2004.
Sahoo, A. K., De Lannoy, G. J., Reichle, R. H., and Houser, P. R.: Assimilation and downscaling of satellite observed soil moisture over the Little River Experimental Watershed in Georgia, USA, Adv. Water Resour., 52, 19–33, 2013.
Samuel, J., Coulibaly, P., Dumedah, G., and Moradkhani, H.: Assessing model state and forecasts variation in hydrologic data assimilation, J. Hydrol., 513, 127–141, 2014.
Schaap, M. G. and Leij, F. J.: Database-related accuracy and uncertainty of pedotransfer functions, Soil Science, 163, 765–779, 1998.
Seneviratne, S. I., Corti, T., Davin, E. L., Hirschi, M., Jaeger, E. B., Lehner, I., Orlowsky, B., and Teuling, A. J.: Investigating soil moisture–climate interactions in a changing climate: A review, Earth-Sci. Rev., 99, 125–161, 2010.
Sheng, M., Lei, H., Jiao, Y., and Yang, D.: Evaluation of the runoff and river routing schemes in the Community Land Model of the Yellow River basin, J. Adv. Model. Earth Syst., 9, 2993–3018, 2017.
Shock, C. C., Barnum, J. M., and Seddigh, M.: Calibration of Watermark Soil Moisture Sensors for Irrigation Management, Plant Soil, 143, 213–217, https://doi.org/10.1007/bf00007875, 1998.
Shrestha, P., Sulis, M., Masbou, M., Kollet, S., and Simmer, C.: A scale-consistent terrestrial systems modeling platform based on COSMO, CLM, and ParFlow, Mon. Weather Rev., 142, 3466–3483, 2014.
Simmer, C., Adrian, G., Jones, S., Wirth, V., Göber, M., Hohenegger, C., Janjic, T., Keller, J., Ohlwein, C., and Seifert, A.: Herz: The german hans-ertel centre for weather research, B. Am. Meteorol. Soc., 97, 1057–1068, 2016.
Springer, A., Eicker, A., Bettge, A., Kusche, J., and Hense, A.: Evaluation of the Water Cycle in the European COSMO-REA6 Reanalysis Using GRACE, Water, 9, 289, https://doi.org/10.3390/w9040289, 2017.
Sridhar, V., Hubbard, K. G., You, J., and Hunt, E. D.: Development of the soil moisture index to quantify agricultural drought and its “user friendliness” in severity-area-duration assessment, J. Hydrometeorol., 9, 660–676, 2008.
Stöckli, R., Lawrence, D. M., Niu, G.-Y., Oleson, K. W., Thornton, P. E., Yang, Z.-L., Bonan, G. B., Denning, A. S., and Running, S. W.: Use of FLUXNET in the Community Land Model development, J. Geophys. Res.-Biogeo., 113, 001025, https://doi.org/10.1029/2007jg000562, 2008.
Trenberth, K. E., Smith, L., Qian, T., Dai, A., and Fasullo, J.: Estimates of the global water budget and its annual cycle using observational and model data, J. Hydrometeorol., 8, 758–769, 2007.
Vereecken, H., Schnepf, A., Hopmans, J. W., Javaux, M., Or, D., Roose, T., Vanderborght, J., Young, M. H., Amelung, W., Aitkenhead, M., Allison, S. D., Assouline, S., Baveye, P., Berli, M., Brüggemann, N., Finke, P., Flury, M., Gaiser, T., Govers, G., Ghezzehei, T., Hallett, P., Franssen, H. J. H., Heppell, J., Horn, R., Huisman, J. A., Jacques, D., Jonard, F., Kollet, S., Lafolie, F., Lamorski, K., Leitner, D., McBratney, A., Minasny, B., Montzka, C., Nowak, W., Pachepsky, Y., Padarian, J., Romano, N., Roth, K., Rothfuss, Y., Rowe, E. C., Schwen, A., Šimunek, J., Tiktak, A., Dam, J. V., van der Zee, S. E. A. T. M., Vogel, H. J., Vrugt, J. A., Wöhling, T., and Young, I. M.: Modeling soil processes: Review, key challenges, and new perspectives, Vadose Zone J., 15, https://doi.org/10.2136/vzj2015.09.0131, 2016.
Verhoest, N. E. C., van den Berg, M. J., Martens, B., Lievens, H., Wood, E. F., Pan, M., Kerr, Y. H., Al Bitar, A., Tomer, S. K., Drusch, M., Vernieuwe, H., De Baets, B., Walker, J. P., Dumedah, G., and Pauwels, V. R. N.: Copula-based downscaling of coarse-scale soil moisture observations with implicit bias correction, IEEE T. Geosci. Remote, 53, 3507–3521, 2015.
Vinukollu, R. K., Wood, E. F., Ferguson, C. R., and Fisher, J. B.: Global estimates of evapotranspiration for climate studies using multi-sensor remote sensing data: Evaluation of three process-based approaches, Remote Sens. Environ., 115, 801–823, 2011.
Wagner, W., Dorigo, W., de Jeu, R., Fernandez, D., Benveniste, J., Haas, E., and Ertl, M.: Fusion of active and passive microwave observations to create an essential climate variable data record on soil moisture, ISPRS Annals, 7, 315–321, 2012.
Wagner, W., Hahn, S., Kidd, R., Melzer, T., Bartalis, Z., Hasenauer, S., Figa-Saldaña, J., de Rosnay, P., Jann, A., and Schneider, S.: The ASCAT soil moisture product: A review of its specifications, validation results, and emerging applications, Meteorol. Z., 22, 5–33, 2013.
Wang, J.: Microwave Emission from Smooth Bare Fields and Soil Moisture Sampling Depth, IEEE T. Geosci. Remote, GE-25, 616–622, https://doi.org/10.1109/TGRS.1987.289840, 1987.
Wahl, S., Bollmeyer, C., Crewell, S., Figura, C., Friederichs, P., Hense, A., Keller, J. D., and Ohlwein, C.: A novel convective-scale regional reanalysis COSMO-REA2: Improving the representation of precipitation, Meteorol. Z., 26, 345–361, https://doi.org/10.1127/metz/2017/0824, 2017.
Western, A. W., Zhou, S.-L., Grayson, R. B., McMahon, T. A., Blöschl, G., and Wilson, D. J.: Spatial correlation of soil moisture in small catchments and its relationship to dominant spatial hydrological processes, J. Hydrol., 286, 113–134, 2004.
Wood, E. F., Roundy, J. K., Troy, T. J., van Beek, L. P. H., Bierkens, M. F. P., Blyth, E., de Roo, A., Döll, P., Ek, M., Famiglietti, J., Gochis, D., van de Giesen, N., Houser, P., Jaffé, P. R., Kollet, S., Lehner, B., Lettenmaier, D. P., Peters-Lidard, C., Sivapalan, M., Sheffield, J., Wade, A., and Whitehead, P.: Hyperresolution global land surface modeling: Meeting a grand challenge for monitoring Earth's terrestrial water: OPINION, Water Resour. Res., 47, W05301, https://doi.org/10.1029/2010WR010090, 2011.
Xiao, Z., Liang, S., Wang, J., Chen, P., Yin, X., Zhang, L., and Song, J.: Use of General Regression Neural Networks for Generating the GLASS Leaf Area Index Product From Time-Series MODIS Surface Reflectance, IEEE T. Geosci. Remote., 52, 209–223, https://doi.org/10.1109/TGRS.2013.2237780 2014.
Xie, X. and Zhang, D.: Data assimilation for distributed hydrological catchment modeling via ensemble Kalman filter, Adv. Water Resour., 33, 678–690, 2010.
Yang, Z.-L. and Niu, G.-Y.: The versatile integrator of surface and atmosphere processes: Part 1. Model description, Global Planet. Change, 38, 175–189, 2003.
Yin, J., Zhan, X., Zheng, Y., Hain, C. R., Liu, J., and Fang, L.: Optimal ensemble size of ensemble Kalman filter in sequential soil moisture data assimilation, Geophys. Res. Lett., 42, 6710–6715, https://doi.org/10.1002/2015GL063366, 2015.
Zeng, X. and Decker, M.: Improving the numerical solution of soil moisture-based Richards equation for land models with a deep or shallow water table, J. Hydrometeorol., 10, 308–319, 2009.