the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Using GRACE in a streamflow recession to determine drainable water storage in the Mississippi River basin
Heloisa Ehalt Macedo
Ralph Edward Beighley
Cédric H. David
John T. Reager
The study of the relationship between water storage and runoff generation has long been a focus of the hydrological sciences. NASA's Gravity Recovery and Climate Experiment (GRACE) mission provides monthly depth-integrated information on terrestrial water storage anomalies derived from time-variable gravity observations. As the first basin-scale storage measurement technique, these data offer potentially novel insight into the storage–discharge relationship. Here, we apply GRACE data in a streamflow recession analysis with river discharge measurements across several subdomains of the Mississippi River basin. Nonlinear regression analysis was used for 12 watersheds to determine that the fraction of baseflow in streams during non-winter months varies from 52 % to 75 % regionally. Additionally, the first quantitative estimate of absolute drainable water storage was estimated. For the 2002–2014 period, the drainable storage in the Mississippi River basin ranged from 2900±400 to 3600±400 km3.
- Article
(2058 KB) -
Supplement
(138 KB) - BibTeX
- EndNote
The amount of water that a watershed stores is a key descriptor of the functionality of that watershed and its role in the Earth system (Wagener et al., 2007; Sayama et al., 2011; Black, 1997). As water can reside for periods ranging from months to thousands of years in subsurface soils, storage is often a critical yet under-observed variable in hydrology and rainfall–runoff models. Water storage helps to define the amount of water available for water resource applications, as well as the resilience of a watershed to changes in climate (e.g., Brutsaert, 2005; Kirchner, 2009) with implications for society and the environment.
Despite the importance of characterizing watershed storage, relatively little work has been undertaken to understand the relationship between storage and discharge. Most of the existing work is based on remotely sensed observations of storage (e.g., Riegger and Tourian, 2014; Reager et al., 2014; Sproles et al., 2015; Tourian et al., 2018; Riegger, 2018). Across scales, subsurface heterogeneity in soils and geology can make the storage–discharge relationship complex and challenging to observe and model (Beven, 2006). Additionally, observations of storage over large domains such as an entire river basin are challenging to obtain using traditional in situ methods.
During the periods when soils and surface waters are not frozen, time series of streamflow can be partitioned into two primary components: “event flow”, which is a transient response to increased precipitation forcing; and “baseflow”, which represents the background or ambient drainage of the water stored in soils beneath the surface (Beven, 2001; Hall, 1968; Appleby, 1970; Horton, 1935). Streamflow recession analysis is a classical tool that has been used to investigate the ways in which storage contributes to streamflow, and to derive information on storage properties and regional unconfined aquifer characteristics (Tallaksen, 1995; Rupp and Selker, 2005; Brutsaert, 2008; Rupp and Woods, 2008; Tague and Grant, 2004; Clark et al., 2009; Biswal and Marani, 2010; Shaw and Riha, 2012; Biswal and Nagesh Kumar, 2015). Brutsaert and Nieber (1977) first proposed plotting an observed recession slope of hydrograph to estimate the storage–discharge relationship. After decades of use in the hydrological sciences, this framework was expanded by Kirchner (2009) in the simple dynamical systems approach, under the fundamental assumption that the discharge of the stream depends solely on the amount of water stored in the catchment. The motivation was to create a functional relationship between discharge and storage that could then be used to model discharge using only precipitation and evapotranspiration data. To date, there have been few studies on how low-flows or baseflow relate to total water storage (Krakauer and Temimi, 2011; Wittenberg and Sivapalan, 1999; Thomas et al., 2015; Wittenberg, 1999).
The relatively recent (e.g., 2000–current) availability of satellite-based Earth observations has generally improved our understanding of water stores and fluxes at varying scales, during normal and under extreme conditions (Alsdorf et al., 2010; Beighley et al., 2011; Swenson and Wahr, 2009; Kim et al., 2009; Reager et al., 2014; Sproles et al., 2015; Riegger and Tourian, 2014; Riegger, 2018; Tourian et al., 2018). For example, the Gravity Recovery and Climate Experiment (GRACE) satellites launched in 2002 provide monthly changes in total water storage resulting from water mass effect on the Earth's gravity field (Tapley et al., 2004). These changes are computed as total terrestrial water storage anomalies (TWSA) and describe the monthly difference in storage state from the record-length mean. Due to of the ability of the satellite to measure changes in the entire vertical column, including surface and subsurface water storage, these first-of-their-kind measurements have provided a valuable tool for understanding seasonal and interannual subsurface changes in water storage.
Building on these previous efforts and concepts, exponential relationships between monthly, non-winter discharge and GRACE TWSAs are developed at 12 US Geological Survey streamflow gauge locations distributed throughout the Mississippi River basin (Fig. 1, Table 1) for a 12.5-year period (April 2002 to October 2014). A forward-looking, low-flow filter is applied to the sorted discharge–TWSA pairs as a baseflow proxy. Exponential relationships between discharge and TWSA are developed for all non-winter flows and approximated baseflows. Results are used to investigate the fraction of non-winter monthly discharge approximated as baseflow throughout the Mississippi River basin.
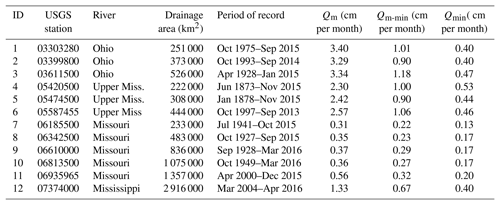
Table 1USGS gauge information and streamflow statistics: mean annual non-winter monthly discharge (Qm), mean annual minimum non-winter monthly discharge (Qm-min) and minimum non-winter monthly discharge (Qmin) observed during the study period.
We define drainable water storage as “the volume of water in a basin that is connected to streamflow and would drain out of the basin as time went towards infinity with no additional precipitation inputs”. Tourian et al. (2018) was the first study to estimate a total drainable water storage from a large river basin. This was done by estimating a linear relationship between the storage variability with the discharge at the mouth and applying a phase shift between the two time-series using a Hilbert transform. Here, to characterize the drainable storage from the subbasins, GRACE TWSAs are transformed into drainable water storages (i.e., not anomalies) using the derived discharge–TWSA relationships. Applying baseflow recession allows for nonlinearity in the storage–discharge relationship by treating only the case of storage driven flow (baseflow). For the first time, we demonstrate the direct relationship between storage and discharge on a basin and subbasin scale, we estimate parameters in the baseflow recession equation and we give the first estimate of a new quantity (drainable basin storage) that has never been estimated using only observations.
2.1 Data
The GRACE data used here are the GRCTellus global mascons (JPL RL05; mass concentration) solution data (Watkins et al., 2015; Wiese, 2015). This GRACE total water storage anomaly (TWSA) product is a 0.5∘ grid based on the spatial variability of the 3∘ measurements. The TWSA data for the Mississippi subbasins are aggregated over each subbasin using the area-weighted averaging method presented by Riegger and Tourian (2014). Due to satellite battery management and other issues, there are some missing months in the GRACE dataset. In total, 12 of the 151 monthly values are missing in our period of study. To fill missing months, linear interpolation between the previous and following months was used.
Monthly streamflow measurements (Qo) were obtained for select discharge gauge stations (US Geological Survey, 2015). The gauge stations were selected based on data availability, drainage area and location throughout the Mississippi River basin (i.e., along major tributaries). The 12 sites were distributed throughout the Mississippi River basin with 3 along the Ohio River (1–3), 3 along the upper Mississippi River (4–6), 5 along the Missouri River (7–11) and 1 near the outlet of the Mississippi River (12) (Fig. 1). Rodell and Famiglietti (1999) estimated that the minimum region size in which GRACE could resolve water mass variability would be about 200 000 km2, a smaller size than our smallest basin. The GRACE mascons (Watkins et al., 2015) are statistically independent and are at a 3∘ resolution (around 90 000 km2). Although multiple sites are from individual tributaries, they are distributed along the river such that the difference in drainage area between two sites is roughly 100 000 km2 or more.
All relevant gauge information, such as river name, drainage area and period of record, is contained in Table 1. It is essential to note that potential cold weather months (November through March) were excluded from this analysis for USGS streamflow to minimize the impacts of snow and ice influence on the total water storage. For example, if basin-wide storage increases due to snow accumulation, it is likely that there will be no correlated change in discharge at that time. Thus, the storage change measured by GRACE for those months is not directly linked to discharge until some later period. The sensitivity of the results of this study to the selection of April through October as the non-frozen period is likely to be minimal in this region.
There are other possible sources of storage variability that should be considered when using GRACE measurements, such as vegetation growth and groundwater pumping. Regarding vegetation biomass, Rodell et al. (2007) affirms that the seasonal and interannual biomass variations are typically smaller than the uncertainty in the GRACE TWSA measurements, and based on the global maps of vegetation biomass (Rodell et al., 2005), this holds true for the Mississippi River basin. Significant pumping occurs in the High Plains located in the basin; however, as it is a shallow-water-table aquifer (Scanlon et al., 2012; Brookfield et al., 2018; Nie et al., 2018), the storage changes would still be linked to baseflow generation. In other words, the portions of the basin which are experiencing water table decline due to human activities would still exhibit the same general storage–discharge relationship.
2.2 Methods
To identify potential relationships between monthly discharge (Q) and basin storage (S), GRACE TWSA data are used to represent storage variability and paired time series of Q–S are determined for each subbasin. Mean monthly observed discharge (m3 s−1) is converted to depth units (cm per month) by cumulating flow rates for each month and dividing by the drainage area upstream of each site (Table 1). Only non-winter months were selected to limit the impacts of snow processes on Qo–S relationships. Following work by Kim et al. (2009), we focus on the fact that most summer storage variability in the Mississippi River basin is not due to surface water storage, but instead to subsurface storage (including the vadose zone). Our assumptions are applied to the recession of the streamflow records, namely that baseflow drives the portion of streamflow that underlies monthly peaks, and that this baseflow amount can be regressed against storage to achieve the storage minimum with calculated uncertainty. Pairing Qo with S, we also assume that an average monthly discharge corresponds to the GRACE TWSA for the same month, which derives from a single measurement in the month concerned. However, the GRACE solution integrates temporal information from several ground tracks through the study region into the monthly gravity field, a single value carrying information for a whole month. Note that we focus on storage anomalies rather than absolute water storage to determine the discharge relationships because of the inability to quantify absolute storage based only on GRACE measurements.
To investigate baseflow (Qb) relationships, a forward-looking “low-flow filter” is developed and applied. The rationale for the filter is that both baseflow and event flow are represented in the discharge record at any time, but only the baseflow portion of streamflow serves to infer drainable storage. Hence, we assume that the storage-driven portion of discharge generally increases with increasing S, here represented by GRACE TWSA. To build the Qb–S relationship, the Qo–S paired series is sorted from the minimum to maximum value of S. Because Qo is assumed to increase with S, Qb for a given S is set to the forward-looking minimum Qo. Next, a Qb value is estimated for each S, based on minimum measured values of Qo:
where n is the number of forward-looking values remaining in the paired series. In other words, the filter looks at the next nQo values paired to the next n larger S values, selecting the minimum Qo as baseflow. The value of n can be subjective depending on the series size. Here, we used 20 % of the number of pairs (18 months), after analyzing the model's sensitivity to n (Fig. S1 in the Supplement). The process defines the low-flow envelope in the Qo–S series, where the variations in discharge above the minimum value are due to short duration rainfall–runoff events not captured in the monthly GRACE TWSAs. Here, we term the low-flow series as baseflow (Qb) but acknowledge our definition of baseflow may differ from other studies.
Building on previous studies (e.g., Kirchner, 2009; Reager et al., 2014), which suggest that summer river discharge and drainable storage generally show an exponential relationship, we assume a relationship for total discharge and estimated baseflow in the form of Eq. (2):
where Q is the non-winter discharge (Qo) or estimated baseflow (Qb), α and β are coefficients, and S is basin storage defined here as GRACE TWSA.
To transform TWSA into an absolute water storage value, referenced herein as drainable storage (Se) that directly influences discharge, a storage offset must best estimated. For example, Riegger and Tourian (2014) proposed a definition of time-dependent water absolute storage Se(t), using Eq. (3):
where TWSA(t) is the monthly storage anomaly, and So is an unknown constant storage offset. So only shifts the Se(t) series without impacting its temporal variability. Figure 2 shows how the TWSAs provide the same fit (e.g., R2) and exponential coefficient (β) accounting for the change in discharge with changing storage. Only the leading coefficient (α) changes in response to the value of the storage offset (So) being added to each TWSA. The intent of Fig. 2 is to demonstrate that TWSA and S can be used interchangeably by replacing α to account for the resulting desired storage units. The storage offset cannot be measured directly but should correspond to the long-term mean water storage for the region of interest. Based on the assumption that baseflow is driven by storage (Se) and therefore a linear function of storage, the relationship between discharge and TWSA can provide insights for estimating the representative So value, which provides an opportunity to estimate drainable storage.
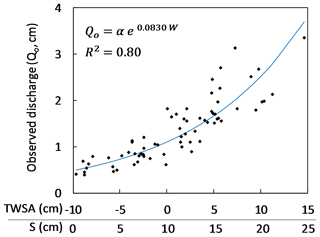
Figure 2Storage–discharge for the Mississippi River basin (site 12) based on Eq. (3) and an assumed So value of 10 cm, which is arbitrarily selected to illustrate the effects on Q–S relationships, where W represents storage in GRACE TWSA units (x axis, TWSA, in cm) or absolute units (x axis, S, in cm) and α is 1.101 if W is TWSA or 0.4934 if W is S.
3.1 Storage–discharge relationships
As discussed, we assume there is an exponential relationship between storage and discharge. However, because we only base our Q–S relationship on measurements, we use GRACE TWSA as a surrogate of storage. Figure 3 shows all non-winter (April–October) monthly observed discharges (Qo) and the relationships between discharge and storage for all 12 subbasins. In general, the figure shows that the Ohio and Upper Mississippi subbasins (1–6) exhibit similar behavior in terms of magnitude and variability of discharge, whereas the Missouri subbasins (7–11) have much less variability and smaller discharges for a given storage. Note that, the variability observed in the Missouri subbasins (7–11) series is due to high Q–S points resulting from flooding in April to July 2011 (Reager et al., 2014), where the four largest storages are from these months. Figure 3 also shows how the Qb–S relationships capture the minimum flow conditions for the observed storage–discharge series (i.e., minimum flow envelope). The variability above the Qb–S curve represents short-duration event discharges not captured by storage-driven discharge.

Figure 3Non-winter (April–October) monthly observed discharge (Qo, y axis, in cm) and storage (S, x axis, in cm represented by TWSAs); the lines represent the relationship between observed discharge (blue) or baseflow (red) and storage. The plot IDs correspond to the site IDs listed Table 1 and shown in Fig. 1. All relationships are significant at a 99 % confidence interval (p value < 0.00001), based on a t test.
The resulting α, β and R2 values for the Qo–S and Qb–S relationships are shown in Fig. 3 and listed in Table S1 in the Supplement. In general, the relationships fit the Qb–S pairs with a median R2 of 0.89 ranging from 0.46 to 0.92. For overall discharge, which includes event variability, the median R2 drops to 0.63 ranging from 0.40 to 0.80. The α values range from 0.15 to 1.5 (cm per month) for baseflow and 0.22 and 2.7 (cm per month) for streamflow and differ between the major tributaries. In general, α tends to decrease as minimum observed discharge decreases. For example, values along the Missouri River are noticeably lower than those along the upper Mississippi and Ohio rivers. As expected, both αb and αo are highly correlated with mean annual low-flow (R is 0.99 for baseflow and 0.96 for streamflow).
Comparing the two relationships, αb is equal to roughly 65 % of αo ranging from 52 % to 75 %. Note that, the ratio αb∕αo represents the mean baseflow fraction at each station when the TWSA is zero (i.e., Qb=αb and Qo=αo), which corresponds to the mean storage observed during the GRACE period. Although baseflow fractions are difficult to assess and vary based on estimation methods (Cheng et al., 2016; Eckhardt, 2008; Gonzales et al., 2009; Lott and Stewart, 2016; Zhang et al., 2017), the values reported here are consistent with those in the literature. Zhang and Schilling (2006) reported ratios ranging from 65 % to 75 % for sites along the Mississippi River. Arnold et al. (2000) reported a ratio of 65 % in the upper Mississippi River. Beighley et al. (2002) reported a median ratio of 55 % for the Susquehanna River, which boarders the Ohio on its eastern boundary.
The β values (i.e., exponential coefficient that scales discharge based on S) range from 0.02 to 0.1 for baseflow and 0.04 to 0.1 for streamflow and differ between the major tributaries. Based on a qualitative assessment, β appears to decrease as the amount of water regulation increases. For example, the Missouri River is known to be highly regulated and the associated β values are noticeably lower than those for the upper Mississippi and Ohio rivers. In a regulated system, basin storage can increase with little change in river discharge because water is being stored in lakes/reservoirs. In this case, the Missouri river has several very large reservoirs (e.g., Lake Oahe, Lake Sakakawea, Fort Peck Lake), which may explain the relative weaker relation between Q–S. This is one of this method's limitations, creating an uncertainty from the inability to include specific basin characteristics. For this reason, the relationships for heavily regulated rivers only reflect the reservoir storage availability observed during the study period. Of interest is the difference in βo and βb along the Missouri River, where βb is roughly 35 %–62 % of βo compared with the other rivers where βb is 84 %–110 % of βo. This difference, which is due to disproportionally lower βo values for the Missouri River, suggests that storage changes are mitigated more for baseflow than for event-flow conditions in regulated systems (Fig. 3). As expected, the β values are correlated with streamflow variability, defined here as the ratio of mean annual low-flow divided by mean annual flow for non-winter months (Qm-min∕Qm), where R is −0.89 and −0.94 for baseflow and streamflow, respectively. The correlation of α to low-flows and β to streamflow variability supports the physical meaning of Q–S relationships (Kirchner, 2009; Reager et al., 2014).
3.2 Absolute water storage
A unique aspect of the Q–TWSA relationship described in Eq. (2) is that it can be used to estimate the storage offset (So) in Eq. (3), which enables the conversion of TWSA to drainable storage. For example, solving Eq. (2) for TWSA when streamflow is approximately zero, yields the maximum negative TWSA for the associated Q–TWSA relationship. If we set the storage offset to the maximum negative TWSA in Eq. (3), we can convert TWSA to drainable storages, where the basin storage is zero for the near zero flow condition. This is the fundamental concept supporting the assumed Q–S relationships. The challenge is defining near zero streamflow because an exponential relationship cannot be solved for S if Q is zero. Here, we assume near zero streamflow is approximately 0.01 % to 0.1 % of the minimum monthly non-winter observed discharge (see Qmin in Table 1). Although this is not exact, it is bounded by observed streamflow and provides discharges that capture the extreme hydrologic conditions associated with zero drainable storage. For example, 0.1 % Qmin corresponds to mean monthly discharges ranging from only 0.1 to 4.5 m3 s−1 between sites. Using the above approach and the Qo–TWSA relationships in Fig. 3, Fig. 4 shows the non-winter (April–October) drainable storage for each subbasin during the study period, where the colored regions represent the range in storage measured by GRACE for the two estimates of storage offset (So for 0.1 % Qmin and 0.01 % Qmin).
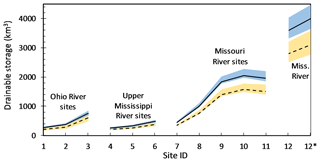
Figure 4Estimated drainable basin storages (S) for non-winter months (April–October) during the period 2002–2014 based on storage offsets derived using a zero-flow condition of 0.1 % and 0.01 % of Qmin; shaded regions show corresponding measured storage ranges from GRACE; subbasin outlet locations are shown in Fig. 1; site ID 12* corresponds to estimated storage based on area-weighted values from the Ohio, upper Mississippi and Missouri River basins.
As the Mississippi River station (site 12) resulting storage offset ranges from 96 to 123 cm (i.e. 109±14 cm) and the observed basin-wide TWSA ranges from −9.7 to 14.6 cm, we estimate the absolute drainable storage as 2900±400 to 3600±400 km3. Considering that the Mississippi River site drains all 11 subbasins with sites 3, 6 and 11 representing the upper Mississippi, Ohio and Missouri river outlets, respectively (2.3 million km2). There is roughly 600 000 km2 of drainage area above site 12 not captured by three outlet gauges. Using the average storage per square kilometer from the three subbasins, we estimate storage for the remaining area. Cumulating the subbasin and ungauged storages, we estimate that the Mississippi River basin storage offset varies from 3100 to 4000 km3 for non-winter months (site 12* in Fig. 4), i.e. approximately one-tenth of the maximum storage in the largest US reservoir: Lake Mead. Although there should be no difference in the storage offset from the two approaches, a difference of roughly 10 % is found, which may result from the storage per unit area from the subbasins overestimating the storage in the ungauged area. Although the range of mean storage is 800 to 900 km3, it represents less than 30 % of the lowest storage estimates. Thus, we provide one of the first drainable storage estimates for the Mississippi River basin and its major tributaries. These values cannot be validated as there are no current measurements of such an amount. Most large-scale models (e.g, PCR-GLOBWB, van Beek and Bierkens, 2009) are not fully coupled with groundwater models and contain structural errors in their ability to represent the GRACE-observed storage variability (Houborg et al., 2012; Scanlon et al., 2018). Thus, the comparison would not be direct. The storage offsets listed in Table S2 can be used to covert GRACE TWSA time series to absolute drainable storage time series and determine corresponding α values.
Given the importance of knowing how much water is available for societal demands and the complexity of measuring this quantity using traditional methods, the primary goals of this research are to estimate total drainable water storage and the fraction of baseflow in the Mississippi River basin using remotely sensed measurements.
In summary, our approach focuses on non-winter months (April–November) for the period from April 2002 through October 2014 for 12 watersheds distributed throughout the Mississippi River basin. A forward-looking, low-flow filter is used to approximate baseflow from measured discharges. Exponential relationships between discharge and NASA's GRACE total water storage anomalies are developed for all 12 sub-areas. The relationships show that the fraction of baseflow in the subbasins varies from 52 % to 75 % regionally. The provided approach can be used to provide estimates of drainable water storage for watersheds larger than roughly 200 000 km2 using only measurements derived the GRACE mission and monthly streamflow gauge observations.
As we base our analysis on observed quantities, a certain level of empiricism is required to validate the methodology. Still, we believe that this analysis is an initial step towards further understanding the relationship between storage and discharge. Future research is recommended to investigate the effects of temporal subsampling in developing Q–S relationships, explore additional methods for estimating baseflow values for each increasing storage change value, explore additional methods to estimate So with and/or without measured discharges, and integrate winter months into the analysis to characterize year-round storage–discharge relationships. Our long-term goal is to estimate discharge (e.g., baseflow) without gauge measurements, in order to characterize and model hydrologic and ecological cycles in regions with limited or no in situ measurements.
The GRACE mascon solution data (Wiese, 2015) can be accessed at https://doi.org/10.5067/TEMSC-OCL05, and the monitored discharge data (US Geological Survey, 2015) are provided by the National Water Information System and can be accessed at https://doi.org/10.17616/R3S333.
The supplement related to this article is available online at: https://doi.org/10.5194/hess-23-3269-2019-supplement.
All authors conceptualized the project. HEM and REB performed the analysis, investigation and validation. HEM prepared the paper with contributions from all co-authors.
The authors declare that they have no conflict of interest.
We would like to thank Nandita Basu for editing the paper and the reviewers for their constructive comments and suggestions, which led to substantial improvements in the paper. We would also like to thank NASA's SWOT science team and the GRACE science team as well as the Brazilian government (through a CAPES-Coordenação de Aperfeiçoamento de Pessoal de Nível Superior scholarship) for funding this project. A portion of this research was performed at the Jet Propulsion Laboratory, California Institute of Technology, under contract with NASA.
This research has been supported by NASA (grant nos. NNX16AQ39G, NNN13D505T and NNX14AJ95G), and a Coordenação de Aperfeiçoamento de Pessoal de Nível Superior scholarship (grant no. 88888.076230/2013-00).
This paper was edited by Nandita Basu and reviewed by two anonymous referees.
Alsdorf, D., Han, S. C., Bates, P., and Melack, J.: Seasonal water storage on the Amazon floodplain measured from satellites, Remote Sens. Environ., 114, 2448–2456, https://doi.org/10.1016/j.rse.2010.05.020, 2010.
Appleby, F. V.: Recession and the Baseflow Problem, Water Resour. Res., 6, 1398–1403, https://doi.org/10.1029/WR006i005p01398, 1970.
Arnold, J. G., Muttiah, R. S., Srinivasan, R., and Allen, P. M.: Regional estimation of base flow and groundwater recharge in the Upper Mississippi river basin, J. Hydrol., 227, 21–40, https://doi.org/10.1016/S0022-1694(99)00139-0, 2000.
Beighley, R. E., Johnson, D. L., and Miller, A. C.: Subsurface response model for storm events within Susquehanna River Basin, J. Hydrol. Eng., 7, 185–191, https://doi.org/10.1061/(Asce)1084-0699(2002)7:2(185), 2002.
Beighley, R. E., Ray, R. L., He, Y., Lee, H., Schaller, L., Andreadis, K. M., Durand, M., Alsdorf, D. E., and Shum, C. K.: Comparing satellite derived precipitation datasets using the Hillslope River Routing (HRR) model in the Congo River Basin, Hydrol. Process., 25, 3216–3229, https://doi.org/10.1002/hyp.8045, 2011.
Beven, K. J.: Rainfall-Runoff Modelling: The Primer, John Wiley and Sons, 2001.
Beven, K.: Searching for the Holy Grail of scientific hydrology: Qt=(S, R, Δt)A as closure, Hydrol. Earth Syst. Sci., 10, 609–618, https://doi.org/10.5194/hess-10-609-2006, 2006.
Biswal, B. and Marani, M.: Geomorphological origin of recession curves, Geophys. Res. Lett., 37, L24403, https://doi.org/10.1029/2010GL045415, 2010.
Biswal, B. and Nagesh Kumar, D.: Estimation of `drainable' storage – A geomorphological approach, Adv. Water Resour., 77, 37–43, https://doi.org/10.1016/j.advwatres.2014.12.009, 2015.
Black, P. E.: Watershed Functions, J. Am. Water Resour. Assoc., 33, 1–11, https://doi.org/10.1111/j.1752-1688.1997.tb04077.x, 1997.
Brookfield, A. E., Hill, M. C., Rodell, M., Loomis, B. D., Stotler, R. L., Porter, M. E., and Bohling, G. C.: In Situ and GRACE-Based Groundwater Observations: Similarities, Discrepancies, and Evaluation in the High Plains Aquifer in Kansas, Water Resour. Res., 54, 8034–8044, https://doi.org/10.1029/2018wr023836, 2018.
Brutsaert, W.: Hydrology: an introduction, Cambridge University Press, Cambridge, 2005.
Brutsaert, W.: Long-term groundwater storage trends estimated from streamflow records: Climatic perspective, Water Resour. Res., 44, W02409, https://doi.org/10.1029/2007WR006518, 2008.
Brutsaert, W. and Nieber, J. L.: Regionalized drought flow hydrographs from a mature glaciated plateau, Water Resour. Res., 13, 637–643, https://doi.org/10.1029/WR013i003p00637, 1977.
Cheng, L., Zhang, L., and Brutsaert, W.: Automated Selection of Pure Base Flows from Regular Daily Streamflow Data: Objective Algorithm, J. Hydrol. Eng., 21, 06016008, https://doi.org/10.1061/(ASCE)HE.1943-5584.0001427, 2016.
Clark, M. P., Rupp, D. E., Woods, R. A., Tromp-van Meerveld, H. J., Peters, N. E., and Freer, J. E.: Consistency between hydrological models and field observations: linking processes at the hillslope scale to hydrological responses at the watershed scale, Hydrol. Process., 23, 311–319, https://doi.org/10.1002/hyp.7154, 2009.
Eckhardt, K.: A comparison of baseflow indices, which were calculated with seven different baseflow separation methods, J. Hydrol., 352, 168–173, https://doi.org/10.1016/j.jhydrol.2008.01.005, 2008.
Gonzales, A. L., Nonner, J., Heijkers, J., and Uhlenbrook, S.: Comparison of different base flow separation methods in a lowland catchment, Hydrol. Earth Syst. Sci., 13, 2055–2068, https://doi.org/10.5194/hess-13-2055-2009, 2009.
Hall, F. R.: Base-flow recessions – a review, Water Resour. Res., 4, 973–983, https://doi.org/10.1029/WR004i005p00973, 1968.
Horton, R.: Surface runoff phenomena. Part 1 – Analysis of the hydrograph, Publication 101, Horton Hydrological Laboratory,Voorheesville, NY, 1935.
Houborg, R., Rodell, M., Li, B., Reichle, R., and Zaitchik, B. F.: Drought indicators based on model-assimilated Gravity Recovery and Climate Experiment (GRACE) terrestrial water storage observations, Water Resour. Res., 48, W07525, https://doi.org/10.1029/2011wr011291, 2012.
Kim, H., Yeh, P. J. F., Oki, T., and Kanae, S.: Role of rivers in the seasonal variations of terrestrial water storage over global basins, Geophys. Res. Lett., 36, L17402, https://doi.org/10.1029/2009GL039006, 2009.
Kirchner, J. W.: Catchments as simple dynamical systems: Catchment characterization, rainfall-runoff modeling, and doing hydrology backward, Water Resour. Res., 45, W02429, https://doi.org/10.1029/2008WR006912, 2009.
Krakauer, N. Y. and Temimi, M.: Stream recession curves and storage variability in small watersheds, Hydrol. Earth Syst. Sci., 15, 2377–2389, https://doi.org/10.5194/hess-15-2377-2011, 2011.
Lott, D. A. and Stewart, M. T.: Base flow separation: A comparison of analytical and mass balance methods, J. Hydrol., 535, 525–533, https://doi.org/10.1016/j.jhydrol.2016.01.063, 2016.
Nie, N., Zhang, W., Chen, H., and Guo, H.: A Global Hydrological Drought Index Dataset Based on Gravity Recovery and Climate Experiment (GRACE) Data, Water Resour. Manage., 32, 1275–1290, https://doi.org/10.1007/s11269-017-1869-1, 2018.
Reager, J., Thomas, B., and Famiglietti, J.: River basin flood potential inferred using GRACE gravity observations at several months lead time, Nat. Geosci., 7, 588–592, https://doi.org/10.1038/Ngeo2203, 2014.
Riegger, J.: Quantification of Drainable Water Storage Volumes in Catchments and in River Networks on Global Scales using the GRACE and/or River Runoff, Hydrol. Earth Syst. Sci. Discuss., https://doi.org/10.5194/hess-2018-38, in review, 2018.
Riegger, J. and Tourian, M. J.: Characterization of runoff–storage relationships by satellite gravimetry and remote sensing, Water Resour. Res., 50, 3444–3466, https://doi.org/10.1002/2013WR013847, 2014.
Rodell, M. and Famiglietti, J.: Detectability of variations in continental water storage from satellite observations of the time dependent gravity field, Water Resour. Res., 35, 2705–2723, https://doi.org/10.1029/1999wr900141, 1999.
Rodell, M., Chao, B. F., Au, A. Y., Kimball, J. S., and McDonald, K. C.: Global Biomass Variation and Its Geodynamic Effects: 1982–98, Earth Interact., 9, 1–19, https://doi.org/10.1175/ei126.1, 2005.
Rodell, M., Chen, J., Kato, H., Famiglietti, J. S., Nigro, J., and Wilson, C. R.: Estimating groundwater storage changes in the Mississippi River basin (USA) using GRACE, Hydrogeol. J., 15, 159–166, https://doi.org/10.1007/s10040-006-0103-7, 2007.
Rupp, D. E. and Selker, J. S.: Drainage of a horizontal Boussinesq aquifer with a power law hydraulic conductivity profile, Water Resour. Res., 41, W11422, https://doi.org/10.1029/2005WR004241, 2005.
Rupp, D. E. and Woods, R. A.: Increased flexibility in base flow modelling using a power law transmissivity profile, Hydrol. Process., 22, 2667–2671, https://doi.org/10.1002/hyp.6863, 2008.
Sayama, T., McDonnell, J. J., Dhakal, A., and Sullivan, K.: How much water can a watershed store?, Hydrol. Process., 25, 3899–3908, https://doi.org/10.1002/hyp.8288, 2011.
Scanlon, B. R., Faunt, C. C., Longuevergne, L., Reedy, R. C., Alley, W. M., McGuire, V. L., and McMahon, P. B.: Groundwater depletion and sustainability of irrigation in the US High Plains and Central Valley, P. Natl. Acad. Sci. USA, 109, 9320–9325, https://doi.org/10.1073/pnas.1200311109, 2012.
Scanlon, B. R., Zhang, Z., Save, H., Sun, A. Y., Müller Schmied, H., van Beek, L. P. H., Wiese, D. N., Wada, Y., Long, D., Reedy, R. C., Longuevergne, L., Döll, P., and Bierkens, M. F. P.: Global models underestimate large decadal declining and rising water storage trends relative to GRACE satellite data, P. Natl. Acad. Sci. USA, 115, E1080–E1089, https://doi.org/10.1073/pnas.1704665115, 2018.
Shaw, S. B. and Riha, S. J.: Examining individual recession events instead of a data cloud: Using a modified interpretation of dQ∕dt−Q streamflow recession in glaciated watersheds to better inform models of low flow, J. Hydrol., 434–435, 46–54, https://doi.org/10.1016/j.jhydrol.2012.02.034, 2012.
Sproles, E. A., Leibowitz, S. G., Reager, J. T., Wigington, P. J., Famiglietti, J. S., and Patil, S. D.: GRACE storage-runoff hystereses reveal the dynamics of regional watersheds, Hydrol. Earth Syst. Sci., 19, 3253–3272, https://doi.org/10.5194/hess-19-3253-2015, 2015.
Swenson, S. and Wahr, J.: Monitoring the water balance of Lake Victoria, East Africa, from space, J. Hydrol., 370, 163–176, https://doi.org/10.1016/j.jhydrol.2009.03.008, 2009.
Tague, C. and Grant, G. E.: A geological framework for interpreting the low-flow regimes of Cascade streams, Willamette River Basin, Oregon, Water Resour. Res., 40, W04303, https://doi.org/10.1029/2003WR002629, 2004.
Tallaksen, L. M.: A review of baseflow recession analysis, J. Hydrol., 165, 349–370, https://doi.org/10.1016/0022-1694(94)02540-R, 1995.
Tapley, B. D., Bettadpur, S., Watkins, M., and Reigber, C.: The gravity recovery and climate experiment: Mission overview and early results, Geophys. Res. Lett., 31, L09607, https://doi.org/10.1029/2004GL019920, 2004.
Thomas, B. F., Vogel, R. M., and Famiglietti, J. S.: Objective hydrograph baseflow recession analysis, J. Hydrol., 525, 102–112, https://doi.org/10.1016/j.jhydrol.2015.03.028, 2015.
Tourian, M. J., Reager, J. T., and Sneeuw, N.: The Total Drainable Water Storage of the Amazon River Basin: A First Estimate Using GRACE, Water Resour. Res., 54, 3290–3312, https://doi.org/10.1029/2017WR021674, 2018.
US Geological Survey. National Water Information System data available on the World Wide Web (USGS Water Data for the Nation), available at: http://waterdata.usgs.gov/nwis/ (last access: 16 June 2015), https://doi.org/10.17616/R3S333, 2015.
van Beek, L. and Bierkens, M. F.: The global hydrological model PCR-GLOBWB: conceptualization, parameterization and verification, Department of Physical Geography, Utrecht University, Utrecht, the Netherlands, 2009.
Wagener, T., Sivapalan, M., Troch, P., and Woods, R.: Catchment Classification and Hydrologic Similarity, Geogr. Compass, 1, 901–931, https://doi.org/10.1111/j.1749-8198.2007.00039.x, 2007.
Watkins, M. M., Wiese, D. N., Yuan, D. N., Boening, C., and Landerer, F. W.: Improved methods for observing Earth's time variable mass distribution with GRACE using spherical cap mascons, J. Geophys. Res.-Solid, 120, 2648–2671, https://doi.org/10.1002/2014jb011547, 2015.
Wiese, D.: GRACE monthly global water mass grids NETCDF RELEASE 5.0, Ver. 5.0, available at: ftp://podaac-ftp.jpl.nasa.gov/allData/tellus/L3/mascon/RL05/JPL/non-CRI/netcdf (last acess: 16 June 2015), https://doi.org/10.5067/TEMSC-OCL05, 2015.
Wittenberg, H.: Baseflow recession and recharge as nonlinear storage processes, Hydrol. Process., 13, 715–726, https://doi.org/10.1002/(SICI)1099-1085(19990415)13:5<715::AID-HYP775>3.0.CO;2-N, 1999.
Wittenberg, H. and Sivapalan, M.: Watershed groundwater balance estimation using streamflow recession analysis and baseflow separation, J. Hydrol., 219, 20–33, https://doi.org/10.1016/S0022-1694(99)00040-2, 1999.
Zhang, J., Zhang, Y., Song, J., and Cheng, L.: Evaluating relative merits of four baseflow separation methods in Eastern Australia, J. Hydrol., 549, 252–263, https://doi.org/10.1016/j.jhydrol.2017.04.004, 2017.
Zhang, Y. K. and Schilling, K. E.: Increasing streamflow and baseflow in Mississippi River since the 1940s: Effect of land use change, J. Hydrol., 324, 412–422, https://doi.org/10.1016/j.jhydrol.2005.09.033, 2006.






