the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Flooding in the Mekong Delta: the impact of dyke systems on downstream hydrodynamics
Vo Quoc Thanh
Dano Roelvink
Mick van der Wegen
Johan Reyns
Herman Kernkamp
Giap Van Vinh
Vo Thi Phuong Linh
Building high dykes is a common measure of coping with floods and plays an important role in agricultural management in the Vietnamese Mekong Delta. However, the construction of high dykes causes considerable changes in hydrodynamics of the Mekong River. This paper aims to assess the impact of the high-dyke system on water level fluctuations and tidal propagation in the Mekong River branches. We developed a coupled 1-D to 2-D unstructured grid using Delft3D Flexible Mesh software. The model domain covered the Mekong Delta extending to the East (South China Sea) and West (Gulf of Thailand) seas, while the scenarios included the presence of high dykes in the Long Xuyen Quadrangle (LXQ), the Plain of Reeds (PoR) and the Trans-Bassac regions. The model was calibrated for the year 2000 high-flow season. Results show that the inclusion of high dykes changes the percentages of seaward outflow through the different Mekong branches and slightly redistributes flow over the low-flow and high-flow seasons. The LXQ and PoR high dykes result in an increase in the daily mean water levels and a decrease in the tidal amplitudes in their adjacent river branches. Moreover, the different high-dyke systems not only have an influence on the hydrodynamics in their own branch, but also influence other branches due to the Vam Nao connecting channel. These conclusions also hold for the extreme flood scenarios of 1981 and 1991 that had larger peak flows but smaller flood volumes. Peak flood water levels in the Mekong Delta in 1981 and 1991 are comparable to the 2000 flood as peak floods decrease and elongate due to upstream flooding in Cambodia. Future studies will focus on sediment pathways and distribution as well as climate change impact assessment.
Rivers are the major source of fresh water for human use (Syvitski and Kettner, 2011). In addition, the fresh water supply is an important resource for ecosystems. When river discharge exceeds the bankfull discharge, the floodplains inundate. Fluvial floods cause both advantages and disadvantages for local residents. Floods are the main source of fresh water supply and deliver sediments that act as a natural and valuable fertiliser source for agricultural crops (Chapman and Darby, 2016). This is an important process in the Mekong Delta as the majority of local citizens are farmers. In contrast, extreme floods may damage both crops and infrastructure.
In order to maintain agricultural cultivation during the high-flow seasons, dyke rings have been built to protect agricultural crops in the Vietnamese Mekong Delta (VMD). As a result, the river system in the VMD has significantly changed, especially following the severe floods in 2000 (Biggs et al., 2009; Renaud and Kuenzer, 2012). A dense canal system has been created in flood-prone areas to efficiently drain flood waters from the Long Xuyen Quadrangle and the Plain of Reeds to the West Sea (Gulf of Thailand) and to the Vamco River respectively (Fig. 1).
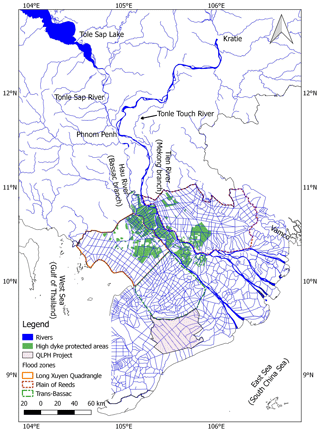
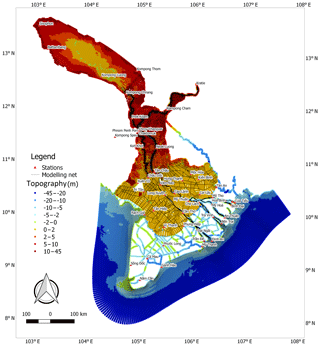
Figure 1Location of the Mekong Delta. Adapted from the Department of Agriculture and Rural Development of An Giang and Dong Thap (2012).
Recently, large hydraulic structures have been built not only in the flood-prone areas but also in coastal areas to protect cropping systems from saline intrusion. Therefore, hydrodynamic processes have changed considerably. Understanding the prevailing hydrodynamics is essential for sustainable water management in these regions.
The high-dyke system is intended to reduce local natural flood hazards but may alter the hazard downstream (Triet et al., 2017). Furthermore, this system also increases the potential risk due to dyke breaks. Following different approaches, Tran et al. (2018) found that the high-dyke system upstream of the VMD causes an increase in the peak water levels in downstream areas. However, water levels at these downstream stations are dominated by tidal motion. In fact, tides may result in an increase in water levels in the central VMD. Thus, an analysis of tidal fluctuation is needed to investigate water level changes on the Mekong River. The high-dyke system may be an important factor, but sea level rise in combination with land subsidence enhances peak water levels at the central stations to a larger extent (Triet et al., 2017). The high-dyke system influences not only the downstream hydrodynamics by reducing inundated floodplain areas, but also impacts fluvial sediment deposition on floodplains.
There are a number of large-scale numerical models used to simulate the annual floods and suspended sediment transport and to evaluate the impacts of dyke construction in the Mekong Delta (Manh et al., 2014; Tran et al., 2018; Triet et al., 2017; Van et al., 2012; Wassmann et al., 2004). For instance, Tran et al. (2018) investigated the impacts of the upstream high-dyke system on the downstream part of the VMD. Using a MIKE hydrodynamic model for the Mekong Delta, they found that the high-dyke system in the Long Xuyen Quadrangle (LXQ) can reduce the discharge of the Tien River, diverting around 7 % of the total volume to the Hau River. In addition, the yearly discharge variations have slight effects on the peak water levels at the Can Tho station, while Triet et al. (2017) found that the high-dyke system caused an increase from 9 to 13 cm in the flood peaks at the central VMD stations. Moreover, Triet et al. (2017) showed that the development of the dyke system upstream of the VMD reduced flood retention in this area, leading to an increase of 13.5 and 8.1 cm in the peak water levels in the downstream part of the VMD at Can Tho and My Thuan respectively.
The above-mentioned studies evaluated the impact of high dykes in the LXQ and the high dykes developed up until 2011. However, the impacts of the other floodplain regions need to be considered, including the LXQ, the Plain of Reeds (PoR) and Trans-Bassac. Additionally, Manh et al. (2014), Tran et al. (2018) and Triet et al. (2017) used a common 1-D version of the MIKE11 model for the Mekong Delta, and the downstream boundaries are defined at the Mekong's river mouths. However, Kuang et al. (2017) found that river flows can contribute to a rise in the water level at the river mouths. Thus, in the present study another modelling approach is used in order to address these issues.
This study aims to assess the impacts of the high-dyke system on water level fluctuation and tidal propagation in the Mekong River branches. An unstructured, combined 1-D to 2-D grid is used to simulate the flood dynamics in 2000. The model domain covers the Mekong Delta and extends from Kratie in Cambodia to the East (South China Sea) and West (Gulf of Thailand) seas. Simulated scenarios present the impact of high dykes in different floodplain regions and the entire VMD. The specific objectives are
-
to develop a calibrated and validated hydrodynamic model using Delft3D Flexible Mesh that is able to simulate the annual floods in the Mekong Delta;
-
to analyse the spatial–temporal distribution of the Mekong River's flows for different extreme river flow scenarios; and
-
to evaluate how the development of high dykes, which are built to protect floodplains, influences the downstream hydrodynamics, particularly with respect to tidal propagation.
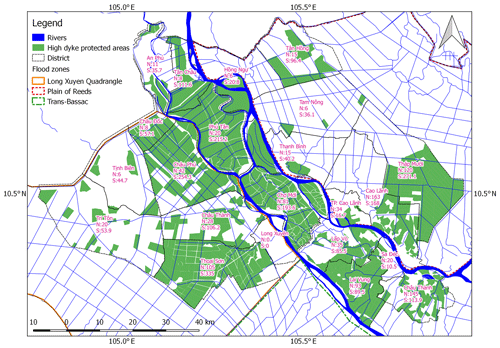
Figure 2Spatial distribution of high dykes that were built up until 2011. The high dykes are presented by district. The number of high dykes (N) is shown as well as the area that they protect (S) in square kilometres (km2). Adapted from the Department of Agriculture and Rural Development of An Giang and Dong Thap (2012).
1.1 The Mekong Delta
The Mekong is one the largest rivers in the world (MRC, 2010). It starts in Tibet (China) and flows through five riparian countries before reaching the ocean via (originally nine branches but now) seven estuaries. It has a length of 4800 km and a total catchment area of 795 000 km2 (MRC, 2005). The Mekong Delta starts in Phnom Penh (Fig. 1), where the Mekong River is separated into two branches, namely the Mekong and the Bassac (Gupta and Liew, 2007; Renaud et al., 2013). The Mekong Delta is formed by sediment deposition from the Mekong River, which provides an annual water volume of 416 km3 as well as 73 Mt yr−1 of sediment at Kratie, which is mainly distributed in the high-flow season (Koehnken, 2014; MRC, 2005). The Mekong Delta has a complex river network, especially in the Vietnamese region. The Mekong Delta's river network is illustrated in Fig. 2. It has resulted from extensive artificial canal development that began in 1819 (Hung, 2011).
Regarding land resources, the VMD area comprises about 4×106 ha, and three-quarters of this region is used for agricultural production (Kakonen, 2008). The livelihoods of the local citizens are primarily based on agriculture and aquaculture. Thus, the river infrastructure has been developing with agriculture as a priority. The area provides just over half of the rice yields in Vietnam and provides up to approximately 90 % of the exported rice yields from Vietnam (GSOVN, 2010). However, the rice cultivation is highly influenced by annual floods (MRC, 2009a).
The most intensive agricultural production in the VMD is found in An Giang Province (Fig. 2). Although it is also a flood-prone area, the inundation periods are slightly shorter due to flood withdraw to the West Sea. In the deep flooded zones (the Long Xuyen Quadrangle and the Plain of Reeds), high dykes have been densely constructed in the downstream direction. This is due to the fact that the areas downstream of the LXQ and PoR experience low flood peaks, meaning that the dyke rings do not need to be as high as they do in the regions upstream of the LXQ and PoR.
The Mekong Delta is dominated by a tropical monsoonal climate. There are two dominant monsoons. The southwest monsoon occurs from May to October, coinciding with the high-flow season. The other, drier monsoon period is from November to March and is followed by a transition period (MRC, 2010). The mean temperature is approximately 26.5 ∘C. Although the climate is seasonally changing, monthly average temperature differences are 4 ∘C between the hottest and coldest months (Le Sam, 1996). However, seasonal rainfall is drastically different in terms of time and space. The high-flow season contributes approximately 90 % of the total annual rainfall intensity, whereas the low-flow season (from December to April) accounts for 10 % of the total rainfall. The yearly mean rainfall is about 1600 mm in the VMD. The highest rainfall is found in the western coastal area of the Mekong Delta and ranges between 2000 and 2400 mm. The eastern coast receives about 1600 mm of rainfall, whereas the lowest rainfall is recorded in the centre of the VMD (Le Sam, 1996; Thanh et al., 2014).
1.2 High-dyke development in the Vietnamese Mekong Delta
The Mekong Delta has been modified extensively over the last 2 decades following the devastating flood in 2000. One noticeable change is the hydraulic infrastructure, especially the dyke development. Before the dykes were built, a dense canal network was developed to drain floods to the West Sea and to clean acid sulfate soils.
Depending on the dyke function, dykes can be classified into two categories. Low dykes are built to protect the rice harvest from summer–autumn crops in August. This is the rising phase of the annual floods. The low dykes allow flood overflows and the inundation of floodplains, so the crests of low dykes are designed to just equal the maximum water level in August. High dykes are constructed in order to completely prevent the annual floods and enable intensive agricultural production. Generally high dykes are designed at a crest level of 0.5 m above the year 2000 flood peak. The 2000 flood was a severe event that has a 50-year recurrence interval in terms of flood volume (MRC, 2005). In An Giang, there are two types of high dykes. The first type of high dyke only has a single dyke ring. The hydrodynamics just outside of the dyke ring are dominated by floods. These dykes have a straightforward floodplain protection function but a high risk of breaching. The other type of high dyke contains the above-mentioned single dyke ring which is then protected by a large outer dyke. The hydrodynamics outside of these high dykes are controlled by structures (sluice gates) in the outer dyke.
Several studies have mapped the high dykes in the VMD using remotely sensed images (e.g. Duong et al., 2016; Fujihara et al., 2016; Kuenzer et al., 2013). Using this method, the high dykes are identified via flooded and non-flooded areas. However, these results are easily affected by the water management of the high-dyke rings. For example, in An Giang, the high-dyke areas are managed according to the cropping cycle rule. In other words, these areas are cultivated for eight () agricultural crops over 3 years and are allowed to inundate during part of the year once every 3 years. Thus, the results need to be verified with observations to ensure the reliability of the maps.
High dykes were rarely constructed in the VMD before 2000 (Duong et al., 2016). However, as previously stated, the year 2000 historical flood caused enormous damage to infrastructure and residents' properties. After the flood event, the local authorities planned and built a cascade of high dykes in order to protect residents as well as crops, which are the major livelihood in this region. In addition, the VMD has great potential with respect to the intensification of agricultural production. In 2009, the area protected by high dykes was about 1222 km2, covering around 35 % of An Giang Province; in 2011, this percentage had increased to over 40 % (about 1431 km2). Dong Thap has a much lower coverage of about 30 %, corresponding to an area of 990 km2; however, Dong Thap has deep, inundated areas and its soil contains a high concentration of sulfates, resulting in a low potential for agriculture (Kakonen, 2008).
Figure 2 presents the numbers of high dykes and the areas protected by these structures by district in An Giang and Dong Thap provinces until 2011. In 2011, the number of high dykes in An Giang and Dong Thap were 329 and 657 respectively. The total area protected by high dykes in An Giang was larger than in Dong Thap (about 14 compared with 10 km2 respectively). As a result, the mean area of a high dyke in An Giang is larger than in Dong Thap. In fact, high dykes are located mainly along the banks of the Tien River and Hau River (Fig. 2), where the soils are alluvial (Nguyen et al., 2015).
1.3 Flood dynamics in the Mekong Delta
The Mekong Delta is spatially separated into inner and outer sections. The former is dominated by fluvial processes, whereas the latter is dominated by marine processes, including tides and waves (Ta et al., 2002). The Mekong River supplies approximately 416 km3 of water annually, or 13 200 m3 s−1 through Kratie on average (MRC, 2005). Figure 3 shows that water discharge varies from 1700 to 40 000 m3 s−1 between the low-flow and high-flow seasons (Frappart et al., 2006; Le et al., 2007; MRC, 2009b; Wolanski et al., 1996). During the high-flow season, high water discharge causes inundation in the delta floodplains in Cambodia and Vietnam. The annual floods in the Mekong Delta can be indicated by their peaks and volumes. The analysis of flood peaks and volumes at Kratie from 1961 to 2017 shows that the floods in 1991 and 2000 were extreme (Fig. 4).
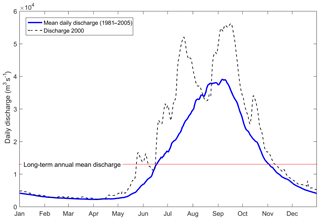
Figure 3Temporal distribution of daily water discharge at Kratie (available data from Darby et al., 2016).
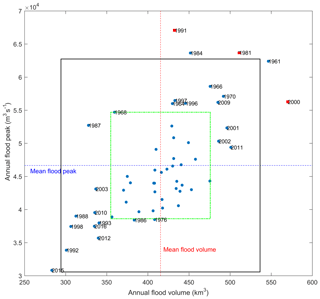
Figure 4The annual flood peaks and volumes at Kratie from 1961 to 2017. The green and black boxes indicate significant (mean ± SD) and extreme (mean ± 2 SD) drought or flood years respectively. (SD refers to standard deviation.)
From Kratie to Phnom Penh, the hydrodynamics of the Mekong River are dominated by fluvial flows. The river banks are lower than the water levels in the high-flow seasons, which leads to water overflow into the floodplains. The floodplains on the west side convey water to the Tonle Sap River, while the flood water flows into the Tonle Touch River on the east side (Fig. 1). The floodplains on the west receive less water than those on the east, with water volumes of 24.7 and 35.4 km3 respectively. The peak discharges of the Mekong River to the respective left and right floodplains are approximately 5400 and 7800 m3 s−1 (Fujii et al., 2003). These floodplains in combination with the Tonle Sap River encompass about half of the Mekong's peak discharge.
At Phnom Penh, the Mekong is divided into two branches (the Mekong and the Bassac). In addition the Mekong River joins with the Tonle Sap River. The Tonle Sap Lake is the largest freshwater body in Southeast Asia and has a crucially important role in controlling the water levels in the Mekong Delta. Its surface area covers an area of approximately 3500 km2 during the low-flow season and is about 4 times larger during the high-flow season (MRC, 2005). The water volume of the lake can reach 70 km3 in the high-flow season (MRC, 2005). The Tonle Sap Lake functions as a natural flood retention basin for the Mekong River, leading to a reduction in the annual variations of water discharge flowing into the delta. The flood flows to the lake and reverses back to the Mekong River at the Phnom Penh confluence during low flows. Figure 5 shows the long-term daily average water discharge flowing in and out of Tonle Sap Lake at the Prek Kdam station. When water levels at Kampong Luong increase, reaching a peak of over 9 m, the lake supplies water to the delta, increasing the Mekong River flows after the flood season and helping to reduce saline intrusion in coastal areas during the low-flow season. From May to September, Mekong water feeds into the Tonle Sap Lake. From October until the following April it then drains back into the Mekong.
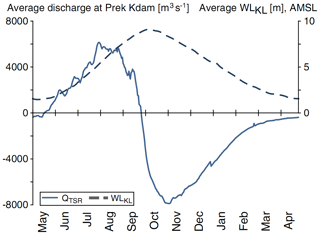
Figure 5Daily averaged (from 1997 to 2004) water discharge hydrograph at Prek Kdam and water level variation at Kampong Luong (Kummu et al., 2014). The solid line presents the river flow entering Tonle Sap Lake at the Prek Kdam station, and the dashed line shows water levels at the Kampong Luong station.
From Phnom Penh to the Cambodian–Vietnamese (CV) border, the Mekong River flows mainly through the Mekong branch, reaching up to 26 800 m3 s−1 during flood peaks (Fujii et al., 2003). During these peaks, the floods discharge onto the VMD through the Mekong and Bassac branches as well as via the floodplain overflow comprising 73 %, 7 % and 20 % of the total discharge respectively (Fig. 1).
In the VMD, the Mekong River flow partly diverts from the Tien River (Mekong branch) to the Hau River (Bassac branch). Regarding flood distribution, water discharge at Tan Chau (Tien River) and Chau Doc (Hau River) is estimated to be 80 % and 20 % of the total flood flow respectively. However, the Vam Nao connecting channel leads to a relative balance between the Tien River (at My Thuan) and the Hau River (at Can Tho) downstream (Fig. 6). At these stations water levels are strongly dominated by the tides of the East Sea. The water levels in the coastal VMD region fluctuate due to tides from both the East Sea and the West Sea, but the tidal range of the East Sea is much higher than that of the West Sea. Therefore, the East Sea's tides play a more important role and become the main dominant factor controlling hydrodynamics in VMD coastal areas.
This section introduces the methodology of our study. Section 2.1 describes the model set-up. Section 2.2 provides the model calibration and validation. Section 2.3 and 2.4 elaborate on the high-dyke development scenarios and on further analysis of these scenarios respectively.
2.1 Model description and set-up
2.1.1 Software description
The hydrodynamic model applied in this study is the Delft3D Flexible Mesh (DFM) Model Suite which has been developed by Deltares (deltares.nl). DFM is a multidimensional model which includes one, two and three dimensions in the same set-up. It solves the 2-D and 3-D shallow water equations (Kernkamp et al., 2011). These equations describe mass and momentum conservation (Deltares, 2018).
where , ζ is the water level, h is the water depth, u is the velocity vector, g is the gravitational acceleration, ν is the viscosity, ρ is the water mass density and τ is the bottom friction.
DFM allows computation on unstructured grids, so it is suitable for regions with complex geometry (Achete et al., 2015), including combinations of 1-D, 2-D and 3-D grids. This feature is efficient for taking small canals into account. Therefore, in this study, DFM is selected for simulating flood dynamics in the Mekong Delta which comprises a dense river network and highly variable river widths, dykes and flood plains.
2.1.2 Model set-up
The model in this study was improved from the model used by Thanh et al. (2017). In the present configuration, the model uses a depth-averaged setting.
Grid generation and improvement
The unstructured model was constructed using a multi-scale modelling approach; specifically, it consists of a combination of 1-D (canals) and 2-D (the main branches of the Mekong River, its floodplains and shelf) parts. The approach shows efficiency in the case of complex geometry such as the entire Mekong Delta. To capture the hydrodynamics of the main branches and estuaries of the delta, the main channels are represented in enough horizontal detail to resolve the flow patterns over channels and shoals and at the main bifurcations and confluences. Regarding the shelf, the model extended to approximately 80 km from the coastline of the delta to fully contain the river plume (Fig. 6).
The grid includes the river system of the Mekong River from Kratie to the East Sea and its shelf. The mainstream of the Mekong River, the subaqueous delta and floodplains are represented by 2-D cells, whereas the primary and secondary canals are modelled as 1-D networks. The 2-D cells are a combination of curvilinear (in the main channels) and triangular grid cells. The grid creation was introduced and recommended by Bomers et al. (2019) and Kernkamp et al. (2011). The grid/element sizes vary from about 0.1 km in rivers to 3 km on the delta shelf. The lengths of the grid vary depending on the river geometry. The lengths of cells are generally around 700 m on the Mekong River mainstreams and decrease to approximately 200 m at river bifurcations and confluences. The larger cells of the Tonle Sap Lake, the floodplains and the sea are up to 2000 m. The uniform length of 1-D segments is 400 m. The grid quality is critical for accurate simulations; therefore, the grid has been made orthogonal, smooth and sufficiently dense, to orthogonal values of less than 10 %.
From the survey data, it can occur that a dyke ring in the model can consist of both high dykes and low dykes. This situation may transpire because the model only includes the main rivers and the secondary canal network, and tertiary and small canals are not included. In order to determine whether the dykes are fully protected or partly protected, the ratio of high-dyke area to low-dyke/non-dyke area is calculated. If the ratio is higher than or equal to 1, the dyke is recognised as a high dyke. If the ratio is lower than 1, it is determined not to be a high dyke. In the modelling approach, a high dyke does not allow water flow from linked canals to its protected floodplains, and we did not consider flows over the crest of dykes.
The VMD witnessed three large floods from 2000 to 2002 based on the flood classification of the Tan Chau's flood peaks. Thus, the 2000 and 2001 floods were chosen to calibrate and validate the model respectively. Another reason for selecting the 2000 flood is that the datasets for this flood are comprehensive.
Bathymetry data
When modelling the flood dynamics in the Mekong Delta, bathymetry is a key element. However, available data from the Mekong Delta are limited. For river bathymetry, cross-sectional data were used that were collected by the Mekong River Commission and used to develop the 1-D hydrodynamic model (ISIS) to simulate fluvial flood propagation (Van et al., 2012). To use these profile data for 2-D modelling, the cross-sectional data were interpolated to river bathymetry for the main branches, whereas the primary and secondary canals directly used the cross-sectional data from the 1-D ISIS model. The bathymetry of the sea area is extracted from ETOPO1 (Amante and Eakins, 2009). The floodplains' topography is obtained from the freely available SRTM90m (Reuter et al., 2007) digital elevation model. Although SRTM is not a high-quality digital elevation model, it was reasonably used for flood modelling in the Mekong Delta (e.g. Dung et al., 2011; Tran et al., 2018).
Boundary conditions
Open boundaries are defined as water discharge (at Kratie) and water levels (the sea). The measured water discharges were used for the upstream boundary at Kratie and were collected from the Mekong River Commission. The latter were defined as astronomical tidal constituents and extracted from a global tidal model (TPXO; Egbert and Erofeeva, 2002). Furthermore, in order to allow for alongshore transport, the northern cross-shore boundary is defined as a Neumann boundary which is driven by the alongshore water level gradient (Tu et al., 2019).
Initial conditions
Water levels in the Mekong Delta vary highly in space due to large-scale flood retention. Thus, the model takes a long time to capture the system behaviour, especially with respect to arriving at the correct flood storage for the Tonle Sap Lake. The Tonle Sap Lake plays a significant role in controlling upstream discharge in the low-flow season. Therefore, the model was spun up over the year 1999; simulated results at the end of this year were used as initial conditions for the year 2000 simulation.
2.2 Model calibration and validation
The years 2000 and 2001 were chosen to calibrate and validate the model respectively. The model calibration parameter is the roughness coefficient. This parameter is also selected for calibration without any sensitivity analysis as it is commonly used for calibrating hydrodynamic models (Manh et al., 2014; Wood et al., 2016). In this study, the “trial and error” method is used for calibration. The roughness coefficients are extracted from the previous calibrated models, including ISIS (Van et al., 2012) and MIKE11 (Manh et al., 2014), in order to speed up the calibration process. The model was calibrated against measured data, with the objective function of the Nash–Sutcliffe efficiency (NSE). The NSE is a normalised statistical indicator that uses the comparison of the residual variance and the measured data variance (Nash and Sutcliffe, 1970); it is calculated as follows:
where is the mean of the observed discharges, is the simulated discharges and is the observed discharge at time t.
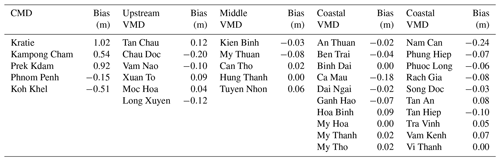
In this study, we used different temporal intervals of observation data. Daily data are used in the Cambodian Mekong Delta (CMD), and hourly data are used in the VMD. The reason for this is that hydrodynamics in the CMD are unlikely to be affected by tides, particularly in the high-flow season, whereas hydrodynamics in the VMD are strongly dominated by tides, even in the high-flow season; thus, the hourly data are better for representing tidal fluctuation.
The NSE is commonly used for evaluating hydrological models. Model performance is acceptable if the NSE is higher than 0 (Moriasi et al., 2007). If the NSE is higher than 0, the simulation is a better predictor than the mean observation. A NSE of 1 corresponds to a perfect match between the modelled results and the observed data. The hydrodynamic model is defined as well calibrated if the NSE, in terms of water levels and discharges, is higher than 0.5. Moriasi et al. (2007) classified model performance based on the NSE as “very good” (NSE > 0.75), “good” (0.75 ≤ NSE ≤ 0.65), “satisfactory” (0.65 ≤ NSE ≤ 0.5) and “unsatisfactory” (NSE < 0.5).
In addition, we used a bias index in order to recognise if the model systematically under- or overestimated water levels. In this study, a commonly used bias measure – the mean error – is used to represent the systematic error of the model (Walther and Moore, 2005). The bias is computed based on the following equation:
where is the simulated yearly mean, and is the observed yearly mean. The bias is calculated for water levels over the year 2000.
2.3 High-dyke development scenarios
To investigate the roles of different floodplains in the VMD and the impact of these floodplains on the VMD's hydrodynamics and downstream tidal propagation, we developed scenarios that include the contributions of each floodplains' water retention. These scenarios used the hydrograph of the year 2000 flood, which was an extremely wet year, in order to estimate the maximum impacts of high dykes. The results of a statistical analysis of flood peaks and volumes encouraged the selection of the year 2000 flood (Fig. 4).
The hydrodynamic forcing is the same in these scenarios; the only difference is development of high dykes. The scenarios are as follows:
-
Scenario 1 (Base) is the base scenario for the 2000 flood, without high dykes. The floodplains in the VMD were not protected by high dykes before 2000 (Duong et al., 2016); therefore, no high dykes are considered in this scenario.
-
Scenario 2 (Dyke 2011) includes the high-dyke system in 2011, as illustrated in Fig. 2. The number of high dykes and the protected floodplain areas are described in Sect. 1.2.
-
Scenario 3 (Dyke LXQ) only includes the high-dyke system developed in the LXQ. The floodplain area protected by the high dykes in the LXQ is approximately 3034 km2.
-
Scenario 4 (Dyke PoR) only includes the high-dyke system developed in the PoR. The PoR is a deeply inundated region in the high-flow season (Kakonen, 2008). In this scenario, the high dykes in PoR protect a floodplain area of around 5020 km2.
-
Scenario 5 (Dyke Trans-Bassac) only includes the high-dyke system developed in the Trans-Bassac region. This region is a shallowly inundated area comprising 3152 km2.
-
Scenario 6 (Dyke VMD) assumes that the high-dyke system is totally developed throughout the VMD's floodplains. This scenario is used to investigate the possible impacts of high dykes if they are built to protect the entire VMD floodplain area. The total floodplain area considered in the model is about 13 059 km2.
2.4 Analysis of simulations
2.4.1 Tidal harmonic analysis
The peak water level is a good index for indicating extreme events in flooded areas. Tran et al. (2018) and Triet et al. (2017) used the flood peaks to assess the impact of high dykes in the VMD. However, the VMD coastal area is drastically dominated by tides. As a result, the amplitudes of tidal constituents are good indices for presenting average variations in water levels in coastal areas. The water levels at the stations along the Tien River and Hau River were analysed over the whole of the year 2000 using T_TIDE (Pawlowicz et al., 2002).
where N is a number of tidal constituents. We analysed the eight main tidal constituents. Each constituent has a frequency σk, which is known, and a complex amplitude αk, which is not known. x(t) is a time series. αk and α−k are complex conjugates.
2.4.2 Water balance calculation
To understand flow dynamics, the water balance analysis is conducted using hourly discharge data from simulations. The targeted stations for this analysis are located on the Mekong's mainstreams and boundaries of the flood-prone zones.
where is total water volume flowing in the target regions in accordance with the Mekong's flow direction, Q is hourly simulated discharge, dt is the temporal interval, and t is selected periods of an entire year and seasons.
In this section we present results of model performance and analysis. The model performance with respect to calibration and validation is indicated by the NSE values (Sect. 3.1). The results for the spatial distribution and temporal variation are shown in Sect. 3.2. In addition, Sect. 3.3 presents the impact of high dykes on water levels and tidal propagation.
3.1 Model calibration and validation
The overall model performance is generally satisfactory with respect to simulating flood dynamics in the Mekong Delta. For water level calibration, up to 36 stations are used for calibration and the majority of these stations have NSE values higher than the satisfactory level of 0.5. The model performance shows its stability in validation, as the NSE values are higher than 0.7. Generally, the model slightly overestimates water levels. Large biases were found in the CMD, with the largest bias of around 1 m at Kratie. The absolute values of the biases decrease to less than 0.2 m at the stations in the VMD. Particularly, the biases at the middle and coastal VMD stations are smaller than 0.1 m (Appendix A).

Figure 7The spatial distribution of the water volume (km3) throughout the VMD in 2000. The low-flow season is calculated from 1 January to 30 June and the high-flow season runs from 1 July to 30 October.
The annual flood flows through the VMD via the Mekong mainstreams and over floodplains; therefore, discharge data from stations in these areas are employed for calibration. A total of 11 stations on the mainstreams and across the CV border are used for calibration. Simulated and measured discharges at these stations show good agreement, and this is indicated by high NSE values. As a result, the Manning roughness coefficient values of the Mekong River reaches and its floodplains after calibration and validation are illustrated in Table 1. The range of roughness coefficients found is relatively similar to previous modelling efforts (Dang et al., 2018a; Manh et al., 2014; Tran et al., 2018; Triet et al., 2017; Van et al., 2012).
3.2 Spatial distribution and temporal variation of water volume in the VMD
3.2.1 Spatial distribution
Water enters the VMD in three ways: the Tien River, the Hau River and flows across the CV border. Figure 7 presents the spatial distribution of the water volume in the VMD. The VMD received around 580 km3 in 2000, with volumes of 405, 83, 61 and 31 km3 via the Tien River, Hau River, and the right and left CV border respectively. The Tien River diverts a considerable amount (152 km3) of water to the Hau River via the Vam Nao canal. This is the major mechanism that balances the flows seaward between the Tien River and Hau River. In fact, the streamflows are relatively equal between the Tien River and Hau River, with volumes of 247 (at My Thuan) and 235 km3 (at Can Tho) respectively. The Tien River is drained by its five estuary branches, whereas the Hau River only has two branches. The Hau River flows into the East Sea discharging 162 and 69 km3 via the Dinh An and Tran De branches respectively. The Tien River's estuary branches, namely the Cung Hau, Co Chien, Ham Luong, Dai and Tieu, drain a similar volume to the East Sea, with a range of between 54 and 63 km3, except for the Tieu branch which discharges only 34 km3.
In addition to the mainstreams of the Mekong River, floodplains have a substantial role in changing the hydrodynamics in the VMD. Hence, we analysed the water balance in the three main flood-prone areas: the LXQ, the PoR and the Trans-Bassac. Among these regions, the PoR harbours the largest amount of floodwater; thus, it is a main flood storage for the VMD. Water primarily flows into the PoR across the eastern part of the CV border in the delta area. In fact, this pathway conveyed approximately 61 km3 in 2000. The simulated results show a volume deficit of 29 km3 from the western and southern boundary of the PoR, which is drained to the Tien River. The southern PoR drains a volume of around 38 km3 to the Soai Rap estuarine branch via the Vamco River. Analysing the water balance of the LXQ shows that it receives water from the northern and eastern sides, while it drains water to the western and southern sides. The yearly inflow to the LXQ is about 44 km3, with volumes of 31 and 13 km3 from the northern and eastern boundaries respectively. It is found that a similar amount of water drains out of the LXQ. The LXQ mainly releases water from the western boundary (32 km3) into the West Sea, followed by the southern boundary (13 km3). The drained water (11 km3) from the southern LXQ mostly enters the Trans-Bassac floodplains. An additional source to the Trans-Bassac region is the Hau River, with an annual volume of 6 km3. The sum of the inflows is drained via the southern canals in this region.
The principal dynamical characteristic of the Mekong Delta floods is their seasonal variation. Figures 7 and 8 illustrate the seasonal variation of the water volume and the percentage volume (compared with the yearly and seasonal entering volumes at Kratie) respectively. Obviously, the flows in the high-flow season are significantly higher than those in the low-flow season. The flood flows contribute up to between 53 % and 65 % of the annual flows throughout the mainstreams and the percentages increase to over 80 % on the floodplains. The Mekong River that flowed into the VMD in 2000 was about 97 % of the total flow at Kratie. However, the water volume entering the VMD was higher than the entry volume at Kratie in the low-flow season.
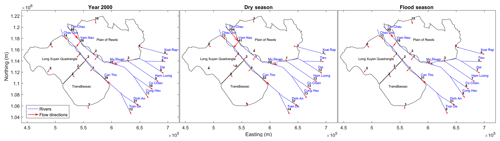
Figure 8Percentages (compared with the total water volume at Kratie) of water distribution throughout the VMD in 2000.

Figure 9Fortnightly average discharges at stations along the Mekong branches (a) and cumulative water volumes of the major floodplains in the VMD (b).
Table 2Increases in the annual mean water levels (in cm) over the year 2000 at the selected stations along the Tien River and the Hau River under different high-dyke development scenarios.
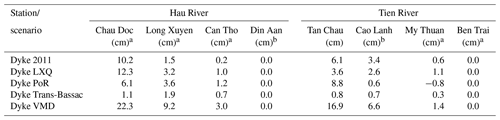
a The differences fall within the model error variations. b No measured data are available.
In the low-flow season, there are slight discrepancies in the water volumes in the segments of the Mekong River, e.g. from Tan Chau to My Thuan. A part of the discrepant proportion is stored in the river segment. As evidence, the water level at Tan Chau at the beginning of the low-flow season is about 2 m, and it then increases to 3.5 m at the beginning of the high-flow season.
3.2.2 Temporal variation
Figure 9 presents the simulated fortnightly average discharges at in- and outflows of the Mekong branches as well as cumulative water storage in the main VMD floodplains from April 2000 to April 2001. The yearly average inflows of the Mekong branches at Tan Chau and Chau Doc are approximately 13 000 and 2700 m3 s−1 respectively. Playing a great role in water diversion between the two Mekong branches, the Vam Nao canal causes water discharges from the Tien River and Hau River to be more balanced seaward of the canal (Fig. 7). Consequently, the water discharges at My Thuan (Tien River) and Can Tho (Hau River) stations become similar, with annual average amounts of about 7900 and 7500 m3 s−1 respectively. The above-mentioned water at Can Tho station is simultaneously drained through the Hau River mouths. The total outflow from the Tien River is slightly greater than at My Thuan due to added flows from the southern PoR, discharging around 8400 m3 s−1.
The water discharges from the Tien River and Hau River are highly variable over time. As shown for the results of discharge variations, the high-flow season is from the beginning of July to the end of October and the remaining period is defined as the low-flow season. The largest seasonal difference is at Tan Chau, with maximum and minimum discharges of about 21 000 and 4500 m3 s−1 in the high-flow and low-flow seasons respectively. The flood flow at Chau Doc reaches a peak of 5600 m3 s−1, while the lowest flow is only 500 m3 s−1 in the low-flow season. However, the high and low flows on the Hau River at Can Tho increase to over 14 100 and 2200 m3 s−1 respectively. A similar fluctuation is found at the Hau River's mouths. On the Tien River, the flood discharge at My Thuan is only 14 800 m3 s−1 and increases slightly to 17 000 m3 s−1 at the Tien River mouths, but the low flows are similar (2400 m3 s−1) at these stations.
The hydrographs in the upstream area of the VMD are flatter than those of the downstream region. The hydrograph shapes are indicated by their kurtosis and are illustrated in Fig. 9. The kurtosis index is a measure of the peakedness of the distribution. Downstream, the hydrographs are narrower at Can Tho, My Thuan and the outflows of the Tien River and Hau River, with kurtosis values higher than 1.5. One of the noticeable points is that flows at the Can Tho and My Thuan stations are relatively lower at the beginning of the high-flow season than at the end, while the flood flows are stable throughout the high-flow season at Tan Chau and Chau Doc stations. This clearly shows how the early flood peak is stored in the major floodplains of the VMD. Figure 9 depicts the cumulative volumes in the major floodplains. At the beginning of the high-flow season, these floodplains are almost empty. By early October, storage increases to 11, 8 and 2 km3 in the PoR, LXQ and Trans-Bassac respectively. When these floodplains are filled, the flood flows at Can Tho and My Thuan reach their maxima during the year.
3.3 Water level changes under high-dyke development
Figure 10 shows that including high dykes increases the daily mean water levels for the Hau River (Chau Doc, Long Xuyen and Can Tho) and the Tien River (Tan Chau, Cao Lanh and My Thuan), especially in the high-flow season. The highest increase was found at Chau Doc and Tan Chau stations while increases decline more seaward.
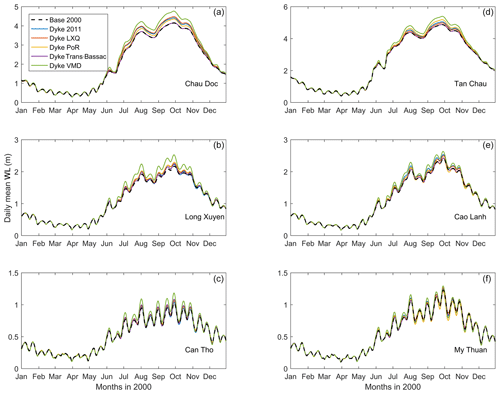
Figure 10Daily mean water level (WL) variations at selected stations along the Hau River (a, b, c) and Tien River (d, e, f) under different high-dyke development scenarios.
3.3.1 Daily water levels
On the Hau River the floodplains protected by dykes in the LXQ, PoR and Trans-Bassac cause increases of 12.3, 6.1 and 1.1 cm in the annual mean water levels at Chau Doc station respectively. However, Table 2 shows that the effect of the PoR dykes on the water levels at Long Xuyen and Can Tho is larger than that of the LXQ dykes. With the high dykes built until 2011, the yearly averaged water levels would increase by 10.2 cm (Chau Doc), 1.5 cm (Long Xuyen) and 0.2 cm (Can Tho). If the high dykes were extended over the VMD (Scenario 6), the yearly mean water levels would increase to 22.3 cm at Chau Doc station.
Generally, water levels on the Tien River are less affected by high dykes. Among the floodplains considered, the PoR has the largest effect on the Tien River's water levels as they are directly connected. For example, the yearly mean water level at Tan Chau increases by about 8.8 cm, but only by 0.6 cm at Cao Lanh station. Interestingly, the PoR slightly reduces water levels at My Thuan due to a reduction in the conveyance capacity of floodwater from the CV border. Although the LXQ is not directly linked to the Tien River, it causes increases in the water levels of around 3.6 and 1.1 at Tan Chau and My Thuan respectively. As the high dykes covered 2421 km2 until 2011, the mean water levels are projected to rise by approximately 0.6 cm at My Thuan and up to 6.1 cm at Tan Chau. In addition, the mean water level at Tan Chau could increase by 16.9 cm if the VMD's floodplains were fully protected by dykes. Noticeably, the model errors at these stations were comparable to the variability of water level changes among the scenarios. The differences at the selected stations, except Tan Chau, fell within the model error variations (Table 2). The differences in water levels among the scenarios may be influenced by the model set-up.
3.3.2 Tidal amplitudes
The hydrodynamics in the Mekong Delta are significantly influenced by tides from the East Sea. A tidal harmonic analysis is conducted over the year 2000 to explore possible changes in the main tidal constituents. Figure 11 depicts the projected changes in tidal amplitudes along the Tien River and Hau River from the river mouths to approximately 195 km landward under a high-dyke development scenario.
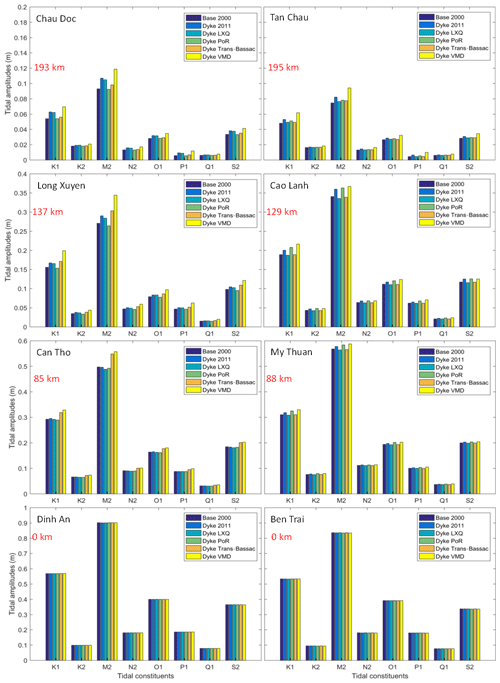
Figure 11Tidal amplitudes of the eight main constituents at the selected stations along the Tien River (right) and Hau River (left) from the river mouths to about 195 km landward in the high-dyke development scenarios.
Tidal amplitudes at the river mouths are unlikely to change. However, differences become significant further inland. At Chau Doc, the LXQ causes the largest increase in tidal amplitudes compared with the other zones. It slightly increases the M2 and K1 tidal amplitude by about 13 % and 15 % respectively. The Trans-Bassac area has a major role in the tidal amplitude change from Long Xuyen to Can Tho. Its dyked floodplains lead to an increase in the tidal amplitudes from 8 % to 13 %. Additionally, the M2 and K1 amplitudes could rise by close to 28 %, 27 % and 12 % at Chau Doc, Long Xuyen and Can Tho respectively. In contrast, high dykes in the PoR result in a marginal reduction in the amplitudes on the Hau River. Similarly, the LXQ and Trans-Bassac cause slight decreases in tidal variation on the Tien River. High dykes constructed on the PoR lead to higher tidal amplitudes on the Tien River, with increases of about 6 %. These increases could reach up to 28 % at Tan Chau, 11 % at Cao Lanh and 4.4 % at My Thuan.
4.1 Model performance
The calibration presented in this study considered a larger number of stations compared with previous studies (e.g. Thanh et al., 2017; Tran et al., 2018; Triet et al., 2017; Van et al., 2012). These stations are mainly located in the VMD (Fig. A1). The majority of stations on the branches of the main Mekong River have a NSE higher than 0.8 (good). In contrast, the stations located further away from the main stream have a lower NSE values. The NSE values of the Phuoc Long and Ca Mau stations are lower than the acceptable level because the water levels at these stations are highly influenced by local infrastructure, specifically the Quan Lo Phung Hiep (QLPH, see Fig. 1) project. The QLPH has been constructed to protect this area from saline intrusion. Flows entering the QLPH are controlled by a series of sluice gates that are mainly located along the coast to prevent saline intrusion into areas of rice cultivation and to control fresh water sources. We did not consider these sluice gates in the model, as they do not have a fixed operation schedule: their operation is based on crop calendars and in situ hydrodynamics (Manh et al., 2014). For example, the observed water level at Phuoc Long station is relatively unchanged at 0.2 m over the year 2000, while the model estimates that water levels at this station have semi-diurnal variations between −0.2 m and 0.6 due to the tidal effects from the East Sea. During validation, a better fit was found at My Thuan station, whereas the other stations have comparable NSE values. As such, we are confident that the model is capable of capturing hydrodynamics in the Mekong Delta accurately.
The modelling approach in this study overcomes a limitation of previous 1-D models that define their boundaries at the river mouths. The boundary conditions (usually water levels) at these locations are not always available, as the water level measurement system in the VMD is not installed at all river mouth locations. Imposing a simple tidal forcing is not justifiable because river flow will impact the mean water level as well as the tidal characteristics in river mouths. Our model grid, which considers part of the shelf, allows for a proper description of these dynamics.
4.2 Spatiotemporal distribution of water volume in the VMD
The total net water volume flow through the Mekong Delta at Kratie was approximately 600 km3 in 2000, as the annual flood contributed about 480 km3 at this location. This is considerably higher than the average volume of 330 km3. However, the annual flood peak in 2000 is only slightly higher than the mean flood peak of 52 000 m3 s−1 (MRC, 2009a). Thus, the 2000 flood is characterised by a broader than usual hydrograph.
Table 3Distribution of water discharge throughout the river mouths (following Nguyen et al., 2008).
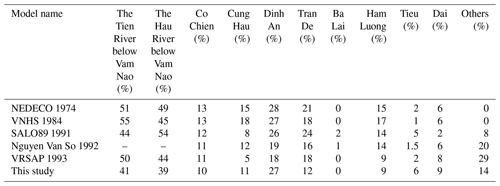
Note that the percentages in this study are calculated based on the total volume at Kratie.
Several studies have investigated the distribution of the flood volume in the Mekong Delta (e.g. Manh et al., 2014; Nguyen et al., 2008; Renaud and Kuenzer, 2012). Manh et al. (2014) calculated the flood volume distribution for the floods between 2009 and 2011 in the upper VMD and concluded that the flood distribution changed marginally over the above-mentioned period. However, they did not estimate flow distribution through the river mouths. We found a similar pattern with respect to the flood volume distribution on the mainstreams, but our model estimated a larger discharge across the VC border to the VMD. A possible explanation for this is that the 2000 flood was considerably larger than the floods during the 2009–2011 period. Table 3 shows a comparison of the VMD's outflows from the current study and from five other models, as summarised by Nguyen et al. (2008). There is only a small variation among the models used which is attributed to different topographical data and boundary conditions (Nguyen et al., 2008). The flow distribution from the current study falls within the range of variation of the other five models, although it differs regarding some important branches, such as the Tien River and Hau River, below Vam Nao.
The water distributions slightly vary over the high-flow and low-flow seasons. The largest changes are found in the discharges to the floodplains. For instance, water volumes are highly seasonal at the CV border stations. The water flows in the low-flow season contribute to 2 %–6 % of the annual flows at these stations. The relative percentages of the Mekong flow, exiting via the Hau River estuaries in the low-flow season are higher than those in the high-flow season, whereas the percentages at the Tien River estuaries are relatively constant.
Several studies have investigated the roles of the Tonle Sap Lake in regulating the flood regimes on the Mekong River (Fujii et al., 2003; Kummu et al., 2014; Manh et al., 2014). Kummu et al. (2014) estimated that the Tonle Sap Lake is capable of reducing about 20 % of the Mekong mainstream discharge and that its greatest storage volume is in August, with an amount of around 15 km3 from the Mekong River flows. The highest monthly released volume occurs in November and peaks at nearly 20 km3. Consequently, Tonle Sap Lake has a crucial role in regulating the Mekong River flows on a temporal scale. The VMD floodplains have a different role than the Tonle Sap Lake with respect to changing the Mekong mainstream flows. They mainly store early flood waters in August. This leads to reduce flood flows at downstream stations along these floodplains. These stations reach peak discharges when the VMD floodplains are almost fully filled. Therefore, the peak flows at the downstream stations occur in October. These results are consistent with the analysis of Dang et al. (2018b).
4.3 Impact of high-dyke development
The Mekong Delta is presently facing several threats, such as the impact of hydropower dams, sea level rise, delta land subsidence and hydraulic infrastructure (Dang et al., 2018a; Kondolf et al., 2018). The impacts of these threats are highly various in terms of their timescales. Among these, hydraulic infrastructure (especially high dykes) has a considerable influence on the hydrodynamics in the region on a short timescale. The high dykes in the VMD are built to protect agricultural land during floods. As a result, flood discharges on the rivers increase and hydrodynamics in the VMD change. Specifically, the results indicate that a lack of flood retention in the LXQ leads to an increase in the water levels on the Hau River, with a downward trend of increases from Chau Doc to Can Tho. This rising pattern was also found by Tran et al. (2018), albeit with different magnitudes due to the different years. They compared the peak water levels, whereas we used daily mean water levels for comparison. Tran et al. (2018) found that the water level peaks would be drastically higher if high dykes were built. These peaks especially increased in the upper VMD (e.g. by 66 cm at Chau Doc and only 4 cm at Can Tho).
Interestingly, the high dykes in the PoR have slightly stronger impacts on water levels at Long Xuyen station than those in the LXQ region. The reason for this is an increase in the water levels on the Tien River, which causes an increase in the water diversion from the Tien River to the Hau River. Due to the Vam Nao connecting canal, the PoR floodplains influence water level fluctuation not only on the Tien River, but also on the Hau River. In addition, the LXQ floodplains affect water levels on both the Tien River and Hau River. Nevertheless, the increasing water levels on the Tien River remain slightly lower than the levels on the Hau River, as the Tien River has more river mouths and a higher conveyance capacity in comparison with the Hau River.
Recent studies on the impact of high dykes in the VMD (e.g. Tran et al., 2018; Triet et al., 2017) have only compared the maximum water levels. However, we found that high dykes also resulted in a reduction in the minimum water levels. This means that high dykes have effects on tidal fluctuation on the main branches. We analysed the tidal amplitudes of the eight main constituents over the year 2000 in order to quantify how water levels on the main branches changed. Noticeably, the complete implementation of the high-dyke system over the VMD floodplains can cause increases of about 12 % and 4 % in the tidal amplitudes at Can Tho and My Thuan stations respectively. Additionally, high dykes in the PoR directly adjacent to Tien River cause a reduction in the tidal amplitude on the Hau River and vice versa. The reason for this is that river water cannot flow into the floodplains, which leads to an increase in river discharge in the main streams. This increased river discharge causes a significant M2 amplitude reduction (Guo et al., 2016). The amplitudes and mean water level at the river mouth stations are unlikely to change under high-dyke development (Table 2). This is due to the fact that flood retention loss due to floodplain areas protected by high dykes causes an insignificant change in the water discharge at that location. In contrast, and as an example, Kuang et al. (2017) found that if water discharges from the Yangtze River upstream increased by 20 000 m3 s−1, the water levels at the mouth could rise by approximately 1 cm. An explanation for this is that the water discharge change due to high-dyke development is not large enough to increase water levels at the river mouths.
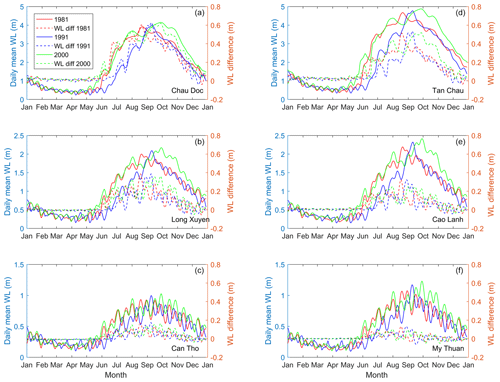
Figure 12Simulated daily mean water levels in the high-flood years of 1981, 1991 and 2000 at selected stations on the Mekong River. The dashed lines indicate water level differences due to the impacts of high dykes.
The impacts of high-dyke development on the downstream hydrodynamics are considered to be different and not as significant as those of hydropower dams, climate change and sea level rise. Dang et al. (2018a) revealed that hydropower development increases the monthly water levels at Tan Chau by 0.4 m and at My Thuan by 0.05 m in a wet year. Sea level rise causes a gradual but drastic increase in water levels. For instance, the water level at My Thuan could increase by 0.3 m due to a sea level rise of 0.38 m. However, high-dyke development in the VMD causes another distinct effect on the floodplains: it prevents flood waters from entering the floodplains, thereby excluding sediment deposition on these floodplains. Sediment deposition on the floodplains benefits agricultural production. Chapman et al. (2016) estimated that annual sediment deposition in An Giang would be worth USD 26 million.
4.4 Flood discharge and volume scenarios
In order to investigate the impact of the distribution of hydrological conditions, we selected 1981, 1991 and 2000 for comparison, as these years include extreme floods in terms of the flood peaks and highest volumes. The simulations considered conditions with and without high dykes. Figure 12 shows that the water levels at the VMD stations are comparable for all 3 years, although the 1991 peak flood at Kratie is about 20 % larger than the 2000 peak flood. Furthermore, the year 2000 flood – which had the largest flood volume – led to the highest water levels. Thus, flood volume is more important than flood peak flows for extreme flood conditions. The reason for this is that high flood peaks flood the area and fill the Tonle Sap Lake in Cambodia; thus, the peak flood flow decreases and elongates downstream (Triet et al., 2017). In addition, Fig. 12 shows that the water level difference for scenarios with and without high dykes is similar and decreases downstream for all 3 years.
4.5 Estimated uncertainties
The quality of input data directly influences the uncertainty of the model results. There are varying sources of uncertainty such as topography, river discharge, initial condition and model parameters (Abily et al., 2016; Di Baldassarre and Montanari, 2009; Bates et al., 2004; Savage et al., 2016; Teng et al., 2017). The river discharge data contain uncertainty due to the use of a rating curve to generate a discharge value from the water level. The interpolated and extrapolated discharge have been shown to be uncertain by between 6.2 % and 42.8 % (Di Baldassarre and Montanari, 2009). The initial condition includes water levels as the initial state of the rivers and floodplains, especially for the Tonle Sap Lake. However, there is a general lack of measured water levels throughout the entire Mekong Delta. To overcome this limitation, we adopted a long spin-up time. River bathymetry in this study was reconstructed from cross sections. Although the river bathymetry was reconstructed using an efficient interpolation method, it contains an error of 0.74 m (Thanh et al., 2019). One of the major sources of uncertainty stems from the SRTM data. Although the SRTM data were used for the VMD floodplains, they contribute to the model error. Recently, several studies have reported that the SRTM data contain high uncertainties, including stripe noise, speckle noise, absolute bias and tree height bias (Hawker et al., 2018; Tarekegn and Sayama, 2013; Yamazaki et al., 2017). In fact, Hawker et al. (2018) revealed that the SRTM data could contain vertical height errors ranging from 1.0 to 4.8 m. These studies suggest that the SRTM data should be processed to remove these errors. However, the model in this study enables one to better understand the hydrodynamics in the Mekong Delta and might serve as a tool for comparative studies. Future work will explore the impact of model input uncertainties on the model outcomes.
In this study, we applied a process-based model (DFM) in order to simulate hydrodynamics in the entire Mekong Delta from Kratie to the shelf areas. The model was calibrated using a dataset of water levels and discharge at 36 stations over the Mekong Delta. The model shows good agreement between simulations and observations. This model is an improved version of the model used by Thanh et al. (2017), as it takes the Cambodian and Vietnamese floodplains as well as the dense river/canal network in the VMD into account. Nevertheless, it does not contain tertiary rivers/canals and hydraulic structures for salinity regulation.
We found that the change in seasonal flow distribution throughout the Mekong's mouths is insignificant, except at the Dinh An mouth which shows a slight increase in the low-flow season. In contrast, the Mekong River network discharging to the sea via the Soai Rap mouth and the western LXQ dramatically dropped in the low-flow season compared with the high-flow season due to overflow reduction at the CV border.
This study found that the floodplains protected by dykes in the LXQ and PoR influence water regimes not only on the directly linked Mekong branch, but also on other branches. The LXQ high dykes cause an increase in the daily mean water levels, but a decrease in tidal amplitudes on the Tien River (after the Vam Nao connecting channel). A similar pattern is also found for the interaction between the PoR high dykes and the Hau River. The high dykes built in the PoR, LXQ and Trans-Bassac regions have demonstrated an impact on water levels at Tan Chau, Chau Doc and Can Tho respectively. These outcomes will benefit sustainable water management and planning in the VMD.
For water level calibration, up to 36 stations are used for calibration. Based on the above-mentioned classification, the NSE values at 33 of 36 stations are higher than the acceptable value of 0.5: 23, 4 and 6 stations are classified as very good, good and satisfactory respectively (Fig. A1). The three unsatisfactory stations are at Ca Mau, Phuoc Long and Rach Gia. Regarding the model validation, only 14 stations are used due to the availability of observed data. Over the validation period, these stations have NSE values that are in the same groups as the calibration values. However, while they are in the good and very good classes, the values at the My Thuan stations increase from 0.69 in calibration to 0.74 in validation.
For water discharge calibration, 11 stations on the mainstreams and across the CV border are used for calibration. A total of 9 of the 11 stations have NSE values in the very good category (Fig. A2). The two stations cross-border stations, namely the right border (to the PoR) and left border (to the LXQ), are in the satisfactory and unsatisfactory categories respectively; however, the NSE values are 0.49 at the left border and 0.54 at the right border, fluctuating around the acceptable criteria. Data at these stations are not available for validation. All stations used for validation are in the very good group. Compared with the calibration, the NSE values for the validation are relatively stable, except for My Thuan station, which increases from 0.84 to 0.95.

Figure A1The NSE values of the water levels at the gauging stations in the Mekong Delta. The calibration (the year 2000) and validation (the year 2001) are presented in panels (a) and (b) respectively.

Figure A2The NSE values of the water discharges at the gauging stations in the Mekong Delta. The calibration (the year 2000) and validation (the year 2001) are presented in panels (a) and (b) respectively.
The data used in this paper are not publicly accessible; however, the data and codes can be made available from the corresponding author upon reasonable request.
VQT, DR and MVDW were responsible for conceptualising this study and for the formal analysis. VQT, JR and HK designed and executed the modelling framework. GVV and VTPL were responsible for data curation. VQT wrote the initial draft of the paper, and all authors contributed to the paper by providing comments and suggestions.
The authors declare that they have no conflict of interest.
This project is part of the ONR Tropical Deltas DRI and is funded under grant nos. N00014-12-1-0433 and N00014-15-1-2824. The authors would like to thank Tran Duc Dung and the Mekong River Commission for providing the data. Simulations were carried out on the Dutch national e-infrastructure with the support of the SURF cooperative. We highly appreciate the three anonymous reviewers for their comments and suggestions that improved this paper.
This research has been supported by the ONR Tropical Deltas DRI (grant nos. N00014-12-1-0433 and N00014-15-1-2824).
This paper was edited by Giuliano Di Baldassarre and reviewed by three anonymous referees.
Abily, M., Bertrand, N., Delestre, O., Gourbesville, P., and Duluc, C. M.: Spatial Global Sensitivity Analysis of High Resolution classified topographic data use in 2D urban flood modelling, Environ. Model. Softw., 77, 183–195, https://doi.org/10.1016/j.envsoft.2015.12.002, 2016.
Achete, F. M., van der Wegen, M., Roelvink, D., and Jaffe, B.: A 2-D process-based model for suspended sediment dynamics: a first step towards ecological modeling, Hydrol. Earth Syst. Sci., 19, 2837–2857, https://doi.org/10.5194/hess-19-2837-2015, 2015.
Amante, C. and Eakins, B. W.: ETOPO1 1 arc-minute global relief model: Procedures, data sources and analysis, NOAA Tech. Memo. NESDIS, NGDC-24, NOAA, 19 pp., 2009.
Bates, P. D., Horritt, M. S., Aronica, G., and Beven, K.: Bayesian updating of flood inundation likelihoods conditioned on flood extent data, Hydrol. Process., 18, 3347–3370, https://doi.org/10.1002/hyp.1499, 2004.
Biggs, D., Miller, F., Hoanh, C. T., and Molle, F.: The delta machine: water management in the Vietnamese Mekong Delta in historical and contemporary perspectives, in: Contested waterscapes in the Mekong region: hydropower, livelihoods and governance, edited by: Molle, F., Foran, T., and Kakonen, M., Routledge, London, UK, 203–225, 2009.
Bomers, A., Schielen, R. M. J., and Hulscher, S. J. M. H.: The influence of grid shape and grid size on hydraulic river modelling performance, Environ. Fluid Mech., 19, 1273–1294, https://doi.org/10.1007/s10652-019-09670-4, 2019.
Chapman, A. and Darby, S.: Evaluating sustainable adaptation strategies for vulnerable mega-deltas using system dynamics modelling: Rice agriculture in the Mekong Delta's An Giang Province, Vietnam, Sci. Total Environ., 559, 326–338, https://doi.org/10.1016/j.scitotenv.2016.02.162, 2016.
Chapman, A. D., Darby, S. E., Hoang, H. M., Tompkins, E. L., and Van, T. P. D.: Adaptation and development trade-offs: fluvial sediment deposition and the sustainability of rice-cropping in An Giang Province, Mekong Delta, Climatic Change, 137, 593–608, https://doi.org/10.1007/s10584-016-1684-3, 2016.
Dang, D. T., Cochrane, T. A., Arias, M. E., and Dang, V. P.: Future hydrological alterations in the Mekong Delta under the impact of water resources development, land subsidence and sea level rise, J. Hydrol. Reg. Stud., 15, 119–133, https://doi.org/10.1016/j.ejrh.2017.12.002, 2018a.
Dang, T. H., Ouillon, S., and Van Vinh, G.: Water and suspended sediment budgets in the Lower Mekong from high-frequency, Water, 10, 846, https://doi.org/10.3390/w10070846, 2018b.
Darby, S. E., Hackney, C. R., Leyland, J., Kummu, M., Lauri, H., Parsons, D. R., Best, J. L., Nicholas, A. P., and Aalto, R.: Fluvial sediment supply to a mega-delta reduced by shifting tropical-cyclone activity, Nat. Publ. Gr., 539, 276–279, https://doi.org/10.1038/nature19809, 2016.
Deltares: D-Flow Flexible Mesh: User Manual, Delft, the Netherlands, 2018.
Department of Agriculture and Rural Development of An Giang and Dong Thap: Maps of hydraulic infrastructure in An Giang and Dong Thap, An Giang and Dong Thap, 2012.
Di Baldassarre, G. and Montanari, A.: Uncertainty in river discharge observations: A quantitative analysis, Hydrol. Earth Syst. Sci., 13, 913–921, https://doi.org/10.5194/hess-13-913-2009, 2009.
Dung, N. V., Merz, B., Bárdossy, A., Thang, T. D., and Apel, H.: Multi-objective automatic calibration of hydrodynamic models utilizing inundation maps and gauge data, Hydrol. Earth Syst. Sci., 15, 1339–1354, https://doi.org/10.5194/hess-15-1339-2011, 2011.
Duong, V. H. T., Nestmann, F., Van, T. C., Hinz, S., Oberle, P., and Geiger, H.: Geographical impact of dyke measurement for land use on flood water in geographical impact of dyke measurement for land use on flood water in the Mekong Delta, in: 8th Eastern European Young Water Professionals Conference – IWA, 12–14 May 2016, Gdansk, Poland, 308–317, 2016.
Egbert, G. D. and Erofeeva, S. Y.: Efficient inverse modeling of barotropic ocean tides, J. Atmos. Ocean. Tech., 19, 183–204, 2002.
Frappart, F., Do Minh, K., L'Hermitte, J., Cazenave, A., Ramillien, G., Le Toan, T., and Mognard-Campbell, N.: Water volume change in the lower Mekong from satellite altimetry and imagery data, Geophys. J. Int., 167, 570–584, https://doi.org/10.1111/j.1365-246X.2006.03184.x, 2006.
Fujihara, Y., Hoshikawa, K., Fujii, H., Kotera, A., Nagano, T., and Yokoyama, S.: Analysis and attribution of trends in water levels in the Vietnamese Mekong Delta, Hydrol. Process., 30, 835–845, https://doi.org/10.1002/hyp.10642, 2016.
Fujii, H., Garsdal, H., Ward, P., Ishii, M., Morishita, K., and Boivin, T.: Hydrological roles of the Cambodian floodplain of the Mekong River, Int. J. River Basin Manage., 1, 1–14, https://doi.org/10.1080/15715124.2003.9635211, 2003.
GSOVN – Genaral Statistics Office of Viet Nam: Statistical yearbook of Vietnam, Hanoi, 2010.
Guo, L., van der Wegen, M., Wang, Z. B., Roelvink, D., and He, Q.: Exploring the impacts of multiple tidal constituents and varying river flow on long-term, large-scale estuarine morphodynamics by means of a 1-D model, J. Geophys. Res.-Earth, 121, 1000–1022, https://doi.org/10.1002/2016JF003821, 2016.
Gupta, A. and Liew, S. C.: The Mekong from satellite imagery: A quick look at a large river, Geomorphology, 85, 259–274, https://doi.org/10.1016/j.geomorph.2006.03.036, 2007.
Hawker, L., Rougier, J., Neal, J., Bates, P., Archer, L., and Yamazaki, D.: Implications of simulating global digital elevation models for flood inundation studies, Water Resour. Res., 54, 7910–7928, https://doi.org/10.1029/2018WR023279, 2018.
Hung, N. N.: Sediment dynamics in the floodplain of the Mekong Delta, Vietnam, Universität Stuttgart, Stuttgart, 2011.
Kakonen, M.: Mekong Delta at the crossroads: More control or adaptation??, Ambio, 37, 205–212, 2008.
Kernkamp, H. W. J., Van Dam, A., Stelling, G. S., and De Goede, E. D.: Efficient scheme for the shallow water equations on unstructured grids with application to the continental shelf, Ocean Dynam., 61, 1175–1188, https://doi.org/10.1007/s10236-011-0423-6, 2011.
Koehnken, L.: IKMP discharge and dediment monitoring program review, recommendations and data analysis. Part 2: Data analysis of preliminary results, Mekong River Commission, Phnom Penh, Cambodia, 2012.
Kondolf, G. M., Schmitt, R. J. P., Carling, P., Darby, S., Arias, M., Bizzi, S., Castelletti, A., Cochrane, T. A., Gibson, S., Kummu, M., Oeurng, C., Rubin, Z., and Wild, T.: Changing sediment budget of the Mekong: Cumulative threats and management strategies for a large river basin, Sci. Total Environ., 625, 114–134, https://doi.org/10.1016/j.scitotenv.2017.11.361, 2018.
Kuang, C., Chen, W., Gu, J., Su, T. C., Song, H., Ma, Y., and Dong, Z.: River discharge contribution to sea-level rise in the Yangtze River Estuary, China, Cont. Shelf Res., 134, 63–75, https://doi.org/10.1016/j.csr.2017.01.004, 2017.
Kuenzer, C., Guo, H., Huth, J., Leinenkugel, P., Li, X., and Dech, S.: Flood mapping and flood dynamics of the mekong delta: ENVISAT-ASAR-WSM based time series analyses, Remote Sens., 5, 687–715, https://doi.org/10.3390/rs5020687, 2013.
Kummu, M., Tes, S., Yin, S., Adamson, P., Józsa, J., Koponen, J., Richey, J., and Sarkkula, J.: Water balance analysis for the Tonle Sap Lake-floodplain system, Hydrol. Process., 28, 1722–1733, https://doi.org/10.1002/hyp.9718, 2014.
Le, T. V. H., Nguyen, H. N., Wolanski, E., Tran, T. C., and Haruyama, S.: The combined impact on the flooding in Vietnam's Mekong River delta of local man-made structures, sea level rise, and dams upstream in the river catchment, Estuar. Coast. Shelf Sci., 71, 110–116, https://doi.org/10.1016/j.ecss.2006.08.021, 2007.
Le Sam: Thùy nông 'o đông băng sông Cúu Long – [Agriculture irrigation in the Mekong Delta], Agriculture Publisher, Ho Chi Minh city, 1996.
Manh, N. V., Dung, N. V., Hung, N. N., Merz, B., and Apel, H.: Large-scale suspended sediment transport and sediment deposition in the Mekong Delta, Hydrol. Earth Syst. Sci., 18, 3033–3053, https://doi.org/10.5194/hess-18-3033-2014, 2014.
Moriasi, D. N., Arnold, J. G., Van Liew, M. W., Bingner, R. L., Harmel, R. D., and Veith, T. L.: Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations, T. ASABE, 50, 885–900, https://doi.org/10.13031/2013.23153, 2007.
MRC: Overview of the Hydrology of the Mekong Basin, Vientiane, Laos, 2005.
MRC: Annual Mekong Flood Report 2008, Vientiane, 2009a.
MRC: MRC Management Information Booklet No. 2: The Flow of the Mekong, available at: http://www.mrcmekong.org/assets/Publications/report-management-develop/MRC-IM-No2-the-flow-of-the-mekong.pdf (last access: 15 April 2014), 2009b.
MRC: State of the Basin Report 2010, Vientiane, Laos, 2010.
Nash, J. E. and Sutcliffe, J. V: River flow forecasting through conceptual models Part I – a discussion of principles, J. Hydrol., 10, 282–290, https://doi.org/10.1016/0022-1694(70)90255-6, 1970.
Nguyen, A. D., Savenije, H. H. G., Pham, D. N., and Tang, D. T.: Using salt intrusion measurements to determine the freshwater discharge distribution over the branches of a multi-channel estuary: The Mekong Delta case, Estuar. Coast. Shelf Sci., 77, 433–445, https://doi.org/10.1016/j.ecss.2007.10.010, 2008.
Nguyen, P. M., Le, K. Van, Botula, Y., and Cornelis, W. M.: Evaluation of soil water retention pedotransfer functions for Vietnamese Mekong Delta soils, Agr. Water Manage., 158, 126–138, https://doi.org/10.1016/j.agwat.2015.04.011, 2015.
Pawlowicz, R., Beardsley, B., and Lentz, S.: Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE, Comput. Geosci., 28, 929–937, https://doi.org/10.1016/S0098-3004(02)00013-4, 2002.
Renaud, F. G. and Kuenzer, C.: The Mekong Delta System, Springer, Dordrecht, Heidelberg, New York, London, 2012.
Renaud, F. G., Syvitski, J. P. M., Sebesvari, Z., Werners, S. E., Kremer, H., Kuenzer, C., Ramesh, R., Jeuken, A. D., and Friedrich, J.: Tipping from the Holocene to the Anthropocene: How threatened are major world deltas?, Curr. Opin. Environ. Sustain., 5, 644–654, https://doi.org/10.1016/j.cosust.2013.11.007, 2013.
Reuter, H. I., Nelson, A., and Jarvis, A.: An evaluation of void-filling interpolation methods for SRTM data, Int. J. Geogr. Inf. Sci., 21, 983–1008, https://doi.org/10.1080/13658810601169899, 2007.
Savage, J. T. S., Bates, P., Freer, J., Neal, J., and Aronica, G.: When does spatial resolution become spurious in probabilistic flood inundation predictions?, Hydrol. Process., 30, 2014–2032, https://doi.org/10.1002/hyp.10749, 2016.
Syvitski, J. P. M. and Kettner, A.: Sediment flux and the Anthropocene, Philos. T. Roy. Soc. A, 369, 957–975, https://doi.org/10.1098/rsta.2010.0329, 2011.
Ta, T. K. O., Nguyen, V. L., Tateishi, M., Kobayashi, I., Saito, Y., and Nakamura, T.: Sediment facies and Late Holocene progradation of the Mekong River Delta in Bentre Province, southern Vietnam: An example of evolution from a tide-dominated to a tide- and wave-dominated delta, Sediment. Geol., 152, 313–325, https://doi.org/10.1016/S0037-0738(02)00098-2, 2002.
Tarekegn, T. H. and Sayama, T.: Correction of SRTM dem artefacts by Fourier transform for flood inundation modeling, J. Jpn. Soc. Civ. Eng. Ser. B1, 69, 193–198, 2013.
Teng, J., Jakeman, A. J., Vaze, J., Croke, B. F. W., Dutta, D., and Kim, S.: Flood inundation modelling: A review of methods, recent advances and uncertainty analysis, Environ. Model. Softw., 90, 201–216, https://doi.org/10.1016/j.envsoft.2017.01.006, 2017.
Thanh, V. Q., Hoanh, C. T., Trung, N. H., and Tri, V. P. D.: A bias-correction method of precipitation data generated by regional climate model, in: International Symposium on Geoinformatics for Spatial Infrastructure Development in Earth and Allied Sciences 2014, Japan-Vietnam Geoinformatics Consortium, 6–9 December 2019, Da Nang, Vietnam, 2014.
Thanh, V. Q., Reyns, J., Wackerman, C., Eidam, E. F., and Roelvink, D.: Modelling suspended sediment dynamics on the subaqueous delta of the Mekong River, Cont. Shelf Res., 147, 213–230, https://doi.org/10.1016/j.csr.2017.07.013, 2017.
Thanh, V. Q., Roelvink, D., van der Wegen, M., Tu, L. X., Reyns, J., and Linh, V. T. P.: Spatial topographic interpolation for meandering channels, J. Waterw. Port Coast. Ocean Eng., in review, 2019.
Tran, D. D., van Halsema, G., Hellegers, P. J. G. J., Phi Hoang, L., Quang Tran, T., Kummu, M., and Ludwig, F.: Assessing impacts of dike construction on the flood dynamics of the Mekong Delta, Hydrol. Earth Syst. Sci., 22, 1875–1896, https://doi.org/10.5194/hess-22-1875-2018, 2018.
Triet, N. V. K., Dung, N. V., Fujii, H., Kummu, M., Merz, B., and Apel, H.: Has dyke development in the Vietnamese Mekong Delta shifted flood hazard downstream?, Hydrol. Earth Syst. Sci., 21, 3991–4010, https://doi.org/10.5194/hess-21-3991-2017, 2017.
Tu, L. X., Thanh, V. Q., Reyns, J., Van, S. P., Anh, D. T., Dang, T. D., and Roelvink, D.: Sediment transport and morphodynamical modeling on the estuaries and coastal zone of the Vietnamese Mekong Delta, Cont. Shelf Res., 186, 64–76, https://doi.org/10.1016/j.csr.2019.07.015, 2019.
Van, P. D. T., Popescu, I., Van Griensven, A., Solomatine, D. P., Trung, N. H., and Green, A.: A study of the climate change impacts on fluvial flood propagation in the Vietnamese Mekong Delta, Hydrol. Earth Syst. Sci., 16, 4637–4649, https://doi.org/10.5194/hess-16-4637-2012, 2012.
Walther, B. A. and Moore, J. L.: The concepts of bias, precision and accuracy, and their use in testing the performance of species richness estimators, with a literature review of estimator performance, Ecography, 28, 815–829, 2005.
Wassmann, R., Hien, N. X., Hoanh, C. T., and Tuong, T. P.: Sea level rise affecting the Vietnamese Mekong Delta: water elevation in the flood season and implications for rice production, Climatic Change, 66, 89–107, https://doi.org/10.1023/B:CLIM.0000043144.69736.b7, 2004.
Wolanski, E., Huan, N. N., Dao, L. T., Nhan, N. H., and Thuy, N. N.: Fine-sediment dynamics in the Mekong River estuary, Viet Nam, Estuar. Coast. Shelf Sci., 43, 565–582, 1996.
Wood, M., Hostache, R., Neal, J., Wagener, T., Giustarini, L., Chini, M., Corato, G., Matgen, P., and Bates, P.: Calibration of channel depth and friction parameters in the LISFLOOD-FP hydraulic model using medium-resolution SAR data and identifiability techniques, Hydrol. Earth Syst. Sci., 20, 4983–4997, https://doi.org/10.5194/hess-20-4983-2016, 2016.
Yamazaki, D., Ikeshima, D., Tawatari, R., Yamaguchi, T., O'Loughlin, F., Neal, J. C., Sampson, C. C., Kanae, S., and Bates, P. D.: A high-accuracy map of global terrain elevations, Geophys. Res. Lett., 44, 5844–5853, https://doi.org/10.1002/2017GL072874, 2017.