the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Conditional simulation of surface rainfall fields using modified phase annealing
András Bárdossy
Sebastian Hörning
Tao Tao
The accuracy of quantitative precipitation estimation (QPE) over a given region and period is of vital importance across multiple domains and disciplines. However, due to the intricate temporospatial variability and the intermittent nature of precipitation, it is challenging to obtain QPE with adequate accuracy. This paper aims to simulate rainfall fields while honoring both the local constraints imposed by the point-wise rain gauge observations and the global constraints imposed by the field measurements obtained from weather radar. The conditional simulation method employed in this study is modified phase annealing (PA), which is practically an evolution from the traditional simulated annealing (SA). Yet unlike SA, which implements perturbations in the spatial field, PA implements perturbations in Fourier space, making it superior to SA in many respects. PA is developed in two ways. First, taking advantage of the global characteristic of PA, the method is only used to deal with global constraints, and the local ones are handed over to residual kriging. Second, except for the system temperature, the number of perturbed phases is also annealed during the simulation process, making the influence of the perturbation more global at initial phases and decreasing the global impact of the perturbation gradually as the number of perturbed phases decreases. The proposed method is used to simulate the rainfall field for a 30 min event using different scenarios: with and without integrating the uncertainty of the radar-indicated rainfall pattern and with different objective functions.
Quantitative precipitation estimation (QPE) over a given region and period is of vital importance across multiple domains and disciplines. Yet the intricate temporospatial variability, together with the intermittent nature of precipitation in both space and time, has hampered the accuracy of QPE (Kumar and Foufoula-Georgiou, 1994; Emmanuel et al., 2012; Cristiano et al., 2017).
The point-wise observations of precipitation measured by rain gauges are accurate but only available at limited locations. Meanwhile, precipitation-related measurements produced by meteorological radars have become standard outputs of weather offices in many places in the world. However, the problem with radar-based QPE is the nonguaranteed accuracy, which could be impaired by various sources of errors, such as static/dynamic clutter, signal attenuation, anomalous propagation of the radar beam, uncertainty in the Z–R relationship, etc. (see Doviak and Zrnić, 1993; Collier, 1999; Fabry, 2015, for details). Despite the various sources of error, weather radar has been widely acknowledged as a valid indicator of precipitation patterns (e.g., Mendez Antonio et al., 2009; Fabry, 2015). Considering the pros and cons of the two most usual sources of precipitation information, the QPE obtained by merging the point-wise rain gauge observations and the radar-indicated precipitation pattern has become a research problem in both meteorology and hydrology (Hasan et al., 2016; Yan and Bárdossy, 2019).
In the context of merging radar and rain gauge data, we consider two types of constraints: the local constraints imposed by the point-wise rain gauge observations and the global constraints imposed by the field measurement from weather radar. This paper focuses on simulating surface rainfall fields conditioned on the two types of constraints. There exists a variety of geostatistical methods aiming to simulate conditional Gaussian fields with a given covariance function, such as turning bands simulation, LU-decomposition-based methods, sequential Gaussian simulation, etc. (see Deutsch and Journel, 1998; Chilès and Delfiner, 2012; Lantuéjoul, 2013, for details). The common goal of these methods is to ensure that the simulated realizations comply with the additional information available (Lauzon and Marcotte, 2019). The additional information could be observed values of the simulated targets, measurements that are related linearly or nonlinearly to the simulated targets, third- or higher-order statistics (Guthke and Bárdossy, 2017; Bárdossy and Hörning, 2017), etc.
The conditional simulation method used in this work is phase annealing (PA). It was first proposed in Hörning and Bárdossy (2018) and is essentially a product of the general-purpose metaheuristics method of simulated annealing (SA) (Kirkpatrick et al., 1983; Geman and Geman, 1984; Deutsch, 1992; Deutsch and Journel, 1994). It utilizes the sophisticated optimization scheme of SA in the search for the global optimum. Yet compared to SA, the distinction or evolvement of PA lies in the fact that the perturbation, or swapping in the nomenclature of SA, is implemented in Fourier space. Or, to be more exact, the perturbation is implemented on the phase component of the Fourier transform, while the power spectrum is preserved such that the spatial covariance is invariant at all iterations according to the well-known Wiener–Khinchin theorem (Wiener, 1930; Khintchine, 1934). Compared to SA, PA alleviates the singularity problem, namely the undesired discontinuities or poor embedding of the conditional points within the neighborhood (Hörning and Bárdossy, 2018), and in general, PA has a much higher convergence rate compared to SA.
A remarkable feature of PA is that it is a global method: any perturbation imposed on the phase component is reflected in the entire field. Yet admittedly, if the perturbation is implemented at lower frequencies where the corresponding wave lengths are relatively large, the impact is more global and vice versa. The global characteristic of PA makes it a valuable methodology for global constraints. However, PA is found to be insufficient in the treatment of local constraints (Hörning and Bárdossy, 2018). Note that by local constraints, we refer primarily to point equality constraints when the total number of constraints is far less than that of the grid points. In the algorithm of PA, the local constraints are normally ensured by inserting a component measuring the dissimilarity between the simulated and the target values. On the other hand, one could argue that if the information on the measurement error is explicitly known, then this piece of information could be considered in the simulation, and the inability of PA to handle the local constraints can be utilized in turn. However, in the general case, the local constraints can only be approximated by PA.
Respecting the fact that the specialty of PA is the treatment of the global constraints, we separate the global from the local. In particular, PA is only used to handle the global constraints, and local ones are handled separately by residual kriging at each iteration. As an extension of PA, except for annealing the system temperature, the number of perturbed phases is annealed in parallel to render the algorithm to work more globally at initial phases of the simulation. The global impact of the perturbation is weakened as the number of perturbed phases decreases.
This paper is divided into six sections. After the general introduction, the methodology of PA is introduced in Sect. 2, including three stages: presimulation, simulation, and postsimulation. Section 3 provides two options to integrate the uncertainty of the radar-indicated rainfall pattern into the simulation. Section 4 introduces the study domain and the two types of data used in this study. In Sect. 5, the proposed algorithm is used to simulate the rainfall field for a 30 min event, where different simulation scenarios are applied. Section 6 ends this paper with conclusions.
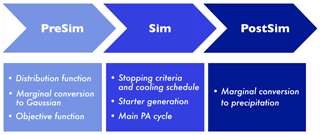
Figure 1 summarizes the procedure of simulating surface rainfall fields using the algorithm of PA, including three stages: presimulation (PreSim), simulation (Sim), and postsimulation (PostSim). Each stage and the corresponding substages are described in the following subsections in the same sequence as shown in the flowchart.
2.1 Presimulation
2.1.1 Distribution function of surface rainfall
PA is embedded in Gaussian space. The direct output of the PA algorithm is a spatial field whose marginal distribution function is standard normal; hence the distribution function of surface rainfall is essential to transform the simulated Gaussian fields into rainfall fields of interest.
The scenario is as follows: based on K rain gauge observations and a regular grid of radar quantiles (representing the spatial pattern of the rainfall field), the distribution function of surface rainfall is generated. The procedure was first introduced in Yan and Bárdossy (2019), and we specify the modified version here.
- a.
For all rain gauge observations rk, the collocated quantiles in the radar quantile map U are determined and denoted as uk. The two datasets are then sorted in ascending order, i.e., and .
- b.
Set the spatial intermittency u0, i.e., the quantile corresponding to zero precipitation. u0 is estimated as the ratio of the number of zero-valued pixels to the total number of pixels in the domain of interest. If the small quantiles of the field are properly sampled by the rain gauges, one could use the smallest sampled quantile u1 to estimate u0:
where r1 is the smallest gauge observation corresponding to u1. As an alternative, if the small quantiles of the field are not properly sampled by the rain gauges, we propose to estimate u0 from the original radar displays in dBZ, namely a series of instantaneous maps of radar reflectivity within the relevant accumulation time. A zero-valued pixel is defined when the maximum of the collocated pixel values of these maps is smaller than a given threshold (say 20 dBZ).
- c.
Let G(r) denote the distribution function of surface rainfall to be estimated. A linear interpolation is applied for rainfall values of less than the maximum recorded gauge observations, i.e., r≤rK:
with rk−1, rk being the two nearest neighbors of r () and being the quantiles corresponding to rk−1, rk, respectively.
- d.
Extrapolate rainfall values r>rK. A modification is made here: the minimum of exponential and linear extrapolation is used as the result, as expressed in Eq. (3). We have learned from practice that the exponential extrapolation tends to overestimate the rainfall extremes, so a linear component is used to restrict the extrapolation result.
where the only parameter λ of the exponential distribution is determined from the last pair (rK, uK):
It is recommended that the methodology described above is used to estimate the distribution function of accumulated rainfall, not rain intensity, because it is built on the assumption that rain gauge observations can represent the ground truth. Yet in general, rain gauges are considered to be poor in capturing the instantaneous rain intensity, while the measurement error diminishes rapidly as the integration time increases (Fabry, 2015).
As we only use the radar-indicated spatial ranks, i.e., the scaled radar map following a uniform distribution in [0, 1], there is no requirement for the accuracy of the Z–R relation given the monotonic relationship of the two quantities. One could use a Z–R relation at hand to transform radar reflectivity into rain intensity and then make the accumulation. Nevertheless, a normal quality control for radar data, as described in Sect. 4, is necessary to maintain the accuracy of radar-indicated spatial ranks.
2.1.2 Marginal conversion to Gaussian
As PA is embedded in Gaussian space, all the constraints, including the point equality targets rk (mm) imposed by rain gauges and the quantile map U (–) imposed by weather radar, are converted to a standard normal marginal distribution by
where Φ−1 is the inverse of the cumulative standard normal distribution function and G is the distribution function of surface rainfall obtained according to the procedure described in Sect. 2.1.1.
2.1.3 Objective function
We impose two kinds of constraints: local and global. As has been explained in the introduction, PA is a powerful method for handling global constraints. In order not to interfere with the logic behind PA and to fulfill the point equality constraints (local constraints) exactly, residual kriging is implemented at each iteration to obtain the observed values at rain gauge locations. Thus the objective function only needs to measure the fulfillment of the global constraints.
We impose two global constraints: field pattern and directional asymmetry. Note that both constraints are evaluated from the simulated Gaussian field and are compared with the radar-based Gaussian field Z*, as obtained in Eq. (6). We term Z* the reference field hereafter.
The first global constraint, field pattern, requires the simulated field to be similar to the reference field. The similarity of the two fields is quantified by the Pearson correlation coefficient:
In the ideal case, equals 1, and we use the difference () to measure the distance from the ideal.
The second global constraint is directional asymmetry, as given by
where [A(h)]Z (abbreviated as AZ hereafter) is the asymmetry function evaluated from the simulated Gaussian field Z, N(h) is the number of pairs fulfilling , and Φ is the cumulative standard normal distribution function. Directional asymmetry was first introduced in Bárdossy and Hörning (2017) and Hörning and Bárdossy (2018). It is a third-order statistic, and the physical phenomenon revealed by this statistic could be significant for advection-dominant processes, such as storms. We use the entire field to compute the directional asymmetry function and compare the simulated one with the reference asymmetry function, i.e., the directional asymmetry function evaluated from the reference field, abbreviated as . There exist multiple choices to define the distance of the two asymmetry functions, and we have used the L∞ norm .
Different schemes could be used to combine the two components, linear or nonlinear, and we have chosen the maximum of the two components. Finally, the objective function we have used to quantify the fulfillment of the two global constraints is expressed as
where w is the relative weight of the component directional asymmetry, and Ascal, as expressed in Eq. (10), is the scaling factor that scales the L∞ norm of the difference of the two asymmetry functions between 0 and 1.
It is worth mentioning that the proposed methodology is flexible, and any global statistic could be used to constrain the simulated fields. One could even combine several statistics in the objective function.
2.2 Simulation
2.2.1 Stopping criteria and cooling schedule
There are many choices of stopping criteria for an optimization algorithm, such as (a) the total number of iterations, (b) the predefined value of the objective function, (c) the rate of decrease of the objective function, (d) the number of continuous iterations without improvement, (e) the predefined threshold of the initial objective function value, and so forth. One could use one criterion or combine several.
As for the cooling schedule, the system temperature of PA decreases according to the cooling schedule as the optimization process develops: the lower the system temperature, the less likely a bad perturbation is accepted. A bad perturbation occurs when the perturbation does not decrease the objective function value. A reasonable cooling schedule is capable of preventing the optimization from being trapped prematurely at a local minimum. Yet one should be aware that there is always a compromise between the statistical guarantee of the convergence and the computational cost: the slower the temperature decreases, the higher the probability of the convergence. However, cooling slowly also means more iterations and therefore higher computational costs.
Comparative studies of the performance of SA using the most important cooling schedules, i.e., multiplicative monotonic, additive monotonic, and nonmonotonic adaptive cooling, have been made by, e.g., Nourani and Andresen (1998), Martín and Sierra (2020), and others. The results show that annealing works properly when the cooling curve has a moderate slope at the initial and central stages of the process and tends to have a softer slope at the final stage. Many cooling schedules satisfy these conditions. As PA utilizes the optimization strategy of SA, the rules also apply for PA. Our choice of the cooling schedule is the multiplicative monotonic one.
Specifically, we search for two parameters – the initial temperature T0 and the final temperature Tmin – by decreasing the temperature exponentially and discretely. At each fixed temperature, N perturbations, say 1000, are implemented, and the corresponding acceptance rate and improvement rate are computed. Acceptance means the perturbation is accepted by the system, and the system state is updated irrespective of whether the perturbation brings improvement to the system, while improvement means the perturbation does decrease the objective function value. In short, a perturbation that brings improvement must be an accepted perturbation, yet an accepted perturbation does not necessarily bring improvement to the system. We refer to the experiment as a temperature cycle, where N perturbations are implemented, and the two mentioned rates are computed at a fixed temperature.
T0 is first set by starting a temperature cycle with an initial guess of T0. If the acceptance rate is lower than the predefined limit, say 98 %, then the temperature is increased and vice versa. The goal is to find a T0 with a relatively high acceptance rate. Then, Tmin is set by decreasing T0 exponentially until the predefined stopping criterion is met. It is clear in our case that if more iterations are implemented, better realizations (realizations with lower objective function values) could be produced, yet it is again a compromise between a satisfactory destination and the computational cost.
We note that from the determination of T0, the total number of temperature cycles m (to anneal T0 to Tmin) is recorded. Thus the total number of perturbations is estimated as L=mN. A continuous cooling schedule is then computed from T0, Tmin, and L. The temperature at Iteration l is computed as
where αT is the attenuation factor of the system temperature, given as
In parallel with the temperature annealing we also anneal the number of phases being perturbed in Fourier space, starting with a relatively large number N0 (say 5 % to 20 % of the total number of valid Fourier phases) and decreasing all the way down to 1. The number of phases to be perturbed at Iteration l is computed by
where αN is the attenuation factor with respect to the number of perturbed Fourier phases. It is computed as
The logic behind annealing the number of perturbed phases is to render the perturbation to have a more global impact initially when the distance from the destination is relatively large and to decrease the impact of the perturbation gradually as the optimization process develops.
2.2.2 Starter generation
PA requires a starting Gaussian random field with the prescribed spatial covariance, abbreviated as starter. Various methods could be used to generate such a random field, e.g., fast Fourier transformation for regular grids (Wood and Chan, 1994; Wood, 1995; Ravalec et al., 2000), turning bands simulation (Journel, 1974), or the Cholesky transformation of the covariance matrix. Considering the fact that the gauge observations used in this work cannot provide enough information to derive the spatial covariance, the radar-based Gaussian field, i.e., the reference field Z*, is used instead to derive the covariance.
It should be noted that if a fast Fourier transformation (FFT) is used to generate the starter, the inherent periodic property of the FFT should be treated with care. Specifically, the simulation should be embedded in a larger domain. The original domain is enlarged in all directions by a finite range, i.e., the range bringing the covariance function from the maximum to approaching zero. If covariance models with asymptotic ranges (e.g., exponential, Matérn, and Gaussian covariances) are employed, the extension in domain size could be significant (Chilès and Delfiner, 2012).
2.2.3 Main PA cycle
The starting point of PA is a Gaussian random field ZK with the prescribed spatial covariance as described in Sect. 2.2.2. A little modification in our case is that the values at the observational locations are fixed by residual kriging, as indicated by the subscript K. In particular, the procedure of residual kriging is explained in the following (Step 6). The procedure of the PA algorithm applied in this paper is specified as follows:
-
The discrete Fourier transform (DFT) of ZK is computed as
-
The system temperature Tl and the number of perturbed phases Nl at Iteration l are computed by Eqs. (11) and (13).
-
Nl vectors (un, vn) are generated, where n=0, ⋯, Nl−1. un, vn are randomly drawn from the two discrete uniform distributions [1, ⋯, U′] and [1, ⋯, V′], respectively, where U′, V′ are the highest frequencies considered for perturbation in the x and y directions, respectively. Note that zero frequencies in both directions should be excluded from the perturbation. One could use the entire frequency range or select a subarea to impose the perturbation.
-
Nl phases θn are randomly drawn from the uniform distribution [−π, π).
-
The Fourier coefficients at the selected locations (un, vn) and the corresponding symmetrical locations are expressed as
where U, V are the number of grid points in x and y directions, respectively, and are also the highest frequencies in both directions. These coefficients are then updated in terms of the Fourier phases using θn, while the corresponding amplitudes remain unchanged:
The perturbed Fourier transform is denoted as . The corresponding perturbed spatial random field is obtained by the inverse DFT:
-
Due to the perturbation, no longer satisfies the point equality constraints (note the removal of the subscript K). Thus kriging is applied for the residuals , where zk represents the point equality constraints defined in Eq. (5). The results of kriging r are superimposed on :
As kriging is a geostatistical method that depends only on the configuration of the data points, the weight matrix of individual grid points does not change with iterations. One needs to compute the weight matrices for all the grid points only once. Thus residual kriging is cheap to use and causes almost no additional computational cost.
-
is then subject to the objective function defined in Eq. (9). If , the perturbation is accepted. Otherwise, the perturbation is accepted with the probability
-
If the perturbation is accepted, the system state is updated; namely ZK, 𝒵K and 𝒪(ZK) are replaced by , , and , respectively.
-
If the stopping criterion is met, the optimization is stopped and ZK is a realization in Gaussian space, satisfying the predefined optimization criterion. Otherwise go to Step 2.
2.3 Postsimulation
The Gaussian field ZK is transformed into a rainfall field by
where Φ is the cumulative standard normal distribution function, and G−1 is the inverse of the distribution function of surface rainfall, as obtained in Sect. 2.1.1. The resultant R is a realization of the surface rainfall field.
The two datasets – gauge observations rk and the collocated radar quantiles uk – are supposed to have the same rankings; namely large gauge observations should correspond to large quantiles and vice versa. Yet it is not always the case, which reveals the conflict of radar and gauge data. To quantify the conflict, we employ the (Spearman's) rank correlation ρS that measures the monotonic relationship of two variables: the closer ρS is to 1, the more accordance (or less conflict) of radar and gauge data.
The conflict of the two could be partially explained by the fact that weather radar measures at some distance above the ground (a few hundred to more than a thousand meters aloft). It is therefore reasonable to suspect the correctness of comparing the ground-based rain gauge observations with the collocated radar data by assuming the vertical descent of the hydrometeors. In fact, hydrometeors are very likely to be laterally advected during their descent by wind, which occurs quite frequently concurrently with precipitation. To take the possible wind-induced displacement into account, the procedure described in Yan and Bárdossy (2019) is adopted. Here we recall the procedure briefly in three steps.
-
A rank correlation matrix is generated by first shifting the original radar quantile map U with all the vectors defined by a regular grid hij, i.e., locations of all the grid cells in hij, and then calculating the rank correlation between gauge observations and the collocated radar quantiles in the shifted map. Note that the radar quantile map shifted by vector hij (a certain grid cell in hij) is denoted as Uij.
Both hij and have the same spatial resolution as U. The center of hij is (0, 0), with the corresponding entry in denoted as , meaning that zero shift is imposed on U. The farther a grid cell is from the center, the larger the shift imposed on U is. One should limit the number of grid cells in hij depending on the radar measurement height.
-
A probability matrix Pij is generated from the rank correlation matrix :
where H is a monotonic function, such as power function, exponential function, or logarithmic function. The first derivative (dH∕dx) matters as a large dH∕dx means that more weights are assigned to those displacement vectors (or shifted fields) that produce a higher-rank correlation. Our choice of function H is simply H(x)=x2.
-
The probability matrix Pij is scaled to ensure that the sum of all entries equals 1:
Pij quantifies the uncertainty of the radar-indicated rainfall pattern by giving the probability of individual shifted quantile fields in analogy with a probability mass function. The logic behind it is that only those displacement vectors that increase the accordance of radar and gauge data are accepted and given strong probability.
The method described above is built on the assumption that the entire field is displaced by a single vector. The extent of the domain in this work is 19 km × 19 km (see Sect. 4 for details), and the selection of the extent is limited by the gauge data availability. With this spatial extent, we could quite often find dozens of displacement vectors that bring up the concordance of radar and gauge data. If gauge data accessibility is not the limiting factor, one could enlarge the extent (say to 40 km × 40 km), provided that the resultant probability matrix has some pattern (not a random field).
There are two options to integrate the uncertainty of the radar-indicated rainfall pattern, i.e., the information carried by the probability matrix Pij, into the simulation.
Option 1: the expectation of the shifted quantile fields is computed using the probability matrix, and then the corresponding Gaussian field is computed, as given in Eq. (26). The result is used as the reference field when applying the PA algorithm.
Option 2: those (marginally converted) shifted quantile fields Φ−1(Uij) bearing a positive probability are considered as reference fields, and the algorithm described in Sect. 2 is applied independently for all these reference fields. The results are multiple realizations of the surface rainfall field with different references, denoted as Rij. The estimate of the surface rainfall field (with the uncertainty of the radar-indicated rainfall pattern integrated) is obtained as the expectation of these realizations:
Both options are capable of producing estimates of the surface rainfall field with the uncertainty of the radar-indicated rainfall pattern integrated, yet the results are distinct, as presented in Sect. 5.
The study domain is located in Baden-Württemberg, in the southwest of Germany. As shown in Fig. 2, it is a square domain with a side length of 19 km. The domain is discretized to a 39×39 grid with a spatial resolution of 500 m × 500 m. A gauge network consisting of 12 pluviometers is available within the domain, as denoted by the red dots in Fig. 2.
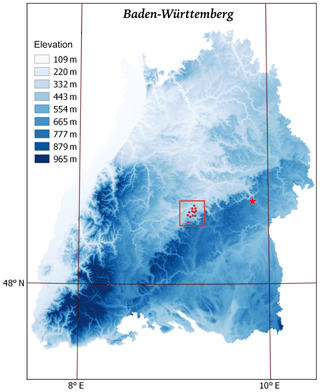
Figure 2The elevation map of Baden-Württemberg with the study domain marked by the red square, the rain gauges marked by the red dots, and the site of Radar Türkheim marked by the red star.
The radar data used in this study are the raw data with 5 min temporal resolution, measured by Radar Türkheim, a C-band radar operated by the German Weather Service (DWD). Radar Türkheim is located about 45 km from the domain center, as denoted by the red star in Fig. 2. The raw data are subject to a processing chain consisting of (1) clutter removal (Gabella and Notarpietro, 2002), (2) attenuation correlation (Krämer and Verworn, 2008; Jacobi and Heistermann, 2016), (3) reprojection from polar to Cartesian coordinates, and (4) clipping of the square data for the study domain. All these quality control steps are operated in the wradlib environment, an open-source library for weather radar data processing (Heistermann et al., 2013).
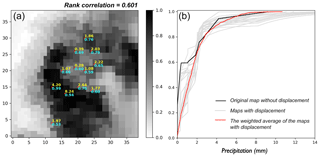
Figure 3(a) Original radar quantile map (–) for the 30 min event (4 May 2017, 13:20–13:50 LT), with the rain gauge observations (mm) labeled in yellow and the collocated radar quantiles labeled in cyan. (b) Distribution functions of surface rainfall. Black: original radar map without displacement; gray: radar maps with displacement; red: the weighted average of the radar maps with displacement.
We selected a 30 min event to apply the algorithm of PA. The event was selected not only due to the relatively prominent rain intensity reflected by the rain gauge data, but more importantly because the event was properly captured by a few rain gauges unevenly distributed in the domain of interest, as shown by the red dots in Fig. 3a. From the figure, it can be clearly seen that the sampled quantiles (indicated by the text in cyan) cover the entire range [0, 1]: not only the small or large ones, but the sampled quantiles as well are more or less evenly distributed. One might have noticed that the smallest sampled quantile is 0.53. Yet in this case, u0=0.26 (the spatial intermittency) and the quantile value 0.53 correspond to the rainfall value 0.28 mm after the re-ordering.
The conflict of radar and gauge data is obviously reflected in Fig. 3 (left), for example, the collocation of 4.20 mm rainfall with the quantile 0.99 in contrast with the collocation of 8.24 mm rainfall with the quantile 0.94. The rank correlation of the gauge observations and the collocated radar quantiles is 0.601, as labeled in the title of the figure. The distribution function of the surface rainfall field based on the two original datasets is shown by the black line in Fig. 3b.
However, using the algorithm described in Sect. 3 to evaluate the uncertainty of the radar-indicated rainfall pattern, one can obtain multiple distribution functions of surface rainfall, as shown by the gray lines in Fig. 3b. Note that only the distribution functions associated with those shifted fields possessing a positive probability (as indicated by the probability matrix) are shown in the figure.
With these distribution functions, one can transform the corresponding shifted quantile fields into rainfall fields, and with the probability matrix, the expectation of these rainfall fields can be computed, as shown in Fig. 4b. Also with the probability matrix, one can compute the expectation of the shifted quantile fields, as shown in Fig. 4a. From the expected quantile map, a tangible improvement in terms of the concordance of radar and gauge data is observed: the rank correlation increases from 0.601 to 0.769, as labeled in the title of Figs. 3 and 4.
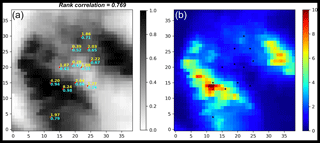
Figure 4(a) The expected quantile map (–), with the rain gauge observations (mm) labeled in yellow and the collocated radar quantiles labeled in cyan. (b) The expected rainfall field (mm).
It is noteworthy that the data configuration used in this work is not good enough to maximize the performance of the proposed methodology as the distribution of the rain gauges is relatively centered. Thus we have to select events whose storm center is relatively centered according to the radar map. To enlarge the applicability, it is recommended that rain gauges are uniformly distributed in the domain of interest. In addition to the distribution of the rain gauges, as shown in the following, the effect of conditioning on gauge observations is local (in consistency with the terminology local constraints); hence, with a denser network of rain gauges, a good performance of the methodology is more likely guaranteed.
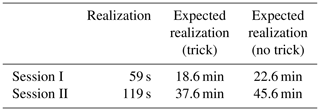
We open up two simulation sessions, depending on the different objective functions used when applying the PA algorithm. In Session I, the objective function contains only the component field pattern . In Session II, the component directional asymmetry comes into play, and the objective function expressed in Eq. (9) is employed, where the relative weight of the component directional asymmetry w equals 0.5. Technically, for both simulation sessions, the optimization process stops when the objective function falls below 0.05.
5.1 Simulation Session I
We present an evolution in terms of the simulation strategy where the algorithm of PA is applied differently in three stages:
-
using the original quantile map as the reference
-
using the expected quantile map as the reference, i.e., integrating the uncertainty of the radar-indicated rainfall pattern via Option 1 in Sect. 3
-
simulating independently using those shifted quantile maps with a positive probability as the reference and computing the expectation, i.e., integrating the uncertainty of the radar-indicated rainfall pattern via Option 2 in Sect. 3.
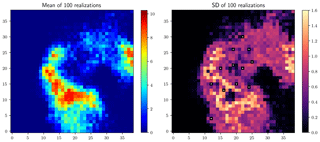
Figure 5Stage 1 results: mean and standard deviation of 100 realizations (mm), obtained using the original quantile map as the reference.
Stage 1 (simulating rainfall fields using the original quantile map as the reference) means the uncertainty of the radar-indicated rainfall pattern is not integrated. Figure 5 shows the mean of 100 such realizations on the left and the corresponding standard deviation map on the right. The standard deviation map reflects the variability of different realizations, and the pixel values, collocated with the rain gauges, are zeros, as marked by the white points in Fig. 5 (right), which shows the fulfillment of the point equality constraints and the local effect of conditioning to the gauge observations. And this local effect is reflected in all the standard deviation maps shown in the following.
Stage 2 (simulating rainfall fields using the expected quantile map as the reference) integrates the uncertainty of the radar-indicated rainfall pattern via Option 1, as described in Sect. 3. Similarly, the mean of 100 such realizations and the corresponding standard deviation map are shown in Fig. 6. Comparing Figs. 5 and 6, one could observe the displacements of the peak regions in both the rainfall and the standard deviation maps. Compared to Fig. 5, a visible reduction in the standard deviation is observed in Fig. 6, showing the reduced estimation uncertainty by integrating the uncertainty of the radar-indicated rainfall pattern.
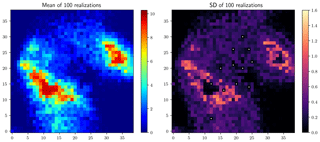
Figure 6Stage 2 results: mean and standard deviation of 100 realizations (mm), obtained using the expected quantile map as the reference.
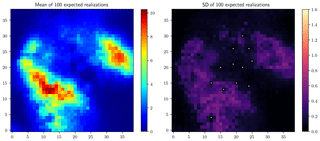
Stage 3 involves a simulation strategy that is slightly more complicated than before. The simulation is applied independently using the shifted quantile map associated with a positive probability as the reference, and the single simulation cycle is applied to all the components possessing a positive probability. Finally, the expectation of these realizations is computed, termed the expected realization hereafter. Yet the computational cost to obtain such an expected realization is much higher as multiple realizations are required to make up an expected realization (see Table 1 for details). Similarly, the mean of 100 expected realizations and the corresponding standard deviation map are shown in Fig. 7. Comparing Figs. 6 and 7, the positions of the peak regions remain unchanged in both the rainfall and the standard deviation maps. Yet compared to Fig. 6, the reduction in the standard deviation is remarkable in Fig. 7, showing further reduction in terms of the estimation uncertainty.
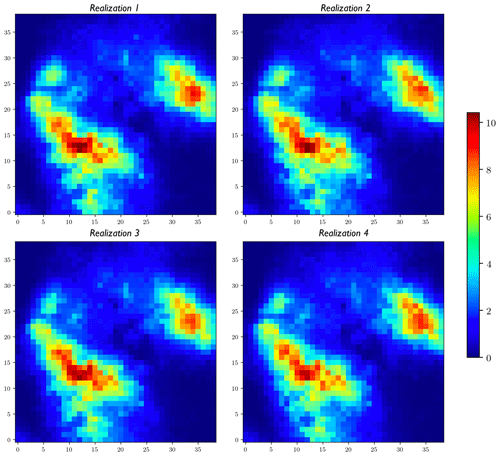
In addition, the mean field and the standard deviation map of the results from Stage 3 are much smoother compared to the other alternatives shown previously. Figure 8 displays four randomly selected expected realizations to show the similarity of different expected realizations and the smoothness of individual expected realizations.
5.2 Simulation Session II
In the previous session, the objective function only contains the component field pattern. In this session, the component directional asymmetry (abbreviated as asymmetry hereafter) comes into play in the objective function. It should be noted that the evaluation cost of the objective function in Session II is higher than that in Session I, and more time is needed to generate a single realization if the same stopping criterion is used (see Table 1 for details).
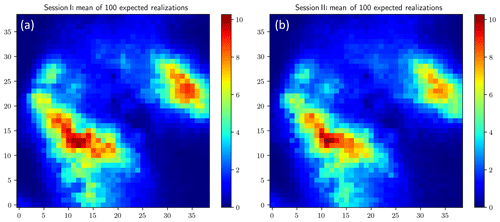
We still adopt the three-stage evolution when applying the PA algorithm as in Simulation Session I. Differences between realizations from Session I and Session II do exist, but they are not that remarkable. Therefore, in the presentation of the results from Session II, we omit the results from Stages 1 and 2 and only display the results from Stage 3 in Figs. 9 and 10 (both panels on the right of each figure). The corresponding results from Session I are presented on the left just for the sake of comparison and identifying the effect of adding the component asymmetry in the objective function. Comparing the two mean fields in Fig. 9, the distinction is in the peak values: the two have similar estimates for the peak values of the large rain cell yet different estimates for those of the small cell. As for the comparison of the standard deviation maps in Fig. 10, a slight reduction in the standard deviation of Session II can be observed.
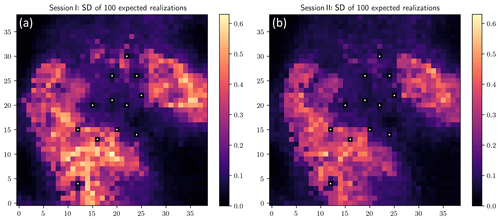
Figure 10Standard deviation of 100 expected realizations (mm) from Session I (a) and Session II (b).
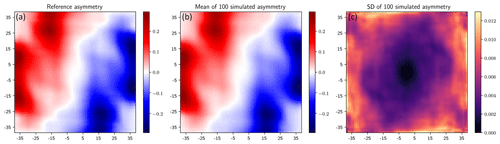
Figure 11(a) Reference asymmetry function. (b, c) Mean and standard deviation of 100 simulated asymmetry functions. Unit: –.
From the results shown in Figs. 9 and 10, the effect of adding the component asymmetry in the objective function seems to be minor, which is due to the fact that the two components (field pattern and asymmetry) share a special relationship: high similarity in terms of the pattern between the reference and the simulated field suggests high similarity in the asymmetry of the two as well. Yet, it does not work in reverse.
To show the capability of the proposed method in terms of fulfilling the component asymmetry, the mean of 100 simulated asymmetry functions is displayed in the middle in Fig. 11 in comparison with the reference asymmetry function (the one evaluated from the reference field) on the left. As for the analysis of the asymmetry function: first, it is a symmetrical function with respect to the origin (0, 0) (see the formula given in Eq. (8)); second, the value of each pixel is obtained by (a) shifting the simulated field by the coordinate of the pixel and then (b) evaluating Eq. (8) for the intersection of the shifted and the original field. This statistic could be computed more efficiently in Fourier space by generalizing the approach presented in Marcotte (1996). As shown in Fig. 11, the extremes of the asymmetry functions for both the reference and the mean simulated ones approach ±0.3. If one computes the asymmetry function for a spatial field obeying a multivariate Gaussian distribution, where symmetric behavior of the field is assumed, the function value approaches zero.
As shown in Fig. 11, the reference and the mean asymmetry are barely distinguishable. The standard deviation map, displayed on the right, reveals the small variability between the simulated asymmetry functions. Note that the presented asymmetry functions are evaluated from realizations of Stage 1. But a similar standard in terms of the fulfillment of the component asymmetry can be achieved by all the other results from Session II.
It is worth mentioning that a trick is used to reduce the computational cost substantially at a fairly low cost in terms of the estimation quality. In Sect. 3, when using multiple shifted quantile fields to produce the expected realization, one should be aware that these individual fields make fairly different contributions to the final estimate. By analyzing the Lorenz curve of the contribution of these individual fields (as shown in Fig. 12), i.e., the weights indicated by the probability matrix, one could see that the lowest several weights contribute very little to the accumulated total. Specifically, the top 9 weights (out of 23) contribute to 90 % of the accumulated total, the top 13 contribute to 95 %, the top 18 contribute to 99 %, and the top 19 contribute to 99.5 %. Being slightly conservative, we have chosen to use the top 19 contributors to produce the expected realization. Note that the top 19 weights should be scaled such that the sum of them equals 1. We have tested this trick (using 19 to represent 23) on the results from Session I (Stage 3). As expected, the difference between the expected realizations, obtained with and without using the trick, is tiny: the maximum difference is 0.050 mm, the minimum difference −0.058 mm, and the mean difference 0.001 mm. The results, shown in Figs. 9 and 10, are produced by using the trick, which helps in saving the computational cost (see Table 1 for details).
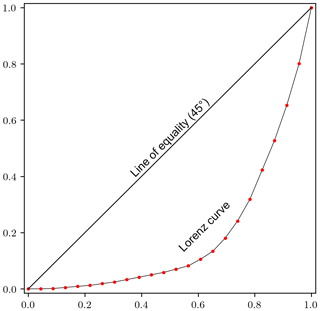
Figure 12Lorenz curve of the contribution of the individual shifted field, where the x axis denotes the cumulative share of population ordered by contribution from the lowest to the highest, and the y axis denotes the cumulative share of contribution.
The focus of this paper is to simulate rainfall fields conditioned on the local constraints imposed by the point-wise rain gauge observations and the global constraints imposed by the field measurements from weather radar. The innovation of this work comes in three aspects. The first aspect is the separation of the global and local constraints. The global characteristic of PA makes it a powerful methods for handling the global constraints. Thus PA is only used to deal with the global constraints, and the local ones are handed over to residual kriging. The separation of different constraints makes the best use of PA and avoids its insufficiency in terms of the fulfillment of the local constraints. The second is the extension of the PA algorithm. Except for annealing the system temperature, the number of perturbed phases is also annealed during the simulation process, making the algorithm work more globally in initial phases. The global influence of the perturbation decreases gradually at iterations as the number of perturbed phases decreases. The third is the integration of the uncertainty of the radar-indicated rainfall pattern by (a) simulating using the expectation of multiple shifted fields as the reference or (b) applying the simulation independently using multiple shifted fields as the reference and combining the individual realizations as the final estimate.
The proposed method is used to simulate the rainfall field for a 30 min event. The algorithm of PA is applied using different scenarios: with and without integrating the uncertainty of the radar-indicated rainfall pattern and with different objective functions. The capability of the proposed method in fulfilling the global constraints, both the field pattern and the directional asymmetry, is demonstrated by all the results. Practically, the estimates, obtained by integrating the uncertainty of the radar-indicated rainfall pattern, show a reduced estimation variability. And obvious displacements of the peak regions are observed compared to the estimates, obtained without integrating the uncertainty of the radar-indicated rainfall pattern. As for the two options to integrate the uncertainty of the radar-indicated rainfall pattern, (b) seems to be superior to (a) in terms of the substantial reduction in the estimation variability and the smoothness of the final estimates. As for the two simulation sessions using different objective functions, the impact of adding the component directional asymmetry in the objective function does exist, but it is not that prominent. This is due to the special relationship between the two global constraints: high similarity in the field pattern is a sufficient condition for high similarity in the directional asymmetry function (although the inverse is not true). Yet, compared to the results using the objective function containing solely the component field pattern, a slight reduction in the estimation variability is observed from the results using the objective function containing also the component directional asymmetry.
Four basic datasets required for simulating the 30 min rainfall event are available at https://doi.org/10.6084/m9.figshare.11515395.v1 (Yan, 2020). The other files and figures archived under this link are secondary and generated based on the four basic datasets. The displays of the input data are provided in the Python script inputDisplay.py.
The first author, JY, did the programming work, all the computations, and the manuscript writing. The second author, AB, contributed to the research idea and supervised the research. The third author, SH, provided a good opportunity to improve the program in terms of the efficiency. The fourth author, TT, provided valuable suggestions for the revision of this article.
The authors declare that they have no conflict of interest.
The radar and gauge data that support the findings of this study are kindly provided by the German Weather Service (DWD) and Stadtentwässerung Reutlingen, respectively.
This research has been supported by the National Natural Science Foundation of China (grant nos. 51778452 and 51978493).
This paper was edited by Nadav Peleg and reviewed by Geoff Pegram and two anonymous referees.
Bárdossy, A. and Hörning, S.: Process-Driven Direction-Dependent Asymmetry: Identification and Quantification of Directional Dependence in Spatial Fields, Math. Geosci., 49, 871–891, https://doi.org/10.1007/s11004-017-9682-1, 2017. a, b
Chilès, J. P. and Delfiner, P.: Geostatistics: Modeling Spatial Uncertainty, in: Series In Probability and Statistics, Wiley, https://doi.org/10.1002/9781118136188, 2012. a, b
Collier, C.: The impact of wind drift on the utility of very high spatial resolution radar data over urban areas, Phys. Chem. Earth Pt. B, 24, 889–893, https://doi.org/10.1016/S1464-1909(99)00099-4, 1999. a
Cristiano, E., ten Veldhuis, M.-C., and van de Giesen, N.: Spatial and temporal variability of rainfall and their effects on hydrological response in urban areas – a review, Hydrol. Earth Syst. Sci., 21, 3859–3878, https://doi.org/10.5194/hess-21-3859-2017, 2017. a
Deutsch, C. V. and Journel, A. G.: The application of simulated annealing to stochastic reservoir modeling, SPE Adv. Technol. Ser., 2, 222–227, https://doi.org/10.2118/23565-PA, 1994. a
Deutsch, C. V. and Journel, A.: GSLIB – Geostatistical Software Library and User's Guide, Technometrics, 40, 132–145, https://doi.org/10.2307/1270548, 1998. a
Deutsch, C. V.: Annealing techniques applied to reservoir modeling and the integration of geological and engineering (well test) data, PhD thesis, Stanford University, Stanford, CA, 1992. a
Doviak, R. J. and Zrnić, D. S.: Doppler radar and weather observations, 2nd Edn., Academic Press, San Diego, 523–545, 1993. a
Emmanuel, I., Andrieu, H., Leblois, E., and Flahaut, B.: Temporal and spatial variability of rainfall at the urban hydrological scale, J. Hydrol., 430, 162–172, 2012. a
Fabry, F.: Radar meteorology: principles and practice, Cambridge University Press, Cambridge, 2015. a, b, c
Gabella, M. and Notarpietro, R.: Ground clutter characterization and elimination in mountainous terrain, in: vol. 305, Proceedings of ERAD, Delft, the Netherlands, 2002. a
Geman, S. and Geman, D.: Stochastic Relaxation, Gibbs Distributions, and the Bayesian Restoration of Images, IEEE T. Patt. Anal. Mach. Intel., PAMI-6, 721–741, 1984. a
Guthke, P. and Bárdossy, A.: On the link between natural emergence and manifestation of a fundamental non-Gaussian geostatistical property: Asymmetry, Spat. Stat., 20, 1–29, https://doi.org/10.1016/j.spasta.2017.01.003, 2017. a
Hasan, M. M., Sharma, A., Johnson, F., Mariethoz, G., and Seed, A.: Merging radar and in situ rainfall measurements: An assessment of different combination algorithms, Water Resour. Res., 52, 8384–8398, https://doi.org/10.1002/2015WR018441, 2016. a
Heistermann, M., Jacobi, S., and Pfaff, T.: Technical Note: An open source library for processing weather radar data (wradlib), Hydrol. Earth Syst. Sci., 17, 863–871, https://doi.org/10.5194/hess-17-863-2013, 2013. a
Hörning, S. and Bárdossy, A.: Phase annealing for the conditional simulation of spatial random fields, Comput. Geosci., 112, 101–111, 2018. a, b, c, d
Jacobi, S. and Heistermann, M.: Benchmarking attenuation correction procedures for six years of single-polarized C-band weather radar observations in South-West Germany, Geomatics, Nat. Hazards Risk, 7, 1785–1799, 2016. a
Journel, A. G.: Geostatistics for conditional simulation of ore bodies, Econ. Geol., 69, 673–687, 1974. a
Khintchine, A.: Korrelationstheorie der stationären stochastischen Prozesse, Math. Annal., 109, 604–615, 1934. a
Kirkpatrick, S., Gelatt, C. D., and Vecchi, M. P.: Optimization by Simulated Annealing, Science, 220, 671–680, 1983. a
Krämer, S. and Verworn, H.: Improved C-band radar data processing for real time control of urban drainage systems, in: Proceedings of the 11th International Conference on Urban Drainage, 31 August–5 September 2008, Edinburgh, Scotland, UK, 1–10, 2008. a
Kumar, P. and Foufoula-Georgiou, E.: Characterizing multiscale variability of zero intermittency in spatial rainfall, J. Appl. Meteorol., 33, 1516–1525, 1994. a
Lantuéjoul, C.: Geostatistical Simulation: Models and Algorithms, Springer Science & Business Media, Berlin, 2013. a
Lauzon, D. and Marcotte, D.: Calibration of random fields by FFTMA-SA, Comput. Geosci., 127, 99–110, https://doi.org/10.1016/j.cageo.2019.03.003, 2019. a
Marcotte, D.: Fast variogram computation with FFT, Comput. Geosci., 22, 1175–1186, https://doi.org/10.1016/S0098-3004(96)00026-X, 1996. a
Martín, J. F. D. and Sierra, J. M. R.: A Comparison of Cooling Schedules for Simulated Annealing, in: Encyclopedia of Artificial Intelligence, edited by: Dopico, J. R. R., Dorado, J., and Pazos, A., 344–352, https://doi.org/10.4018/978-1-59904-849-9.ch053, 2020. a
Mendez Antonio, B., Magaña, V., Caetano, E., Da Silveira, R., and Domínguez, R.: Analysis of daily precipitation based on weather radar information in México City, Atmósfera, 22, 299–313, 2009. a
Nourani, Y. and Andresen, B.: A comparison of simulated annealing cooling strategies, J. Phys. A, 31, 8373–8385, 1998. a
Ravalec, M. L., Noetinger, B., and Hu, L. Y.: The FFT Moving Average (FFT-MA) Generator: An Efficient Numerical Method for Generating and Conditioning Gaussian Simulations, Math. Geol., 32, 701–723, https://doi.org/10.1023/A:1007542406333, 2000. a
Wiener, N.: Generalized harmonic analysis, Acta Math., 55, 117–258, 1930. a
Wood, A. T.: When is a truncated covariance function on the line a covariance function on the circle?, Stat. Probabil. Lett., 24, 157–164, https://doi.org/10.1016/0167-7152(94)00162-2, 1995. a
Wood, A. T. and Chan, G.: Simulation of stationary Gaussian processes in [0, 1] d, J. Comput. Graph. Stat., 3, 409–432, 1994. a
Yan, J.: Input data for conditional simulation of surface rainfall field (30 min accumulated rainfall) using phase annealing, Figshare, https://doi.org/10.6084/m9.figshare.11515395.v1, 2020. a
Yan, J. and Bárdossy, A.: Short time precipitation estimation using weather radar and surface observations: With rainfall displacement information integrated in a stochastic manner, J. Hydrol., 574, 672–682, https://doi.org/10.1016/j.jhydrol.2019.04.061, 2019. a, b, c