the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Worldwide lake level trends and responses to background climate variation
Benjamin M. Kraemer
Anton Seimon
Rita Adrian
Peter B. McIntyre
Lakes provide many important benefits to society, including drinking water, flood attenuation, nutrition, and recreation. Anthropogenic environmental changes may affect these benefits by altering lake water levels. However, background climate oscillations such as the El Niño–Southern Oscillation and the North Atlantic Oscillation can obscure long-term trends in water levels, creating uncertainty over the strength and ubiquity of anthropogenic effects on lakes. Here we account for the effects of background climate variation and test for long-term (1992–2019) trends in water levels in 200 globally distributed large lakes using satellite altimetry data. The median percentage of water level variation associated with background climate variation was 58 %, with an additional 10 % explained by seasonal variation and 25 % by the long-term trend. The relative influence of specific axes of background climate variation on water levels varied substantially across and within regions. After removing the effects of background climate variation on water levels, long-term water level trend estimates were lower (median: +0.8 cm yr−1) than calculated from raw water level data (median: +1.2 cm yr−1). However, the trends became more statistically significant in 86 % of lakes after removing the effects of background climate variation (the median p value of trends changed from 0.16 to 0.02). Thus, robust tests for long-term trends in lake water levels which may or may not be anthropogenic will require prior isolation and removal of the effects of background climate variation. Our findings suggest that background climate variation often masks long-term trends in environmental variables but can be accounted for through more comprehensive statistical analyses.
- Article
(6147 KB) - Full-text XML
-
Supplement
(267 KB) - BibTeX
- EndNote
The water level of a lake is an integrative indicator of local and regional hydrology. By extension, variation in lake water levels through time captures the dynamic nature of the water cycle, particularly when coherent patterns are observed across many lakes (Crétaux et al., 2016; Molinos et al., 2015; Zhang et al., 2011). Water level variation is often associated with oscillatory dynamics in earth's hydroclimate such as the El Niño–Southern Oscillation (ENSO) (Ghanbari and Bravo, 2008; Stager et al., 2007), the Pacific Decadal Oscillation (PDO) (Benson et al., 2003; Wang et al., 2010), the North Atlantic Oscillation (NAO) (Benson et al., 1998), and the Indian Ocean Dipole (IOD) (Marchant et al., 2007). For instance, water levels in multiple lakes in Poland can increase by 20 cm or more during the positive phase of the NAO (Wrzesiński et al., 2018). When multiple axes of background climate variation overlap, the effects can be even more intense – due to strong oceanic temperature anomalies in the late 1990s associated with both the ENSO and the IOD, water levels in eight East African Great Lakes went up by more than 1 m in less than a year (Mercier et al., 2002). This constituted a combined increase in water storage of more than 266 km3 – more than half the volume of Lake Erie.
Human activities can also directly affect lake water levels, creating variation that is independent of background climate dynamics (Aladin et al., 2009; Pekel et al., 2016; Rodell et al., 2018; Tao et al., 2015). For instance, in the 1970s, the two main inflowing rivers to the Aral Sea were diverted in an attempt to irrigate cotton plantations in Central Asian deserts (Aladin et al., 2009; Micklin, 1988). As a result, the water level in the Aral Sea dropped by 2 m in the first decade following the onset of irrigation, and continued to decline as water use in the watershed intensified. In this case, attribution of water level variation to human activity was robust because an abrupt change in surface water management coincided with a comparably abrupt change in the water level of downstream lakes. However, attributing water level variation to human activity is more difficult when anthropogenic effects are subtle relative to the effects of background climate variation (Corti et al., 1999). This challenge is especially salient when attributing water level variation to anthropogenic climate change (Hassanzadeh et al., 2012; Rodell et al., 2018), especially at the global scale (Rodell et al., 2018). Indeed, there is an ongoing debate about the global extent and strength of climate change effects on water level variation in lakes (Muller, 2018).
Climate change can affect water levels through a complex web of forces linking surface temperature with hydrology (Block and Strzepek, 2012; Ramanathan et al., 2001; Rodell et al., 2018). While warming has been observed across the earth's surface, hydrological responses to warming are highly variable, with some areas becoming wetter and others becoming dryer (Greve et al., 2014; Rodell et al., 2018; Wang et al., 2012). However, more than three-quarters of earth's land mass has seen no substantial change in total wetness or dryness in response to recent climate change (Greve et al., 2014; Greve and Seneviratne, 2015). Thus, the effects of climate change on water levels may be subtle relative to background climate variation (Jöhnk et al., 2004), calling for statistical approaches that can effectively account for the effects of background climate variation. Analyzing water levels from lakes worldwide may be especially helpful in reducing uncertainty about the potential contribution of background climatic variation to long-term trends.
Here, we build off previous studies focused on specific lake regions (Clites et al., 2014; Molinos and Donohue, 2014; Molinos et al., 2015; Pasquini et al., 2008) and attempt to disentangle the effects of background climate variation from other drivers of water levels in 200 globally distributed lakes using time series of remotely sensed water levels from 1992 to 2019. We investigate two key areas of uncertainty: (1) whether apparent anthropogenic water level trends in specific lakes can be explained by background climate variation and (2) whether trends in water levels can be detected in specific lakes only after accounting for and removing the influence of background climate variation. We use boosted regression trees (BRTs) as a means of removing the effects of background climate variation on water levels in each lake, enabling us to achieve more robust quantification of the multi-decadal trends which may or may not be anthropogenic. This approach differs from other recently published approaches (Chanut et al., 1988; Molinos et al., 2015) in that it allows for nonlinear relationships, high levels of interactions between axes of climate variation, nonstationarity, and missing data. Finally, we assess patterns across lakes to generalize about which regions are most strongly influenced by background climate variation. Our overall goal is to better understand the impact of large-scale background climate forcing on lakes in ways that will help communities manage the benefits derived from lakes in the face of global climate dynamics and anthropogenic influences.
2.1 Overview
The 200 lakes included in our study contain much of the earth's liquid surface freshwater and a large proportion of freshwater biodiversity (Vadeboncoeur et al., 2011). They span a wide range of lake characteristics including surface area (23 to 377 002 km2), catchment area (93 to 2 764 126 km2), perimeter (62 to 15 829 km), latitude (−50.22 to 66.14∘ N), and elevation (−71 to 5194 m above sea level) (Supplement). All continents were represented except for Antarctica and Australia. According to the HydroLAKES database (Messager et al., 2016), at least 78 of these lakes are reservoirs, and 18 of them have some water level regulatory structure such as a dam. The global scope of this analysis builds off similar analyses which aimed to disentangle background climate variation's influence on lake water levels using smaller numbers of lakes from specific regions (Mercier et al., 2002; Molinos et al., 2015) or specific lakes (Cohn and Robinson, 1975; Stager et al., 2005; Tomasion and Valle, 2000).
Our first objective was to estimate trends in water levels in this global sample of lakes based on average annual water level. Annual water levels were used in the trend analysis instead of raw water levels so that trend residuals would not be serially autocorrelated. We calculated trends using Theil–Sen non-parametric regression using the “zyp” package in R. Theil–Sen slopes represent the median of slopes derived from all pairwise combinations of points in a time series. The statistical significance of each trend (p value) was calculated using a bootstrapped one-sample Wilcoxon signed-rank test with 1000 repetitions where the input data for the test was the complete list of all slopes derived from all pairwise combinations of points in the time series. The number of pairwise slopes used in each repetition of the Wilcoxon signed-rank test was equal to the number of years of water level data for each lake.
Our second objective was to characterize and account for the effects of background global climate variation on lake water levels. We did this by using BRTs to model water level variation in each lake as a function of the year, the month of the year, and a large set of global climate indices. We calculated the relative importance of each global climate index in the models for each lake to assess its sensitivity to different axes of background climate variation. We use the partial dependence of water level variation on the year term in the model to reflect the long-term variation in water levels that is not attributable to background climate variation. We repeat the Theil–Sen slope calculation and p-value calculation based on the partial dependence data for the year term as an estimate of the long-term trend that is not attributable to background climate variation. This remaining variation could be attributable to human activity, though we cannot draw causal conclusions or distinguish between the various aspects of human activity which can affect water levels.
We derived the background global climate indices for each lake's BRT using principal component analysis (PCA) applied to global variation in monthly earth surface air temperature data through time. This approach is widely applied in the climate sciences to global grids of temperature, pressure, or rainfall data and is analogous to empirical orthogonal function (EOF) analysis (Dommenget and Latif, 2008; Hannachi et al., 2009; Kim and Wu, 1999). Temperature time series at each pixel were included as separate variables in the PCA with each time step as a separate observation of those variables. We linearly detrended temperature variation at each pixel such that the temperature values were equivalent to the residuals from a Theil–Sen regression through time. Temperatures were detrended because long-term temperature trends could be considered potentially related to anthropogenic climate change, which we wanted to separate from the principal components (PCs) representing background climate (Stenseth et al., 2003). Thus, the effect of all PCs on water levels in the BRTs were interpreted as the collective effects of background surface air temperature variation and its associated hydrological effects on lake levels.
Using the PCs was preferred over using the commonly recognized climate indices (NAO, ENSO, IOD, etc.) directly in each lake's BRTs for several reasons. First, many commonly recognized global climate indices are correlated, which makes them problematic for simultaneous use as predictors, whereas the PCs used here are uncorrelated by definition. Second, using the commonly recognized global climate indices alone would miss a substantial amount of variation in air temperature that may still drive climate and hydrological variation in lakes but is not yet well recognized. Third, many of the commonly recognized global climate indices are defined subjectively (e.g., average temperature difference between two subjectively defined areas of the ocean), whereas the PCs used here are less subjective.
Our modeling approach is based on the recognition that much of the variation in water levels is directly or indirectly driven by global patterns in earth's surface air temperature via the effects of global temperatures on hydrological fluxes (Dommenget and Latif, 2008). This relationship is well supported because earth's surface air temperature is a key control on earth's hydrological cycle through the Clausius–Clapeyron relation, which, in turn, drives lake water budgets and water levels (Christensen et al., 2004; Fowler et al., 2007; Nijssen et al., 2001; Tierney et al., 2008). Earth's surface air temperature may also be a key control on the positioning of atmospheric rivers, which can also drive lake water budgets and water levels (Gimeno et al., 2014; Lorenzo et al., 2008). This assumption is empirically well supported by studies showing that earth surface air temperature variation described by ENSO, PDO, and IOD is strongly associated with water level variation across the globe (Stager et al., 2007; Tierney et al., 2013; Wang et al., 2010).
Disentangling the direct and indirect effects of earth surface air temperature variation on water level variation could be done using a reductionist approach, i.e., by constructing lake hydrological budgets with all of the water inputs and outputs and modeling the effect of human activity on each of those fluxes. But, for most lakes in our dataset, we lack the field measurements required to model the forces linking earth surface air temperature to water level variation for the entire 28-year water level time series (Hegerl et al., 2015; Stenseth et al., 2003). So instead, we use BRTs which mimic the complex web of forces linking earth surface air temperature variation to water level variation. We use BRTs for this purpose because the model structure accommodates high levels of interactions among predictor variables and mimics the interactive and indirect effects we tried to capture. This approach also differs from other recently published approaches (Chanut et al., 1988; Molinos et al., 2015) in that it allows for nonlinear relationships, nonstationarity, and missing data. We fit BRTs separately for each lake because the influence of a particular climate oscillation could differ across lakes due to geographic forcing, orographic forcing, or other local factors (Stenseth et al., 2003). We used backward-elimination variable selection techniques to identify the PCs for each specific lake that, when fit against a training dataset, performed the best when predicting water level variation in a test dataset with which the model had not been fit. Then, we used the resulting BRTs to determine the relative importance of different axes of background climate variation separately for each lake.
2.2 Data
Water level data were acquired from the NASA/CNES Topex/Poseidon and Jason satellite missions via the Global Reservoir and Lake Monitoring (G-REALM) project version 2.3 (Crétaux and Birkett, 2006) and can be obtained from http://www.pecad.fas.usda.gov/cropexplorer/global_reservoir (last access: 24 January 2020). Although these altimeters were developed to map ocean surface height, they have also been used to detect water level changes in lakes (Birkett, 1995). Only a small subset of the world's lakes can be monitored in this way because the spaceborne sensors must pass directly over the lake with sufficient regularity to produce accurate and complete time series. The US Department of Agriculture (USDA) uses these data to monitor water level variation for many inland water bodies globally. The lakes in this study comprise the 200 lakes with the longest (> 28 years) and highest-temporal-resolution time series (greatest number of samples per year). Validation of satellite altimeter data over inland water bodies is typically performed by comparing satellite altimeter measurements and in situ measurements. The root mean squared error of elevation variations derived from the NASA/CNES Topex/Poseidon and Jason-1 satellite missions is typically ∼5 cm for large lakes based on the USDA G-REALM website (https://ipad.fas.usda.gov/cropexplorer/global_reservoir/validation.aspx, last access: 24 January 2020). Thus, it is justifiable to use altimetry water level observations in place of in situ gauge measurements (Birkett et al., 2011).
Water levels are typically measured every 10 d, but the exact dates on which water levels are measured vary from lake to lake. To make water level data temporally consistent, we linearly interpolated each lake's time series to the daily scale using the “deseasonalize” and “zoo” packages in R (R Core Team, 2017). Monthly averages were calculated so that all lakes had time series of the same interval that also matches the temporal resolution of surface air temperature data used in the PCA. Seventy of the 200 water level time series had a data gap from late 2002 through the middle of 2008. The missing data were not estimated; instead, our analyses treated these lakes in the same way as lakes with complete data.
Monthly average land and ocean surface air temperature anomaly data were acquired from the Goddard Institute for Space Studies (GISS) land–ocean temperature index analysis for a 2×2∘ grid with 1200 km smoothing (Hansen et al., 2010). These temperature data are derived from meteorological station observations distributed across the globe and processed according to methods developed at the National Aeronautics and Space Administration (NASA) (Hansen et al., 2010). They are publicly available at https://data.giss.nasa.gov/gistemp/ (last access: 24 January 2020).
2.3 Principal component analysis
We used PCA to distill the spatial complexity of surface air temperatures for inclusion in each lake's BRT. PCA is an ordination-based statistical tool that converts potentially correlated variables into a set of orthogonal vectors that capture the variation across locations. PCA uses orthogonal linear transformation to identify vectors that account for as much of the total variation in a set of variables as possible. The first PC (PC1) explains the largest percentage of the variation in the underlying set of variables, followed by the second (PC2), third (PC3), and so on. Each succeeding PC is linearly uncorrelated to the others and accounts for as much of the remaining variation as possible. PCA can, therefore, be used to summarize the consistent aspects of time dynamics across space and reduce redundant spatial variation (stemming from spatial autocorrelation and teleconnections) in temperature.
To identify which known oscillations in surface air temperature are related to individual PCs, we calculated a complete correlation matrix between each PC and all of the 43 major climate indices recognized by NOAA's Earth System Research Laboratory. For indices that are not updated to the present, we calculated the correlation over the longest time period over which each major climate index was available. Monthly time series of major climate indices were sourced from https://www.esrl.noaa.gov/psd/data/climateindices/list/ (last access: 24 January 2020). In cases where a PC is highly correlated to one of the major climate indices (PCs), we renamed it with a subscript (e.g., PCENSO) to facilitate interpretation. In all remaining cases, PCs were named with a numeric subscript which matched their order in the PCA (e.g., “PC18”)
2.4 Boosted regression trees (BRTs) and model selection
BRTs were used to model mean monthly water levels in the lakes as a function of year, the month of the year, and a large set of PCs. A BRT is an ensemble machine learning approach that differs from conventional statistical techniques which use a single parsimonious model. Instead, BRTs combine the strengths of standard regression trees and boosting – a method for aggregating many models to improve the predictive capacity. The main advantages of BRTs over other statistical models are that they have higher predictive performance, do not require data transformation or outlier elimination, automatically handle complex nonlinear relationships and interactions, and allow for many types of predictor variables and partial missing data. Through these interactions, the BRT allows for nonstationarity of the times eries (e.g., the effect of each PC is allowed to change over time). We fit BRTs using the “dismo” and “gbm” packages (Hijmans et al., 2017) in R (R Core Team, 2017). To cross-validate the BRTs for each lake, we fit the model using a training dataset and then used the fit BRT to predict monthly water levels using the PC values from a test dataset. For each lake, we fit six starting models using six different training and test dataset combinations. To get these dataset combinations, we first split the lake level time series for each lake into training and test datasets along its time series using 40–60, 50–50, and 60–40 splits. We split the data serially along the time series into training and test datasets instead of by randomly selecting observations for the training and test datasets because the data are temporally autocorrelated and we wanted to ensure that the training and test datasets were independent. For each of the three splits, the starting model was fit twice, once using the first part of the split as a training dataset and the second part as a test dataset, and once using the second part of the split as a training dataset and the first part as a test dataset, resulting in a total of six train–test dataset combinations. For each lake's six train–test dataset combinations, we repeatedly refit the starting model after dropping the PC with the lowest relative importance averaged across all six train–test dataset combinations (see explanation of relative importance below) until the starting model had only two predictors – the minimum number of predictors allowed in a BRT. Each time a variable was dropped from one of the six starting models, we calculated the average change in predicted residual error sum of squares (PRESS; the sum of squares of the prediction residuals calculated using the test data) which resulted from dropping it.
Variables which, when dropped from the model, resulted in an average increase in PRESS across the six starting models were selected in that lake's “best BRT”. We combined information across models so that the selection of a variable did not depend on the arbitrary decisions of where to split the time series and whether to use the first or second part as the training dataset. All 336 PCs were used as predictors at the beginning of the model selection process because even very high order PCs can be important variables in a model (Phinyomark et al., 2015), and many of the high-order PCs calculated here were statistically distinguishable from random noise (Supplement). Thus, the best BRT included the year, the month, and the combination of PCs from PC1 to PC336 which consistently improved its performance in cross-validation. A maximum of 336 PCs could be calculated from 336 monthly observations of temperature over the 28-year span of the lake level time series. This best combination of PCs, specific to each lake, was used for determining the relative importance of the variables selected in the best model. We refit the best BRT for each lake to the full time series to calculate the final relative importance values of each PC. The relative importance of each predictor variable in the model is a function of the frequency with which it was included in the BRT's individual regression trees and the improvement to the model that resulted from its inclusion (Elith et al., 2008). The relative importance of variables that were not selected in each lake's best BRT was set to zero.
We observed considerable variation in water levels within the 200 lakes in our analyses (Fig. 1). Prior to accounting for the effects of background climate variation, water levels increased at a median rate of 1.2 cm yr−1 (interquartile range: −0.3 to 4.1 cm yr−1) (Fig. 1). Water levels were decreasing in 60 lakes (30 %), of which 14 were statistically significant (p < 0.05 level), and increasing in 140 lakes (70 %), of which 51 were statistically significant (p < 0.05 level). In total, 65 lakes (32.5 %) in our analyses had significant trends in water level (Fig. 1). Given a significance level of α=0.05, we would expect only 10 of our 200 lakes to show “significant” trends by chance; thus, we observed far more significant long-term trends than predicted by chance alone (Fig. 1). A comparable disparity was observed across a range of different arbitrary thresholds for statistical significance (i.e., 0.01, 0.05, and 0.1).
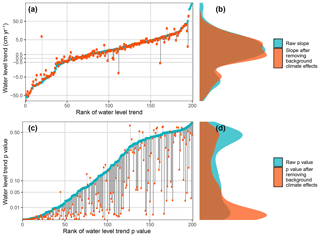
Figure 1The change in each lake's water level trend (a, b) and their trend p value (c, d) which resulted from removing the effects of background climate variation on water level variation in 200 globally distributed large lakes. After removing the effects of background climate variation on water levels, long-term water level trend estimates (orange) were slightly more conservative overall compared to rates calculated from the raw water level data (turquoise). The median value of water level trends across lakes changed from +1.2 to +0.8 cm yr−1 after removing the effects of background climate variation. The trends became more statistically significant in most (86 %, black lines below the curve) but not all lakes (14 %, gray lines above the curve) after accounting for the effects of background climate variation. The median p value of water level trends across lakes changed from 0.16 to 0.02 after removing the effects of background climate variation. Lakes are ranked independently in panels (a) and (c).
Changes in water levels from 1992 to 2019 displayed a moderate level of regional consistency in the direction and magnitude of water level trends (Fig. 2). In particular, lakes in the Middle East and the southwest United States tended to have decreasing water levels (Fig. 2). Lakes in Canada and Europe tended to have weak or increasing water level trends. Water level trends in East Asia and Africa were highly variable from lake to lake (Fig. 2).

Figure 2Long-term trends in water levels prior to removing the effects of background climate variation. Some lakes – including those in the southwest United States, parts of Africa, and the Middle East – show regionally consistent patterns in water levels.
BRTs performed well for most lakes in our cross-validation and model optimization procedure; the median PRESS of the best model was 7.0 cm (interquartile range: 3.5–85.7 cm) across lakes. Two lakes with known anthropogenic water level dynamics, both of which are reservoirs on the Mekong River in China, performed poorly in cross-validation because they had water level increases > 50 m as a result of dam construction in the middle of the time series (Nuozhadu and Xiaowan dams). Across lakes, the best model included a median of 11 of the 336 PCs (interquartile range: 3–19 PCs) that were fed into our model selection procedure. One hundred fifty-four out of 336 PCs were never selected in any lake, and the overall frequency of inclusion across lakes decreased with PC order (Kendall's tau , p < 0.01). The median percentage of water level variation associated with background climate variation was 58 % (inner quartile range: 33–74 %) with an additional 10 % (inner quartile range: 4–22 %) explained by seasonal variation and 25 % (inner quartile range: 13–50 %) explained by the long-term trend.
The relative importance of each specific predictor variable varied substantially from lake to lake. Based on the median relative importance values across lakes, the year and the month most strongly influenced water level variability. PC1, PC4, PC5, and PC6 were the predictor variables with the third (2.6), fourth (1.6), fifth (1.5), and sixth (1.4) highest median relative importance in the best-performing BRTs (Fig. 3). PC1 was strongly correlated with the multivariate El Niño index (MEI; Kendall's tau =0.68, p < 0.01), PC4 was correlated with the Atlantic Multidecadal Oscillation (AMO; Kendall's tau =0.26, p < 0.01), PC5 was correlated with the Arctic Oscillation (AO; Kendall's tau =0.30, p < 0.01), and PC6 was correlated with the Indian Ocean Dipole (IOD; Kendall's tau =0.21, p < 0.01), so we renamed them here as PCENSO, PCAMO, PCAO, and PCIOD, respectively (Figs. 3–4). These four PCs together encompass 22.0 % of the variation in surface air temperature anomalies according to the eigenvalues from the PCA (PCENSO=9.2 %, PCAMO=5.5 %, PCAO=4.0 %, and PCIOD=3.3 %). PCENSO, PCAMO, PCAO, and PCIOD were selected in the best models for 107, 78, 69, and 70 lakes, respectively, but the direction of their effects differed among lakes (Fig. 3). Many of the remaining PCs of high mean relative importance across waterbodies were only moderately correlated to indices from NOAA (Kendall's correlation coefficient < 0.2). For instance, PC18 was not substantially correlated with any climate index recognized by NOAA (maximum Kendall's tau =0.14, p < 0.01) yet exhibited the 11th-highest median relative importance in explaining water levels across lakes (Fig. 5).
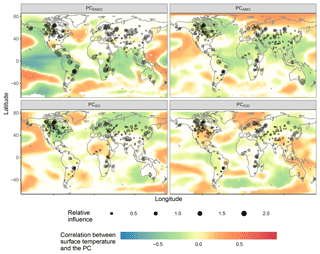
Figure 3The relative influence of different axes of background climate variation (PCs) on water level variation. Empty dots represent lakes for which the PC was not selected in its “best model”. The opacity of each colored pixel in each map is related to the significance of the correlation between the PC and temperature at that pixel, with less significant correlations appearing white.
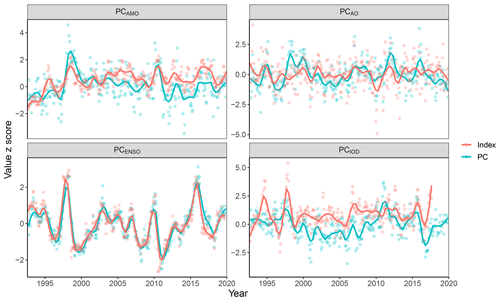
Figure 4Time series of background climate variation for the four PCs that were most influential in the best models of water level variation on average across lakes. PCs (PCAMO, PCAO, PCENSO, and PCIOD) and their corresponding climate indices (AMO, AO, ENSO, and IOD) are transformed to their z scores so that they can be more easily compared on the same unit-less scale. The dots represent raw values, and the lines represent locally weighted scatterplot (LOWESS)-smoothed time series.
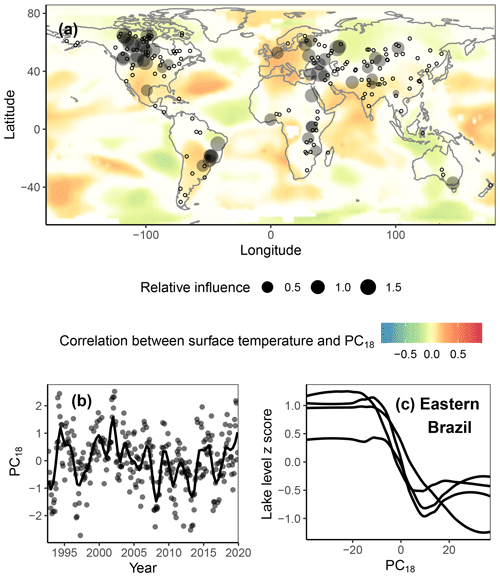
Figure 5PC18 is an example of a PC which was important for explaining water levels but was not strongly correlated with any of the climate indices recognized by NOAA. In panel (a), empty dots represent lakes for which PC18 was not selected in its “best model”. The opacity of each colored pixel in each map is related to the significance of the correlation between the PC and temperature at that pixel, with less significant correlations appearing white. In panel (b), the dots represent raw values of PC18, and in panels (b) and (c) the lines represent LOWESS-smoothed values.
PCENSO, PCAMO, PCAO, and PCIOD were strongly related to water level variation in lakes around the world, but the strength and directionality of those effects were regionally concentrated (Fig. 6). The strongest effects of PCENSO were concentrated in the tropics, where it had positive effects on water levels (Fig. 6). PCAMO was more positively associated with water levels in the Midwestern United States and negatively associated with water levels in northern Canada and East Africa. PCAO was also selected in the best models of lakes that were regionally concentrated; it was positively associated with water levels in Central Asia, while it was negatively associated with water levels in parts of Canada, Alaska, northern Europe, Brazil, and East Africa (Fig. 6). PCIOD was positively associated with water levels in Europe (Fig. 6).
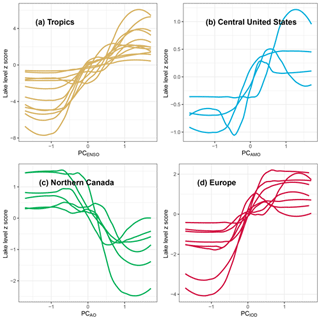
Figure 6Regional consistency in the directionality of PCENSO, PCAMO, PCAO, and PCIOD effects on water level variation. Each line represents a LOWESS-smoothed relationship between water level variation in a specific lake and one of the four PCs. Water levels have been transformed into z scores so that they may all be plotted on the same axis.
After removing the effects of background climate variation on water levels using the fitted BRTs, water level trend estimates were shallower compared to estimates from the original time series (Fig. 1). The median water level trend across lakes dropped from +1.2 to +0.8 cm yr−1 after correcting for background climate variation (Fig. 1). Even though they were lower on average, the trends became more statistically significant in 86 % of lakes (Fig. 1). Indeed, the median p value of water level trends across lakes changed from 0.16 to 0.02 after removing the effects of background climate variation (Fig. 1). For instance, prior to removing the effects of background climate variation, Becharof Lake in Alaska had an increasing trend (+0.40 cm yr−1) with relatively low statistical significance (p value =0.15). However, after accounting for the effects of background climate variation, the trend was not substantially affected (from +0.40 to +0.51 cm yr−1) but became substantially more statistically significant (p value from 0.15 to < 0.01). Based on inspection of the time series of water levels in Lake Becharof, we suspect that the strong climate oscillations affecting lake levels throughout the time series, in particular the water level local minima in 1998 and 2017 as well as the local maxima in 2003 and 2013, masked the long-term trend (Fig. 7). In contrast, prior to removing the effects of background climate variation, Gods Lake in Canada had an increasing trend (+1.26 cm yr−1) with a relatively low statistical significance (p value =0.35). However, after accounting for the effects of background climate variation, the trend flipped sign and was much weaker (from +1.26 to −0.10 cm yr−1) and less statistically significant (p value from 0.35 to 0.58). Based on inspection of the time series, we suspect that a series of three local water level minima early in the lake level time series in 1996, 2000, and 2004 created a specious appearance of a long-term trend in Gods Lake (Fig. 7) that went away when those minima were attributed to background climate.
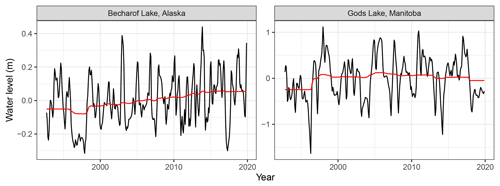
Figure 7Water level time series for two North American lakes which show the potential for background climate variation to mask long-term trends (Becharof Lake) and the potential for climate variation to give rise to the false appearance of long-term trends (Gods Lake). The water level trend in Becharof Lake in Alaska became more significant after accounting for background climate variation, and the water level trend in Gods Lake in Manitoba became less significant after accounting for background climate variation. Raw data are shown here, but all trends were calculated based on annual averages. The black line is the raw water level data, and the red line is the partial dependence of water level on the year term in the boosted regression trees.
We detected long-term trends in water levels before and after accounting for background climate variation in most lakes in our analyses. The evidence of trends in the majority of lakes belies reports that most of the earth has experienced no consistent changes in annual wetness and dryness (Greve et al., 2014; Greve and Seneviratne, 2015). This contrast highlights the potential for waterbody surface levels to serve as integrative metrics of regional water budgets, thereby enhancing our ability to detect hydrological changes.
Background climate variation had significant effects on water levels in most large lakes between 1992 and 2019. Infrequently, the effects of multiple axes of background climate variation gave rise to the appearance of long-term trends which became less significant once background climate variation was factored out. But more often, background climate variation masked underlying trends in water levels which were detected when the effects of background climate were factored out (Supplement Table S2). Thus, attempting to detect anthropogenic effects on water levels using water level time series without accounting for background climate variation may over- or underestimate the multi-decadal water level trends in lakes.
The trends in water levels estimated here differed widely among lakes, presumably reflecting the heterogeneity of underlying changes in regional hydrological fluxes. Rising water levels in the majority of lakes may be attributable to increases in precipitation within their watersheds (Bintanja and Selten, 2014; Chadwick et al., 2013; IPCC, 2014; O'Gorman et al., 2012). However, even in watersheds which have experienced increased precipitation, greater inputs of water may be offset or even exceeded by increases in evapotranspiration (Dorigo et al., 2012; Vinukollu et al., 2011; Vörösmarty et al., 2000; Vörösmarty and Sahagian, 2006) that yield net decreases in water levels.
Not all of the lakes with significant trends in water levels followed the “wet gets wetter and dry gets dryer” pattern that is often predicted to occur with climate change (Wang et al., 2012). According to such predictions, surface water storage would be expected to decrease in many dry mid-latitude and subtropical regions, and to increase at high latitudes and in humid mid-latitude regions (IPCC, 2014). Several lakes with the strongest decreases in water levels (Aral, Mosul, Powell, Rakshastal, Salton, Tharthar, and Urmia) are indeed located in relatively dry regions (average long-term discharge/watershed area < 5000 cm3 s−1 km−2). Furthermore, several lakes with the strongest increases in water levels (Zeyaskoye and Atitlán) are located in relatively wet regions (average long-term discharge/watershed area > 5000 cm3 s−1 km−2). However, the intensification of wet–dry contrasts was violated in many places as some lakes in wet regions got dryer (Vermelha, Winnebago, and Woods) and some lakes in dry regions got wetter (Balkhash, Cahora Bassa, Kapachagay, Kariba, and Ulungar). This finding adds to others showing that a range of hydrological fluxes contradict the “wet gets wetter and dry gets dryer” pattern over land (Byrne et al., 2015). As a specific example from our study, Lake Turkana had a significant increase in water level from 1992 to 2019 despite being in a very dry region. Thus, intensification of contrasts in precipitation may be a useful heuristic for predicting water level trends in some regions but is clearly inapplicable at the global scale (Greve et al., 2014; Greve and Seneviratne, 2015).
The changes in water levels in response to the four most important PCs (PCENSO, PCAMO, PCAO, and PCIOD) often matched the direction of change predicted from the hydrological changes associated with these particular climate oscillations. For instance, we observed strong negative relationships between PCENSO and water levels for many waterbodies in sub-Saharan Africa, the equatorial Americas, and central Canada, as would be predicted based on studies of the global effects of ENSO on precipitation (Dai and Wigley, 2000; Ropelewski and Halpert, 1987). We also observed water level changes in North America as a function of PCAMO that are consistent with predictions from observed regional changes in rainfall associated with AMO (Wang et al., 2017). However, we also detected relationships between water levels and PCs that were not consistent with the known hydrological effects of the ENSO, AO, AMO, and IOD. For example, we found that PCAO had a strong effect on water levels in East Africa, where the AO is not typically considered to be a major driver of hydrological fluxes. However, the correlation between PCAO and the AO was relatively weak, so the apparent influence of PCAO could be driven by climate variation that was captured by PCAO and not the actual AO index.
Fifty-eight percent of the explained variation in water levels (median across lakes) could be attributed to large-scale climate drivers as represented by the 336 PCs derived from air temperature records. We included higher-order PCs because they might have accounted for additional variation in water levels. But we note that higher-order PCs encompassed far less of the variation in surface air temperatures, and they were included in far fewer of the lakes' best water level models, so their implications for water levels are far weaker. For example, PC100 explained only 0.1 % of variation in global surface air temperatures and was included in our best-performing model for four lakes, albeit with very low explanatory contribution in those cases. Thus, excluding high-order PCs is unlikely to lead to substantial improvements or changes to our conclusions. The performance of the BRTs might be improved by including lag effects (Hansen et al., 1998; Hidalgo and Dracup, 2003). However, the computation time required to include lag effects was prohibitive.
Our interpretations of the statistical patterns reported herein require several caveats. First, there is substantial debate over which aspect of human activity (e.g., climate change, land use change, or dam construction/management) is most important for driving water levels (Gyau-Boakye, 2001; Lenters, 2001; Mercier et al., 2002; Ricko et al., 2011; Wurtsbaugh et al., 2017). Our modeling approach does not discern whether the trends we calculated are anthropogenic or which aspects of human activity are driving water level trends. Hence, future work is needed to disentangle the various anthropogenic forces which may influence water levels. Detecting anthropogenic water level trends and distinguishing between the effects of different aspects of human activity on water levels could be achieved by including water level dynamics in earth system models. To date, lake ecosystems are generally oversimplified in such models, in which lakes are often assumed to be relatively static, inert bodies on the landscape.
Second, we interpreted the trend in the partial dependence values for the year term in each lake's BRT as being potentially anthropogenic. However, we cannot exclude the possibility that anthropogenic water level variation was attributed to background climate PCs themselves in cases where PCs are highly correlated with human activity. Human water extraction may consistently be a larger proportion of total water fluxes during certain phases of the ENSO cycle, for example. In the BRTs, this aspect of anthropogenic water level variation would have been captured by PCENSO rather than the year term and would have been erroneously attributed to background climate variation. However, if the correlation between human water extraction and ENSO changed over time, it would be correctly attributed to the year variable in the BRTs, in general accordance with our simplified interpretations.
Third, we distinguish between anthropogenic climate change and background climate variation in our interpretations because background climate indices like those used here are generally considered to be modes of natural variation. However, human activity may influence background climate variation as well, perhaps making certain phases of various climate oscillations more likely (Cai et al., 2015; Capotondi and Sardeshmukh, 2017; Timmermann et al., 1999). We partially accounted for this by removing any linear trend through time in temperature prior to the PCA. Detrending the temperature data in this way helped to separate the background climate indices from any ongoing climate change. However, more complex interactions between climate change and background climate variation would not be removed by this approach, as in a scenario where climate change enhances both positive and negative phases of background climate oscillations yet has no impact on trends of the mean. Research on such complex relationships is still inconclusive (Allen and Ingram, 2002; Cane, 2005; Collins, 2000; Guilyardi et al., 2009; van Oldenborgh et al., 2005), so we performed only linear detrending of PCs. We also recognize that our 28-year time series could also reflect longer-period climate oscillations such as the Pacific Decadal Oscillation, but the limited duration of altimeter-based satellite monitoring of lake levels precludes testing for such influences.
The lakes represented in our study comprise a substantial portion of the global liquid surface freshwater on the planet. Our study includes the 10 most voluminous freshwater lakes on earth's surface (Baikal, Tanganyika, Superior, Michigan, Huron, Malawi, Victoria, Great Bear, Ontario, and Great Slave), which collectively contain more freshwater (total 80 241 km3) than has been withdrawn from the environment by humans at the global scale over the last 20 years (Food and Agriculture Organization of the United Nations, 2016). But the lakes in this study are not representative of all lakes, which tend to have smaller surface area and shallower maximum depths on average. Thus, the relative importance of background climate oscillations in the remainder of lakes other than the 200 large lakes studied here over the last 28 years remains uncertain and should be investigated further.
Our modeling approach could be widely applied to disentangle the effects of background climate on other hydrological changes, including streamflow and pan evaporation rates. The novel statistical method presented here using BRTs could be used to describe or factor out the effects of long-term variation in background climate variation on a wide variety of environmental variables, including fires, floods, heat waves, and droughts – all of which have been shown to be sensitive to climate teleconnections (Chen et al., 2016; Lau and Kim, 2012; Stenseth et al., 2003). Instead of using common climate indices, we encourage the use of the complete set of PCs calculated here, because important climate oscillations could otherwise be missed. To illustrate this point, the PC with the 11th-highest median relative importance in explaining water level variation was not strongly correlated with any of the reported NOAA climate indices (Fig. 5).
Wherever water levels are affected by background climate and human activity, there is the potential to affect lake ecosystems and the benefits that humans derive from them (Clites et al., 2014). More than 2 billion people live in water stressed regions of the world where human demand for surface freshwater exceeds the available supply (Mekonnen and Hoekstra, 2016; Vörösmarty et al., 2000, 2010). Meeting the competing demands for surface freshwater, especially in water-scarce regions and in the face of anthropogenic environmental change, is a key challenge for society. Our capacity to disentangle the effects of background climate oscillations on water levels is key to sustaining our freshwater resources (Clites et al., 2014; Gronewold et al., 2013). By applying this BRT statistical approach, we partially disentangled the effects of background global climate indices on water levels. Many of the large lakes in our analyses were remarkably resilient to long-term changes from 1992 to 2019. Thus, large lakes may be an increasingly important resource as water scarcity intensifies in the future. Abrupt changes in water levels in large lakes remain possible due to human activities and climate change, but our analyses suggest that we have not yet observed such changes in many of earth's largest lakes.
On average, water levels in the world's large lakes are increasing but are highly variable from lake to lake. Background climate variability often masks these long-term trends in water levels and occasionally gives rise to the appearance of false trends that wane after background climate variation is factored out. Background climate variation alone can explain a large proportion of water level variability in lakes worldwide due to the strong influence of earth surface air temperatures on lake levels via climate–lake level teleconnections. These findings highlight further opportunities to investigate the specific mechanisms that couple climate and lake levels. The novel statistical method presented here using BRTs could be used to describe or factor out the effects of long-term variation in background climate variation on a wide variety of environmental variables, including fires, floods, heat waves, and droughts. Tests for long-term trends in environmental variables which may or may not be anthropogenic will likely benefit from prior isolation and removal of the effects of background climate variation using this method.
All code used in the production of this paper, including data analysis and figures, are published in the Zenodo online repository with DOI https://doi.org/10.5281/zenodo.3363187 (Kraemer, 2019).
Water level data products are courtesy of the USDA/NASA G-REALM program, which can be found at https://www.pecad.fas.usda.gov/cropexplorer/global_reservoir/ (United States Department of Agriculture Foreign Agricultural Service and United States National Aeronautics and Space Administration, 2020). All GISS data can be found at https://data.giss.nasa.gov/gistemp/ (United States National Aeronautics and Space Administration Goddard Institute for Space Studies, 2020).
The supplement related to this article is available online at: https://doi.org/10.5194/hess-24-2593-2020-supplement.
BMK designed the study, developed the model code, and performed the analyses. BMK prepared the initial manuscript. BMK, RA, AS, and PBM contributed to the manuscript's revision and editing.
The authors declare that they have no conflict of interest.
The lead author is grateful for support from the IGB Leibniz Institute for Freshwater Ecology and Inland Fisheries through their international visiting scholars program and from the German Research Foundation within the LimnoScenES project (AD 91/22-1). We are also grateful for financial support from the John D. and Catherine T. MacArthur Foundation grants G-108015-0 and G-1609-151200 to Appalachian State University, and for further support from the Packard Fellowship in Science and Engineering.
This research has been supported by the Deutsche Forschungsgemeinschaft (grant no. AD 91/22-1) and the John D. and Catherine T. MacArthur Foundation (grant nos. G-108015-0 and G-1609-151200).
The publication of this article was funded by the
Open Access Fund of the Leibniz Association.
This paper was edited by Stacey Archfield and reviewed by three anonymous referees.
Aladin, N. V., Plotnikov, I. S., Micklin, P., and Ballatore, T.: Natural Resources and Environmental Issues Aral Sea: Water level, salinity and long-term changes in biological communities of an endangered ecosystem-past, present and future, Nat. Resour. Env. Iss., 15, 177–183, 2009.
Allen, M. R. and Ingram, W. J.: Constraints on future changes in climate and the hydrologic cycle, Nature, 419, 224–232, https://doi.org/10.1038/nature01092, 2002.
Benson, L., Linsley, B., Smoot, J., Mensing, S., Lund, S., Stine, S., and Sarna-Wojcicki, A.: Influence of the Pacific decadal oscillation on the climate of the Sierra Nevada, California and Nevada, Quaternary Res., 59, 151–159, https://doi.org/10.1016/S0033-5894(03)00007-3, 2003.
Benson, L. V., Lund, S. P., Burdett, J. W., Kashgarian, M., Rose, T. P., Smoot, J. P., and Schwartz, M.: Correlation of Late-Pleistocene Lake-Level Oscillations in Mono Lake, California, with North Atlantic Climate Events, Quaternary Res., 49, 1–10, https://doi.org/10.1006/qres.1997.1940, 1998.
Bintanja, R. and Selten, F. M.: Future increases in Arctic precipitation linked to local evaporation and sea-ice retreat, Nature, 509, 479–482, https://doi.org/10.1038/nature13259, 2014.
Birkett C., Reynolds C., Beckley B., and Doorn B.: From Research to Operations: The USDA Global Reservoir and Lake Monitor, in: Vignudelli S., Kostianoy A., Cipollini P., and Benveniste, J., Coastal Altimetry, Springer, Berlin, Heidelberg, 2011.
Birkett, C. M. C.: The contribution of TOPEX/POSEIDON to the global monitoring of climatically sensitive lakes, J. Geophys. Res., 100, 25179–25204, https://doi.org/10.1029/95JC02125, 1995.
Block, P. and Strzepek, K.: Power Ahead: Meeting Ethiopia's Energy Needs Under a Changing Climate, Rev. Dev. Econ., 16, 476–488, https://doi.org/10.1111/j.1467-9361.2012.00675.x, 2012.
Byrne, M. P., O'Gorman, P. A., and O'Gorman, P. A.: The response of precipitation minus evapotranspiration to climate warming: Why the “Wet-get-wetter, dry-get-drier” scaling does not hold over land, J. Climate, 28, 8078–8092, https://doi.org/10.1175/JCLI-D-15-0369.1, 2015.
Cai, W., Santoso, A., Wang, G., Yeh, S. W., An, S. Il, Cobb, K. M., Collins, M., Guilyardi, E., Jin, F. F., Kug, J. S., Lengaigne, M., Mcphaden, M. J., Takahashi, K., Timmermann, A., Vecchi, G., Watanabe, M., and Wu, L.: ENSO and greenhouse warming, Nat. Clim. Chang., 5, 849–859, https://doi.org/10.1038/nclimate2743, 2015.
Cane, M. A.: The evolution of El Niño, past and future, Earth Planet. Sc. Lett., 230, 227–240, https://doi.org/10.1016/j.epsl.2004.12.003, 2005.
Capotondi, A. and Sardeshmukh, P. D.: Is El Niño really changing?, Geophys. Res. Lett., 44, 8548–8556, https://doi.org/10.1002/2017GL074515, 2017.
Chadwick, R., Boutle, I., and Martin, G.: Spatial patterns of precipitation change in CMIP5: Why the rich do not get richer in the tropics, J. Climate, 26, 3803–3822, https://doi.org/10.1175/JCLI-D-12-00543.1, 2013.
Chanut, J. P., D'astous, D., and El-Sabh, M. I.: Modelling the Natural and Anthropogenic Variations of the St. Lawrence Water Level, in Natural and Man-Made Hazards, 377–394, Springer Netherlands, Dordrecht, 1988.
Chen, Y., Morton, D. C., Andela, N., Giglio, L., and Randerson, J. T.: How much global burned area can be forecast on seasonal time scales using sea surface temperatures?, Environ. Res. Lett., 11, 045001, https://doi.org/10.1088/1748-9326/11/4/045001, 2016.
Christensen, N. S., Wood, A. W., Voisin, N., Lettenmaier, D. P., and Palmer, R. N.: The Effects of Climate Change on the Hydrology and Water Resources of the Colorado River Basin, Clim. Change, 62, 337–363, https://doi.org/10.1023/B:CLIM.0000013684.13621.1f, 2004.
Clites, A. H., Smith, J. P., Hunter, T. S., and Gronewold, A. D.: Visualizing relationships between hydrology, climate, and water level fluctuations on Earth's largest system of lakes, J. Great Lakes Res., 40, 807–811, https://doi.org/10.1016/j.jglr.2014.05.014, 2014.
Cohn, B. P. and Robinson, J. E.: Cyclic fluctuations of water levels in Lake Ontario, Comput. Geosci., 1, 105–108, https://doi.org/10.1016/0098-3004(75)90010-2, 1975.
Collins, M.: Understanding uncertainties in the response of ENSO to greenhouse warming, Geophys. Res. Lett., 27, 3509–3512, https://doi.org/10.1029/2000GL011747, 2000.
Corti, S., Molteni, F., Palmer, T. N., Corti, S., and Molteni, F.: Signature of recent climate change in frequencies of natural atmospheric circulation regimes, Nature, 398, 799–802, https://doi.org/10.1038/19745, 1999.
Crétaux, J.-F. and Birkett, C.: Lake studies from satellite radar altimetry, Comptes Rendus – Geosci., 338, 1098–1112, https://doi.org/10.1016/j.crte.2006.08.002, 2006.
Crétaux, J.-F., Abarca-del-Río, R., Bergé-Nguyen, M., Arsen, A., Drolon, V., Clos, G., and Maisongrande, P.: Lake Volume Monitoring from Space, Surv. Geophys., 37, 269–305, https://doi.org/10.1007/s10712-016-9362-6, 2016.
Dai, A. and Wigley, T. M. L.: Global patterns of ENSO-induced precipitation, Geophys. Res. Lett., 27, 1283–1286, https://doi.org/10.1029/1999GL011140, 2000.
Dommenget, D. and Latif, M.: Generation of hyper climate modes, Geophys. Res. Lett., 35, L02706, https://doi.org/10.1029/2007GL031087, 2008.
Dorigo, W., de Jeu, R., Chung, D., Parinussa, R., Liu, Y., Wagner, W., and Fernández-Prieto, D.: Evaluating global trends (1988–2010) in harmonized multi-satellite surface soil moisture, Geophys. Res. Lett., 39, L18405, https://doi.org/10.1029/2012GL052988, 2012.
Elith, J., Leathwick, J., and Hastie, T.: A working guide to boosted regression trees, J. Anim. Ecol., 77, 802–813, 2008.
Food and Agriculture Organization of the United Nations: AQUASTAT, available at: http://www.fao.org/nr/water/aquastat/main/index.stm (last access: 11 July 2018), 2016.
Fowler, H. J., Blenkinsop, S., and Tebaldi, C.: Linking climate change modelling to impacts studies: recent advances in downscaling techniques for hydrological modelling, Int. J. Climatol., 27, 1547–1578, https://doi.org/10.1002/joc.1556, 2007.
Ghanbari, R. N. and Bravo, H. R.: Coherence between atmospheric teleconnections, Great Lakes water levels, and regional climate, Adv. Water Resour., 31, 1284–1298, https://doi.org/10.1016/j.advwatres.2008.05.002, 2008.
Gimeno, L., Nieto, R., VÃ!`zquez, M., and Lavers, D. A.: Atmospheric rivers: a mini-review, Front. Earth Sci., 2, 2, https://doi.org/10.3389/feart.2014.00002, 2014.
Greve, P. and Seneviratne, S. I.: Assessment of future changes in water availability and aridity, Geophys. Res. Lett., 42, 5493–5499, https://doi.org/10.1002/2015GL064127, 2015.
Greve, P., Orlowsky, B., Mueller, B., Sheffield, J., Reichstein, M., and Seneviratne, S. I.: Global assessment of trends in wetting and drying over land, Nat. Geosci., 7, 716–721, https://doi.org/10.1038/NGEO2247, 2014.
Gronewold, A. D., Fortin, V., Lofgren, B., Clites, A., Stow, C. A., and Quinn, F.: Coasts, water levels, and climate change: A Great Lakes perspective, Clim. Change, 120, 697–711, https://doi.org/10.1007/s10584-013-0840-2, 2013.
Guilyardi, E., Wittenberg, A., Fedorov, A., Collins, M., Wang, C., Capotondi, A., van Oldenborgh, G. J., and Stockdale, T.: Understanding El Niño in ocean-atmosphere general circulation models: Progress and challenges, B. Am. Meteorol. Soc., 90, 325–340, https://doi.org/10.1175/2008BAMS2387.1, 2009.
Gyau-Boakye, P.: Environmental impacts of the Akosombo dam and effects of climate change on the lake levels, Environ. Dev. Sustain., 3, 17–29, https://doi.org/10.1023/A:1011402116047, 2001.
Hannachi, A., Unkel, S., Trendafilov, N. T., and Jolliffe, I. T.: Independent component analysis of climate data: A new look at EOF rotation, J. Climate, 22, 2797–2812, https://doi.org/10.1175/2008JCLI2571.1, 2009.
Hansen, J., Ruedy, R., Sato, M., and Lo, K.: Global surface temperature change, Rev. Geophys., 48, RG4004, https://doi.org/10.1029/2010RG000345, 2010.
Hansen, J. W., Hodges, A. W., and Jones, J. W.: ENSO influences on agriculture in the southeastern United States, J. Climate, 11, 404–411, https://doi.org/10.1175/1520-0442(1998)011<0404:EIOAIT>2.0.CO;2, 1998.
Hassanzadeh, E., Zarghami, M., and Hassanzadeh, Y.: Determining the Main Factors in Declining the Urmia Lake Level by Using System Dynamics Modeling, Water Resour. Manag., 26, 129–145, https://doi.org/10.1007/s11269-011-9909-8, 2012.
Hegerl, G. C., Black, E., Allan, R. P., Ingram, W. J., Polson, D., Trenberth, K. E., Chadwick, R. S., Arkin, P. A., Sarojini, B. B., Becker, A., Dai, A., Durack, P. J., Easterling, D., Fowler, H. J., Kendon, E. J., Huffman, G. J., Liu, C., Marsh, R., New, M., Osborn, T. J., Skliris, N., Stott, P. A., Vidale, P. L., Wijffels, S. E., Wilcox, L. J., Willett, K. M., and Zhang, X.: Challenges in quantifying changes in the global water cycle, B. Am. Meteorol. Soc., 96, 1097–1115, https://doi.org/10.1175/BAMS-D-13-00212.1, 2015.
Hidalgo, H. G. and Dracup, J. A.: ENSO and PDO Effects on Hydroclimatic Variations of the Upper Colorado River Basin, J. Hydrometeorol., 4, 5–23, https://doi.org/10.1175/1525-7541(2003)004<0005:EAPEOH>2.0.CO;2, 2003.
Hijmans, R. J., Phillips, S., Leathwick, J. R., and Elith, J.: Package “dismo”, October, https://doi.org/10.1016/j.jhydrol.2011.07.022, 2017.
IPCC: IPCC Fifth Assessment Report, Fifth Assess. Rep., 10–12, available at: https://www.ipcc.ch/report/ar5/index.shtml (last access: 8 May 2019), 2014.
Jöhnk, K. D., Straile, D., and Ostendorp, W.: Water level variability and trends in lake constance in the light of the 1999 centennial flood, Limnologica, 34, 15–21, https://doi.org/10.1016/S0075-9511(04)80017-3, 2004.
Kim, K. Y. and Wu, Q.: A comparison study of EOF techniques: Analysis of nonstationary data with periodic statistics, J. Climate, 12, 185–199, https://doi.org/10.1175/1520-0442-12.1.185, 1999.
Kraemer, B. M.: GlobalLakeLevels, Zenodo, https://doi.org/10.5281/zenodo.3363187, 2019.
Lau, W. K. M. and Kim, K. M.: The 2010 Pakistan flood and Russian heat wave: Teleconnection of hydrometeorological extremes, J. Hydrometeorol., 13, 392–403, https://doi.org/10.1175/JHM-D-11-016.1, 2012.
Lenters, J. D.: Long-term Trends in the Seasonal Cycle of Great Lakes Water Levels, J. Great Lakes Res., 27, 342–353, https://doi.org/10.1016/S0380-1330(01)70650-8, 2001.
Lorenzo, D., E, Lorenzo, E. Di, Schneider, N., Cobb, K. M., Franks, P. J. S., Chhak, K., Miller, A. J., Mcwilliams, J. C., Bograd, S. J., Arango, H., Curchitser, E., Powell, T. M., Rivie, P., Di Lorenzo, E., Schneider, N., Cobb, K. M., Franks, P. J. S., Chhak, K., Miller, A. J., Mcwilliams, J. C., Bograd, S. J., Arango, H., Curchitser, E., Powell, T. M., and Rivière, P.: North Pacific Gyre Oscillation links ocean climate and ecosystem change, Geophys. Res. Lett., 35, L08607, https://doi.org/10.1029/2007GL032838, 2008.
Marchant, R., Mumbi, C., Behera, S., and Yamagata, T.: The Indian Ocean dipole – the unsung driver of climatic variability in East Africa, Afr. J. Ecol., 45, 4–16, https://doi.org/10.1111/j.1365-2028.2006.00707.x, 2007.
Mekonnen, M. M. and Hoekstra, A. Y.: Four billion people facing severe water scarcity, Sci. Adv., 2, e1500323, https://doi.org/10.1126/sciadv.1500323, 2016.
Mercier, F., Cazenave, A., and Maheu, C.: Interannual lake level fluctuations (1993–1999) in Africa from Topex/Poseidon: connections with ocean–atmosphere interactions over the Indian Ocean, Global Planet. Change, 32, 141–163, https://doi.org/10.1016/S0921-8181(01)00139-4, 2002.
Messager, M. L., Lehner, B., Grill, G., Nedeva, I., and Schmitt, O.: Estimating the volume and age of water stored in global lakes using a geo-statistical approach, Nat. Commun., 7, 13603, https://doi.org/10.1038/ncomms13603, 2016.
Micklin, P. P.: Desiccation of the Aral Sea: A Water Management Disaster in the Soviet Union, Science, 241, 1170–1176, https://doi.org/10.1126/science.241.4870.1170, 1988.
Molinos, J. and Donohue, I.: Downscaling the non-stationary effect of climate forcing on local-scale dynamics: The importance of environmental filters, Clim. Change, 124, 333–346, https://doi.org/10.1007/s10584-014-1077-4, 2014.
Molinos, J. G., Viana, M., Brennan, M., and Donohue, I.: Importance of long-term cycles for predicting water level dynamics in natural lakes, edited by I. Álvarez, PLoS One, 10, e0119253, https://doi.org/10.1371/journal.pone.0119253, 2015.
Muller, M.: Cape Town's drought: don't blame climate change, Nature, 559, 174–176, https://doi.org/10.1038/d41586-018-05649-1, 2018.
Nijssen, B., O'Donnell, G. M., Hamlet, A. F., and Lettenmaier, D. P.: Hydrologic sensitivity of global rivers to climate change, Clim. Change, 50, 143–175, https://doi.org/10.1023/A:1010616428763, 2001.
O'Gorman, P. A., Allan, R. P., Byrne, M. P., and Previdi, M.: Energetic Constraints on Precipitation Under Climate Change, Surv. Geophys., 33, 585–608, https://doi.org/10.1007/s10712-011-9159-6, 2012.
Pasquini, A. I., Lecomte, K. L., and Depetris, P. J.: Climate change and recent water level variability in Patagonian proglacial lakes, Argentina, Global Planet. Change, 63, 290–298, https://doi.org/10.1016/j.gloplacha.2008.07.001, 2008.
Pekel, J.-F., Cottam, A., Gorelick, N., and Belward, A. S.: High-resolution mapping of global surface water and its long-term changes, Nature, 540, 418–422, https://doi.org/10.1038/nature20584, 2016.
Phinyomark, A., Hettinga, B. A., Osis, S., and Ferber, R.: Do intermediate- and higher-order principal components contain useful information to detect subtle changes in lower extremity biomechanics during running?, Hum. Movement Sci., 44, 91–101, https://doi.org/10.1016/j.humov.2015.08.018, 2015.
Ramanathan, V., Crutzen, P. J., Kiehl, J. T., and Rosenfeld, D.: Aerosols, climate, and the hydrological cycle, Science, 294, 2119–2124, https://doi.org/10.1126/science.1064034, 2001.
R Core Team: R: A Language and Environment for Statistical Computing, R Found. Stat. Comput., available at: http://www.r-project.org/ (last access: 16 November 2018), 2017.
Ricko, M., Carton, J. A., and Birkett, C.: Climatic Effects on Lake Basins. Part I: Modeling Tropical Lake Levels, J. Climate, 24, 2983–2999, https://doi.org/10.1175/2010JCLI3602.1, 2011.
Rodell, M., Famiglietti, J. S., Wiese, D. N., Reager, J. T., Beaudoing, H. K., Landerer, F. W., and Lo, M.-H.: Emerging trends in global freshwater availability, Nature, 557, 651–659, https://doi.org/10.1038/s41586-018-0123-1, 2018.
Ropelewski, C. F. and Halpert, M. S.: Global and Regional Scale Precipitation Patterns Associated with the El Niño/Southern Oscillation, Mon. Weather Rev., 115, 1606–1626, https://doi.org/10.1175/1520-0493(1987)115<1606:GARSPP>2.0.CO;2, 1987.
Stager, J. C., Ryves, D., Cumming, B. F., David Meeker, L., and Beer, J.: Solar variability and the levels of Lake Victoria, East Africa, during the last millenium, J. Paleolimnol., 33, 243–251, https://doi.org/10.1007/s10933-004-4227-2, 2005.
Stager, J. C., Ruzmaikin, A., Conway, D., Verburg, P., and Mason, P. J.: Sunspots, El Niño, and the levels of Lake Victoria, East Africa, J. Geophys. Res.-Atmos., 112, D15106, https://doi.org/10.1029/2006JD008362, 2007.
Stenseth, N. C., Ottersen, G., Hurrell, J. W., Mysterud, A., Lima, M., Chan, K. S., Yoccoz, N. G., and Ådlandsvik, B.: Studying climate effects on ecology through the use of climate indices: The North Atlantic Oscillation, El Niño Southern Oscillation and beyond, P. R. Soc. B-Biol. Sci., 270, 2087–2096, https://doi.org/10.1098/rspb.2003.2415, 2003.
Tao, S., Fang, J., Zhao, X., Zhao, S., Shen, H., Hu, H., Tang, Z., Wang, Z., Guo, Q., and Turner, B. L.: Rapid loss of lakes on the Mongolian Plateau, P. Natl. Acad. Sci. USA, 112, 2281–2286, https://doi.org/10.1073/pnas.1411748112, 2015.
Tierney, J. E., Russell, J. M., Huang, Y., Damsté, J. S. S., Hopmans, E. C., and Cohen, A. S.: Northern hemisphere controls on tropical southeast African climate during the past 60,000 years., Science, 322, 252–255, 2008.
Tierney, J. E., Smerdon, J. E., Anchukaitis, K. J., and Seager, R.: Multidecadal variability in East African hydroclimate controlled by the Indian Ocean., Nature, 493, 389–392, https://doi.org/10.1038/nature11785, 2013.
Timmermann, A., Oberhuber, J., Bacher, A., Esch, M., Latif, M., and Roeckner, E.: Increased El Niño frequency in a climate model forced by future greenhouse warming, Nature, 398, 694–697, https://doi.org/10.1038/19505, 1999.
Tomasion, M. and Valle, F. D.: Natural climatic changes and solar cycles: An analysis of hydrological time series, Hydrolog. Sci. J., 45, 477–489, https://doi.org/10.1080/02626660009492344, 2000.
United States Department of Agriculture Foreign Agricultural Service and United States National Aeronautics and Space Administration: Global Reservoirs and Lakes Monitoring Program, available at: https://www.pecad.fas.usda.gov/cropexplorer/global_reservoir/, last access: 24 January 2020.
United States National Aeronautics and Space Administration Goddard Institute for Space Studies: Goddard Institute for Space Studies Surface Temperature Analysis, available at: https://data.giss.nasa.gov/gistemp/, last access: 24 January 2020.
Vadeboncoeur, Y., McIntyre, P. B., and Vander Zanden, M. J.: Borders of biodiversity: life at the edge of the world's large lakes, Bioscience, 61, 526–537, https://doi.org/10.1525/bio.2011.61.7.7, 2011.
van Oldenborgh, G. J., Philip, S. Y., and Collins, M.: El Niño in a changing climate: a multi-model study, Ocean Sci., 1, 81–95, https://doi.org/10.5194/os-1-81-2005, 2005.
Vinukollu, R. K., Meynadier, R., Sheffield, J., and Wood, E. F.: Multi-model, multi-sensor estimates of global evapotranspiration: climatology, uncertainties and trends, Hydrol. Process., 25, 3993–4010, https://doi.org/10.1002/hyp.8393, 2011.
Vörösmarty, C. J. and Sahagian, D.: Anthropogenic Disturbance of the Terrestrial Water Cycle, Bioscience, 50, 753, https://doi.org/10.1641/0006-3568(2000)050[0753:adottw]2.0.co;2, 2006.
Vörösmarty, C. J., Green, P., Salisbury, J., and Lammers, R. B.: Global water resources: Vulnerability from climate change and population growth, Science, 289, 284–288, https://doi.org/10.1126/science.289.5477.284, 2000.
Vörösmarty, C. J., McIntyre, P. B., Gessner, M. O., Dudgeon, D., Prusevich, A., Green, P., Glidden, S., Bunn, S. E., Sullivan, C. A., Liermann, C. R., and Davies, P. M.: Global threats to human water security and river biodiversity, Nature, 467, 555–561, https://doi.org/10.1038/nature09440, 2010.
Wang, B., Liu, J., Kim, H. J., Webster, P. J., and Yim, S. Y.: Recent change of the global monsoon precipitation (1979–2008), Clim. Dynam., 39, 1123–1135, https://doi.org/10.1007/s00382-011-1266-z, 2012.
Wang, J., Yang, B., Ljungqvist, F. C., Luterbacher, J., Osborn, T. J., Briffa, K. R., and Zorita, E.: Internal and external forcing of multidecadal Atlantic climate variability over the past 1,200 years, Nat. Geosci., 10, 512–517, https://doi.org/10.1038/ngeo2962, 2017.
Wang, S. Y., Gillies, R. R., Jin, J., and Hipps, L. E.: Coherence between the great salt lake level and the Pacific quasi-decadal oscillation, J. Climate, 23, 2161–2177, https://doi.org/10.1175/2009JCLI2979.1, 2010.
Wrzesiński, D., Ptak, M., and Plewa, K.: Effect of the north Atlantic oscillation on water level fluctuations in lakes of northern Poland, Geogr. Pol., 91, 243–259, https://doi.org/10.7163/gpol.0119, 2018.
Wurtsbaugh, W. A., Miller, C., Null, S. E., Justin De Rose, R., Wilcock, P., Hahnenberger, M., Howe, F., and Moore, J.: Decline of the world's saline lakes, Nat. Geosci., 10, 816–821, https://doi.org/10.1038/NGEO3052, 2017.
Zhang, G., Xie, H., Kang, S., Yi, D., and Ackley, S. F.: Monitoring lake level changes on the Tibetan Plateau using ICESat altimetry data (2003–2009), Remote Sens. Environ., 115, 1733–1742, https://doi.org/10.1016/j.rse.2011.03.005, 2011.





