the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Projected increases in magnitude and socioeconomic exposure of global droughts in 1.5 and 2 °C warmer climates
Jie Chen
Sylvia C. Sullivan
Hui-Min Wang
Shenglian Guo
Liping Zhang
Jong-Suk Kim
The Paris Agreement sets a long-term temperature goal to hold global warming to well below 2.0 ∘C and strives to limit it to 1.5 ∘C above preindustrial levels. Droughts with either intense severity or a long persistence could both lead to substantial impacts such as infrastructure failure and ecosystem vulnerability, and they are projected to occur more frequently and trigger intensified socioeconomic consequences with global warming. However, existing assessments targeting global droughts under 1.5 and 2.0 ∘C warming levels usually neglect the multifaceted nature of droughts and might underestimate potential risks. This study, within a bivariate framework, quantifies the change in global drought conditions and corresponding socioeconomic exposures for additional 1.5 and 2.0 ∘C warming trajectories. The drought characteristics are identified using the Standardized Precipitation Evapotranspiration Index (SPEI) combined with the run theory, with the climate scenarios projected by 13 Coupled Model Inter-comparison Project Phase 5 (CMIP5) global climate models (GCMs) under three representative concentration pathways (RCP 2.6, RCP4.5 and RCP8.5). The copula functions and the most likely realization are incorporated to model the joint distribution of drought severity and duration, and changes in the bivariate return period with global warming are evaluated. Finally, the drought exposures of populations and regional gross domestic product (GDP) under different shared socioeconomic pathways (SSPs) are investigated globally. The results show that within the bivariate framework, the historical 50-year droughts may double across 58 % of global landmasses in a 1.5 ∘C warmer world, while when the warming climbs up to 2.0 ∘C, an additional 9 % of world landmasses would be exposed to such catastrophic drought deteriorations. More than 75 (73) countries' populations (GDP) will be completely affected by increasing drought risks under the 1.5 ∘C warming, while an extra 0.5 ∘C warming will further lead to an additional 17 countries suffering from a nearly unbearable situation. Our results demonstrate that limiting global warming to 1.5 ∘C, compared with 2 ∘C warming, can perceptibly mitigate the drought impacts over major regions of the world.
- Article
(11309 KB) - Full-text XML
-
Supplement
(3729 KB) - BibTeX
- EndNote
Climate warming mainly due to greenhouse gas emissions has altered the global hydrological cycle and resulted in more frequent and persistent natural hazards such as droughts, which have imposed considerable economic, societal, and environmental challenges across the globe (Handmer et al., 2012; Chang et al., 2016; EM-DAT, 2018). With the aspiration to mitigate these adverse consequences, the Paris Agreement proposed to cut greenhouse gas emissions for holding the increase in global temperature to well below 2.0 ∘C and pursuing efforts to limit the warming to 1.5 ∘C above preindustrial levels (UNFCCC, 2015). Regardless of the socioeconomic and technological achievability of the Paris Agreement goals, portraying the drought evolution with different warming trajectories would provide valuable information and references for mankind to enable appropriate adaptation strategies in a warmer future.
To examine the sensitivity of drought risks with different warming targets, numerous approaches have emerged. One way is to employ a set of ensemble simulations produced by a single coupled climate model (e.g., Community Earth System Model, CESM) which is designed specifically to perform the impact assessments at near-equilibrium scenarios of 1.5 or 2 ∘C additional warming (Sanderson et al., 2017; Lehner et al., 2017). This single model type cannot reflect the structural uncertainty of climate models, which is important in impact assessments, and thus raises doubts about the robustness of such drought condition assessments (Liu et al., 2018a). Emerging modeling efforts such as the “Half a degree Additional warming, Projections, Prognosis and Impacts” (HAPPI) model inter-comparison project provided a new dataset with experiments designed to explicitly target impacts of 1.5 and 2 ∘C above preindustrial warming (Mitchell et al., 2016). However, the HAPPI model employed prescribed climatological sea surface temperatures and could not consider the internal variability of ocean–atmosphere circulation, which is crucial in physically simulating climatic variability and persistence (Seager et al., 2005; Routson et al., 2016). Current studies usually utilize CMIP5 climate models to project climate scenarios under different representative concentration pathways (RCPs), identify the time period for a warming target and then examine the drought conditions associated with different levels of global warming. For instance, Su et al. (2018) used 13 CMIP5 models based on RCP2.6 and RCP4.5 to compare the drought conditions for two warming targets over China and reported that tremendous losses will emerge even under the ambitious 1.5 ∘C warming target.
These prevailing tides of the literature almost reach a consensus that, with a higher saturation threshold and more intense and frequent dry spells driven by rising temperatures, drought conditions would considerably worsen in many regions of the world (Mitchell et al., 2016; Liu et al., 2018a, b). The potentially devastating impacts of more severe drought conditions on society raise considerable concerns, motivating a number of global socioeconomic assessments of future drought change impact (e.g., Below et al., 2007; Schilling et al., 2012). For instance, Liu et al. (2018a) investigated global drought evolution and corresponding population exposures in additional 1.5 and 2 ∘C warming conditions using a set of CMIP5 models under RCP4.5 and RCP8.5. Naumann et al. (2018) assessed the development of drought conditions across the world for different warming targets in the Paris Agreement. These studies concluded that there are considerable benefits for the environment and society in limiting warming to 1.5 ∘C relative to 2.0 ∘C, although 1.5 ∘C warming still implies a substantial challenge for global sustainable development. However, most previous socioeconomic assessments (e.g., Peters, 2016; Park et al., 2018; Liu and Sun, 2019) have focused on a static socioeconomic scenario, probably due to data constraint. These studies cannot capture the dynamic nature of population and assets over time, which has been identified as crucial for simulating realistic societal development paths (Smirnov et al., 2016). Recently, five shared socioeconomic pathways (SSPs) have been proposed, providing a more reasonable dataset to characterize a set of plausible alternative futures of societal development with consideration of climate change and policy impacts over the 21st century (Leimbach et al., 2017). To date, the SSPs have not yet been incorporated into the drought impact assessments with warming at the global scale.
More importantly, among existing global drought impact assessments, especially those targeting different warming levels proposed by the Paris Agreement, drought variables such as severity and duration are usually separately investigated through probability modeling and stochastic theories (e.g., Sanderson et al., 2017; Lehner et al., 2017; Su et al., 2018). Knowing that droughts are multifaceted phenomena (Xu et al., 2015; Tsakiris et al., 2016) usually characterized by duration and severity, univariate frequency analysis is unable to describe the probability of occurrence for the drought events physically and may lead to underestimation of drought risks and societal hazards. For instance, droughts with a moderate severity but a long persistence are seldom identified as severe events in univariate analysis; nevertheless, they may pose substantial socioeconomic losses because of rapid stored water depletion and low resilience to subsequent droughts (Lehner et al., 2017). Therefore, there is an urgent necessity to incorporate the joint modeling of multiple drought features into impact assessments (Genest and Favre, 2007; Liu et al., 2015). The copula function that shows good feasibility of marginal distributions in modeling inter-correlated variables has been introduced in multivariate analysis for droughts (e.g., Wong et al., 2013; Zhang et al., 2015; Ayantobo et al., 2017). However, to the authors' knowledge, no previous work links the high interdependence of drought characteristics to a global impact assessment under different warming levels.
In the multivariate framework, selection of variable combinations along the quantile curve poses a new challenge, as the choice of the joint return period (JRP) leads to infinitely many such combinations. To meet the needs of infrastructure design and adaptivity, many researchers (e.g., Chen et al., 2010; Li et al., 2016; Zscheischler and Seneviratne, 2017) have assumed that the correlated variables have the same probability of occurrence under a given JRP, which is called the equivalent frequency combination (EFC) method. Despite the fact that the EFC method has low calculation complexity, the statistical and theoretical basis of the equal frequency assumption is questionable (Yin et al., 2018a). To develop a more rational design for a multivariate approach, a novel concept of “most likely design realization” to choose the point with the highest likelihood along the quantile curve has been proposed in frequency analysis (Salvadori et al. 2011; Yin et al., 2019a). It would be very important to evaluate and characterize these different likelihoods of drought events in bivariate drought impact assessment under a warming climate.
In this study, under a bivariate framework, we quantify changes in global drought conditions and socioeconomic exposure with additional levels of 1.5 and 2.0 ∘C warming. The drought characteristics are identified using the Standardized Precipitation Evapotranspiration Index (SPEI) combined with the run theory and with climate scenarios simulated by 13 CMIP5 global climate models (GCMs) under three RCPs (RCP2.6, RCP4.5, and RCP8.5). The copula functions and most likely realization are incorporated to model the drought severity and duration concurrently, and changes in the bivariate return period with global warming are systematically investigated. Finally, the drought exposures of populations and regional gross domestic product (GDP) under different SSPs are assessed globally.
2.1 Climatic and socioeconomic scenarios
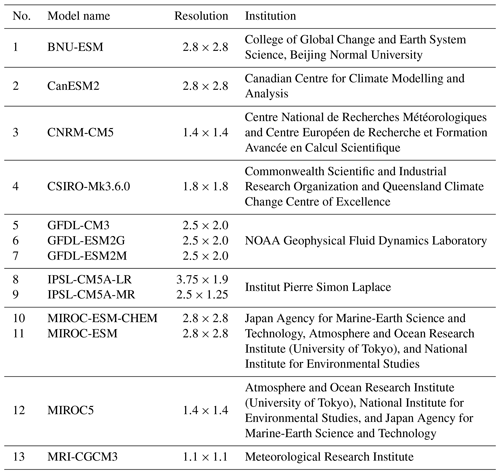
Climate projections are based on ensemble runs (r1i1p1) by 13 models from CMIP5 (Table 1), covering the period 1976–2100 under three RCPs (i.e., RCP2.6, RCP4.5, and RCP8.5).
Ten climate variables were used in this study. Specifically, 9 out of the 10 variables were applied for the calculation of potential evapotranspiration (PET). These nine variables include surface maximum, mean, and minimum air temperatures, surface wind speed, relative humidity, surface downwelling and upwelling longwave fluxes, and surface downwelling and upwelling shortwave fluxes. The 10th variable is the precipitation. Then the calculated PET and GCM-simulated precipitation were employed to calculate drought indices. The PET was initially calculated at the daily scale. Then both the daily-scale PET and precipitation were aggregated to the monthly scales and bilinearly interpolated to a spatial resolution of 1.0∘ × 1.0∘ on latitude and longitude for each model simulation.
To assess the exposures of populations and assets to droughts, which will eventually lead to higher drought losses in the future, instead of using a static socioeconomic scenario as many studies have (e.g., Hirabayashi et al., 2013; Smirnov et al., 2016), we employ the spatially explicit global shared SSPs. This dataset includes gridded population and GDP data under five SSPs, covering the period 2010–2100 at a spatial resolution of 0.5∘ × 0.5∘ (Jiang et al., 2017, 2018; Su et al., 2018; Huang et al., 2019). It involves a sustainable scenario (SSP1), a pathway of continuing historical trends (SSP2), a strongly fragmented world (SSP3), a highly unequal world (SSP4), and a growth-oriented world (SSP5). Among combinations of different RCP trajectories and socioeconomic pathways, some SSP–RCP combinations are unlikely to occur, e.g., SSP3–RCP2.6 and SSP1–RCP8.5 (Jones and O'Neill, 2016). Considering the socioeconomic challenges for mitigation along different development paths, the RCP2.6 scenario is associated with SSP1 (SSP126), which will face a lower challenge of mitigation in the future. The RCP4.5 scenario is associated with SSP2 (SSP245), while the highest emission scenario RCP8.5 is associated with SSP5 (SSP585), by which a relatively higher challenge is expected under foreseeable warming conditions (Samir and Lutz, 2017).
2.2 Definition of a baseline, 1.5 and 2 ∘C global warming
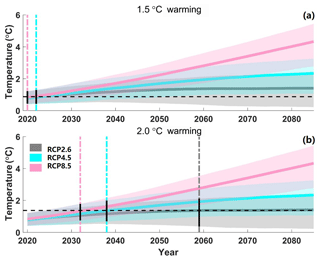
The sensitivity of annual global temperature to climate variability significantly varies in models and RCPs. Therefore, the time period with additional global warming of 1.5 and 2 ∘C with respect to preindustrial conditions also varies between different climate scenarios. Here, the time periods for different global warming levels are determined using the 30-year running mean of a multi-model ensemble mean of global-mean surface air temperature, following previous studies (Vautard et al., 2014; Su et al., 2018). We first select a baseline period of 1976–2005, during which the observed global average temperature was approximately 0.46–0.66 ∘C warmer than pre-industrial conditions (IPCC, 2018). This reference period is widely adopted for climate impact assessment (e.g., Vautard et al., 2014), and we set the warming degree during the baseline period as 0.51 ∘C; hence the 1.5 and 2.0 ∘C warming targets are determined by additional warming of 0.99 and 1.49 ∘C, respectively. For each RCP, we define the 1.5 and 2 ∘C warmer worlds by using the multi-model ensemble mean of global temperature. In other words, the reaching year is the same for all 13 GCMs under a specific RCP scenario and is determined as the 30-year period with mean temperature closest to the warming target for each RCP (see Fig. 1).
2.3 Drought indices and event identification
2.3.1 Standardized Precipitation Evapotranspiration Index
The drought condition is quantified with the SPEI developed by Vicente-Serrano et al. (2010), which has been widely adopted in characterizing drought conditions (e.g., Ayantobo et al., 2018; Wen et al., 2019). The SPEI quantifies the extent of atmospheric water surplus and deficit relative to the long-term average condition by standardizing the difference between precipitation and potential evapotranspiration (PET). The SPEI with a 3-month timescale (SPEI-3) is used in this study because it captures well the shallow soil moisture available to crops and reflects seasonal water loss processes (Yu et al., 2014).
The PET is first calculated using the Penman–Monteith approach suggested by the Food and Agriculture Organization of the United Nations (FAO) (Allen et al., 1998):
where Δ is the slope of saturation vapor pressure vs. air temperature curve (kPa ∘C−1) and is calculated by
where tmean is the surface mean air temperature (∘C). Rn is the net radiation (MJ m−2 d−1) and is calculated by
where rsds and rsus (rlds and rlus) are surface downwelling and upwelling shortwave flux (surface downwelling and upwelling longwave flux), respectively (w m−2). G is the soil heat flux (MJ m−2 d−1) and is close to zero at the daily scale. γ is a psychometric constant (kPa ∘C−1) and is calculated by
where P is the atmospheric pressure (kPa). u2 is the wind speed at 2 m height (m s−1), transferred from
where u10 is the surface wind speed at the 10 m height simulated by GCMs. es and ea are saturation and actual vapor pressure (kPa), respectively:
where RH is the relative humidity (%) and tmp is temperature (i.e., daily maximum and minimum air temperature). Due to the non-linearity of Eq. (6), it would be more appropriate to apply the average saturated vapor pressure derived from the daily maximum and minimum air temperature.
The widely used log-logistic distribution is employed for fitting the 3-month deficit of precipitation and PET (P − PET) (Touma et al., 2015):
where F(x) denotes the cumulative distribution function; α, β and λ represent shape, scale and location parameters, which are estimated by the maximum likelihood method (Ahmad et al., 1988).
The SPEI-3 can then be derived by standardizing the F(x) into a standard normal function with a transforming function Φ−1 as follows:
2.3.2 Drought event identification
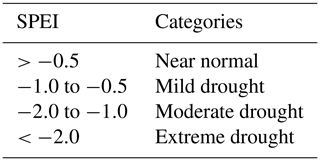
After calculating the SPEI-3 for global terrestrial grid cells, we derive the drought duration, intensity, and severity using the run theory for the reference and the 1.5 and 2 ∘C warmer worlds. The run theory proposed by Yevjevich. (1967) is a useful and objective method for drought event identification, where a run represents a subset of time series, in which SPEI-3 is either beneath (i.e., negative run) or over (i.e., positive run) a fixed threshold. A run with SPEI-3 that continuously stays below −0.5 is defined as a drought event (Mishra and Singh, 2010; Zargar et al., 2011), which generally includes drought characteristics of duration and severity. The persistent time period during a drought event is further defined as the drought duration, while drought severity (dimensionless) is defined as a cumulative deficit below −0.5.
2.4 Bivariate return period and most likely realization method
Previous studies usually independently examined the change either in drought duration or severity under climate warming, neglecting the multiplex nature of droughts (Naumann et al., 2018). This study jointly models drought duration (D) and severity (S) via the copula function, which is versatile for describing dependent hydrological variables due to its good flexibility of marginal distributions. The widely used Gamma distribution was adopted for fitting drought variables in each grid over the globe, and we selected the Gumbel copula to model the joint distribution of drought duration and severity. Within the copula-based approaches, different definitions of joint return periods (JRPs) have been proposed, such as OR, AND, Kendall, dynamic, and structure-based return periods (Yin et al., 2019a). Among these, the OR case (Tor) is usually adopted in drought occurrence assessment (Zhang et al., 2015):
where El represents the expected inter-arrival time of drought events, the joint distribution F(d, s) could be described by a copula function C[FD(d), FS(s)], and FD(d) and FS(s) indicate the marginal distribution functions of D and S, respectively.
Under the bivariate framework, the choice of an appropriate Tor leads to infinite combinations of drought duration and severity. The drought events along the Tor-level curve are generally not equivalent in terms of environmental and societal consequences, and hence the likelihood of each event must be taken into consideration when selecting appropriate joint quantiles. In this paper, the most likely realization method (Salvadori et al., 2011; Yin et al., 2019a) is used to choose the drought scenario with the highest likelihood along the Tor-level isoline. For a given Tor, the most likely combination point among all possible events can be derived by the following formula (Gräler et al., 2013):
where f(d, s) represents the joint probability density function of drought duration and severity, c[FD(d), FS(s)]=dC(FD(d), FS(s))∕d(fD(d))d(fS(s)) indicates the density function of the copula, and fD(d) and fS(s) are probability density functions of drought duration and severity, respectively. Due to the complexity of deriving analytical solutions in Eq. (11), the harmonic mean Newton method (Yin et al., 2018a) is applied to estimate the most likely realizations.
2.5 Calculation of socioeconomic exposure under warmer conditions
To calculate the socioeconomic exposures by droughts in different warming environments, we evaluate the change in drought occurrence frequency in a bivariate context. Firstly, we estimate the bivariate quantiles of drought duration and severity (i.e., most likely realization) under one given JRP during the historical period. As the 50-year drought events usually gained great attention by the scientific community and socio-climatic policymakers (Zhang et al., 2015; Naumann et al., 2018), we adopt this level as a reference for assessing possible drought implications. With the historical 50-year bivariate quantiles, we can recalculate the joint occurrence frequency under future additional 1.5 and 2.0 ∘C warming conditions, respectively. It can be inferred that areas with a JRP lower than 50 years are projected to suffer from more severe drought conditions. To explicitly assess the drought risk changes from 1.5 to 2.0 ∘C warming climates, we estimate the ratio of the recalculated recurrence frequency between these two warming periods. Taking the 50-year drought events as an example, we first determine the magnitudes (duration and severity) of the 50-year drought events in the historical period. Then we input the determined magnitudes of the 50-year drought events into the future joint distribution functions, recalculate the joint recurrence frequencies and convert them into new return periods at the 1.5 and 2.0 ∘C warming climates. The ratio is then calculated by dividing the new return period in the 2.0 ∘C warming future by the new return period in the 1.5 ∘C warming. A ratio less than 1.0 suggests that the new return period in 2.0 ∘C warming climates further reduces compared to that in the 1.5 ∘C warming level, which means that reference drought events are more common under the 0.5 ∘C warming impacts and implies worrisome conditions.
To evaluate socioeconomic implications of drought with additional warming, we record the population and GDP in those areas with more severe drought conditions and define them as exposures by increasing drought risks. As previously stated, we consider the dynamic nature of socioeconomic development pathways by employing different SSPs and used the multi-year average populations and GDPs during 30-year periods determined by different warming levels. After estimating the socioeconomic exposures for each GCM simulation, we use the multi-model ensemble mean as an indication for each grid cell to reduce model bias. Note that we select three RCPs and corresponding SSPs under two warming targets so that the analysis is performed on six scenarios.
3.1 Projected changes in dryness
We first examine changes in the mean and standard deviation of SPEI-3 from the historical reference period (1976–2005) to the 1.5 ∘C warmer worlds (Fig. 2), indicated by the multi-model ensemble mean results. We find that mean SPEI-3 decreases at the global scale (across 85 % of the land areas, excluding Antarctica), except in very limited regions in high-latitude areas (e.g., Siberia in Russia), where it exhibits a slight increase. The descending changes in the mean SPEI-3 imply that, over the majority of the globe, the probability distribution function of SPEI-3 would shift towards lower values and hence more severe dryness. Particularly, dramatic decreases combined with strong model agreement (in terms of sign of change) are presented in South America, Australia, and northern Africa. This may be attributed to higher evaporative demands and more frequent and persistent dry spells associated with rising temperatures (Naumann et al., 2018). On the other hand, we also observe an increase in the standard deviation of SPEI-3 with additional 1.5 ∘C warming, particularly in northern Africa and southwestern Asia. As the SPEI-3 follows the standard normal distribution, the increasing standard deviation means more variability in dryness, which hinders resilience efforts in a 1.5 ∘C warmer world. These changes are consistent under three different RCPs, indicating the robustness of this globally drier future.
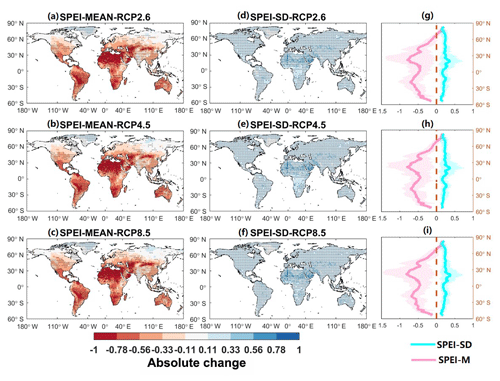
Figure 2Projected changes in the mean and standard deviation of the SPEI under the 1.5 ∘C warming target.
How would the dryness pattern change from 1.5 to 2.0 ∘C warming climates? A progressive descending change in mean values of SPEI-3 is observed across 58 % of the land surface with the global mean temperature increasing between 1.5 and 2.0 ∘C, although several high-latitude regions (i.e., Russia, Canada) show an insignificant opposite change (Fig. 3). This may be mechanically explained by thick clouds in these regions that strengthen the reflectance of shortwave radiation and limit the increase in latent heat flux as well as evapotranspiration, thus contributing to the mitigation of atmospheric aridity (Huang et al., 2017). For the change in the standard deviation of SPEI-3, we find that increases occur over continental regions almost globally, accompanied by minor spatial variability. Overall, the climatic metric SPEI-3 shows a strong negative response to the warming climate, suggesting that dryness will intensify in a future warming world.
3.2 Projected changes in drought characteristics
Figure 4 shows the relative change in global drought duration and severity derived from SPEI-3 in the 1.5 ∘C warmer world relative to the historical period under three different RCPs. The drought duration is projected to slowly prolong with warming across 78 % of the land surface, and 44% of land areas have an increase of higher than 10 %, although the change is not significant in the Russian and Sahel areas. The drought severity shows a much more pronounced rise globally, with significant increases (exceeding 50 %) over 46 % of global landmasses. Moreover, several regions experience compound increases (with strong model agreement) in both drought severity and duration, such as Southeast Asia, the Mediterranean, southern Africa, southern North America, and South America, suggesting an urgent need to increase societal and environmental resilience to a warming climate there. In the tropics and high-latitude areas, the drought severity is projected to increase, while the duration will decrease. In these regions, mitigation strategies should target short, intense bursts of drought.
When the global temperature rises from additional 1.5 to 2.0 ∘C warming, the world will experience more severe drought conditions, with a further increase in drought severity accounting for 75 % of the land surface (differences in effects between the 1.5 and 2.0 ∘C warming levels) and a persistent lengthening in duration across 58 % of the land areas (Fig. 5). Similar to the changing pattern from the baseline to a 1.5 ∘C warming climate, the drought severity shows a more rapidly increasing rate than drought duration globally under the 2.0 ∘C warming world. Comparing the 2.0 ∘C to the 1.5 ∘C warming condition, the increase in drought severity is greater than 10 % over 35 % of the land areas, while only 8 % of the land areas show such an increase (>10 %) in drought duration. This drought-prone condition is more severe in several regions such as Mediterranean regions, South Africa and South America, posing large challenges for existing socio-hydrological systems there.
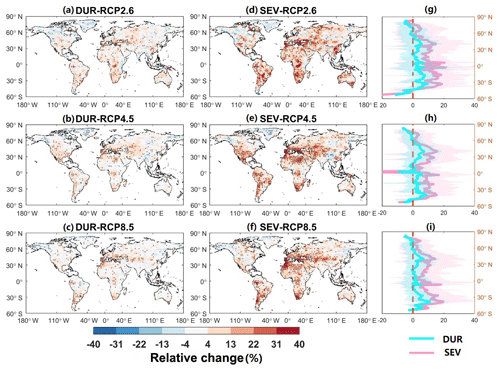
Figure 5Projected changes in drought duration and severity between the 1.5 and 2.0 ∘C warming targets.
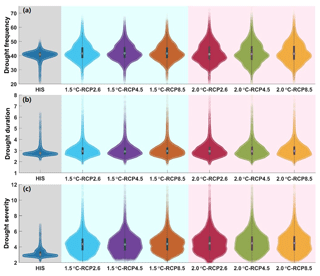
To explicitly investigate the changes in drought characteristics under warming conditions, we also show statistics of drought frequency, duration and severity in the historical period and future additional warmer worlds in violin plots (Fig. 6), in which the distributions comprise drought characteristics across all land pixels of the multi-model ensemble mean results. The violin plots (Hintze and Nelson, 1998) consist of a boxplot inside and an outside violin shape which displays the probability distribution of drought characteristics. Apparently, the drought frequency based on SPEI-3 is also projected to pronouncedly lengthen under three RCPs, accompanied by large variability capturing by the kernel density estimation in Fig. 6. This rapid increasing tendency also holds true for drought duration and severity, and extreme conditions are projected to occur more frequently under warming climates. For example, the 90 % uncertainty range of drought duration (severity) increases from 2.2–6.5 to 1.8–7.8 months (from 2.1–6.6 to 2.0–12) under the 2.0 ∘C warming climate relative to the historical period.
3.3 Projected changes in drought risks
As evidence is accumulating that high-impact events are typically multivariate in nature (Zhang et al., 2015; Ayantobo et al., 2017), we now consider a deeper focus on changes in drought severity and duration within a bivariate framework under different warming levels. Using the copula-based approach in Sect. 2.4, we show the median projected change in the historical 50-year drought conditions over multi-model ensembles under a 1.5 ∘C warming climate (Fig. 7). Generally, in regions with a substantial increase in drought duration and severity (Fig. 5), the 50-year drought events exhibit a rapid increase in occurrence with warming. More than 88 % of global landmasses will be subject to more frequent historical 50-year droughts, and the frequency of such severe droughts would double over 58 % of the global land surface. For most areas of South America (except for the zone around the Equator), northeastern America, central and western Asia, and Northwest China, the historical 50-year droughts are projected to occur 2 to 10 times more frequently under the ambitious 1.5 ∘C warming level. Regions with a lower frequency of historical 50-year drought events indicate a reduction in drought risks, which are only limited in Siberia, the Indian peninsula, and Alaska.
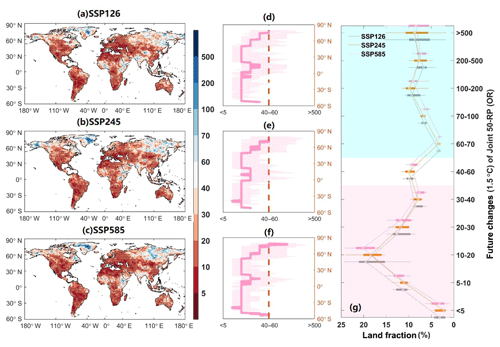
Figure 7Projected changes in joint 50-year return periods of droughts under the 1.5 ∘C warming target.
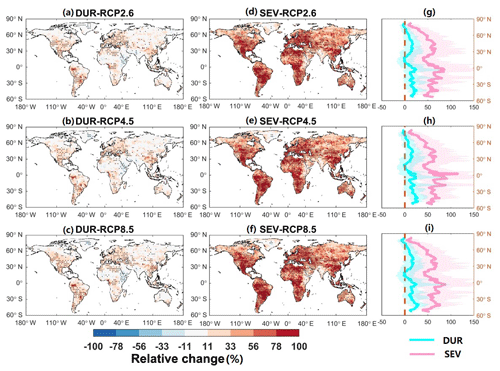
To closely assess the drought conditions with an extra 0.5 ∘C warming, we derive the ratio of an adjusted 50-year return period between 2.0 and 1.5 ∘C warming worlds (Fig. 8). In regions with a ratio of less than 1.0, the present drought events are projected to occur more frequently under the half-degree additional warming, which accounts for 71 % of continental areas. In addition, the frequency of the historical 50-year droughts would double across 67 % of the global landmasses under the 2.0 ∘C warming level. That is, 9 % increase in the world land areas compares to the 1.5 ∘C warming level (i.e., 58 %). Although over some regions such as northern Canada and East Asia, the occurrence of the extreme droughts will be less frequent to some degree, strong rises in recurrence frequency with warming are projected to dominate large parts of Europe, the southern United States, Australia, South America, northern Africa, and the Mediterranean.
3.4 Population and GDP exposure from increasing drought risks
To understand the socioeconomic influences induced by increasing drought risks (here defined as more frequent historical 50-year events), we combine the drought projection with population and GDP information based on SSPs and estimate exposures by droughts in the 1.5ãnd 2.0 ∘C warmer worlds. Here, instead of using the absolute value of population (and GDP) to assess the nation-wide drought exposures, the nation-wide population (and GDP) fraction is employed. This can avoid covering up badly drought-affected countries where the national populations (or GDP) are small (or low) in terms of the world level. Specifically, for a country (e.g., the United States), the fraction of drought-affected population (and GDP) divided by the total population (and GDP) of this country is employed as the indicator. Therefore, the most drought-affected countries are presented by high fractions. Globally, three SSPs suggest a consistent projection that large percentages of population and GDP will be exposed to increasing drought risks. In more than 67 (140) countries, 100 % (50 %) of both populations and GDPs are exposed to more severe droughts under the 1.5 ∘C warming target (Fig. 9). The two socioeconomic factors of GDP and population are highly correlated (O'Neill et al., 2014). Economically prosperous regions are associated with higher population and immigration (Fig. S1 in the Supplement); thus, the drought-affected GDP exposures usually exhibit similar changing patterns with the population. In regions with low GDP and population density, even when total socioeconomic exposures to droughts seem small, droughts can still cause fatal and destructive losses for those countries if their drought resilience is poor. To give a fairer and more impartial assessment of droughts' socioeconomic consequences, we define and assess the fraction of drought-affected population (or GDP) divided by total national population (or total GDP) based on different countries in a 1.5 ∘C warming world. In addition, we see some interesting results. For example, the US and China are no longer the most drought-affected countries, while 100 % of the population and GDP in the Mexico, southern Europe, central and southern Africa, and Mediterranean regions (i.e., Turkey, Ukraine) are projected to experience more severe drought, suggesting large policy challenges there.
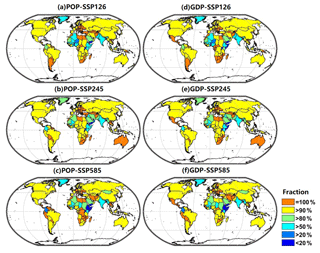
Figure 9National population and GDP fraction exposure to more frequent severe droughts under the 1.5 ∘C warming target.
To illustrate the consequences of limiting warming to 2.0 ∘C above the preindustrial levels, we also calculate the socioeconomic exposures under three SSPs (Fig. 10) and the differences in percentage between the 1.5 and 2.0 ∘C warming levels (Fig. S2). Most regions of the globe are projected to exhibit a generally increasing fraction (relative to 1.5 ∘C warming) in populations and GDPs (except for central Africa and East Asia). To be specific, under the extra half-degree warming, an additional 17 countries are projected to exhibit a 100 % fraction in socioeconomic exposure. More than 10 countries would experience a 30 % increase in population and GDP exposure if the global warming level increased from 1.5 to 2.0 ∘C. These increases illustrate the benefit of holding global warming to 1.5 ∘C instead of 2 ∘C, particularly for the mitigation of population and GDP exposure to drought. It should be noted that when climate warming climbs from 1.5 to 2.0 ∘C, there is some spatial heterogeneity with regards to drought exposure variations. Specifically, drought exposures for some countries (i.e., Canada) can be slightly decreased in the 2 ∘C warming level compared to the 1.5 ∘C warming level. This decrease in population and GDP exposure fraction can be attributed to the decreasing land fraction exposure to more frequent droughts (Table S2). For example, the land fraction suffering more frequent severe droughts in Canada will decrease (−12.77 %) in the 2.0 ∘C warming level compared to 1.5 ∘C warming under the SSP126 scenario. In other words, the additional 0.5 ∘C warming will not lead to drought risk deterioration globally, partly due to the increasing column-precipitable water with a warming environment (Dong et al., 2019; Yin et al., 2019b), although it holds for the majority of global landmasses. Anyway, the spatial heterogeneity should be given attention, especially when assessing the climate change impacts on extreme events at regional or local scales (Liu et al., 2018b).
3.5 National assessment of socioeconomic exposure in typical countries
The large spatial variability of drought risks and socioeconomic exposures under climate warming motivates a more systematic and in-depth assessment on national scales, particularly for the countries vulnerable to droughts. Therefore, we investigate more thoroughly the drought-affected land fractions (Figs. 11 and 12) and corresponding socioeconomic exposure (Figs. S3 and S4) in eight hotspot countries spanning different socio-climatic regions: Argentina, Australia, Canada, China, United States, South Africa, Brazil, and Mexico.
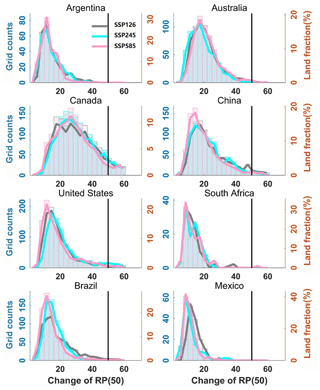
Figure 11Projected changes in drought risks for eight typical drought-prone countries under the 1.5 ∘C warming target.
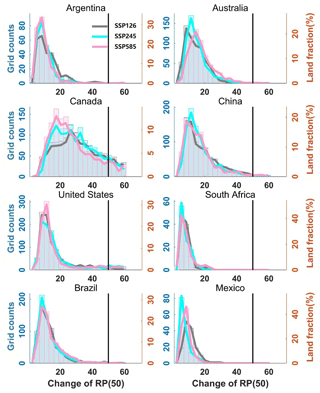
Figure 12Projected changes in drought risks for eight typical drought-prone countries under the 2.0 ∘C warming target.
For assessment at the national scale, spatially aggregating mean changes are more helpful than per-grid cell changes for indicating the risk of a particular land fraction being impacted by climate change (Fischer et al., 2013; Lehner et al., 2017). The land fractions of each grid cell are binned and plotted against the change in drought return period (relative to historical 50-year drought) (Figs. 11 and 12). The bin number is fixed to 20 groups for the eight example countries. In a 1.5 ∘C warming world (Fig. 11), these spatially aggregated changes explicitly show a significant increase in drought risks over these hotspot countries, with more than 90 % of grid cells projected to suffer from more frequent droughts.
Nevertheless, we still observe a difference between the tropics and extratropical regions. The increasing drought risks are more profound in tropical regions (e.g., Mexico and Brazil) than those over the high-latitude country (e.g., Canada). For instance, in a 1.5 ∘C warming world, more than 85 % of the grid cells (associated with around 65 %–97 % of the national populations and GDPs) over Mexico and Brazil could be exposed to the historical 50-year drought every 20 years. This pronounced increase in drought risks over tropical countries may be attributed to an oceanic forcing that favors the formation of deep convection over the ocean and thus weakened the continental convergence associated with the monsoon (Giannini et al., 2013). This finding suggests that the tropics may confront more severe, frequent droughts and worse socioeconomic influences (Figs. S3 and S4) under a warming climate. When the additional warming target rises up to 2.0 ∘C, drought conditions worsen over all these example countries (Fig. 12). The increase in drought risks is still more pronounced in the tropical countries. More than 90 % of the grid cells (associated with around 90 %–100 % of the national population and GDP) across Brazil and Mexico will experience drought frequency double that of the historical 50-year drought.
Overall, increasing drought risks under warming climates can cause major challenges for sustainable development and existing infrastructure systems, while ambitiously limiting warming to 1.5 ∘C would substantially mitigate future drought risks and corresponding socioeconomic exposures.
Among the warming-induced hydrological changes, one of the most definitive and detectable changes is the simultaneous increase in precipitation and evaporative demand, which are governed by the Clausius–Clapeyron relationship (Scheff and Frierson, 2014). Observations and model simulations have reported a variety of scaling rates between precipitation and global temperature, where the daily and hourly precipitation extremes (i.e., 99th/95th percentile precipitation) usually exhibit a sub-C–C scaling at regional scales, accompanied by spatial and decadal variability (Yin et al., 2018b). For global average precipitation, however, most climate models project an increase of 1 %–3 % per degree warming (Liu et al., 2013). This deviation from the C–C relation law is due to a global radiative energy constraint (Held and Soden, 2006) and atmospheric moisture limitation by decreasing relative humidity and increasing the potential for intense tropical and subtropical thunderstorms under warming (Muller et al., 2011; Yin et al., 2018b). Potential evapotranspiration, on the other hand, is predicted to increase by 1.5 %–4 % per degree warming (Scheff and Frierson, 2014; Naumann et al., 2018). Therefore, we expect climate warming to lead to a general intensification of drought conditions, as the drying of the surface is enhanced with water scarcity. This is confirmed by the decreasing SPEI-3 and significantly increasing drought severity and duration with warming globally found here (Figs. 2–8).
The reference crop Penman–Monteith model is employed to calculate potential evapotranspiration (and thus SPEI) in the current study. In this process, surface resistance (rs) is fixed to 70 s m−1. However, according to recent studies (e.g., Roderick et al., 2015; Yang et al., 2019), an elevated CO2 environment can drive stomatal closure, increasing stomatal resistance and further increasing rs. Subsequently, this increasing rs causes the decline in the potential evapotranspiration, especially across vegetated lands where the photo-synthetic rate is high. From this perspective, the neglect of increasing rs may overestimate future drying conditions and corresponding drought risk changes to some extent. However, on the other hand, the increase in total leaf area with CO2 and growing-season length can cause countervailing decreases in rs (Greve et al., 2019). Overall, accurate and robust quantification of rs scaling with CO2 still needs additionally explicit work and substantial observed data. Though the impact of rs on the drought assessments deserves further studies, it is beyond the scope of this study. Therefore, the traditional fixed rs method is used in this study to calculate potential evapotranspiration.
In the run theory, once the threshold (e.g., −0.5) is determined, drought events with different severity magnitudes are identified and constitute a sample for the selected time period. This sample contains different magnitudes in severity and different lengths in the duration, therefore characterizing the distribution of different levels of drought (ranging from the mild, moderate, to extreme conditions). On the other hand, different threshold values in identifying a drought event may cause disparities regarding drought risk changes and may challenge the robustness of our results. Generally, the threshold value usually ranges between −1 and 0 (Xu et al., 2015; Ayantobo et al., 2017, 2018; Yuan et al., 2017; Jiao and Yuan, 2019). Herein, the threshold of −0.5 is employed to identify droughts varying from mild to extremely dry levels (Table 2, Chen et al., 2018), which has been widely adopted in drought-related studies (Liu and Jiang, 2015; Xiao et al., 2017; Chen et al., 2018). The inclusion of minor drought events can enlarge the sample size in bivariate frequency analysis and thus circumvents the problem of insufficient samples. Moreover, to verify the robustness of our results, we also use the −0.8 threshold to serve as a comparison. Relevant results are shown in Figs. 13–15. Figure 13 displays comparisons of distributions comprising drought characteristics (i.e., drought frequency, drought duration and drought severity) across all land pixels between using −0.8 and −0.5 as the thresholds. Figures 14 and 15 show comparisons of projected changes in joint 50-year return periods of droughts between using −0.8 and −0.5 as the thresholds under different warming levels. As shown in the figure (Fig. 13), drought characteristics tend to slightly decrease across different periods. However, future drought risk changes as indicated by the 50-year joint return period deriving from the −0.8 threshold are similar to those from the −0.5 threshold (Figs. 14 and 15). In addition, we also derive changes in drought risks for the 20- or 100-year drought events to explore risk variations caused by different extents of drought (Figs. S5 and S6). Results show that although the magnitudes of changes are different, they present quite similar spatial patterns. Furthermore, since the calculation of socioeconomic exposures to droughts is based on the variations of drought risks when employing the same dynamic population (and GDP) pathways, similar changes in the drought risks will lead to analogical socioeconomic exposures. As a reference, we analyze the socioeconomic exposures in the case when −0.8 is used as the threshold (Figs. S7 and S8). Compared with the results of the −0.5 threshold (Figs. 9 and 10), the overall characteristics of the drought exposures are mostly the same. This confirms the conclusions of our study.

Figure 13Distribution for drought characteristics when using −0.5 as the threshold and −0.8 as the threshold, respectively.
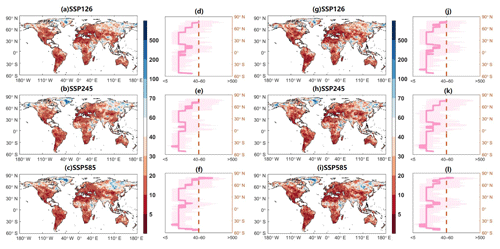
Figure 14Projected changes in joint 50-year return periods of droughts when using −0.5 as the threshold and −0.8 as the threshold under the 1.5 ∘C warming target.
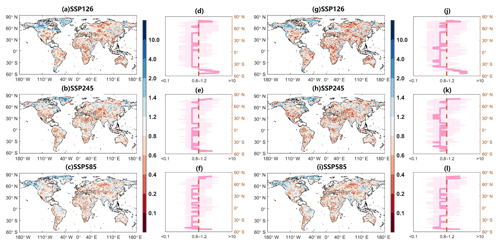
Figure 15Projected changes in joint 50-year return periods of droughts when using −0.5 as the threshold and −0.8 as the threshold between the 1.5 and 2.0 ∘C warming targets.
Although aggravated drought risks are projected globally, the changing patterns exhibit large spatial variability, with more significant increases over mid-latitudes and tropical regions than those over high-latitude landmasses. It should be noticed that regions (e.g., the Mediterranean, southern Africa, southern North America) with large projected changes generally display strong model agreement (in terms of sign of change), which implies high confidence in these drought-prone areas. Conversely, substantial model uncertainty of drought projections is particularly clear for regions with small changing amplitudes, as indicated by weak model agreement (e.g., Southeast Asia and Russia). For example, 100 % of the population in tropical regions like Brazil and Mexico would be affected by increasing drought risks. Indeed, our finding that the tropical and mid-latitude regions, where the vast majority of the global population resides, would bear the greatest drought risks should be precautious under the foreseeable warming future. Previous studies have reported that the increases in El Niño frequency (Xie et al., 2010), an extension of the Hadley cell (Lu et al., 2007), and poleward moisture transport by transient eddies (Chou et al., 2009) under warming all contribute to the drying tendency in the tropics; however, our work does not quantitatively examine these underlying physical mechanisms behind the spatial variability due to paucity of data.
When investigating socioeconomic exposure (i.e., population and GDP) under different warming levels, we notice that drought risks and population (GDP) both contribute to the exposure change. However, the use of population and GDP for a single year (i.e., 2005 or 2100), which have been used by some earlier studies (e.g., Peters, 2016; Park et al., 2018; Liu et al., 2018a), has ignored the role of dynamic socioeconomic impacts. This neglect may lead to biased conclusions. In this study, the dynamic characteristics are considered differences in population (and GDP) between the fixed 30-year 1.5 and 2.0 ∘C warming periods (Table 3). Accordingly, the exposure is defined as the number of people (GDP) being exposed to areas where the bivariate drought risks increase under the warming climate. Under the 1.5 ∘C warming climate, there are around 88 % of global landmasses being exposed to increasing drought risks, which corresponds to USD 1386.9 million population (and USD 33311.1 billion) according to the average of the three SSPs from a global perspective. At the 2.0 ∘C warming level, though there are still 88 % of the global land areas being exposed to increasing drought risks, the affected population (and GDP) will soar to 1538.2 million (and USD 72852.2 billion). In this light, the increase in population (and GDP) contributes to the increasing exposures. Therefore, it is important to incorporate the dynamic population (and GDP) into exposure-calculating processes. Nevertheless, when further investigating the affected population (and GDP) between the two warming climates, the role of drought risk changes should also be given attention. Specifically, though the percentage of landmasses with increasing drought risks stays unchanged for both the 1.5 and 2.0 ∘C warming climates (both approximately 88 %), the magnitudes of risk changes are different. For instance, drought risks will double across around 58 % of the global landmasses at the 1.5 ∘C warming level, while the same drought risks will occur over 67 % of the global landmasses at the 2.0 ∘C warming level. Those differences in the magnitudes of drought risk changes can definitely bring about divergent impacts to the local population and economy. Therefore, our study strengthens the benefits and necessity of controlling the global warming at the 1.5 ∘C level.
For a complete analysis of climate change impact assessment, it is important to know the role of corresponding uncertainty especially induced by GCMs and RCP scenarios. Measured by the 90 % range of the changing characteristics of SPEI-3 from historical to 1.5 ∘C warming worlds and from 1.5 to 2.0 ∘C warming targets, the uncertainties induced by multi-model ensembles are quantified in each grid under three RCPs (Figs. S9 and S10). Compared with the ensemble mean change in SPEI-3 shown in Figs. 2 and 3, we find that the model uncertainty is relatively large, particularly for South America and Africa, where the 90 % range even exceeds the ensemble mean change. This finding also holds true when evaluating the drought duration and severity (Figs. S11 and S12), suggesting that model uncertainty cannot be ignored in climate change impact studies.
To fully consider model uncertainty on drought conditions, we also present the bivariate return period of the present 50-year drought condition for each model under RCP4.5 in a 1.5 ∘C warming world and the occurrence change under an additional 0.5 ∘C warming (Figs. S13 and S14). As expected, different climate models show large variations, and several models even exhibit opposite changes over certain regions. Despite this uncertainty, most models still project general increasing risks at the global scale under climate warming, particularly for mid-latitude areas and the tropics. For RCP uncertainty, although we notice that the three scenarios present similar variations to some extent, there are still discernable differences especially when the warming increases from the 1.5 warming level to the 2.0 ∘C warming level. Generally, the warming trajectories are dependent on RCP scenarios. In other words, different RCP scenarios correspond to various temperature levels for the fixed time period. However, this study fixed the warming level. It can be expected that the differences among RCP scenarios are largely reduced. Nevertheless, the complex circulation system can still result in some differences in hydro-meteorological variables (e.g., precipitation, wind speed and relative humidity) among RCP scenarios, even at the same warming level, because they are not linearly related to the warming temperature. Since drought conditions are evaluated by using such hydro-meteorological variables, those differences at the same warming level can lead to variations in drought evolutions. Furthermore, drought variations under three scenarios are even to some extent significant at the regional or national scales. For example, when the warming level increases from 1.5 to 2.0 ∘C, the GDP exposure for Colombia will decrease at the SSP126 scenario, while it will increase at the SSP585 scenario. Future studies may explore their potential physical mechanisms (i.e., connecting drought evolution with land–atmosphere interactions). For other uncertainty sources, several previous studies (Wang et al., 2018; Gu et al., 2019; Chen and Brissette, 2019) have been devoted to detecting and attributing uncertainty to GCM structure, RCPs, internal climate variability, and even drought indices. Here, it is challenging to consider all these uncertainties systematically; future work could focus on including the integrated uncertainty and quantifying relative contributions to drought evolution and impact assessments.
Finally, there are some extra issues that need attention. For instance, to fully consider the robustness of the results, we use the warming level of a multi-model ensemble mean to serve as the warming trajectory. Firstly, compared to the method of determining warming level by individual model output, the use of the multi-model ensemble mean method involves more future projections/GCMs and thus guarantees the reliability of the conclusions (Chen et al., 2011; Mehran et al., 2014). This multi-model ensemble mean method is also consistent with some previous studies (Liu et al., 2018a; Liu and Sun, 2019; Su et al., 2018). Secondly, the application of the multi-model ensemble mean method keeps the consistency of the sample size under each RCP and for each warming level. This can exclude the differences originating from the sample size when assessing different warming level impacts or evaluating RCP uncertainty. It is true that different warming-level calculating methods can result in divergent model ensembles and may thus affect the results. For example, some studies (Sanderson et al., 2017; Lehner et al., 2017) used a single model to conduct climate warming impact assessments, while some studies (James et al., 2017; Thober et al., 2018) employed pooled future projections (i.e., 1.5∕2.0 ∘C) to perform analyses without considering RCP discrepancies. Future studies may explore the impacts of different warming-level calculation methods, but this is beyond the scope of the current study.
In addition, considering the relative coarseness of the CMIP5 models, it may be more appropriate to re-grid the GCM outputs to a common rough grid (e.g., 2∘). However, the spatial resolution of population and GDP used in this study is 0.5∘ × 0.5∘, which has to be upscaled to the same resolution of GCM outputs. But a coarse grid may be larger than the largest city in the world; thus, it is inappropriate to reflect the regional population and GDP exposures. Besides, some national territory areas are small, and a finer resolution (e.g., 1∘ × 1∘) may be more appropriate to obtain reliable population and GDP exposure results at the national scale. The same spatial resolution has been used in other studies (e.g., Schneider and Reusch, 2016; Li et al., 2018; Yang et al., 2019). Nevertheless, in order to validate the rationality of interpolation to 1∘ spatial resolution, we also re-gridded the data to a 2∘ grid and further re-conducted our studies (Figs. S15 and S16). Overall, there are only slight differences between the results of 1 and 2∘ resolution, confirming the reliability of our results.
Motivated by the 2015 Paris Agreement proposal, we quantify the changes in global drought bivariate magnitudes and socioeconomic consequences in the 1.5 and 2.0 ∘C warmer worlds, with climate projected by the multi-model ensemble under three representative concentration pathways (RCP2.6, RCP4.5, and RCP8.5). The drought characteristics are identified using the SPEI combined with the run theory, and the changes in occurrence are measured by both drought duration and severity, with the incorporation of the copula functions and most likely realization method. The main conclusions are summarized as follows (Table S1 in the Supplement).
-
The means of SPEI-3 from the historical period to the 1.5 and 2.0 ∘C warmer worlds are projected to descend at a global scale, while the standard deviation exhibits large increases. As the SPEI-3 following the normal distribution, these changes suggest that the distribution of SPEI-3 would shift towards the negative side with a flatter tendency, implying a more severe drying condition in a future warming world.
-
The drought duration is projected to slowly prolong across 78 % of the land surface, while the drought severity shows a much more pronounced rise globally in the 1.5 ∘C warming world. Compared to the 1.5 ∘C warming condition, there will be a further increase in drought severity and a persistent lengthening in drought duration under the additional 2.0 ∘C warming level. Several regions in mid-latitude regions and the tropics would experience substantial increases in drought magnitude, such as Southeast Asia, the Mediterranean, southern Africa, southern North America, and South America.
-
More than 58 % of global landmasses would be subject to twice more frequent historical 50-year droughts even under the ambitious 1.5 ∘C mitigation target. The drought condition will further worsen under a 2.0 ∘C warming climate, with around a 9 % increase in the world landmasses experiencing such severe deterioration compared to the 1.5 ∘C warming level.
-
More than 75 (73) countries are projected to exhibit a 100 % fraction in the population (GDP) exposed to increasing drought risks even under the ambitious 1.5 ∘C warming trajectories. An extra 0.5 ∘C warming will lead to an additional 17 countries exhibiting a 100 % fraction in socioeconomic exposure. Moreover, the tropical countries (i.e., Mexico and Brazil) will be subject to dramatically increased drought risks, with 85 % of the land fraction experiencing a doubled frequency of severe historical droughts under the 1.5 ∘C warming target; when the warming increases to 2.0 ∘C, the corresponding land fraction is projected to approach 90 %.
The climate simulation data can be accessed from the CMIP5 archive (https://esgf-node.llnl.gov/projects/esgf-llnl/ (last access: 1 July 2019) (Taylor et al., 2012). The SSP data are provided by Buda Su and Tong Jiang in the National Climate Center, China Meteorological Administration.
The supplement related to this article is available online at: https://doi.org/10.5194/hess-24-451-2020-supplement.
JC conceived the original idea, and LG designed the methodology. JC, LPZ and JSK collected the data. LG developed the code and performed the study, with some contributions from JC and HMW. LG, JC, JBY, SCS and SLG contributed to the interpretation of the results. LG and JBY wrote the paper, and JC, SCS, SLG, LPZ and JSK revised the paper.
The authors declare that they have no conflict of interest.
This work was partially supported by the National Key Research and Development Program of China (no. 2017YFA0603704; no. 2016YFC0402206), the National Natural Science Foundation of China (grant nos. 51779176, 51539009, and 51811540407), the Overseas Expertise Introduction Project for Discipline Innovation (111 Project) funded by the Ministry of Education and State Administration of Foreign Experts Affairs, P. R. China (grant no. B18037), and the Thousand Youth Talents Plan from the Organization Department of the CCP Central Committee (Wuhan University, China). The authors would like to thank the World Climate Research Programme Working Group on Coupled Modelling and all climate modeling institutions listed in Table 1 for making GCM outputs available. We also thank Buda Su and Tong Jiang at the National Climate Center, China Meteorological Administration, for sharing the SSP data.
This research has been supported by the National Key Research and Development Program of China (grant nos. 2017YFA0603704 and 2016YFC0402206), the National Natural Science Foundation of China (grant nos. 51779176, 51539009, and 51811540407), the Overseas Expertise Introduction Project for Discipline Innovation (111 Project) funded by the Ministry of Education and State Administration of Foreign Experts Affairs, P. R. China (grant no. B18037), and the Thousand Youth Talents Plan from the Organization Department of the CCP Central Committee (Wuhan University, China).
This paper was edited by Xing Yuan and reviewed by two anonymous referees.
Ahmad, M. I., Sinclair, C. D., and Werritty, A.: Log-logistic flood frequency analysis, J. Hydrol., 98, 205–224, 1988.
Allen, R. G., Pereira, L. S., Raes, D., and Smith, M.: Crop evapotranspiration – Guidelines for computing crop water requirements, FAO Irrigation and drainage paper 56, Fao, Rome, available at: http://www.scscourt.org/complexcivil/105CV049053/volume3/172618e_5xAGWAx8.pdf (last access: January 2020), 1998.
Ayantobo, O. O., Li, Y., Song, S., and Yao, N.: Spatial comparability of drought characteristics and related return periods in mainland China over 1961–2013, J. Hydrol., 550, 549–567, 2017.
Ayantobo, O. O., Li, Y., Song, S., Javed, T., and Yao, N.: Probabilistic modelling of drought events in China via 2-dimensional joint copula, J. Hydrol., 559, 373–391, 2018.
Below, R., Grover-Kopec, E., and Dilley, M.: Documenting drought-related disasters: a global reassessment, J. Environ. Dev., 16, 328–344, 2007.
Chang, J., Li, Y., Wang, Y., and Yuan, M.: Copula-based drought risk assessment combined with an integrated index in the Wei River Basin, China, J. Hydrol., 540, 824–834, 2016.
Chen, J., Brissette, F. P., Poulin, A., and Leconte, R.: Overall un-certainty study of the hydrological impacts of climate change for a Canadian watershed, Water Resour. Res., 47, W12509, https://doi.org/10.1029/2011wr010602, 2011.
hen, J., Liu, Y., Pan, T., Liu, Y., Sun, F., and Ge, Q.: Population exposure to droughts in China under the 1.5 ∘C global warming target, Earth Syst. Dynam., 9, 1097–1106, https://doi.org/10.5194/esd-9-1097-2018, 2018.
Chen, J. and Brissette, F. P.: Reliability of climate model multi-member ensembles in estimating internal precipitation and temperature variability at the multi-decadal scale, Int. J. Climatol., 39, 843–856, 2019.
Chen, L., Guo, S., Yan, B., Liu, P., and Fang, B.: A new seasonal design flood method based on bivariate joint distribution of flood magnitude and date of occurrence, Hydrolog. Sci. J., 55, 1264–1280, 2010.
Chou, C., Neelin, J. D., Chen, C. A., and Tu, J. Y.: Evaluating the “rich-get-richer” mechanism in tropical precipitation change under global warming, J. Climate, 22, 1982–2005, https://doi.org/10.1175/2008JCLI2471.1, 2009.
Dong, W., Lin, Y., Wright, J. S., Xie, Y., Yin, X., and Guo, J.: Precipitable water and CAPE dependence of rainfall intensities in China, Clim. Dynam., 52, 3357–3368, 2019.
EM-DAT: The OFDA/CRED international disaster database (Univ Catholique de Louvain, Brussels), available at: https://www.emdat.be, last access: 15 September 2018.
Fischer, E. M., Beyerle, U., and Knutti, R.: Robust spatially aggregated projections of climate extremes, Nat. Clim. Change, 3, 1033, https://doi.org/10.1038/nclimate2051, 2013.
Genest, C. and Favre, A. C.: Everything you always wanted to know about copula modelling but were afraid to ask, J. Hydrol. Eng., 12, 347–368, 2007.
Giannini, A., Saravanan, R., and Chang, P.: Oceanic forcing of Sahel rainfall on interannual to interdecadal time scales, Science, 302, 1027–1030, 2013.
Gräler, B., van den Berg, M. J., Vandenberghe, S., Petroselli, A., Grimaldi, S., De Baets, B., and Verhoest, N. E. C.: Multivariate return periods in hydrology: a critical and practical review focusing on synthetic design hydrograph estimation, Hydrol. Earth Syst. Sci., 17, 1281–1296, https://doi.org/10.5194/hess-17-1281-2013, 2013.
Greve, P., Roderick, M., Ukkola, A. M., and Wada, Y.: The Aridity Index under global warming, Environ. Res. Lett., 14, 124006, https://doi.org/10.1088/1748-9326/ab5046, 2019.
Gu, L., Chen, J., Xu, C. Y., Kim, J. S., Chen, H., Xia, J., and Zhang, L.: The contribution of internal climate variability to climate change impacts on droughts, Sci. Total Environ., 684, 229–246, 2019.
Handmer, J., Honda, Y., Arnell, N., Benito, G., Hatfield, J., Mohamed, I. F., Peduzzi, P., Wu, S., Sherstyukov, B., Takahashi, K., and Yan, Z.: Changes in impacts of climate extremes: Human systems and ecosystems. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation, in: A Special Report of Working Groups I and II of the Intergovernmental Panel on Climate Change (IPCC), edited by: Field, C. B., Barros, V., Stocker, T. F., Qin, D., Dokken, D. J., Ebi, K. L., Mastrandrea, M. D., Mach, K. J., Plattner, G.-K., Allen, S. K., Tignor, M., and Midgley, P. M., Cambridge University Press, Cambridge, UK, 231–290, 2012.
Held, I. M. and Soden, B. J.: Robust responses of the hydrological cycle to global warming, J. Climate, 19, 5686–5699, 2006.
Hintze, J. L. and Nelson, R. D.: Violin plots: a box plot-density trace synergism, Am. Statist., 52, 181–184, 1998.
Hirabayashi, Y., Mahendran, R., Koirala, S., Konoshima, L., Yamazaki, D., Watanabe, S., and Kanae, S.: Global flood risk under climate change, Nat. Clim. Change, 3, 816–821, https://doi.org/10.1038/nclimate1911, 2013.
Huang, J., Yu, H., Dai, A., Wei, Y., and Kang, L.: Drylands face potential threat under 2 ∘C global warming target, Nat. Clim. Change, 7, 417–422, https://doi.org/10.1038/nclimate3275, 2017.
Huang, J., Qin, D., Jiang, T., Wang, Y., Feng, Z., Zhai, J., and Su, B.: Effect of Fertility Policy Changes on the Population Structure and Economy of China: From the Perspective of the Shared Socioeconomic Pathways, Earth's Future, 7, 250–265, 2019.
IPCC – Intergovernmental Panel on Climate Change: Special Report on Global Warming of 1.5 ∘C, Intergovernmental Panel on Climate Change (IPCC), in: Special report on global warming of 1.5 ∘C [M], Cambridge University Press, Cambridge, UK, 2018.
James, R., Washington, R., Schleussner, C. F., Rogelj, J., and Conway, D.: Characterizing half-a-degree difference: a review of methods for identifying regional climate responses to global warming targets, Wiley Interdisciplin. Rev.: Clim. Change, 8, e457, https://doi.org/10.1002/wcc.457, 2017.
Jiang, T., Zhao, J., Jing, C., Cao, L. G., Wang, Y. J., Sun, H. M., and Wang, R.: National and provincial population projected to 2100 under the shared socioeconomic pathways in China, Clim. Change Res., 13, 128–137, 2017.
Jiang, T., Zhao, J., Cao, L., Wang, Y., Su, B., Jing, C., and Gao, C.: Projection of national and provincial economy under the shared socioeconomic pathways in China, Adv. Clim. Change Res., 14, 50–58, 2018.
Jiao, Y. and Yuan, X.: More severe hydrological drought events emerge at different warming levels over the Wudinghe watershed in northern China, Hydrol. Earth Syst. Sci., 23, 621–635, https://doi.org/10.5194/hess-23-621-2019, 2019.
Jones, B. and O'Neill, B. C.: Spatially explicit global population scenarios consistent with the Shared Socioeconomic Pathways, Environ. Res. Lett., 11, 084003, https://doi.org/10.1088/1748-9326/11/8/084003, 2016.
Lehner, F., Coats, S., Stocker, T. F., Pendergrass, A. G., Sanderson, B. M., Raible, C. C., and Smerdon, J. E.: Projected drought risk in 1.5 ∘C and 2 ∘C warmer climates, Geophys. Res. Lett., 44, 7419–7428, 2017.
Leimbach, M., Kriegler, E., Roming, N., and Schwanitz, J.: Future growth patterns of world regions-A GDP scenario approach, Global Environ. Change, 42, 215–225, 2017.
Li, T., Guo, S., Liu, Z., Xiong, L., and Yin, J.: Bivariate design flood quantile selection using copulas, Hydrol. Res., 48, 997–1013, 2016.
Li, W., Jiang, Z., Zhang, X., Li, L., and Sun, Y.: Additional risk in extreme precipitation in China from 1.5 ∘C to 2.0 ∘C global warming levels, Sci. Bull., 63, 228–234, 2018.
Liu, J., Wang, B., Cane, M. A., Yim, S. Y., and Lee, J. Y.: Divergent global precipitation changes induced by natural versus anthropogenic forcing, Nature, 493, 656–659, https://doi.org/10.1038/nature11784, 2013.
Liu, K. and Jiang, D.: Analysis of dryness/wetness over China using standardized precipitation evapotranspiration index based on two evapotranspiration algorithms, Chin. J. Atmos. Sci., 39, 23–36, 2015.
Liu, W. and Sun, F.: Increased adversely-affected population from water shortage below normal conditions in China with anthropogenic warming, Sci. Bull., 64, 567–569, 2019.
Liu, W., Sun, F., Lim, W. H., Zhang, J., Wang, H., Shiogama, H., and Zhang, Y.: Global drought and severe drought-affected populations in 1.5 and 2 ∘C warmer worlds, Earth Syst. Dynam., 9, 267–283, https://doi.org/10.5194/esd-9-267-2018, 2018a.
Liu, W., Lim, W. H., Sun, F., Mitchell, D., Wang, H., Chen, D., Bethke I., Shiogama, H., and Fischer, E.: Global freshwater availability below normal conditions and population impact under 1.5 and 2 ∘C stabilization scenarios, Geophys. Res. Lett., 45, 9803–9813, https://doi.org/10.1029/2018GL078789, 2018b.
Liu, X. F., Wang, S. X., Zhou, Y., Wang, F. T., Li, W. J., and Liu, W. L.: Regionalization and spatiotemporal variation of drought in china based on standardized precipitation evapotranspiration index (1961–2013), Adv. Meteorol., 2015, 1–18, https://doi.org/10.1155/2015/950262, 2015.
Lu, J., Vecchi, G. A., and Reichler, T.: Expansion of the Hadley cell under global warming, Geophys. Res. Lett., 34, L06805, https://doi.org/10.1029/2006GL028443, 2007.
Mehran, A., AghaKouchak, A., and Phillips, T. J.: Evaluation of CMIP5 continental precipitation simulations relative to satellite-based gauge-adjusted observations, J. Geophys. Res.- Atmos., 119, 1695–1707, https://doi.org/10.1002/2013jd021152, 2014.
Mishra, A. K. and Singh, V. P.: A review of drought concepts, J. Hydrol., 391, 202–216, 2010.
Mitchell, D., James, R., Forster, P. M., Betts, R. A., Shiogama, H., and Allen, M.: Realizing the impacts of a 1.5 ∘C warmer world, Nat. Clim. Change, 6, 735–737, https://doi.org/10.1038/nclimate3055, 2016.
Muller, C. J., O'Gorman, P. A., and Back, L. E.: Intensification of precipitation extremes with warming in a cloud-resolving model, J. Climate, 24, 2784–2800, 2011.
Naumann, G., Alfieri, L., Wyser, K., Mentaschi, L., Betts, R. A., Carrao, H., and Feyen, L.: Global changes in drought conditions under different levels of warming, Geophys. Res. Lett., 45, 3285–3296, 2018.
O'Neill, B. C., Kriegler, E., Riahi, K., Ebi, K. L., Hallegatte, S., Carter, T. R., and van Vuuren, D. P.: A new scenario framework for climate change research: the concept of shared socioeconomic pathways, Climatic Change, 122, 387–400, 2014.
Park, C. E., Jeong, S. J., Joshi, M., Osborn, T. J., Ho, C. H., Piao, S., and Kim, B. M.: Keeping global warming within 1.5 ∘C constrains emergence of aridification, Nat. Clim. Change, 8, 70–74, https://doi.org/10.1038/s41558-017-0034-4, 2018.
Peters, G. P.: The best available science to inform 1.5 ∘C policy choices, Nat. Clim. Change, 6, 646–649, https://doi.org/10.1038/nclimate3000, 2016.
Roderick, M. L., Greve, P., and Farquhar, G. D.: On the assessment of aridity with changes in atmospheric CO2, Water Resour. Res., 51, 5450–5463, 2015.
Routson, C. C., Woodhouse, C. A., Overpeck, J. T., Betancourt, J. L., and McKay, N. P.: Teleconnected ocean forcing of Western North American droughts and pluvials during the last millennium, Quaternary Sci. Rev., 146, 238–250, 2016.
Salvadori, G., De Michele, C., and Durante, F.: On the return period and design in a multivariate framework, Hydrol. Earth Syst. Sci., 15, 3293–3305, https://doi.org/10.5194/hess-15-3293-2011, 2011.
Samir, K. C. and Lutz, W.: The human core of the shared socioeconomic pathways: Population scenarios by age, sex and level of education for all countries to 2100, Global Environ. Change, 42, 181–192, 2017.
Sanderson, B. M., Xu, Y., Tebaldi, C., Wehner, M., O'Neill, B., Jahn, A., Pendergrass, A. G., Lehner, F., Strand, W. G., Lin, L., Knutti, R., and Lamarque, J. F.: Community climate simulations to assess avoided impacts in 1.5 and 2 ∘C futures, Earth Syst. Dynam., 8, 827–847, https://doi.org/10.5194/esd-8-827-2017, 2017.
Scheff, J. and Frierson, D. M.: Scaling potential evapotranspiration with greenhouse warming, J. Climate, 27, 1539–1558, 2014.
Schilling, J., Freier, K. P., Hertig, E., and Scheffran, J.: Climate change, vulnerability and adaptation in North Africa with focus on Morocco, Agric. Ecosyst. Environ., 156, 12–26, 2012.
Schneider, D. P. and Reusch, D. B.: Antarctic and Southern Ocean surface temperatures in CMIP5 models in the context of the surface energy budget, J. Climate, 29, 1689–1716, 2016.
Seager, R., Kushnir, Y., Herweijer, C., Naik, N., and Velez, J.: Modeling of tropical forcing of persistent droughts and pluvials over western North America: 1856–2000, J. Climate, 18, 4065–4088, https://doi.org/10.1175/JCLI3522.1, 2005.
Smirnov, O., Zhang, M., Xiao, T., Orbell, J., Lobben, A., and Gordon, J.: The relative importance of climate change and population growth for exposure to future extreme droughts, Climatic Change, 138, 41–53, 2016.
Su, B., Huang, J., Fischer, T., Wang, Y., Kundzewicz, Z. W., Zhai, J., and Tao, H.: Drought losses in China might double between the 1.5 ∘C and 2.0 ∘C warming, P. Natl. Acad. Sci. USA, 115, 10600–10605, 2018.
Taylor, K. E., Stouffer, R. J., and Meehl, G. A.: An Overview of CMIP5 and the Experiment Design, B. Am. Meteorol. Soc., 93, 485–498, https://doi.org/10.1175/bams-d-11-00094.1, 2012.
Thober, S., Kumar, R., Wanders, N., Marx, A., Pan, M., Rakovec, O., Samaniego, L., Sheffield, J., Wood, E., and Zink, M.: Multi-model ensemble projections of European river floods and high flows at 1.5, 2, and 3 degrees global warming, Environ. Res. Lett., 13, 014003, https://doi.org/10.1088/1748-9326/aa9e35, 2018.
Touma, D., Ashfaq, M., Nayak, M. A., Kao, S.-C., and Diffenbaugh, N. S.: A multi-model and multi-index evaluation of drought characteristics in the 21st century, J. Hydrol., 526, 196–207, https://doi.org/10.1016/j.jhydrol.2014.12.011, 2015.
Tsakiris, G., Kordalis, N., Tigkas, D., Tsakiris, V., and Vangelis, H.: Analysing drought severity and areal extent by 2D Archimedean copulas, Water Resour. Manage., 30, 1–13, 2016.
UNFCCC: Conference of the Parties. Adoption of the Paris Agreement, Paris, 1–32, 2015.
Vautard, R., Gobiet, A., Sobolowski, S., Kjellström, E., Stegehuis, A., Watkiss, P., and Jacob, D.: The European climate under a 2 ∘C global warming, Environ. Res. Lett., 9, 034006, https://doi.org/10.1088/1748-9326/9/3/034006, 2014.
Vicente-Serrano, S. M., Beguería, S., and López-Moreno, J. I.: A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index, J. Climate, 23, 1696–1718, https://doi.org/10.1175/2009jcli2909.1, 2010.
Wang, H.-M., Chen, J., Cannon, A. J., Xu, C.-Y., and Chen, H.: Transferability of climate simulation uncertainty to hydrological impacts, Hydrol. Earth Syst. Sci., 22, 3739–3759, https://doi.org/10.5194/hess-22-3739-2018, 2018.
Wen, S. S., Wang, A. Q., Tao, H., Malik, K., Huang, J., Zhai, J., Jing, C., Rasul, G. and Su, B.: Population exposed to drought under the 1.5 ∘C and 2.0 ∘C warming in the Indus River Basin, Atmos. Res., 218, 296–305, 2019.
Wong, G., Van Lanen, H. A. J., and Torfs, P. J. J. F.: Probabilistic analysis of hydrological drought characteristics using meteorological drought, Hydrolog. Sci. J., 58, 253–270, 2013.
Xiao, M., Zhang, Q., Singh, V. P., and Chen, X.: Probabilistic forecasting of seasonal drought behaviors in the Huai River basin, China, Theor. Appl. Climatol., 128, 667–677, 2017.
Xie, S. P., Deser, C., Vecchi, G. A., Ma, J., Teng, H., and Wittenberg, A.: Global warming pattern formation: Sea surface temperature and rainfall, J. Climate, 23, 966–986, https://doi.org/10.1175/2009JCLI3329.1, 2010.
Xu, K., Yang, D. W., Xu, X. Y., and Lei, H. M.: Copula based drought frequency analysis considering the spatio-temporal variability in Southwest China, J. Hydrol., 527, 630–640, 2015.
Yang, Y., Roderick, M. L., Zhang, S., McVicar, T. R., and Donohue, R. J.: Hydrologic implications of vegetation response to elevated CO2 in climate projections, Nat. Clim. Change, 9, 44–48, https://doi.org/10.1038/s41558-018-0361-0, 2019.
Yevjevich, V. M.: Objective approach to definitions and investigations of continental hydrologic droughts, An. Hydrology papers, Colorado State University, Colorado, 1–17, 1967.
Yin, J. B., Guo, S. L., He, S. K., Guo, J. L., Hong, X. J., and Liu, Z. J.: A copula-based analysis of projected climate changes to bivariate flood quantiles, J. Hydrol., 566, 23–42, 2018a.
Yin, J. B., Gentine, P., Zhou, S., Sullivan, C. S., Wang, R., Zhang, Y., and Guo, S. L.: Large increase in global storm runoff extremes driven by climate and anthropogenic changes, Nat. Commun., 9, 4389, https://doi.org/10.1038/s41467-018-06765-2, 2018b.
Yin, J. B., Guo, S., Wu, X., Yang, G., Xiong, F., and Zhou, Y.: A meta-heuristic approach for multivariate design flood quantile estimation incorporating historical information, Hydrol. Res., 50, 526–544, 2019a.
Yin, J. B., Gentine, P., Guo, S., Zhou, S., Sullivan, S. C., Zhang, Y., Gu, L., and Liu, P.: Reply to `Increases in temperature do not translate to increased flooding', Nat. Commun., 10, 1–5, https://doi.org/10.1038/s41467-019-13613-4, 2019b.
Yu, M., Li, Q., Hayes, M. J., Svoboda, M. D., and Heim, R. R.: Are droughts becoming more frequent or severe in China based on the standardized precipitation evapotranspiration index: 1951–2010?, Int. J. Climatol., 34, 545–558, 2014.
Yuan, X., Zhang, M., Wang, L., and Zhou, T.: Understanding and seasonal forecasting of hydrological drought in the Anthropocene, Hydrol. Earth Syst. Sci., 21, 5477–5492, https://doi.org/10.5194/hess-21-5477-2017, 2017.
Zargar, A., Sadiq, R., Naser, B., and Khan, F. I.: A review of drought indices, Environ. Rev., 19, 333–349, 2011.
Zhang, Q., Xiao, M. Z., and Singh, V. P.: Uncertainty evaluation of copula analysis of hydrological droughts in the East River basin, China, Global Planet. Change, 129, 1–9, 2015.
Zscheischler, J. and Seneviratne, S. I.: Dependence of drivers affects risks associated with compound events, Sci. Adv., 3, e1700263, https://doi.org/10.1126/sciadv.1700263, 2017.