the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Dual state/rainfall correction via soil moisture assimilation for improved streamflow simulation: evaluation of a large-scale implementation with Soil Moisture Active Passive (SMAP) satellite data
Yixin Mao
Wade T. Crow
Soil moisture (SM) measurements contain information about both pre-storm hydrologic states and within-storm rainfall estimates, both of which are required inputs for event-based streamflow simulations. In this study, an existing dual state/rainfall correction system is extended and implemented in the 605 000 km2 Arkansas–Red River basin with a semi-distributed land surface model. The Soil Moisture Active Passive (SMAP) satellite surface SM retrievals are assimilated to simultaneously correct antecedent SM states in the model and rainfall estimates from the Global Precipitation Measurement (GPM) mission. While the GPM rainfall is corrected slightly to moderately, especially for larger events, the correction is smaller than that reported in past studies due primarily to the improved baseline quality of the new GPM satellite product. In addition, rainfall correction is poorer in regions with dense biomass due to lower SMAP quality. Nevertheless, SMAP-based dual state/rainfall correction is shown to generally improve streamflow estimates, as shown by comparisons with streamflow observations across eight Arkansas–Red River sub-basins. However, more substantial streamflow correction is limited by significant systematic errors present in model-based streamflow estimates that are uncorrectable via standard data assimilation techniques aimed solely at zero-mean random errors. These findings suggest that more substantial streamflow correction will likely require better quality SM observations as well as future research efforts aimed at reducing systematic errors in hydrologic systems.
- Article
(1081 KB) -
Supplement
(1088 KB) - BibTeX
- EndNote
Accurate streamflow simulation is important for water resources management applications such as flood control and drought monitoring. Reliable streamflow simulation requires accurate estimates of pre-storm soil moisture (SM) that control the partitioning of infiltration and surface runoff during rainfall events, as well as longer-memory subsurface flow (Freeze and Harlan, 1969; Western et al., 2002; Aubert et al., 2003). Good streamflow simulations also require realistic rainfall time series estimates.
SM measurements contain information about both antecedent hydrologic states and within-storm rainfall events. With advances in the quality and availability of in situ and satellite-measured SM products, researchers have started to explore the potential of using SM measurements to improve the estimates of both pre-storm SM and within-storm rainfall. For example, multiple studies have attempted to assimilate SM measurements to improve the representation of antecedent SM states in hydrologic models via Kalman-filter-based techniques (e.g., Francois et al., 2003; Brocca et al., 2010, 2012; Wanders et al., 2014; Alvarez-Garreton et al., 2014; Lievens et al., 2015, 2016; Massari et al., 2015; Mao et al., 2019). Other studies have explored the use of SM measurements to back-calculate within-storm rainfall or to correct existing rainfall time series products (e.g., Crow et al., 2011; Chen et al., 2012; Brocca et al., 2013, 2014, 2016; Koster et al., 2016).
In the past decade, so-called dual state/rainfall correction systems have been implemented that combine both SM state update and rainfall correction schemes to optimally improve streamflow simulations (e.g., Crow and Ryu, 2009; Chen et al., 2014; Alvarez-Garreton et al., 2016). Specifically, SM measurements (typically from satellite observation) are used to simultaneously update model states and correct the (typically satellite-observed) rainfall time series product used to force the model. The updated antecedent states and corrected rainfall are then combined as inputs into a hydrologic model to produce an improved streamflow simulation (see Fig. 1 for illustration of the dual-correction system). Past studies have suggested that such systems generally outperform either state-update-only or rainfall-correction-only schemes (Crow and Ryu, 2009; Chen et al., 2014; Alvarez-Garreton et al., 2016), with the rainfall correction contributing more during high-flow events and the state updating contributing more during low flow periods (also see Massari et al., 2018).
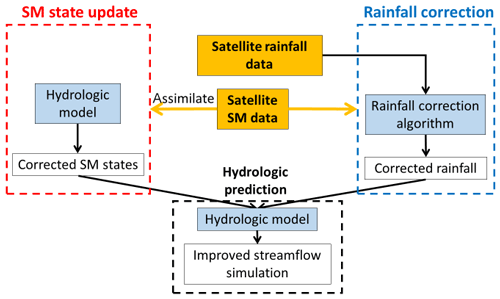
Figure 1The dual state/rainfall correction framework applied in this study. Satellite-based soil moisture (SM) data are integrated into a hydrological simulation system via two correction schemes: (1) a standard data assimilation system to correct modeled SM states (shown in the red box on the left) and (2) a rainfall correction algorithm to correct rainfall forcing data (shown in the blue box on the right). Finally, these two contributions are combined to improve streamflow simulations (shown in the black box at the bottom).
While these past studies were encouraging, they applied the dual-correction system only to catchment-scale, lumped hydrologic models. In this study, a semi-distributed land surface model, the Variable Infiltration Capacity (VIC) model, is implemented instead. The VIC model, compared to the previous lumped models, includes a more detailed representation of both energy and water balance processes (Liang et al., 1994; Hamman et al., 2018). The macroscale grid-based VIC also better matches the true spatial resolution of satellite SM measurements and provides a means for correcting large-scale streamflow analysis. In addition, earlier dual-correction studies used previous-generation satellite products such as the Advanced Scatterometer (ASCAT) satellite SM data, the Soil Moisture Ocean Salinity (SMOS) satellite SM data, and the Tropical Rainfall Measuring Mission (TRMM) precipitation data. Here, we use newer data products from the more recent Global Precipitation Measurement (GPM) mission (Hou et al., 2014) and the NASA Soil Moisture Active Passive (SMAP) mission (Entekhabi et al., 2010). Both the SMAP and GPM products provide near-real-time measurements over much of the global land surface, making them especially useful for regions with scarce ground-based rainfall and SM observations.
The main objective of this study is to assess the effectiveness of such a dual-correction system to improve streamflow simulations using recent satellite SM and precipitation products. To address this main objective, we introduce methodological advances. Specifically, we (1) extended the system to provide a probabilistic streamflow estimate via ensemble simulation and analysis techniques (note that past studies focused solely on deterministic improvement), (2) updated the rainfall correction scheme to take full advantage of the higher accuracy and temporal resolution of newer satellite data products, and (3) investigated the potential cross-correlation of errors in the dual system, thus validating the theoretical basis of our analysis system. These methodological contributions will be presented throughout the paper.
The remainder of this paper is organized as follows. Section 2 describes the dual-correction system and our novel methodological contributions, as well as the study domain, hydrologic model, and datasets used. Results are presented in Sect. 3. Section 4 discusses our results and identifies lessons learned, and Sect. 5 summarizes our conclusions.
2.1 Study domain
The dual state/rainfall correction system is applied in the Arkansas–Red River basin (approximately 605 000 km2) located in the south-central United States (Fig. 2). This basin consists of the Arkansas River and the Red River, both converging eastward into the Mississippi River. This domain has a strong climatic gradient and is wetter in the east and drier in the west (Fig. 2). The basin experiences little snow cover in winter except for the mountainous areas along its far western edge. Vegetation cover tends to be denser in the east (deciduous forest) than in the west (wooded grassland, shrubs, crops, and grassland).

Figure 2The Arkansas–Red River basin with climatology-averaged annual precipitation (calculated from NLDAS-2 precipitation data over 1979–2017). The pink shaded areas show the upstream sub-basins of the eight USGS streamflow sites evaluated in this study, with basin numbers labeled on the plot (see Table 1 for basin numbers and corresponding sites).
2.2 Data
2.2.1 SMAP satellite SM data
The SMAP mission provides SM estimates for the top 5 cm of the soil column, with an average revisit time of 2–3 d, a resolution of 36 km, and a 50 h data latency. Both ascending (afternoon; PM) and descending (morning; AM) retrievals from the SMAP L3 Passive product data Version 4 (O'Neill et al., 2016) from 31 March 2015 to 31 December 2017 were used in this study. A few SMAP pixels with obvious quality flaws (i.e., near-constant retrieval values) were manually masked out. The internal quality flags provided by the SMAP mission were not applied in this study to preserve the measurements in the eastern half of the domain, where the data quality of the entire region is flagged as unrecommended due to relatively heavy vegetation cover. The native 36 km SMAP retrievals were used throughout the study without spatial remapping or temporal aggregation.
2.2.2 GPM satellite precipitation data
The Integrated Multi-satellitE Retrievals for GPM (IMERG) Level 3 Version 05 Early Run precipitation data were used in this study (Huffman et al., 2018). IMERG merges multiple satellite observations and provides a near-global precipitation product with a spatial resolution of 0.1∘ (Huffman et al., 2015). We used the “Early Run” version of this product since its short latency (4 h) makes it suitable for near-real-time data assimilation applications. However, this short latency also prevents correction of the IMERG Early Run product using ground-based rain gauge observations. We aggregated the original 30 min IMERG precipitation product to our every 3 h modeling time step and remapped it onto our 1∕8∘ model spatial resolution.
2.2.3 Other meteorological forcing data
Other than precipitation, the VIC model requires air temperature, shortwave and longwave radiation, air pressure, vapor pressure, and wind speed as forcing inputs. These variables were taken from the 1∕8∘ gridded North American Land Data Assimilation System Phase 2 (NLDAS-2) meteorological forcing data product (Xia et al., 2009). We aggregated the original hourly NLDAS-2 meteorological variables to the every 3 h modeling time step.
2.2.4 Validation data
Daily streamflow data at eight USGS streamflow sites in the study domain (USGS, 2018) were used to evaluate the streamflow time series from the dual-correction system (Fig. 2 and Table 1). These eight sites were selected for their lack of human regulation and their dense rain gauge coverage (Crow et al., 2017). We separately evaluated the rainfall correction scheme, in which the NLDAS-2 precipitation data were treated as the benchmark. The NLDAS-2 precipitation data were based on daily gauge-based rainfall measurements that were disaggregated into hourly intervals using ground-based weather radar (Xia et al., 2012). The reliance of NLDAS-2 on gauge observations (to obtain daily rainfall accumulations) ensures that it is more reliable (in a relative sense) than the remote-sensing-only Early Run IMERG products used in this study. Consequently, it provides an adequate evaluation benchmark for subsequent attempts to correction IMERG.
2.3 Hydrologic modeling
We used Version 5 of the VIC model (Liang et al., 1994; Hamman et al., 2018). VIC is a large-scale, semi-distributed model that simulates various land surface processes. In this study, the VIC model was implemented in the Arkansas–Red River basin with the same setup as in Mao et al. (2019). Specifically, the model was set up at 1∕8∘ spatial resolution with each grid cell further divided into multiple vegetation tiles via statistical distributions. Each grid cell was simulated by VIC separately using a soil column discretized into three vertical layers (with domain-average thicknesses of 0.10, 0.40, and 0.93 m, respectively). In VIC, runoff can be generated by fast-response surface runoff and by slow-response runoff from the bottom soil layer. All vegetation cover and soil property parameters in the model were taken from Maurer et al. (2002), which were calibrated against streamflow observations at the most downstream outlet of the combined Arkansas and Red River basins. The simulation period was from March 2015 to December 2017 when both the SMAP and GPM products are available. The VIC model was spun up by running the period 1979–2015 twice using NLDAS-2 forcing.
The local runoff simulated by VIC at each grid cell was routed through the stream network using the RVIC, the routing model of VIC (Hamman et al., 2017), which is an adapted version of the routing model developed by Lohmann et al. (1996, 1998).
2.4 The dual-correction system
In this section, we describe our methodological updates to the rainfall correction scheme, followed by a description of the state update scheme. Next, we describe how the two schemes are combined to produce the final ensemble streamflow analysis.
2.4.1 The SMART rainfall correction scheme updates and adaption
The Soil Moisture Analysis Rainfall Tool (SMART) rainfall correction algorithm (Crow et al., 2009, 2011; Chen et al., 2012) is based on sequential assimilation of SM measurements into an Antecedent Precipitation Index (API) model.
where t is a time step index, P is the original IMERG precipitation observation (mm), and γ is a unitless loss coefficient. We implemented an every 3 h version of SMART (instead of the daily version in past studies) to receive the every 3 h IMERG rainfall input and both the ascending (PM) and descending (AM) SMAP retrievals at the correct time of day. We also extended the ensemble Kalman filter (EnKF) version of SMART introduced by Crow et al. (2011) to an ensemble Kalman smoother (EnKS), in which the API state is not only updated at time steps when SMAP is available but also updated during measurement gaps (see Sect. S1 in the Supplement for mathematical details underlying the SMART EnKS approach). We set γ to 0.98 such that the uncorrected API time series approximately captures the dynamics of SMAP retrievals (i.e., with high correlation; see Sect. S3 for a sensitivity analysis on γ). SMAP was rescaled to the API regime through cumulative distribution function (CDF) matching over the 2.5-year simulation period prior to assimilation. CDF matching was performed separately for SMAP AM and PM retrievals to account for their mutual systematic differences.
The SMART algorithm then uses the API increment, δt, to estimate the rainfall correction amount via a simple linear relation. We implemented an ensemble rainfall correction rather than the single deterministic rainfall correction used in past SMART applications.
where the superscript (j) denotes the jth ensemble member (ensemble size M=32), Pcorr,t is the corrected precipitation for time t, Ppert,t is the perturbed IMERG precipitation, and λ is a scaling factor that linearly relates the API increment to rainfall correction, which was set to a domain-constant of 0.1 (–) (see Sect. S4 for discussion on the choice of λ). We applied the rainfall correction only at time steps when the original IMERG rainfall observation was nonzero, taking advantage of the enhanced rain/no rain detection accuracy of IMERG (Gebregiorgis et al., 2018). This tactic mitigates the spurious introduction of low-intensity rainfall events by SMART (see also Sect. 3.1). Finally, following Crow et al. (2009, 2011), negative Pcorr,t values were set to zero, and the final corrected precipitation time series was multiplicatively rescaled to be unbiased over the entire simulation period against the original IMERG estimates (so that the long-term mean of the IMERG rainfall time series was preserved).
In this study, the SMART algorithm was run at each of the 36 km SMAP pixels individually. The original 0.1∘ IMERG product was remapped to the coarser 36 km resolution prior to SMART, and the corrected 36 km rainfall was then downscaled to the VIC 1∕8∘ model resolution. In our implementation of an EnKS-based SMART system, the original IMERG precipitation was multiplicatively perturbed by log-normally distributed noise with the mean and standard deviation equal to one. SMAP measurement error ranges from 0.03 to 0.045 m3 m−3 across the domain, which was estimated from the SMAP ground validation studies (e.g., Colliander et al., 2017; Chan et al., 2017), and its spatial distribution was set to be proportional to the leaf area index (LAI) (denser vegetation cover corresponds to larger SMAP error). The API state was directly perturbed by zero-mean Gaussian noise to represent API model error. The perturbation variance was set to 0.3 mm2 over the entire domain such that the normalized filter innovation has variance of approximately one (which is a necessary condition for the proper parameterization of a Kalman filter; see Mehra, 1971, and Crow and Bolten, 2007). The SMAP measurement error and the state perturbation variance are the two primary variables impacting innovation statistics. Since we had a relatively good estimate of the measurement error, the state perturbation level can be uniquely determined via an analysis of normalized innovation variances (Crow and van den Berg, 2010).
2.4.2 State updating via EnKF
As illustrated in Fig. 1 (the red box on the left), the SMAP SM retrievals were also assimilated into the VIC model to update model states using an EnKF. The EnKF implementation in this study generally follows Mao et al. (2019). Specifically, a 1-D filter was implemented for each 36 km SMAP pixel separately and at each pixel SMAP was assimilated to update the SM states of multiple underlying finer 1∕8∘ VIC grid cells. Resolution differences between the coarser assimilation observations and finer modeling grid were accounted for via the inclusion of a spatial averaging step within the observation operator (Mao et al., 2019). Following Lievens et al. (2015, 2016) and Mao et al. (2019), only the upper two layers of SM states in VIC were updated by the EnKF, although the bottom-layer SM does respond to the update of the upper two layers through drainage (see Sect. S2 for mathematical details of the EnKF implemented here). An ensemble of 32 Monte Carlo model run ensembles was used for the EnKF.
The SMAP retrievals were rescaled (separately for AM and PM retrievals) to match the 2.5-year mean and standard deviation of the VIC-simulated surface-layer SM time series prior to assimilation. The error statistics of IMERG precipitation and unscaled SMAP retrievals were assumed to be the same as those applied in SMART (Sect. 2.4.1). Following Mao et al. (2019), VIC SM states were directly perturbed during the EnKF forecast step by zero-mean, additive Gaussian noise with a standard deviation of 0.5 mm over the entire study domain. This noise represents uncertainty in VIC's ability to propagate states estimates forward in time (note that the bottom-layer SM was perturbed, even though not directly updated by EnKF, to create a realistic ensemble spread for probabilistic estimates of baseflow and, thus, streamflow).
Although VIC modeling errors are likely spatially auto-correlated, we tested whether accounting for spatial correlation improved filter performance. Since it did not significantly improve the results, we did not account for spatial correlation in our EnKF implementation. This finding is consistent with Gruber et al. (2015) who described the limited benefit of 2-D filtering, versus a 1-D baseline, when assimilating distributed SM retrievals into a land surface model. We will further discuss this point in Sect. 4.
2.4.3 Combining the state update and the rainfall correction schemes
The ensemble of updated model states and the corrected rainfall forcing were combined to produce final streamflow estimates (black box in the bottom of Fig. 1). We first randomly paired ensemble members of corrected rainfall and updated VIC states and selected 32 such pairs to balance competing considerations of computational cost and statistical stability. For each pair, the VIC model was rerun with the updated states inserted sequentially over time and forced by the corrected rainfall. Other meteorological forcings were kept unchanged. The runoff output from VIC for each pair was then routed to the gauge locations, resulting in an ensemble of basin-outlet streamflow time series. To further separate the relative contribution of the state update and the rainfall correction schemes to overall streamflow improvement, two additional streamflow simulations were performed. The first was the “state-updated streamflow” case, where VIC was rerun with the updated states and forced by the original IMERG precipitation. The resulting streamflow reflects only the impact of state updating on streamflow simulations. The second was the “rainfall-corrected streamflow” case, where VIC was forced by the SMART-corrected rainfall ensemble but without inserting the updated states. The resulting streamflow reflects only the effect of SMART rainfall correction.
The EnKF state update and SMART rainfall correction schemes were executed independently to minimize the risk of cross-correlated error (Crow et al., 2009). In particular, note that VIC state estimates created using SMART forcing – see the black “Hydrologic prediction” box in Fig. 1 – were not fed back into the EnKF state update analysis. Nevertheless, cross-correlated error in (EnKF) state and (SMART) rainfall estimates potentially may still be present since the two schemes are informed by the same SM measurement time series. Such cross-correlated error could, in turn, degrade the quality of probabilistic streamflow estimates. In fact, due to this concern, Massari et al. (2018) intentionally avoided combining the state and rainfall correction schemes. To further investigate this risk, we performed a set of synthetic experiments where we compared probabilistic streamflow estimates obtained via the following two scenarios: (1) a single set of synthetically generated SM measurements assimilated into the state and rainfall correction schemes, mimicking the original dual-correction system and (2) two separate sets of SM measurements with mutually independent errors assimilated separately into the two schemes, thereby explicitly avoiding error cross-correlation in the system. Results show that the two scenarios achieve very similar streamflow correction performance and, therefore, minimal risk of degraded streamflow estimates (see Sect. S5).
2.5 Evaluation strategies and metrics
We evaluated the rainfall correction results in addition to the dual-corrected streamflow results in terms of both deterministic and probabilistic metrics.
The 1∕8∘ gauge-informed NLDAS-2 precipitation data were remapped to the 36 km SMART resolution grid as the benchmark for evaluating rainfall. Deterministically, the ensemble-mean SMART-corrected rainfall was compared to the original IMERG precipitation (remapped to 36 km), and its improvement was evaluated in terms of (1) the time series correlation coefficient (r), (2) the percent error reduction (PER) in terms of the root-mean-squared error (RMSE), and (3) additional categorical skill metrics, including the false alarm ratio (FAR), probability of detection (POD), and threat score (TS) (Wilks, 2011; Crow et al., 2011; Chen et al., 2012; Brocca et al., 2016). Probabilistically, the normalized ensemble skill (NENSK) was calculated, which measures the ensemble-mean error normalized by ensemble spread.
where the ensemble skill (ENSK) is the temporal mean of ensemble-mean squared error, and the ensemble spread (ENSP) is the temporal mean of ensemble variance (De Lannoy et al., 2006; Brocca et al., 2012; Alvarez-Garreton et al., 2014; Mao et al., 2019). If an ensemble of time series correctly represents the uncertainty of an analysis, NENSK will equal one (Talagrand et al., 1997; Wilks, 2011). NENSK > 1 indicates an underdispersed ensemble, while NENSK < 1 indicates an overdispersed ensemble. For all metrics, precipitation datasets were aggregated to multiple temporal accumulation periods (the native every 3 h period without aggregation and every 1 and 3 d) for evaluation at different timescales.
The dual-corrected streamflow was evaluated at the outlet of the eight USGS sub-basins shown in Fig. 2. Deterministically, the ensemble-median-corrected streamflow was compared to the baseline streamflow, or the so-called “open-loop” streamflow, which is simply the single VIC simulation forced by IMERG precipitation without any correction, in terms of (1) PER and (2) the Kling–Gupta efficiency (KGE) (Gupta et al., 2009). The latter combines the performance of correlation, variance, and bias. The ensemble-median and not the ensemble-mean streamflow was used for more stable evaluation results in the case of a skewed streamflow ensemble caused by model nonlinearity. In addition to ensemble-median evaluations, NENSK was calculated for the entire streamflow ensembles.
3.1 SMART rainfall correction
3.1.1 The impact of SMART methodological choices
Figure 3 shows the rainfall improvement in terms of correlation coefficient r based on both an EnKS- (the left column) and EnKF-based (the right column) implementation of SMART. For EnKF results, both δ and P in Eq. (2) were aggregated to windows prior to correction every 3 d to ensure SM data availability in every correction window (and the every 3 d correction was subsequently downscaled to every 3 h time steps uniformly). Overall, the EnKF implementation results in less r improvement than the EnKS implementation, which confirms the benefit of applying SMART using a smoothing approach.
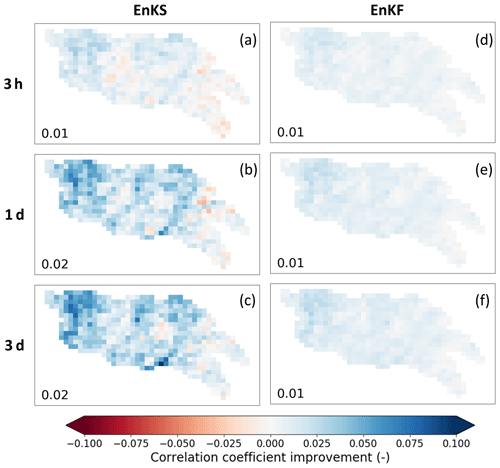
Figure 3Maps of correlation coefficient improvement after SMART rainfall correction (i.e., improvement of correlation with respect to NLDAS-2 benchmark rainfall realized upon implementation of SMART). Shown in (a–c) are the SMART EnKS experiments, and shown in (d–f) are the EnKF experiments. Each row shows results based on different temporal accumulation periods (i.e., every 3 h and every 1 and 3 d aggregation, respectively). The number on the lower left corner of each subplot shows the domain-median correlation improvement.
The impact of our (previous choice) to update rainfall only at nonzero IMERG time steps is examined via domain-median categorical metrics (Fig. 4). When we correct rainfall every time step (Fig. 4, Column 1), FAR is largely degraded (by 0.1–0.4) at low rainfall event thresholds especially with shorter accumulation periods (every 3 h and every 1 d; see Fig. 4a). This is likely due to SMART misinterpreting SM retrieval noise as small rainfall events (Chen et al., 2014). POD is improved at these low thresholds (Fig. 4b), but it is not enough to compensate for the large FAR degradation. Therefore, TS, which accounts for both false alarms and missed events, is also degraded at low thresholds (by as large as 0.2 at every 3 h). In contrast, when we only correct rainfall at nonzero IMERG time steps (Fig. 4, Column 2), the FAR degradation is much less (note the different y axes in the two columns in Fig. 4). While this approach does sacrifice POD at low thresholds (Fig. 4e), the overall TS for every 1 and 3 d aggregation is improved for most event thresholds, especially the higher ones. As mentioned in Sect. 2.4.1, one possible reason for the success of this SMART choice is the improved rain/no rain detection quality of the baseline IMERG precipitation product, which was found to have an improved miss-rain, false-rain, and hit rate relative to older TMPA-RT (Real-Time TRMM Multi-Satellite Precipitation Analysis) products over the contiguous US (CONUS; Gebregiorgis et al., 2018). It is thus beneficial to retain the IMERG rain/no rain detection skill and not subject it to SMART-based correction.

Figure 4Change in categorical metrics (FAR, POD, and TS) before and after SMART correction for every 3 h and every 1 and 3 d accumulation periods. Metrics at different rainfall thresholds are shown on the x axis (e.g., the 80th percentile means that an event is defined as exceeding the 80th percentile of nonzero rainfall accumulation over the listed time accumulation period). Shown in (a–c) are the SMART rainfall-corrected data at all time steps; shown in (d–f) are the SMART rainfall-corrected data only at nonzero time steps. Note that the y-axis range is different for the two columns.
With regards to binary rain/no-rain determination, one strategy for mitigating FAR problems is to arbitrarily set a (greater-than-zero) minimum accumulation threshold that must be exceeded for an event to be registered. To this end we carried out a sensitivity analysis to examine the impact of using a nonzero rain/no rain threshold versus our baseline assumption of a zero threshold. However, this analysis was unable to isolate an optimized threshold value for distinguishing rain/no rain cases. Instead, a continuous trade-off exists between POD and FAR at different rainfall thresholds. However, a zero rain/no rain threshold does appear slightly beneficial for PER and the correlation coefficient improvement (see Sect. S6).
3.1.2 Rainfall correction evaluation
After rainfall correction at every 1 and 3 d accumulation periods, PER exhibits a domain-median error reduction of ∼8 % (Fig. 5, Column 1). The PER improvement is consistent with the improvement of the categorical metrics at high-event thresholds (Fig. 4, Column 2), since PER is more sensitive to high rainfall values. PER every 3 h shows little improvement (Fig. 5a), suggesting that the deterministic correction is more effective at an accumulation period that more closely matches the SMAP retrieval interval. The same finding can also be drawn from the correlation and categorical results (Fig. 3, Column 2 and Fig. 4, Column 2). Overall, the correlation coefficient improves more in the western part of the domain, which is likely attributable to the better quality of SMAP retrievals in the lightly vegetated western portion of the basin. However, RMSE is reduced more in the eastern part of the domain, which is likely due to the increased frequency of large rainfall events in this region and SMART's tendency to be more effective for the correction of moderate-to-large precipitation events. Note that SMART rainfall correction cannot be evaluated in terms of overall bias, since – like all SM data assimilation systems – the SMART algorithm rescales the corrected time series back to the uncorrected mean prior to its evaluation.
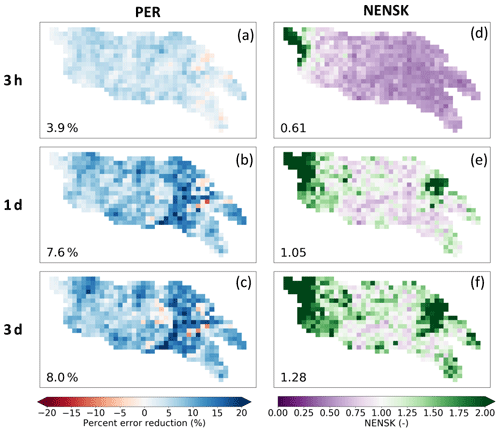
Figure 5Maps of SMART rainfall correction results (with λ=0.1, EnKS, and rainfall corrected only during time steps with nonzero rainfall). Each column shows the following metrics, respectively: percent RMSE reduction (PER) (a–c) and ensemble NENSK (d–f). Each row shows results based on different temporal accumulation period: every 3 h and every 1 and 3 d, respectively. The number in the lower left corner of each subplot shows the domain-median statistic.
The probabilistic metric NENSK (Fig. 5, Column 2) is less than one for most of the domain at an every 3 h time step, indicating an overdispersed ensemble on average. However, when evaluating at every 1 and 3 d accumulation periods, NENSK is closer to one, indicating a better representation of the uncertainty of the rainfall estimates. As we aggregate over longer accumulation windows (e.g., every 3 d), NENSK becomes slightly greater than one (i.e., underdispersed ensemble), since the SMART algorithm assumes only a random rainfall error but no systematic bias. As a result, it slightly underestimates the uncertainty range over longer-term periods. Ensemble rainfall tends to be underdispersed on the west edge of the domain with low rainfall, indicating that we are underestimating rainfall uncertainty in this region.
In summary, SMART successfully uses SMAP SM retrievals to correct IMERG rainfall during relatively larger events, with slight-to-moderate deterministic improvement. However, SMART correction is less successful for small rainfall events and can even lead to slight degradation. The correction is more effective, and the ensemble representation is better, when rainfall estimates are temporally aggregated to periods consistent with SMAP retrieval intervals (i.e., every 1 to 3 d accumulation periods).
3.2 Streamflow from the dual-correction system
3.2.1 Evaluation of streamflow improvement
The final daily streamflow performance from the dual-correction system is listed in Table 2 (the “dual” columns) for each sub-basin. Overall, streamflow estimates are improved but with large variability across sub-basins. Specifically, PER ranges from approximately 6 % to 34 %, and KGE improvement ranges from slightly negative to +0.95 across all sub-basins. For sub-basins with better baseline streamflow performance (as measured by KGE, i.e., the Ninnescah, Walnut, and Chikaskia sub-basins), the relative improvement after the dual correction is generally smaller.
Table 2Daily streamflow results from the dual-correction system for the eight USGS sub-basins shown in Fig. 1. In addition to the deterministic KGE improvement, PER, and probabilistic NENSK results from the dual system (“dual” columns), the table also lists the open-loop streamflow KGE (“open-loop KGE” column), KGE improvement, and PER as a result of state update or rainfall correction scheme alone (“state update only” and “rainfall correction only” columns, respectively), and KGE improvement and PER when forced by the NLDAS-2 benchmark precipitation without state update (“NLDAS-2 forced” column).
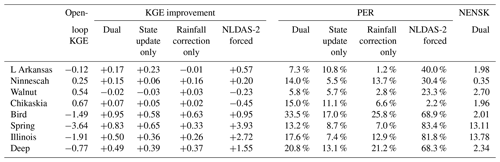
Table 2 also summarizes the streamflow improvement from each of the correction schemes alone (i.e., the “state update only” and “rainfall correction only” columns). For sub-basins with relatively better open-loop model performance, the contribution of state updating generally surpasses that of rainfall correction. Conversely, at sub-basins with relatively poorer open-loop model performance (i.e., the Bird, Spring, Illinois, and Deep sub-basins), streamflow improvement is primarily attributable to the SMART rainfall correction.
3.2.2 Impact of rainfall forcing error
To further understand the relationship between open-loop simulation performance, rainfall forcing error, and correction performance, we forced the VIC model by the NLDAS-2 benchmark rainfall (without state update). The subsequent streamflow improvement level is assumed to approximate the maximum improvement achievable via rainfall correction alone (Table 2 “NLDAS-2 forced” columns). While almost all sub-basins show streamflow improvement simply by switching to NLDAS-2 rainfall forcing, the improvement is especially large for sub-basins with poorer open-loop streamflow estimates. In these basins, PER is over 65 %, and the negative KGE for the open loop case improves to near zero or positive values for the NLDAS-forced case. This suggests that, despite advances in the quality of remotely sensed rainfall data products, poor open-loop streamflow simulations at these sub-basins are still largely attributable to poor-quality IMERG rainfall forcing error. In these basins, the SM-based rainfall correction scheme can potentially play an important role in improving VIC streamflow estimates. Unfortunately, this potential is not always realized. Note how the SMART-based rainfall-correction-only case generally fails to match the NLDAS-forced case in the Spring, Illinois, and Deep sub-basins (Table 2). This is likely because these basins are located in relatively high-biomass areas where SMAP retrievals (and thus SMART corrections) are less accurate.
In contrast, the sub-basins with better open-loop streamflow results (i.e., the Ninnescah, Walnut, and Chikaskia sub-basins) demonstrate less streamflow improvement when switching to the NLDAS-2 rainfall forcing. The sub-basin with the best (IMERG-forced) open-loop streamflow results, Chikaskia, even experiences a small degradation when forced by the NLDAS-2 rainfall (Table 2). This suggests that the NLDAS-2 benchmark rainfall at this sub-basin is not obviously superior to the IMERG baseline. Nevertheless, SMART is still able to extract information from SMAP and slightly correct IMERG rainfall and subsequent streamflow estimates.
3.2.3 Impact of model parameterization
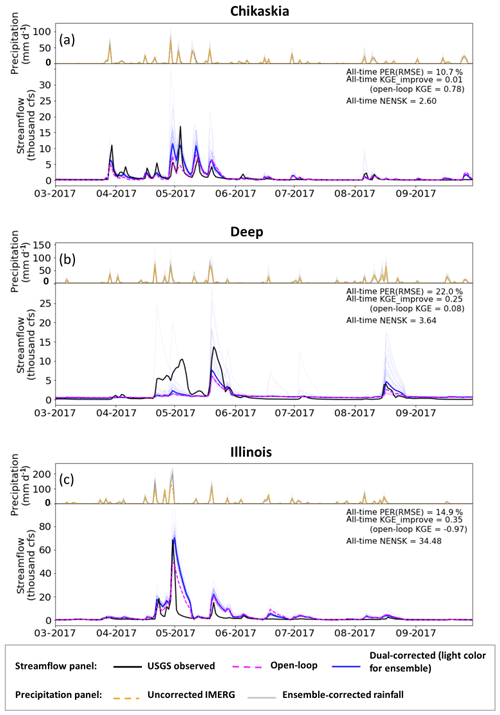
The dual-correction scheme presented in this study is designed to correct only the random error present in a hydrologic simulation system. It does not correct systematic error or overall bias. Figure 6 shows example time series of the open-loop, USGS-observed and dual-corrected streamflow at three sub-basins (the Chikaskia, Deep, and Illinois) with various levels of open-loop performance. Although the dual system often nudges the simulated streamflow in the correct direction (especially during high-flow periods) and results in overall improved evaluation statistics, systematic error (in the model process representation as well as rainfall forcing) clearly exists. This systematic error, although difficult to quantify, cannot be corrected by the data assimilation approach discussed here. The NENSK statistic partly reflects such systematic error. NENSK is significantly above one at most sub-basins, indicating an underdispersed ensemble on average. In other words, at most sub-basins the ensemble spread created by the dual system only represents the random uncertainty around the open-loop streamflow and neglects systematic error that accounts for a significant fraction of total streamflow error.
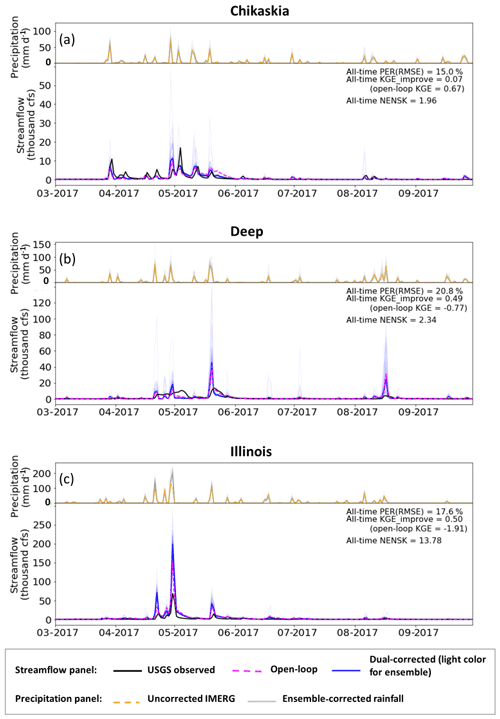
Figure 6Example time series of streamflow results from the dual-correction system. In the upper part of each panel, orange line: uncorrected IMERG rainfall aggregated to the sub-basin-average; light-grey lines: ensemble-corrected rainfall. Only part of the simulation period is shown for clear display; however, statistics shown on each panel are based on the entire simulation period (approximately 2.5 years). In the lower part of each panel, black line: USGS observed streamflow; magenta line: baseline VIC simulation; light-blue lines: ensemble-updated streamflow results; solid blue line: ensemble-mean-updated streamflow; cfs: cubic feet per second (0.0283 m3 s−1).
The level of systematic error is tied closely to the quality of the hydrologic model parameters often estimated through calibration. The VIC parameters used in this study were taken from Maurer et al. (2002) and derived based on streamflow at the outlets of large basins. To further examine the effect of systematic error on data assimilation, we calibrated the model parameters for the eight sub-basins separately using streamflow acquired from the USGS (Table 1). Specifically, VIC parameters that control infiltration, soil conductivity, and baseflow generation as well as the recession rate of the grid-cell-scale unit hydrograph in RVIC were calibrated using the multi-objective autocalibration method (MOCOM; Yapo et al., 1998). Basin-constant parameters were calibrated toward USGS streamflow time series during 2015 to 2017 (forced by the baseline IMERG precipitation) to optimize daily KGE and monthly bias. Only a subset of the eight sub-basins achieved better-than-open-loop streamflow results via this traditional calibration method, due mainly to the relatively large IMERG forcing error present in some sub-basins that prevents the calibration scheme from finding an improved parameterization. Figure 7 shows three example sub-basins (i.e., Chikaskia, Deep, and Illinois) with relatively good calibration outcomes. Comparing Fig. 7 to Fig. 6, we observe that the streamflow improvement achieved by parameter calibration (i.e., systematic error reduction) alone is as important as, or more important than, that achieved by data assimilation (via random-error reduction) in all three sub-basins. In both cases (i.e., the default and calibrated VIC parameters), NENSK is significantly above one, indicating that we underestimate the streamflow simulation uncertainty when only random errors are considered.
4.1 SMART rainfall correction
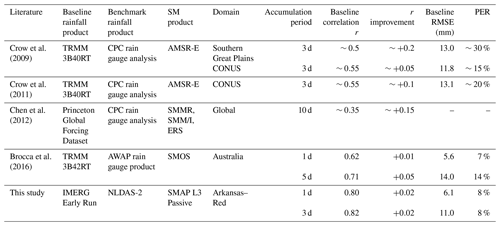
Overall, SMART improves the IMERG rainfall product (see Figs. 3 to 5); however, the magnitude of improvement is somewhat smaller than that found in previous studies, especially in terms of correlation r (domain-median improvement of 0.01 to 0.02). Table 3 summarizes results from past studies that applied remotely sensed SM to correct rainfall time series. Over the past decade, the quality of the baseline satellite-derived rainfall product has improved considerably, from the TRMM 3B40-RT product used by Crow et al. (2009, 2011) with to the TRMM 3B42-RT product used by Brocca et al. (2016) with –0.7 to the IMERG product used in our study with r over 0.8. This tendency is confirmed by Gebregiorgis et al. (2018) who demonstrated the improved accuracy of IMERG relative to TRMM over the contiguous US in terms of correlation, RMSE, bias, and categorical metrics. This improvement is relevant here because the marginal value of data assimilation tends to decrease as the skill of the background land surface model increases (Reichle et al., 2008; Qing et al., 2011; Bolten and Crow, 2012; Dong et al., 2019). Since SMART is fundamentally a data assimilation approach, the added value of its SM-based correction tends to decrease as the accuracy of the baseline product (it is correcting) increases. This tendency, previously noted in Crow and Ryu (2009) and Crow et al. (2011), is clearly illustrated in Table 3. Therefore, large improvement over time in the quality of satellite-based rainfall products appears to have partially undercut the value of SM-based rainfall correction. It should be noted that the SM/rainfall correction algorithms applied in Table 3 differ slightly. However, Brocca et al. (2016) found comparable performance even when intercomparing very different rainfall correction approaches, suggesting that the various studies listed in Table 3 are relatively intercomparable.
Table 3Review of SMART rainfall correction results in literature along with the results in this study. CPC: Climate Prediction Center; AMSR-E: Advanced Microwave Scanning Radiometer for the Earth Observing System; SMMR: Scanning Multichannel Microwave Radiometer; SSM/I: Special Sensor Microwave Imager; ERS: European Remote Sensing satellites; AWAP: Australian Water Availability Project.
4.2 Dual correction for streamflow
Although we applied the dual-correction system to the entire Arkansas–Red River basin, we selected only eight smaller sub-basins for our streamflow evaluation due to the limited availability of unregulated streamflow observations at basin outlets. While the dual-correction approach generally improved VIC streamflow estimates, especially during relatively high-flow events in areas with poor IMERG data, the magnitude of this correction was relatively modest. Results in Sect. 3 indicated three general reasons for this. First, the latest generation of satellite rainfall products (e.g., IMERG) has significantly improved precision compared to its predecessors. The already high-quality rainfall estimates are more difficult for SM retrievals to contribute substantial rainfall correction skill (see discussion in Sect. 4.1 above). Second, the dual-correction approach is designed to correct only the zero-mean random-error component in the total streamflow error but not systematic error or bias. However, systematic error sources, typically associated with inaccurate model structure and/or parameterization and large rainfall bias, can account for a significant fraction of overall streamflow error (Sect. 3.2.3). The existence of systematic error is particularly problematic from a probabilistic perspective, since the ensemble streamflow produced by the dual system only represents random error, and it therefore largely underestimates simulation uncertainty. Finally, in certain sub-basins (i.e., the Bird, Spring, Illinois, and Deep sub-basins) where VIC streamflow is substantially degraded by random error in IMERG data products, SMART-based dual correction often underperformed due to the reduced accuracy of SMAP-based rainfall correction in eastern areas of the domain with relatively dense biomass (see Fig. 3).
In addition to these factors, additional research is needed to fully investigate the impact of several simplifications applied in the dual-correction data assimilation system. For example, the impact of error spatial correlation on downstream streamflow performance should be fully examined before extending our findings to large-scale river systems. Specifically, while a 1-D filter with spatially uncorrelated model representation error may be appropriate for small-basin correction, ignoring the spatial correlation structure of errors could potentially have a more profound impact on the correction performance at large river outlets where streamflow originates from runoff from a large number of grid cells. Multiple studies have investigated the effects of spatial error patterns in hydrologic data assimilation. For example, Reichle and Koster (2003) investigated the impact of spatial error correlation in the model SM states on its assimilation performance; Gruber et al. (2015) examined the impact of a 2-D filter with spatially autocorrelated error versus a 1-D filter on SM updating quality; Pan et al. (2009) and Pan and Wood (2009, 2010) evaluated the surface SM assimilation performance with VIC by comparing a 1-D filter, a 2-D filter, and a multiscale autoregressive filtering approach and considered the spatial and temporal structure of precipitation error. However, all these studies focused exclusively on the performance of SM simulations. Direct assessment of the impact of spatial error patterns on the routed streamflow results is needed, especially from a probabilistic perspective since the ignorance of spatial error patterns (and therefore their potential to mutually cancel as runoff is routed through a river network) will lead to an incorrect ensemble representation of streamflow uncertainty.
Another factor that may have limited the dual-correction performance, particularly the state updating scheme, is the rescaling of the SMAP retrievals to the VIC top-layer SM regime. Matching a satellite-observed SM product with that represented in a land surface model (LSM) is a necessary pre-processing step in a data assimilation system; however, it has the well-known limitation of neglecting potential bias-correction information contained in the satellite-observed product. While this problem is well-discussed in the literature (see, e.g., Yilmaz and Crow, 2013; Kumar et al., 2015; Nearing et al., 2018), no robust solutions currently exist. Ideally, the physical source of remote sensing and modeling biases could be isolated and addressed. However, this is very difficult to do in practice. For instance, although SMAP is typically described as measuring the top ∼5 cm of SM, the actual vertical support depth is unclear and varies nonlinearly as a function of SM and vegetation water content. In addition, the relationship between the top-layer depth and its SM dynamics in an LSM is complex and driven by multiple poorly known model parameters (although, Shellito et al., 2018, found that changing the top-layer depth from 10 to 5 cm in the Noah LSM did not significantly affect surface SM dynamics). Therefore, like other existing SM data assimilation applications, we are forced to resort to an ad hoc solution where satellite-based observations are rescaled to match the climatological characteristics of equivalent model products.
In this paper, we applied a dual state/rainfall correction data assimilation system in the Arkansas–Red River basin. Built upon the dual system developed in past studies, we have made several methodological advances. First, we implemented the dual-correction system with a more complex, semi-distributed land surface model (VIC) and applied it in a regional-scale basin. Second, the latest satellite products, the SMAP SM product and the IMERG rainfall product, were incorporated into the system. Third, the existing dual-correction algorithm was extended to maximize the use of information contained in the more accurate, and temporally more frequent, satellite data products. Fourth, the SMART approach has been modified to produce an ensemble streamflow product to generate probabilistic estimates. Fifth, we confirmed via a formal synthetic experiment that error cross-correlation that potentially exists in the dual-correction system does not cause noticeable degradation of streamflow improvement, and the dual-correction scheme applied here is optimal.
Our results show that, overall, the SMART algorithm is able to correct IMERG rainfall slightly to moderately, and the correction is more effective during larger rainfall events and at daily-to-multi-daily timescales. The ensemble produced by the correction scheme represents the rainfall uncertainty relatively well. However, the rainfall correction we achieved is generally smaller than that found by previous studies, mainly due to the improved quality of the baseline satellite rainfall product over time. In addition, although SMAP arguably also has a higher quality than older remotely sensed SM products, its quality remains relatively low in dense-biomass regions, resulting in reduced rainfall correction via SMART.
Combined with analogous improvement in pre-storm SM states, the relatively small rainfall correction is propagated into VIC and generally results in improved streamflow estimates. However, the improvements found are relatively small and vary greatly between sub-basins. Due to its deleterious impact on SMAP retrieval uncertainty, small improvement is found in sub-basins containing dense biomass. Furthermore, the dual-data-assimilation system is only designed to correct zero-mean random errors and not systematic errors or bias. However, systematic errors can account for a substantial fraction of the total streamflow error. This results in relatively modest streamflow correction via the Kalman-filter-based correction system and the significant underestimation of uncertainty in VIC streamflow estimates.
Given the above findings, we provide the following recommendations for future research:
-
Higher-quality SM retrievals are necessary to push the current limit of rainfall correction (and, consequently, streamflow correction), especially in areas of dense vegetation.
-
However, even with better SM data quality, data assimilation techniques aimed solely at random-error sources are unlikely to substantially reduce streamflow errors in many sub-basins, since random errors often account for only a relatively small portion of the total error. Instead, approaches that reduce systematic errors in streamflow simulation are needed. To date, this is still a challenging task in large-scale hydrologic modeling, since robust calibration is difficult to achieve with limited streamflow data and many distributed parameters. With the availability of the near-global and distributed satellite products such as SMAP and IMERG, more creative methods are needed to extract useful information from the large volume of remote sensing observations. For example, the characteristics of SM dynamics and its response to rainfall can be directly extracted from the datasets themselves, which can potentially inform hydrologic model representation. These new areas of research have the potential to improve hydrologic modeling beyond the correction of random errors.
The VIC model used in the study can be found at Hamman et al. (2017), with a modification to the calculation of drainage between soil layers (https://github.com/UW-Hydro/VIC/releases/tag/Mao_etal_stateDA_May2018). The data assimilation code used in this study is available at Mao (2019).
The supplement related to this article is available online at: https://doi.org/10.5194/hess-24-615-2020-supplement.
All co-authors designed the experiments. YM developed the system code and carried out the experiments. WTC and BN supervised the study. YM prepared the paper with contributions from all co-authors.
The authors declare that they have no conflict of interest.
We would like to thank Andrew Wood from NCAR for collaborating.
This research has been supported by the NASA Terrestrial Hydrology Program (grant nos. NNX16AC50G and 13-THP13-0022) and the Pathfinder Fellowship by CUAHSI with support from the National Science Foundation (NSF) (grant no. EAR-1338606).
This paper was edited by Niko Wanders and reviewed by Christian Massari and one anonymous referee.
Alvarez-Garreton, C., Ryu, D., Western, A. W., Crow, W. T., and Robertson, D. E.: The impacts of assimilating satellite soil moisture into a rainfall-runoff model in a semi-arid catchment, J. Hydrol., 519, 2763–2774, https://doi.org/10.1016/j.jhydrol.2014.07.041, 2014.
Alvarez-Garreton, C., Ryu, D., Western, A. W., Crow, W. T., Su, C.-H., and Robertson, D. R.: Dual assimilation of satellite soil moisture to improve streamflow prediction in data-scarce catchments, Water Resour. Res., 52, 5357–5375, https://doi.org/10.1002/2015WR018429, 2016.
Aubert, D., Loumagne, C., and Oudin, L.: Sequential assimilation of soil moisture and streamflow data in a conceptual rainfall-runoff model, J. Hydrol., 280, 145–161, https://doi.org/10.1016/S0022-1694(03)00229-4, 2003.
Bolten, J. D. and Crow, W. T.: Improved prediction of quasi-global vegetation conditions using remotely-sensed surface soil moisture, Geophys. Res. Lett., 39, L19406, https://doi.org/10.1029/2012GL053470, 2012.
Brocca, L., Melone, F., Moramarco, T., Wagner, W., Naeimi, V., Bartalis, Z., and Hasenauer, S.: Improving runoff prediction through the assimilation of the ASCAT soil moisture product, Hydrol. Earth Syst. Sci., 14, 1881–1893, https://doi.org/10.5194/hess-14-1881-2010, 2010.
Brocca, L., Moramarco, T., Melone, F., Wagner, W., Hasenauer, S., and Hahn, S.: Assimilation of surface-and root-zone ASCAT soil moisture products into rainfall–runoff modeling, IEEE T. Geosci. Remote, 50, 2542–2555, https://doi.org/10.1109/TGRS.2011.2177468, 2012.
Brocca, L., Moramarco, T., Melone, F., and Wagner, W.: A new method for rainfall estimation through soil moisture observations, Geophys. Res. Lett., 40, 853–858, https://doi.org/10.1002/grl.50173, 2013.
Brocca, L., Ciabatta, L., Massari, C., Moramarco, T., Hahn, S., Hasenauer, S., Kidd, R., Dorigo, W., Wagner, W., and Levizzani, V.: Soil as a natural rain gauge: Estimating global rainfall from satellite soil moisture data, J. Geophys. Res.-Atmos., 119, 5128–5141, https://doi.org/10.1002/2014JD021489, 2014.
Brocca, L., Pellarin, T., Crow, W. T., Ciabatta, L., Massari, C., Ryu, D., Su, C.-H., Rüdiger, C., and Kerr, Y.: Rainfall estimation by inverting SMOS soil moisture estimates: A comparison of different methods over Australia, J. Geophys. Res.-Atmos., 121, 12062–12079, https://doi.org/10.1002/2016JD025382, 2016.
Chan, S., Bindlish, R., O’Neill, P., Jackson, T., Chaubell, J., Piepmeier, J., Dunbar, S., Colliander, A., Chen, F., Entekhabi, D., Yueh, S., Cosh, M., Caldwell, T., Walker, J., Wu, X., Berg, A., Rowlandson, T., Pacheco, A., McNairn, H., Thibeault, M., Martínez-Fernández, J., González-Zamora, Á., Lopez-Baeza, E., Uldall, F., Seyfried, M., Bosch, D., Starks, P., Holifield C., Prueger, J., Su, Z., van der Velde, R., Asanuma, J., Palecki, M., Small, E., Zreda, M., Calvet, J.-C., Crow, W., and Kerr, Y.: Development and validation of the SMAP enhanced passive soil moisture product, in: 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), July 2017 Fort Worth, TX, United States, https://doi.org/10.1109/IGARSS.2017.8127512, 2017.
Chen, F., Crow, W. T., and Holmes, T. R. H.: Improving long-term, retrospective precipitation datasets using satellite-based surface soil moisture retrievals and the Soil Moisture Analysis Rainfall Tool, J. Appl. Remote Sens., 6, 063604, https://doi.org/10.1117/1.JRS.6.063604, 2012.
Chen, F., Crow, W. T., and Ryu, D.: Dual forcing and state correction via soil moisture assimilation for improved rainfall–runoff modeling, J. Hydrometeorol., 15, 1832–1848, https://doi.org/10.1175/JHM-D-14-0002.1, 2014.
Colliander, A., Jackson, T. J., Bindlish, R., Chan, S., Das, N., Kim, S. B., Cosh, M. H., Dunbar, R. S., Dang, L., Pashaian, L., Asanuma, J., Aida, K., Berg, A., Rowlandson, T., Bosch, D., Caldwell, T., Caylor, K., Goodrich, D., al Jassar, H., Lopez-Baeza, E., Martínez-Fernández, J., González-Zamora, A., Livingston, S., McNairn, H., Pacheco, A., Moghaddam, M., Montzka, C., Niedrist, C., Pellarin, T., Prueger, J., Pulliainen, J., Notarnicola, C., Rautiainen, K., Ramos, J., Seyfried, M., Starks, P., Su, Z., Zeng, Y., van der Velde, R., Thibeault, M., Dorigo, W., Vreugdenhil, M., Walker, J. P., Wu, X., Monerris, A., O'Neill, P. E., Entekhabi, D., Njoku, E. G., and Yueh, S.: Validation of SMAP surface soil moisture products with core validation sites, Remote Sens. Environ., 191, 215–231, https://doi.org/10.1016/j.rse.2017.01.021, 2017.
Crow, W. T. and Bolten, J. D.: Estimating precipitation errors using spaceborne surface soil moisture retrievals, Geophys. Res. Lett., 34, L08403, https://doi.org/10.1029/2007GL029450, 2007.
Crow, W. T. and Ryu, D.: A new data assimilation approach for improving runoff prediction using remotely-sensed soil moisture retrievals, Hydrol. Earth Syst. Sci., 13, 1–16, https://doi.org/10.5194/hess-13-1-2009, 2009.
Crow, W. T. and van den Berg, M. J.: An improved approach for estimating observation and model error parameters for soil moisture data assimilation, Water Resour. Res., 46, W12519, https://doi.org/10.1029/2010WR009402, 2010.
Crow W. T., Huffman, G. J., Bindlish, R., and Jackson, T. J.: Improving satellite-based rainfall accumulation estimates using spaceborne surface soil moisture retrievals, J. Hydrometeorol., 10, 199–212, https://doi.org/10.1175/2008JHM986.1, 2009.
Crow, W. T., van den Berg, M. J., Huffman, G. J., and Pellarin, T.: Correcting rainfall using satellite-based surface soil moisture retrievals: The Soil Moisture Analysis Rainfall Tool (SMART), Water Resour. Res., 47, W08521, https://doi.org/10.1029/2011WR010576, 2011.
Crow, W. T., Chen, F., Reichle, R. H., and Liu, Q.: L band microwave remote sensing and land data assimilation improve the representation of prestorm soil moisture conditions for hydrologic forecasting, Geophys. Res. Lett., 44, 5495–5503, https://doi.org/10.1002/2017GL073642, 2017.
De Lannoy, G. J. M., Houser, P. R., Pauwels, V. R. N., and Verhoest, N. E. C.: Assessment of model uncertainty for soil moisture through ensemble verification, J. Geophys. Res., 111, D10101, https://doi.org/10.1029/2005JD006367, 2006.
Dong, J., Crow, W. T., Reichle, R., Liu, Q., Lei, F., and Cosh, M.: A global assessment of added value in the SMAP Level 4 soil moisture product relative to its baseline land surface model, Geophys. Res. Lett., 46, 6604–6613, https://doi.org/10.1029/2019GL083398, 2019.
Entekhabi, D., Njoku, E. G., O’Neill, P. E., Kellogg, K. H., Crow, W. T., Edelstein, W. N., Entin, J. K., Goodman, S. D., Jackson, T. J., Johnson, J., Kimball, J., Piepmeier, J. R., Koster, R. D., Martin, N., McDonald, K. C., Moghaddam, M., Moran, S., Reichle, R., Shi, J. C., Spencer, M. W., Thurman, S. W., Tsang, L., and Van Zyl, J.: The Soil Moisture Active and Passive (SMAP) Mission, Proc. IEEE, 98, 704–716, https://doi.org/10.1109/JPROC.2010.2043918, 2010.
Francois, C., Quesney, A., and Ottle, C.: Sequential assimilation of ERS-1 SAR data into a coupled land surface-hydrological model using an extended Kalman filter, J. Hydrometeorol., 4, 473–487, https://doi.org/10.1175/1525-7541(2003)4<473:SAOESD>2.0.CO;2, 2003.
Freeze, R. A. and Harlan, R. L.: Blueprint for a physically-based, digitally-simulated hydrologic response model, J. Hydrol., 9, 237–258, https://doi.org/10.1016/0022-1694(69)90020-1, 1969.
Gebregiorgis, A. S., Kirstetter, P.-E., Hong, Y. E., Gourley, J. J., Huffman, G. J. Petersen, W. A., Xue, X., and Schwaller, M. R.: To what extent is the day 1 GPM IMERG satellite precipitation estimate improved as compared to TRMM TMPA-RT?, J. Geophys. Res.-Atmos., 123, 1694–1707, https://doi.org/10.1002/2017JD027606, 2018.
Gruber, A., Crow, W. T., Dorigo, W., and Wagner, W.: The potential of 2D Kalman filtering for soil moisture data assimilation, Remote Sens. Environ., 171, 137–148, https://doi.org/10.1016/j.rse.2015.10.019, 2015.
Gupta, H. V., Kling, H., Yilmaz, K. K., and Martinez, G. F.: Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling, J. Hydrol., 377, 80–91, https://doi.org/10.1016/j.jhydrol.2009.08.003, 2009.
Hamman, J. J., Nijssen, B., Bohn, T., Franssen, W., Gergel, D., Mao, Y., Flores-Cervantes, J. H., Helgason, H., Peng, B., Craig, T., and The Gitter Badger: VIC 5.0.1, https://doi.org/10.5281/zenodo.267178, 2017.
Hamman, J. J., Nijssen, B., Roberts, A., Craig, A., Maslowski, W., and Osinski, R.: The coastal streamflow flux in the Regional Arctic System Model, J. Geophys. Res., 122, 1683–1701, https://doi.org/10.1002/2016JC012323, 2017.
Hamman, J. J., Nijssen, B., Bohn, T. J., Gergel, D. R., and Mao, Y.: The Variable Infiltration Capacity Model, Version 5 (VIC-5): Infrastructure improvements for new applications and reproducibility, Geosci. Model Dev., 11, 3481–3496, https://doi.org/10.5194/gmd-11-3481-2018, 2018.
Hou, A. Y., Kakar, R. K., Neeck, S., Azarbarzin, A. A., Kummerow, C. D., Kojima, M., Oki, R., Nakamura, K., and Iguchi, T.: The Global Precipitation Measurement mission, B. Am. Meteorol. Soc., 95, 701–722, https://doi.org/10.1175/BAMS-D-13-00164.1, 2014.
Huffman, G. J., Bolvin, D. T., and Nelkin, E. J.: Integrated Multi-Satellite Retrievals for GPM (IMERG) Technical Documentation, Tech. Doc., NASA GSFC, available at: https://docserver.gesdisc.eosdis.nasa.gov/public/project/GPM/IMERG_doc.05.pdf, 2015.
Huffman, G. J., Stocker, E. F., Bolvin, D. T., and Nelkin, E. J.: last updated 2018: IMERG L3 Early Run Data Sets. NASA/GSFC, Greenbelt, MD, USA, available at: https://gpm1.gesdisc.eosdis.nasa.gov/opendap/hyrax/GPM_L3/GPM_3IMERGHHL.05/, last access: 29 August 2018.
Koster, R. D., Brocca, L., Crow, W. T., Burgin, M. S., and De Lannoy, G. J. M.: Precipitation estimation using L-band and C-band soil moisture retrievals, Water Resour. Res., 52, 7213–7225, https://doi.org/10.1002/2016WR019024, 2016.
Kumar, S. V., Peters-Lidard, C. D., Santanello, J. A., Reichle, R. H., Draper, C. S., Koster, R. D., Nearing, G., and Jasinski, M. F.: Evaluating the utility of satellite soil moisture retrievals over irrigated areas and the ability of land data assimilation methods to correct for unmodeled processes, Hydrol. Earth Syst. Sci., 19, 4463–4478, https://doi.org/10.5194/hess-19-4463-2015, 2015.
Liang, X., Lettenmaier, D. P., Wood, E. F., and Burges, S. J.: A simple hydrologically based model of land surface water and energy fluxes for general circulation models, J. Geophys. Res., 99, 14415–14428, https://doi.org/10.1029/94JD00483, 1994.
Lievens, H., Tomer, S. K., Al Bitar, A., De Lannoy, G. J. M., Drusch, M., Dumedah, G., Hendricks Franssen, H.-J., Kerr, Y. H., Martens, B., Pan, M., Roundy, J. K., Vereecken, H., Walker, J. P., Wood, E. F., Verhoest, N. E. C., and Pauwels, V. R. N.: SMOS soil moisture assimilation for improved hydrologic simulation in the Murray Darling Basin, Australia, Remote Sens. Environ., 168, 146–162, https://doi.org/10.1016/j.rse.2015.06.025, 2015.
Lievens, H., De Lannoy, G. J. M., Al Bitar, A., Drusch, M., Dumedah, G., Hendricks Franssen, H.-J., Kerr, Y. H., Tomer, S. K., Martens, B., Merlin, O., Pan, M., Roundy, J. K., Vereecken, H., and Walker, J. P.: Assimilation of SMOS soil moisture and brightness temperature products into a land surface model, Remote Sens. Environ., 180, 292–304, https://doi.org/10.1016/j.rse.2015.10.033, 2016.
Lohmann, D., Nolte-Holube, R., and Raschke, E.: A large-scale horizontal routing model to be coupled to land surface parametrization schemes, Tellus A, 48, 708–721, https://doi.org/10.1034/j.1600-0870.1996.t01-3-00009.x, 1996.
Lohmann, D., Raschke, E., Nijssen, B., and Lettenmaier, D. P.: Regional scale hydrology: I. Formulation of the VIC-2L model coupled to a routing model, Hydrolog. Sci. J., 43, 131–141, https://doi.org/10.1080/02626669809492107, 1998.
Mao, Y.: Dual state/rainfall correction via soil moisture assimilation for improved streamflow simulation: Evaluation of a large-scale implementation with SMAP satellite data, https://doi.org/10.5281/zenodo.3547877, 2019.
Mao, Y., Crow, W. T., and Nijssen, B.: A framework for diagnosing factors degrading the streamflow performance of a soil moisture data assimilation system, J. Hydrometeorol., 20, 79–97, https://doi.org/10.1175/JHM-D-18-0115.1, 2019.
Massari, C., Brocca, L., Tarpanelli, A., and Moramarco, T.: Data Assimilation of Satellite Soil Moisture into Rainfall-Runoff Modelling: A Complex Recipe?, Remote Sens., 7, 11403–11433, https://doi.org/10.3390/rs70911403, 2015.
Massari, C., Camici, S., Ciabatta, L., and Brocca, L.: Exploiting satellite-based surface soil moisture for flood forecasting in the Mediterranean area: State update versus rainfall correction, Remote Sens., 10, 292 https://doi.org/10.3390/rs10020292, 2018.
Maurer, E. P., Wood, A. W., Adam, J. C., Lettenmaier, D. P., and Nijssen, B.: A long-term hydrologically-based data set of land surface fluxes and states for the conterminous United States, J. Climate, 15, 3237–3251, https://doi.org/10.1175/1520-0442(2002)015<3237:ALTHBD>2.0.CO;2, 2002.
Mehra, R. K.: On-line identification of linear dynamic systems with applications to Kalman filtering, IEEE T. Autom. Control., 16, 12–21, https://doi.org/10.1109/TAC.1971.1099621, 1971.
Nearing, G., Yatheendradas, S., Crow, W. T., Chen, F., and Zhan, X: The efficiency of data assimilation, Water Resour. Res., 54, 6374–6392, https://doi.org/10.1029/2017WR020991, 2018.
O'Neill, P. E., Chan, S., Njoku, E. G., Jackson, T., and Bindlish, R.: SMAP L3 Radiometer Global Daily 36 km EASE-Grid Soil Moisture, Version 4, NASA National Snow and Ice Data Center Distributed Active Archive Center, Boulder, Colorado, USA, https://doi.org/10.5067/OBBHQ5W22HME, 2016.
Pan, M. and Wood, E. F.: A multiscale ensemble filtering system for hydrologic data assimilation. Part II: Application to land surface modeling with satellite rainfall forcing, J. Hydrometeorol., 10, 1493–1506, https://doi.org/10.1175/2009JHM1155.1, 2009.
Pan, M. and Wood, E. F.: Impact of accuracy, spatial availability, and revisit time of satellite-derived surface soil moisture in a multiscale ensemble data assimilation system, IEEE J. Select. Top. Appl. Earth Obs. Rem. Sens., 3, 49–56, https://doi.org/10.1109/JSTARS.2010.2040585, 2010.
Pan, M., Wood, E. F., McLaughlin, D. B., and Entekhabi, D.: A multiscale ensemble filtering system for hydrologic data assimilation. Part I: Implementation and synthetic experiment, J. Hydrometeorol., 10, 794–806, https://doi.org/10.1175/2009JHM1088.1, 2009.
Qing, L., Reichle, R., Bindlish, R., Cosh, M. H., Crow, W. T., de Jeu, R., de Lannoy, G., Huffman, G. J., and Jackson, T. J.: The contributions of precipitation and soil moisture observations to the skill of soil moisture estimates in a land data assimilation system, J. Hydrometeorol., 12, 750–765, https://doi.org/10.1175/JHM-D-10-05000.1, 2011.
Reichle, R. H. and Koster, R. D.: Assessing the impact of horizontal error correlations in background fields on soil moisture estimation, J. Hydrometeorol., 4, 1229–1242, https://doi.org/10.1175/1525-7541(2003)004<1229:ATIOHE>2.0.CO;2, 2003.
Reichle, R. H., Crow, W. T., Koster, R. D., Sharif, H., and Mahanama, S.: Contribution of soil moisture retrievals to land data assimilation products, Geophys. Res. Lett., 35, L01404, https://doi.org/10.1029/2007GL031986, 2008.
Shellito, P. J., Small, E. E., and Livneh B.: Controls on surface soil drying rates observed by SMAP and simulated by the Noah land surface model, Hydrol. Earth Syst. Sci., 22, 1649–1663, https://doi.org/10.5194/hess-22-1649-2018, 2018.
Talagrand, O., Vautard, R., and Strauss, B.: Evaluation of probabilistic prediction systems, technical report, Eur. Cent. for Medium-Range Weather Forecast., Reading, UK, 1997.
USGS – United States Geological Survey: USGS Surface-water daily data for the nation, available at: https://waterdata.usgs.gov/nwis/dv/?referred_module=sw, last access: 21 March 2018.
Wanders, N., Karssenberg, D., De Roo, A., De Jong, S. M., and Bierkens, M. F. P.: The suitability of remotely sensed soil moisture for improving operational flood forecasting, Hydrol. Earth Syst. Sci., 18, 2343–2357, https://doi.org/10.5194/hess-18-2343-2014, 2014.
Western, A. W., Grayson, R. B., and Blöschl, G.: Scaling of soil moisture: a hydrologic perspective, Annu. Rev. Earth Planet. Sci., 30, 149–180, https://doi.org/10.1146/annurev.earth.30.091201.140434, 2002.
Wilks, D. S.: Statistical methods in the atmospheric sciences, 3rd Edn., Elsevier/Academic Press, Amsterdam, Boston, 2011.
Xia, Y., et al.: NCEP/EMC: NLDAS Primary Forcing Data L4 Hourly 0.125×0.125 degree V002, in: NASA/GSFC/HSL, edited by: Mocko, D., Goddard Earth Sciences Data and Information Services Center (GES DISC), Greenbelt, Maryland, USA, https://doi.org/10.5067/6J5LHHOHZHN4, 2009.
Xia, Y., Mitchell, K., Ek, M., Sheffield, J., Cosgrove, B., Wood, E., Luo, L., Alonge, C., Wei, H., Meng, J., Livneh, B., Lettenmaier, D., Koren, V., Duan, Q., Mo, K., Fan, Y., and Mocko, D.: Continental-scale water and energy flux analysis and validation for the North American LandData Assimilation System project phase 2 (NLDAS-2): 1. Intercomparison and application of model products, J. Geophys. Res., 117, D03109, https://doi.org/10.1029/2011JD016048, 2012.
Yapo, P. O., Gupta, H. V., and Sorooshian, S.: Multi-objective global optimization for hydrologic models, J. Hydrol., 204, 83–97, https://doi.org/10.1016/S0022-1694(97)00107-8, 1998.
Yilmaz, M. T. and Crow, W. T.: The optimality of potential rescaling approaches in land data assimilation, J. Hydrometeorol., 14, 650–660, https://doi.org/10.1175/JHM-D-12-052.1, 2013.