the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Temperature controls production but hydrology regulates export of dissolved organic carbon at the catchment scale
Julia Perdrial
Benjamin W. Abbott
Susana Bernal
Rémi Dupas
Sarah E. Godsey
Adrian Harpold
Donna Rizzo
Kristen Underwood
Thomas Adler
Gary Sterle
Lateral carbon flux through river networks is an important and poorly understood component of the global carbon budget. This work investigates how temperature and hydrology control the production and export of dissolved organic carbon (DOC) in the Susquehanna Shale Hills Critical Zone Observatory in Pennsylvania, USA. Using field measurements of daily stream discharge, evapotranspiration, and stream DOC concentration, we calibrated the catchment-scale biogeochemical reactive transport model BioRT-Flux-PIHM (Biogeochemical Reactive Transport–Flux–Penn State Integrated Hydrologic Model, BFP), which met the satisfactory standard of a Nash–Sutcliffe efficiency (NSE) value greater than 0.5. We used the calibrated model to estimate and compare the daily DOC production rates (Rp; the sum of the local DOC production rates in individual grid cells) and export rate (Re; the product of the concentration and discharge at the stream outlet, or load).
Results showed that daily Rp varied by less than an order of magnitude, primarily depending on seasonal temperature. In contrast, daily Re varied by more than 3 orders of magnitude and was strongly associated with variation in discharge and hydrological connectivity. In summer, high temperature and evapotranspiration dried and disconnected hillslopes from the stream, driving Rp to its maximum but Re to its minimum. During this period, the stream only exported DOC from the organic-poor groundwater and from organic-rich soil water in the swales bordering the stream. The DOC produced accumulated in hillslopes and was later flushed out during the wet and cold period (winter and spring) when Re peaked as the stream reconnected with uphill and Rp reached its minimum.
The model reproduced the observed concentration–discharge (C–Q) relationship characterized by an unusual flushing–dilution pattern with maximum concentrations at intermediate discharge, indicating three end-members of source waters. A sensitivity analysis indicated that this nonlinearity was caused by shifts in the relative contribution of different source waters to the stream under different flow conditions. At low discharge, stream water reflected the chemistry of organic-poor groundwater; at intermediate discharge, stream water was dominated by the organic-rich soil water from swales; at high discharge, the stream reflected uphill soil water with an intermediate DOC concentration. This pattern persisted regardless of the DOC production rate as long as the contribution of deeper groundwater flow remained low (<18 % of the streamflow). When groundwater flow increased above 18 %, comparable amounts of groundwater and swale soil water mixed in the stream and masked the high DOC concentration from swales. In that case, the C–Q patterns switched to a flushing-only pattern with increasing DOC concentration at high discharge. These results depict a conceptual model that the catchment serves as a producer and storage reservoir for DOC under hot and dry conditions and transitions into a DOC exporter under wet and cold conditions. This study also illustrates how different controls on DOC production and export – temperature and hydrological flow paths, respectively – can create temporal asynchrony at the catchment scale. Future warming and increasing hydrological extremes could accentuate this asynchrony, with DOC production occurring primarily during dry periods and lateral export of DOC dominating in major storm events.
- Article
(6778 KB) -
Supplement
(952 KB) - BibTeX
- EndNote
Soil organic carbon (SOC) is the largest terrestrial stock of organic carbon, containing approximately 4 times more carbon than the atmosphere (Stockmann et al., 2013; Hugelius et al., 2014). Understanding the SOC balance requires the consideration of lateral fluxes in water, including dissolved organic and inorganic carbon (DOC and DIC, respectively), and vertical fluxes of gases such as CO2 and CH4 (Chapin et al., 2006). Both lateral and vertical fluxes influence SOC mineralization to the atmosphere (Campeau et al., 2019), although lateral fluxes are arguably less understood and integrated into Earth system models (Aufdenkampe et al., 2011; Raymond et al., 2016). Lateral fluxes from terrestrial to aquatic ecosystems are similar in magnitude to net vertical fluxes (Regnier et al., 2013; Battin et al., 2009), highlighting the importance of quantifying the controls on the lateral carbon (C) flux. In addition to its role in the global C cycle, DOC is an important water quality parameter that can mobilize metals and contaminants as well as imposing challenges for water treatment (Sadiq and Rodriguez, 2004; Bolan et al., 2011). DOC also regulates food web structures by acting as an energy source for heterotrophic organisms and interacts with other biogeochemical cycles (Malone et al., 2018; Abbott et al., 2016).
SOC decomposition and DOC production have been studied extensively (Abbott et al., 2015; Hale et al., 2015; Humbert et al., 2015; Lambert et al., 2013; Neff and Asner, 2001), yet the interactions between SOC and DOC and their response to climate change at catchments or larger scales remain unresolved (Laudon et al., 2012; Clark et al., 2010). Some regions have experienced long-term increases in DOC, potentially due to recovery from acid rain or climate-induced changes in temperature (T) and hydrological flow (Laudon et al., 2012; Perdrial et al., 2014; Evans et al., 2012; Monteith et al., 2007), whereas others have observed decreases or no change (Skjelkvale et al., 2005; Worrall et al., 2018). Generally, the linkages among SOC processing, hydrological conditions, and DOC export or concentration remain poorly understood. Recent analyses indicate that the relationship between DOC concentration and discharge (C–Q) at stream outlets is primarily positive (Moatar et al., 2017; Zarnetske et al., 2018). Approximately 80 % of watersheds in the USA and France show a flushing C–Q pattern (i.e., the stream DOC concentration increases with discharge), whereas the rest shows dilution (decreasing DOC with discharge) or chemostatic behavior (negligible concentration change with discharge). These C–Q patterns generally correlate with catchment characteristics, including topography, wetland area, and climate characteristics, but it remains uncertain how hydrological and biogeochemical processes regulate SOC decomposition, DOC production, and DOC export (Jennings et al., 2010; Worrall et al., 2018). This gap in process understanding limits the integration of lateral carbon dynamics into projections of future ecosystem response to environmental change.
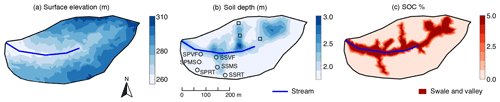
Figure 1Attributes of the Susquehanna Shale Hills Critical Zone Observatory (SSHCZO): (a) surface elevation, (b) soil depth, and (c) soil organic carbon (SOC). The surface elevation was generated from lidar topographic data (criticalzone.org/shale-hills/data), whereas soil depths and SOC were interpolated using ordinary kriging based on field surveys with 77 and 56 sampling locations, respectively (Andrews et al., 2011; Lin, 2006). The SOC distribution in panel (c) is further simplified using the high, uniform SOC (5 % v∕v) in swales and valley soils based on field survey information (Andrews et al., 2011). Swales and valley floor areas were defined based on surface elevation via field survey and a 10 m resolution digital elevation model (Lin, 2006). Additional sampling instrumentation is shown in panel (b), including six soil water sites (circles) and three soil Tsites (squares).
Stream DOC can be influenced by a variety of factors that control SOC decomposition and DOC production rates. DOC production generally increases as T increases; however, there may be multiple thermal optima, and the local rates can vary with SOC characteristics, soil type, and soil biota (Davidson and Janssens, 2006; Jarvis and Linder, 2000; Yan et al., 2018; Zarnetske et al., 2018). DOC production rates can exhibit low temperature sensitivity in highly weathered soils with a high clay content (Davidson and Janssens, 2006). They have also been shown to increase with soil water content in sandy loam soils (Yuste et al., 2007) and to have an optimum with a volumetric water content of approximately 0.75 in fine sands (Skopp et al., 1990). Because DOC export (or load) is the product of discharge and DOC concentration, it may differ from local DOC production rates in complex ways. For example, high T can produce a peak soil water DOC concentration but not necessarily stream concentration or export, due to temporal or spatial mismatches (D'Amore et al., 2015). These confounding factors present significant challenges to quantify the predominant mechanisms that regulate DOC production and export under varying environmental conditions.
One approach to understanding DOC production and export is the use of reactive transport models (RTM). These models integrate multiple production, consumption, and export processes, enabling the differentiation of individual and coupled processes (Steefel et al., 2015; Li, 2019; Li et al., 2017b). The use of RTMs complements statistical tools for the identification of influential factors (Correll et al., 2001; Herndon et al., 2015; Zarnetske et al., 2018). Historically, RTMs have been used in groundwater systems, where direct observations are particularly challenging (Kolbe et al., 2019; Li et al., 2009; Wen and Li, 2018; Wen et al., 2018). At the catchment scale, biogeochemical modules have been developed as add-ons to hydrological models. For example, a DOC production module was coupled to the HBV hydrological model using a static SOC pool that emphasized the influence of active-layer dynamics and slope aspect (Lessels et al., 2015). The INCA-C (Futter et al., 2007) and extended LPJ-GUESS (Tang et al., 2018) models have investigated the importance of land cover in determining DOC terrestrial routing and lateral transport. Terrestrial and aquatic carbon processes have also been integrated into the Soil and Water Assessment Tool (SWAT) to simulate aquatic DOC dynamics (Du et al., 2019). These modules typically simulate individual reactions without considering multicomponent reaction thermodynamics and kinetics.
In this context, the recently developed BioRT-Flux-PIHM model (BFP, Biogeochemical Reactive Transport–Flux–Penn State Integrated Hydrologic Model) fills an important gap by incorporating coupled elemental cycling, stoichiometry, and rigorous thermodynamics and kinetics (Bao et al., 2017; Zhi et al., 2019). We used the BFP to address the following question: how do hydrology and T interact to determine rates of DOC production and export at the catchment scale? We applied the BFP to a temperate forest catchment in the Susquehanna Shale Hills Critical Zone Observatory (SSHCZO). This small catchment (<0.1 km2) has gentle topography with a network of shallow depressions or swales that have high SOC and deep soils (detailed in Sect. 2). It is underlain by one type of lithology (shale) and land use (forest), providing a useful test bed to evaluate biogeochemical and hydrological functions (Brantley et al., 2018). Previous lab and field work have identified non-chemostatic C–Q patterns of DOC at SSHCZO that are attributable to differences in the hydrologic connectivity of organic-rich soils during different flow conditions (Andrews et al., 2011; Herndon et al., 2015). SSHCZO has spatially extensive and high-frequency measurements of soil properties, hydrology, and biogeochemistry (Brantley et al., 2018). These data facilitate detailed benchmarking of the BFP model and evaluation of processes controlling DOC production and export. We expected that T and soil moisture would drive DOC production in the soil, whereas DOC export and, thus, C–Q patterns would be most related to hydrological connectivity. Therefore, we predicted that DOC production and export might be asynchronous (i.e., not occurring at the same time) because they respond differently to changes in T and hydrology. Although soil respiration is an important process, this study focuses on the net production and export of DOC.
2.1 Study site: a small catchment with an intermittent stream
The Shale Hills catchment is a 0.08 km2, V-shaped, first-order watershed with an intermittent stream in central Pennsylvania. It is forested with coniferous trees and is situated on the Rose Hill shale formation. The annual mean air T is 9.8±1.9 ∘C (± SD) and the annual mean precipitation is 1029±270 mm over the past decade. The watershed is characterized by large areas of swales and valley floors with deep and wet soils (Fig. 1b). These lowland soils contain more SOC (∼5 % v∕v) than the hillslopes and uplands (∼1 % v∕v; Fig. 1c).
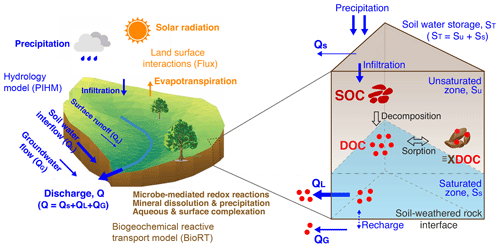
Figure 2A schematic representation of major processes in the catchment reactive transport model BFP (BioRT-Flux-PIHM). Stream discharge Q includes surface runoff QS, soil water interflow (lateral flow) QL, and groundwater flow QG. In the vertical direction, soil pores are not saturated with water in the shallow unsaturated zone and water flows vertically until it reaches the saturated zone where water forms interflows and moves laterally to the stream. Soil water total storage ST is the sum of water in the unsaturated (Su) and saturated zones (Ss). Some water also recharges further into deeper groundwater. Within the soil zone, SOC decomposes and releases DOC, which also sorbs onto the soil surface to become ≡XDOC.
Soil water DOC samples were collected using lysimeters with a diameter of 5 cm installed at 10 or 20 cm intervals from the soil surface to a depth of hand-auger refusal, which varied from 30 to 160 cm depending on soil thickness. There were a total of six sampling locations (Fig. 1b), including three at the south planar sites – valley floor (SPVF), mid-slope (SPMS), and ridgetop (SPRT) – and three at the swale sites – valley floor (SSVF), mid-slope (SSMS), and ridgetop (SSRT). No soil water DOC samples were collected on the north side of the catchment. Stream water DOC samples were collected daily in glass bottles at the stream outlet weir. All soil water and stream water DOC samples were filtered to 0.45 µm using Nylon syringe filters and were analyzed with a Shimadzu TOC-5000A analyzer (detailed in Andrews et al., 2011). Real-time soil T (every 10 min) was measured at the ridgetop, mid-slope, and valley floor (squares in Fig. 1b) using automatic monitoring stations at depths of 0.20, 0.40, 0.70, 0.90, 1.00, and 1.30 m (Lin and Zhou, 2008).
2.2 The BioRT-Flux-PIHM (BFP) model
BFP is the catchment reactive transport model of the general PIHM (Penn State Integrated Hydrologic Modeling System) family of code (Duffy et al., 2014). The code includes three modules (Fig. 2): the surface hydrological module PIHM, the land surface module Flux, and the multicomponent reactive transport module BioRT (Biogeochemical Reactive Transport). The code has been applied to simulate conservative solute transport, chemical weathering, surface complexation, and biogeochemical reactions at the catchment scale (Bao et al., 2017; Zhi et al., 2019; Li, 2019). Here, we only introduce the salient features that are relevant to this study; readers are referred to earlier publications for further details. Flux-PIHM separates the subsurface flow into active interflow in shallow soil zones and groundwater flow deeper than the soil-weathered rock interface. Note that this “deeper groundwater” is the groundwater that actively interacts with the stream and shallow layer, not necessarily the water in the deep groundwater aquifer. The PIHM module simulates hydrological processes including precipitation, infiltration, surface runoff QS, soil water interflow (lateral flow) QL, and discharge Q (Fig. 2). The Flux module simulates processes including solar radiation and evapotranspiration. Flux-PIHM calculates water variables (e.g., water storage, soil moisture, and water table depth) in unsaturated and saturated zones and assumes a no-flow boundary at the soil–bedrock interface with high permeability contrast. In this version of Flux-PIHM, the deeper groundwater flow QG is a separate input to the stream and is decoupled from the shallow soil water. This is supported by field data that show negligible seasonal variation in groundwater chemistry (Jin et al., 2014; Thomas et al., 2013; Kim et al., 2018). The QG is estimated using conductivity mass-balance hydrograph separation (Lim et al., 2005).
The BioRT module takes in water calculated at each time step to simulate reactive transport processes. BFM discretizes the domain into prismatic elements and uses a finite volume approach based on mass conservation. The mass conservation governing equation for the reactive transport of a single solute m is as follows:
where i and j represent the grid block i and the neighboring grid j; the subscript x distinguishes between flow in the unsaturated zone (infiltration and recharge) and saturated zone (recharge and lateral flow); V is the total bulk volume (m3) of each grid block; Sw is the soil moisture (m3 water m−3 pore volume); θ is porosity; C is the aqueous species concentration (mol m−3 water); t is time (s); N is the index of elements sharing surfaces; A is the grid interface area (m2); D is the diffusion/dispersion coefficient (m2 s−1); l is the distance (m) between the center of two neighboring grid blocks; q is the flow rate (m3 s−1); rm is the kinetically controlled reaction rates (mol s−1) involving species m, which is the DOC production rate from SOC decomposition at the grid block i; and np is the total number of independent solutes.
2.3 DOC production and sorption
In the model, DOC is produced by the decomposition of SOC via the kinetically controlled reaction SOC(s)→DOC. With abundant SOC and O2 in soils serving as electron donors and acceptors, a typical dual Monod kinetics can be simplified into zero-order kinetics with additional temperature and soil moisture dependence:
where rp is the local DOC production rate in individual grids (rm in Eq. 1, m is DOC); k is the kinetic rate constant of net DOC production (10−10 mol m−2 s−1) (Zhi et al., 2019; Wieder et al., 2014); and A is a lumped “surface area” (m2, ( m2 g−1) × (g of SOC mass)) that quantifies SOC content and biomass abundance (Chiou et al., 1990; Kaiser and Guggenberger, 2003; Zhi et al., 2019). The functions f(T) and f(Sw) describe the rate dependence on soil T and moisture, respectively. f(T) follows a widely used Q10-based formation: , where Q10 quantifies the rate increases with T, with the superscript 10 referring to a T value of 10 ∘C (Davidson and Janssens, 2006). Q10 in the base case is set at 2.0, within the typical range of 1.2–3.8 for forest ecosystems (Liu et al., 2017). The f(Sw) has the form f(Sw)=(Sw)n in the base case, where n is the saturation exponent with a value of 1.0, which is within the typical range of 0.75–3.0 for most soils (Yan et al., 2018; Hamamoto et al., 2010). The dependence of production rates on soil T and moisture have been described using multiple forms in existing studies (Davidson and Janssens, 2006; Yan et al., 2018) and will be further explored via sensitivity analysis, as detailed in Sect. 2.6. The SOC content typically decreases with depth (Billings et al., 2018; Bishop et al., 2004), although the specific pattern may vary with soil texture, landscape position, vegetation, and climate (Jobbagy and Jackson, 2000). The depth function of SOC at Shale Hills has been observed to be exponential (Andrews et al., 2011), which is typical of many soils (Billings et al., 2018; Currie et al., 1996). To take this into account, we use the equation , where Cd is SOC at depth z below the surface; C0 is the SOC level at the ground surface, and bm quantified the decline rate with depth, which is set here to a value of 0.3 (Weiler and McDonnell, 2006).
DOC produced from SOC can also sorb on soils via the following reaction: , where ≡X and ≡XDOC represent the functional group without and with sorbed DOC, respectively (Rasmussen et al., 2018). This reaction is considered fast and is thermodynamically controlled with an equilibrium constant Keq that links the activity (here approximated by concentrations) of the three chemicals via . The DOC concentrations calculated from Eq. (1) were used to establish the concentrations of ≡X and ≡XDOC. The Keq value represents the thermodynamic limit of the sorption, i.e., the sorption affinity of the soil for DOC. It depends on temperature but also on soil properties such as the clay content and the abundance of iron oxides (Kaiser et al., 2001; Conant et al., 2011). A Keq value of 100.2 was obtained by fitting the stream and soil water DOC data (detailed in Sect. 2.4). The sum of [≡X] and [≡XDOC] represents the soil sorption capacity. A value ranging from to mol g−1 soil was used for Shale Hills (Jin et al., 2010; Li et al., 2017a) depending on the mineralogy in different zones of the catchment.
2.4 Domain setup
BFP is a model with full discretization in the horizontal direction and partial discretization in the vertical direction with three layers: ground surface, unsaturated, and saturated zones. Although a new version of BFP explicitly includes a groundwater zone, it was not released in time for this work, so the groundwater fluxes were estimated separately. The study watershed was discretized into 535 prismatic land elements and 20 stream segments using PIHMgis (http://www.pihm.psu.edu/pihmgis_home.html, last access: 11 February 2020), a GIS interface for BFP. The land elements are unstructured triangles with mesh sizes varying from 10 to 100 m. The simulation domain was set up using national datasets: the USGS National Elevation Dataset for topography; the National Land cover Database for vegetation distribution; the National Hydrography Dataset for water drainage network; the North American Land Data Assimilation Systems Phase 2 (NLDAS-2) for hourly meteorological forcing; and the Moderate Resolution Imaging Spectroradiometer (MODIS) for leaf area index. In addition, extensive characterization and measurement data at Shale Hills were used to define soil depth and soil mineralogical properties such as surface area and ion exchange capacity that are heterogeneously distributed across the catchment (Andrews et al., 2011; Lin, 2006; Jin and Brantley, 2011; Jin et al., 2010; Shi et al., 2013) (http://criticalzone.org/shale-hills/data/, last access: 11 February 2020). Other soil matrix properties include conductivity, porosity, and van Genuchten parameters. Soil macropores such as cracks, fractures, and roots can generate preferential flows. Their properties are represented using the area macropore fraction, depth, and conductivities. They are parameterized based on values quantified in previous studies at Shale Hills (Shi et al., 2013; Lin, 2006), as shown in Fig. S1 and Table S1 in the Supplement.
Based on field measurements, the SOC content in swales and valley areas is relatively high (Andrews et al., 2011) and was set at 5 % (v∕v solid phase) compared with 1 % in the rest of the catchment (Fig. 1c). The clay minerals were set at 23 % (v∕v solid phase) along the ridgetop and 33 % at the valley floor (Jin et al., 2010; Li et al., 2017a). The input DOC concentrations in rainfall and groundwater (below soils) were set at reported medians of 0.6 and 1.2 mg L−1, respectively (Andrews et al., 2011; Iavorivska et al., 2016), as high-frequency DOC observations were not available. The initial DOC concentration in soil water was set at 2.0 mg L−1, which was the average concentration from the six field sampling locations in Fig. 1.
2.5 Model calibration
We used stream (daily) and soil pore water (biweekly) DOC concentration data from April to October 2009 for model calibration and the year 2008 as spin-up until a “steady state” for both water and DOC was reached. The “steady state” here refers to a state where the inter-annual difference between stored mass within the catchment is less than 5 % of the total mass. The water input is precipitation, and its output is ET and discharge. The DOC mass input is from rainfall, groundwater, and production, and the DOC output is the export load at the stream outlet. The model performance was evaluated using the monthly Nash–Sutcliffe efficiency (NSE) (Nash and Sutcliffe, 1970) that quantified the residual variance of modeling output compared to measurements. The general satisfactory range for monthly average outputs for hydrological models is NSE >0.5 (Moriasi et al., 2007), and we used similar standards for biogeochemical solutes (Li et al., 2017a). To reproduce the DOC data, we first set the SOC surface area A using a literature range of 10−3–100 m2 g−1 (Zhi et al., 2019; Chiou et al., 1990; Kaiser and Guggenberger, 2003). We also set Keq using a literature range of 100–101 (Oren and Chefetz, 2012; Ling et al., 2006). Once the simulated output captured the temporal trend of data, we refined QG based on the estimation from hydrograph separation (Fig. S2) to capture the peaks of stream DOC concentration, especially under low-discharge periods. Because not all soils are in contact with water, the calibrated surface area represents the effective solid–water contact area, and is orders of magnitude lower than the reported SOC surface areas from laboratory experiments (Kaiser and Guggenberger, 2003). The calibrated hydrological parameters are mostly from Shi et al. (2013), except groundwater estimation. Groundwater estimates were based on Li et al. (2017a) and further refined using conductivity mass-balance hydrograph separation (Lim et al., 2005) and then by reproducing the stream DOC concentration. In other words, stream and groundwater chemistry data together helped constrain the groundwater flow.

Figure 3Temporal dynamics of (a) daily precipitation, stream discharge Q, and evapotranspiration ET on the arithmetic scale; (b) stream discharge Q, soil water interflow QL, and groundwater QG on a logarithmic scale with soil T on an arithmetic axis (right); (c) soil water storage ST (unsaturated water storage Su+ saturated water storage Ss) and hydrological connectivity Ics∕Width. The yellow dots in panel (b) represent the average soil T from three sampling locations (square symbols in Fig. 1b) with the shading reflecting variation in measurement. Q was highly responsive to intense precipitation events in spring and winter. Note high soil T, high ET, low Ss, and lowIcs∕Width during July–August 2009. Stream discharge was primarily comprised of QL, except in July–October when the relative contribution of QG increased.
2.6 Quantification of water and DOC dynamics
2.6.1 Hydrological connectivity
Saturated soil water storage calculated from the model was used to quantify hydrological connectivity Ics∕Width. With “Width” defined as the average width of catchment in the direction perpendicular to the stream (230 m), the term Ics∕Width quantifies the average proportional width of the catchment connected to the stream (e.g., , 0.35, and 0.70 in Fig. S3). Depending on the catchment geometry and the extent of connectivity, Ics∕Width may vary from 0 to 1.0. A high Ics∕Width value (i.e., high hydrological connectivity) indicates that a large catchment area is connected to the stream. To determine whether two grids are hydrologically connected, the spatial distribution of saturated water storage was used to calculate connectivity following the equation and an algorithm in the literature (Allard, 1994; Western et al., 2001; Xiao et al., 2019). Here τ(h) is the probability of two grid blocks being connected at a separation distance of h. Two grids are considered “connected” if they are joined by a continuous flow path and have saturated storages exceeding the threshold of the 75th percentile of saturated storage (over the whole catchment). Note that Ics∕Width here only quantifies the hydrological connectivity in soils and does not reflect the groundwater in shallow aquifers below the soil–bedrock interface.
2.6.2 DOC concentration–discharge relationships
At the catchment scale, we differentiate the DOC production rates and export rates. The production rate Rp is the sum of the local DOC production rate rp in individual grid blocks (Eq. 2) across the whole catchment. The export rate Re is the product of discharge and the DOC concentration at the stream outlet. Total stored DOC is the difference between stream output and input from production, rainfall, and groundwater. The DOC input from the rainfall Rr (mg d−1) is the precipitation rate (m d−1) times the rainfall DOC concentration ( mg m 0.6 mg L L m−3) and the catchment drainage area (m2). The DOC input from groundwater Rg (mg d−1) is the total groundwater influx (flow rate) times the groundwater DOC concentration (1.2 mg L−1).
C–Q patterns were quantified using two complementary approaches: the power law equation C=aQb (Godsey et al., 2009) and the ratio of the coefficients of variation of the DOC concentration and discharge (Musolff et al., 2015). The slope of the power law equation b does not account for the goodness of fit of the C–Q pattern itself. For example, a slope of b=0 would be considered chemostatic (i.e., relatively small variation of concentration compared with discharge), although high variability in solute concentrations would in fact reflect a chemodynamic behavior (i.e., solute concentrations are sensitive to changes in discharge). We considered two general categories based on these metrics (Musolff et al., 2015): if b values fell between −0.2 and 0.2 and , C–Q patterns were considered chemostatic; values of or , indicated a chemodynamic behavior. In the chemodynamic category, values of b>0.2 indicate flushing, whereas values of indicate dilution. We used the MATLAB curve-fitting toolbox to obtain the best fit model parameters.
2.7 Sensitivity analysis
We used a sensitivity analysis to explore the influence of soil T and moisture in the DOC production kinetics. The Q10 in was explored using a minimum value of 1.0 (i.e., no dependence on T) and a maximum value of 4.0 (Davidson and Janssens, 2006) (Fig. S4a), i.e., f(T)=1 and . The rate dependence on soil moisture was explored using the base case f1(Sw)=(Sw)n (increase behavior), and three additional functions (f2, f3, and f4) representing the most commonly observed forms (Fig. S4b), including decrease behavior, constant behavior, and threshold behavior (Gomez et al., 2012; Yan et al., 2018):
the decrease behavior function was
the constant behavior function was
and the threshold behavior function was
The constants in Eqs. (3)–(5) were selected to ensure similar averages of f(Sw) across the whole Sw range such that trajectories rather than absolute values of f(Sw) were compared (Fig. S4b). The sensitivity of DOC sorption onto soils was tested using Keq values of 0 (no sorption), 100.5 and 101.0.
The sensitivity of C–Q patterns and Re to changes in groundwater was also tested with groundwater flow contribution and DOC concentration. The groundwater flow rates were varied from negligible (QG=0) to 2.5 times those of the base case ( and m d−1 for the wet and dry periods, respectively). The corresponding fractions (QG∕Q) of groundwater flow to the total annual discharge for the two cases were 0 % and 18.8 %, respectively. The groundwater DOC concentration (DOCGW) was varied by 2 orders of magnitude (0.12 and 12.0 mg L−1). Results from these analyses were compared with the base case, in which the groundwater contributed to 7.5 % of the total annual streamflow at 1.2 mg L−1.
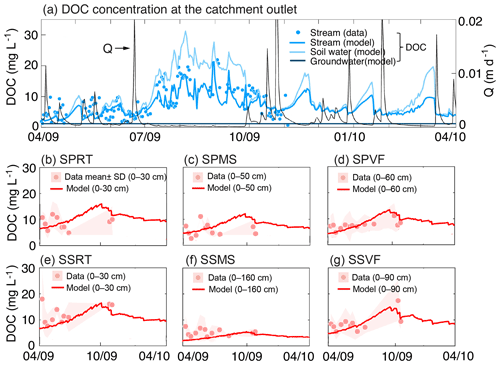
Figure 4(a) Temporal dynamics of measured and simulated stream DOC concentrations as well as groundwater and soil water DOC. The stream DOC (bright blue line) was from the soil water (light blue line) and groundwater QG (dark blue line). Under low-discharge conditions (e.g., July–September), QG contributed a larger proportion of discharge and stream DOC was more similar to groundwater DOC. Under wet conditions, stream DOC resembled soil water DOC from QL. (b–g) The local soil water DOC concentration for the six sampling locations shown in Fig. 1b, including three planar (panels b–d) and three swale locations (panels e–g). The mean ±SD for each location was calculated based on measurements at different depths with 10 or 20 cm intervals from the soil surface down to a depth of hand-auger refusal.
3.1 Water dynamics
The total precipitation from 1 April 2009 to 31 March 2010 was 1130 mm. Stream discharge was highly responsive to intense precipitation events and was high ( m d−1) in spring and fall compared with summer with high soil T and high ET ( m d−1). The model captured the temporal dynamics of daily discharge, ET, and soil T with NSE values of 0.68, 0.72, and 0.62, respectively (Fig. 3a, b). The model estimated that 47.5 % of annual precipitation contributed to discharge, whereas the rest contributed to ET. The stream discharge has three components: surface runoff QS, soil water interflow QL (lateral flow), and groundwater flow QG from the shallow subsurface that interacts with the stream (Fig. 2). On average, lateral flow QL is about 90.2 % and surface runoff QS is about 2.3 %. Following the conductivity mass-balance hydrograph separation (Lim et al., 2005), QG was estimated to be and m d−1 for the wet and dry periods (August–September), which is equivalent to 6.9 % and 42.2 % of average stream discharge at the corresponding times, respectively. Overall QG accounted for ∼7.5 % of the annual Q, similar to previously reported values (Li et al., 2017a; Hoagland et al., 2017). In the dry months from August to September, the stream was almost dry with no visible flow, and the relative contribution of groundwater to discharge was comparable to that of QL (Fig. 3b). The unsaturated water storage Su was typically more than 10 times larger than the saturated storage Ss such that the ST and Su curves almost overlapped (Fig. 3c). Ss was negligible in the dry period (close to 0 m), contributing negligibly to the stream. Hydrological connectivity (Ics∕Width) covaried with Ss but showed significant temporal fluctuations. High summer ET drove the catchment to drier conditions, thereby decreasing the connectivity to the stream.
3.2 Temporal patterns of DOC concentrations
The model captured the general trend of stream DOC (NSE of 0.55 for the monthly DOC concentration; Fig. 4). Under dry conditions (e.g., m d−1), QG contributed substantially to Q (∼32 %–71 %; Fig. 3), and the stream DOC concentration reflected the mixing of groundwater and soil water (Fig. 4a), with a contribution from groundwater DOC of 7 %–17 %. Under wet conditions, the stream DOC concentration overlapped with the soil water DOC concentration (light blue line in Fig. 4). Only ∼1 %–8 % of stream DOC was sourced from groundwater at these times.
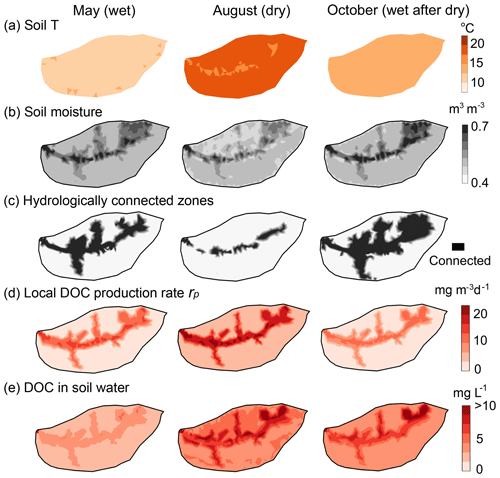
Figure 5Spatial profiles in May (wet), August (dry), and October (wet after dry) of 2009: (a) soil T, (b) soil moisture, (c) hydrologically connected zones, (d) local DOC production rates rp, and (e) soil water DOC concentration. The soil DOC and rp were high in swales and the valley that had a relatively high soil water and SOC content (Fig. 1c). Although water content in August was relatively low compared with May and October, high soil T led to high rp, with most DOC production and accumulation in zones that were disconnected from the stream.
The temporal dynamics of soil water data showed relatively small temporal variation compared with stream DOC (Fig. 4b, c, d, e, f, g), and local soil pools were not always hydrologically connected to the stream. The simulated soil water DOC captured this small-variation trend with acceptable overall model performance (i.e., NSE >0.5), although the goodness of fit was lower in some locations, e.g., a NSE value of 0.36 (SPRT), 0.42 (SPMS), 0.60 (SPVF), 0.46 (SSRT), 0.40 (SSMS), and 0.51 (SSVF). The variation in model performance at different locations may arise from the lack of detailed information on local soil properties and organic carbon content. Although the model explicitly considered spatial heterogeneities such as topography and soil properties, averaged values represented grid sizes from 10 to 100 m, and this local scale was large compared with the field sampling size (e.g., lysimeters with a diameter of 5 cm). Geochemical processes are sensitive to local properties, including SOC %, SOC surface area, and sorption sites, and the representation of these properties was based on a few measurements that were only coarsely defined as ridgetop, mid-slope, and valley floor.
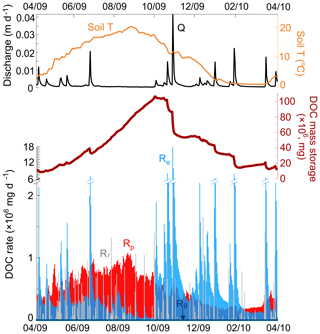
Figure 6Temporal dynamics of DOC storage, influent rate (rainfall Rr, groundwater Rg, production Rp), and outflow rate (effluent Re) at the catchment scale. The stored DOC mass (dark red line) was calculated as follows: (DOC influent rate − outflow rate) × time. The temporal Re dynamics mostly followed the trend of discharge (black line, top panel), whereas Rp mostly followed the trend of soil T (orange line, top panel).
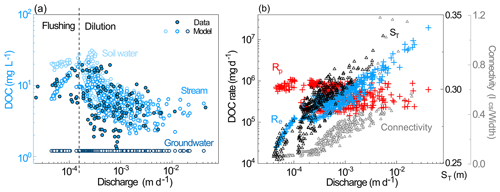
Figure 7(a) Relationship of daily discharge (Q) with stream DOC concentration: open circles are simulations and filled circles with a black outline are data. (b) Relationship of daily discharge (Q) with soil water storage ST, connectivity (Ics∕Width), the catchment-scale DOC export rate Re, and the DOC production rate Rp. At low Q, the stream water transitioned from organic-poor groundwater to organic-rich water from the valley floor and swales, leading to a flushing (positive) pattern. At higher Q, the stream water shifted from organic-rich soil water from swales and valley areas to lower DOC water from planar hillslopes and uplands, decreasing the stream DOC concentration and resulting in a dilution C–Q pattern. Re increased by 2 orders of magnitude with increasing Q, whereas Rp varied within an order of magnitude.

Figure 8The catchment-scale DOC production rate Rp and export rate Re as a function of (a) soil T, (b) soil water storage ST, and (c) hydrological connectivity (Ics∕Width). Cross symbols are daily values in the base case. Rp increased with soil T and decreased slightly with ST and connectivity. In contrast, Re increased with ST and connectivity but decreased with soil T. Re tended to decrease with soil T in the hot, dry summer due to low discharge during that period.
3.3 Spatial patterns and mass balance
Spatial patterns vary between May (wet), August (dry), and October (wet after dry) (Fig. 5). In May, the average soil T was around 12 ∘C with small spatial variations (<3 ∘C). Most flow-convergent areas (valley areas and swales) were well connected to the stream and had a high water content (Fig. 5b, c). The distribution resembles that of SOC (Fig. 1c) and water content (Fig. 5b), with a high rp and soil water DOC concentration in swales and valley. Low rp in relatively dry planar hillslopes and uplands led to a low soil water DOC concentration. In August, the average soil T increased to around 20 ∘C. The hydrologically connected zones shrank to the immediate vicinity of the stream, but rp increased 2-fold from May. The simulated soil water DOC concentration increased by a factor of 2 across the whole catchment, especially in hillslope and uplands on the north side, because the DOC produced was trapped in low soil moisture areas that were not hydrologically connected to the stream. This indicates that DOC samples collected on the south side may not represent the DOC dynamics of the entire catchment, especially in the summer and fall dry months. In October, rp decreased as soil cooled down, but increased precipitation and decreased ET expanded the hydrologically connected zones beyond swales and valley areas (Fig. 5c), promoting the desorption and the flushing of stored DOC. The soil water DOC concentration, however, remained high because of the large store of sorbed DOC produced during the antecedent dry times.
Figure 6 shows the catchment-scale DOC production and export rates and mass balance. Generally, the daily Rp (5.1×105 mg d−1) was greater than the daily Rr from rainfall (1.6×105 mg d−1) or groundwater Rg (1.2×104 mg d−1). During storm events, Rr occasionally exceeded Rp. Rp was generally high in summer, despite low water storage. The export rate Re did not follow the temporal patterns of the total input rate () or Rp. Instead, it primarily followed the discharge patterns: large rainfall events exported disproportionally high DOC, plummeting the DOC mass within the catchment. From the wet to dry period, as water levels dropped, DOC accumulated within the catchment (Fig. 5e, May to August). During the dry-to-wet transition, as the catchment became wetter, the contributing areas expanded to the uplands and the DOC was flushed out, reducing the overall DOC soil pool to much lower values (Fig. 5e, August–October). The DOC mass storage increased by 1.8×106 mg over the year, which was about 1.0 % of the overall DOC production, indicating a general mass balance at the catchment scale.
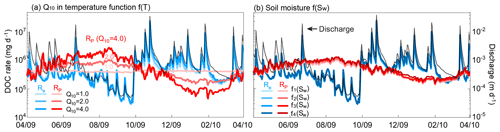
Figure 9Sensitivity analysis of temporal DOC rates for (a) soil temperature f(T) and (b) soil moisture f(Sw). A varying Q10 value in f(T) had a larger influence on Rp than varying f(Sw). Neither f(T) nor f(Sw) had a significant influence on Re. Instead, Re mostly followed the temporal trend of discharge, indicating the predominant control of hydrological conditions.
3.4 C–Q patterns and rate dependence
The C–Q relationships showed a slightly positive correlation at low Q followed by a negative correlation at higher Q (Fig. 7a). The simulated C–Q relationship captured this trend but overestimated the positive relationship at low Q. The simulated C–Q relationships showed a general dilution behavior with the C–Q slope and , which was consistent with the general pattern exhibited in the field data (Fig. 7a). This C–Q pattern can be explained by the dynamics of different water sources with different DOC contributing to the stream. At low discharges ( m d−1) with small water storage (0.25–0.28 m) and connectivity () (Fig. 7b), the stream DOC was a mix of organic-poor groundwater and organic-rich swales and valley floor zones. As connectivity and discharge increased and the stream expanded, the contribution of organic-rich swales increased, elevating the DOC concentration to its maximum. Under even wetter conditions with connectivity exceeding 0.1, the contribution from planar hillslopes and uplands with a lower DOC concentration increased, diluting the organic-rich DOC from swales and valley areas. Daily Re correlated positively with ST, hydrological connectivity, and Q, and increased by 2 orders of magnitude as Q rose by 3 order of magnitude. The variation of daily Rp with Q was small (105–106 mg d−1) compared with that of Re (Fig. 7b). Values of Rp depended more on soil T than on soil water storage and hydrological connectivity (Ics∕Width) (Fig. 8). In contrast, Re increased with soil water storage ST but notably decreased with soil T (>17 ∘C) due to the low discharge during the hot and dry summer.
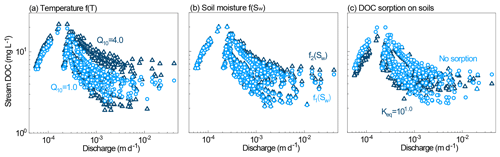
Figure 11C–Q relationships under different (a) T, (b) f(Sw), and (c) sorption equilibrium constants Keq for the two extreme cases. The C–Q patterns were similar in all cases, although the extent of dilution slightly changed. This indicates potential factors other than reaction kinetics and thermodynamics that regulate C–Q patterns.
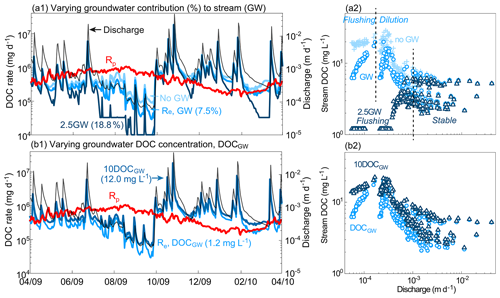
Figure 12Sensitivity analysis of groundwater on rates (Rp and Re) and C–Q relationships: (a) scenarios with a different groundwater volume contribution (%) to stream discharge and (b) scenarios with a different groundwater DOC concentration (DOCGW). DOCGW and GW (QG∕Q) in the base case were 1.2 mg L−1 and 7.5 %, respectively. “2.5 GW” in panel (a) represents the case with 2.5 times QG compared with the base case. Increases in the relative groundwater contribution lowered Re and shifted the C–Q pattern from an overall dilution pattern to an overall flushing pattern; changing DOCGW had negligible influence on the DOC rates and C–Q patterns.
3.5 Sensitivity analysis
3.5.1 Control of temperature, soil moisture, and sorption
Higher Q10 values in f(T) led to more pronounced seasonality in Rp (Fig. 9a). The Rp for Q10=4.0 was more than 4 times higher than that of Q10=1.0 in summer, and much lower in winter with low soil T (<10 ∘C). In contrast, the temporal pattern of Re almost overlapped at different Q10 values, and it mostly followed the discharge dynamics (black line in Fig. 9). Daily Rp varied only slightly (within 15 %) with different f(Sw) (Fig. S4b), while Re showed very little change (Fig. 9b). Although we varied Q10 from 1.0 to 4.0 in f(T), it is worth noting that varying the kinetic rate constant, SOC surface area, volume fraction, and biomass amount could have similar effects (not shown here) because they are all multiplied in Eq. (2).
Simulations showed that strong DOC sorption (Keq=101.0) did not change Rp but lowered the stream DOC concentration and resulted in smaller Re (Fig. 10a). DOC sorption had little impact on Rp, but strong sorption decreased the magnitude of Re by 10 %–69 %. The sorbed DOC concentration differed by more than a factor of 3, with more sorbed DOC with larger Keq values (Fig. 10b). Large amounts of sorbed DOC persisted until early fall, when large rainfall events flushed out sorbed DOC and reduced DOC storage (Fig. 6). This means that catchments can store large quantities of DOC, although the specific amount of DOC stored depends on sorption capacity.
Varying DOC production kinetics did not change the overall C–Q patterns, although the magnitude of overall dilution changed slightly in cases with different f(T) and Keq (Fig. 11). High Q10 values in f(T) led to less dilution, due to more accumulated soil DOC in the dry period (low discharge) and, thus, more DOC flushing as discharge increased in the dry-to-wet period. High Keq resulted in less dilution as the higher sorption capacity acts as a stronger buffer to compensate for the concentration variations.
3.5.2 Groundwater control on DOC export
As shown in Fig. 12, changing the groundwater volume contribution to stream (GW) had more significant impacts than changing the groundwater DOC concentration (DOCGW), especially at low discharges ( m d−1). Increasing the GW contribution from no GW to 2.5 GW (i.e., 18.8 %) lowered stream DOC at low discharges, shifting the C–Q pattern from overall dilution (or a chevron pattern) to overall flushing (or flushing until stable). More specifically, the threshold that separated distinct phases of these segmented C–Q responses (Fig. 12a2) shifted from to about m d−1. This reflects the relative groundwater contribution to streamflow for each case. In contrast, varying the groundwater DOC concentration (DOCGW) by 2 orders of magnitude while keeping the same groundwater contribution (GW) did not change C–Q pattern.
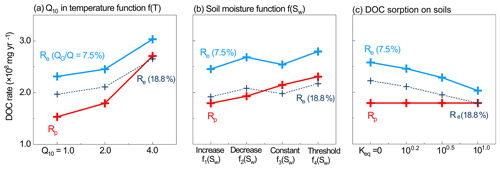
Figure 13Total annual Rp (red) and Re (blue) under two groundwater volume contribution conditions ( % and 18.8 %) for three different variables: (a) soil T, (b) soil moisture, and (c) sorption equilibrium Keq. Rp was not influenced by a deeper groundwater contribution, so there is only one curve for each variable. Rp has higher dependence on temperature than on soil moisture function form and sorption capacity.
Figure 13 summarizes the annual total Rp and Re in all sensitivity test scenarios. Annual Rp was more sensitive to T than to Sw or sorption thermodynamics. Annual Re was less sensitive to T variation, although it also increased with Q10 because a higher production led to higher DOC export. Annual Rp also depended on f(Sw), with the threshold function f4(Sw) (Sect. 2.6) having the highest production rates. However, Re did not follow the trend of Rp (Fig. 13b). Generally, under the same hydrological conditions, a doubling of Rp only led to about a 50 % increase in Re. Higher sorption affinity (higher Keq) did not change production rates but could reduce DOC export by about 30 % due to high DOC storage in soils. High relative groundwater inputs (18.8 % versus 7.5 %) lowered Re in all scenarios because more water came from deeper organic-poor groundwater.
This study revealed that DOC production was primarily regulated by temperature, but the lateral export of DOC was controlled by hydrological conditions. This work contributes to the growing body of research concluding that lateral carbon flux is determined by water routing and hydrological connectivity and only secondarily by biological activity (Zarnetske et al., 2018). Although soil respiration and vertical CO2 fluxes are closely related, this work focuses on the net production and export of DOC because it has been studied and understood to a much lesser extent than soil respiration (Tank et al., 2018). To better appreciate the relative importance of land–water–atmosphere carbon fluxes, future research needs to fully integrate lateral DOC fluxes in concert with vertical fluxes of CO2 across terrestrial and freshwater ecosystems.
4.1 DOC production
The DOC production rate Rp depends more on T than on water storage or soil moisture. This finding is expected, as DOC production is biologically mediated and, thus, influenced by temperature and the metabolic dependence on temperature (Gillooly et al., 2001). Although the local-scale soil moisture varies from 0.40 at the ridgetop to 0.70 in swales and riparian zones (Fig. 5b), the averaged catchment-scale soil moisture has relatively small variations across different seasons in this temperate humid catchment (0.46 to 0.56 on average over the whole catchment), especially compared with places where water is limited and soil moisture can drop below 0.15 (Korres et al., 2015). This small variation is due to the capability of the shale-derived, clay-rich soils at Shale Hills to hold water (Xiao et al., 2019). The influence of soil moisture on DOC production is likely higher in catchments with more pronounced seasonal changes and more fluctuations in soil moisture.
This work also suggests that catchment-scale (Rp) and local-scale (rp) production rates have different controls. The rate law used at the local scale is measured at relatively small scales, i.e., 0.1–2.0 m in soil pedons (Bauer et al., 2008; Yan et al., 2016). Our results show that even when the rate law with an optimum soil moisture was used at the local scale (f4(Sw) in Fig. S4b), the catchment-scale rates do not exhibit maximum rates at an “optimal” soil moisture (Fig. 8), indicating different controls at the local scale versus the catchment scale. In addition, due to the spatial heterogeneities of T, soil moisture, and SOC content, the temporal variations of Rp and rp may be not consistent. The daily Rp spanned less than an order of magnitude with its maximum in the dry, hot summer and its minimum in the wet, cold winter and spring (Fig. 6). Local-scale rp exhibited similar temporal dynamics but varied by more than 2 orders of magnitude, with rapid production mostly in “hot spots” (swales and riparian zones) with persistently high water and SOC content (Fig. 5). Note that the local-scale rate laws are often used directly at the catchment scale or at even larger scales (Crowther et al., 2016; Conant et al., 2011; Fissore et al., 2009; Moyano et al., 2012). This work suggests that although local-scale rate laws have been developed extensively, direct extrapolation of rates from local to catchment scales can be misleading. This speaks to the importance of understanding controls on biogeochemical transformation rates and developing reaction rate theories at the catchment scale for regional-scale and global-scale simulations.
The simulations here suggest that DOC storage depends on the sorbing capacity of soils such that clay content and the presence of organo-mineral aggregates might play a role in mediating DOC dynamics (Lehmann et al., 2007; Cincotta et al., 2019).
DOC production depends on catchment size, hydrogeologic structure, vegetation, and climatic setting. Geomorphological and ecological processes have been shown to co-generate systematic differences in the vertical and lateral distribution of SOC and plant biomass, with a greater concentration of organic carbon in the valley floor than in hillslopes in some catchments (Piney et al., 2018; Temnerud et al., 2016; Campeau et al., 2019; Thomas et al., 2016) and enriched SOC in the uplands in other catchments (Herndon et al., 2015). These differences may explain the large variation of stream DOC in catchments under diverse climate conditions (Moatar et al., 2017). The median stream DOC at Shale Hills is relatively high (10.0 mg L−1), compared with 3.0 mg L−1 in temperate humid catchments in Germany (Musolff et al., 2018), 4.1 mg L−1 in some UK catchments with oceanic climate (Monteith et al., 2015), and 4.5 mg L−1 in France (Moatar et al., 2017). It is also close to 9.5 mg L−1 in boreal catchments in Sweden (Winterdahl et al., 2014), and 8.1 mg L−1 measured in boreal wet and 10.5 mg L−1 in boreal dry catchments in Norway and Finland (de Wit et al., 2016). These differences suggest that climate, vegetation, and landscape heterogeneity may together shape how much DOC can be produced as well as when, where, and to what degree a hill is connected to a stream and the export of DOC at different times.
4.2 Temporal asynchrony of DOC production and export
The contrasting temporal patterns of simulated DOC production and export reflect the asynchronous nature of the two processes at the catchment scale. Local DOC production is influenced by the seasonal pattern of soil T, whereas the export is predominantly controlled by precipitation events and antecedent conditions that modulate the degree to which DOC production zones are hydrologically connected to the stream. This differs from studies showing the synchronization of DOC production and export in temperate climatic regions at soil pedons (Michalzik et al., 2001). This may be due to the relatively short water residence time and high connectivity at the pedon scale. The temporal asynchrony between DOC production and export is therefore strongly influenced by the seasonality of temperature and precipitation, which is shaped by local climate. At Shale Hills the wet winter and spring happens to be the cold season, whereas the dry summer is hot. In the summer, the catchment essentially produces and stores DOC in soil water and soil surfaces and waits for the arrival of the next storm to export. In other words, low hydrological connectivity in the summer imposes a lag period with respect to DOC export such that the DOC we see today is often the DOC produced a while ago. As such, the catchment acts as a DOC producer in the summer and a DOC exporter in spring and winter when the soil is wetter.
These findings indicate a strong climatic control over DOC production and export. In places where climate seasonality is not as strong and catchments are hydrologically connected to streams throughout the year, we can expect to see DOC export all year long and, therefore, much less asynchrony. In places with strong seasonality, a few high-flow events can dominate the DOC export of the whole year. Under the Mediterranean climate with strong seasonality, for example, antecedent moisture conditions have been observed to be essential for understanding the temporal pattern of DOC and nutrient (N) export (Bernal et al., 2005, 2002). Hydrological connectivity and water flow paths become dominant as subsurface saturation expands across valley floors and into hillslopes (Covino, 2017; Abbott et al., 2016).
4.3 Implications for vertical and lateral carbon fluxes
This work focuses on DOC lateral fluxes and does not simulate the carbon loss through soil respiration and associated vertical CO2 fluxes, which has been the focus of some previous work (Brantley et al., 2018; Hasenmueller et al., 2015). Soil respiration is an important pathway of carbon flux that, similar to DOC production, can be shaped by soil temperature and moisture. Generally, warm temperature and medium soil moisture provide optimal conditions for microbial respiration, leading to significant vertical losses of carbon during summer months (Perdrial et al., 2018; Stielstra et al., 2015). In contrast, low temperature and high soil moisture can hinder aerobic respiration and associated carbon losses as CO2 (Smith et al., 2018), effectively accumulating DOC until the arrival of large storms. This pattern is consistent with observations that the total CO2 release and DOC production are positively correlated (Neff and Hooper, 2002). The dependence of DOC production and export on soil T and soil moisture might also hold true for soil respiration. Conversely, as part of the sorbed DOC may be respired by microbes into CO2, our model might overestimate the DOC accumulation in the catchment, especially in summer.
This work does not consider the transport of particulate organic carbon (POC) in soil water and stream water, although POC can play an important role in the carbon budget and biogeochemical cycles in some cases (Ludwig et al., 1996; Diem et al., 2013). In Shale Hills, DOC comprises a major fraction (between 70 % and 80 %) of the total organic carbon export (Jordan et al., 1997). Similar patterns have been reported for organic carbon export at the global scale (Alvarez-Cobelas et al., 2012). However, POC export can be significant in anthropogenically impacted areas (Correll et al., 2001; Mattsson et al., 2005) with significant disturbance (Abbott et al., 2016). They follow a different temporal pattern from DOC, due to different sources, transport mechanisms, and sensitivity to hydrologic variations (Dhillon and Inamdar, 2014; Alvarez-Cobelas et al., 2012).
4.4 Regulation of C–Q patterns
During dry periods, stream water mostly reflects the carbon-poor groundwater. As precipitation wets the catchment, the valley floor area that is characterized by a high SOC and DOC concentration is connected to the stream (Figs. 5, 7), elevating the stream DOC. This increase in DOC concentration continues until the catchment becomes wetter and expands the connected zones to the whole valley and swales. Under these conditions, the influence of high DOC in the vicinity of the stream fades and the DOC concentration decreases. This occurs at a threshold connectivity of about ∼0.1 (≈ the valley width divided by the catchment width). In other words, during wet periods when the whole catchment is hydrologically connected to the stream, the stream DOC reflects the “average” concentration across the catchment (∼2.5 mg L−1). The increase and subsequent decrease pattern (or chevron pattern) therefore indicates the presence of three end-members from different sources: the groundwater with a very low DOC concentration, the soil water at stream beds and in organic-rich swales with the highest DOC content, and the uphill soil water with a DOC level in between these two.
The overall dilution (or chevron) C–Q pattern observed here with a maximum at a mid-range discharge contrasts the commonly observed flushing pattern for DOC (Moatar et al., 2017). In fact, it more closely resembles the hysteresis behavior often observed in storm and snowmelt events for metals and nutrients (Zhi et al., 2019; Duncan et al., 2017). Previous field studies have illustrated that the hydrological connectivity to the stream versus the distribution of SOC ultimately dictates the spatial and temporal dynamics of the DOC concentration in soil and stream water, leading to different C–Q relationships (dilution versus flushing) (Bernhardt et al., 2017; Bernal and Sabater, 2012; Covino, 2017). This has been illustrated by different C–Q relationships at Shale Hills (USA) and Plynlimon (UK) (Herndon et al., 2015). Stream water at Shale Hills is derived from SOC-rich swales with a high DOC concentration at low flow and from both swales and hillslopes with a low DOC concentration when discharge increases. Conversely, at Plynlimon, SOC is enriched in uplands; therefore, concentrations are high at high flow when water flows connect SOC-rich uplands. Our reactive transport modeling provides a quantitative and mechanistic approach to explain the overall C–Q patterns, which have generally been interpreted as a production/source limitation (Covino, 2017; Zarnetske et al., 2018). Our results suggest that the spatial distribution of source zones and the degree of their connectivity to the stream determine when they are flushed out. Modeling approaches such as the one presented here can help us understand the mechanisms underlying C–Q patterns, and, thus, improve our ability to predict the evolution of C–Q trajectories under changing conditions.
C–Q patterns also relate to the mixture of different sources of water in the stream, which is composed of the time-varying relative contribution from the shallow soil water and relatively deep groundwater. Their DOC contribution can be affected by the vertical distribution of reacting materials (Musolff et al., 2017; Bishop et al., 2004; Seibert et al., 2009; Winterdahl et al., 2016) and the relative volume contribution of source water (soil water versus groundwater below the soil-weathered rock interface) to the stream (Zhi et al., 2019; Radke et al., 2019; Weigand et al., 2017). Within the shale bedrock, the groundwater contribution to the stream is relatively small (∼7.5 %) at Shale Hills. Soil water (although from a very limited swale area) dominates inflow to the stream even during the summer dry period. When the groundwater volume input increases to about 18.8 % of the streamflow by volume (2.5 times the actual case; Fig. 12), the C–Q relationships shift to an overall flushing pattern. This may provide a potential explanation for the DOC C–Q flushing pattern at sandstone-dominant Garner Run (a neighboring catchment of Shale Hills), where the groundwater contributions to the stream are typically higher (Hoagland et al., 2017; Li et al., 2018). More interestingly, when the groundwater contribution is “sufficiently” high, it can mask the signature of the swale-derived soil water such that the three-end-member chevron C–Q pattern become a two-end-member pattern with monotonic flushing pattern that is similar to the observation in Coal Creek where groundwater contributes about 20 % annually (Zhi et al., 2019). C–Q relationships have been categorized into nine patterns, including three monotonic and six segmented types (Moatar et al., 2017; Underwood et al., 2017). The shifting threshold that separates segments of C–Q responses by the relative groundwater contribution in this work (Fig. 12) suggests that the relative contribution of groundwater to streamflow may play a pivotal role in shaping the C–Q patterns. This threshold value can potentially provide a rough estimation for the relative contribution of different end-members to the stream.
The mechanisms that regulate DOC C–Q patterns – seasonally variable hydrological connectivity and groundwater contribution – are consistent with previous literature on geogenic species (Mn, Fe), isotopes, and particle fluxes at Shale Hills (Herndon et al., 2018; Kim et al., 2018; Sullivan et al., 2016; Thomas et al., 2013). For example, Mn is associated with DOC via biotic cycling and storage in plant species, and Fe is associated with DOC via aqueous complexation. Therefore, both solutes are more abundant in shallow soils. The C–Q pattern of Fe and Mn shows a dilution pattern with concentrations decreasing as discharge increases (Herndon et al., 2015; 2018). In the dry summer, stream water derives from rich-organic swales and riparian zones with high concentrations of soluble Fe and Mn (Herndon et al., 2018), leading to corresponding high stream concentrations. At high flows, these solutes are diluted by the influx of uphill soil water without as much DOC. This again emphasizes the key role of solute sources and hydrological dynamics in controlling stream chemistry.
The production and export of DOC remain central uncertainties in determining the ecosystem-level carbon balance. These uncertainties persist because of complex interacting controls on DOC production and export. Indeed, few studies have quantitatively addressed the linkages between SOC processing, hydrological conditions, and corresponding DOC processing and export at the catchment scale. We found that DOC production was the major DOC source at Shale Hills (75 % compared with 23 % from precipitation and 2 % from groundwater). The simulations showed that the temporal dynamics of DOC export rates (Re) were more linked to hydrological flow paths and precipitation events. A sensitivity analysis further confirmed that the DOC production rates Rp were primarily controlled by temperature: changing the temperature dependence altered DOC concentrations significantly, whereas the effects of changing soil moisture dependence were relatively small. Conversely, DOC export was most sensitive to changes in hydrology, rendering more than 2 orders of magnitude differences in dry and wet periods. This difference in environmental drivers led to an asynchrony between DOC production and export. During the wet period (spring and winter), the catchment was well connected and DOC production and export occurred simultaneously. During summer, DOC accumulated (often in sorbed form) in soils disconnected from the stream, and DOC export was limited and constrained to the near-stream areas. In other words, the catchment serves as a DOC producer in the dry and hot summer but as an exporter in the wet and cold winter.
This work quantitatively demonstrates the key role of hydrological flow paths and the degree of connectivity in determining the C–Q patterns exhibited at the catchment outlet. At low discharges where connectivity is limited (Ics∕Width < 0.1), stream DOC was mainly sourced from groundwater or from the valley floor and swales with enriched SOC. At higher discharges, an increasing contribution of soil lateral flow from planar hillslopes and uplands with low soil water DOC decreased the stream DOC concentration, ultimately rendering a dilution C–Q pattern. Although changing DOC reaction characteristics alters the soil water DOC concentration, there is little change in the overall C–Q patterns. However, when groundwater contributes 18.8 % of total annual discharge, the stream DOC concentration increases with discharge and flushing patterns emerge. This underscores the significance of the relative contribution and chemical signature of different water sources in shaping DOC export patterns. This study provides new insights into how DOC production and export interact at multiple scales and emphasizes the importance of considering different constraints when projecting the response of lateral and vertical carbon fluxes to climate changes.
The field data have been digitized and are accessible from the national CZO data portal (http://criticalzone.org/shale-hills/data/datasets/; Brantley and Duffy, 2012). The source code of BFP (BioRT-Flux-PIHM) and the input files necessary to reproduce the results are available from the authors upon request (lili@engr.psu.edu).
The supplement related to this article is available online at: https://doi.org/10.5194/hess-24-945-2020-supplement.
HW, LL, and the co-authors conceived the idea and designed the numerical experiments based on ideas generated from a workshop and monthly discussions. HW ran the simulations, analyzed the simulation results, and wrote the first draft of the paper. All co-authors participated in editing the paper.
The authors declare that they have no conflict of interest.
We acknowledge financial support from the US National Science Foundation Geobiology and Low-Temperature Geochemistry program (grant EAR-1724171). We appreciate data from the Susquehanna Shale Hills Critical Zone Observatory (SSHCZO), which is supported by the National Science Foundation (grant no. EAR-0725019: principal investigator Christopher J. Duffy; grant no. EAR-1239285: principal investigator Susan L. Brantley; and grant no. EAR-1331726: principal investigator Susan L. Brantley). Data were collected in Penn State's Stone Valley Forest, which is funded by the Penn State College of Agricultural Sciences, Department of Ecosystem Science and Management and managed by the staff of the Forestlands Management Office. We thank the ISU Center for Ecological Research and Education and EPSCoR (grant no. IIA 1301792) that stimulated ideas in this paper. Susana Bernal's work was funded by CANTERA (grant no. RTI-2018-094521-B-101) and a Ramón y Cajal fellow (grant no. RYC-2017-22643) from the Spanish Ministry of Science, Innovation, and Universities.
This research has been supported by the US National Science Foundation Geobiology and Low-Temperature Geochemistry program (grant no. EAR-1724171).
This paper was edited by Christian Stamm and reviewed by two anonymous referees.
Abbott, B. W., Jones, J. B., Godsey, S. E., Larouche, J. R., and Bowden, W. B.: Patterns and persistence of hydrologic carbon and nutrient export from collapsing upland permafrost, Biogeosciences, 12, 3725–3740, https://doi.org/10.5194/bg-12-3725-2015, 2015.
Abbott, B. W., Baranov, V., Mendoza-Lera, C., Nikolakopoulou, M., Harjung, A., Kolbe, T., Balasubramanian, M. N., Vaessen, T. N., Ciocca, F., Campeau, A., Wallin, M. B., Romeijn, P., Antonelli, M., Goncalves, J., Datry, T., Laverman, A. M., de Dreuzy, J. R., Hannah, D. M., Krause, S., Oldham, C., and Pinay, G.: Using multi-tracer inference to move beyond single-catchment ecohydrology, Earth-Sci. Rev., 160, 19–42, https://doi.org/10.1016/j.earscirev.2016.06.014, 2016.
Allard, D.: Simulating a geological lithofacies with respect to connectivity information using the truncated Gaussian model, in: Geostatistical Simulations, edited by: Armstrong M., and Dowd P.A., Springer, Dordrecht, the Netherlands, 197–211, https://doi.org/10.1007/978-94-015-8267-4_16, 1994.
Alvarez-Cobelas, M., Angeler, D. G., Sanchez-Carrillo, S., and Almendros, G.: A worldwide view of organic carbon export from catchments, Biogeochemistry, 107, 275–293, https://doi.org/10.1007/s10533-010-9553-z, 2012.
Andrews, D. M., Lin, H., Zhu, Q., Jin, L. X., and Brantley, S. L.: Hot Spots and Hot Moments of Dissolved Organic Carbon Export and Soil Organic Carbon Storage in the Shale Hills Catchment, Vadose Zone J., 10, 943–954, https://doi.org/10.2136/vzj2010.0149, 2011.
Aufdenkampe, A. K., Mayorga, E., Raymond, P. A., Melack, J. M., Doney, S. C., Alin, S. R., Aalto, R. E., and Yoo, K.: Riverine coupling of biogeochemical cycles between land, oceans, and atmosphere, Front. Ecol. Environ., 9, 53–60, https://doi.org/10.1890/100014, 2011.
Bao, C., Li, L., Shi, Y. N., and Duffy, C.: Understanding watershed hydrogeochemistry: 1. Development of RT-Flux-PIHM, Water Resour. Res., 53, 2328–2345, https://doi.org/10.1002/2016wr018934, 2017.
Battin, T. J., Luyssaert, S., Kaplan, L. A., Aufdenkampe, A. K., Richter, A., and Tranvik, L. J.: The boundless carbon cycle, Nat. Geosci., 2, 598–600, https://doi.org/10.1038/ngeo618, 2009.
Bauer, J., Herbst, M., Huisman, J. A., Weihermuller, L., and Vereecken, H.: Sensitivity of simulated soil heterotrophic respiration to temperature and moisture reduction functions, Geoderma, 145, 17–27, https://doi.org/10.1016/j.geoderma.2008.01.026, 2008.
Bernal, S. and Sabater, F.: Changes in discharge and solute dynamics between hillslope and valley-bottom intermittent streams, Hydrol. Earth Syst. Sci., 16, 1595–1605, https://doi.org/10.5194/hess-16-1595-2012, 2012.
Bernal, S., Butturini, A., and Sabater, F.: Variability of DOC and nitrate responses to storms in a small Mediterranean forested catchment, Hydrol. Earth Syst. Sci., 6, 1031–1041, https://doi.org/10.5194/hess-6-1031-2002, 2002.
Bernal, S., Butturini, A., and Sabater, F.: Seasonal variations of dissolved nitrogen and DOC : DON ratios in an intermittent Mediterranean stream, Biogeochemistry, 75, 351–372, https://doi.org/10.1007/s10533-005-1246-7, 2005.
Bernhardt, E. S., Blaszczak, J. R., Ficken, C. D., Fork, M. L., Kaiser, K. E., and Seybold, E. C.: Control Points in Ecosystems: Moving Beyond the Hot Spot Hot Moment Concept, Ecosystems, 20, 665–682, https://doi.org/10.1007/s10021-016-0103-y, 2017.
Billings, S. A., Hirmas, D., Sullivan, P. L., Lehmeier, C. A., Bagchi, S., Min, K., Brecheisen, Z., Hauser, E., Stair, R., Flournoy, R., and Richter, D. D.: Loss of deep roots limits biogenic agents of soil development that are only partially restored by decades of forest regeneration, Elem. Sci. Anth., 6, 34, https://doi.org/10.1525/elementa.287, 2018.
Bishop, K., Seibert, J., Köhler, S., and Laudon, H.: Resolving the Double Paradox of rapidly mobilized old water with highly variable responses in runoff chemistry, Hydrol. Process., 18, 185–189, https://doi.org/10.1002/hyp.5209, 2004.
Bolan, N. S., Adriano, D. C., Kunhikrishnan, A., James, T., McDowell, R., and Senesi, N.: Dissolved organic matter: biogeochemistry, dynamics, and environmental significance in soils, in: Advances in Agronomy, vol. 110, edited by: Sparks, D. L., Advances in Agronomy, Elsevier Academic Press Inc, San Diego, USA, 1–75, 2011.
Brantley, S. L. and Duffy, C. J.: CZO Dataset: Shale Hills – Streamflow (2006–2012) and Stream Water Chemistry (2006–2010), available at: http://criticalzone.org/shale-hills/data/datasets/ (last access: 11 February 2020), 2012.
Brantley, S. L., White, T., West, N., Williams, J. Z., Forsythe, B., Shapich, D., Kaye, J., Lin, H., Shi, Y. N., Kaye, M., Herndon, E., Davis, K. J., He, Y., Eissenstat, D., Weitzman, J., DiBiase, R., Li, L., Reed, W., Brubaker, K., and Gu, X.: Susquehanna Shale Hills Critical Zone Observatory: Shale Hills in the Context of Shaver's Creek Watershed, Vadose Zone J., 17, 180092–180110, https://doi.org/10.2136/vzj2018.04.0092, 2018.
Campeau, A., Bishop, K., Amvrosiadi, N., Billett, M. F., Garnett, M. N., Laudon, H., Oquist, M. G., and Wallin, M. B.: Current forest carbon fixation fuels stream CO2 emissions, Nat. Commun., 10, 1876, https://doi.org/10.1038/s41467-019-09922-3, 2019.
Chapin, F. S., Woodwell, G. M., Randerson, J. T., Rastetter, E. B., Lovett, G. M., Baldocchi, D. D., Clark, D. A., Harmon, M. E., Schimel, D. S., Valentini, R., Wirth, C., Aber, J. D., Cole, J. J., Goulden, M. L., Harden, J. W., Heimann, M., Howarth, R. W., Matson, P. A., McGuire, A. D., Melillo, J. M., Mooney, H. A., Neff, J. C., Houghton, R. A., Pace, M. L., Ryan, M. G., Running, S. W., Sala, O. E., Schlesinger, W. H., and Schulze, E. D.: Reconciling carbon-cycle concepts, terminology, and methods, Ecosystems, 9, 1041–1050, https://doi.org/10.1007/s10021-005-0105-7, 2006.
Chiou, C. T., Lee, J. F., and Boyd, S. A.: THE SURFACE-AREA OF SOIL ORGANIC-MATTER, Environ. Sci. Technol., 24, 1164–1166, https://doi.org/10.1021/es00078a002, 1990.
Cincotta, M., Perdrial, J. N., Shavitz, A., Shanley, J., Perdrial, N., Armfield, J., Liebenson, A., Landsman, M., and Adler, T.: Soil aggregates as source of dissolved organic carbon to streams: an experimental study on the effect of solution chemistry on water extractable carbon, Frontiers in Earth Science, 7, 172, https://doi.org/10.3389/fenvs.2019.00172, 2019.
Clark, J. M., Bottrell, S. H., Evans, C. D., Monteith, D. T., Bartlett, R., Rose, R., Newton, R. J., and Chapman, P. J.: The importance of the relationship between scale and process in understanding long-term DOC dynamics, Sci. Total Environ., 408, 2768–2775, https://doi.org/10.1016/j.scitotenv.2010.02.046, 2010.
Conant, R. T., Ryan, M. G., Agren, G. I., Birge, H. E., Davidson, E. A., Eliasson, P. E., Evans, S. E., Frey, S. D., Giardina, C. P., Hopkins, F. M., Hyvonen, R., Kirschbaum, M. U. F., Lavallee, J. M., Leifeld, J., Parton, W. J., Steinweg, J. M., Wallenstein, M. D., Wetterstedt, J. A. M., and Bradford, M. A.: Temperature and soil organic matter decomposition rates - synthesis of current knowledge and a way forward, Glob. Change Biol., 17, 3392–3404, https://doi.org/10.1111/j.1365-2486.2011.02496.x, 2011.
Correll, D. L., Jordan, T. E., and Weller, D. E.: Effects of precipitation, air temperature, and land use on organic carbon discharges from rhode river watersheds, Water Air Soil Poll., 128, 139–159, https://doi.org/10.1023/a:1010337623092, 2001.
Covino, T.: Hydrologic connectivity as a framework for understanding biogeochemical flux through watersheds and along fluvial networks, Geomorphology, 277, 133–144, https://doi.org/10.1016/j.geomorph.2016.09.030, 2017.
Crowther, T. W., Todd-Brown, K. E. O., Rowe, C. W., Wieder, W. R., Carey, J. C., Machmuller, M. B., Snoek, B. L., Fang, S., Zhou, G., Allison, S. D., Blair, J. M., Bridgham, S. D., Burton, A. J., Carrillo, Y., Reich, P. B., Clark, J. S., Classen, A. T., Dijkstra, F. A., Elberling, B., Emmett, B. A., Estiarte, M., Frey, S. D., Guo, J., Harte, J., Jiang, L., Johnson, B. R., Kroel-Dulay, G., Larsen, K. S., Laudon, H., Lavallee, J. M., Luo, Y., Lupascu, M., Ma, L. N., Marhan, S., Michelsen, A., Mohan, J., Niu, S., Pendall, E., Penuelas, J., Pfeifer-Meister, L., Poll, C., Reinsch, S., Reynolds, L. L., Schmidt, I. K., Sistla, S., Sokol, N. W., Templer, P. H., Treseder, K. K., Welker, J. M., and Bradford, M. A.: Quantifying global soil carbon losses in response to warming, Nature, 540, 104–108, https://doi.org/10.1038/nature20150, 2016.
Currie, W. S., Aber, J. D., McDowell, W. H., Boone, R. D., and Magill, A. H.: Vertical transport of dissolved organic C and N under long-term N amendments in pine and hardwood forests, Biogeochemistry, 35, 471–505, https://doi.org/10.1007/bf02183037, 1996.
D'Amore, D. V., Edwards, R. T., Herendeen, P. A., Hood, E., and Fellman, J. B.: Dissolved Organic Carbon Fluxes from Hydropedologic Units in Alaskan Coastal Temperate Rainforest Watersheds, Soil Sci. Soc. Am. J., 79, 378–388, https://doi.org/10.2136/sssaj2014.09.0380, 2015.
Davidson, E. A. and Janssens, I. A.: Temperature sensitivity of soil carbon decomposition and feedbacks to climate change, Nature, 440, 165–173, https://doi.org/10.1038/nature04514, 2006.
de Wit, H. A., Ledesma, J. L. J., and Futter, M. N.: Aquatic DOC export from subarctic Atlantic blanket bog in Norway is controlled by seasalt deposition, temperature and precipitation, Biogeochemistry, 127, 305–321, https://doi.org/10.1007/s10533-016-0182-z, 2016.
Dhillon, G. S. and Inamdar, S.: Storm event patterns of particulate organic carbon (POC) for large storms and differences with dissolved organic carbon (DOC), Biogeochemistry, 118, 61–81, https://doi.org/10.1007/s10533-013-9905-6, 2014.
Diem, S., von Rohr, M. R., Hering, J. G., Kohler, H. P. E., Schirmer, M., and von Gunten, U.: NOM degradation during river infiltration: Effects of the climate variables temperature and discharge, Water Res., 47, 6585–6595, https://doi.org/10.1016/j.watres.2013.08.028, 2013.
Du, X. Z., Zhang, X. S., Mukundan, R., Hoang, L., and Owens, E. M.: Integrating terrestrial and aquatic processes toward watershed scale modeling of dissolved organic carbon fluxes, Environ. Pollut., 249, 125–135, https://doi.org/10.1016/j.envpol.2019.03.014, 2019.
Duffy, C., Shi, Y., Davis, K., Slingerland, R., Li, L., Sullivan, P. L., Goddéris, Y., Brantley, S. L. J. P. E., and Science, P.: Designing a suite of models to explore critical zone function, Procedia Earth and Planetary Science, 10, 7–15, https://doi.org/10.1016/j.proeps.2014.08.003, 2014.
Duncan, J. M., Welty, C., Kemper, J. T., Groffman, P. M., and Band, L. E.: Dynamics of nitrate concentration-discharge patterns in an urban watershed, Water Resour. Res., 53, 7349–7365, https://doi.org/10.1002/2017WR020500, 2017.
Evans, C. D., Jones, T. G., Burden, A., Ostle, N., Zielinski, P., Cooper, M. D. A., Peacock, M., Clark, J. M., Oulehle, F., Cooper, D., and Freeman, C.: Acidity controls on dissolved organic carbon mobility in organic soils, Glob. Change Biol., 18, 3317–3331, https://doi.org/10.1111/j.1365-2486.2012.02794.x, 2012.
Fissore, C., Giardina, C. P., Kolka, R. K., and Trettin, C. C.: Soil organic carbon quality in forested mineral wetlands at different mean annual temperature, Soil Biol. Biochem., 41, 458–466, https://doi.org/10.1016/j.soilbio.2008.11.004, 2009.
Futter, M. N., Butterfield, D., Cosby, B. J., Dillon, P. J., Wade, A. J., and Whitehead, P. G.: Modeling the mechanisms that control in-stream dissolved organic carbon dynamics in upland and forested catchments, Water Resour. Res., 43, W02424, https://doi.org/10.1029/2006wr004960, 2007.
Gillooly, J. F., Brown, J. H., West, G. B., Savage, V. M., and Charnov, E. L.: Effects of size and temperature on metabolic rate, Science, 293, 2248–2251, https://doi.org/10.1126/science.1061967, 2001.
Godsey, S. E., Kirchner, J. W., and Clow, D. W.: Concentration-discharge relationships reflect chemostatic characteristics of US catchments, Hydrol. Process., 23, 1844–1864, https://doi.org/10.1002/hyp.7315, 2009.
Gomez, R., Arce, M. I., Sanchez, J. J., and Sanchez-Montoya, M. D.: The effects of drying on sediment nitrogen content in a Mediterranean intermittent stream: a microcosms study, Hydrobiologia, 679, 43–59, https://doi.org/10.1007/s10750-011-0854-6, 2012.
Hale, R. L., Turnbull, L., Earl, S. R., Childers, D. L., and Grimm, N. B.: Stormwater Infrastructure Controls Runoff and Dissolved Material Export from Arid Urban Watersheds, Ecosystems, 18, 62–75, https://doi.org/10.1007/s10021-014-9812-2, 2015.
Hamamoto, S., Moldrup, P., Kawamoto, K., and Komatsu, T.: Excluded-volume expansion of Archie's law for gas and solute diffusivities and electrical and thermal conductivities in variably saturated porous media, Water Resour. Res., 46, W06514, https://doi.org/10.1029/2009wr008424, 2010.
Hasenmueller, E. A., Jin, L. X., Stinchcomb, G. E., Lin, H., Brantley, S. L., and Kaye, J. P.: Topographic controls on the depth distribution of soil CO2 in a small temperate watershed, Appl. Geochem., 63, 58–69, https://doi.org/10.1016/j.apgeochem.2015.07.005, 2015.
Herndon, E. M., Dere, A. L., Sullivan, P. L., Norris, D., Reynolds, B., and Brantley, S. L.: Landscape heterogeneity drives contrasting concentration–discharge relationships in shale headwater catchments, Hydrol. Earth Syst. Sci., 19, 3333–3347, https://doi.org/10.5194/hess-19-3333-2015, 2015.
Herndon, E. M., Steinhoefel, G., Dere, A. L. D., and Sullivan, P. L.: Perennial flow through convergent hillslopes explains chemodynamic solute behavior in a shale headwater catchment, Chem. Geol., 493, 413–425, https://doi.org/10.1016/j.chemgeo.2018.06.019, 2018.
Hoagland, B., Russo, T. A., Gu, X., Hill, L., Kaye, J., Forsythe, B., and Brantley, S. L.: Hyporheic zone influences on concentration-discharge relationships in a headwater sandstone stream, Water Resour. Res., 53, 4643–4667, https://doi.org/10.1002/2016wr019717, 2017.
Hugelius, G., Strauss, J., Zubrzycki, S., Harden, J. W., Schuur, E. A. G., Ping, C.-L., Schirrmeister, L., Grosse, G., Michaelson, G. J., Koven, C. D., O'Donnell, J. A., Elberling, B., Mishra, U., Camill, P., Yu, Z., Palmtag, J., and Kuhry, P.: Estimated stocks of circumpolar permafrost carbon with quantified uncertainty ranges and identified data gaps, Biogeosciences, 11, 6573–6593, https://doi.org/10.5194/bg-11-6573-2014, 2014.
Humbert, G., Jaffrezic, A., Fovet, O., Gruau, G., and Durand, P.: Dry-season length and runoff control annual variability in stream DOC dynamics in a small, shallow groundwater-dominated agricultural watershed, Water Resour. Res., 51, 7860–7877, https://doi.org/10.1002/2015wr017336, 2015.
Iavorivska, L., Boyer, E. W., Miller, M. P., Brown, M. G., Vasilopoulos, T., Fuentes, J. D., and Duffy, C. J.: Atmospheric inputs of organic matter to a forested watershed: Variations from storm to storm over the seasons, Atmos. Environ., 147, 284–295, https://doi.org/10.1016/j.atmosenv.2016.10.002, 2016.
Jarvis, P. and Linder, S.: Botany – Constraints to growth of boreal forests, Nature, 405, 904–905, https://doi.org/10.1038/35016154, 2000.
Jennings, E., Jarvinen, M., Allott, N., Arvola, L., Moore, K., Naden, P., Aonghusa, C. N., Noges, T., and Weyhenmeyer, G. A.: Impacts of Climate on the Flux of Dissolved Organic Carbon from Catchments, in: Impact of Climate Change on European Lakes, edited by: George, G., Aquatic Ecology Series, Springer, Dordrecht, the Netherlands, 199–220, 2010.
Jin, L. and Brantley, S. L.: Soil chemistry and shale weathering on a hillslope influenced by convergent hydrologic flow regime at the Susquehanna/Shale Hills Critical Zone Observatory, Supplement, Appl. Geochem., 26, S51–S56, https://doi.org/10.1016/j.apgeochem.2011.03.027, 2011.
Jin, L. X., Ravella, R., Ketchum, B., Bierman, P. R., Heaney, P., White, T., and Brantley, S. L.: Mineral weathering and elemental transport during hillslope evolution at the Susquehanna/Shale Hills Critical Zone Observatory, Geochim. Cosmochim. Ac., 74, 3669–3691, https://doi.org/10.1016/j.gca.2010.03.036, 2010.
Jin, L. X., Ogrinc, N., Yesavage, T., Hasenmueller, E. A., Ma, L., Sullivan, P. L., Kaye, J., Duffy, C., and Brantley, S. L.: The CO2 consumption potential during gray shale weathering: Insights from the evolution of carbon isotopes in the Susquehanna Shale Hills critical zone observatory, Geochim. Cosmochim. Ac., 142, 260–280, https://doi.org/10.1016/j.gca.2014.07.006, 2014.
Jobbagy, E. G. and Jackson, R. B.: The vertical distribution of soil organic carbon and its relation to climate and vegetation, Ecol. Appl., 10, 423–436, https://doi.org/10.1890/1051-0761(2000)010[0423:Tvdoso]2.0.Co;2, 2000.
Jordan, T. E., Correll, D. L., and Weller, D. E.: Relating nutrient discharges from watersheds to land use and streamflow variability, Water Resour. Res., 33, 2579–2590, https://doi.org/10.1029/97wr02005, 1997.
Kaiser, K. and Guggenberger, G.: Mineral surfaces and soil organic matter, Eur. J. Soil Sci., 54, 219–236, https://doi.org/10.1046/j.1365-2389.2003.00544.x, 2003.
Kaiser, K., Kaupenjohann, M., and Zech, W.: Sorption of dissolved organic carbon in soils: effects of soil sample storage, soil-to-solution ratio, and temperature, Geoderma, 99, 317–328, https://doi.org/10.1016/s0016-7061(00)00077-x, 2001.
Kim, H., Gu, X., and Brantley, S. L.: Particle fluxes in groundwater change subsurface shale rock chemistry over geologic time, Earth Planet. Sc. Lett., 500, 180–191, https://doi.org/10.1016/j.epsl.2018.07.031, 2018.
Kolbe, T., de Dreuzy, J. R., Abbott, B. W., Aquilina, L., Babey, T., Green, C. T., Fleckenstein, J. H., Labasque, T., Laverman, A. M., Marcais, J., Peiffer, S., Thomas, Z., and Pinay, G.: Stratification of reactivity determines nitrate removal in groundwater, P. Natl. Acad. Sci. USA, 116, 2494–2499, https://doi.org/10.1073/pnas.1816892116, 2019.
Korres, W., Reichenau, T. G., Fiener, P., Koyama, C. N., Bogena, H. R., Comelissen, T., Baatz, R., Herbst, M., Diekkruger, B., Vereecken, H., and Schneider, K.: Spatio-temporal soil moisture patterns – A meta-analysis using plot to catchment scale data, J. Hydrol., 520, 326–341, https://doi.org/10.1016/j.jhydrol.2014.11.042, 2015.
Lambert, T., Pierson-Wickmann, A. C., Gruau, G., Jaffrezic, A., Petitjean, P., Thibault, J. N., and Jeanneau, L.: Hydrologically driven seasonal changes in the sources and production mechanisms of dissolved organic carbon in a small lowland catchment, Water Resour. Res., 49, 5792–5803, https://doi.org/10.1002/wrcr.20466, 2013.
Laudon, H., Buttle, J., Carey, S. K., McDonnell, J., McGuire, K., Seibert, J., Shanley, J., Soulsby, C., and Tetzlaff, D.: Cross-regional prediction of long-term trajectory of stream water DOC response to climate change, Geophys. Res. Lett., 39, L18404, https://doi.org/10.1029/2012gl053033, 2012.
Lehmann, J., Kinyangi, J., and Solomon, D.: Organic matter stabilization in soil microaggregates: implications from spatial heterogeneity of organic carbon contents and carbon forms, Biogeochemistry, 85, 45–57, https://doi.org/10.1007/s10533-007-9105-3, 2007.
Lessels, J. S., Tetzlaff, D., Carey, S. K., Smith, P., and Soulsby, C.: A coupled hydrology-biogeochemistry model to simulate dissolved organic carbon exports from a permafrost-influenced catchment, Hydrol. Process., 29, 5383–5396, https://doi.org/10.1002/hyp.10566, 2015.
Li, L.: Watershed reactive transport, Rev. Mineral. Geochem., 85, 381–418, 2019.
Li, L., Steefel, C. I., Williams, K. H., Wilkins, M. J., and Hubbard, S. S.: Mineral Transformation and Biomass Accumulation Associated With Uranium Bioremediation at Rifle, Colorado, Environ. Sci. Technol., 43, 5429–5435, https://doi.org/10.1021/es900016v, 2009.
Li, L., Bao, C., Sullivan, P. L., Brantley, S., Shi, Y., and Duffy, C.: Understanding watershed hydrogeochemistry: 2. Synchronized hydrological and geochemical processes drive stream chemostatic behavior, Water Resour. Res., 53, 2346–2367, https://doi.org/10.1002/2016wr018935, 2017a.
Li, L., Maher, K., Navarre-Sitchler, A., Druhan, J., Meile, C., Lawrence, C., Moore, J., Perdrial, J., Sullivan, P., Thompson, A., Jin, L., Bolton, E. W., Brantley, S. L., Dietrich, W. E., Mayer, K. U., Steefel, C. I., Valocchi, A., Zachara, J., Kocar, B., McIntosh, J., Tutolo, B. M., Kumar, M., Sonnenthal, E., Bao, C., Beisman, J.: Expanding the role of reactive transport models in critical zone processes, Earth-Sci. Rev., 165, 280–301, 2017b.
Li, L., DiBiase, R. A., Del Vecchio, J., Marcon, V., Hoagland, B., Xiao, D., Wayman, C., Tang, Q., He, Y., Silverhart, P., Forsythe, B., Williams, J. Z., Shapich, D., Mount, G. J., Kaye, J., Guo, L., Lin, H., Eissenstat, D., Dere, A., Brubaker, K., Kaye, M., Davis, K., Russo, T., and Brantley, S.: Investigating the effect of lithology and agriculture at the Susquehanna Shale Hills Critical Zone Observatory (SSHCZO): The Garner Run and Cole Farm subcatchments, Vadose Zone J., 17, 180063–180077, https://doi.org/10.2136/vzj2018.03.0063, 2018.
Lim, K. J., Engel, B. A., Tang, Z. X., Choi, J., Kim, K. S., Muthukrishnan, S., and Tripathy, D.: Automated Web Gis based hydrograph analysis tool, what, J. Am. Water Resour. As., 41, 1407–1416, https://doi.org/10.1111/j.1752-1688.2005.tb03808.x, 2005.
Lin, H.: Temporal stability of soil moisture spatial pattern and subsurface preferential flow pathways in the shale hills catchment, Vadose Zone J., 5, 317–340, https://doi.org/10.2136/vzj2005.0058, 2006.
Lin, H. and Zhou, X.: Evidence of subsurface preferential flow using soil hydrologic monitoring in the Shale Hills catchment, Eur. J. Soil Sci., 59, 34–49, https://doi.org/10.1111/j.1365-2389.2007.00988.x, 2008.
Ling, W. T., Xu, J. M., and Gao, Y. Z.: Dissolved organic matter enhances the sorption of atrazine by soil, Biol. Fertil. Soils, 42, 418–425, https://doi.org/10.1007/s00374-006-0085-6, 2006.
Liu, Y., Wang, C. H., He, N. P., Wen, X. F., Gao, Y., Li, S. G., Niu, S. L., Butterbach-Bahl, K., Luo, Y. Q., and Yu, G. R.: A global synthesis of the rate and temperature sensitivity of soil nitrogen mineralization: latitudinal patterns and mechanisms, Glob. Change Biol., 23, 455–464, https://doi.org/10.1111/gcb.13372, 2017.
Ludwig, W., Probst, J. L., and Kempe, S.: Predicting the oceanic input of organic carbon by continental erosion, Global Biogeochem. Cy., 10, 23–41, https://doi.org/10.1029/95gb02925, 1996.
Malone, E. T., Abbott, B. W., Klaar, M. J., Kidd, C., Sebilo, M., Milner, A. M., and Pinay, G.: Decline in Ecosystem delta C-13 and Mid-Successional Nitrogen Loss in a Two-Century Postglacial Chronosequence, Ecosystems, 21, 1659–1675, https://doi.org/10.1007/s10021-018-0245-1, 2018.
Mattsson, T., Kortelainen, P., and Raike, A.: Export of DOM from boreal catchments: impacts of land use cover and climate, Biogeochemistry, 76, 373–394, https://doi.org/10.1007/s10533-005-6897-x, 2005.
Michalzik, B., Kalbitz, K., Park, J. H., Solinger, S., and Matzner, E.: Fluxes and concentrations of dissolved organic carbon and nitrogen – a synthesis for temperate forests, Biogeochemistry, 52, 173–205, https://doi.org/10.1023/a:1006441620810, 2001.
Moatar, F., Abbott, B. W., Minaudo, C., Curie, F., and Pinay, G.: Elemental properties, hydrology, and biology interact to shape concentration-discharge curves for carbon, nutrients, sediment, and major ions, Water Resour. Res., 53, 1270–1287, https://doi.org/10.1002/2016WR019635, 2017.
Monteith, D. T., Stoddard, J. L., Evans, C. D., de Wit, H. A., Forsius, M., Hogasen, T., Wilander, A., Skjelkvale, B. L., Jeffries, D. S., Vuorenmaa, J., Keller, B., Kopacek, J., and Vesely, J.: Dissolved organic carbon trends resulting from changes in atmospheric deposition chemistry, Nature, 450, 537–539, https://doi.org/10.1038/nature06316, 2007.
Monteith, D. T., Henrys, P. A., Evans, C. D., Malcolm, I., Shilland, E. M., and Pereira, M. G.: Spatial controls on dissolved organic carbon in upland waters inferred from a simple statistical model, Biogeochemistry, 123, 363–377, https://doi.org/10.1007/s10533-015-0071-x, 2015.
Moriasi, D. N., Arnold, J. G., Van Liew, M. W., Bingner, R. L., Harmel, R. D., and Veith, T. L.: Model evaluation guidelines for systematic quantification of accuracy in watershed simulations, T. Asabe, 50, 885–900, 2007.
Moyano, F. E., Vasilyeva, N., Bouckaert, L., Cook, F., Craine, J., Curiel Yuste, J., Don, A., Epron, D., Formanek, P., Franzluebbers, A., Ilstedt, U., Kätterer, T., Orchard, V., Reichstein, M., Rey, A., Ruamps, L., Subke, J.-A., Thomsen, I. K., and Chenu, C.: The moisture response of soil heterotrophic respiration: interaction with soil properties, Biogeosciences, 9, 1173–1182, https://doi.org/10.5194/bg-9-1173-2012, 2012.
Musolff, A., Schmidt, C., Selle, B., and Fleckenstein, J. H.: Catchment controls on solute export, Adv. Water Resour., 86, 133–146, https://doi.org/10.1016/j.advwatres.2015.09.026, 2015.
Musolff, A., Fleckenstein, J. H., Rao, P. S. C., and Jawitz, J. W.: Emergent archetype patterns of coupled hydrologic and biogeochemical responses in catchments, Geophys. Res. Lett., 44, 4143–4151, https://doi.org/10.1002/2017GL072630, 2017.
Musolff, A., Fleckenstein, J. H., Opitz, M., Büttner, O., Kumar, R., and Tittel, J.: Spatio-temporal controls of dissolved organic carbon stream water concentrations, J. Hydrol., 566, 205–215, https://doi.org/10.1016/j.jhydrol.2018.09.011, 2018.
Nash, J. E. and Sutcliffe, J. V.: River flow forecasting through conceptual models part I – A discussion of principles, J. Hydrol., 10, 282–290, 1970.
Neff, J. C. and Asner, G. P.: Dissolved organic carbon in terrestrial ecosystems: Synthesis and a model, Ecosystems, 4, 29–48, https://doi.org/10.1007/s100210000058, 2001.
Neff, J. C. and Hooper, D. U.: Vegetation and climate controls on potential CO2, DOC and DON production in northern latitude soils, Glob. Change Biol., 8, 872–884, https://doi.org/10.1046/j.1365-2486.2002.00517.x, 2002.
Oren, A. and Chefetz, B.: Sorptive and Desorptive Fractionation of Dissolved Organic Matter by Mineral Soil Matrices, J. Environ. Qual., 41, 526–533, https://doi.org/10.2134/jeq2011.0362, 2012.
Perdrial, J., McIntosh, J., Harpold, A., Brooks, P. D., Zapata-Rios, X., Ray, J., Meixner, T., Kanduc, T., Litvak, M., Troch, P. A., and Chorover, J.: Stream water carbon controls in seasonally snow-covered mountain catchments: impact of inter-annual variability of water fluxes, catchment aspect and seasonal processes, Biogeochemistry, 118, 273–290, https://doi.org/10.1007/s10533-013-9929-y, 2014.
Perdrial, J., Brooks, P. D., Swetnam, T., Lohse, K. A., Rasmussen, C., Litvak, M., Harpold, A. A., Zapata-Rios, X., Broxton, P., Mitra, B., Meixner, T., Condon, K., Huckle, D., Stielstra, C., Vázquez-Ortega, A., Lybrand, R., Holleran, M., Orem, C., Pelletier, J., and Chorover, J.: A net ecosystem carbon budget for snow dominated forested headwater catchments: linking water and carbon fluxes to critical zone carbon storage, Biogeochemistry, 138, 225–243, https://doi.org/10.1007/s10533-018-0440-3, 2018.
Piney, G., Bernal, S., Abbott, B. W., Lupon, A., Marti, E., Sabater, F., and Krause, S.: Riparian corridors: a new conceptual framework for assessing nitrogen buffering across biome, Front. Environ. Sci., 6, 47, https://doi.org/10.3389/fenvs.2018.00047, 2018.
Radke, A. G., Godsey, S. E., Lohse, K. A., McCorkle, E. P., Perdrial, J., Seyfried, M. S., and Holbrook, W. S.: Spatiotemporal heterogeneity of water flowpaths controls dissolved organic carbon sourcing in a snow-dominated, headwater catchment, Front. Ecol. Evol., 7, 46, https://doi.org/10.3389/fevo.2019.00046, 2019.
Rasmussen, C., Heckman, K., Wieder, W. R., Keiluweit, M., Lawrence, C. R., Berhe, A. A., Blankinship, J. C., Crow, S. E., Druhan, J. L., Hicks Pries, C. E., Marin-Spiotta, E., Plante, A. F., Schädel, C., Schimel, J. P., Sierra, C. A., Thompson, A., and Wagai, R.: Beyond clay: towards an improved set of variables for predicting soil organic matter content, Biogeochemistry, 137, 297–306, https://doi.org/10.1007/s10533-018-0424-3, 2018.
Raymond, P. A., Saiers, J. E., and Sobczak, W. V.: Hydrological and biogeochemical controls on watershed dissolved organic matter transport: pulse-shunt concept, Ecology, 97, 5–16, https://doi.org/10.1890/14-1684.1, 2016.
Regnier, P., Friedlingstein, P., Ciais, P., Mackenzie, F. T., Gruber, N., Janssens, I. A., Laruelle, G. G., Lauerwald, R., Luyssaert, S., Andersson, A. J., Arndt, S., Arnosti, C., Borges, A. V., Dale, A. W., Gallego-Sala, A., Godderis, Y., Goossens, N., Hartmann, J., Heinze, C., Ilyina, T., Joos, F., LaRowe, D. E., Leifeld, J., Meysman, F. J. R., Munhoven, G., Raymond, P. A., Spahni, R., Suntharalingam, P., and Thullner, M.: Anthropogenic perturbation of the carbon fluxes from land to ocean, Nat. Geosci., 6, 597–607, https://doi.org/10.1038/ngeo1830, 2013.
Sadiq, R. and Rodriguez, M. J.: Disinfection by-products (DBPs) in drinking water and predictive models for their occurrence: a review, Sci. Total Environ., 321, 21–46, https://doi.org/10.1016/j.scitotenv.2003.05.001, 2004.
Seibert, J., Grabs, T., Köhler, S., Laudon, H., Winterdahl, M., and Bishop, K.: Linking soil- and stream-water chemistry based on a Riparian Flow-Concentration Integration Model, Hydrol. Earth Syst. Sci., 13, 2287–2297, https://doi.org/10.5194/hess-13-2287-2009, 2009.
Shi, Y. N., Davis, K. J., Duffy, C. J., and Yu, X.: Development of a Coupled Land Surface Hydrologic Model and Evaluation at a Critical Zone Observatory, J. Hydrometeorol., 14, 1401–1420, https://doi.org/10.1175/jhm-d-12-0145.1, 2013.
Skjelkvale, B. L., Stoddard, J. L., Jeffries, D. S., Torseth, K., Hogasen, T., Bowman, J., Mannio, J., Monteith, D. T., Mosello, R., Rogora, M., Rzychon, D., Vesely, J., Wieting, J., Wilander, A., and Worsztynowicz, A.: Regional scale evidence for improvements in surface water chemistry 1990–2001, Environ. Pollut., 137, 165–176, https://doi.org/10.1016/j.envpol.2004.12.023, 2005.
Skopp, J., Jawson, M. D., and Doran, J. W.: Steady-State Aerobic Microbial Activity As A Function Of Soil-Water Content, Soil Sci. Soc. Am. J., 54, 1619–1625, https://doi.org/10.2136/sssaj1990.03615995005400060018x, 1990.
Smith, K. A., Ball, T., Conen, F., Dobbie, K. E., Massheder, J., and Rey, A.: Exchange of greenhouse gases between soil and atmosphere: interactions of soil physical factors and biological processes, Eur. J. Soil Sci., 69, 10–20, https://doi.org/10.1111/ejss.12539, 2018.
Steefel, C. I., Appelo, C. A. J., Arora, B., Jacques, D., Kalbacher, T., Kolditz, O., Lagneau, V., Lichtner, P. C., Mayer, K. U., Meeussen, J. C. L., Molins, S., Moulton, D., Shao, H., Simunek, J., Spycher, N., Yabusaki, S. B., and Yeh, G. T.: Reactive transport codes for subsurface environmental simulation, Comput. Geosci., 19, 445–478, https://doi.org/10.1007/s10596-014-9443-x, 2015.
Stielstra, C., Brooks, P. D., Lohse, K. A., McIntosh, J. M., Chorover, J., Barron-Gafford, G., Perdrial, J. N., Barnard, H. R., and Litvak, M.: Climatic and landscape influences on soil moisture are primary determinants of soil carbon fluxes in seasonally snow-covered forest ecosystems, Biogeochemistry, 123, 447–465, https://doi.org/10.1007/s10533-015-0078-3, 2015.
Stockmann, U., Adams, M. A., Crawford, J. W., Field, D. J., Henakaarchchi, N., Jenkins, M., Minasny, B., McBratney, A. B., de Courcelles, V. D., Singh, K., Wheeler, I., Abbott, L., Angers, D. A., Baldock, J., Bird, M., Brookes, P. C., Chenu, C., Jastrow, J. D., Lal, R., Lehmann, J., O'Donnell, A. G., Parton, W. J., Whitehead, D., and Zimmermann, M.: The knowns, known unknowns and unknowns of sequestration of soil organic carbon, Agr. Ecosyst. Environ., 164, 80–99, https://doi.org/10.1016/j.agee.2012.10.001, 2013.
Sullivan, P. L., Ma, L., West, N., Jin, L., Karwan, D. L., Noireaux, J., Steinhoefel, G., Gaines, K. P., Eissenstat, D. M., Gaillardet, J., Derry, L. A., Meek, K., Hynek, S., and Brantley, S. L.: CZ-tope at Susquehanna Shale Hills CZO: Synthesizing multiple isotope proxies to elucidate Critical Zone processes across timescales in a temperate forested landscape, Chem. Geol., 445, 103–119, https://doi.org/10.1016/j.chemgeo.2016.05.012, 2016.
Tang, J., Yurova, A. Y., Schurgers, G., Miller, P. A., Olin, S., Smith, B., Siewert, M. B., Olefeldt, D., Pilesjo, P., and Poska, A.: Drivers of dissolved organic carbon export in a subarctic catchment: Importance of microbial decomposition, sorption-desorption, peatland and lateral flow, Sci. Total Environ., 622, 260–274, https://doi.org/10.1016/j.scitotenv.2017.11.252, 2018.
Tank, S. E., Fellman, J. B., Hood, E., and Kritzberg, E. S.: Beyond respiration: Controls on lateral carbon fluxes across the terrestrial-aquatic interface, Limnol. Oceanogr. Lett., 3, 76–88, https://doi.org/10.1002/lol2.10065, 2018.
Temnerud, J., von Brömssen, C., Fölster, J., Buffam, I., Andersson, J.-O., Nyberg, L., and Bishop, K.: Map-based prediction of organic carbon in headwater streams improved by downstream observations from the river outlet, Biogeosciences, 13, 399–413, https://doi.org/10.5194/bg-13-399-2016, 2016.
Thomas, E. M., Lin, H., Duffy, C. J., Sullivan, P. L., Holmes, G. H., Brantley, S. L., and Jin, L. X.: Spatiotemporal patterns of water stable isotope compositions at the Shale Hills Critical Zone Observatory: Linkages to subsurface hydrologic processes, Vadose Zone J., 12, 1–16, https://doi.org/10.2136/vzj2013.01.0029, 2013.
Thomas, Z., Abbott, B. W., Troccaz, O., Baudry, J., and Pinay, G.: Proximate and ultimate controls on carbon and nutrient dynamics of small agricultural catchments, Biogeosciences, 13, 1863–1875, https://doi.org/10.5194/bg-13-1863-2016, 2016.
Underwood, K. L., Rizzo, D. M., Schroth, A. W., and Dewoolkar, M. M.: Evaluating Spatial Variability in Sediment and Phosphorus Concentration-Discharge Relationships Using Bayesian Inference and Self-Organizing Maps, Water Resour. Res., 53, 10293–10316, https://doi.org/10.1002/2017wr021353, 2017.
Weigand, S., Bol, R., Reichert, B., Graf, A., Wiekenkamp, I., Stockinger, M., Luecke, A., Tappe, W., Bogena, H., Puetz, T., Amelung, W., and Vereecken, H.: Spatiotemporal analysis of dissolved organic carbon and nitrate in waters of a forested catchment using wavelet analysis, Vadose Zone J., 16, 1–14, https://doi.org/10.2136/vzj2016.09.0077, 2017.
Weiler, M. and McDonnell, J. J.: Testing nutrient flushing hypotheses at the hillslope scale: A virtual experiment approach, J. Hydrol., 319, 339–356, https://doi.org/10.1016/j.jhydrol.2005.06.040, 2006.
Wen, H. and Li, L.: An upscaled rate law for mineral dissolution in heterogeneous media: The role of time and length scales, Geochim. Cosmochim. Ac., 235, 1–20, https://doi.org/10.1016/j.gca.2018.04.024, 2018.
Wen, H., Pan, Z. Z., Giammar, D., and Li, L.: Enhanced Uranium Immobilization by Phosphate Amendment under Variable Geochemical and Flow Conditions: Insights from Reactive Transport Modeling, Environ. Sci. Technol., 52, 5841–5850, https://doi.org/10.1021/acs.est.7b05662, 2018.
Western, A. W., Bloschl, G., and Grayson, R. B.: Toward capturing hydrologically significant connectivity in spatial patterns, Water Resour. Res., 37, 83–97, https://doi.org/10.1029/2000wr900241, 2001.
Wieder, W. R., Grandy, A. S., Kallenbach, C. M., and Bonan, G. B.: Integrating microbial physiology and physio-chemical principles in soils with the MIcrobial-MIneral Carbon Stabilization (MIMICS) model, Biogeosciences, 11, 3899–3917, https://doi.org/10.5194/bg-11-3899-2014, 2014.
Winterdahl, M., Erlandsson, M., Futter, M. N., Weyhenmeyer, G. A., and Bishop, K.: Intra-annual variability of organic carbon concentrations in running waters: Drivers along a climatic gradient, Global Biogeochem. Cy., 28, 451–464, https://doi.org/10.1002/2013GB004770, 2014.
Winterdahl, M., Laudon, H., Lyon, S. W., Pers, C., and Bishop, K.: Sensitivity of stream dissolved organic carbon to temperature and discharge: Implications of future climates, J. Geophys. Res.-Biogeo., 121, 126–144, https://doi.org/10.1002/2015JG002922, 2016.
Worrall, F., Howden, N. J. K., Burt, T. P., and Bartlett, R.: Declines in the dissolved organic carbon (DOC) concentration and flux from the UK, J. Hydrol., 556, 775–789, https://doi.org/10.1016/j.jhydrol.2017.12.001, 2018.
Xiao, D., Shi, Y., Brantley, S., Forsythe, B., DiBiase, R., Davis, K., and Li, L.: Streamflow generation from catchments of contrasting lithologies: the role of soil properties, topography, and catchment size, Water Resour. Res.55, 9234–9257, https://doi.org/10.1029/2018WR023736, 2019.
Yan, Z. F., Liu, C. X., Todd-Brown, K. E., Liu, Y. Y., Bond-Lamberty, B., and Bailey, V. L.: Pore-scale investigation on the response of heterotrophic respiration to moisture conditions in heterogeneous soils, Biogeochemistry, 131, 121–134, https://doi.org/10.1007/s10533-016-0270-0, 2016.
Yan, Z. F., Bond-Lamberty, B., Todd-Brown, K. E., Bailey, V. L., Li, S. L., Liu, C. Q., and Liu, C. X.: A moisture function of soil heterotrophic respiration that incorporates microscale processes, Nat. Commun., 9, 2562, https://doi.org/10.1038/s41467-018-04971-6, 2018.
Yuste, J. C., Baldocchi, D. D., Gershenson, A., Goldstein, A., Misson, L., and Wong, S.: Microbial soil respiration and its dependency on carbon inputs, soil temperature and moisture, Glob. Change Biol., 13, 2018–2035, https://doi.org/10.1111/j.1365-2486.2007.01415.x, 2007.
Zarnetske, J. P., Bouda, M., Abbott, B. W., Saiers, J., and Raymond, P. A.: Generality of Hydrologic Transport Limitation of Watershed Organic Carbon Flux Across Ecoregions of the United States, Geophys. Res. Lett., 45, 11702–11711, https://doi.org/10.1029/2018gl080005, 2018.
Zhi, W., Li, L., Dong, W., Brown, W., Kaye, J., Steefel, C., and Williams, K. H.: Distinct Source Water Chemistry Shapes Contrasting Concentration-Discharge Patterns, Water Resour. Res., 55, 4233–4251, https://doi.org/10.1029/2018WR024257, 2019.